
Prognose von Zeitreihen (Teil 1): Methode der Empirischen Modus Dekomposition (Empirical Mode Decomposition, EMD)
Einführung
Der Erfolg eines jeden Händlers hängt in erster Linie von seiner Fähigkeit ab, einen "Blick in die Zukunft zu werfen", d.h. zu erraten, wie sich der Preis nach einer bestimmten Zeitspanne verändert. Um dieses Problem zu lösen, ist es wichtig, über eine Vielzahl von Werkzeugen und Funktionen zu verfügen, von den neuesten Aktualisierungen der grundlegenden Marktmerkmale bis hin zu den Algorithmen der technischen Analyse. Alle können mehr oder weniger stark verbessert werden, indem man die mathematischen Methoden der Zeitreihenprognose verwendet, sowohl die Preise selbst als auch technische Indikatoren, die Volatilität, makroökonomische Indizes, die Bilanz des Handelsportfolios oder etwas anderes, das als solche Zeitreihen fungieren kann.
Die Vorhersage ist ein sehr weitreichendes Thema und wurde auf der Website mql5.com bereits mehrfach thematisiert. Einer der ersten einführenden und dennoch seriösen Artikel, Prognose von Finanzzeitreihen, wurde bereits 2008 in Englisch veröffentlicht. Neben vielen anderen Artikeln und Veröffentlichungen in der CodeBase werden beispielsweise MetaTrader-fähige Lösungen angeboten:
- "Zeitreihenvorhersage mit exponentieller Glättung (Fortsetzung)".
- Suche nach ähnlichen Mustern in der Historie, mit der dynamischen Transformation der Zeitachse (WmiFor+DTW);
- Back propagation (von Fehlern) Neuronales Netz (BPNN);
- Neuronales Netz der Kohonen (SOM);
Die vollständige Liste erhalten Sie über die Suche in den relevanten Rubriken der Website (Artikel, CodeBase).
Zu diesem Zweck werden wir die Liste der verfügbaren Prognoseinstrumente um zwei neue erweitern. Das erste von ihnen basiert auf der Methode der Empirical Mode Decomposition (EMD, empirische Modus Zerlegung), die bereits im Artikel mit dem Titel Einführung in die Empirical Mode Decomposition besprochen, aber nicht auf die Vorhersage angewendet wurde. EMD wird im ersten Teil dieses Artikels betrachtet.
Das zweite Instrument verwendet die Methode Support-Vektor-Maschine (SVM), in der Version Least-Squares-Support-Vektor-Maschine (LS-SVM). Wir werden es in unserem zweiten Teil thematisieren.
EMD-basierter Prognose-Algorithmus
Eine detaillierte Einführung in die EMD-Technologie finden Sie im Artikel Einführung in die empirische Bandzerlegung (EMD). Es geht um die Zerlegung einer Zeitreihe in einzelne Bänder — den sogenannten Intrinsic Mode Functions (IMFs). Jede Form ist die Spline-Interpolation von Zeitreihen-Maxima und -Minima, wobei die Extremwerte zunächst in der Anfangsreihe gesucht werden. Dann wird die soeben gefundene IMF davon abgezogen, woraufhin die Spline-Interpolation für die Extremwerte der modifizierten Reihe durchgeführt wird, und diese Konstruktion mehrerer IMFs wird so lange fortgesetzt, bis der Rest niedriger als der spezifizierte Rauschpegel ist. Optisch ähneln die Ergebnisse der Fourier-Reihenerweiterung; im Gegensatz zu letzterer sind die typischen EMD-Formen jedoch keine frequenzbestimmenden, harmonischen Schwingungen. Die Anzahl der erhaltenen IMF-Expansionsfunktionen hängt von der Glätte der Anfangsreihe und von den Einstellungen des Algorithmus ab.
In dem oben erwähnten Artikel werden fertige Klassen zur Berechnung der EMD vorgestellt, aber es wird vorgeschlagen, das Zerlegungsergebnis als Graph in eine externe HTML-Datei zu überführen. Wir werden uns auf diese Klassen stützen und notwendige Ergänzungen schreiben, um den Algorithmus vorhersagbar zu machen.
2 Dateien wurden den Artikeln beigefügt: CEMDecomp.mqh und CEMD_2.mqh. Die zweite Datei ist eine leicht verbesserte Version der ersten, so dass wir hier von der zweiten Datei ausgehen werden. Kopieren wir sie unter dem neuen Namen EMD.mqh und binden wir sie, noch ohne Änderungen, in den Indikator EMD.mq5 ein.
#include <EMD.mqh>
Wir werden auch spezielle Klassen für die vereinfachte Deklaration des Arrays von Pufferindikatoren, IndArray.mqh, verwenden (seine englische Beschreibung ist verfügbar im Blog, die aktuelle Version davon ist dem Artikel beigefügt). Wir werden viele Puffer benötigen, und sie werden in einer einheitlichen Weise verarbeitet werden.
#define BUF_NUM 18 // 16 IMF maximum (including input at 0-th index) + residue + reconstruction #property indicator_separate_window #property indicator_buffers BUF_NUM #property indicator_plots BUF_NUM #include <IndArray.mqh> IndicatorArray buffers(BUF_NUM); IndicatorArrayGetter getter(buffers);
Wie Sie sehen, wird der Indikator in einem separaten Fenster angezeigt und verfügt über 18 Puffer, die für die Anzeige reserviert sind:
- Erste Zeitreihe;
- 16 Komponenten seiner Zerlegung (wahrscheinlich werden nicht alle davon verwendet);
- Rest ("Trend"); und
- Rekonstruktion.
Der letzte Punkt ist der faszinierendste. Es geht darum, dass wir, nachdem wir die Funktionen des IMF erhalten haben, einige (aber nicht alle) von ihnen zusammenfassen und eine geglättete Version der ersten Serie erhalten können. Es ist die geglättete Rekonstruktion der Quelle, die für die Vorhersage dienen wird, da sie die Summe der bekannten Splines ist, die für die noch nicht gekommenen Balken extrapoliert werden kann (Spline-Extrapolation). Die Prognosetiefe sollte jedoch auf mehrere Balken begrenzt werden, da die gefundenen IMFs irrelevant werden, sobald sie sich vom letzten bekannten Punkt, für den sie ermittelt wurden, entfernen.
Aber zurück zur Datei EMD.mqh. Darin ist die Klasse CEMD definiert, die die gesamte Arbeit leistet. Der Prozess wird durch den Aufruf der Methode Decomp gestartet, der das Zeitreihen-Zählfeld, y, übergeben wird. Es ist die Größe dieses Arrays, die die Länge N der richtigen Funktionen — IMFResult — bestimmt. Die Methode arrayprepare bereitet Hilfsarrays vor, um sie zu berechnen:
class CEMD { private: int N; // Input and output data size double IMFResult[]; // Result double X[]; // X-coordinate for the TimeSeries. X[]=0,1,2,...,N-1. ... public: int N; // Input and output data size double Mean; // Mean of input data ... int decomp(double &y[]) { ... N = ArraySize(y); arrayprepare(); for(i = 0; i < N; i++) X[i] = i; Mean = 0; for(i = 0; i < N; i++) Mean += (y[i] - Mean) / (i + 1.0); // Mean (average) of input data for(i = 0; i < N; i++) { a = y[i] - Mean; Imf[i] = a; IMFResult[i] = a; } // The loop of decomposition ... extrema(...); ... ... } private: int arrayprepare(void) { if(ArrayResize(IMFResult, N) != N) return (-1); ... } };
Um die Anzahl der berechneten Punkte zu erhöhen, fügen wir der Methode Decomp einen neuen Parameter Extrapolation hinzu, der die Tiefe der Prognose angibt. Erhöhen wir N um die Anzahl der für die Extrapolation angeforderten Anzahl, nachdem wir zuvor die reale Länge der Ausgangsreihe in der lokalen Variablen Nf gespeichert haben (im Code sind die Änderungen mit "+" und "*" für Ergänzungen bzw. Änderungen gekennzeichnet).
int decomp(const double &y[], const int extrapolate = 0) // * { ... N = ArraySize(y); int Nf = N; // + preserve actual number of input data points N += extrapolate; // + arrayprepare(); for(i = 0; i < N; i++) X[i] = i; Mean = 0; for(i = 0; i < Nf; i++) // * was N Mean += (y[i] - Mean) / (i + 1.0); for(i = 0; i < N; i++) { a = y[MathMin(i, Nf - 1)] - Mean; // * was y[i] Imf[i] = a; IMFResult[i] = a; } // The loop of decomposition ... extrema(...); ... for(i = 0; i < N; i++) { IMFResult[i + N * nIMF] = IMFResult[i]; IMFResult[i] = y[MathMin(i, Nf - 1)] - Mean; // * was y[i] } }
Die Konstruktion von IMFs auf den zu prognostizierenden Balken beginnt mit dem letzten bekannten Wert der Zeitreihe.
Dies sind fast alle für die Prognose erforderlichen Änderungen. Der vollständige Code dessen, was wir erhalten haben, ist in der angehängten Datei EMDloose.mqh zu sehen. Aber warum EMDloose.mqh und nicht EMD.mqh?
Die Sache ist die, dass diese Prognosemethode nicht ganz korrekt ist. Da wir die N-Größe aller Arrays des Objekts vergrößert haben, schließt dies auch die Balken ein, die bei der Suche nach Extremwerten vorhergesagt werden sollen, was in der Methode extrema durchgeführt wird. Technisch gesehen gibt es in Zukunft keine Extremwerte mehr. Alle Extremwerte, die während der Berechnungen gebildet werden, sind diejenigen der Summe der Spline-Extrapolationen (ohne die Anfangsreihe, die in Zukunft nicht mehr existiert). Infolgedessen beginnen sich die Funktionen Spline aneinander anzupassen und versuchen, ihre Stapel zu glätten. In gewisser Weise ist es bequem, da die Vorhersage ein Selbstgleichgewicht erhält — der Schwingungsprozess bleibt in der Nähe der Werte der Zeitreihe und geht nicht ins Unendliche. Der Wert einer solchen Vorhersage ist jedoch minimal — er charakterisiert die anfängliche Zeitreihe nicht mehr. Diese Methode kann jedoch zweifellos verwendet werden, und diejenigen, die dies wünschen, können sie verwenden und genau dafür EMDloose.mqh in das Projekt einbeziehen.
Um das Problem zu beheben, werden wir einige weitere Änderungen vornehmen und die endgültige Arbeitsversion von EMD.mqh erhalten. Um die Auswirkungen der beiden Prognosemethoden zu vergleichen, werden wir im Folgenden prüfen, wie der Indikator mit EMD.mqh und mit EMDloose.mqh funktioniert.
Nun, die IMF-Funktionen müssen in Zukunft auf den Splines des letzten realen Punktes der Zeitreihe konstruiert werden. In diesem Fall hat die Prognosetiefe eine physikalische (angewandte) Beschränkung, da kubische Splines, wenn sie nicht rekonstruiert werden, zur Unendlichkeit tendieren. Dies ist nicht kritisch, da die Prognosetiefe ganz am Anfang durch sekundäre Balken begrenzt werden sollte.
Der Sinn der Änderungen besteht darin, die Länge der anfänglichen Zeitreihe in der Variablen des Objekts zu speichern, nicht lokal in der Methode Decomp.
class CEMD { private: int N; // Input and output data size int Nf; // + public: int decomp(const double &y[], const int extrapolate = 0) { ... N = ArraySize(y); Nf = N; // + preserve actual number of input data points in the object N += extrapolate; // + ... } };
Dann können wir die Variable Nf innerhalb der Methode extrema verwenden, nachdem wir sie an relevanten Stellen an die Stelle des erhöhten N gesetzt haben. Auf diese Weise werden nur reale Extremwerte berücksichtigt, die aus der ersten Zeitreihe stammen. Am einfachsten ist es, alle Änderungen durch den Kontextvergleich der Dateien EMD.mqh und EMDloose.mqh zu sehen.
Damit ist der Prognosealgorithmus eigentlich abgeschlossen. Ein weiterer kleiner Schritt zum Erhalt der Dekompositionsergebnisse. In der Klasse CEMD ist dafür die Methode getIMF gedacht. Anfänglich wurden 2 Parameter eingepasst: Zielfeld — x und die Anzahl der gewünschten IMF-Oberschwingungen — nn.
void CEMD::getIMF(double &x[], const int nn, const bool reverse = false) const { ... if(reverse) ArrayReverse(x); // + }
Hier wird der optionale Parameter reverse hinzugefügt, mit dem Sie das Array in umgekehrter Reihenfolge sortieren können. Dies ist notwendig, um das Arbeiten mit Indikatorpuffern zu gewährleisten, für die eine zeitreihenartige Indizierung bequem ist (0. Element ist das jüngste).
Damit ist die Erweiterung der CEMD-Klasse für Prognosezwecke abgeschlossen, so dass wir mit der Implementierung eines EMD-basierten Indikators fortfahren können.
Der Indikator EMD.mq5
Zu Demonstrationszwecken wird der Indikator direkt mit Kursen arbeiten; dieser Ansatz ist jedoch für den absoluten realen Handel nicht gerade geeignet. Die Prognose einer Preisreihe mittels Extrapolation legt zumindest einen Nachrichtenfilter nahe, um starke externe Einflüsse auf den Prognosehorizont auszuschließen. Für kürzere Zeiträume ist die nächtliche Seitwärtsbewegung wahrscheinlich die erste Wahl. Außerdem können wir längere Zeiträume empfehlen, da sie weniger empfindlich gegenüber dem Marktrauschen sind, oder ausgewogene synthetische Symbolkörbe aus mehreren Instrumenten.
Lassen Sie uns die Eingaben des Indikators definieren:
input int Length = 300; // Length (bars, > 5) input int Offset = 0; // Offset (0..P bars) input int Forecast = 0; // Forecast (0..N bars) input int Reconstruction = 0; // Reconstruction (0..M IMFs)
Die Parameter Offset und Length legen den Offset und die Anzahl der Balken für die zu analysierende Serie fest. Um die Analyse von Vorhersagen über die Historie zu erleichtern, wird der Parameter Offset auch in der Schnittstelle durch eine gestrichelte vertikale Linie dargestellt, die Sie mit der Maus innerhalb des Diagramms ziehen und die Vorhersage interaktiv neu berechnen können (beachten Sie, dass die Berechnungen je nach Länge und Form der Serie und je nach Prozessorleistung sehr viel Zeit in Anspruch nehmen können).
Parameter Forecast — Anzahl der vorherzusagenden Balken. Für den rigorosen Algorithmus EMD.mqh ist es nicht empfehlenswert, einen Wert von mehr als 5-10 anzunehmen. Größere Werte sind für den vereinfachten Algorithmus EMDloose.mqh zulässig.
Die Parameter-Rekonstruktion definiert die Anzahl der IMF-Funktionen, die bei der Rekonstruktion der Zeitreihe weggelassen werden können, so dass andere die Prognose bilden. Wenn hier 0 angegeben wird, fällt die Rekonstruktion vollständig mit der Ausgangsreihe zusammen, und eine Prognose ist unmöglich (im Grunde ist sie gleich der Konstante — dem letzten Preiswert und daher bedeutungslos). Wird er auf 1 gesetzt, so wird die Rekonstruktion geglättet, indem die kleinsten Schwingungen weggelassen werden; wird er auf 2 gesetzt, so werden die zwei höchsten Harmonischen weggelassen, usw. Wenn wir eine Zahl eingeben, die der Anzahl der gefundenen IMF-Funktionen entspricht, fällt die Rekonstruktion mit dem Rest ("Trend") zusammen. In all diesen Fällen verfügt die geglättete Reihe über eine Prognose (eine eigene für jede Kombination der Anzahl der IMF-Funktionen). Wenn eine Zahl festgelegt wird, die die Anzahl der IMFs überschreitet, sind die Rekonstruktion und die Prognose unbestimmt. Der empfohlene Wert für diesen Parameter ist 2.
Je geringer der Wert der Rekonstruktion ist, desto beweglicher und näher an der Anfangsreihe wird die Rekonstruktion sein (es ist wie eine kurzzeitige MA), aber die Prognose wird sehr volatil sein. Je höher dieser Wert ist, desto glatter und stabiler wird die Rekonstruktion und Prognose sein (wie bei einem längerfristigen MA).
In OnInit() werden wir den Offset der Puffer entsprechend der Prognosetiefe einstellen.
int OnInit() { IndicatorSetString(INDICATOR_SHORTNAME, "EMD (" + (string)Length + ")"); for(int i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE); PlotIndexSetInteger(i, PLOT_SHIFT, Forecast); } return INIT_SUCCEEDED; }
Der Indikator wird auf der Grundlage der Eröffnungspreis im Modus "Bar-für-Bar" berechnet. Hier sind die wichtigsten Punkte für OnCalculate().
Wir definieren die lokalen Variablen und legen die Indizierung der als Zeitreihe verwendeten Open und Time fest.
int OnCalculate(const int rates_total, const int prev_calculated, const datetime& Time[], const double& Open[], const double& High[], const double& Low[], const double& Close[], const long& Tick_volume[], const long& Volume[], const int& Spread[]) { int i, ret; ArraySetAsSeries(Time, true); ArraySetAsSeries(Open, true);
Sicherstellen des Modus Bar-für-Bar.
static datetime lastBar = 0; static int barCount = 0; if(Time[0] == lastBar && barCount == rates_total && prev_calculated != 0) return rates_total; lastBar = Time[0]; barCount = rates_total;
Warten auf die ausreichende Datenmenge.
if(rates_total < Length || ArraySize(Time) < Length) return prev_calculated; if(rates_total - 1 < Offset || ArraySize(Time) - 1 < Offset) return prev_calculated;
Initialisierung der Indikatorpuffer.
for(int k = 0; k < BUF_NUM; k++) { buffers[k].empty(); }
Verteilen des lokalen Arrays, yy, um die Anfangsreihe in das Objekt zu übergeben und dann die Ergebnisse zu erhalten.
double yy[]; int n = Length; ArrayResize(yy, n, n + Forecast);
Ausfüllen des Arrays für die Analyse mit den Daten der Zeitreihen
for(i = 0; i < n; i++) { yy[i] = Open[n - i + Offset - 1]; // we need to reverse for extrapolation }
Start des EMD-Algorithmus unter Verwendung des entsprechenden Objekts
CEMD emd;
ret = emd.decomp(yy, Forecast);
if(ret < 0) return prev_calculated;
Im Erfolgsfall werden die gewonnenen Daten — in erster Linie die Anzahl der IMF-Funktionen und der Mittelwert — gelesen.
const int N = emd.getN(); const double mean = emd.getMean();
Erweitertes Array yy, in das wir die Punkte jeder Funktion für zukünftige Balken schreiben werden.
n += Forecast;
ArrayResize(yy, n);
Einrichten der Visualisierung: Anfangsreihen, Rekonstruktion und Prognose werden mit fetten Linien dargestellt, alle anderen einzelnen IMFs mit feinen Linien. Da sich die Anzahl der IMFs dynamisch ändert (abhängig von der Form der Ausgangsserie), kann diese Einstellung nicht einmalig in OnInit() vorgenommen werden.
for(i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_SHOW_DATA, i <= N + 1); PlotIndexSetInteger(i, PLOT_LINE_WIDTH, i == N + 1 ? 2 : 1); PlotIndexSetInteger(i, PLOT_LINE_STYLE, STYLE_SOLID); }
Anzeige der ersten Zeitreihe im letzten Puffer (nur zur Kontrolle der übertragenen Daten, da wir sie in der Praxis z.B. aus dem EA-Code nicht benötigen).
emd.getIMF(yy, 0, true); if(Forecast > 0) { for(i = 0; i < Forecast; i++) yy[i] = EMPTY_VALUE; } buffers[N + 1].set(Offset, yy);
Verteilen der Array-Summe für die Rekonstruktion (Summen der IMFs). In der Schleife Durchsuchen aller an der Rekonstruktion beteiligten IMFs und Aufsummieren der Zählerstände in diesem Array (Summen der IMFs). Gleichzeitig wird jeder IMF in seinen eigenen Puffer gestellt.
double sum[]; ArrayResize(sum, n); ArrayInitialize(sum, 0); for(i = 1; i < N; i++) { emd.getIMF(yy, i, true); buffers[i].set(Offset, yy); if(i > Reconstruction) { for(int j = 0; j < n; j++) { sum[j] += yy[j]; } } }
Der vorletzte Puffer nimmt den Rest auf und wird als gepunktete Linie angezeigt.
PlotIndexSetInteger(N, PLOT_LINE_STYLE, STYLE_DOT); emd.getIMF(yy, N, true); buffers[N].set(Offset, yy);
Tatsächlich enthalten die Puffer vom ersten bis zum vorletzten alle Zerlegungsharmonien in aufsteigender Reihenfolge (zuerst die kleinen, dann die größeren, bis zum "Trend").
Schließlich wird die Summierung der Komponenten durch die Zählungen in Array-Summe vervollständigt, um die endgültige Rekonstruktion zu erhalten.
for(int j = 0; j < n; j++) { sum[j] += yy[j]; if(j < Forecast && (Reconstruction == 0 || Reconstruction > N - 1)) // completely fitted curve can not be forecasted (gives a constant) { sum[j] = EMPTY_VALUE; } } buffers[0].set(Offset, sum); return rates_total; }
Anzeige der Summe zusammen mit der Prognose im Puffer Null. Der Index Null wird gewählt, um das Lesen von EAs zu erleichtern. Die Anzahl der beteiligten IMFs und Puffer ändert sich in der Regel mit dem Eintreffen eines neuen Balkens, so dass die anderen Pufferindizes variabel sind.
Im Artikel werden einige Nuancen ausgelassen, die sich auf die Formatierung von Beschriftungen und die interaktive Arbeit mit der Offsetlinie der Historie beziehen. Der vollständige Quellcode ist am Ende des Artikels angehängt.
Die einzige erwähnenswerte Unterschied hängt damit zusammen, dass der Indikator beim Ändern des Abstands des Offset-Parameters mit Hilfe einer vertikalen Linie eine Aktualisierung des Diagramms durch den Aufruf von ChartSetSymbolPeriod anfordert. Diese Funktion ist in MetaTrader 5 so implementiert, dass sie die Caches aller Zeiträume des aktuellen Symbols zurücksetzt und neu aufbaut. Abhängig von der durch die Anzahl der Balken in den Charts gewählten Einstellung und von der Computerleistung kann dieser Vorgang bemerkenswert lange dauern (in einigen Fällen Dutzende von Sekunden, wenn es z.B. M1-Charts mit Millionen von Balken gibt). Leider bietet die MQL-API keine effizientere Methode zur Wiederherstellung eines einzelnen Indikators. In diesem Zusammenhang empfiehlt es sich, falls dieser Fall auftritt, den Offset über das Dialogfeld für die Indikatoreinstellungen zu ändern oder die Anzahl der in den Diagrammen angezeigten Balken zu verringern (Terminal sollte neu gestartet werden). Eine vertikale Cursorlinie wird hinzugefügt, um eine einfache und präzise Positionierung am voraussichtlichen Beginn der Datenprobe zu gewährleisten.
Überprüfen wir, wie der Indikator im strikten Modus und im vereinfachten Modus mit den gleichen Einstellungen funktioniert (es sei daran erinnert, dass der vereinfachte Modus durch Neukompilierung mit der Datei EMDloose.mqh erreicht wird, da es sich nicht um den Hauptarbeitsmodus handelt). Für EURUSD D1 verwenden wir die folgenden Einstellungen:
- Length = 250;
- Offset = 0;
- Forecast = 10;
- Reconstruction = 2;
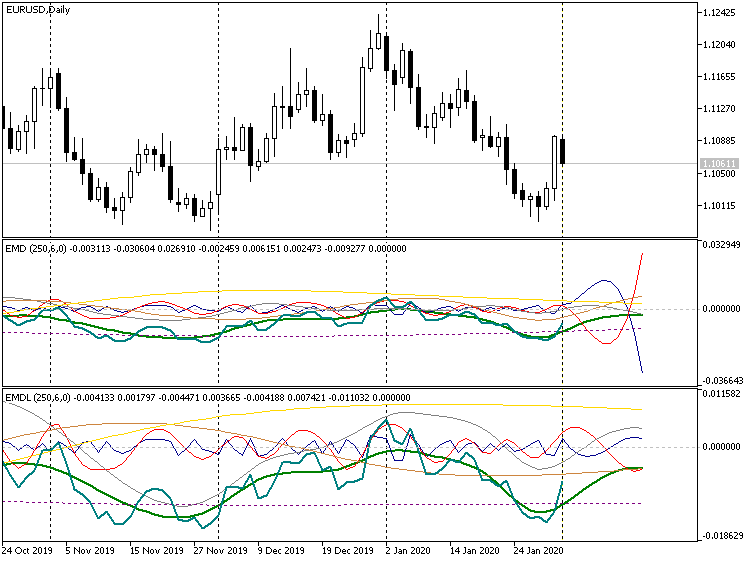
Kurzprognose, Indikator EMD, EURUSD D1
Im obigen Screenshot sind 2 Indikatorversionen dargestellt, die strikte oben und die vereinfachte unten. Beachten Sie, dass in der strikten Version einige Obertöne dazu neigen, in verschiedene Richtungen, nach oben und unten, "wegzulaufen". Aus diesem Grund ist sogar die Skala des ersten Indikators kleiner geworden als die des zweiten (die Neuskalierung ist eine visuelle Warnung vor der Unzulänglichkeit der prognostizierten Tiefe). Im vereinfachten Modus schweben alle Zerlegungskomponenten weiterhin um Null. Dies kann verwendet werden, um eine längerfristige Prognose zu erhalten, indem z.B. der Wert 100 im Parameter Prognose gesetzt wird. Das sieht schön aus, ist aber meist weit von der Realität entfernt. Die einzige Anwendung einer solchen Prognose scheint die Schätzung der zukünftigen Preisbewegungsbandbreite zu sein, in der Sie versuchen können, auf Preiskontraktion nach innen oder auf einen Ausbruch zu handeln.
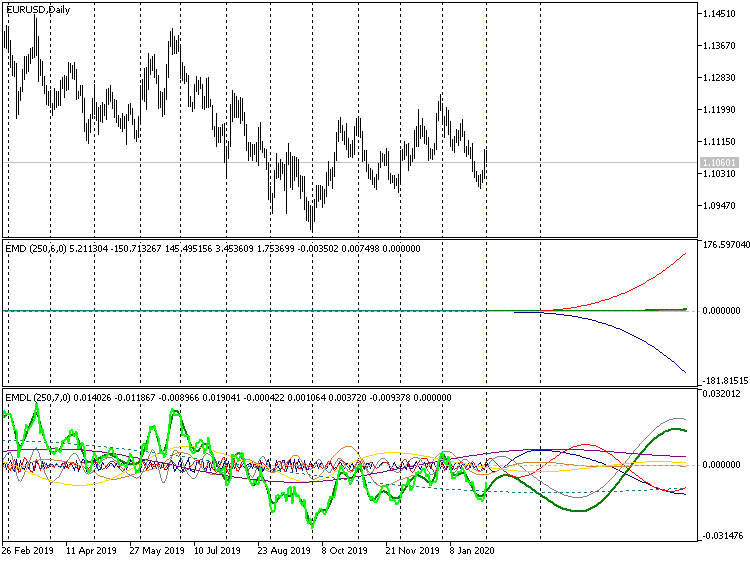
Lange Prognose, Indikatoren EMD, EURUSD D1
In der strikten Version führt dies dazu, dass nur die Enden der Polynome in die Unendlichkeit divergieren, während der informative Teil des Diagramms um Null "zusammengebrochen" ist.
Im Falle des erweiterten Prognosehorizonts sind Unterschiede in der Überschrift der Indikatoren zu erkennen: Wurden anfangs in beiden Fällen 6 eigene Funktionen gefunden (die zweite Zahl in Klammern, nach der Anzahl der zu analysierenden Balken), so verwendet die vereinfachte Version nun 7, da in ihrem Fall die 100 für die Vorhersage geforderten Balken an den Berechnungen der Extremwerte teilnehmen. Die Vorhersage auf 10 Balken liefert einen solchen Effekt (für diese Zeitreihe) nicht. Wir können eine Vorhersage = 10, die maximal zulässige vorschlagen, das ist aber eine nicht empfohlene Vorhersagelänge. Die empfohlene Länge beträgt 2-4 Balken.
Zur visuellen Referenz der rekonstruierten anfänglichen Zeitreihe und der Prognose ist es einfach, einen ähnlichen Indikator zu erstellen, der direkt auf dem Preisdiagramm angezeigt wird, EMDPrice. Seine interne Struktur folgt vollständig der des betrachteten EMD-Indikators, aber es gibt nur einen Puffer (einige IMFs sind an den Berechnungen beteiligt, werden aber nicht angezeigt, um eine Überladung des Charts zu vermeiden).
In EMDPrice verwenden wir eine Kurzform von OnCalculate(), die es uns erlaubt, den Preistyp für die Berechnungen zu wählen, wie z.B. den 'typical' Preis. Bei jedem Typ Eröffnungspreis ist jedoch zu berücksichtigen, dass der Indikator auf Eröffnungsbalken berechnet wird und daher Balken 1 der zuletzt gebildete ist (d.h. alle Preistypen hat). Mit anderen Worten, der Offset kann nur bei offenen Preisen 0 sein, während er in anderen Fällen mindestens 1 sein muss.
In der Abbildung unten sehen Sie, wie der Indikator EMDPrice mit einem Offset von 15 Balken in die Vergangenheit arbeitet.
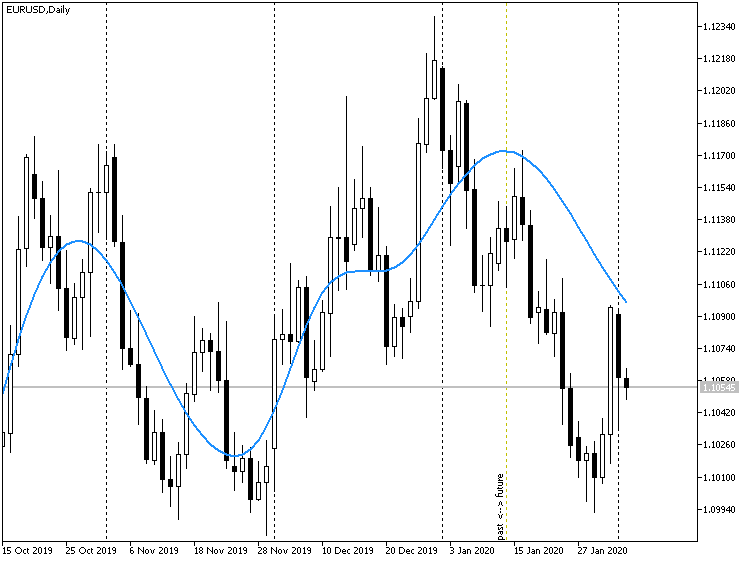
Die Prognose des EMD-Preisindikators auf dem Preisdiagramm EURUSD D1, auf Basis der Historie
Um die Prognosefähigkeit des EMD-Indikators zu testen, werden wir einen speziellen EA entwickeln.
Ein Expert Advisor für EMD-basierte Tests
Lassen Sie uns einen einfachen EA, TestEMD, erstellen, der eine Instanz des EMD-Indikators und des Handels auf der Grundlage seiner Prognosen erstellt. Er wird mit dem Eröffnungspreis der Balken arbeiten, da der Indikator die Eröffnungspreise für die Prognose verwendet.
Die grundlegenden Eingaben des EA:
- Length — Länge der Zeitreihe, die dem Indikator übergeben wird;
- Forecast — Anzahl der Prognosebalken, die dem Indikator übergeben werden;
- Reconstruction — Anzahl der kleineren Harmonischen, die bei der Rekonstruktion der Prognose ausgelassen und dem Indikator übergeben werden sollen;
- SignalBar — Nummer des Balkens, für den der Vorhersagewert aus dem Indikatorpuffer angefordert wird.
Als Handelssignal nehmen wir die Differenz zwischen den Indikatorwerten der SignalBar (dieser Parameter sollte negativ sein, um in die zu prognostizierende Zukunft zu blicken) und auf dem aktuellen Nullbalken. Eine positive Differenz ist das Kaufsignal, während die negative ein Verkaufssignal ist.
Da der Indikator EMD eine Prognose für die Zukunft erstellt, sind die Balkenzahlen in SignalBar in der Regel negativ und in absoluten Werten gleich den Werten der Prognose (grundsätzlich kann das Signal auch von einem weniger entfernten Balken genommen werden; in diesem Fall ist jedoch unklar, warum eine Prognose für eine größere Anzahl von Balken berechnet werden soll). Dies ist ein Fall des normalen Arbeitsmodus bei der Durchführung von Handelsoperationen. In diesem Modus, wenn der Indikator EMD aufgerufen wird, ist sein Offset-Parameter immer Null, da wir keine Prognosen über die Geschichte untersuchen.
Der EA unterstützt jedoch auch einen anderen, speziellen Nicht-Handelsmodus, der es erlaubt, schnell eine Optimierung aufgrund der theoretischen Berechnungen der Rentabilität der virtuellen Transaktionen auf den letzten Prognosebarren durchzuführen. Die Berechnung wird sequentiell für jeden neuen Balken innerhalb des gewählten Datumsbereichs durchgeführt, und die allgemeine Statistik in Form des Gewinnfaktors der Multiplikation der Prognose mit der realen Kursbewegung wird von OnTester zurückgegeben. Im Tester sollten Sie das Kriterium nutzerdefinierte Optimierung als Optimierungspreis auswählen. Geben Sie 0 ein, um diesen Modus in den SignalBar-Parameter aufzunehmen. Gleichzeitig wird der EA selbst automatisch Offset gleich Prognose setzen. Dies ist genau das, was es dem EA ermöglicht, die Prognose und die Preisänderung auf den letzten Prognosebalken zu vergleichen.
Natürlich kann der EA im normalen Betriebsmodus zusammen mit der Durchführung von Handelsoperationen und der Auswahl eines beliebigen eingebetteten Optimierungsindexes optimiert werden. Dies gilt vor allem deshalb, weil der recheneffektive Nicht-Handelsmodus ziemlich grob ist (insbesondere berücksichtigt er keine Spreads). Die Maxima und Minima der beiden Fitnessfunktionen müssen jedoch ungefähr gleich sein.
Da eine Vorhersage auf mehrere Balken im Voraus gemacht werden kann und die entsprechend gerichtete Position für den gleichen Zeitraum eröffnet wird, können entgegengesetzt gerichtete Positionen zur gleichen Zeit existieren. Wenn z.B. die Prognose 3 ist, dann wird jede Position innerhalb des Marktes für 3 Balken gehalten, und zu jedem Zeitpunkt sind 3 Positionen offen, die von unterschiedlichem Typ sein können. In dieser Hinsicht ist ein Hedging-Konto erforderlich.
Der vollständige Quellcode des EA ist dem Artikel beigefügt und wird hier nicht im Detail beschrieben. Sein Handelsteil basiert auf der Bibliothek MT4Orders, die den Aufruf von Handelsfunktionen erleichtert. Im EA gibt es keine "Freund-Feind"-Kontrolle von Aufträgen mittels der Magicnummer, keine strikte Fehlerverarbeitung und keine Einrichtung für Slippages, StopLosses und TakeProfits. Die feste Losgröße wird im Eingabeparameter Lot festgelegt, und es wird mit Marktaufträgen gehandelt. Wenn Sie EMD in funktionierenden EA verwenden möchten, können Sie diese Test-EA bei Bedarf um die entsprechenden Funktionen erweitern oder den mit dem Indikator EMD arbeitenden Teil in ähnlicher Weise in Ihre bestehenden EAs einfügen.
Beispielhafte Einstellungen zur Optimierung sind dem Artikel als Datei TestEMD.set beigefügt. Eine Optimierung mit EURUSD D1 für das Jahr 2018 im beschleunigten Modus liefert die folgenden optimalen Einstellungen:
- Length=110
- Forecast=4
- Reconstruction=2
Dementsprechend muss SignalBar gleich minus der Vorhersage sein, also -4.
Ein einziger Test mit diesen Einstellungen für den Zeitraum von Anfang 2018 bis Februar 2020, d.h. mit einem Forward für das Jahr 2019 und Anfang 2020, ergibt das folgende Bild:
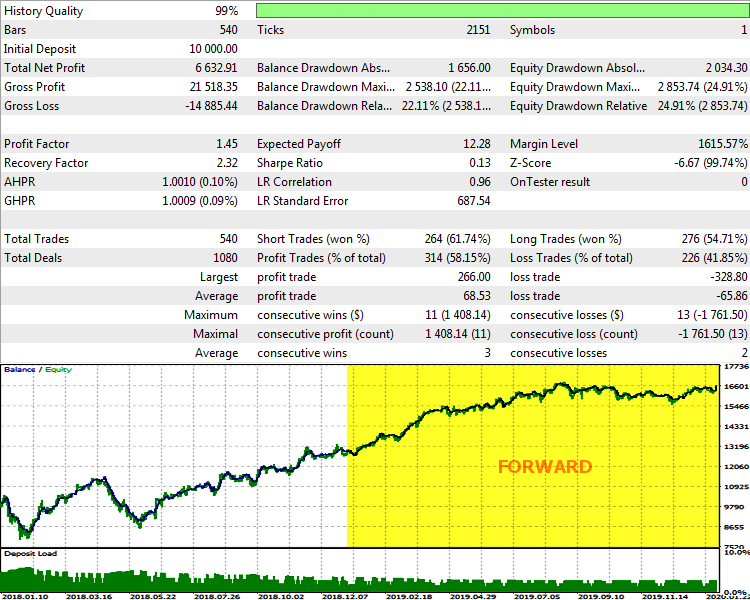
TestEMD Testbericht mit EURUSD D1, 2018-2020
Wie wir sehen, profitiert das System, auch wenn die Indizes zeigen, dass es Raum für Verbesserungen gibt. Insbesondere ist es logisch anzunehmen, dass eine häufigere Neuoptimierung in einem Schritt-für-Schritt-Betrieb und die Suche nach der Schrittgröße die Leistung des Roboters verbessern kann.
Grundsätzlich kann man sagen, dass der EMD-Algorithmus es ermöglicht, in einem größeren Zeitrahmen die fundamentalen, in gewissem Sinne momentanen Schwankungen der Notierungen zu identifizieren und darauf aufbauend ein profitables Handelssystem zu schaffen.
EMD ist nicht die einzige Technologie, die wir hier in Betracht ziehen werden. Bevor wir jedoch zum zweiten Teil übergehen, müssen wir die Mathematik für das Studium von Zeitreihen etwas "auffrischen".
Analyse der Hauptmerkmale von Zeitreihen in MQL — Indikator TSA
Auf der Website mql5.com wurde bereits ein Artikel mit ähnlichem Titel veröffentlicht: Analyse der wesentlichen Merkmale von Zeitreihen. Er bietet eine detaillierte Betrachtung der Berechnungswerte, wie Mittelwert, Median, Streuung, Schiefe und Wölbungsfaktoren, Verteilungshistogramm, Autokorrelationsfunktionen, partielle Autokorrelation und vieles mehr. All dies wird in der Klasse TSAnalysis in der Datei TSAnalysis.mqh gesammelt, die dann zu Demonstrationszwecken im Skript TSAexample.mq5 verwendet wird. Zur Visualisierung der Klassenleistung wurde der Ansatz leider mit der Generierung einer externen HTML-Datei angewandt, die im Browser analysiert werden muss. Gleichzeitig bietet MetaTrader 5 verschiedene grafische Werkzeuge zur Anzeige von Datenfeldern, vor allem von Indikatorpuffern. Wir werden die Klasse leicht modifizieren und sie "freundlicher" gegenüber Indikatoren gestalten, wonach wir einen Indikator implementieren werden, der die Analyse von Kursen direkt im Terminal ermöglicht.
Wir werden die neue Datei mit der Klasse TSAnalysisMod.mqh benennen. Das Hauptarbeitsprinzip bleibt dasselbe: Mit der Methode Calc wird eine Zeitreihe in das Objekt übergeben, für die während der Verarbeitung die gesamte Menge der Indizes berechnet wird. Sie werden alle in 2 Typen unterteilt — skalare Typen und Arrays. Der aufrufende Code kann dann jedes der Merkmale lesen.
Lassen Sie uns die skalaren Merkmale in einer einzigen Struktur von TSStatMeasures zusammenführen:
struct TSStatMeasures { double MinTS; // Minimum time series value double MaxTS; // Maximum time series value double Median; // Median double Mean; // Mean (average) double Var; // Variance double uVar; // Unbiased variance double StDev; // Standard deviation double uStDev; // Unbiaced standard deviation double Skew; // Skewness double Kurt; // Kurtosis double ExKurt; // Excess Kurtosis double JBTest; // Jarque-Bera test double JBpVal; // JB test p-value double AJBTest; // Adjusted Jarque-Bera test double AJBpVal; // AJB test p-values double maxOut; // Sequence Plot. Border of outliers double minOut; // Sequence Plot. Border of outliers double UPLim; // ACF. Upper limit (5% significance level) double LOLim; // ACF. Lower limit (5% significance level) int NLags; // Number of lags for ACF and PACF Plot int IP; // Autoregressive model order };
Wir werden die Arrays durch die Enumeratoren von TSA_TYPE bezeichnen:
enum TSA_TYPE { tsa_TimeSeries, tsa_TimeSeriesSorted, tsa_TimeSeriesCentered, tsa_HistogramX, tsa_HistogramY, tsa_NormalProbabilityX, tsa_ACF, tsa_ACFConfidenceBandUpper, tsa_ACFConfidenceBandLower, tsa_ACFSpectrumY, tsa_PACF, tsa_ARSpectrumY, tsa_Size // }; // ^ non-breaking space (to hide aux element tsa_Size name)
Um eine vollständige Struktur von TSStatMeasures mit den Arbeitsergebnissen zu erhalten, steht die Methode getStatMeasures zur Verfügung. Um eines der Arrays mit Hilfe von Makros zu erhalten, werden Methoden desselben Typs generiert, die als getARRAYNAME erscheinen, wobei ARRAYNAME dem Suffix eines der Enumeratoren von TSA_TYPE entspricht. Um zum Beispiel eine sortierte Zeitreihe zu lesen, sollten Sie die Methode getTimeSeriesSorted aufrufen. Alle derartigen Methoden haben eine Signatur:
int getARRAYNAME(double &result[]) const;
Wir füllen das übergebene Array aus, und geben die Anzahl der Elemente zurück.
Darüber hinaus gibt es eine universelle Methode zum Lesen eines beliebigen Arrays:
int getResult(const TSA_TYPE type, double &result[]) const
Die virtuelle Methodenschau wird vollständig aus der ursprünglichen Klasse entfernt, da sie nutzlos ist. Dem aufrufenden Code wird die vollständige Kontrolle über alle schnittstellenbezogenen Aufgaben übertragen.
Es ist bequem, Codes mit Hilfe der Klasse TSAnalysis von einem speziellen Indikator — dem TSA.mq5 — zu verarbeiten. Sein Hauptziel ist die Visualisierung von Merkmalen, die Arrays repräsentieren. Wenn Sie es wünschen, können Sie ihm bei Bedarf eine Option zur Anzeige skalarer Werte hinzufügen (sie werden jetzt zur Protokollierung ausgedruckt).
Da einige Arrays logisch in Dreiergruppen miteinander verbunden sind (z.B. hat die Autokorrelationsfunktion eine obere und eine untere Grenze von 95-% Konfidenzintervall), sind im Indikator 3 Puffer reserviert. Die Anzeigearten der Puffer passen sich je nach Bedeutung der angeforderten Daten dynamisch an.
Des Indikators Eingabe-Parameter:
- Type — Typ des angeforderten Arrays, Enumerator TSA_TYPE;
- Length — Länge der analysierten Zeitreihe in Balken;
- Offset — Anfangsversatz der Zeitreihe, 0 — Startpunkt;
- Differencing — Differenzierungsmodus, der definiert, ob er Kurse so lesen soll, wie sie sind, oder ob er die Differenz erster Ordnung nehmen soll;
- Smoothing — Mittelungszeitraum;
- Method — Methode der Mittelwertbildung;
- Price — Preistyp (standardmäßig Eröffnungspreis);
Der Indikator wird durch Balken berechnet.
Dies ist ein Beispiel dafür, wie die Funktion der partiellen Autokorrelation für EURUSD D1 auf 500 Balken mit Differenzierung aussieht:
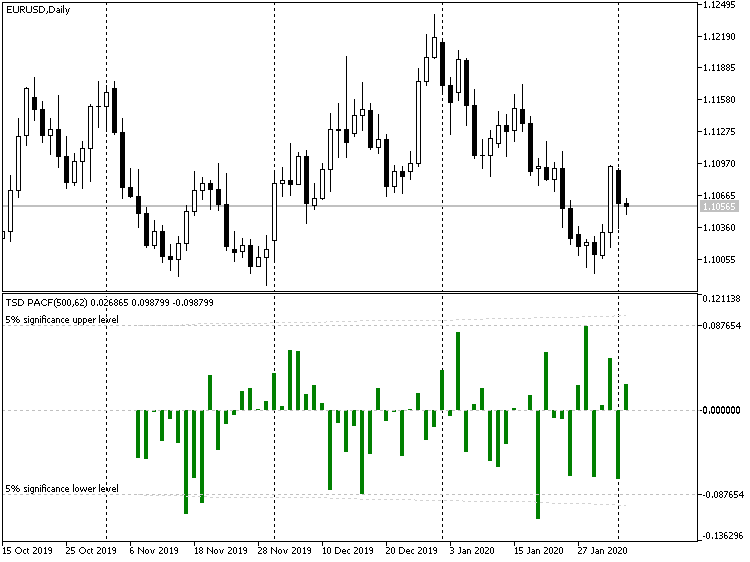
Indikator TSD, EURUSD D1
Wenn man die Unterschiede erster Ordnung nimmt, kann man die Stationarität (und Vorhersagbarkeit) einer Serie erhöhen. Im Grunde genommen wird die Differenz zweiter Ordnung noch stationärer sein, die dritter Ordnung — noch mehr, usw. Dies hat jedoch seine negativen Seiten, die später (in Teil 2) diskutiert werden.
Die partielle Autokorrelationsfunktion ist auch hier nicht zufällig gewählt. Wir werden sie im nächsten Schritt brauchen, wenn wir zu einer anderen Prognosemethode übergehen. Da wir jedoch eine ziemlich große Menge an Material studieren müssen, haben wir dieses vorbereitende Kapitel für diesen Artikel verwendet. Darüber hinaus stellt die statistische Analyse von Zeitreihen einen universellen Wert dar und kann bei anderen kundenspezifischen Entwicklungen im MQL-Bereich verwendet werden.
Schlussfolgerungen
In diesem Artikel haben wir die besonderen Aspekte des Algorithmus der empirischen Modus-Dekompensation besprochen, die es uns erlauben, seine Anwendbarkeit auf den Bereich der kurzfristigen Vorhersage von Zeitreihen zu erweitern. Die in MQL implementierten Klassen, Indikatoren und EA erlauben es, die EMD-Prognose als zusätzlichen Faktor bei Handelsentscheidungen sowie als Teil automatisierter Handelssysteme zu verwenden. Darüber hinaus haben wir das Toolkit aktualisiert, um die statistische Analyse von Zeitreihen durchzuführen, die wir in unserem nächsten Artikel benötigen werden, um die Vorhersage mit der LS-SVM-Methode zu berücksichtigen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/7601
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Die Handelssignale mehrerer Währungen überwachen (Teil 2): Implementierung des visuellen Teils der Anwendung
Die Handelssignale mehrerer Währungen überwachen (Teil 2): Implementierung des visuellen Teils der Anwendung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Vielen Dank für diesen interessanten Artikel, aber die Dateien funktionieren nicht, sie haben Syntaxfehler und nicht deklarierte Variablen.
Mit freundlichen Grüßen
Bitte stellen Sie Ihre Fehlerprotokolle zur Verfügung und geben Sie genau an, was Sie getan haben.
Vielen Dank an Stanislav für den sehr guten Artikel. Ich habe die Codes heruntergeladen und bin beim Kompilieren auf einen Fehler gestoßen.
Der Fehler lautet: 'Offset' -irgendein Operator erwartet in der Zeile
puffer[0].set(Versatz,Summe);
Bitte zeigen Sie mir, wie ich das lösen kann.
Vielen Dank
Vielen Dank an Stanislav für den sehr guten Artikel. Ich habe die Codes heruntergeladen und bin beim Kompilieren auf einen Fehler gestoßen.
Der Fehler lautet: 'Offset' - irgendein Operator wird in der Zeile erwartet
puffer[0].set(Versatz,Summe);
Bitte zeigen Sie, wie Sie das Problem lösen können.
Danke
Ich habe gerade die Quellen neu heruntergeladen und alle Indikatoren und den Experten ohne Probleme kompiliert.
Sie machen etwas falsch. Stellen Sie sicher, dass Sie den Inhalt des Archivs mit erhaltener Ordnerstruktur extrahiert haben.
Dies sind die Ergebnisse, wenn ich das Datum vom 1.1.2020 bis jetzt geändert habe