Using Deep Reinforcement Learning to Enhance Ilan Expert Advisor

Introduction

In the world of algorithmic trading, some strategies, like eternal stars in the ever-changing firmament of financial markets, leave an indelible mark on the history of trading. Among them is Ilan, a once legendary grid Expert Advisor that captivated the minds and accounts of traders in the 2010s with its deceptive simplicity and potential effectiveness during periods of low volatility.

However, time does not stand still. In the age of quantum computing, neural networks, and machine learning, the strategies of yesterday require fundamental reimagining. What if we combine the classical mechanics of Ilan grid averaging with advanced artificial intelligence algorithms? What if, instead of hard-coded rules, we let the system adapt on its own and constantly improve?

In this article, we challenge established ideas about trading models and undertake an ambitious attempt to revive classic Ilan by equipping it with deep reinforcement learning (Q-learning) with a dynamic Q-table. We are not just modifying existing code, we are creating a fundamentally new intelligent model capable of learning from our own experience, adapting to market changes and optimizing trading solutions in real time.

Our journey will take you through the labyrinths of algorithmic trading, where mathematical rigor meets computational elegance, and classic Martingale techniques take on new life thanks to innovative machine learning approaches. Whether you are an experienced algorithmic trader, a trading architecture developer, or just a financial technology enthusiast, this article offers a unique perspective on the future of automated trading.

Fasten your seat belts — we are embarking on an exciting journey to create Ilan 3.0 AI, where tradition meets innovation, and the past evolves into the future.

Studying the classic Ilan from the inside

Before diving into the world of artificial intelligence, it is necessary to understand what made Ilan such a popular Expert Advisor in the 2010s. The key idea of its work was the concept of averaging positions. When the price moved against the open position, the Expert Advisor would not close the loss, but added new orders, improving the average entry price.

Here is a simplified code snippet illustrating this logic:

// Simplified averaging logic in the original Ilan
if(positionCount == 0) {
   // Opening first position on signal
   if(OpenSignal()) {
      OpenPosition(ORDER_TYPE_BUY, StartLot);
   }
} else {
   // Calculating level for averaging
   double averagePrice = CalculateAveragePrice();
   double gridLevel = averagePrice - GridSize * Point();
   
   // If price has reached grid level, add position
   if(Bid <= gridLevel) {
      double newLot = StartLot * MathPow(LotMultiplier, positionCount);
      OpenPosition(ORDER_TYPE_BUY, newLot);
   }
   
   // Checking for closing of all TP positions
   if(Bid >= averagePrice + TakeProfit * Point()) {
      CloseAllPositions();
   }
}

The Magic of Martingale: Why traders fell in love with Ilan

The popularity of Ilan can be explained by several factors. First of all, its work was intuitive even to novice traders. In a sideways market, the system showed almost magical results — every price fluctuation turned into a source of profit. Averaging positions made it possible to "save" trades that were initially at a loss, creating a trader's feeling of invincibility of the architecture.

Another attractive factor was the feature to customize the strategy using a minimal set of parameters:

// Key parameters of Ilan Expert Advisor
input double   StartLot = 0.01;          // Initial lot size
input double   LotMultiplier = 1.5;      // Lot multiplier for each new position
input int      GridSize = 30;            // Grid size in points
input int      TakeProfit = 40;          // Profit for closing all positions
input int      MaxPositions = 10;        // Maximum number of positions to open

This simplicity of setup created the illusion of control. The trader could experiment with different combinations of parameters, achieving impressive results based on historical data.

Attempts at evolution: What has changed in Ilan 2.0

In Ilan 2.0, developers tried to solve some of these problems. Dynamic calculation of the grid step based on market volatility, work with several currency pairs and analysis of their correlation, additional filters for opening positions and protection mechanisms against excessive losses have been added.

// Dynamic calculation of grid step in Ilan 2.0
double CalculateGridStep(string symbol) {
   double atr = iATR(symbol, PERIOD_CURRENT, ATR_Period, 0);
   return atr * ATR_Multiplier;
}

// Protective mechanism to limit losses
bool EquityProtection() {
   double currentEquity = AccountInfoDouble(ACCOUNT_EQUITY);
   double maxAllowedDrawdown = AccountInfoDouble(ACCOUNT_BALANCE) * MaxDrawdownPercent / 100.0;
   
   if(AccountInfoDouble(ACCOUNT_BALANCE) - currentEquity > maxAllowedDrawdown) {
      CloseAllPositions();
      return true;
   }
   return false;
}

These improvements did make the system more resilient, but they did not solve the fundamental problem of lack of adaptability. Ilan 2.0 was still based on static rules and could not learn from its experience or adapt to changing market conditions.

Why did traders keep using Ilan

Despite obvious disadvantages, many traders continued to use Ilan and its modifications. This is due to a number of psychological factors. Those who went broke were usually silent, while successful stories were actively published. Traders would notice successful periods and ignored the warning signs. It seemed that fine-tuning the parameters could solve all the problems. In addition, the Martingale strategy activated the same psychological triggers as gambling.

To be fair, it's worth noting that in certain market conditions — especially during periods of low volatility and sideways movement — the EA could actually show impressive results for a long time. The problem was that market conditions would inevitably change, and the expert advisor did not adapt to these changes.

Why Ilan inevitably broke down and lost deposit

The real problem of Ilan was revealed in the long run. The strategy that worked perfectly in a sideways market proved to be catastrophically vulnerable to prolonged trend movements. Consider a typical crash scenario.

Firstly, the first buy position is opened. Then the market starts a steady downward movement. The EA adds positions by increasing lots exponentially. After several levels of averaging, the position size becomes so large that even a small further movement leads to a margin call.

Mathematically, this problem can be expressed as follows: with a Martingale strategy with a multiplication factor of 1.5 and an initial lot of 0.01, the tenth consecutive position will have a size of about 0.57 lots, which is 57 times larger than the initial one. The total size of all open positions will be about 1.1 lots, which for an account of $1,000 with a leverage of 1:100 means using almost the entire available margin.

// Calculation of total size of martingale positions
double totalVolume = 0;
double currentLot = StartLot;
for(int i = 0; i < MaxPositions; i++) {
   totalVolume += currentLot;
   currentLot *= LotMultiplier;
}
// At StartLot = 0.01 and LotMultiplier = 1.5 after 10 positions
// totalVolume will be about 1.1 lots!

The key problem was the lack of a mechanism to determine when the averaging strategy should be discontinued. Ilan was like a gambler who doesn't know when to stop and keeps betting more and more in the hope of winning back.

Why Ilan needs AI

Analyzing Ilan's strengths and weaknesses, it becomes obvious that its key problem is the inability to learn and adapt. The Expert Advisor follows the same rules, no matter how successful or disastrous its previous actions were.

This is where artificial intelligence comes on the scene. What if we keep the basic mechanism of Ilan operation, but add it with a feature to analyze the results of its actions and adjust the strategy? What if, instead of hard-coded rules, we let the model independently find optimal parameters and entry points based on accumulated experience?

This idea is at the heart of our Ilan 3.0 AI project, where we integrate a time-tested averaging strategy with advanced machine learning methods. In the next section, we consider how Q-learning technology can make this concept a reality.

How Q-learning will improve Ilan Expert Advisor

Transition from the classical Ilan model to an intelligent system capable of learning requires a fundamental change in EA’s architecture. Q-learning algorithm becomes the heart of Ilan 3.0 AI. It is one of the most important technologies in the field of reinforcement learning.

The basics of Q-learning based on your actions

Q-learning is so named because of the "Quality function," which determines the value of an action in a particular condition. In our implementation, we use a Q-table, a data structure that stores scores for each “state-action” pair:

// Structure for Q-table
struct QEntry {
    string state;     // Discretized state of market
    int action;       // Action (0-nothing, 1-buy, 2-sell)
    double value;     // Q-value
};

// Global array for Q-table
QEntry QTable[];
int QTableSize = 0;

A key feature of Q-learning is the system's ability to learn from its own experience. After each action, the algorithm receives a reward (profit) or a penalty (loss) and adjusts its assessment of the value of this action in a specific market situation:

// Updating Q-value using Bellman formula
void UpdateQValue(string stateStr, int action, double reward, string nextStateStr, bool done)
{
    double currentQ = GetQValue(stateStr, action);
    double nextMaxQ = 0;
    
    if(!done)
    {
        // Find maximum Q for following state
        nextMaxQ = GetMaxQValue(nextStateStr);
    }
    
    // Updating Q-value
    double newQ = currentQ + LearningRate * (reward + DiscountFactor * nextMaxQ - currentQ);
    
    // Saving updated value
    SetQValue(stateStr, action, newQ);
}

This formula, known as the Bellman equation, is the cornerstone of our approach. The LearningRate parameter determines the learning rate, and DiscountFactor determines the importance of future rewards relative to current ones.

A balance between finding new solutions and using experience

One of the key challenges in reinforcement learning is the need to balance between exploring new strategies and exploiting already known optimal solutions. To solve this problem, we use the ε-greedy strategy:

// Choosing action with balance between exploration and exploiting
int SelectAction(string stateStr)
{
    // With epsilon probability choose random action (research)
    if(MathRand() / (double)32767 < currentEpsilon)
    {
        return MathRand() % ActionCount;
    }
    
    // Otherwise, choose action with maximum Q-value (exploiting)
    int bestAction = 0;
    double maxQ = GetQValue(stateStr, 0);
    
    for(int a = 1; a < ActionCount; a++)
    {
        double q = GetQValue(stateStr, a);
        if(q > maxQ)
        {
            maxQ = q;
            bestAction = a;
        }
    }
    
    return bestAction;
}

The currentEpsilon parameter determines the probability of a random choice of action. Over time, its value decreases, which allows the system to move from active research to the preferential use of accumulated knowledge:

// Reducing epsilon for a gradual transition from exploration to exploiting
if(currentEpsilon > MinExplorationRate)
    currentEpsilon *= ExplorationDecay;

Digital sensory organ: how the algorithm perceives the market

To effectively train an algorithm, it must "see" the market, that is to have a formalized idea of the current situation. In Ilan 3.0 AI, we use a comprehensive state vector that includes technical indicators, open position metrics, and other market data:

// Getting current market state for Q-learning
void GetCurrentState(string symbol, double &state[])
{
    ArrayResize(state, StateDimension);
    
    // Technical indicators
    double rsi = iRSI(symbol, PERIOD_CURRENT, RSI_Period, PRICE_CLOSE, 0);
    double cci = iCCI(symbol, PERIOD_CURRENT, CCI_Period, PRICE_TYPICAL, 0);
    double macd = iMACD(symbol, PERIOD_CURRENT, 12, 26, 9, PRICE_CLOSE, MODE_MAIN, 0);
    
    // Normalization of indicators
    double normalized_rsi = rsi / 100.0;
    double normalized_cci = (cci + 500) / 1000.0;
    
    // Metrics of positions
    int positions = (symbol == "EURUSD") ? euroUsdPositions : audUsdPositions;
    double normalized_positions = (double)positions / MaxTrades;
    
    // Calculating price difference
    double point = SymbolInfoDouble(symbol, SYMBOL_POINT);
    double currentBid = SymbolInfoDouble(symbol, SYMBOL_BID);
    double avgPrice = CalculateAveragePrice(symbol);
    double price_diff = (currentBid - avgPrice) / (100 * point);
    
    // Filling in state vector
    state[0] = normalized_rsi;
    state[1] = normalized_cci;
    state[2] = normalized_positions;
    state[3] = price_diff;
    state[4] = macd / (100 * point);
    state[5] = AccountInfoDouble(ACCOUNT_EQUITY) / AccountInfoDouble(ACCOUNT_BALANCE);
}

To work with the Q-table, continuous state values must be discretized, that is be converted into a string representation with a finite number of options:

// Converting state to string for Q-table
string StateToString(double &state[])
{
    string stateStr = "";
    
    for(int i = 0; i < ArraySize(state); i++)
    {
        // Rounding to 2 decimal places for discretization
        double discretized = MathRound(state[i] * 100) / 100.0;
        stateStr += DoubleToString(discretized, 2);
        
        if(i < ArraySize(state) - 1)
            stateStr += ",";
    }
    
    return stateStr;
}

This discretization process enables the system to generalize experience by applying it to similar but not identical market situations.

Incentive system: Carrot and stick in the AI world

The correct definition of a reward approach is probably the most critical aspect in building an effective reinforcement learning system. In Ilan 3.0 AI, we have developed a multi-level incentive system that guides algorithm development in the right direction.

Economics of awards: How to motivate the algorithm

When closing positions with profit, the model receives a positive reward proportional to the amount of profit:

// Reward at closing profitable positions
if(shouldClose)
{
    if(ClosePositions(symbol, magic))
    {
        if(isTraining)
        {
            double reward = profit; // Reward is equal to profit
            UpdateQValue(stateStr, action, reward, stateStr, true);
            
            // Learning statistics
            episodeCount++;
            totalReward += reward;
            
            Print(“Episode ", episodeCount, " completed with reward: ", reward, 
                 ". Average reward: ", totalReward / episodeCount);
        }
    }
}

When averaging loss positions, the system receives a small penalty, which encourages it to look for optimal entry points and avoid situations that require averaging:

// Penalty at averaging positions
if(OpenPosition(symbol, ORDER_TYPE_BUY, CalculateLot(positionsCount, symbol), StopLoss, TakeProfit, magic))
{
    if(isTraining)
    {
        double reward = -1; // Small penalty for averaging
        UpdateQValue(stateStr, action, reward, stateStr, false);
    }
}

Absence of an immediate reward when opening the first position forces the system to focus on long-term results rather than on short-term actions.

Fine balancing of the model

Effectiveness of the Q-learning system strongly depends on the correct setting of its key parameters. In Ilan 3.0 AI, we provide a feature to fine tune all aspects of learning:

// Reinforcement learning parameters
input double   LearningRate = 0.01;      // Learning rate
input double   DiscountFactor = 0.95;    // Discount factor
input double   ExplorationRate = 0.3;    // Initial probability of exploration
input double   ExplorationDecay = 0.995; // Exploration reduction factor
input double   MinExplorationRate = 0.01;// Minimal probability of exploration

LearningRate determines the update rate of Q-values. High values lead to rapid learning, but they can cause instability. Low values ensure stable but slow learning.

DiscountFactor determines the importance of future rewards. Values closer to 1 force the model to strive for long-term profit maximization, sometimes sacrificing immediate benefits.

Research parameters control the balance between the search for new strategies and the exploitation of known optimal solutions. Over time, the probability of research decreases, enabling the system to rely more and more on accumulated experience.

From theory to practice: Implementation

Implementing Ilan 3.0 AI requires integrating Q-learning mechanisms with traditional logic of a trading expert advisor. The key component is the trade management function, which uses Q-learning to make decisions:

// Trade management function using Q-learning
void ManagePairWithDQN(string symbol, int &positionsCount, CArrayDouble &trades, 
                     int magic, datetime &firstTradeTime)
{
    // Getting current market data
    double currentBid = SymbolInfoDouble(symbol, SYMBOL_BID);
    double currentAsk = SymbolInfoDouble(symbol, SYMBOL_ASK);
    double point = SymbolInfoDouble(symbol, SYMBOL_POINT);
    
    // Forming current state
    double state[];
    GetCurrentState(symbol, state);
    string stateStr = StateToString(state);
    
    // Selecting action using Q-table
    int action = SelectAction(stateStr);
    
    // Converting action into trading operation
    bool shouldTrade = (action > 0);
    ENUM_ORDER_TYPE orderType = (action == 1) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL;
    
    // Logic of opening and managing positions
    if(shouldTrade)
    {
        // Logic of opening first position or averaging
        // ...
    }
    
    // Checking need to close positions
    double profit = CalculatePositionsPnL(symbol, magic);
    if(profit > 0 && positionsCount > 0)
    {
        // Logic of closing profitable positions
        // ...
    }
}

Saving system experience

To save the accumulated experience, we implemented a mechanism for saving and loading the Q-table between sessions:

// Saving Q-table to file
bool SaveQTable(string filename)
{
    int handle = FileOpen(filename, FILE_WRITE|FILE_BIN);
    if(handle == INVALID_HANDLE)
    {
        Print("Error when opening file for writing Q-table: ", GetLastError());
        return false;
    }
    
    // Writing table size
    FileWriteInteger(handle, QTableSize);
    
    // Writing values
    for(int i = 0; i < QTableSize; i++)
    {
        FileWriteString(handle, QTable[i].state);
        FileWriteInteger(handle, QTable[i].action);
        FileWriteDouble(handle, QTable[i].value);
    }
    
    FileClose(handle);
    return true;
}

// Downloading Q-table from file
bool LoadQTable(string filename)
{
    if(!FileIsExist(filename))
    {
        Print("Q-table file does not exist: ", filename);
        return false;
    }
    
    int handle = FileOpen(filename, FILE_READ|FILE_BIN);
    if(handle == INVALID_HANDLE)
    {
        Print("Error when opening file to read Q-table: ", GetLastError());
        return false;
    }
    
    // Reading table size
    int size = FileReadInteger(handle);
    
    // Allocating memory for table
    if(size > ArraySize(QTable))
    {
        ArrayResize(QTable, size);
    }
    
    // Reading values
    for(int i = 0; i < size; i++)
    {
        QTable[i].state = FileReadString(handle);
        QTable[i].action = FileReadInteger(handle);
        QTable[i].value = FileReadDouble(handle);
        QTableSize++;
    }
    
    FileClose(handle);
    return true;
}

Let's consider the test of this expert advisor. The test was obtained using OHLC modeling on a 15-minute chart, on AUDUSD and EURUSD pairs for 2020-2025 (the main symbol is EURUSD, but the Expert Advisor also loads AUDUSD).

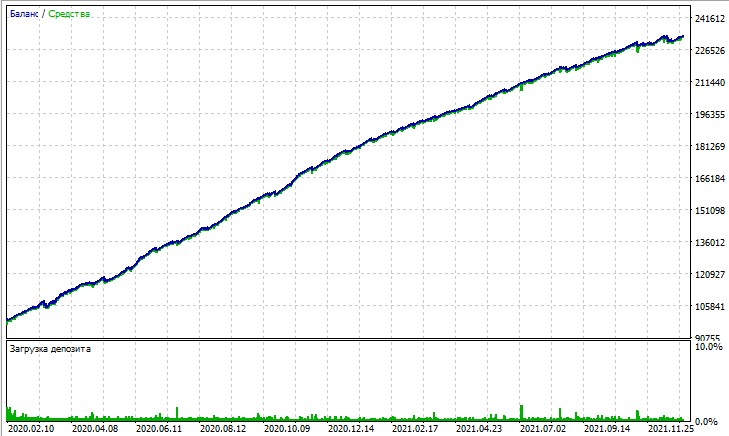
But the "All Ticks" test mercilessly highlights the large drawdowns that occur due to the Martingale. Despite the penalties, sometimes the model falls into a series of averaging trades. Perhaps in future versions we will remove drawdowns using DQN risk management:

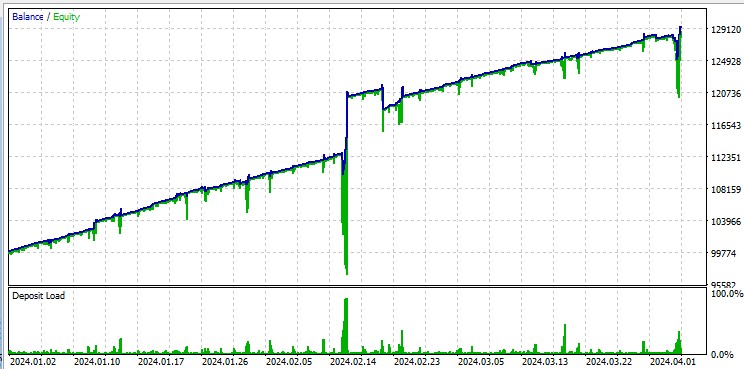
It should also be noted that the robot trades huge lots, which is useful for getting rebates per turnover from the broker.

Ways to improve the algorithm

Despite significant improvements, Ilan 3.0 AI represents only the first step in the evolution of intelligent trading systems. Promising areas for further development include:

1. Replacing the Q-table with a full-fledged neural network for a better generalization of experience
2. Implementation of deep reinforcement learning (DQN, DDPG, PPO) algorithms
3. Using meta-learning techniques to quickly adapt to new market conditions
4. Integration with news and fundamental data analysis architectures

Conclusion

Implementation of Ilan 3.0 AI demonstrates a fundamental change in the approach to algorithmic trading. We are moving from static systems based on fixed rules to adaptive algorithms capable of learning and evolving.

The integration of the classic Ilan strategy with modern machine learning methods opens up new horizons in the development of trading systems. Instead of endless parameter optimization, we implement systems that are able to independently find optimal strategies and adapt to changing market conditions.

The future of algorithmic trading lies in hybrid approaches combining time-tested trading strategies with innovative artificial intelligence techniques. Ilan 3.0 AI is not just an improved version of the classic Expert Advisor, but a fundamentally new class of intelligent trading systems capable of learning, adapting and developing together with the market.

We are on the threshold of a new era in algorithmic trading — an era of models that not only follow set rules, but are constantly evolving, finding optimal strategies in the ever-changing world of financial markets.