Neural Networks Made Easy (Part 85): Multivariate Time Series Forecasting
286
1
Introduction
Forecasting timeseries is one of the most important elements in building an effective trading strategy. When performing a trading operation in one direction or another, we proceed from our own vision (forecast) of the upcoming price movement. Recent advances in deep learning models, especially architecture-based Transformer models, have demonstrated significant progress in this area, offering a great potential for solving the multifaceted problems associated with long-term timeseries forecasting.
However, the question arises about the efficiency of using the Transformer architecture for timeseries forecasting purposes. Most of the Transformer-based models we have previously considered used the Self-Attention mechanism to record long-term dependencies of various time steps in the analyzed sequence. However, some studies argue that most existing Transformer models based on intertemporal attention are unable to adequately study intertemporal dependencies. Sometimes a simple linear model outperforms some Transformer models.
The authors of the paper "Client: Cross-variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting" approached this issue quite constructively. To assess the scale of the problem, they conducted a complex experiment with a series of masking parts of the historical series, randomly replacing individual data with "0". Models that are more sensitive to time dependence show a large performance degradation without correct historical data. Thus, the performance degradation is an indication of the model's ability to capture temporal patterns. The experiment found that the performance of Cross-Attention-based Transformer models does not significantly decrease as the scale of data masking increases. Some such models show virtually unchanged forecasting performance even when up to 80% of historical data is randomly replaced with "0". This may indicate that the forecast results of such models are not sensitive to changes in the analyzed time series.
My personal attitude towards the results of the presented analysis is ambiguous. Of course, the lack of sensitivity to changes in the analyzed timeseries is, to put it mildly, alarming. Furthermore, given that the model is considered a "black box", it is difficult to understand which part of the data the model takes into account and which it ignores.
On the other hand, in the environment of stochastic financial markets, the analyzed timeseries contains quite a lot of noise, which should preferably filtered. In this context, ignoring minor fluctuations or outliers that are not typical of the environment under consideration may help you to identify the most significant part of the analyzed timeseries.
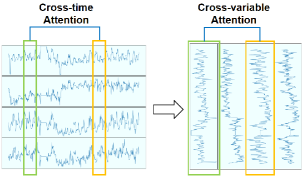
In addition, the authors of the paper noticed that in some multivariate timeseries, different variables exhibit related patterns over time. This suggests the possibility of using attention mechanisms to learn dependencies between variables rather than between time steps. This assumption allows changing the paradigm in which the Self-Attention mechanism is applied.
Although the Transformer proposed by the authors of the paper models nonlinearity well and captures dependencies between variables, it may not work well when extracting trends from the analyzed series. This task is well performed by linear models. In order to combine the best of both worlds, the authors of the paper the Cross-variable Linear Integrated Enhanced Transformer - Client method for multivariate long-term time series forecasting. The proposed algorithm combines the ability of linear models to extract trends with the expressive capabilities of the enhanced Transformer.
1. The "Client" Algorithm
The main idea of Client is move from attention over time to analyzing dependencies between variables and integrating a linear module into the model to better exploit variable dependencies and trend information, respectively.
The authors of the Client method creatively approached the solution to the timeseries forecasting problem. On the one hand, the proposed algorithm incorporates already familiar approaches. On the other hand, it rejects some well-established methods. The inclusion or exclusion of each individual block in the algorithm is accompanied by a series of tests. The tests demonstrate the feasibility of the decision taken from the point of view of the model effectiveness.
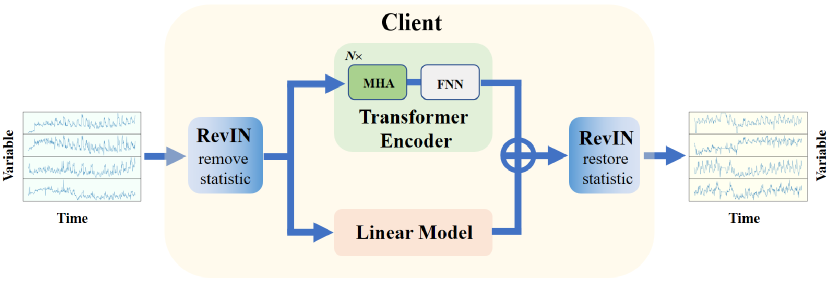
To solve the problem with the distribution bias, the authors of the method use reversible normalization with a symmetric structure (RevIN), which was discussed in the previous article. RevIN is first used to removes statistical information about the timeseries from the original data. After the model processes the data and generates forecast values, the statistical information of the original timeseries is restored in the forecast, which generally allows to increase the stability of model training and the quality of the forecast values of the timeseries.
To enable further analysis in terms of variables rather than time steps, the authors of the method propose transposing the initial data.
The data prepared in this way is fed to the Transformer Encoder, which consists of several layers of multi-headed Self-Attention (MHA) and FeedForward (FFN) blocks.
Please note that the input is fed to the Encoder, bypassing the usually present Embedding layer. Tests conducted by the authors of the method demonstrated the ineffectiveness of its use, since the additional level of data transformation distorts time information and leads to a decrease in the performance of the model. In addition, the positional coding block is removed since there is no time sequence between the different variables.
After feature extraction in the Encoder, the timeseries is passed to the projection layer, which generates predicted values for each variable.
The proposed projection layer replaces the Classic Transformer Decoder. In their paper, the authors of Client found that the addition of a Decoder resulted in a decrease in the overall performance of the model.
In parallel with the attention block, the Client model includes and integrated linear module, which is used to study information about the trends of timeseries in independent channels and individual variables.
The predicted values of the attention block and the linear module are summed taking into account the learnable weights that are applied to the results of the linear module.
At the output of the model, the results are again transposed to bring them into line with the sequence of the original data. The statistical information of the timeseries is restored.
Thus, the Client method uses the linear module to collect trend information and the advanced Transformer module to collect nonlinear information and dependencies between variables. The author's visualization of the method is presented below.
2. Implementing in MQL5
After considering the theoretical aspects of the Client method, we move on to the practical part of our article, in which we implement our vision of the proposed approaches using MQL5.
2.1 Create a new neural layer
First, let's create a new class CNeuronClientOCL, which will combine most of the proposed approaches. We will create this class, like most of those we created earlier, by inheriting from our base neural layer class.CNeuronBaseOCL.
class CNeuronClientOCL : public CNeuronBaseOCL { protected: //--- Attention CNeuronMLMHAttentionOCL cTransformerEncoder; CNeuronConvOCL cProjection; //--- Linear model CNeuronConvOCL cLinearModel[]; //--- CNeuronBaseOCL cInput; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); public: CNeuronClientOCL(void) {}; ~CNeuronClientOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint at_layers, uint count, uint &mlp[], ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronClientOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
The attention block will be created from 2 objects:
- cTransformerEncoder — the object of the CNeuronMLMHAttentionOCL class which allows creating the Encoder block of the multi-head Transformer from a given number of successive layers.
- cProjection — projection layer. Here we use a convolutional layer to make independent predictions on individual variables. The prediction depth determines the number of filters in the layer.
To create a linear module, we will create a dynamic array of convolutional layers cLinearModel[], which will allow us to generate independent forecasts for individual variables.
Note that in this implementation, I decided to move the reversible normalization and data transposition layers outside the class. This is because the Client block can be integrated into a more complex architecture. Therefore, statistical information can be deleted and restored far from this block.
Also, data transposition can also be performed at a distance from the Client block. In addition, in some cases, it is possible to create the required sequence of source data at the data preparation stage.
The set of methods of our new class is quite standard.
We declare all internal objects as static, which allows us to leave the class constructor and destructor empty. With this approach, we can focus less on memory cleaning issues, delegating this functionality to the system.
Initialization of all internal objects is performed in the Init method. In the parameters of this method, we pass to the class object all the information necessary to organize the required architecture.
It should be noted here that in the class body, we create 2 parallel streams:
- The Transformer block
- The linear module
Both of these modules have complex and very different independent architectures, although they work with the same dataset. Therefore, we need a mechanism to pass both modules into the architecture object. For the Transformer block, we will use the previously developed 5 variable approach:
- window: size of the vector of 1 element of the sequence
- window_key: size of the vector of internal representation of 1 element of the sequence
- heads: number of attention heads
- count: number of elements in the sequence
- at_layers: number of layers in the Encoder block
To describe the architecture of the linear module, we use a numerical array mlp[]. The number of elements in the array indicates the number of layers to create. The value of each element indicates the size of the vector describing one element of the sequence at the output of the layer. The linear module works with the same dataset as the attention block. Therefore, the number of elements in the sequence is the same.
Please note that the authors of the Client method propose to analyze the dependencies between variables. Therefore, in this case, the size of the vector describing 1 element of the sequence will be equal to the depth of the analyzed history. And the number of elements in the sequence is equal to the number of variables being analyzed. The input data must be transposed accordingly before being fed into our new CNeuronClientOCL class object.
With this approach, we will indicate the depth of data forecasting in the last element of the mlp[] array.
This is the data transfer logic. Let's implement the proposed approach in code. In the Init method parameters, we specify the variables presented above and supplement them with elements of the base class.
bool CNeuronClientOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint at_layers, uint count, uint &mlp[], ENUM_OPTIMIZATION optimization_type, uint batch) { uint mlp_layers = mlp.Size(); if(mlp_layers == 0) return false;
In the method body, we first check the size of the linear module architecture description array mlp[]. It must contain at least one element indicating the depth of data forecasting. If the array is empty, we terminate the method with the false result.
In the next step, we initialize class objects. First we modify the dynamic array of the linear module.
if(ArrayResize(cLinearModel, mlp_layers + 1) != (mlp_layers + 1)) return false;
Please note that the array size must be 1 element larger than the resulting linear layer architecture. We will talk about the reasons for this step a little later.
Next, we call the same method of the parent class, which initializes all inherited objects.
if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, mlp[mlp_layers - 1] * count, optimization_type, batch)) return false;
After that we call the Transformer Encoder initialization method.
if(!cTransformerEncoder.Init(0, 0, OpenCL, window, window_key, heads, count, at_layers, optimization, iBatch)) return false;
An auxiliary layer for temporary storage of the input data.
if(!cInput.Init(0, 1, open_cl, window * count, optimization_type, batch)) return false;
The next step is to create a loop in which we initialize the layers of the linear module.
uint w = window; for(uint i = 0; i < mlp_layers; i++) { if(!cLinearModel[i].Init(0, i + 2, OpenCL, w, w, mlp[i], count, optimization, iBatch)) return false; cLinearModel[i].SetActivationFunction(LReLU); w = mlp[i]; }
Here it should be remembered that the authors of the Client method propose to apply learning coefficients to the results of the linear module. They have found a rather unusual method for creating learnable multipliers. I decided to replace them with a convolutional layer with the number of filters, window size and convolution stride equal to 1. We add it to the last element (added by us earlier) of the linear module array.
if(!cLinearModel[mlp_layers].Init(0, mlp_layers + 2, OpenCL, 1, 1, 1, w * count, optimization, iBatch)) return false;
There's one more thing here. In the process of normalizing the input data, we convert them to a mean value equal to "0" and a variance of "1". Therefore, the predicted values should also correspond to this distribution. To constrain the predicted values, we use the hyperbolic tangent (tanh) as an activation function.
In a similar way, we initiate the projection layer of the attention block.
cLinearModel[mlp_layers].SetActivationFunction(TANH); if(!cProjection.Init(0, mlp_layers + 3, OpenCL, window, window, w, count, optimization, iBatch)) return false; cProjection.SetActivationFunction(TANH);
As you can see, both output data prediction blocks are activated by the hyperbolic tangent. To ensure correct transmission of the error gradient, we specify a similar activation function for the entire layer.
SetActivationFunction(TANH);
Since we are planning to simply add the values of the two modules, then during the reverse pass we can distribute the error gradient in full across both modules. To eliminate unnecessary data copying operations, we will replace the data buffers storing error gradients in the internal layers.
if(!SetGradient(cProjection.getGradient())) return false; if(!cLinearModel[mlp_layers].SetGradient(Gradient)) return false; //--- return true; }
Do not forget to control operations at every stage. After successful initialization of all nested objects, we return the logical result of the operations to the caller.
After initializing the nested class objects, we move on to organizing the feed-forward pass algorithm in the CNeuronClientOCL::feedForward method. We discussed the basic principles of data transfer when initializing objects. Now let's look at the implementation of the proposed approaches.
In the parameters, the method receives a pointer to the object of the previous neural layer. In the body of the method, we immediately call the feed-forward method of our multi-layer attention block.
bool CNeuronClientOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTransformerEncoder.FeedForward(NeuronOCL)) return false;
After that, we project the forecast values onto the required planning depth.
if(!cProjection.FeedForward(GetPointer(cTransformerEncoder))) return false;
To avoid copying the entire volume of input data to the inner layer, we only copy the pointer to the corresponding data buffer.
if(cInput.getOutputIndex() != NeuronOCL.getOutputIndex())
cInput.getOutput().BufferSet(NeuronOCL.getOutputIndex());
We organize a feed-forward pass loop for the linear module.
uint total = cLinearModel.Size(); CNeuronBaseOCL *neuron = NeuronOCL; for(uint i = 0; i < total; i++) { if(!cLinearModel[i].FeedForward(neuron)) return false; neuron = GetPointer(cLinearModel[i]); }
At this stage we have projections of the forecast values of both modules. The linear module forecasts have already been adjusted for training coefficients. Now we just need to sum add the data from both threads.
if(!SumAndNormilize(neuron.getOutput(), cProjection.getOutput(), Output, 1, false, 0, 0, 0, 0.5 )) return false; //--- return true; }
Similarly, but in reverse order, we implement error gradient propagation through the nested objects up to the previous layer in accordance with their influence on the final result. This is done in the CNeuronClientOCL::calcInputGradients method.
Since we use the substitution of data buffers, the error gradient from the next layer is directly written into the object buffers of both modules. Therefore, we omit the unnecessary operation of distributing the error gradient between Transformer and a linear module. We immediately move on to the distribution of the error gradient through the specified modules. First, we pass the error gradient through the attention block.
bool CNeuronClientOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!cTransformerEncoder.calcHiddenGradients(cProjection.AsObject())) return false; if(!prevLayer.calcHiddenGradients(cTransformerEncoder.AsObject())) return false;
Then we pass it in the backpropagation loop through the linear module.
CNeuronBaseOCL *neuron = NULL; int total = (int)cLinearModel.Size() - 1; for(int i = total; i >= 0; i--) { neuron = (i > 0 ? cLinearModel[i - 1] : cInput).AsObject(); if(!neuron.calcHiddenGradients(cLinearModel[i].AsObject())) return false; }
Note that Transformer writes the error gradient to the previous layer's buffer. The linear model writes it to the buffer of the inner layer.
Before finishing the method, we add the error gradients of both streams.
if(!SumAndNormilize(neuron.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(), 1, false)) return false; //--- return true; }
Other methods of this class are constructed in approximately the same way. We call the relevant methods of the internal objects one by one. Within the framework of this article, we will not dwell on the description of their algorithm in detail. I suggest you familiarize yourself with them. You can find the full code of the class and all its methods in the attachment. The attachment also contains the complete code of all programs used in the article.
2.2 Model architecture
We have created a new class CNeuronClientOCL, which implements the main part of the approaches proposed by the authors of the Client method. However, some requirements of the method need to be implemented directly in the model architecture.
The Client method was proposed to solve timeseries forecasting problems. We will use it in our Encoder.
In the structure of our models, the Encoder is used to prepare a compressed representation of the state of the environment. The Actor model uses this representation to generate the optimal action in a given state based on the learned behavior policy. Obviously, to learn the best possible behavior policy, we need a correct and informative condensed representation of the state of the environment.
The concept of "correct and informative condensed representation of the state of the environment" sounds rather abstract and vague. It is logical to assume that since we are training the Actor's policy to perform optimal actions to generate the maximum possible profit under the conditions of the most probable upcoming price movement, the compressed representation should contain the maximum possible information about the most probable upcoming price movement. In addition, we need to assess the risks and the probability of price movement in the opposite direction. We also need to evaluate the possible magnitude of such movement. In such a paradigm, it seems appropriate to train the Encoder to predict future price movements. Then the hidden state of the Encoder will contain the maximum possible information about the upcoming price movement. Therefore, in the architecture of our Encoder we use the approaches of the Client method.
The architecture of the Encoder is presented in the CreateEncoderDescriptions method. In the parameters, the method receives a pointer to one dynamic array, in which the model architecture will be saved.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
In the body of the method, we check the received pointer and, if necessary, create a new instance of the dynamic array object.
As usual, we feed the model with a "raw" description of the state of the environment. To record the raw data, we create a base layer of the neural network with a size sufficient to accept the raw data.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Here, as before, the layer size is determined by the product of two constants:
- HistoryBars — the depth of the analyzed history of states (bars) of the environment
- BarDescr — the size of the vector describing one bar of the environment state
But there is one thing. Previously, at each iteration, we only fed the model with information about the last closed bar within the price movement. All the necessary depth of the analyzed history was accumulated in the form of Embeddings in the stack of the inner layer of our model. Now, the authors of the Client method, assume that the additional embedding layer distorts the time series information and thus they recommend eliminating it. Therefore, we expand the model's input data layer to feed it with data covering the entire depth of the history being analyzed.
So, we have increased the value of the HistoryBars constant up to 120. This allows you to analyze historical data of the last week on the H1 time frame.
#define HistoryBars 120 //Depth of history
The next layer, as before, is a batch normalization layer, in which the input data is brought into a comparable form by removing statistical information from the time series.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Let's remember the identifier of this layer. Because at the output of the model, we will have to return the statistical information of the timeseries to the forecast values.
When preparing the input data, we can form it as a sequence of data of individual indicators (variables in the context of the Client method). Optionally, we can provide it in the form of a sequence of descriptions of time steps (bars), as was done previously. For the purposes of this article, I decided not to change the input data preparation block. Thus, we can use previously created environment interaction EAs with minimal modifications.
But such an implementation requires installing a data transposition layer, which we will add in the next step.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; prev_count = descr.count = HistoryBars; int prev_wout = descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
After the transpose layer, we add an instance of our new layer - the Client block.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronClientOCL; descr.count = prev_wout; descr.window = prev_count; descr.step = 4; descr.window_out = EmbeddingSize; descr.layers = 5; { int temp[] = {1024, 1024, 1024, NForecast}; ArrayCopy(descr.windows, temp); } if(!encoder.Add(descr)) { delete descr; return false; }
Here, for the size of the sequence being analyzed, we specify the number of variables being analyzed (the BarDescr constant). The size of the vector describing one element of the sequence is equal to the depth of the history we are analyzing (the HistoryBars constant). In the Transformer block, we use 4 attention heads and create 5 such layers.
We will create a linear module from 4 layers: 3 hidden layers of size 1024 and the last layer equal to the planning horizon (the NForecast constant).
Next we perform the inverse transposition of the data.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; prev_count = descr.count = BarDescr; prev_wout = descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
We restore statistical information in them.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; prev_count = descr.count = prev_count * prev_wout; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
I should say a few words about the architecture of the Actor. It is almost entirely copied from the previous article. However, it has one detail that will be explained later.
The architecture of the Actor and Critic models is presented in the CreateDescriptions method. In the method parameters, we receive pointers to 2 dynamic arrays for recording the model architecture.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
In the body of the method, we check the received pointers and, if necessary, create new instances of dynamic array objects.
As before, we feed the Actor model with a description of the current account state and open positions.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Next, we form the account state embedding.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Add 3 successive layers of cross-attention, in which we analyze the dependencies between the current state of the account and the compressed representation of future states of the environment formed by the Encoder.
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } }
According to the idea of the Client method, for the cross-analysis we use the data from the hidden state of the Encoder before re-transposing the data. This allows us to analyze the dependencies of the current account state with the predicted values of individual variables. This is reflected in new values of the desc.units and descr.windows arrays.
Next, as before, comes the decision-making block with stochasticity added to the Actor's policy.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Similar changes affected the Critic model. As you remember, the Actor and Critic models have similar architecture. The difference is that the input of the Critic model is an action vector instead of the account state description. At the output of the model, the action vector is replaced by a reward vector. You can find a full description of the architectural solutions of all the models used in the attachment. The attachment also contains the complete code of all programs used in the article.
Additionally, we have changed the value of the constant pointer to the hidden layer of the Encoder for data extraction.
#define LatentLayer 3
Since we have done much work to coordinate the architectural solutions of the models and change the constants used, we can use previously created EAs for interaction with the environment practically without changes. We just need to recompile them taking into account the changed constants and model architecture. However, this does not refer to model training EAs.
2.3 Forecasting model training EA
The model for forecasting environmental conditions is trained in the "...\Experts\Client\StudyEncoder.mq5" EA. In general, the structure of the EA is borrowed from previous works. We will not consider in detail all its methods. Let's consider only the model training stage performed in the Train method.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
In the body of the method, we first generate a vector of probabilities of choosing trajectories from the experience replay buffer according to their actual profitability. Profitable passes are more likely to be used in the learning process. Thus, we shift the training focus towards trajectories with the highest profitability.
After the preparatory work, we organize the model training loop. Unlike some recent works, here we use a simple loop, rather than the nested loop system used before. This is possible because we do not use recurrent elements (stack of embeddings) in the model architecture.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(i <= 0) { iter--; continue; }
In the body of the loop, we sample the trajectory from the experience replay buffer and the state of the environment on it.
We extract the description of the sampled state of the environment from the experiment replay uffer and transfer the obtained values to the data buffer.
bState.AssignArray(Buffer[tr].States[i].state);
This information is enough to run a feed-forward pass of the Encoder.
//--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Next, we need to prepare a vector of target values. In the context of this work, the planning horizon is much less than the depth of the analyzed history. This greatly simplifies our task of preparing target values. We simply extract from the experience replay buffer a description of the environment state with an indentation of the planning horizon. We also take the first elements from the tensor in the required volume.
//--- Collect target data if(!bState.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!bState.Resize(BarDescr * NForecast)) continue;
If you use a planning horizon greater than the depth of the analyzed history, then collecting target values will require creating a loop over states in the experience replay buffer for the planning horizon.
After preparing the target value tensor, we perform the Encoder backpropagation pass to optimize the parameters of the trained model to minimize the data prediction error.
if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Finally, inform the user about the training progress and move on to the next training iteration.
if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Make sure to control the process of performing operations at every step. After all iterations of model training have been successfully completed, we clear the comments field on the chart.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
Display the model training results in the log. Initiate the EA termination.
2.4 Actor policy training EA
Some edits were also made to the Actor policy training EA "...\Experts\Client\Study.mq5". Again, we focus only on the model training method.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
In the body of the method, we first generate a vector of trajectory selection probabilities and do other preparatory work. In this part, you can see an exact repetition of the algorithm of the previous EA.
Next, we also organize a model training loop in which we sample the trajectory from the experience replay buffer and the state of the environment on it.
We load the selected description of the environment state and perform a feed-forward pass of the Encoder.
bState.AssignArray(Buffer[tr].States[i].state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
This completes the "copying" of the algorithm of the previous EA. After generating a condensed representation of the environment, we first optimize the Critic parameters. Here we first load the Actor's actions performed while interacting with the environment in the given state and execute a feed-forward Critic pass.
//--- Critic bActions.AssignArray(Buffer[tr].States[i].action); if(bActions.GetIndex() >= 0) bActions.BufferWrite(); if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
We then extract from the experience replay buffer the actual reward from the environment received for the given actions of the Actor.
result.Assign(Buffer[tr].States[i + 1].rewards); target.Assign(Buffer[tr].States[i + 2].rewards); result = result - target * DiscFactor; Result.AssignArray(result);
We optimize the Critic's parameters in order to minimize the error in assessing the Actor's actions.
Critic.TrainMode(true); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Next comes the block of the two-step Actor's policy training. Here we first extract the account state description corresponding to the selected environment state and transfer it to the data buffer.
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
After that, we add the timestamp harmonics to the buffer.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Then we perform a feed-forward pass of the Actor to generate the action vector.
//--- Actor if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
As mentioned above, the Actor's policy is trained in 2 steps. We first adjust the Actor's policy to keep its actions within the distribution of our training set. To do this, we minimize the error between the vector of actions generated by the Actor and the actual actions from the experience replay buffer.
if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
In the second step, we adjust the Actor's policy in accordance with the Critic's assessment of the generated actions. Here we first need to evaluate the actions.
if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Then we turn off the Critic learning mode and propagate through it the gradient of the deviation of the action assessment from what is actually possible in a given state.
Critic.TrainMode(false); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer) || !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Here we assume that in the process of learning, the Actor's policy should always improve. The reward received must be no worse than what was actually received when interacting with the environment.
After updating the model parameters, we inform the user about the progress of the training process and move on to the next iteration of the loop.
if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Do not forget to control the process of operations at every step.
After all iterations of the model training process have been successfully completed, we clear the comments field on the chart.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
We also output information about the training results to the terminal log and initiate EA termination.
Again you can find the complete code of all programs in the attachment.
3. Testing
In this article, we have discussed the Client method for multivariate time series forecasting and implemented our vision of the proposed approaches in MQL5. Now we move on to the final stage of our work - testing the results. At this stage, we will train the models on real historical data of the EURUSD instrument, with the H1 timeframe, for 2023. After that, we will test the results of the trained model in the MetaTrader 5 Strategy Tester using historical data from January 2024, while using the same symbol and timeframe which we used to train the models.
Note that the elimination of the Embedding layer and the increase in the number of bars describing 1 state of the environment do not allow us to use the training dataset from the previous article. Therefore, we have to collect a new dataset. Anyway, this process completely repeats the algorithm described in the previous article, so I will not provide the details now.
After collecting the initial training data, we first train the timeseries forecasting model. Here comes the first unpleasant surprise: the quality of forecasting turned out to be quite low. Probably the large amount of noise in the input data data and the model's increased attention to timeseries details worsened the result.
But we don't give up and continue the experiment. Let's see if the Actor model can adapt to such forecasts. We execute several iterations to train the Actor and update the training dataset. But alas. We couldn't train a model capable of generating profit on the training, and obviously testing, datasets. The balance line was moving downwards. The profit factor value was around 0.5.
Perhaps, this result is typical only for our implementation. But the fact remains. The implemented model is not able to provide the desired quality of timeseries forecasting in a highly stochastic environment.
Conclusion
In this article, we discussed a rather interesting and complex algorithm called Client, which combines a linear model for studying linear trends and a Transformer model with the analysis of dependencies between individual variables to study nonlinear information. The authors of the method exclude from their model attention between individual states of the environment separated in time. The proposed improved Transformer model also simplifies embedding and positional encoding levels. The Decoder module is replaced by a projection layer, which, according to the authors of the method, significantly increases the efficiency of forecasting. Moreover, the experimental results presented in the cited paper prove that for timeseries forecasting tasks, the analysis of dependencies between variables in Transformer is more important than the analysis of dependencies between individual states of the environment separated by time.
However, the results of our work show that the proposed approaches are not effective in highly stochastic conditions of financial markets.
Please pay attention that this article presents the results of tests of our individual implementation of the proposed approaches. Thus, the results obtained may only be relevant for this implementation. Under other conditions, it is possible that completely opposite results could be obtained.
The purpose of this article is only to familiarize the reader with the Client method and demonstrate one of the options for implementing the proposed approaches. We in no way evaluate the algorithm proposed by the authors. We only try to apply the proposed approaches to solve our problems.
References
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | EA | Example collection EA |
| 2 | ResearchRealORL.mq5 | EA | EA for collecting examples using the Real-ORL method |
| 3 | Study.mq5 | EA | Model training EA |
| 4 | StudyEncoder.mq5 | EA | Encode training EA |
| 5 | Test.mq5 | EA | Model testing EA |
| 6 | Trajectory.mqh | Class library | System state description structure |
| 7 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 8 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/14721
MQL5 Wizard Techniques you should know (Part 36): Q-Learning with Markov Chains
Neural Networks Made Easy (Part 84): Reversible Normalization (RevIN)
Features of Experts Advisors
Creating an MQL5-Telegram Integrated Expert Advisor (Part 4): Modularizing Code Functions for Enhanced Reusability
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Thank you for your hard work!
You have written quite a lot of articles already, your luggage of knowledge is growing faster than I have time to familiarise myself with its product.
Do you plan to write a review article in which you will briefly express your opinion about the methods you have described, share your experience of using this or that method?