Category Theory in MQL5 (Part 8): Monoids

Introduction

In our previous article, on category theory, we uncovered the key concepts of multi-sets, relative sets, and indexed sets and explored their significance in algorithmic trading. Now, in this follow-up, we introduce the concept of monoids. Monoids form an essential foundation in mathematics and computer science, providing a structured approach to modeling operations on sets of elements.

By definition monoids are a collection of 3 things namely a set; a binary operation that takes any two elements of that set and always outputs an element that is also a member of that set; and an identity element that belongs to the set such that when paired with any other member of that set in the afore mentioned binary operation, the output is always the other element that this identity element is paired with. This binary operation is also associative. Said differently, a monoid is a way of combining elements in a set while adhering to predefined rules. Monoids provide a systematic and flexible approach to aggregating and manipulating data.

Formally, a monoid M, with member elements a, b, & c; an identity element e; and binary operation *; may be defined as:

M * M - - > M;                      1

e * a - - > a;                        2

a * e - - > a;                        3

a * (b * c) - - > (a * b) * c     4

So, equation 1 emphasizes the pairing of any 2 members of the set outputs a member of the set. Equations 2 and 3 stress the significance of the identity element in that the output is always the element in the binary operation that is not the identity. And finally, equation 4 highlights associativity of the binary operation *.

Illustration & Methods

To illustrate the possible application of monoids to traders we will consider 5 decisions some or most traders may be faced with before executing trades. These are:

1. The length of the lookback period to consider.
2. The chart time frame to use.
3. The applied price to use.
4. The indicator to select.
5. And whether, given this information, to trade with the range, or the trend.

For each of these decisions we will come up with:

• a set of possible values from which to choose;
•  a binary operation that helps select between any two elements. This operation can be an MQL5 method that is called by another method iteratively through all the sets elements until one selection is made.
• And an index for the identity element of this set. Index because this element will be in a set which is an array.
• The choice of the ideal binary operation which simply chooses between 2 elements will be one of the following:
• The operation that chooses the lesser of the two elements.
•  The operation that chooses the greatest of the two elements being evaluated
•  The operation that chooses from the set, the element closest to the mean of the two elements in the binary operation.
•  And finally, the operation that chooses from the set the element that is furthest from the mean of the two elements in the binary operation.

We are considering 5 decision points of lookback period, timeframe, applied price, indicator, and signal interpretation. Another trader may have different key decision points. It is therefore important to keep in mind this is not a definitive step by step guide but is something that is simply chosen for this article.

When using monoids of category theory to classify data, there are a few precautions that should be undertaken to ensure accurate and meaningful results. Here are a possible list to keep in mind:

1) Have a well-defined Monoid Structure:

You need to ensure that the data you are working with forms a valid monoid structure as per the definition. This means verifying that it satisfies the monoid axioms, such as having an identity element and being associative under the binary operation. Here are three examples of pitfalls that can lead to a poorly defined monoid structure:

Lack of Closure:

If the binary operation used in the monoid does not result in elements that belong to the same set or domain, closure is violated. For example, if you attempt to define a monoid on natural numbers using the subtraction operation, you will encounter elements that are not natural numbers (e.g., subtracting 5 from 3 results in -2, which is not a natural number). An operation strictly speaking is neither an addition, subtraction, multiplication function. It is simply a method with well-defined rules that takes any two elements of the set and returns one element that is a member of that set.

Non-Associativity:

Another pitfall is when the binary operation fails to satisfy the associative property. If elements in your monoid do not combine in an associative manner, it can lead to ambiguous and inconsistent results. For instance, consider a monoid where the operation is multiplication and the elements are matrices. If you have three matrices a, b, and c, then this operation is not associative i.e., (a * b) * c ≠ a * (b * c), thus the monoid structure is compromised.

Lack of Identity Element:

Every monoid must have an identity element, which acts as the neutral element under the binary operation. If the monoid lacks an identity element, it becomes problematic to perform operations with certain elements. For instance, if you define a monoid on real numbers using the division operation, there is no identity element since division by zero is undefined.

On the other hand, here are three examples of proper monoid structures:

Addition of Integers:

The set of integers, equipped with the binary operation of addition (+), forms a monoid. The identity element is 0, and addition is both associative and closed on the set of integers.

Multiplication of Non-zero Rational Numbers:

The set of non-zero rational numbers (fractions), with the binary operation of multiplication (×), forms a monoid. The identity element is 1, and multiplication is associative and closed for non-zero rational numbers.

String Concatenation:

The set of strings, with the binary operation of concatenation, forms a monoid. The identity element is the empty string (""), and concatenation is associative and closed for strings.

These examples demonstrate well-defined monoid structures that satisfy the necessary properties and can be effectively used for classification purposes. Bottom of Form

2) Semantics and Interpretability:

Understand the semantics of the monoid operation and its relation to your data. Consider whether the resulting classifications align with the intended interpretations and make sense in the context of your problem domain. These 5 examples try to illustrate this:

Word Frequency Classification:

Suppose you are using monoids to classify company quarterly guidance from call transcript based on word frequency. While the monoid operation could simply involve summing up word counts, the interpretability of the resulting classifications would need to considered carefully as it depends on the semantics assigned to different frequency ranges. For instance, you might interpret documents with high word frequencies as being more focused on a specific topic, while low frequencies of specific words might indicate broader or more diverse content. What you do not want to do is focus only on the total wordcount and use it as a basis in your key monoid operations.

Sentiment Analysis:

Let's say you're using a monoid to classify text sentiment. The monoid operation could perform better by aggregating sentiment scores from individual words or sentences. Let's consider an example. Suppose you have a set of customer reviews for a product and you want to classify them into three sentiment categories: positive, neutral, and negative. You decide to use a monoid approach where the monoid operation involves aggregating sentiment scores from individual sentences within each review. In this example, you assign sentiment scores ranging from -1 to 1, where -1 represents highly negative sentiment, 0 represents neutral sentiment, and 1 represents highly positive sentiment. The monoid operation would then do a simple summation of the sentiment scores. Now, let's consider a customer review:

Review: "The product is good. However, the customer service was subpar."

The proper way to classify this, would be to split it into individual sentences and assign sentiment scores to each sentence:

Sentence 1: "The product is good." - Sentiment Score: 0.8 (positive)

Sentence 2: "However, the customer service was subpar." - Sentiment Score: -0.7 (negative)

To then obtain the overall sentiment score, for the review, we apply the monoid operation, which in this case is summation:

Overall Sentiment Score = 0.8 + (-0.7) = 0.1

Based on the semantics assigned to the sentiment score ranges, you interpret the overall sentiment score of 0.1 as a slightly positive sentiment. Therefore, you classify this review as "neutral" or "slightly positive" based on the monoid classification. What you do not want to do is consider both sentences as one and assign an anecdotal score because the word ‘good’ is present. It would be good practice to consider the details.

Image Classification:

A monoid to classify images based on visual features like color, texture, or shape would involve combining these features, and the interpretability of these combined features which results in classifications will depend on how you map them into their intended or meaningful categories. The semantics assigned to different combinations of features can greatly influence how you understand the classification results.

Consider this illustration to show the importance of semantics and interpretability in image classification using monoids. Suppose you are using a monoid approach to classify images into two categories: "Dog" and "Cat" (for traders this could be substituted for say bullish and bearish head and shoulder patterns but the principle remains the same) based on visual features. The monoid operation would involve combining color and texture features read from the images. For our purposes, if we assume that you have two key visual features: "Fur Color" and "Texture Complexity." Fur color can be classified as either "Light" or "Dark," while texture complexity can be classified as either "Simple" or "Complex." Now, let's consider two images.

Let Image 1 have a white cat with simple fur texture, meaning:

• Fur Color: Light
• Texture Complexity: Simple
• And Let Image 2 have a black dog with complex fur texture, implying:
• Fur Color: Dark
• Texture Complexity: Complex

To classify these images using the monoid approach, you combine the visual features according to the monoid operation (e.g., concatenation, summation, etc.):

For Image 1: "Light" + "Simple" = "LightSimple"

For Image 2: "Dark" + "Complex" = "DarkComplex"

Now, here comes the crucial part that is the semantics and interpretability. You need to assign meaning to the combined features in order to map them back to meaningful categories. In our case since we are using an overly simple example:

"LightSimple" could be interpreted as a "Cat" category because light fur color and simple texture are common features of cats.

"DarkComplex" could be interpreted as a "Dog" category since dark fur color and complex texture are often associated with dogs.

By assigning appropriate semantics and interpretations to the combined features, you can classify Image 1 as a "Cat" and Image 2 as a "Dog" correctly.

Customer Segmentation:

Suppose you are using monoids to segment customers based on their purchasing behavior. The monoid operation might involve aggregating transaction data or customer attributes. However, the interpretability of the resulting segments relies on how you interpret and label these segments. For example, you might assign labels such as "high-value customers" or "churn-prone customers" based on the semantics and domain knowledge.

Time Series Classification:

Consider using monoids to classify time series data, such as stock market trends. The monoid operation could involve combining various features like price, volume, and volatility. However, the interpretability of the classifications depends on how you define the semantics of the resulting combinations in relation to market conditions. Different interpretations can lead to distinct insights and decision-making implications.

In all these examples, the semantics assigned to the monoid operation and the resulting classifications are crucial for meaningful interpretation and decision-making. Careful consideration of these semantics ensures that the resulting classifications align with the desired interpretations and enable effective analysis and understanding of the data.

3) Data Preprocessing:

This is important for quality control purposes on the data before it is classified with monoids. It would be appropriate to preprocess the data to ensure compatibility with the monoid structure. For instance, all operation function outputs should be definitive members of the monoid set and not floating data with multiple decimal points that on rounding could be ambiguous. Achieving this may be done by normalizing data (regularization), or transforming it into a suitable format for the monoid operation. But also, the handling missing values needs to addressed for better overall consistency of your trading system.

4) Homogeneity of Data:

Ensure that the data you are classifying possesses a certain degree of homogeneity within each category. For example, at the indicator selection stage, the set monoid we will use should have both indicators with consistent and comparable values or weighting. Given that we are using the RSI oscillator and Bollinger Bands this is clearly not the case by default. We will however normalize one of them to ensure both are comparable and homogeneous. Monoids work best when applied to data that exhibits similar characteristics within each class.

5) Cardinality of Categories:

Consider the cardinality or number of distinct categories that can be formed using the monoid. If the number of resulting categories is too high or too low, it may affect the usefulness of the classification or the interpretability of the results.

Let's illustrate the impact of data cardinality of categories with an example:

Suppose you are working on a classification task to predict direction of a forex pair based on the sentiment of calendar news events, and you have a dataset with a target variable "Sentiment" that can take three possible values: "above expectation," "matched expectation," and "below expectation."

Here's an example dataset:

Review	Sentiment
Fed manufacturing Production m/m	below
GDT Price Index	matched
Business Inventories m/m	above
NAHB Housing Market Index	below

In this example, you can observe that the "Sentiment" variable has three categories: "Above," "Matched," and "Below." The cardinality refers to the number of distinct categories in a variable.

The cardinality of the "Sentiment" variable in this dataset is 3 because it has three unique categories.

The data cardinality of categories can have implications for classification tasks. Let's consider two scenarios:

Scenario 1:

Here we have an Imbalanced Data Cardinality leading to an imbalanced dataset where the "Above" sentiment category has a significantly larger number of samples compared to the "Matched" and "Below" categories. For instance, let's assume 80% of the samples are labeled as "Above," while 10% are "Matched" and 10% are "Below."

In this scenario, the imbalanced data cardinality can lead to biases in the classification model. The model might become biased towards predicting the majority class ("Above") more frequently, while struggling to accurately predict the minority classes ("Matched" and "Below"). This can result in lower precision and recall for the minority classes, impacting the overall performance and interpretability of the classification model.

Scenario 2:

In this case, rather than attributing string values to our monoid set elements as was the case above, we use floating point data to more precisely weight and describe each element in the monoid set. This also implies we have unbound cardinality meaning there is no set number of possible weights/ values for each of the set elements as we did in scenario 1.

6) Scalability:

You would need to assess the scalability of the monoid classification especially when handling large datasets. Depending on the computational complexity, it may be necessary to consider alternative techniques or optimizations to handle significant amounts of data efficiently. One approach when dealing with large datasets is to do feature engineering. Monoid homomorphisms can be used in feature engineering for a variety of tasks. One such of these could be public company valuation.

The homomorphisms could transform input features into a new feature space with more incisive predictive power for valuation models. Let’s consider an example if you have a dataset containing various financial metrics such as revenue, earnings, assets, and liabilities for a set of public companies.

One common approach is to use monoid homomorphisms to derive and focus on key financial ratios that are widely used in valuation models. For example, you can define a homomorphism that maps the revenue monoid set to a new normalized monoid set representing the revenue growth rate. This transformation will clearly reduce your data requirements making your monoids more scalable because a lot of companies listed independently in the revenue monoid set will share the same revenue growth rate values in the codomain.

Similarly, you can use a monoid homomorphism to map the earnings monoid to a monoid representing the earnings per share (EPS). EPS is a widely used valuation metric that indicates a company's profitability on a per-share basis. And there are many other crucial ratios that can come in handy, all aiming towards the same goal of keeping your monoid classification model scalable.

On the flip side you want to minimize the reliance on distributed computing frameworks, such as Apache Hadoop or Apache Spark, to process the data in parallel across multiple nodes in a cluster. These approaches allow you to distribute the workload and accelerate the processing time, making it possible to handle large datasets however they will come at significant downstream costs. ‘Downstream’ because all the problems they are trying to solve could have been handled more tactfully at the monoid-design level in the first place.

7) Generalizability:

You would have to evaluate the generalizability of the classification results using new and unseen data. The monoid-based classification methods should provide a reliable and consistent categorization across different datasets and contexts.

Supposing you are developing monoid-based classification for predicting creditworthiness of loan applicants. Your dataset would contain historical loan data, such as income, credit score, debt-to-income ratio, and employment history, and so on.

In order to evaluate the generalizability of the end classification results, you would have to assess how well the model performs on new, unseen data. For example, after training the model on a dataset from a specific region or time period, you would test it on a separate dataset of a different region or time period. If the model shows consistent and reliable categorization performance across this and other diverse datasets, it would indicate good generalizability.

In achieving generalizability in monoid-based classification methods, potential pitfalls include overfitting, data bias, and feature selection bias. To explain, overfitting is when the monoid operation function (for example) becomes too specific to the training data, leading to poor performance on new data. Conversely data bias can happen if the training dataset is not representative of the broader population, thus leading to a biased classification. With feature selection bias, the selection of features that do not capture the relevant information for the given context, will affect the generalizability of the model.

8) Evaluation Metrics:

Define appropriate evaluation metrics to assess the quality and effectiveness of the monoid classification. These metrics should align with your specific problem and goals, taking into account factors such as accuracy, precision, recall, or F1-score.

9) Overfitting and Underfitting:

Guard against overfitting or underfitting of the monoid classification model. Apply techniques such as cross-validation, regularization, or early stopping to prevent these issues and promote model generalization.

10) Interpretability and Explainability:

Consider the interpretability and explainability of the resulting classifications. Monoids can provide powerful classification capabilities, but it is important to understand how the classification decisions are made and be able to explain them in a meaningful way.

Implementation

Lookback Period:

A monoid domain of 8 integers numbered 1 to 8 will be used to represent the options for available lookback periods. One period unit will be equivalent to 4 and our testing timeframe will be fixed at one-hour, even though our analysis timeframes will vary as covered in the next section. On each new bar we will need to select a period. Our unit of measure for each will be the relative percentage size of the move in that period when compared to an equal length previous period. So, for instance if the price change in points over period 1 (4 bars) was A, and that in the one period before it was B, then the weighting or value of period 1 would be given by the formula below:

= ABS(A)/(ABS(A) + ABS(B))

Where ABS () function represents the absolute value. This formula is checked for zero divide by ensuring the minimum of the denominator is at least a point in size of the security being considered.

Our monoid operation and identity element will be selected from optimization on the following the methods at the start of the article.

Timeframe:

The monoid set for timeframe will have 8 timeframe periods namely:

• PERIOD_H1
• PERIOD_H2
• PERIOD_H3,
• PERIOD_H4,
• PERIOD_H6,
• PERIOD_H8,
• PERIOD_H12,
• PERIOD_D1

The weighting and value assignment of each of these timeframes will follow the same pattern above in lookback period meaning we will compare percentage changes in close price based on prior price bar changes in the respective timeframe.

Applied price:

The applied price set monoid will have 4 possible applied prices to choose from:

• MODE_MEDIAN ((High + Low) / 2)
• MODE_TYPICAL ((High + Low + Close) / 3)
• MODE_OPEN
• MODE_CLOSE

The weighting and value assignment here will vary from what we have above. In this case we’ll use the standard deviation of each applied price over the period selected in look back period to determine the weighting or value of each applied price. Operation and identity index selection will be the same as above.

Indicator:

The monoid set for indicator selection will have only two choices namely:

• RSI Oscillator
• Bollinger Bands Envelopes

The RSI oscillator is normalized to the range 0 to 100 but the Bollinger Bands indicator is not only not normalized, it features multiple buffer streams. In order to normalize the Bollinger Bands and make it comparable to the RSI oscillator we’ll take the difference between the current price and the baseline band C, and divide it by the size of the gap between the upper bands and the lower bands, D. So, our value for the bands will first look like this:

= C/(ABS(C) + ABS(D))

As before this value will be checked for zero divides. This value though can be negative and it tends to the decimal value 1.0. In order to normalize these two aspects and have it in the range 0 – 100 like RSI, we add 1.0 to ensure it is always positive and then multiply the sum by 50.0 to ensure it is in the range 0 – 100. So, our values that will now range from 0 – 100 for both RSI and Bollinger Bands will represent our weighting and the operator function and element index will be selected as mentioned in the methods above.

Decision:

For this last and final monoid, our set will also have only two choices. These are:

• Trade with the trend
• Trade with the range

To quantify these two elements we’ll consider, over the selected lookback period, the amount of price points a security pulls back counter to its eventual trend at the end of the period, as a percentage of this periods total price range. This is bound to be a decimal value from 0.0 – 1.0. It will directly measure the weight of trading with the range meaning trading with the trend will be this value subtracted from 1.0. Operation method and index selection is as above.

This is how we would implement our monoid decisions as an instance of the inbuilt expert trailing class

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_8(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<8;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_4(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<4;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            /*printf(__FUNCSIG__+
               " values size: "+IntegerToString(ArraySize(Values))+
               " in indices size: "+IntegerToString(ArraySize(InputIndices))+
               " in indices index: "+IntegerToString(InputIndices[i])
               );*/
               
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_2(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<2;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(m_lookback_operation==OP_LEAST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_MOST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_CLOSEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
      else if(m_lookback_operation==OP_FURTHEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback()
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      for(int i=0;i<8;i++)
      {
         int _period=(__LOOKBACKS[i]*PeriodSeconds(PERIOD_H4))/PeriodSeconds(m_period);
         double _value=fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))/(fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))+fabs(m_close.GetData(_x+_period)-m_close.GetData(_x+_period+_period)));
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_lookback.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_lookback,m_lookback_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_lookback,m_lookback_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_lookback,m_lookback_operation,_v2,_i2_out,_i3_out);
      
      return(4*__LOOKBACKS[_i3_out[0]]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(void)
   {
      for(int i=0;i<8;i++)
      {
         ResetLastError();
         double _value=0.0;
         double _buffer[];ArrayResize(_buffer,3);ArrayInitialize(_buffer,0.0);ArraySetAsSeries(_buffer,true);
         if(CopyClose(m_symbol.Name(),__TIMEFRAMES[i],0,3,_buffer)>=3)
         {
            _value=fabs(_buffer[0]-_buffer[1])/(fabs(_buffer[0]-_buffer[1])+fabs(_buffer[1]-_buffer[2]));
         }
         else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); }
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_timeframe.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_timeframe,m_timeframe_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_timeframe,m_timeframe_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_timeframe,m_timeframe_operation,_v2,_i2_out,_i3_out);
      
      return(__TIMEFRAMES[_i3_out[0]]);
   }

So the 'Operate_8' function pairs up 8 elements in the monoid set and comes up with a selection of 4, one from each pair. Similarly 'Operate_4' function pairs up the 4 elements got from 'Operate_8' and comes up with a selection of 2, again one from each pair and finally 'Operate_2' function pairs up these two elements from 'Operate_4' to come up with the wining element.

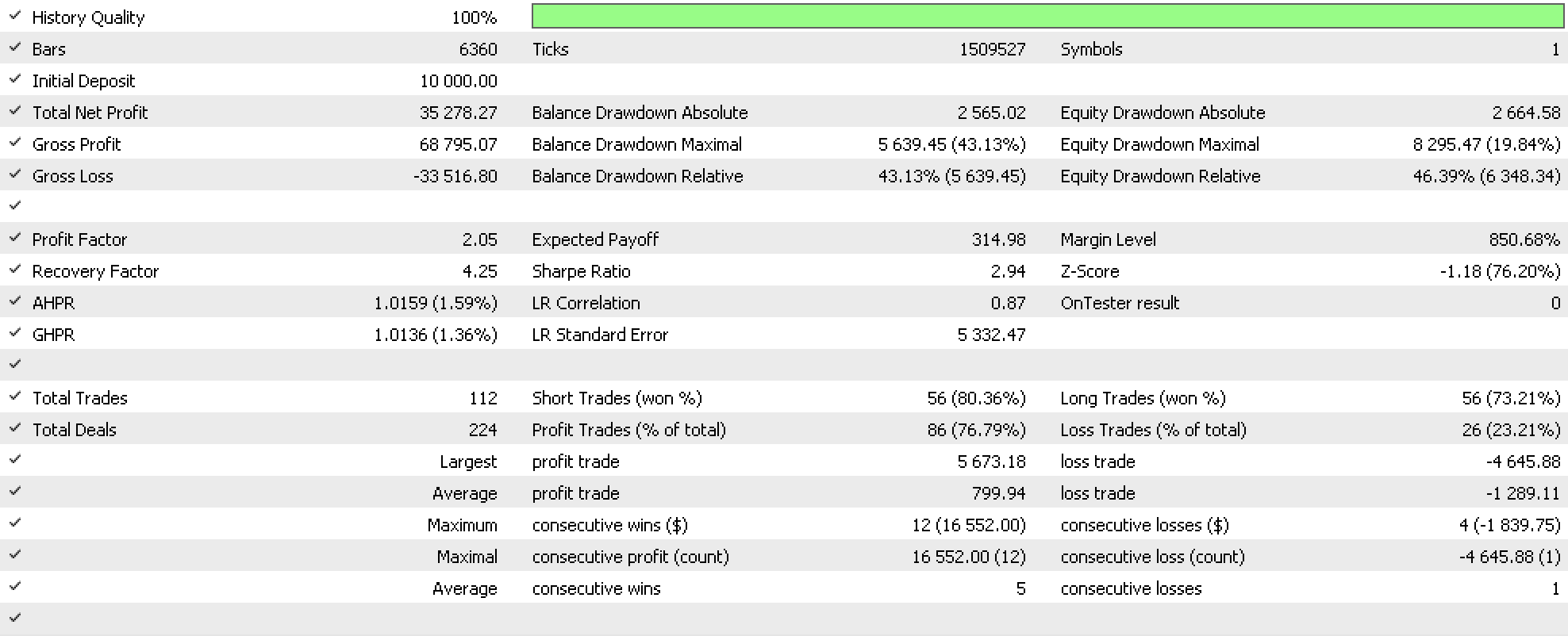
If we run tests with this system on determining the ideal trailing stop for open positions, as part of an expert advisor that uses the inbuilt RSI signal from the expert signal class and fixed money management from the expert money class, we get the report below.

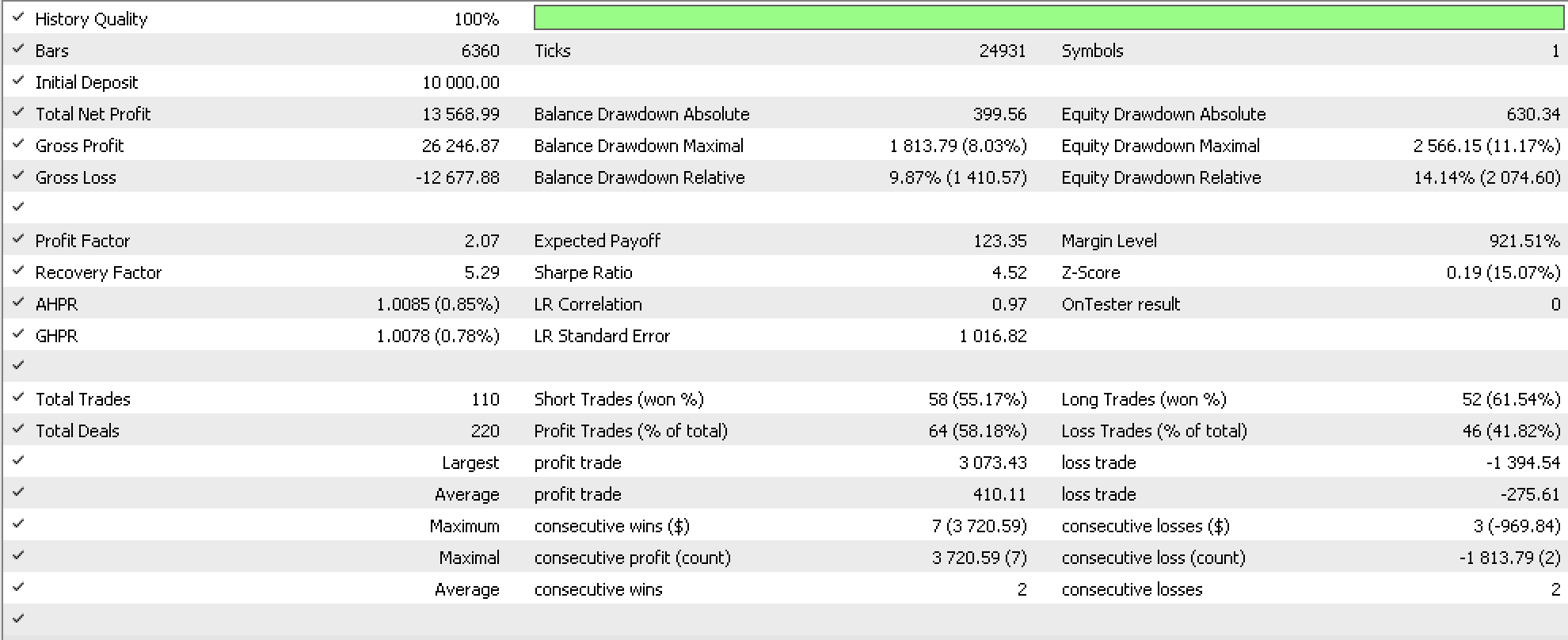
As a control a similar run on a very similar expert advisor whose only difference from our own is the trailing system which is the inbuilt trailing stop based on moving average, yields the report below.

Conclusion

We have looked at monoids as a means of data classification and therefore a decision block. Attention has been drawn to the importance of having well-formed monoids that are generalizable and not curve fitted, as well as other precautions that could be key in realizing a well-rounded system. We have also looked at a possible implementation of this system that adjusts stop loss positions by working as an instance of the inbuilt expert-trailing class.