
MQL5 中的范畴论 (第 8 部分):幺半群(Monoids)
概述
在上一篇文章中,关于范畴论,我们揭示了多集、相对集和索引集的关键概念,并探讨了它们在算法交易中的重要性。 现在,在后续中,我们引入了幺半群(monoids)的概念。 幺半群形成了数学和计算机科学的重要根基,为元素集的建模运算提供了一种结构化的方式。
根据定义,幺半群是 3 个事物的合集,即:一个集合;一个二元运算,它采用该集合的任意两个元素,并始终输出一个元素,该元素也是该集合的成员;以及属于该集合的幺元,这样,当在上述二元运算中与该集合的任何其它成员配对时,输出始终是与该幺元配对的其它元素。 此二元运算也是关联的。 换言之,幺半群是一种在遵守预定义规则的同时,结合集合中元素的方式。 幺半群为聚合和操作数据提供了一种系统而灵活的方式。
形式上,一个幺半群 M,拥有成员元素 a、b 和 c;一个幺元 e;和二元运算 *;可定义为:
M * M - - > M; 1
e * a - - > a; 2
a * e - - > a; 3
a * (b * c) - - > (a * b) * c 4
如此,等式 1 强调集合的任意 2 个成员的配对,其输出变成集合的一个成员。 等式 2 和 3 则强调幺元的重要性,因为输出始终是二元运算中的元素,其不是幺元。 最后,等式 4 高亮显示二元运算 * 的关联性。
描绘 & 方法
为了描绘幺半群在交易者中的可能应用,我们要考虑 5 个决定,都是某些或大多数交易者在执行交易之前也许会面临的。 这些是:
- 要考虑回溯期的长度。
- 要使用的图表时间帧。
- 要使用的应用价格。
- 要选择的指标。
- 以及,这些给定信息,是否采取区间或趋势进行交易。
对于这些决定中的每一个,我们将跟进:
- 一组可供选择的可能数值;
- 一种二元运算,可在任意两个元素之间进行选择。 此运算可以是一个 MQL5 方法,由另一个方法调用,迭代所有集合元素,直到做出一个选择。
- 以及此集合内幺元的索引。 索引,因为此元素所位于的集合是一个数组。
- 理想的二元运算(只需在 2 个元素之间进行选择)的选择将是以下选项之一:
- 选择两个元素中较小元素的运算。
- 从两个正在评估的元素中选择最大元素的运算
- 从集合中进行选择的运算,即二元运算中最接近两个元素中值的元素。
- 最后,从集合中选择距二元运算两个元素的中值最远元素的运算。
我们正在研究 5 个决策要点:回溯期、时间帧、应用价格、指标和信号解释。 其他的交易者也许会有不同的关键决策点。 即如此,重要的是要留意,这并非一个明确的分步指南,而只是本文的简单选择。
当运用范畴论的幺半群进行数据分类时,应采取一些预防措施来确保准确和有意义的结果。 以下是需要留意的可能列表:
1) 具有定义明确的幺半群结构:
您需要确保正在使用的数据是根据定义形成的有效幺半群结构。 这意味着验证它是否满足幺半群公理,譬如拥有幺元元素,并在二元运算下具有关联性。 以下是三个陷阱示例,可能会导致定义不明确的幺半群结构:
缺乏封闭:
如果幺半群中所用的二元运算不会得到属于同一集合或域的元素,则违反封闭。 例如,如果您尝试基于自然数使用减法运算定义幺半群,您将遇到非自然数的元素(例如,从 3 中减去 5 会得到 -2,这不是自然数)。 严格来说,运算既不是加法、减法、乘法函数。 它只是一个具有明确定义规则的方法,它接受集合的任意两个元素,并返回一个元素,该元素是该集合的成员。
非关联性:
另一个缺陷是当二元运算无法满足关联属性时。 如果幺半群中的元素没有以关联方式组合,则可能导致含糊不清和不一致的结果。 举例,考虑一个幺半群,其中运算是乘法,元素是矩阵。 如果您有三个矩阵 a、b 和 c,那么这个运算不是关联的,即 (a * b) * c ≠ a * (b * c),因此幺半群结构会受到损害。
缺少幺元:
每个幺半群都必须有一个幺元,该元素在二元运算下充当中性元素。 如果幺半群缺少幺元,则依据某些元素执行运算会变得有问题。 举例,如果基于实数采用除法运算定义幺半群,则没有幺元,因为除以零是无定义的。
另一方面,这里有三个相应的幺半群结构的例子:
整数加法:
整数集合,等价于加法(+)的二元运算,形成一个幺半群。 幺元为 0,在整数集合上,加法既是关联又是封闭的。
非零有理数的乘法:
非零有理数(分数)的集合,配合乘法(×)的二元运算,形成一个幺半群。 幺元为 1,对于非零有理数,乘法是关联和封闭的。
字符串串联:
字符串集合,配合串联的二元运算,形成一个幺半群。 幺元是空字符串(“”),对于字符串串联是关联和封闭的。
这些示例演示了定义明确的幺半群结构,这些结构满足必要的属性,可以有效地用于分类目的。 形式底部
2) 语义和可解释性:
了解幺半群运算的语义,及其与数据的关系。 研究分类成果是否与预期的解释一致,以及在问题域的语境中是否有意义。 这 5 个例子尝试描绘这一点:
词频分类:
假设您正在利用幺半群从通话记录中依据词频为公司季度指导进行分类。 虽然幺半群运算能简单地涉及对字数求和,但要仔细考虑所得分类的可解释性,因为它取决于分配给不同频率范围的语义。 举例,您可以将含有高词频的文档解释为更专注于特定主题,而特定词的低频可能表示内容更广泛或更多样化。 您不想只关注总体词量,并将其用作关键幺半群运算的基础。
情绪分析:
假设您正在利用幺半群进行文字情绪分类。 通过聚合单个词汇或句子的情感分数,幺半群运算可以执行得更好。 我们研究一个例子。 假设您有一组针对产品的客户评价,并且希望将它们分为三个情绪类别:正面、中性和负面。 您决定运用幺半群方式,其中幺半群运算涉及聚合每条评论中单个句子的情绪分数。 在此示例中,您分配的情绪分数范围为 -1 到 1,其中 -1 表示高度负面情绪,0 表示中性情绪,1 表示高度正面情绪。 然后,幺半群运算将对情绪分数进行简单的求和。 现在,我们来研究一下客户评价:
评论:“产品不错。 但是,客户服务不尽如人意。”
对此进行分类的正确方式,是将其拆分为单独的句子,并为每个句子分配情感分数:
第 1 句:“产品不错。” — 情绪得分:0.8(正面)
第 2 句:“但是,客户服务不尽如人意。” — 情绪得分:-0.7(负面)
然后,为了得到总体情绪分数,对于评价,我们应用幺半群运算,在本例中为求和:
总体情绪得分 = 0.8 + (-0.7) = 0.1
根据分配给情绪分数范围的语义,将总体情绪分数 0.1 解释为略微正面的情绪。 因此,您根据幺半群分类将此评价归类为 “中性” 或 “略微正面”。 您不想只是将两个句子视为一个,并分配一个传闻的分数,因为出现了 “不错” 这个词。 考虑细节将是一种很好的实践。
图像分类:
根据颜色、纹理或形状等视觉特征对图像进行分类的幺半群将涉及组合这些特征,而这些组合特征(分类成果)的可解释性,将取决于您如何将它们映射到其预期或有意义的分类之中。 分配给不同特征组合的语义会极大地影响对分类结果的理解方式。
请考虑此描绘,以便展示语义和可解释性在使用幺半群进行图像分类中的重要性。 假设您使用幺半群方式根据视觉特征将图像分为两类:“狗” 和 “猫”(对于交易者来说,这可以代替看涨和看跌的头肩形态,但原理保持不变)。 幺半群运算将涉及组合从图像中读取的颜色和纹理特征。 就我们的目的而言,如果我们假设您有两个关键的视觉特征:“毛皮颜色” 和 “纹理复杂性”。毛皮颜色可分为“浅色” 或 “深色”,而纹理复杂性可分为“简单” 或 “复杂”。现在,我们研究两个图像。
图像 1 有一只皮毛质地简单的白猫,意思是:
- 毛皮颜色:浅色
- 纹理复杂度:简单
- 且图像· 2 有一只毛皮质地复杂的黑狗,寓意:
- 毛皮颜色:深色
- 纹理复杂度:复杂
为了使用幺半群方式为这些图像进行分类,请根据幺半群运算(例如,串联、求和、等等)组合视觉特征:
对于图像 1:“浅色” + “简单” = “浅色简单”
对于图像 2:“深色” + “复杂” = “深色复杂”
现在,关键部分是语义和可解释性。 您需要为组合特征分配寓意,以便将它们映射到有意义的类别。 在我们的例子中,鉴于我们所用是一个过于简单的例子:
“浅色简单” 可以解释为“猫”类别,因为浅色皮毛和简单的纹理是猫的共同特征。
“深色复杂” 可以解释为“狗”类别,因为深色毛皮颜色和复杂的纹理通常与狗有关。
通过为组合特征分配相应的语义和解释,您就可以正确地将图像 1 分类为 “猫”,将图像 2 分类为 “狗”。
客户细分:
假设您正在运用幺半群基于客户的购买行为对客户进行细分。 幺半群运算可能涉及聚合交易数据或客户属性。 不过,生成的可解释性片段取决于您如何解释和标记这些片段。 例如,您可以根据语义和领域知识分配 “高价值客户” 或 “易流失客户” 等标签。
时间序列分类:
研究运用幺半群对时间序列数据进行分类,譬如股票市场趋势。 幺半群运算可能涉及组合各种特征,如价格、交易量和波动性。 然而,分类的可解释性取决于您如何定义与市场条件相关的组合结果的语义。 不同的解释可以导致不同的见解,并影响决策制定。
在所有这些示例中,分配给幺半群运算的语义,和由此产生的分类,对于有意义的解释和制定决策至关重要。 仔细考虑这些语义,可确保生成的分类与所需的解释保持一致,并能够对数据进行有效的分析和理解。
3) 数据预处理:
出于品控目的,在运用幺半群为数据归类之前,这一步非常重要。 数据预处理与确保幺半群结构的兼容性是相对应的。 举例,所有运算函数输出都应该是幺半群集的确定成员,且不是小数点后带有多位数字的浮点数据,这些浮点数经舍入时可能含义不清。 可以通过规范化数据(常规化)或将其转换为适合幺半群运算的格式来达成这一点。 但还需要解决处理数值缺失的问题,从而提高交易系统的整体一致性。
4) 数据的同质性:
确保要分类的数据在每个类别中都具有一定程度的同质性。 例如,在指标选择阶段,我们将用到的幺半群集合应含有一致性、且具有可比值或权重的两个指标。 我们给出的是 RSI 振荡器和布林带,默认情况下显然不限于这种案例。 不过,我们将对其中之一进行常规化,从而确保两者具有可比性和同质性。 当所应用数据在每个类中都表现出相似特征时,幺半群工作效果最佳。
5) 类别的基数:
研究可运用幺半群来形成不同类别的基数或数量。 如果生成的类别数量过高或过低,可能会影响分类的实用性,或成果的可解释性。
我们通过一个例子来概括类别的基数会产生的影响:
假设您正工作于一项分类任务,基于日历新闻事件的情绪,预测外汇对的方向,并且您有一套数据集包含目标变量 “Sentiment”,该变量可以取三个可能的值:“高于预期”、“符预期”、和 “低于预期”。
下面是一个示例数据集:
| 审评 | 情绪 |
|---|---|
| 美联储制造业生产月率(月度) | 低于 |
| GDT 价格指数 | 符合 |
| 企业库存月率(月度) | 高于 |
| NAHB 住房市场指数 | 低于 |
在此示例中,您能观察到 “Sentiment” 变量有三个类别:“高于”、“符合” 和 “低于”。基数是指变量中不同类别的数量。
此数据集中 “Sentiment” 变量的基数为 3,因为它拥有三个独有类别。
类别的数据基数能对分类任务产生影响。 我们来研究两种场景:
场景 1:
此处,我们有一个不平衡的数据基数,导致一个不平衡的数据集,与 “符合” 和 “低于” 类别相比,“高于” 情绪类别的样本数量要多得多。 举例,假设 80% 的样本标记为 “高于”,而 10% 标记为 “符合”,10% 标记为 “低于”。
在这种情况下,不平衡的数据基数可能会导致分类模型中的偏颇。 该模型可能会更频繁地朝向预测多数类(“高于”)偏颇,而难以准确预测次要类(“符合” 和 “低于”)。 这可能会导致次要类的精度和召回率降低,从而影响分类模型的整体性能和可解释性。
场景 2:
在本例中,我们不像上面那样归因于幺半群集元素采用的是字符串值,我们使用浮点数据来更精确地加权和描述幺半群集中的每个元素。 这也意味着我们的基数未绑定,意即每个集合元素没有固定数量的可能权重/值,就像我们在场景 1 中所做的那样。
6) 可伸缩性:
您需要评估幺半群分类的可伸缩性,尤其是在处理大型数据集时。 取决于计算的复杂性,也许需要研究替代技术或优化,从而更有效地处理大量数据。 处理大型数据集合时的一种方式是进行特征工程。 幺半群同态可用于特征工程中的各种任务。 其中之一可能是上市公司估值。
同态可以将输入特征转到新的特征空间,故估值模型具有更敏锐的预测能力。 我们研究一个示例,如果您有一个数据集,其中包含一组上市公司的营收、收益、资产、和负债等各种财务指标。
一种常见的方式是利用幺半群同态来推导和关注估值模型中广泛使用的关键财务比率。 例如,您可以定义一个同态,将营收幺半群集映射到新常规化幺半群集,表示收入增长率。 这种转换将明显降低您的数据需求,令您的幺半群更具可伸缩性,因为在营收幺半群中列出的许多独立公司将在协域中共享相同的营收增长率数值。
与此类似,您可以使用幺半群同态将收益幺半群映射到表示每股收益(EPS)的幺半群。 每股收益是一种广泛使用的估值指标,用于指示公司每股盈利能力。 还有许多其它关键比率可以派上用场,所有这些都同样旨在实现保持幺半群分类模型可伸缩的目标。
在翻开的另一面,您希望最大限度地减少对分布式计算框架(如 Apache Hadoop 或 Apache Spark)的依赖,以便在集群中的多个节点上并行处理数据。 这些方式允许您分配工作负载,并加速处理时间,从而可以处理大型数据集,但它们将遭遇重大的下游成本。 “下游”,因为它们试图解决的所有问题都可以在幺半群设计层面上得到更巧妙的处理。
7) 普适性:
您必须使用新的和不可见的数据来评估分类结果的普适性。 基于幺半群的分类方法应在不同的数据集和上下文中提供可靠且一致的分类。
假设您正在开发基于幺半群的分类来预测贷款申请人的信誉。 数据集将包含历史贷款数据,例如收入、信用评分、债务收入比、和就业历史、诸如此类。
为了评估最终分类结果的普适性,您必须评估模型在新的、不可见数据上的表现。 例如,模型在特定区域或时间段的数据集上经过训练后,您应在不同区域或时间段的分离数据集上对其进行测试。 如果模型在此数据集和其它不同数据集中展现出一致且可靠的分类性能,则表明具有良好的普适性。
在基于幺半群的分类方法中达成普适性时,潜在的缺陷包括过拟合、数据偏颇、和特征选择偏颇。 解释一下,过拟合是指幺半群运算函数(例如)对训练数据过于依赖,导致在新数据上性能不佳。 相反,如果训练数据集不能代表更广泛的人群,则可能会发生数据偏颇,从而导致有偏颇的分类。 对于特征选择偏颇,特征选择不能捕获给定上下文相关信息,这样会影响模型的普适性。
8) 评估指标:
定义适当的评估指标,来评估幺半群分类的品质和有效性。 这些指标应与您的特定问题和目标保持一致,并参考准确性、精确度、召回率、或 F1-分数、等等因素。
9) 过拟合和欠拟合:
防范幺半群分类模型的过拟合或欠拟合。 应用交叉验证、正则化、或提前停止等技术来防止这些问题,并促进模型普适。
10) 可解释性和可解释性:
研究分类成果的可释义性和可解释性。 幺半群可以提供强大的分类能力,但重要的是要了解分类决策是如何制定的,并能够以有意义的方式解释它们。
实现
回溯期:
一个含 8 个整数的幺半群域,编号从 1 到 8,将用于表示可用回溯期的选项。 一个周期单位相当于 4,我们的测试时间帧将固定为 1 小时,即便我们的分析时间帧将有所不同,如下一节所述。 在每根新柱线上,我们需要选择一个周期。 我们对每个周期的计量单位,将取该周期内移动的大小,相较于前一个相同长度周期内移动的大小,计算相对百分比。 故此,举例,如果跨越周期 1(4 根柱线)的点数变化为 A,而之前的一个周期内为变化 B,则周期 1 的权重或百分比值将由以下公式给出:
= ABS(A)/(ABS(A) + ABS(B))
其中 ABS() 函数表示绝对值。 该公式会检查除零错误,以便确保分母的最小值至少为所考虑证券大小的一个点。
本文开头将根据以下方法优化,选择我们的幺半群运算和幺元。
时间帧:
为时间帧的幺半群集合将有 8 个时间帧周期,即:
- PERIOD_H1
- PERIOD_H2
- PERIOD_H3,
- PERIOD_H4,
- PERIOD_H6,
- PERIOD_H8,
- PERIOD_H12,
- PERIOD_D1
在回溯期内,每个时间帧的权重和价值分配将遵循上述相同的范式,这意味着我们将根据相应时间帧内当前柱线与前期柱线的收盘价进行比较后的百分比。
应用价格:
应用价格集幺半群将有 4 个可能的应用价格可供选择:
- MODE_MEDIAN ((最高价 + 最低价) / 2)
- MODE_TYPICAL ((最高价 + 最低价 + 收盘价) / 3)
- MODE_OPEN
- MODE_CLOSE
这里的权重和数值分配将与我们上面的内容有所区别。 在本例中,我们将使用在回溯期中选择的时间段内每个应用价格的标准差来判定每个应用价格的权重或数值。 运算和幺元索引选择将与上述相同。
指标:
用于指标选择的幺半群集合只有两个选项,即:
- RSI 振荡器
- 布林带轨道线
RSI 振荡器常规化到 0 到 100 的范围,但布林带指标不仅没有常规化,而且具有多个缓冲流。 为了令布林带常规化,并令其与 RSI 振荡器相当,我们将取当前价格与基线带 C 之间的差值,并将其除以上轨线和下轨线之间的差距大小 D。如此,我们的波带值首先如下所示:
= C/(ABS(C) + ABS(D))
和以前一样,将检查此值是否会除零。 然而,此值可以是负数,并且趋向于十进制值 1.0。 为了把这两个方面常规化,并令其像 RSI 一样在 0 – 100 范围内,我们加上 1.0 来确保它始终为正,然后将总和乘以 50.0 从而确保它在 0 – 100 范围之内。 因此,对于 RSI 和布林带,我们现在的取值范围为 0 – 100,将代表我们的权重,并且将按照上述方法中所述选择运算符函数和元素索引。
决策:
对于最后一个也是最后一幺半群,我们的集合也只有两个选择。 这些是:
- 顺势交易
- 区段交易
为了量化这两个要素,我们将研究在选定的回溯期内,证券在期末回落与其最终趋势相反的价格点数量,占该时期总价格范围的百分比。 这必须是 0.0 – 1.0 之间的十进制值。 它将直接衡量该区段交易的权重,这意味着趋势交易将从 1.0 中减去该值。 运算方法和索引选择如上。
这就是我们如何实现我们的幺半群决策,作为内置智能系统尾随类的实例
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CTrailingCT::Operate_8(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[]) { for(int i=0;i<8;i++) { m_element.Let(); if(m_lookback.Get(i,m_element)) { if(!m_element.Get(0,Values[InputIndices[i]])) { printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1)); } } else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); } } // if(O==OP_LEAST) { for(int i=0;i<8;i+=2) { if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; } else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; } else { OutputIndices[i/2]=m_lookback.Identity(); } } } else if(O==OP_MOST) { for(int i=0;i<8;i+=2) { if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; } else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; } else { OutputIndices[i/2]=m_lookback.Identity(); } } } else if(O==OP_CLOSEST) { for(int i=0;i<8;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX; for(int ii=0;ii<8;ii++) { if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[i/2]=_index; } } else if(O==OP_FURTHEST) { for(int i=0;i<8;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0; for(int ii=0;ii<8;ii++) { if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[i/2]=_index; } } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CTrailingCT::Operate_4(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[]) { for(int i=0;i<4;i++) { m_element.Let(); if(m_lookback.Get(i,m_element)) { /*printf(__FUNCSIG__+ " values size: "+IntegerToString(ArraySize(Values))+ " in indices size: "+IntegerToString(ArraySize(InputIndices))+ " in indices index: "+IntegerToString(InputIndices[i]) );*/ if(!m_element.Get(0,Values[InputIndices[i]])) { printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1)); } } else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); } } // if(O==OP_LEAST) { for(int i=0;i<4;i+=2) { if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; } else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; } else { OutputIndices[i/2]=m_lookback.Identity(); } } } else if(O==OP_MOST) { for(int i=0;i<4;i+=2) { if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; } else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; } else { OutputIndices[i/2]=m_lookback.Identity(); } } } else if(O==OP_CLOSEST) { for(int i=0;i<4;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX; for(int ii=0;ii<4;ii++) { if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[i/2]=_index; } } else if(O==OP_FURTHEST) { for(int i=0;i<4;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0; for(int ii=0;ii<4;ii++) { if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[i/2]=_index; } } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CTrailingCT::Operate_2(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[]) { for(int i=0;i<2;i++) { m_element.Let(); if(m_lookback.Get(i,m_element)) { if(!m_element.Get(0,Values[InputIndices[i]])) { printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1)); } } else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); } } // if(m_lookback_operation==OP_LEAST) { for(int i=0;i<2;i+=2) { if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i; } else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; } else { OutputIndices[0]=m_lookback.Identity(); } } } else if(m_lookback_operation==OP_MOST) { for(int i=0;i<2;i+=2) { if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i; } else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; } else { OutputIndices[0]=m_lookback.Identity(); } } } else if(m_lookback_operation==OP_CLOSEST) { for(int i=0;i<2;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX; for(int ii=0;ii<2;ii++) { if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[0]=_index; } } else if(m_lookback_operation==OP_FURTHEST) { for(int i=0;i<2;i+=2) { int _index=-1; double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0; for(int ii=0;ii<2;ii++) { if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;} } // if(_index==-1){ _index=m_lookback.Identity(); } OutputIndices[0]=_index; } } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CTrailingCT::GetLookback() { m_close.Refresh(-1); int _x=StartIndex(); for(int i=0;i<8;i++) { int _period=(__LOOKBACKS[i]*PeriodSeconds(PERIOD_H4))/PeriodSeconds(m_period); double _value=fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))/(fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))+fabs(m_close.GetData(_x+_period)-m_close.GetData(_x+_period+_period))); m_element.Let(); m_element.Cardinality(1); if(m_element.Set(0,_value)) { ResetLastError(); if(!m_lookback.Set(i,m_element,true)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } } //r of 8 double _v1[8];ArrayInitialize(_v1,0.0); int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; } int _i1_out[4];ArrayInitialize(_i1_out,-1); Operate_8(m_lookback,m_lookback_operation,_v1,_i1_in,_i1_out); //r of 4 double _v2[8];ArrayInitialize(_v2,0.0); int _i2_out[2];ArrayInitialize(_i2_out,-1); Operate_4(m_lookback,m_lookback_operation,_v2,_i1_out,_i2_out); //r of 2 double _v3[8];ArrayInitialize(_v3,0.0); int _i3_out[1];ArrayInitialize(_i3_out,-1); Operate_2(m_lookback,m_lookback_operation,_v2,_i2_out,_i3_out); return(4*__LOOKBACKS[_i3_out[0]]); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(void) { for(int i=0;i<8;i++) { ResetLastError(); double _value=0.0; double _buffer[];ArrayResize(_buffer,3);ArrayInitialize(_buffer,0.0);ArraySetAsSeries(_buffer,true); if(CopyClose(m_symbol.Name(),__TIMEFRAMES[i],0,3,_buffer)>=3) { _value=fabs(_buffer[0]-_buffer[1])/(fabs(_buffer[0]-_buffer[1])+fabs(_buffer[1]-_buffer[2])); } else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); } m_element.Let(); m_element.Cardinality(1); if(m_element.Set(0,_value)) { ResetLastError(); if(!m_timeframe.Set(i,m_element,true)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } } //r of 8 double _v1[8];ArrayInitialize(_v1,0.0); int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; } int _i1_out[4];ArrayInitialize(_i1_out,-1); Operate_8(m_timeframe,m_timeframe_operation,_v1,_i1_in,_i1_out); //r of 4 double _v2[8];ArrayInitialize(_v2,0.0); int _i2_out[2];ArrayInitialize(_i2_out,-1); Operate_4(m_timeframe,m_timeframe_operation,_v2,_i1_out,_i2_out); //r of 2 double _v3[8];ArrayInitialize(_v3,0.0); int _i3_out[1];ArrayInitialize(_i3_out,-1); Operate_2(m_timeframe,m_timeframe_operation,_v2,_i2_out,_i3_out); return(__TIMEFRAMES[_i3_out[0]]); }
因此,“Operate_8” 函数将幺半群集合中的 8 个元素配对,并得出 4 个选择,每对一个。 同样,“Operate_4” 函数将从 “Operate_8” 中获得的 4 个元素配对,再得出 2 个元素,同样从每对中选择一个,最后 “Operate_2” 函数将这两个元素从 “Operate_4” 配对里再得出获胜元素。
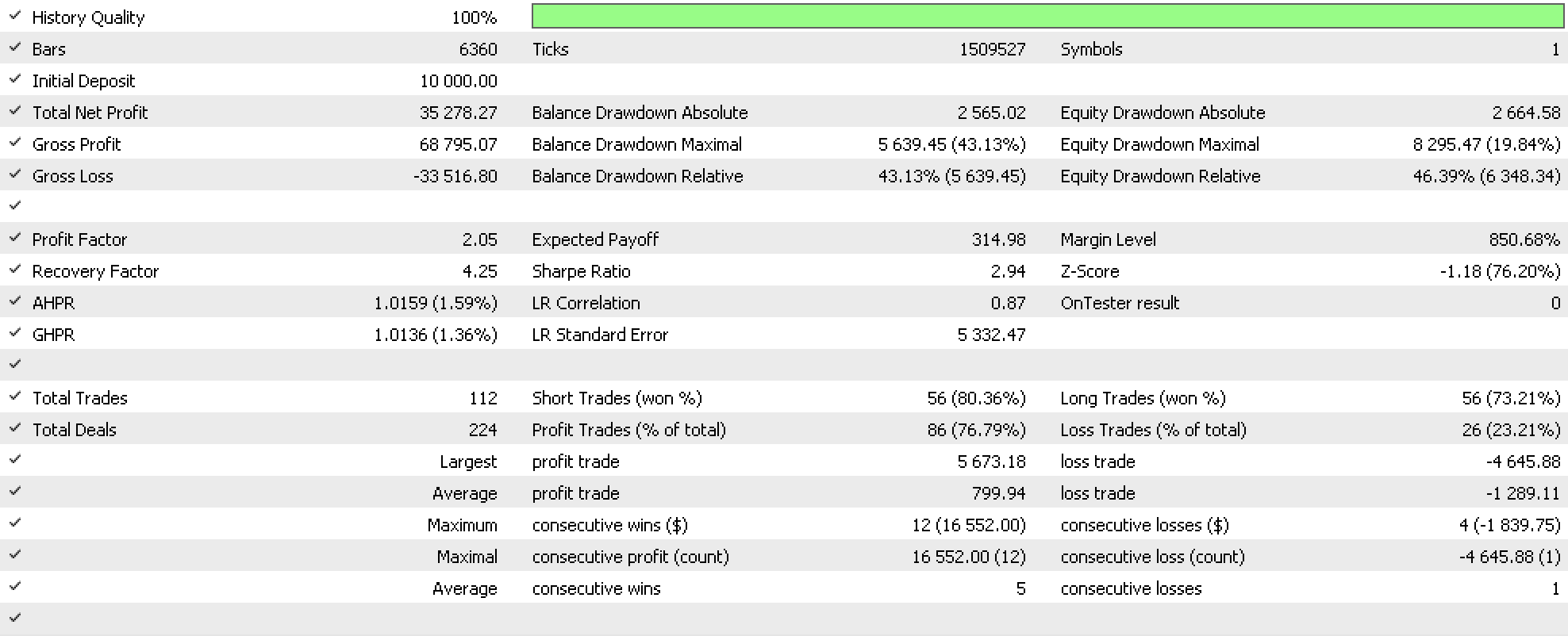
如果我们用此系统进行测试,以便判定持仓的理想尾随停止,作为智能系统的一部分,用到来自智能信号类的内置 RSI 信号,和来自智能资金类的固定资金管理,我们将得到以下报告。
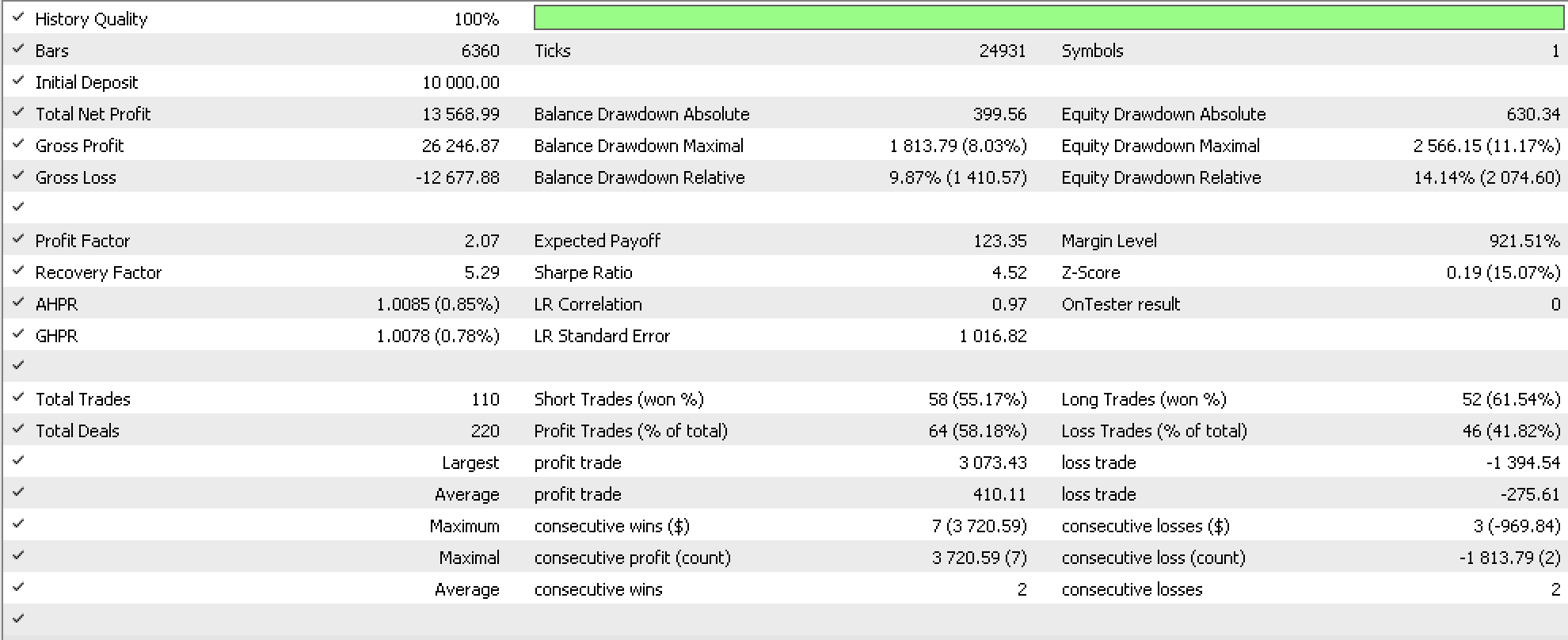
作为对照,在十分类似的智能系统上进行类似的运行,该智能系统与我们自己所做的唯一区别是尾随系统,该系统是基于移动平均线的内置尾随停止,产生以下报告。
结束语
我们已见识到了幺半群可作为数据分类的一种手段,因此也是一种决策模块。 人们已经注意到拥有结构良好幺半群的重要性,其具有普适性,且不会曲线拟合,以及其它预防措施,是实现全能系统的关键。 我们还研究了该系统的可能实现,该系统通过作为内置的智能系统尾随类的实例,调整持仓止损。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/12634
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
非常有用的文章。
谢谢。