
Moral expectation in trading
In this article, I will use the ducat as the currency unit to preserve historical continuity. You can always substitute any other currency you are used to instead of the ducat.
Mathematical expectation
Mathematical expectation in trading is one of the indicators used to evaluate a trading strategy efficiency. Such a user of mathematical expectation (and much more) is considered in detail in the article "Mathematics in Trading. How to estimate trade results.
But we are now interested in the probabilistic definition of mathematical expectation. For example, I offer you a game where you have a 10% chance of winning 100 ducats and a 90% chance of losing 10 ducats. Then the mathematical expectation of such a game will look like this: E = 0.1 * 100 + 0.9 * (-10) = 1 ducat. Thus, we can judge the expected return using mathematical expectation. For instance, if we play this game 100 times, we can assume that our initial deposit can increase by 100 ducats.
Intuition suggests that the greater the mathematical expectation, the more interesting it is to take part in such a game. For example, if we increase the winnings in the game to 200 ducats, then the mathematical expectation will also increase to 11, while the expected profitability from 100 games will rise to 1100 ducats. And what if the mathematical expectation is +100,500. Sounds like a dream! Do you agree with this statement?
If so, today is one of the happiest days of your life. Because I suggest you play the infinite expectation game. Just imagine, you will be a hyper-mega-multi-super-billionaire in an hour (or even faster).
But this game has one small inconvenience. In order to take part in it, you should pay a small entry fee, say 100 ducats. Ok, this sounds a bit mean. Let it be 50 ducats. On another thought, let me offer you a special discount – you pay only 25 ducats, and we will immediately start this wonderful game.
While you are transferring the entry fee, let me tell you the rules of this game. First, you guess the coin toss result: heads or tails. Then I toss a coin and if you guessed right, I will pay you 1 ducat. The second correcr guess will bring you 2 ducats. After the third guess, you will receive 4 ducats, etc. - each next guess will double your previous winnings. Imagine how many ducats I will have to pay you after fifty guesses. And after a hundred? Such numbers have not yet been invented at all, and all the world's wealth will be a trifle compared to your winnings.
If you make a mistake, the game ends. You can make an entry fee again and we will start the game from the very beginning.
Something tells me no one will want to play such a game with me. Why? On one hand, we have an infinite mathematical expectation:
On the other hand, an inner voice suggests that even 25 ducats is too high a price for such infinity. This contradiction is called "St. Petersburg paradox".
Moral expectation
In 1738, Daniel Bernoulli published his work "Specimen theoriae novae de mensura sortis" (Exposition of a New Theory on the Measurement of Risk). In this work, he suggested that in any game, it is necessary to maximize not the expected payoff, but its utility for the player.
This assumption can be illustrated by the following example. Let there be two different players. One has a capital of 100 ducats, and the other has 1000 ducats. They are both offered a game with an expected payoff of 10 ducats. Obviously, for the first player, such a game will be of greater interest, since if he wins, his capital will increase by 10%, while the second player will increase the capital by only 1%. In other words, the same win will be more useful for the first player than for the second one.
Based on this assumption, Daniel Bernoulli derived the moral expectation equation. Let's assume that Deposit is a player's available capital, Profit is an expected payoff, Loss is a possible loss, while p is a probability of winning. In this case, the moral expectation equation looks as follows:
The main difference between moral expectation and mathematical expectation is that moral expectation depends on the player's capital and implicitly takes into account the risk of the game.
Take for example one of the games that I suggested earlier - with a 10% chance you can win 200 ducats, and with a 90% chance you can lose 10 ducats. The mathematical expectation of this game is the same for all players: 0.1*200 + 0.9*(-10) = 11 ducats. But the moral expectation will be different and will give a little more information.
First lay out your ducats on the table and count them. Now weigh the pros and cons and decide on whether you agree to play this game?
- If you agreed to play, and you have more than 73.74 ducats, then everything is in order - you have correctly calculated the risks and opportunities.
- If you have exactly 73.74 ducats, then you are walking on thin ice. On very thin ice.
- If you have less than 73.74 ducats, then ... maybe you should look for other ways to deal with adrenaline addiction. For example, you can try feeding hungry man-eating sharks on the high seas.
- If you have abandoned this game and you have more than 73.74 ducats, then it is quite possible that you are missing the most interesting moments in your life.
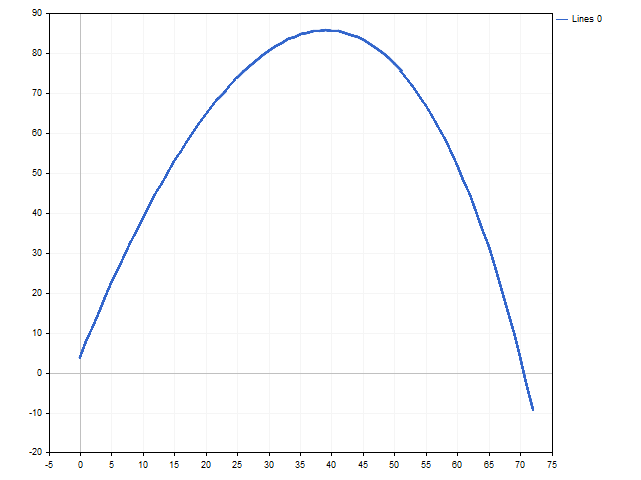
You might ask, where this mysterious sum of 73.74 ducats came from. It comes from the moral expectation of this game:
For a rational player, the moral expectation should be strictly positive:
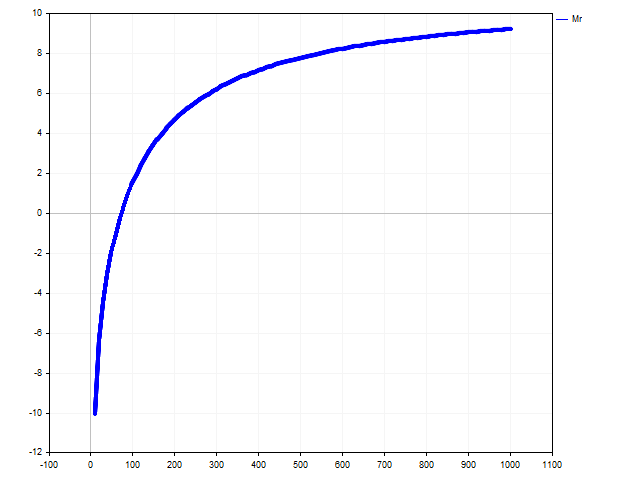
It is easy to find a solution from the inequality Deposit > 73.74. The image below shows how the moral expectation changes depending on the player's capital.
Moral expectation in trading
Some trading strategies include setting a stop loss and take profit. In such trading strategies, it is possible to use moral expectation. In this case, several options for applying moral expectation are possible.
When opening a position, a trader knows an exact balance of the trading account. Also, they can estimate the probability of winning (we will discuss this below). All other position parameters will be represented as variables:
- SL – difference between the position opening price and its stop loss in points (positive integer);
- TP – difference between the position opening price and its take profit in points;
- PV – cost of one point in the deposit currency.
- Lot – position volume.
Then the moral expectation for this position would be:
The first way to apply moral expectation is possible only when the values of any two of the three variables are pre-set – SL, TP and Lot.
For example, when opening a position, we set the position volume and its take profit. Then we can estimate the stop loss level for this trade. Its value should be such that the moral expectation becomes positive. In other words, we find the maximum possible stop loss value.
Let's see how this can be done symbolically. First, we need to find the value of the auxiliary variable:
Then the stop loss will be limited by the inequality:
If we have a lot and a stop loss specified, then we can estimate the take profit level.
Then the take profit for this trade will be as follows:
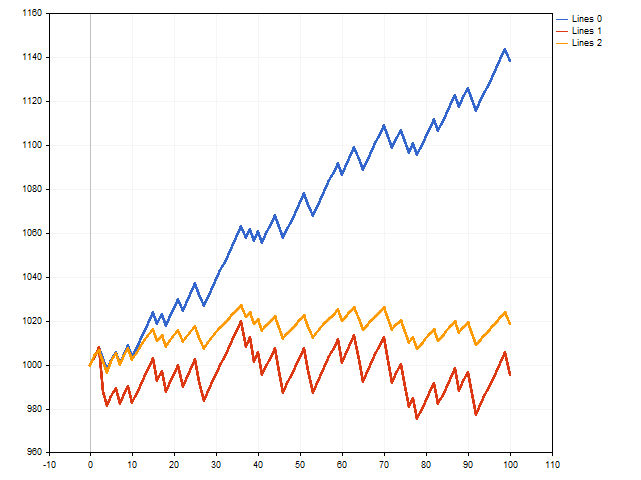
This was a theory. Now let's see what we can do in practice. To do this, write a script that simulate the execution of trades. We will check three options at the same time - with a fixed stop loss and take profit, with a floating stop loss and with a floating take profit.
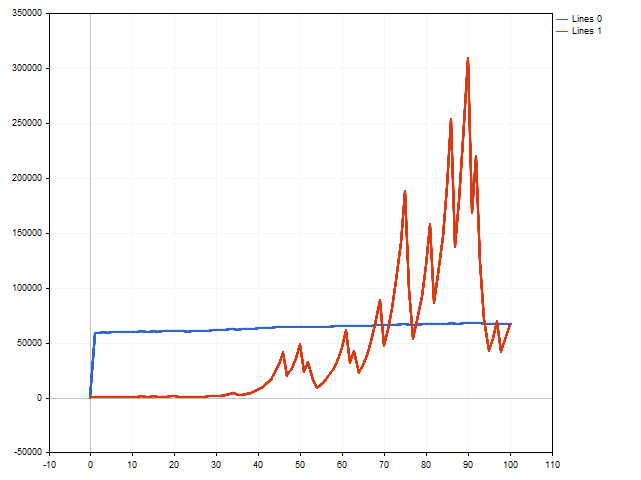
At first glance, the option with the fixed stop loss and take profit (blue line) wins.
However, it should be remembered that we used the maximum stop loss and the minimum take profit possible. What will happen if we move away from these boundaries by slightly reducing the stop loss and increasing the take profit? Then the situation may change.
The red line shows the results of trades with a floating stop loss, and the orange line shows the results of trades with a floating take profit. As we can see, the floating take profit can have a positive impact on trading results.
Moral expectation and money management
Let's break the moral expectation equation into two parts. Let's conditionally call the first part profitable:
The second part is called unprofitable:
If we look closely at the profitable part, we will see that an increase in the lot leads to its growth. However, the same increase in the lot leads to a decrease in the unprofitable part. As a result, the unprofitable part can take on a zero value (or even a negative one). In this case, the moral expectation of such a deal becomes negative. As we remember, this is not the best choice and rational traders do not approve of it.
Our next idea is finding a certain lot value, so that both profitable and unprofitable parts of the equation simultaneously take on the maximum possible values. Then the moral expectation will be maximum for given SL and TP. In the image, you can see how moral expectation changes as the lot size increases.
The numerical experiment gave a positive result. Now let's derive the equation for the optimal position size. To do this, we need to find the derivative of moral expectation with respect to the lot variable, equate it to zero and solve the resulting equation. As a result, we get the following expression:
Let's pay attention to the part of the expression enclosed in square brackets. Here we see the mathematical expectation divided by stop loss and take profit. Please note that for the correct calculation of the lot, the mathematical expectation for the transaction should be strictly positive. In other words, the following condition should always be satisfied:
By the way, if we expand the fraction in square brackets, we get Kelly criterion:
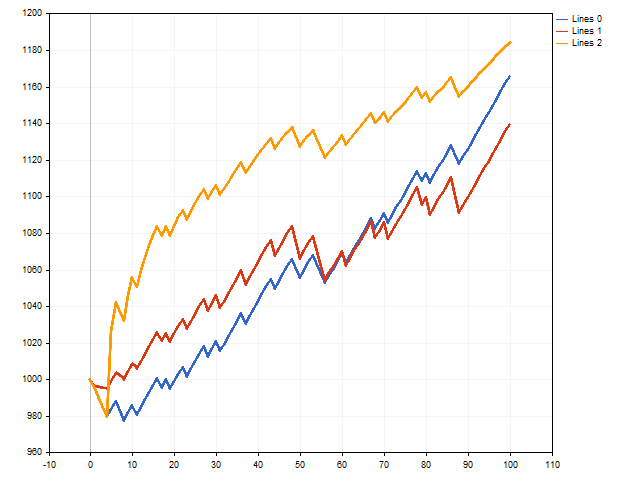
Now let's try to simulate a series of trades, in which the lot is managed with the help of moral expectation. Here we will see a variety of results. For example, the initial deposit can increase by over 160 times.
However, several losing trades in a row can affect the result not in the best way. In the following figure, we can see that the initial deposit has increased by about fifty times. This is quite good. If you do not take into account the fact that near the 90th step, the initial deposit was increased by about three hundred times.
Risk management
As we can see, managing money through moral expectation can lead to both impressive gains and very tangible losses. This raises the question of risk management.
There are two ways here. The first (the most obvious one) is to use not the entire available deposit in the calculations, but only part of it. For example, you can set some fixed amount. Also, you can set a percentage of the current balance. In any case, it will help you reduce the risk when trading.
The second risk management option is to change the calculation of the probability of a profitable trade. Let's look at this option in more detail.
Suppose that n is a total number of trades, while m is a number of winning ones. Then we can evaluate the probability of winning as:
However, this approach is not entirely correct. Since in this way we can estimate the frequency of events that have already occurred. Instead, we need to get the probability of winning in a future trade.
Let's say you have already made 15 trades, 10 of which were winning. You are about to open the next position. Then the total number of trades will increase by 1, but the number of winning trades can either increase or remain the same.
Let's take the average of these options and then the probability of winning for the opened position will be:
This way we get Krichevsky–Trofimov estimator, which in symbolic form looks like this:
Adding a shift allowed for a slightly lower probability of winning, resulting in a lower risk.
Let's generalize the probability estimate as follows: introduce an arbitrary shift s >= 1. Then the probability of winning will be:
By setting s, we can regulate the risk in a fairly wide range - the larger the s value, the lower the risk.
Unfortunately, risk reduction also affects the amount of profit received. Therefore, any trader will be faced with a choice: high risk allows you to get big profits, but losses can also be very large. Low risk allows you to reduce losses, but then the profit will be small.
Let's take a look at how risk can affect trading. I will use the simplest Expert Advisor at the intersection of two moving averages. The EA was tested with the following parameters:
Currency pair: EURUSD,
Timeframe: H1,
Test period: 2021.01.01 – 2022.12.31
All other parameters are defaults.
There were 419 trades during the test period. The balance graph looks as follows:
For different risk values, the following results were obtained.
| Risk | Total Net Profit | Balance Drawdown Absolute | Profit Factor | Expected Payoff | Recovery Factor | Margin Level |
|---|---|---|---|---|---|---|
| 0 | 42 961.51 | 2 699.05 | 1.18 | 102.53 | 1.72 | 89.20% |
| 25 | 28 932.51 | 570.27 | 1.21 | 69.05 | 1.89 | 260.70% |
| 50 | 16 836.83 | 230.64 | 1.21 | 40.18 | 1.92 | 309.53% |
As we can see, risk reduction reduces profits, but can improve other parameters of a trading strategy.
Conclusion
The following programs were used when writing this article:
| Name | Type | Description |
|---|---|---|
| ME SL-TP | Script | The script shows how trading profitability can change if the stop loss and take profit values are selected in accordance with the trade moral expectation. The script parameters:
|
| ME Lot | Script | The script shows how the position size affects the moral expectation of a trade. |
| ME MM | Script | The script compares moral expectation money management and fixed lot trading. At the end of the work, a message is displayed with the result of trading for both options, as well as the size of a rational fixed lot. |
| Two_Moving_Averages_System | Expert Advisor | The EA allows evaluating the impact of risk on trading performance. Its parameters:
|
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/12134
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
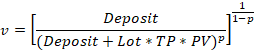


It depends on the probability of a profitable trade and deposit. The use of a large stop loss is due to the fact that a small price movement is more likely. That is, with a ratio of TP = 20 * SL, we are more likely to close the position by taking profit. But this already applies to the theory of optimal foraging.
New Article Moral Expectations in Trading has been published:
By Aleksej Poljakov
Very original theory of trading, kudos!
No, really interesting article) But moral expectation.... There is no such term not in higher, and just in maths) What about indikitars, economic news then? Don't give a damn about them?))))
You are a hostage of textbooks.
Nothing prevents you from describing a phenomenon and giving it a term.
Especially in such a narrow environment
No, really interesting article) But moral expectation.... There is no such term not in higher, and just in maths) What about indikitars, economic news then? Don't care about them?))))
indicators - there is such a thing
https://www.mql5.com/en/articles/14494
I'm not going to write about news - it's too complicated, all that fuzzy logic and so on.... I'd rather tell you something about cycles.
And about terminology. There is "moral expectation".