
Aspettative morali nel trading
In questo articolo utilizzerò il ducato come unità monetaria per preservare la continuità storica. Potete sempre sostituire il ducato con qualsiasi altra valuta a cui siete abituati.
Aspettativa matematica
L'aspettativa matematica nel trading è uno degli indicatori utilizzati per valutare l'efficienza di una strategia di trading. Questo tipo di utilizzo dell'aspettativa matematica (e molto altro ancora) è trattato in dettaglio nell'articolo Mathematics in Trading. How to estimate trade results.
Ma ora siamo interessati alla definizione probabilistica di aspettativa matematica. Ad esempio, vi propongo un gioco in cui avete il 10% di probabilità di vincere 100 ducati e il 90% di perdere 10 ducati. L'aspettativa matematica di un gioco di questo tipo è la seguente: E = 0,1 * 100 + 0,9 * (-10) = 1 ducato. Pertanto, possiamo valutare il rendimento atteso utilizzando l'aspettativa matematica. Per esempio, se giochiamo 100 volte a questo gioco, possiamo supporre che il nostro deposito iniziale possa aumentare di 100 ducati.
L'intuizione suggerisce che quanto maggiore è l'aspettativa matematica, tanto più interessante è partecipare a questo gioco. Ad esempio, se aumentiamo le vincite del gioco a 200 ducati, anche l'aspettativa matematica salirà a 11, mentre la redditività attesa da 100 partite salirà a 1100 ducati. E se l'aspettativa matematica è di +100,500. Sembra un sogno! Siete d'accordo con questa affermazione?
Se è così, oggi è uno dei giorni più felici della vostra vita. Perché vi suggerisco di giocare al gioco delle aspettative infinite. Immaginate di essere un iper-mega-multi-super-miliardario in un'ora (o anche più velocemente).
Ma questo gioco presenta un piccolo inconveniente. Per parteciparvi si deve pagare una piccola quota di iscrizione, diciamo 100 ducati. Ok, sembra un po' meschino. Che siano 50 ducati. A proposito, permettetemi di offrirvi uno sconto speciale: pagate solo 25 ducati e inizieremo immediatamente questo meraviglioso gioco.
Mentre trasferite la quota di iscrizione, lasciate che vi spieghi le regole di questo gioco. Innanzitutto, si indovina il risultato del lancio della moneta: testa o croce. Poi lancio una moneta e se hai indovinato, ti pagherò 1 ducato. La seconda ipotesi corretta ti porterà 2 ducati. Dopo il terzo indovinello, si riceveranno 4 ducati, ecc. - Ogni volta che si indovina si raddoppia la vincita precedente. Immaginate quanti ducati dovrò pagarvi dopo cinquanta indovinelli. E dopo cento? Questi numeri non sono ancora stati inventati e tutte le ricchezze del mondo saranno un'inezia rispetto alle vostre vincite.
Se si commette un errore, il gioco finisce. È possibile versare nuovamente una quota di iscrizione e il gioco ricomincerà dall'inizio.
Qualcosa mi dice che nessuno vorrà fare questo gioco con me. Perché? Da un lato, abbiamo un'aspettativa matematica infinita:
D'altra parte, una voce interiore suggerisce che anche 25 ducati sono un prezzo troppo alto per una tale infinità. Questa contraddizione è chiamata “Paradosso di San Pietroburgo".
Aspettativa morale
Nel 1738, Daniel Bernoulli pubblicò la sua opera “Specimen theoriae novae de mensura sortis" (Esposizione di una Nuova Teoria sulla Misurazione del Rischio). In questo lavoro, ha suggerito che in qualsiasi gioco è necessario massimizzare non la vincita attesa, ma l'utilità per il giocatore.
Questa ipotesi può essere illustrata dal seguente esempio. Ci sono due giocatori differenti. Uno ha un capitale di 100 ducati, l'altro di 1000. A entrambi viene proposto un gioco con una vincita prevista di 10 ducati. Ovviamente, per il primo giocatore tale gioco sarà di maggiore interesse, poiché se vince, il suo capitale aumenterà del 10%, mentre il secondo aumenterà il capitale solo dell'1%. In altre parole, la stessa vincita sarà più utile per il primo giocatore che per il secondo.
Partendo da questo presupposto, Daniel Bernoulli ricavò l'equazione dell’aspettativa morale. Supponiamo che Deposit sia il capitale disponibile di un giocatore, Profit è la vincita prevista, Loss è una possibile perdita, mentre p è la probabilità di vincita. In questo caso, l'equazione dell'aspettativa morale si presenta come segue:
La differenza principale tra aspettativa morale e aspettativa matematica è che l'aspettativa morale dipende dal capitale del giocatore e tiene implicitamente conto del rischio del gioco.
Prendiamo ad esempio uno dei giochi che ho suggerito prima: con il 10% di probabilità si possono vincere 200 ducati e con il 90% di probabilità si possono perdere 10 ducati. L'aspettativa matematica di questo gioco è la stessa per tutti i giocatori: 0,1*200 + 0,9*(-10) = 11 ducati. Ma l'aspettativa morale sarà diversa e darà qualche informazione in più.
Per prima cosa disponete i ducati sul tavolo e contateli. Ora valutate i pro e i contro e decidete se siete d'accordo a giocare a questo gioco?
- Se avete accettato di giocare e avete più di 73,74 ducati, allora tutto è in ordine - avete calcolato correttamente i rischi e le opportunità.
- Se avete esattamente 73,74 ducati, state camminando su ghiaccio sottile. Molto sottile.
- Se avete meno di 73,74 ducati, allora... forse dovreste cercare altri modi per affrontare la dipendenza da adrenalina. Per esempio, potete provare a nutrire squali affamati e mangiatori di uomini in alto mare.
- Se avete abbandonato questo gioco e avete più di 73,74 ducati, è possibile che vi stiate perdendo i momenti più interessanti della vostra vita.
Ci si potrebbe chiedere da dove provenga questa misteriosa somma di 73,74 ducati. È una conseguenza dell'aspettativa morale di questo gioco:
Per un giocatore razionale, l'aspettativa morale dovrebbe essere strettamente positiva:
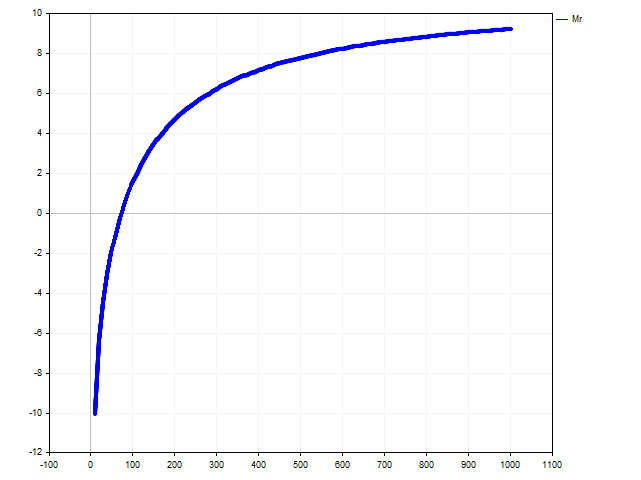
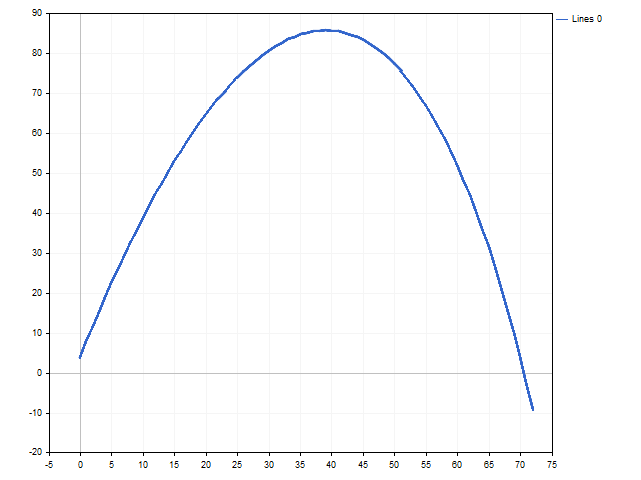
È facile trovare una soluzione dalla disuguaglianza Deposit > 73,74. L'immagine seguente mostra come l'aspettativa morale cambi a seconda del capitale del giocatore.
Aspettative morali nel trading
Alcune strategie di trading prevedono l'impostazione di uno stop loss e di un take profit. In tali strategie di trading è possibile utilizzare l'aspettativa morale. In questo caso, sono possibili diverse opzioni per l'applicazione dell'aspettativa morale.
Quando si apre una posizione, il trader conosce il saldo esatto del conto di trading. Inoltre, si possono stimare le probabilità di vincita (ne parleremo più avanti). Tutti gli altri parametri della posizione saranno rappresentati come variabili:
- SL - differenza tra il prezzo di apertura della posizione e il suo stop loss in punti (numero intero positivo);
- TP - differenza tra il prezzo di apertura della posizione e il suo take profit in punti;
- PV - costo di un punto nella valuta di deposito.
- Lot - volume della posizione.
Allora l'aspettativa morale per questa posizione sarebbe:
Il primo modo di applicare l'aspettativa morale è possibile solo quando i valori di due qualsiasi delle tre variabili sono preimpostati — SL, TP e Lot.
Ad esempio, quando si apre una posizione, si imposta il volume della posizione e il suo take profit. Quindi possiamo stimare il livello di stop loss per questo trade. Il suo valore dovrebbe essere tale da rendere positiva l'aspettativa morale. In altre parole, troviamo il valore massimo possibile di stop loss.
Vediamo come questo può essere fatto simbolicamente. Per prima cosa, dobbiamo trovare il valore della variabile ausiliaria:
Lo stop loss sarà quindi limitato dalla disuguaglianza:
Se abbiamo specificato un lotto e uno stop loss, possiamo stimare il livello di take profit.
Il take profit per questa operazione sarà il seguente:
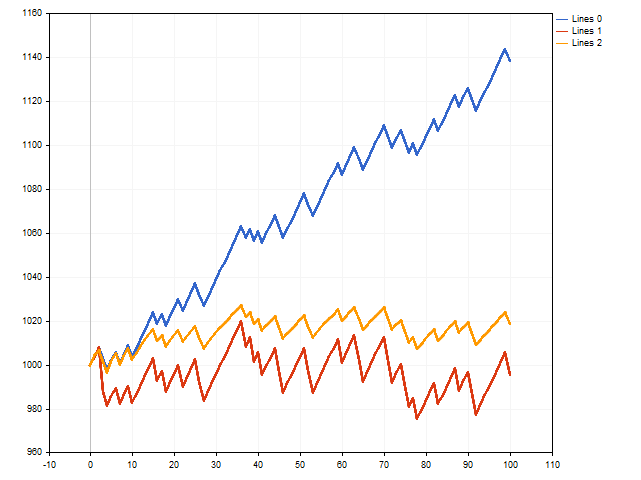
Questa era una teoria. Vediamo ora cosa possiamo fare nella pratica. A tal fine, è necessario scrivere uno script che simuli l'esecuzione dei trade. Verranno controllate tre opzioni contemporaneamente - con stop loss e take profit fissi, con stop loss e take profit flottanti.
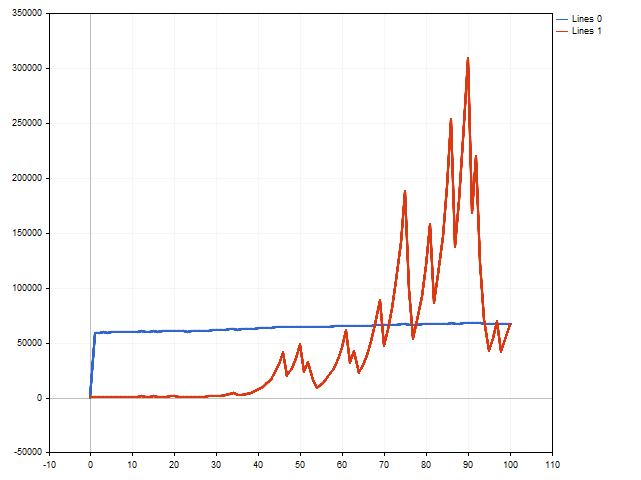
A prima vista, l'opzione con stop loss e take profit fissi (linea blu) risulta vincente.
Tuttavia, va ricordato che abbiamo utilizzato il massimo stop loss e il minimo take profit possibile. Cosa succede se ci allontaniamo da questi limiti riducendo leggermente lo stop loss e aumentando il take profit? Allora la situazione potrebbe cambiare.
La linea rossa mostra i risultati dei trade con uno stop loss flottante, mentre la linea arancione mostra i risultati dei trade con un take profit flottante. Come possiamo vedere, il take profit flottante può avere un impatto positivo sui risultati di trading.
Aspettative morali e gestione del denaro
Scomponiamo l'equazione dell'aspettativa morale in due parti. Chiamiamo condizionatamente redditizia la prima parte:
La seconda parte è chiamata "non redditizia":
Se osserviamo attentamente la parte redditizia, vedremo che un aumento del lotto porta alla sua crescita. Tuttavia, lo stesso aumento del lotto porta a una diminuzione nella parte non redditizia. Di conseguenza, la parte non redditizia può assumere un valore nullo (o addirittura negativo). In questo caso, l'aspettativa morale di una tale operazione diventa negativa. Come ricordiamo, questa non è la scelta migliore e i trader razionali non l'approvano.
La nostra prossima idea è trovare un certo valore del lotto in modo che le parti redditizie e non redditizie dell'equazione assumano contemporaneamente i valori massimi possibili. Allora l'aspettativa morale sarà massima per SL e TP determinati. Nell'immagine si può notare come l'aspettativa morale cambi all'aumentare delle dimensioni del lotto.
L'esperimento numerico ha dato un risultato positivo. Ora ricaviamo l'equazione per la dimensione ottimale della posizione. Per fare ciò, dobbiamo trovare la derivata dell'aspettativa morale rispetto alla variabile Lot, equipararla a zero e risolvere l'equazione risultante. Di conseguenza, si ottiene la seguente espressione:
Prestiamo attenzione alla parte dell'espressione racchiusa tra parentesi quadre. Qui vediamo l'aspettativa matematica divisa per stop loss e take profit. Notare che per il corretto calcolo del lotto, l'aspettativa matematica per la transazione deve essere rigorosamente positiva. In altre parole, la seguente condizione deve essere sempre soddisfatta:
A proposito, se espandiamo la frazione tra parentesi quadre, otteniamo il Criterio di Kelly:
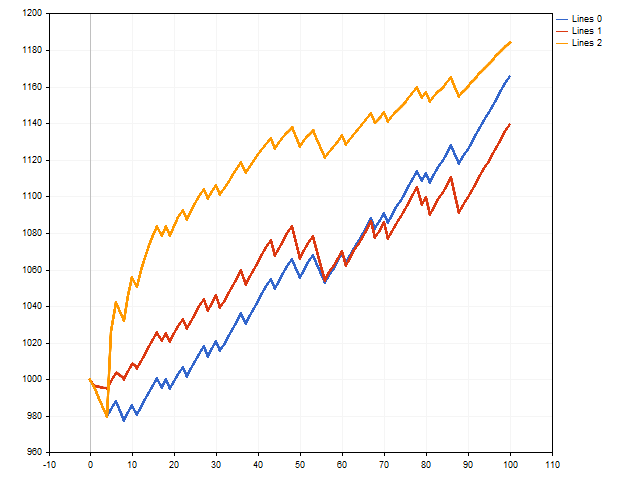
Proviamo ora a simulare una serie di operazioni, in cui il lotto viene gestito con l'aiuto dell'aspettativa morale. Qui vedremo una varietà di risultati. Ad esempio, il deposito iniziale può aumentare di oltre 160 volte.
Tuttavia, diversi trade perdenti di fila possono influenzare il risultato non nel modo migliore. Nella figura seguente si può notare che il deposito iniziale è aumentato di circa cinquanta volte. Questo è abbastanza buono. Se non si tiene conto del fatto che, in prossimità del 90° passaggio, il deposito iniziale è stato aumentato di circa trecento volte.
Gestione del rischio
Come possiamo vedere, la gestione del denaro attraverso l’aspettativa morale può portare sia a guadagni impressionanti che a perdite molto tangibili. Ciò solleva la questione della gestione del rischio.
Ci sono due modi per farlo. Il primo (il più ovvio) consiste nel non utilizzare nei calcoli l'intero deposito disponibile, ma solo una parte di esso. Ad esempio, è possibile impostare un importo fisso. Inoltre, è possibile impostare una percentuale del saldo corrente. In ogni caso, vi aiuterà a ridurre il rischio durante il trading.
La seconda opzione di gestione del rischio consiste nel modificare il calcolo della probabilità di un'operazione profittevole. Analizziamo questa opzione in modo più dettagliato.
Supponiamo che n è il numero totale di trade, mentre m è il numero di operazioni vincenti. Allora possiamo valutare la probabilità di vincita come:
Tuttavia, questo approccio non è del tutto corretto. Poiché In questo modo possiamo stimare la frequenza di eventi che si sono già verificati. Dobbiamo invece ottenere la probabilità di vincita in un'operazione futura.
Supponiamo che abbiate già effettuato 15 operazioni, di cui 10 vincenti. State per aprire la posizione successiva. Il numero totale dei trade aumenterà di 1, ma il numero di operazioni vincenti potrà aumentare o rimanere invariato.
Prendiamo la media di queste opzioni e quindi la probabilità di vincita per la posizione aperta sarà:
In questo modo si ottiene l’estimatore Krichevsky-Trofimov, che in forma simbolica si presenta così:
L'aggiunta di un turno ha permesso di abbassare leggermente la probabilità di vincita, riducendo il rischio.
Generalizziamo la stima della probabilità come segue: introduciamo uno spostamento arbitrario s >= 1. Allora la probabilità di vincere sarà:
Impostando s è possibile regolare il rischio in un intervallo piuttosto ampio - più grande è il valore di s, più basso è il rischio.
Purtroppo, la riduzione del rischio influisce anche sull'ammontare dei profitti percepiti. Pertanto, ogni trader si troverà di fronte ad una scelta: il rischio elevato consente di ottenere grandi profitti, ma anche le perdite possono essere molto elevate. Il basso rischio consente di ridurre le perdite, ma il profitto sarà esiguo.
Vediamo come il rischio può influenzare il trading. Utilizzerò il più semplice Expert Advisor all'intersezione di due medie mobili. L'EA è stato testato con i seguenti parametri:
Coppia di valute: EURUSD,
Timeframe: H1,
Periodo di test: 01.01.2021 - 31.12.2022
Tutti gli altri parametri sono predefiniti.
Durante il periodo di prova sono stati effettuati 419 trade. Il grafico del saldo si presenta come segue:
Per diversi valori di rischio, sono stati ottenuti i seguenti risultati.
| Rischio | Utile netto totale | Saldo Drawdown Assoluto | Fattore di Profitto | Profitto Previsto | Fattore di Recupero | Livello del Margine |
|---|---|---|---|---|---|---|
| 0 | 42 961.51 | 2 699.05 | 1.18 | 102.53 | 1.72 | 89.20% |
| 25 | 28 932.51 | 570.27 | 1.21 | 69.05 | 1.89 | 260.70% |
| 50 | 16 836.83 | 230.64 | 1.21 | 40.18 | 1.92 | 309.53% |
Come si vede, la riduzione del rischio riduce i profitti, ma può migliorare altri parametri di una strategia di trading.
Conclusioni
Per la stesura di questo articolo sono stati utilizzati i seguenti programmi:
| Nome | Tipo | Descrizione |
|---|---|---|
| ME SL-TP | Script | Lo script mostra come la profittabilità del trading possa cambiare se i valori di stop loss e take profit vengono selezionati in base alle aspettative morali del trade. Parametri dello script:
|
| ME Lot | Script | Lo script mostra come la dimensione della posizione influisca sull'aspettativa morale di un'operazione. |
| ME MM | Script | Lo script confronta la gestione del denaro in base alle aspettative morali e il trading a lotti fissi. Al termine del lavoro, viene visualizzato un messaggio con il risultato del trading per entrambe le opzioni, nonché la dimensione di un lotto fisso razionale. |
| Two_Moving_Averages_System | Expert Advisor | L'EA consente di valutare l'impatto del rischio sulla performance di trading. I suoi parametri:
|
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/12134
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.
Questo articolo è stato scritto da un utente del sito e riflette le sue opinioni personali. MetaQuotes Ltd non è responsabile dell'accuratezza delle informazioni presentate, né di eventuali conseguenze derivanti dall'utilizzo delle soluzioni, strategie o raccomandazioni descritte.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
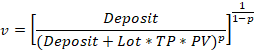


Dipende dalla probabilità di un'operazione redditizia e dal deposito. L'uso di un grande stop loss è dovuto al fatto che un piccolo movimento di prezzo è più probabile. In altre parole, con un rapporto di TP = 20 * SL, è più probabile chiudere la posizione prendendo profitto. Ma questo vale già per la teoria del foraggiamento ottimale.
Pubblicato il nuovo articolo Aspettative morali nel trading:
Di Aleksej Poljakov
Una teoria del trading molto originale, complimenti!
No, articolo davvero interessante) Ma l'aspettativa morale .... Non esiste un termine del genere, non in ambito universitario, e solo in matematica) Che dire poi degli indikitar, delle notizie economiche? Non te ne frega niente di loro?))))
Sei ostaggio dei libri di testo.
Nulla ti impedisce di descrivere un fenomeno e di dargli un termine.
Soprattutto in un ambiente così ristretto
No, articolo davvero interessante) Ma l'aspettativa morale .... Non esiste un termine del genere, non in ambito universitario, e solo in matematica) Che dire poi degli indikitar, delle notizie economiche? Non ti interessano? ))))
indicatori - esiste una cosa del genere
https://www.mql5.com/it/articles/14494
Non ho intenzione di scrivere di notizie - è troppo complicato, tutta quella logica confusa e così via.... Preferisco parlarvi di cicli.
E sulla terminologia. Esiste l'"aspettativa morale".