
Esperança moral na negociação
Neste artigo, usarei o ducado como unidade monetária. Dessa forma, mantenho a continuidade histórica. Mas você sempre pode substituir o ducado por qualquer outra moeda que lhe seja familiar.
Esperança matemática
A esperança matemática ou valor esperado na negociação é um indicador importante para avaliar a eficácia de uma estratégia de negociação. Esse conceito, juntamente com outros aspectos, é detalhado no artigo "Matemática na negociação: Como estimar resultados de trading".
No entanto, agora estamos interessados na definição probabilística da esperança matemática. Por exemplo, vou lhe oferecer um jogo no qual você tem 10% de chance de ganhar 100 ducados e 90% de chance de perder 10 ducados. Nesse caso, a esperança matemática do jogo seria: E = 0,1 * 100 + 0,9 * (-10) = 1 ducado. Dessa forma, podemos usar a esperança matemática para avaliar o retorno esperado. Portanto, se jogarmos esse jogo 100 vezes, podemos supor que nosso depósito inicial poderá aumentar em 100 ducados.
A intuição sugere que quanto maior for a esperança matemática, mais interessante será participar desse jogo. Por exemplo, se aumentarmos os ganhos do jogo para 200 ducados, a esperança matemática também aumentará para 11. Isso significa que a lucratividade esperada de 100 jogos seria de 1100 ducados. E se a esperança matemática fosse +100500, isso seria apenas um sonho! Você concorda com essa afirmação?
Se você concordar, hoje será um dos dias mais felizes da sua vida. Porque estou lhe oferecendo a oportunidade de jogar um jogo com esperança matemática infinita. Apenas imagine, em pouco tempo (até mais rápido do que você imagina), você se tornará um bilionário hipermegaultrasuper rico.
No entanto, esse jogo tem uma pequena desvantagem. Para participar, você precisa pagar uma pequena taxa de entrada, digamos, 100 ducados. Bem, soa um pouco mesquinho da minha parte. Vamos reduzir a taxa para 50 ducados. Ah, mas só para você e somente agora, oferecemos um desconto: você paga apenas 25 ducados, e começaremos imediatamente esse incrível jogo.
Enquanto você envia a taxa de entrada, vou lhe contar as regras desse jogo. Primeiro, você precisa adivinhar qual lado da moeda será sorteado: "cara ou coroa". Em seguida, eu jogarei a moeda e, se você adivinhar corretamente, eu lhe pagarei 1 ducado. No segundo palpite, você receberá 2 ducados. Após o terceiro palpite, serão 4 ducados, e assim por diante. Cada palpite subsequente dobrará seus ganhos anteriores. Imagine quantos ducados eu terei que pagar a você após cinquenta palpites. E depois de cem? Esses números ainda nem foram inventados, e a soma total será uma verdadeira fortuna em comparação com a riqueza mundial.
No entanto, se você errar, o jogo termina. Mas não se preocupe, você pode fazer uma nova taxa de entrada e recomeçaremos o jogo do zero.
Algo me diz que haverá poucas pessoas interessadas em jogar esse jogo comigo. Por quê? De um lado, temos uma esperança matemática infinita:
Por outro lado, uma voz interior sugere que até mesmo 25 ducados é um preço muito alto por tal infinitude. Essa contradição é conhecida como "paradoxo de São Petersburgo".
Esperança moral
Em 1738, Bernoulli publicou "Specimen theoriae novae de mensura sortis" (Um novo exemplo da teoria de medição do acaso). Nesse trabalho, ele propôs que, em qualquer jogo, devemos maximizar não o ganho esperado, mas sim a utilidade desse ganho para o jogador.
Essa suposição pode ser ilustrada com o seguinte exemplo: vamos considerar dois jogadores diferentes. Um deles possui um capital de 100 ducados, enquanto o outro possui 1.000 ducados. Ambos são convidados a participar de um jogo com um ganho esperado de 10 ducados. É evidente que para o primeiro jogador esse jogo despertará maior interesse, já que, em caso de vitória, seu capital aumentará em 10%. Enquanto o segundo jogador verá seu capital aumentar apenas 1%. Ou seja, o mesmo ganho será mais útil para o primeiro jogador do que para o segundo.
Com base nessa suposição, Daniel Bernoulli derivou a fórmula. Seja Deposit o capital disponível para o jogador, Profit o ganho esperado, Loss a possível perda e p a probabilidade de ganhar. A fórmula da esperança moral seria a seguinte:
A principal diferença entre a esperança moral e a esperança matemática reside no fato de que a esperança moral depende do capital do jogador e leva implicitamente em consideração o risco do jogo.
Vamos tomar como exemplo um dos jogos que mencionei anteriormente: com 10% de chance de ganhar 200 ducados e 90% de chance de perder 10 ducados. A esperança matemática desse jogo é a mesma para todos os jogadores: 0,1 * 200 + 0,9 * (-10) = 11 ducados. No entanto, a esperança moral será diferente e fornecerá um pouco mais de informação.
Primeiro, coloque seus ducados na mesa e conte-os. Agora, avalie os prós e os contras e responda: você concorda em jogar este jogo?
- Se concordou em jogar e possui mais de 73,74 ducados, então está tudo bem - você está calculando corretamente os riscos e suas possibilidades.
- Se você tem exatamente 73,74 ducados, está pisando em gelo fino. Em gelo muito fino.
- E se possui menos de 73,74 ducados, talvez seja melhor procurar outras maneiras de lidar com a dependência de adrenalina. Por exemplo, você pode tentar alimentar tubarões famintos em alto mar.
- Se optou por não jogar este jogo e possui mais de 73,74 ducados, é possível que esteja perdendo os momentos mais interessantes da sua vida.
Você deve estar se perguntando de onde veio essa soma misteriosa de 73,74 ducados. Ela vem da esperança moral deste jogo:
Para um jogador racional, a esperança moral deve ser estritamente positiva:
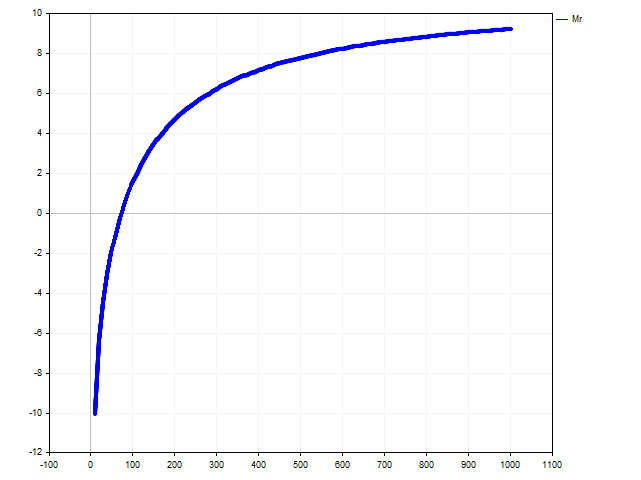
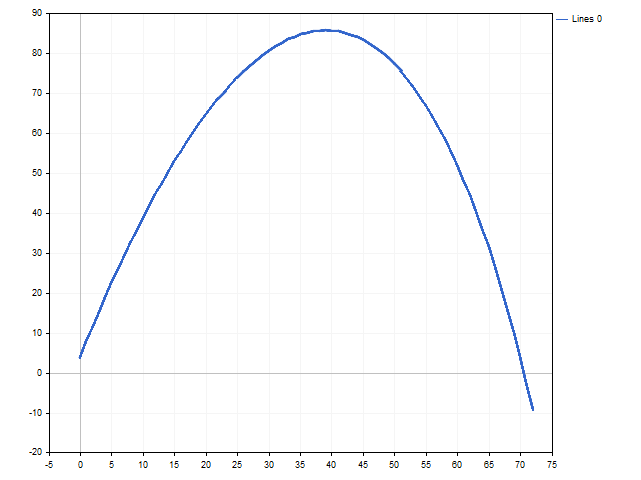
A partir dessa desigualdade, é fácil encontrar a solução Deposit > 73.74. Como a esperança moral varia de acordo com o capital do jogador, você pode ver na figura abaixo.
Esperança moral na negociação
Algumas estratégias de negociação envolvem a definição de um stop loss e de um take profit. Nestas estratégias, é possível utilizar a esperança moral. Existem várias formas de aplicar a esperança moral.
Ao abrir uma posição, o trader conhece o saldo exato da conta de negociação. Além disso, ele pode estimar a probabilidade de ganhar (discutiremos isso mais adiante). Vamos considerar todos os outros parâmetros da posição como variáveis:
- SL – diferença entre o preço de abertura da posição e o valor do stop loss em pontos (um número inteiro positivo);
- TP – diferença entre o preço de abertura da posição e o valor do take profit em pontos;
- PV – valor de um ponto expresso na moeda do depósito;
- Lot – volume da posição.
Assim, a esperança moral para essa posição seria:
A primeira forma de aplicar a esperança moral só é possível quando dois dos três valores - SL, TP e Lot - são previamente definidos.
Por exemplo, ao abrir uma posição, definimos o volume da posição e o seu take profit. Em seguida, podemos estimar o nível do stop loss para essa negociação. Seu valor deve ser tal que a esperança moral se torne positiva. Ou seja, encontraremos o valor máximo possível do stop loss.
Vamos ver como isso pode ser expresso simbolicamente. Primeiro, precisamos encontrar o valor da variável auxiliar:
Em seguida, o stop loss será limitado pela seguinte desigualdade:
Se tivermos o lote e o stop loss definidos, podemos estimar o nível do take profit.
Então, o take profit para essa negociação será o seguinte:
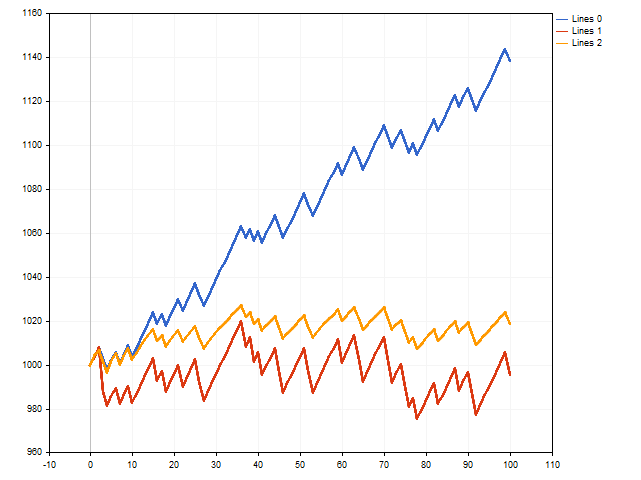
Já vimos os princípios teóricos. Agora, vamos ver se podem ser aplicados na prática. Para isso, escreveremos um script que simulará a realização de transações. Ao mesmo tempo, iremos verificar três opções simultaneamente - com stop loss fixo e take profit, com stop loss flutuante e take profit flutuante.
À primeira vista, a opção com stop loss fixo e take profit (linha azul) é a vencedora.
No entanto, devemos lembrar que usamos o stop loss máximo e o take profit mínimo possível. E o que acontecerá se nos afastarmos desses limites - reduzindo levemente o stop loss e aumentando o take profit? Nesse caso, a situação pode mudar.
A linha vermelha mostra os resultados das negociações com stop loss flutuante, e a linha laranja mostra os resultados das negociações com take profit flutuante. E, como podemos ver, o take profit flutuante pode ter um impacto positivo nos resultados das negociações.
Esperança moral e gerenciamento de capital
Vamos dividir a fórmula da esperança moral em duas partes. Chamaremos condicionalmente a primeira parte de lucrativa:
E chamaremos a segunda parte de não lucrativa:
Ao analisarmos a parte lucrativa com atenção, perceberemos que um aumento no tamanho do lote leva a um aumento nessa parte. No entanto, o mesmo aumento no lote leva a uma diminuição na parte não lucrativa. Como resultado, a parte não lucrativa pode assumir um valor zero (ou até mesmo negativo). Nesse caso, a esperança moral desse acordo se torna negativa. E isso, como já sabemos, não é a melhor escolha e os traders racionais não a aprovam.
Nossa próxima ideia é encontrar um valor para o tamanho do Lot no qual tanto a parte lucrativa quanto a não lucrativa da fórmula assumam os valores máximos possíveis ao mesmo tempo. Assim, a esperança moral será máxima para os valores de SL e TP dados. No gráfico, você pode observar como a esperança moral varia à medida que o tamanho do lote aumenta.
O experimento numérico deu um resultado positivo. Agora vamos derivar a fórmula para o tamanho ideal da posição. Para isso, precisamos encontrar a derivada da esperança moral em relação à variável Lot, igualá-la a zero e resolver a equação resultante. Como resultado, obtemos a seguinte expressão:
Vamos observar a parte da expressão dentro dos colchetes. Aqui, vemos a esperança matemática dividida pelo stop loss e take profit. É importante destacar que, para calcular corretamente o tamanho do lote, a esperança matemática da transação deve ser estritamente positiva. Ou seja, a seguinte condição deve ser sempre atendida:
A propósito, se simplificarmos a fração entre colchetes, obtemos o Critério de Kelly:
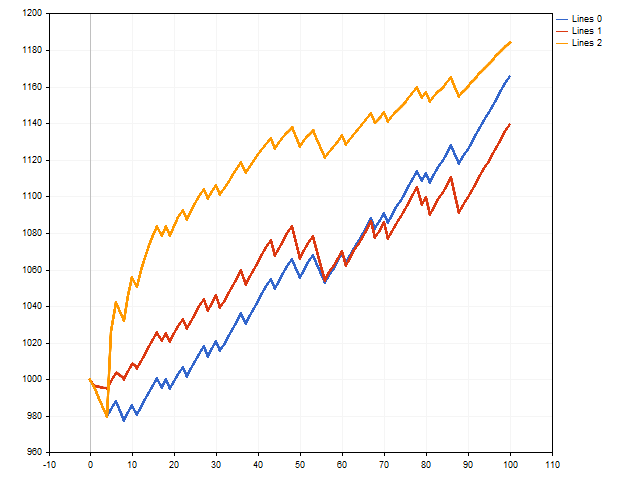
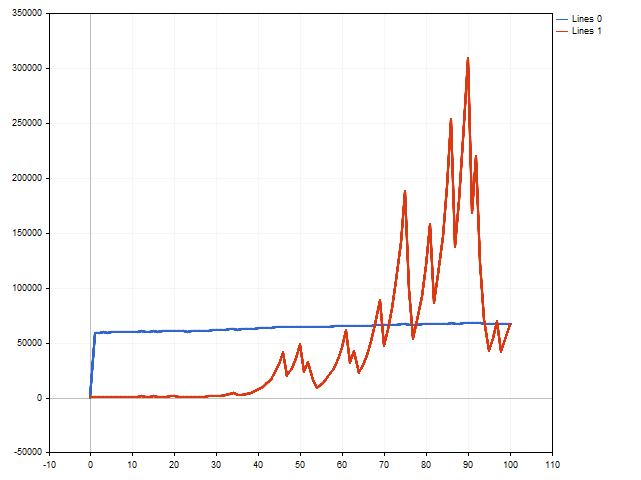
Agora, vamos tentar simular uma série de negociações em que o tamanho do lote é gerenciado com base na esperança moral. Aqui, esperamos uma variedade de resultados. Por exemplo, o depósito inicial pode aumentar mais de 160 vezes.
No entanto, várias negociações perdedoras em sequência podem afetar o resultado de maneira não tão favorável. Na figura a seguir, podemos ver que o depósito inicial aumentou cerca de cinquenta vezes. Isso é bastante positivo. No entanto, devemos levar em consideração que, por volta do 90º passo, o depósito inicial foi aumentado em aproximadamente trezentas vezes.
Gestão de risco
Como vimos, gerenciar o dinheiro por meio da expectativa moral pode levar a ganhos impressionantes ou perdas significativas. Portanto, surge a questão da gestão de risco.
Existem duas abordagens. A primeira, mais óbvia, é não utilizar todo o depósito disponível nos cálculos, mas apenas uma parte dele. Por exemplo, você pode definir um valor fixo ou uma porcentagem do saldo atual. Isso ajudará a reduzir o risco durante as negociações.
A segunda opção de gestão de risco é alterar o cálculo da probabilidade de uma negociação ser lucrativa. Vamos examinar essa opção com mais detalhes.
Seja n o número total de transações e m o número de operações vencedoras. Assim, podemos avaliar a probabilidade de ganhar como:
No entanto, essa abordagem não é totalmente precisa, pois estima a frequência de eventos passados. O que precisamos é obter a probabilidade de ganhar em uma transação futura.
Suponha que você já tenha realizado 15 negociações, das quais 10 foram vencedoras. Agora você está prestes a abrir a próxima posição. Nesse caso, o número total de negociações aumentará em 1, mas o número de negociações vencedoras pode aumentar ou permanecer o mesmo.
Vamos calcular a média dessas opções e assim obter a probabilidade de ganhar para a posição que será aberta:
Dessa forma, obtemos a estimativa de Krichevsky-Trofimov, que pode ser expressa simbolicamente da seguinte maneira:
Ao introduzir um viés, conseguimos obter uma probabilidade ligeiramente menor de ganhar, resultando em um risco reduzido.
Vamos generalizar a estimativa de probabilidade da seguinte forma: vamos introduzir um viés arbitrário s >= 1.
Então, a probabilidade de ganhar será: Ao definir o valor de s, é possível ajustar o risco em uma faixa bastante ampla. Quanto maior o valor de s, menor será o risco.
Infelizmente, a redução do risco também afeta o valor do lucro obtido. Portanto, todo trader se depara com uma escolha: o alto risco permite obter grandes lucros, mas as perdas também podem ser significativas. O baixo risco ajuda a reduzir as perdas, mas o lucro será menor.
Vamos analisar juntos como o risco pode afetar a negociação. Para realizar a verificação, usaremos um EA simples baseado na interseção de duas médias móveis. O Expert Advisor foi testado com os seguintes parâmetros:
Par de moedas: EURUSD,
Período gráfico: H1,
Período de teste: 2021.01.01 – 2022.12.31
Todos os outros parâmetros são padrão.
Houve 419 negociações durante o período de teste. E o balanço fica assim:
Para diferentes valores de risco, foram obtidos os seguintes resultados.
| Risk | Total Net Profit | Balance Drawdown Absolute | Profit Factor | Expected Payoff | Recovery Factor | Margin Level |
|---|---|---|---|---|---|---|
| 0 | 42 961.51 | 2 699.05 | 1.18 | 102.53 | 1.72 | 89.20% |
| 25 | 28 932.51 | 570.27 | 1.21 | 69.05 | 1.89 | 260.70% |
| 50 | 16 836.83 | 230.64 | 1.21 | 40.18 | 1.92 | 309.53% |
Como podemos ver, a redução do risco reduz os lucros, mas pode melhorar outros parâmetros da estratégia de negociação.
Considerações finais
Os seguintes programas foram usados durante a escrita deste artigo:
| Nome | Tipo | Descrição |
|---|---|---|
| ME SL-TP | Script | O script mostra como a lucratividade do trading pode mudar se os valores de stop loss e take profit forem selecionados de acordo com a esperança moral da transação. Parâmetros do script:
|
| ME Lot | Script | O script mostra como o tamanho da posição afeta a esperança moral de uma negociação. |
| ME MM | Script | O script compara a esperança moral de gerenciamento de capital e negociação de lote fixo. Ao final do trabalho, é exibida uma mensagem com o resultado da negociação das duas variantes e também, o tamanho de um lote fixo racional. |
| Two_Moving_Averages_System | Expert Advisor | O Expert Advisor permite avaliar o impacto do risco no desempenho da negociação. Seus parâmetros são:
|
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/12134
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
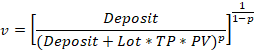


Depende da probabilidade de uma negociação lucrativa e do depósito. O uso de um stop loss grande se deve ao fato de que um pequeno movimento de preço é mais provável. Ou seja, com uma proporção de TP = 20 * SL, é mais provável que fechemos a posição obtendo lucro. Mas isso já se aplica à teoria do forrageamento ideal.
Foi publicado o novo artigo Moral Expectations in Trading (Expectativas morais no comércio ):
Por Aleksej Poljakov
Teoria de negociação muito original, parabéns!
Não, artigo realmente interessante) Mas expectativa moral.... Não existe esse termo nem no ensino superior, nem apenas em matemática) E quanto aos indikitars e às notícias econômicas, então? Não dá a mínima para eles? ))))
Você é refém dos livros didáticos.
Nada impede que você descreva um fenômeno e dê a ele um termo.
Especialmente em um ambiente tão restrito
Não, artigo realmente interessante) Mas expectativa moral.... Não existe esse termo nem no ensino superior, nem apenas em matemática) E quanto às notícias econômicas e indikitars? Você não se importa com eles? ))))
indicadores - existe tal coisa
https://www.mql5.com/pt/articles/14494
Não vou escrever sobre notícias - é muito complicado, toda essa lógica difusa e assim por diante.... Prefiro falar um pouco sobre ciclos.
E sobre terminologia. Existe a "expectativa moral".