
Attentes morales dans le trading
Dans cet article, j'utiliserai le ducat comme unité monétaire afin de préserver la continuité historique. Vous pouvez toujours remplacer le ducat par toute autre monnaie à laquelle vous êtes habitué.
Espérance mathématique
L'espérance mathématique en trading est l'un des indicateurs utilisés pour évaluer l'efficacité d'une stratégie de trading. Un tel utilisateur de l'espérance mathématique (et bien d'autres choses encore) est examiné en détail dans l'article "Mathématiques dans le Trading". Comment estimer les résultats de trading.
Mais nous nous intéressons maintenant à la définition probabiliste de l'espérance mathématique. Par exemple, je vous propose un jeu où vous avez 10% de chances de gagner 100 ducats et 90% de chances de perdre 10 ducats. L'espérance mathématique du jeu est donc la suivante : E = 0,1 * 100 + 0,9 * (-10) = 1 ducat. Nous pouvons donc évaluer le rendement attendu à l'aide de l'espérance mathématique. Par exemple, si nous jouons 100 fois à ce jeu, nous pouvons supposer que notre dépôt initial peut augmenter de 100 ducats.
L'intuition suggère que plus l'espérance mathématique est grande, plus il est intéressant de participer à un tel jeu. Par exemple, si nous augmentons les gains du jeu à 200 ducats, l'espérance mathématique passera également à 11, et la rentabilité attendue de 100 jeux passera à 1100 ducats. Et si l'espérance mathématique est de +100 500. C'est un rêve ! Êtes-vous d'accord avec cette affirmation ?
Si c'est le cas, aujourd'hui est l'un des plus beaux jours de votre vie. Parce que je vous propose de jouer au jeu de l'attente infinie. Imaginez, vous serez hyper-méga-multi-super-milliardaire dans une heure (ou plus rapidement).
Mais ce jeu présente un petit inconvénient. Pour y participer, il faut payer un petit droit d'entrée, par exemple 100 ducats. Ok, cela semble un peu méchant. Qu'il soit de 50 ducats. Par ailleurs, permettez-moi de vous proposer une réduction spéciale : vous ne payez que 25 ducats et nous commençons immédiatement ce jeu merveilleux.
Pendant que vous transférez le droit d'entrée, laissez-moi vous expliquer les règles de ce jeu. Tout d'abord, vous devinez le résultat du tirage au sort : pile ou face. Ensuite, je tire à pile ou face et si vous avez deviné juste, je vous paierai 1 ducat. La deuxième réponse correcte vous rapportera 2 ducats. Après la troisième réponse, vous recevrez 4 ducats, etc. - chaque fois que vous devinez quelque chose, vous doublez vos gains précédents. Imaginez le nombre de ducats que je vais devoir vous payer après cinquante suppositions. Et après cent ans ? Ces chiffres n'ont pas encore été inventés, et toute la richesse du monde ne sera qu'une bagatelle comparée à vos gains.
Si vous faites une erreur, le jeu s'arrête. Vous pouvez à nouveau payer un droit d'entrée et nous recommencerons le jeu depuis le début.
Quelque chose me dit que personne ne voudra jouer à ce jeu avec moi. Mais pourquoi ? D'une part, nous avons une espérance mathématique infinie :
D'un autre côté, une voix intérieure suggère que même 25 ducats est un prix trop élevé pour une telle infinité. Cette contradiction est appelée le "Paradoxe de Saint-Pétersbourg".
Attente morale
En 1738, Daniel Bernoulli publie son ouvrage "Specimen theoriae novae de mensura sortis" (Exposition d'une Nouvelle Théorie sur la Mesure du Risque). Dans ce travail, il a suggéré que dans tout jeu, il est nécessaire de maximiser non pas le gain attendu, mais son utilité pour le joueur.
Cette hypothèse peut être illustrée par l'exemple suivant. Qu'il y ait 2 joueurs différents. L'un a un capital de 100 ducats, l'autre de 1000 ducats. Ils se voient tous deux proposer un jeu dont le gain attendu est de 10 ducats. Il est évident que pour le premier joueur, un tel jeu sera plus intéressant, puisque s'il gagne, son capital augmentera de 10%, alors que le second joueur n'augmentera son capital que de 1%. En d'autres termes, le même gain sera plus utile au premier joueur qu'au second.
Sur la base de cette hypothèse, Daniel Bernoulli a dérivé l'équation de l’utilité espérée. Supposons que le dépôt soit le capital disponible d'un joueur, le profit est le gain attendu, la Perte est la perte possible, et p est la probabilité de gagner. Dans ce cas, l'équation de l'espérance morale se présente comme suit :
La principale différence entre l'espérance morale et l'espérance mathématique est que l'espérance morale dépend du capital du joueur et prend implicitement en compte le risque du jeu.
Prenons l'exemple d'un des jeux que j'ai proposés précédemment : avec 10% de chances, vous pouvez gagner 200 ducats et avec 90% de chances, vous pouvez perdre 10 ducats. L'espérance mathématique de ce jeu est la même pour tous les joueurs : 0,1*200 + 0,9*(-10) = 11 ducats. Mais l'attente morale sera différente et donnera un peu plus d'informations.
Etalez d'abord vos ducats sur la table et comptez-les. Maintenant, pesez le pour et le contre et décidez si vous acceptez de jouer à ce jeu.
- Si vous avez accepté de jouer et que vous disposez de plus de 73,74 ducats, tout est en ordre - vous avez correctement calculé les risques et les opportunités.
- Si vous avez exactement 73,74 ducats, vous marchez sur des œufs. Sur une glace très fine.
- Si vous avez moins de 73,74 ducats, alors ... peut-être devriez-vous chercher d'autres moyens de gérer votre dépendance à l'adrénaline. Par exemple, vous pouvez essayer de nourrir des requins mangeurs d'hommes en haute mer.
- Si vous avez abandonné ce jeu et que vous possédez plus de 73,74 ducats, il est fort possible que vous passiez à côté des moments les plus intéressants de votre vie.
On peut se demander d'où vient cette mystérieuse somme de 73,74 ducats. Cela vient de l'attente morale de ce jeu :
Pour un joueur rationnel, l'espérance morale doit être strictement positive :
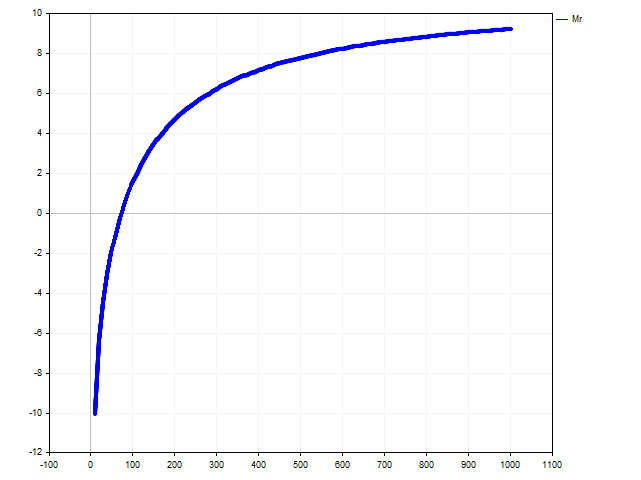
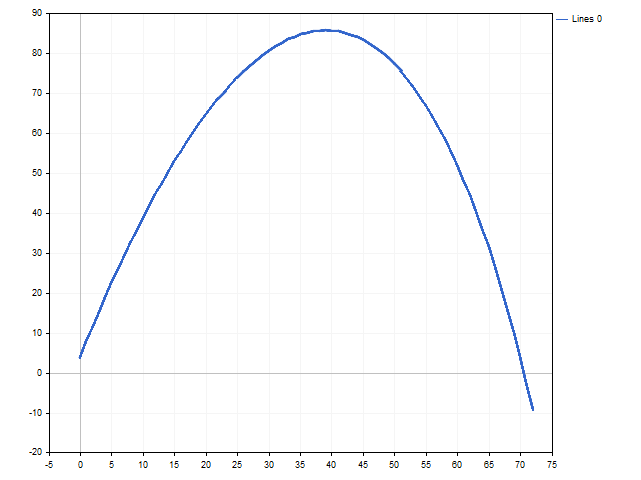
Il est facile de trouver une solution à partir de l'inégalité Dépôt > 73,74. L'image ci-dessous montre comment l'attente morale change en fonction du capital du joueur.
Attentes morales dans le trading
Certaines stratégies de trading incluent la fixation d'un stop loss et d'un take profit. Dans ces stratégies de trading, il est possible d'utiliser l'espérance morale. Dans ce cas, plusieurs options d'application de l'attente morale sont possibles.
Lors de l'ouverture d'une position, le trader connaît le solde exact de son compte de trading. Ils peuvent également estimer la probabilité de gagner (nous y reviendrons plus loin). Tous les autres paramètres de position seront représentés sous forme de variables :
- SL - différence entre le prix d'ouverture de la position et son stop loss en points (nombre entier positif)
- TP - différence entre le prix d'ouverture de la position et son take profit en points
- PV - coût d'un point dans la monnaie du dépôt
- Lot - volume de la position
L'attente morale pour cette position serait alors la suivante :
La première façon d'appliquer l'espérance morale n'est possible que lorsque les valeurs de deux des trois variables sont prédéfinies. SL, TP et Lot.
Par exemple, lors de l'ouverture d'une position, nous définissons le volume de la position et son take profit. Nous pouvons alors estimer le niveau du stop loss pour cette transaction. Sa valeur doit être telle que l'espérance morale devienne positive. En d'autres termes, nous trouvons la valeur maximale possible du stop loss.
Voyons comment cela peut se faire symboliquement. Tout d'abord, nous devons trouver la valeur de la variable auxiliaire :
Le stop loss sera alors limité par l'inégalité :
Si nous avons spécifié un lot et un stop loss, nous pouvons alors estimer le niveau du take profit.
Le take profit pour cette transaction sera alors le suivant :
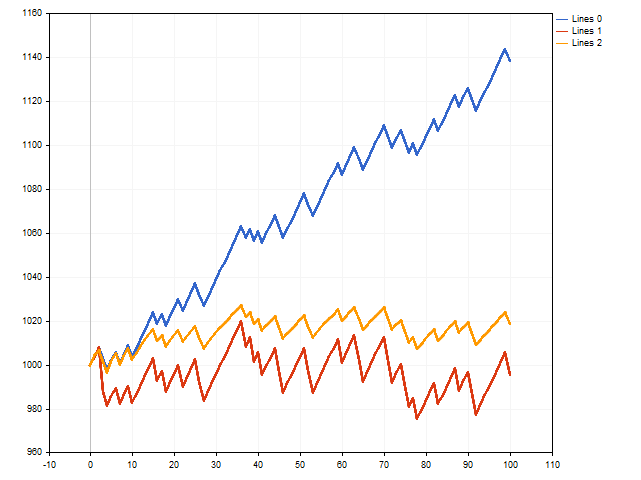
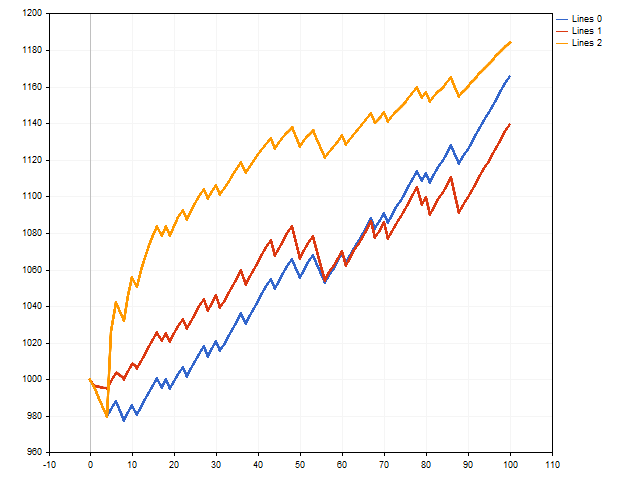
Il s'agissait d'une théorie. Voyons maintenant ce que nous pouvons faire en pratique. Pour ce faire, écrivez un script qui simule l'exécution des transactions. Nous allons vérifier 3 options en même temps : avec un stop loss et un take profit fixes, avec un stop loss flottant et avec un take profit flottant.
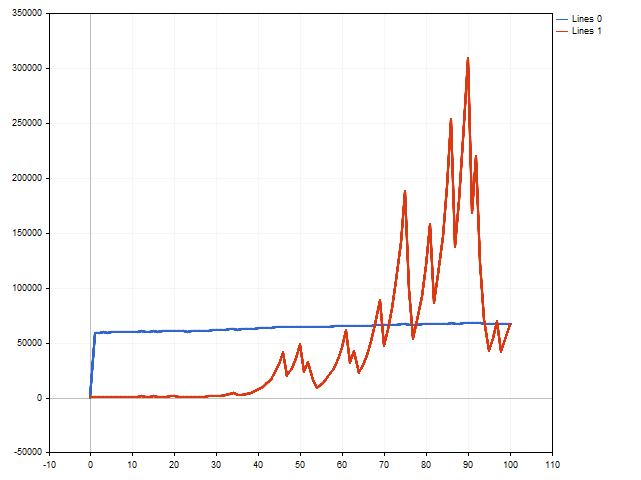
A première vue, l'option avec un stop loss et un take profit fixes (ligne bleue) est gagnante.
Toutefois, il convient de rappeler que nous avons utilisé le maximum de stop loss et le minimum de take profit possible. Que se passera-t-il si nous nous éloignons de ces limites en réduisant légèrement le stop loss et en augmentant le take profit ? La situation peut alors changer.
La ligne rouge montre les résultats des transactions avec un stop loss flottant, et la ligne orange montre les résultats des transactions avec un take profit flottant. Comme nous pouvons le constater, le take profit flottant peut avoir un impact positif sur les résultats de trading.
Attentes morales et gestion de l'argent
Divisons l'équation de l'attente morale en 2 parties. Appelons conditionnellement la première partie rentable :
La deuxième partie est appelée "non rentable" :
Si nous regardons de près la partie rentable, nous verrons qu'une augmentation du lot entraîne sa croissance. Cependant, la même augmentation du lot entraîne une diminution de la partie non rentable. Par conséquent, la partie non rentable peut prendre une valeur nulle (ou même négative). Dans ce cas, l'attente morale d’une transaction devient négative. Comme on s'en souvient, ce n'est pas le meilleur choix et les traders rationnels ne l'approuvent pas.
Notre prochaine idée est de trouver un certain lot de sorte que les parties rentables et non rentables de l'équation prennent simultanément les valeurs maximales possibles. L'espérance morale sera alors maximale pour une valeur donnée de SL et TP. Sur l'image, vous pouvez voir comment l'espérance morale évolue à mesure que la taille du lot augmente.
L'expérience numérique a donné un résultat positif. Déterminons maintenant l'équation de la taille optimale de la position. Pour ce faire, nous devons trouver la dérivée de l'espérance morale par rapport à la variable du lot, l'égaliser à zéro et résoudre l'équation résultante. Nous obtenons ainsi l'expression suivante :
Intéressons-nous à la partie de l'expression entre crochets. Nous voyons ici l'espérance mathématique divisée par le stop loss et le take profit. Veuillez noter que pour le calcul correct du lot, l'espérance mathématique de la transaction doit être strictement positive. En d'autres termes, la condition suivante doit toujours être remplie :
D'ailleurs, si nous développons la fraction entre crochets, nous obtenons le Critère de Kelly :
Essayons maintenant de simuler une série de transactions, dans lesquelles le lot est géré à l'aide de l'espérance morale. Nous verrons ici une variété de résultats. Par exemple, le dépôt initial peut être multiplié par plus de 160.
Mais plusieurs transactions perdantes d'affilée peuvent affecter le résultat de manière négative. Dans la figure suivante, nous pouvons voir que le dépôt initial a été multiplié par cinquante environ. C'est très bien. Si l'on ne tient pas compte du fait qu'à l'approche de la 90e étape, le dépôt initial a été multiplié par près de trois cents.
Gestion des risques
Comme nous pouvons le constater, la gestion de l'argent par le biais d'attentes morales peut conduire à la fois à des gains impressionnants et à des pertes très tangibles. Cela soulève donc la question de la gestion des risques.
Il y a deux façons de procéder. La première (la plus évidente) consiste à ne pas utiliser la totalité du dépôt disponible dans les calculs, mais seulement une partie. Par exemple, vous pouvez fixer un montant fixe. Vous pouvez également fixer un pourcentage du solde actuel. Dans tous les cas, cela vous aidera à réduire les risques lors de vos transactions.
La deuxième option de gestion du risque consiste à modifier le calcul de la probabilité d'une transaction rentable. Examinons cette option plus en détail.
Supposons que n est le nombre total de transactions, et que m est le nombre de transactions gagnantes. Nous pouvons alors évaluer la probabilité de gagner comme suit :
Mais cette approche n'est pas tout à fait correcte. Nous pouvons estimer la fréquence d'événements qui se sont déjà produits. Mais au lieu de cela, nous devons obtenir la probabilité de gagner dans une transaction future.
Supposons que vous ayez déjà effectué 15 transactions, dont 10 ont été gagnantes. Vous êtes sur le point d'ouvrir la position suivante. Le nombre total de transactions augmente alors de 1, mais le nombre de transactions gagnantes peut soit augmenter, soit rester identique.
Prenons la moyenne de ces options et la probabilité de gain pour la position ouverte sera alors la suivante :
Nous obtenons ainsi l'Estimateur Krichevsky-Trofimov qui, sous forme symbolique, se présente comme suit :
L'ajout d'un décalage a permis de réduire légèrement la probabilité de gagner, ce qui a réduit le risque.
Généralisons l'estimation de la probabilité comme suit : introduisons un décalage arbitraire s >= 1. La probabilité de gagner est alors la suivante :
En fixant s, nous pouvons réguler le risque dans une fourchette assez large : plus la valeur de s est grande, plus le risque est faible.
Malheureusement, la réduction du risque affecte également le montant des bénéfices perçus. Par conséquent, tout trader est confronté à un choix : un risque élevé permet de réaliser des bénéfices importants, mais les pertes peuvent également être très lourdes. Un risque faible vous permet de réduire les pertes, mais le bénéfice sera alors faible.
Voyons comment le risque peut influer sur les transactions. J'utiliserai l’Expert Advisor le plus simple à l'intersection de deux moyennes mobiles. L'EA a été testé avec les paramètres suivants :
Paire de devises : EURUSD
Période : H1
Période de test : 01/01/2021 - 31/12/2022
Tous les autres paramètres sont des valeurs par défaut.
Il y a eu 419 transactions pendant la période de test. Le graphique du solde se présente comme suit :
Les résultats suivants ont été obtenus pour différentes valeurs de risque.
| Risque | Bénéfice Net Total | Drawdown Absolu du Solde | Facteur de Profit | Bénéfice Attendu | Facteur de Récupération | Niveau de Marge |
|---|---|---|---|---|---|---|
| 0 | 42 961,51 | 2 699,05 | 1,18 | 102,53 | 1,72 | 89,20% |
| 25 | 28 932,51 | 570,27 | 1,21 | 69,05 | 1,89 | 260,70% |
| 50 | 16 836,83 | 230,64 | 1,21 | 40,18 | 1,92 | 309,53% |
Comme on peut le constater, la réduction du risque réduit les bénéfices, mais peut améliorer d'autres paramètres d'une stratégie de trading.
Conclusion
Les programmes suivants ont été utilisés pour la rédaction de cet article :
| Nom | Type | Description |
|---|---|---|
| ME SL-TP | Scénario | Le script montre comment la rentabilité du trading peut changer si les valeurs du stop loss et du take profit sont sélectionnées en fonction de l'attente morale du trade. Paramètres du script :
|
| ME Lot | Scénario | Le script montre comment la taille de la position affecte l'espérance morale d'une transaction. |
| ME MM | Scénario | Le script compare la gestion de l'argent par espérance morale et le trading par lots fixes. A la fin du travail, un message s'affiche avec le résultat du trading pour les deux options, ainsi que la taille d'un lot fixe rationnel. |
| Système à 2 moyennes mobiles | Expert Advisor | L'EA permet d'évaluer l'impact du risque sur les performances de trading. Ses paramètres sont :
|
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/12134
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
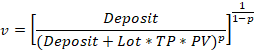


Cela dépend de la probabilité d'un trade rentable et du dépôt. L'utilisation d'un stop loss important est due au fait qu'un petit mouvement de prix est plus probable. En d'autres termes, avec un ratio TP = 20 * SL, nous avons plus de chances de clôturer la position en prenant des bénéfices. Mais cela s'applique déjà à la théorie du butinage optimal.
Un nouvel article intitulé " Moral Expectations in Trading" a été publié :
Par Aleksej Poljakov
Théorie du trading très originale, bravo !
Non, article vraiment intéressant) Mais attente morale.... Il n'y a pas de tel terme, pas dans le supérieur, et seulement en maths) Qu'en est-il des indikitars, des nouvelles économiques alors ? Vous n'en avez rien à faire ? ))))
Vous êtes l'otage des manuels.
Rien ne vous empêche de décrire un phénomène et de lui donner un terme.
Surtout dans un environnement aussi étroit
Non, article vraiment intéressant) Mais attente morale.... Il n'y a pas de terme de ce type, pas dans le supérieur, et seulement en maths) Qu'en est-il des indikitars, des nouvelles économiques alors ? Vous n'en avez rien à faire ? ))))
indicateurs - cela existe
https://www.mql5.com/fr/articles/14494
Je ne vais pas écrire sur les nouvelles - c'est trop compliqué, toute cette logique floue et ainsi de suite.... Je préfère vous parler des cycles.
Et de terminologie. Il y a l'"espérance morale".