MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 85): Verwendung von Mustern des Stochastik-Oszillators und der FrAMA mit Beta-VAE-Inferenzlernen

Einführung

Innerhalb des Ökosystems von MetaTrader 5 ist der MQL5-Assistent ein solides Werkzeug, das es Händlern ermöglicht, schnell neue Handelsideen zu entwickeln und umzusetzen. Wie wir bereits in früheren Artikeln beschrieben haben, geschieht dies alles, ohne dass wir uns mit Low-Level-Coding beschäftigen müssen. Im Kern nutzt der Assistent einen modularen Rahmen, der es Händlern ermöglicht, aus vordefinierten Signalklassen, Geldmanagementstrategien oder Trailing-Stop-Mechanismen zu wählen. Die Möglichkeit, einen Expert Advisor nach dem Plug-and-Play-Prinzip zusammenzustellen, hat die unbeabsichtigte Folge, dass der algorithmische Handel demokratisiert wird, was den Handel für Personen mit unterschiedlichen Fachkenntnissen zugänglicher macht, was langfristig zu einer Erhöhung der Marktliquidität führen dürfte, wenn alles andere gleich bleibt. 

In Teil 85 dieser Serie befassen wir uns mit einer erweiterten Anwendung des Assistenten, wie wir sie bereits in einigen früheren Artikeln beschrieben haben, indem wir maschinelles Lernen integrieren. Konkret geht es um den Beta-Variations-Auto-Encoder-Algorithmus eines Inferenzmodells, das wir in einem kürzlich erschienenen Artikel besprochen hatten, das wir nun aber zur Verarbeitung der binär kodierten Signale des Indikatorpaars aus unserem letzten Artikel verwenden. Zusammenfassend lässt sich sagen, dass der Beta-VAE als unüberwachtes Lernmodell angewendet wird, das hochdimensionale Eingabedaten in einen latenten Raum komprimiert. Auf diese Weise erfasst es zugrunde liegende Strukturen und Beziehungen, die herkömmliche regelbasierte Systeme übersehen könnten. Auf dem Papier soll dieser Automatisierungsprozess nicht nur die Mustererkennung verbessern, sondern auch die inferenzbasierte Entscheidungsfindung innerhalb unserer nutzerdefinierten Signalklassen unterstützen.

Wir verwenden das Indikator-Paar aus unserer letzten Ausgabe, Teil 84, in der wir wie üblich 10 wichtige, eindeutige Muster betrachtet haben, die wir von 0 bis 9 indiziert haben und die vom Stochastik Oszillator und dem Fractal Adaptive Moving Average abgeleitet wurden. Bei den von uns durchgeführten Vorwärtstest haben wir unterschiedliche Leistungen bei diesen 10 Mustern festgestellt. Die Muster von 0 bis 4 sowie von 7 bis 8 erwiesen sich als einigermaßen robust, da sie über die gesamte Bandbreite unserer Vermögenswerte hinweg profitabel waren, die wir ausgewählt hatten, um von den verschiedenen Marktregimen zu profitieren. Die Muster 5, 6 und 9 hinken jedoch stark hinterher, da sie in der Vorwärtsbewegung außerhalb der Stichprobe keine Rentabilität aufweisen.

Es sollte noch einmal betont werden, dass unser Testfenster sehr begrenzt ist. Daher sollten diese Ergebnisse bestenfalls als Hinweis darauf verstanden werden, welche Muster weiter getestet werden müssen, nicht aber, welche Muster zuverlässig sind. Die leistungsschwachen Muster zeigten sich als flache FrAMA mit Stochastik-Kreuzungen für Muster-5, überkaufte/überverkaufte Stochastik-Haken mit fallendem FrAMA für Muster-6 und extreme Stochastik-Oszillator-Niveaus mit entgegengesetzten FrAMA-Steigungen für Muster-9.

Diese Misserfolge könnten auf die mangelnde Flexibilität dieser Muster zurückgeführt werden. Es könnte aber auch sein, dass der Testumfang zu restriktiv war, und dass diese Muster und nicht einige unserer oben genannten „profitablen“ Muster auf lange Sicht belastbar sind. Diese Debatte kann der Leser am besten durch unabhängige Tests klären. Für unsere Zwecke untersuchen wir jedoch, wie maschinelles Lernen das Schicksal der Muster 5, 6 und 9 rehabilitieren könnte, wenn überhaupt.

Kaufsignal (Muster 5): Flaches FrAMA + Stochastik-Kreuz unter 30

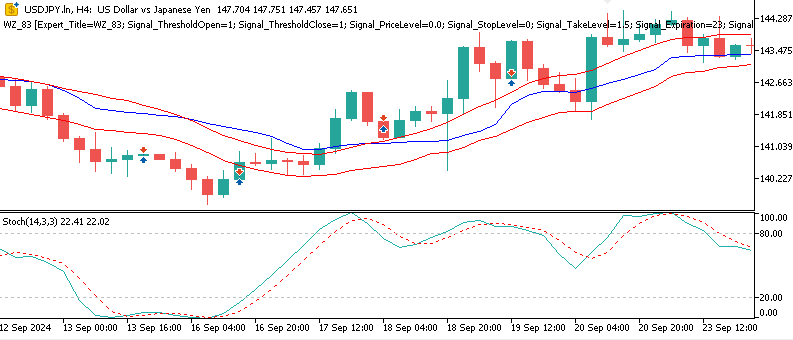
Verkaufssignal (Muster 6): Stochastik-Sptitze „M“ über 80 + steigendem FrAMA

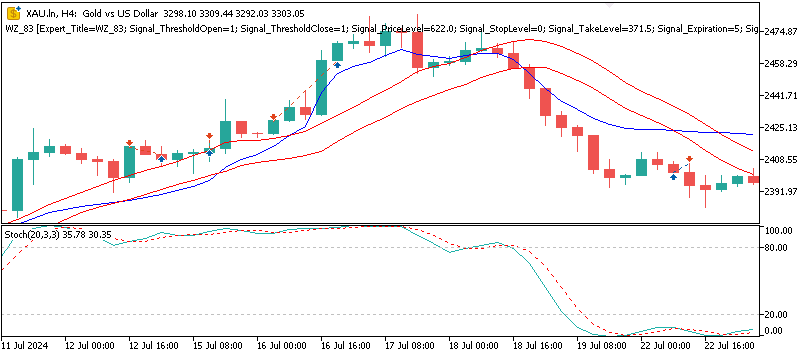
Verkaufssignal (Muster 9): Aufwärtstrend FrAMA + Stoch > 90 und fallend

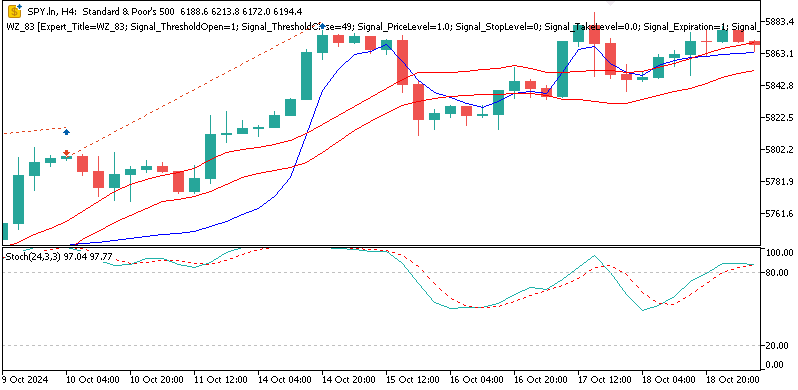
Die These für diesen Artikel lautet, dass der Beta-VAE in der Lage ist, binäre Indikatorwerte, die als Vektoren zusammengesetzt sind, in aussagekräftige latente Repräsentationen umzuwandeln. Da wir dank des Beta-Parameters, der auf ein Gleichgewicht zwischen Rekonstruktionsgenauigkeit und latenter Regularisierung abzielt, den Schwerpunkt auf entwirrte Merkmale legen, ist das Modell in der Lage, versteckte Handelsmuster und -strukturen aufzudecken. Wir können dies anhand historischer Daten für XAUUSD, SPX 500 und USDJPY nachweisen. Nach dem Training exportieren wir unser Modell über ONNX in eine nutzerdefinierte MQL5-Signalklasse für die Montage mit dem MQL5-Assistenten. Unsere Ergebnisse zeigten bescheidene Gewinne des Vorwärtstests für den Vermögenswert XAUUSD, was in gewisser Weise das Potenzial des Inferenzlernens bei der Feinabstimmung einiger unterdurchschnittlicher Rohsignalmuster unterstreicht.

Erkennen von Mustern

Für Modelle des maschinellen Lernens, die für Prognosen und nicht für die Mustererkennung verwendet werden, sind vektorisierte kontinuierliche Eingaben, die normalisierte Preis- oder Indikatorwerte enthalten können, normalerweise der erste Schritt zur Integration des maschinellen Lernens. Sie ermöglichen es, dass große Reihen von Zeitreihendaten ohne manuelle Verzweigungen in das Modell einfließen. Auf diese Weise können die Algorithmen eigenständig Beziehungen zwischen den stochastischen Oszillationen und der Form des FrAMA sowie der Volatilität der Preisbewegung ableiten.

Diese Struktur ist natürlich skalierbar, denn sobald die Indikatorvektoren ausgerichtet und gefenstert sind, können in Python mehrere Balken innerhalb weniger Millisekunden gleichzeitig verarbeitet werden. Beim Export nach MQL5 liefern die Methoden „on-new-bar“ des Strategietesters keine ähnliche Leistung. Bei diesem Ansatz bräuchten wir jedoch keine Wenn-Klauseln, um beispielsweise zu entscheiden, ob der stochastische K-Wert über dem D-Wert liegt oder ob der FrAMA-Wert abflacht, usw. All diese Informationen sind in den Gleitkomma-Tensoren enthalten. Für Systeme, die auf GPUs trainiert werden, bieten diese Tensoren einen eleganten, kompakten Speicherplatz, nicht nur für die Pufferung der Eingaben, sondern vor allem für die Speicherung von Trainingsdeltas, die eine kontinuierliche Berechnung der Unterschiede zwischen Ausgang und Ziel verhindern. 

Dennoch birgt die Eleganz eine gewisse Brüchigkeit. Die kontinuierliche Natur dieser Eingangsvektoren impliziert, dass sie nie rein sind, da sie Marktrauschen, Indikatorverzögerungen und Rundungsartefakte enthalten, die dazu neigen, falsche Korrelationen zu imitieren. In diesem Zusammenhang kann schon ein einziges falsch skaliertes Merkmal den Mittelwert verschieben, die Trainingsgradienten verfälschen und zu einer illusorischen Präzision führen. In Fällen, in denen die Eingabedaten in volatilen Regimen erfasst werden, kann das Modell Fluktuationen lernen, die im Training vorhersagbar erscheinen, sich aber im Live-Handel als nutzlos erweisen. Darüber hinaus können kontinuierliche Signale logische Grenzen verwischen – ein K von 69,8 und 70,1 kann die Klassifizierung ändern, ohne dass sich der Trend sinnvoll ändert. Die Verwendung kontinuierlicher Eingabedaten kann, wie wir in den letzten Artikeln hervorgehoben haben, zu Systemen führen, die in der Simulation gut abschneiden und dennoch schwanken, wenn sich das Marktregime ändert, weil die Glätte der Fließkommazahlen das diskrete Marktverhalten unterdrückt. Das Modell würde, wie manche sagen, „halluzinieren“, indem es z. B. Prognosen auch bei zufälligen Daten angibt.

Ein pragmatischer „Mittelweg“, den wir in diesem Artikel erkunden und in der Vergangenheit empfohlen haben, ist die Destillation der Fließkomma-Eingabedaten in boolesche/binäre Vektoren, die wie Fingerabdrücke für bestimmte Ereignisse wirken. Anstatt das Modell mit erschöpfenden Zahlenbereichen zu füttern, übersetzen wir Muster wie eine Überkreuzung der stochastischen Puffer oder eine Abflachung der FrAMA in eine 1, wenn vorhanden, oder eine 0, wenn nicht vorhanden. Jedes Bit im vermuteten Vektor dieser Werte stellt also eine genau definierte Bedingung dar, die bereits durch eine kleine „if“-Klausel überprüft wurde, die in die Vorverarbeitungsfunktionen aufgenommen wurde. Durch diese binären Muster wird ein niedrigdimensionaler und wohl auch rauschresistenter Input gefälscht, und es wird mehr Wert auf Struktur als auf Größe gelegt. Im Gegensatz zu schwankenden Werten können mit dem Beta-VAE-Modell die zugrunde liegenden Beziehungen zwischen Ereigniskombinationen erlernt werden. Wenn man diese in einem latenten Raum komprimiert, kann man die Marktmodi zuverlässiger widerspiegeln.

Während die Vektorisierung kontinuierlicher Daten uns die Skalierung und die Leistung der Berechnung ermöglicht, da wir die if-Klauseln vollständig umgehen, bringt die binäre Vektorisierung Klarheit in die Entscheidungen. Es ist in der Lage, rohes numerisches „Chaos“ in eine Form von „symbolischer Ordnung“ umzuwandeln, wobei jede 1 oder 0 eine Bedeutung kodiert. Außerdem hängt die Schlussfolgerung nicht nur von empfindlichen Schwellenwerten ab, sondern auch von der bereits kodierten Logik der entscheidenden „Wenn“-Klauseln.

Nachteile des stochastischen Oszillators

Dieser Oszillator, der von George Lane entwickelt wurde, basiert auf dem Momentum. Er misst die Position des Schlusskurses im Vergleich zu seiner jüngsten Spanne und zeigt so die Wahrscheinlichkeit einer Umkehr an. Zusammenfassend lässt sich dies für den Hauptpuffer K wie folgt berechnen:

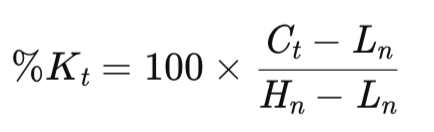
wobei:

• Ct = aktueller Abschluss,
• Hn = höchster Stand in den letzten n Perioden,
• Ln = tiefster Stand in den letzten n Perioden,

Unser Rückblickszeitraum n ist häufig auf 20 voreingestellt, aber wir haben diesen Wert in den letzten beiden Artikeln, in denen wir diese Indikatorpaarung eingeführt haben, als einstellbaren Hyperparameter belassen. Dies ist nicht unbedingt die beste Praxis, da es zu einer Kurvenanpassung führen kann. Der verwendete Rückblickzeitraum wird jedoch über „m“-Perioden geglättet. Dieser Wert ist häufig auf 3 voreingestellt, was wir für unsere Zwecke beibehalten haben. Durch die Glättung erhalten wir ein verfeinertes oder weniger volatiles K. Der D-Puffer, den wir in Teil 83 behandelt haben, hinkt dem K als geglätteter gleitender Durchschnitt hinterher, ebenfalls über einen Zeitraum von 3, den wir standardmäßig beibehalten haben. Er dient dazu, Spitzen im K-Puffer mit Hilfe von Kreuzungen zu lokalisieren. Wie alle stochastischen Oszillatoren gibt er Werte im Bereich von 0-100 aus, wobei die Werte 80 und 20 als wichtige Schwellenwerte dienen.

Auch wenn es sich um einen sehr einfachen Indikator handelt, kann dieser Indikator große Schwächen aufweisen. Wenn sich die Märkte in einem Trend befinden, haben sie die Angewohnheit, stark nachzuziehen. Wenn diese Trends z. B. nach oben gerichtet sind, können sich die K-Puffer-Werte über einen längeren Zeitraum an den oberen Niveaus, d. h. 80 und darüber, „festhalten“, trotz der Überkreuzungen, die innerhalb dieses Bandes rückgängig gemacht werden, ohne auf niedrigere Niveaus zu stoßen. Dies führt zu anhaltenden falschen Verkaufssignalen, da das Momentum weiter anhält. Auf der anderen Seite drücken Abwärtstrends den K-Puffer unter die 20er-Marke, was in der Tat Kaufanreize verzögert, weil wir wieder mit einem Syndrom der kaputten Uhr enden, bei dem viele falsche Signale erzeugt werden, bevor sie schließlich richtig sind.

Diese Verzögerung könnte auf die spannenbasierte Formel zurückzuführen sein, die den Schlusskurs gegenüber seinen Extremwerten normalisiert, aber die Trendpersistenz ignoriert. Dies führt zu „festgefahrenen Messwerten“. Unsere Python-Implementierung ist in der Lage, die K- und D-Puffer als vektorisierte Reihen zu erfassen. Wir haben eine nutzerdefinierte Klasse „SignalFrAMAStochastic“ mit Funktionen wie „cross-up-series“ implementiert, bei der die Verschiebungen von Balken zu Balken wechseln. Nichtsdestotrotz neigt das reale Marktrauschen bei Live-Tests dazu, das Rauschen falscher Kreuzungen zu verstärken, wenn die Märkte im Trend sind. Wir implementieren dies in Python wie folgt;

def Stochastic(
    df: pd.DataFrame,
    k_period: int = 20,
    d_period: int = 3,
    smooth_k: int = 3,
    source_col: str = "close",
    only_stochastic: bool = False
) -> pd.DataFrame:
    """
    Compute Stochastic Oscillator (%K and %D) and append columns to the DataFrame.

    Parameters
    ----------
    df : pd.DataFrame
        Input DataFrame; must include columns 'high', 'low', and the `source_col` (default 'close').
    k_period : int
        Lookback period for %K (highest high / lowest low). Default 14.
    d_period : int
        Period for %D (moving average of %K). Default 3.
    smooth_k : int
        Smoothing window applied to raw %K before computing %D. Default 3.
    source_col : str
        Price column to use for close values (default 'close').
    only_stochastic : bool
        If True, return only the Stochastic columns.

    Returns
    -------
    pd.DataFrame
        DataFrame with appended columns: 'Stoch_%K', 'Stoch_%K_smooth', 'Stoch_%D'
    """
    required_cols = {"high", "low", source_col}
    if not required_cols.issubset(df.columns):
        raise ValueError(f"DataFrame must contain columns: {required_cols}")
    if not all(isinstance(p, int) and p > 0 for p in (k_period, d_period, smooth_k)):
        raise ValueError("k_period, d_period, and smooth_k must be positive integers")

    out = df.copy()

    low_k = out["low"].rolling(window=k_period, min_periods=k_period).min()
    high_k = out["high"].rolling(window=k_period, min_periods=k_period).max()

    # Raw %K (0-100)
    raw_k = (out[source_col] - low_k) / (high_k - low_k)
    raw_k = raw_k * 100.0

    # Smoothed %K (optional smoothing)
    stoch_k = raw_k.rolling(window=smooth_k, min_periods=smooth_k).mean()
    # %D is SMA of smoothed %K
    stoch_d = stoch_k.rolling(window=d_period, min_periods=d_period).mean()

    out['raw_k'] = raw_k
    out["k"] = stoch_k
    out["d"] = stoch_d

    if only_stochastic:
        return out[["raw_k", "k", "d"]].copy()
    return out

class SignalFrAMAStochastic:
    # constructor unchanged — can accept pandas Series too
    def __init__(
        self,
        frama: Sequence[float],
        close: Sequence[float],
        high: Sequence[float],
        low: Sequence[float],
        k: Sequence[float],           # Stochastic %K series
        pips: float,
        point: float,
        past: int,
        x_index: int = 0
    ):
        # store as pandas.Series if possible to help with vectorized operations
        if isinstance(frama, pd.Series): self.frama = frama
        else: self.frama = pd.Series(frama) 
        if isinstance(close, pd.Series): self.close = close
        else: self.close = pd.Series(close)
        if isinstance(high, pd.Series): self.high = high
        else: self.high = pd.Series(high)
        if isinstance(low, pd.Series): self.low = low
        else: self.low = pd.Series(low)
        if isinstance(k, pd.Series): self.k = k
        else: self.k = pd.Series(k)

        self.m_pips = pips
        self.point = point
        self.m_past = past
        self._x = x_index

    # ------------------------
    # Small helpers (vectorized)
    # ------------------------
    @staticmethod
    def cross_up_series(a: pd.Series, b: pd.Series) -> pd.Series:
        """
        Vectorized CrossUp: True where a crossed up b between previous and current bar.
        Equivalent MQL: (a1 <= b1) && (a0 > b0)
        In pandas chronological order: a.shift(1) = previous a, a = current a
        """
        a_prev = a.shift(1)
        b_prev = b.shift(1)
        return (a_prev <= b_prev) & (a > b)

    
    # Trimmed code... 


    # ------------------------
    # Vectorized divergence detection
    # ------------------------
    def bullish_divergence_series(self) -> pd.Series:
        """
        Vectorized detection of bullish divergence:
        - Find local lows (low < low.shift(1) & low < low.shift(-1))
        - For consecutive pairs of local lows (older -> newer), mark the time of the *second*
          low True when:
            low_old < low_new  (price makes lower low)
            K_old   > K_new    (oscillator makes higher low)
        This mirrors the MQL routine that finds two local lows within a lookback and checks them.
        """
        low = self.low
        k = self.k
        # boolean mask of local minima
        is_local_min = (low < low.shift(1)) & (low < low.shift(-1))
        local_idx = np.flatnonzero(is_local_min.to_numpy(copy=False))
        # prepare result array
        res = np.zeros(len(low), dtype=bool)

        # We will iterate adjacent pairs of local extrema (sparse).
        # Only consider pairs where the two minima are not more than (m_past+? ) apart is optional;
        # Here we mimic original by not imposing an explicit global window; user can post-filter if needed.
        for i in range(1, len(local_idx)):
            older = local_idx[i - 1]
            newer = local_idx[i]
            # compare values (note: these are numpy indices; preserve pandas indexing by assigning by position)
            if low.iat[older] < low.iat[newer] and k.iat[older] > k.iat[newer]:
                # mark the time of the newer local low
                res[newer] = True

        return pd.Series(res, index=low.index)

    def bearish_divergence_series(self) -> pd.Series:
        """
        Vectorized detection of bearish divergence:
        - Find local highs (high > high.shift(1) & high > high.shift(-1))
        - For consecutive pairs of local highs (older -> newer), mark the time of the *second*
          high True when:
            high_old > high_new (price makes higher high)
            K_old   < K_new   (oscillator makes lower high)
        """
        high = self.high
        k = self.k
        is_local_max = (high > high.shift(1)) & (high > high.shift(-1))
        local_idx = np.flatnonzero(is_local_max.to_numpy(copy=False))
        res = np.zeros(len(high), dtype=bool)

        for i in range(1, len(local_idx)):
            older = local_idx[i - 1]
            newer = local_idx[i]
            if high.iat[older] > high.iat[newer] and k.iat[older] < k.iat[newer]:
                res[newer] = True

        return pd.Series(res, index=high.index)

    # ------------------------
    # Convenience wrappers for CrossUp/Down using stored Series
    # ------------------------
    def cross_up(self, a_col: pd.Series, b_col: pd.Series) -> pd.Series:
        return self.cross_up_series(a_col, b_col)

    def cross_down(self, a_col: pd.Series, b_col: pd.Series) -> pd.Series:
        return self.cross_down_series(a_col, b_col)

Die Leistung dieses Indikators kann auch zwischen verschiedenen Marktregimen stark divergieren. Wenn sich das Devisenpaar USDJPY beispielsweise in einer Phase geringer Volatilität befindet, kann die Stochastik glänzen, da überverkaufte und überkaufte Phasen häufig vorkommen und in der Regel gut mit Gleichgewichtsausschlägen übereinstimmen. Bei momentumgesteuerten Setups, zu denen auch die seltenen Ausbrüche von XAUUSD gehören können, wird er jedoch häufig ins Stocken geraten, weil er die Beschleunigung mit Umkehrungen verwechselt. Die Rücktests im letzten Artikel haben gezeigt, dass die Muster 5 und 9 stark von den extremen Werten unter 10 und nach 90 abhängen. Die Kreuzungen waren unterdurchschnittlich und die unrentablen Vorwärtstests, die wir bekamen, können auf Regime-Mismatches zurückgeführt werden, wir waren im Trend und nicht in der Range. Der Aufwärtstrend des SPX 500 in diesem Jahr, insbesondere seit den Tiefstständen im April, verschärfte dies noch, da der Stochastik-Oszillator aufgrund seiner Empfindlichkeit gegenüber kurzfristigen Marktstörungen dazu führen kann, dass er breitere Marktimpulse ignoriert. 

Um diese Mängel zu beheben, ist der kontextbezogene Filter des FrAMA von entscheidender Bedeutung. Unser adaptiver Durchschnittsindikator, der Alpha auf Basis fraktaler Dimensionen verwendet, passt seine Glättung an die Marktstruktur an. Der Mittelungszeitraum wird bei gleichmäßigen Trends verkürzt und bei unruhigen Märkten verlängert, um die allgemeine Marktentwicklung zu erfassen. Indem wir die Neigung des FrAMA oder seine Flachheit überlagern, sorgen wir dafür, dass die stochastischen Signale, wie die Validierung des Musters 5, nur dann Kreuze machen, wenn der FrAMA flach ist. Wir filtern im Wesentlichen volatilitätsbedingtes Rauschen. Diese symbiotische Beziehung prägt die Eingaben in das Beta-VAE-Modell, bei dem die binären Flaggen Interaktionen kodieren, die „regime-aware“ sind, was wiederum ein latentes Lernen ermöglicht, eine Entflechtung der Verzögerung zwischen echten Kanten, was auf dem Papier Expertenberater widerstandsfähiger machen sollte.

FrAMA in Python

Mit unserem adaptiven gleitenden Durchschnitt vollziehen wir einen Paradigmenwechsel von der statischen Glättung hin zu einer dynamischen und damit reaktionsfähigeren. Dieser Indikator stützt sich auf die Chaostheorie, indem er die fraktale Dimension einbezieht, um das Volumen des Marktrauschens gegenüber der Marktstruktur zu beziffern. Für ein Fenster von n Balken ist die typische Vorgabe also ebenfalls 20 wie bei der Stochastik, aber FrAMA halbiert diesen Zeitraum in zwei. Dies ermöglicht die Berechnung der Entfernungsverhältnisse N1 und N2 in den Teilfenstern sowie N(1+2) für das gesamte Fenster. Um noch einmal auf unseren früheren Artikel zurückzukommen: D ist definiert als:

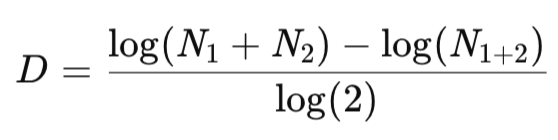
Dabei sind N1 und N2 die oben genannten Bereichsverhältnisse. Seine Werte werden zwischen 1 für einen gleichmäßigen Trend und 2 als Indikator für reines Rauschen festgelegt. Alpha, das adaptive Gewicht, ist ebenfalls von 0,01 bis 1,0 begrenzt, und wir verwenden dies zusammen mit den Puffern für die Preismittelung, um einen adaptiven Durchschnitt auszugeben, wie bereits in früheren Artikeln hervorgehoben wurde, insbesondere im vorletzten Artikel, der zum Zeitpunkt der Erstellung dieses Artikels noch nicht veröffentlicht wurde. In MQL5 haben wir diese Formel ohne Rücksicht auf all ihre Feinheiten mit Hilfe der eingebauten Indikatorklasse „CiFrAMA“ implementiert. Mit Python ist unser Ansatz jedoch folgender:

def FrAMA(
    df: pd.DataFrame,
    period: int = 20,
    price_col: str = "close",
    min_alpha: float = 0.01,
    max_alpha: float = 1.0,
    only_frama: bool = False
) -> pd.DataFrame:
    """
    Compute Fractal Adaptive Moving Average (FRAMA) per John Ehlers' formulation.

    Parameters
    ----------
    df : pd.DataFrame
        Input DataFrame; must include 'high', 'low', and price_col (default 'close').
    period : int
        Window length used to compute fractal dimension (commonly 16). Must be >= 4.
    price_col : str
        Column name to use as price (commonly 'close').
    min_alpha : float
        Minimum alpha clamp (commonly 0.01).
    max_alpha : float
        Maximum alpha clamp (commonly 1.0).
    only_frama : bool
        If True, return only the FRAMA column.

    Returns
    -------
    pd.DataFrame
        DataFrame with appended column: 'FRAMA'
    """
    required_cols = {"high", "low", price_col}
    if not required_cols.issubset(df.columns):
        raise ValueError(f"DataFrame must contain columns: {required_cols}")
    if not (isinstance(period, int) and period >= 4):
        raise ValueError("period must be an integer >= 4")
    if not (0.0 < min_alpha <= max_alpha <= 1.0):
        raise ValueError("min_alpha and max_alpha must satisfy 0 < min_alpha <= max_alpha <= 1")

    out = df.copy()
    n = period
    half = n // 2

    price = out[price_col].to_numpy(dtype=float)
    high = out["high"].to_numpy(dtype=float)
    low = out["low"].to_numpy(dtype=float)
    length = len(out)

    frama = np.full(length, np.nan, dtype=float)

    # Seed: before we have enough bars, set FRAMA to price (common practice)
    # We'll start the loop at index 0 and set initial FRAMA to price[0].
    if length == 0:
        out["frama"] = frama
        return out if not only_frama else out[["frama"]].copy()

    frama[0] = price[0]

    # iterate; we need at least 'n' bars to compute a fractal dimension
    for i in range(1, length):
        if i < n:
            # not enough history to compute full fractal measure -> fallback to price
            frama[i] = price[i]
            continue

        start = i - n + 1
        # first half window: start .. start+half-1
        fh_start = start
        fh_end = start + half - 1
        # second half window: start+half .. i
        sh_start = fh_end + 1
        sh_end = i

        # compute ranges per sub-window (using highs and lows)
        mH = np.max(high[fh_start: fh_end + 1])   # max high in first half
        mL = np.min(low[fh_start: fh_end + 1])    # min low in first half
        N1 = (mH - mL) / float(max(1, half))

        HH = np.max(high[sh_start: sh_end + 1])   # max high in second half
        LL = np.min(low[sh_start: sh_end + 1])    # min low in second half
        N2 = (HH - LL) / float(max(1, half))

        # entire window:
        Mx = np.max(high[start: i + 1])
        Mn = np.min(low[start: i + 1])
        N3 = (Mx - Mn) / float(max(1, n))

        # compute fractal dimension D according to Ehlers:
        # D = (log(N1 + N2) - log(N3)) / log(2)
        # Use guard clauses when N1, N2, N3 are zero or negative
        if (N1 > 0.0) and (N2 > 0.0) and (N3 > 0.0):
            D = (np.log(N1 + N2) - np.log(N3)) / np.log(2.0)
        else:
            # fallback to D = 1 (line-like) when not computable
            D = 1.0

        # alpha conversion using Ehlers' exponential mapping (clamped)
        alpha = np.exp(-4.6 * (D - 1.0))
        if alpha < min_alpha:
            alpha = min_alpha
        if alpha > max_alpha:
            alpha = max_alpha

        # EMA-like update
        frama[i] = alpha * price[i] + (1.0 - alpha) * frama[i - 1]

    out["frama"] = frama
    if only_frama:
        return out[["frama"]].copy()
    return out

Die Hauptstärke von FrAMA liegt wohl in seiner chamäleonartigen Anpassungsfähigkeit an einen Trend. Bei effizienten Trends, bei denen D niedrig ist und Alpha gegen 0,01 schrumpft, kopiert FrAMA einen langperiodischen einfachen gleitenden Durchschnitt, eine Form der verzögerungsreduzierten Nachbildung. Auf der anderen Seite würde sich im fraktalen Chaos, wenn D seine Höchststände erreicht, Alpha dem Wert 1,0 annähern, und der FrAMA würde sich im Wesentlichen wie ein schneller EMA verhalten, der den Preis umarmt, um Wipsaws auszuweichen. In Fällen, in denen es zu einem Regimewechsel kommt, ist dies tendenziell besser als gleitende Durchschnitte mit festen Rückblickszeiträumen. Ein Beispiel: Wenn wir uns auf die volatilen Ausschläge des XAUUSD in diesem Jahr konzentrieren, als der Goldpreis seinen Aufwärtstrend begann, reagieren die hohen Alphawerte des FrAMA besser und würden leicht mit der Verzögerung der Stochastik oder dem Syndrom der kaputten Uhr fertig werden, das wir oben hervorgehoben haben. Wir implementieren dies in Python wie folgt

class SignalFrAMAStochastic:
    # constructor unchanged — can accept pandas Series too
    def __init__(
        self,
        frama: Sequence[float],
        close: Sequence[float],
        high: Sequence[float],
        low: Sequence[float],
        k: Sequence[float],           # Stochastic %K series
        pips: float,
        point: float,
        past: int,
        x_index: int = 0
    ):
        # store as pandas.Series if possible to help with vectorized operations
        if isinstance(frama, pd.Series): self.frama = frama
        else: self.frama = pd.Series(frama) 
        if isinstance(close, pd.Series): self.close = close
        else: self.close = pd.Series(close)
        if isinstance(high, pd.Series): self.high = high
        else: self.high = pd.Series(high)
        if isinstance(low, pd.Series): self.low = low
        else: self.low = pd.Series(low)
        if isinstance(k, pd.Series): self.k = k
        else: self.k = pd.Series(k)

        self.m_pips = pips
        self.point = point
        self.m_past = past
        self._x = x_index

    # Trimmed Code...

    @staticmethod
    def frama_slope_series(frama: pd.Series) -> pd.Series:
        """
        Vectorized FrAMASlope: FrAMA(t) - FrAMA(t-1)  (maps MQL FrAMA(ind) - FrAMA(ind+1))
        Note: first value will be NaN because shift(1) yields NaN at the start.
        """
        return frama - frama.shift(1)

    def flat_frama_series(self, window: Optional[int] = None) -> pd.Series:
        """
        Return boolean Series: True where absolute FRAMA slope stayed <= tol
        for `window` bars including current bar and previous (window-1) bars.
        - window default: self.m_past
        - tol = self.m_pips * self.point
        """
        if window is None:
            window = self.m_past
        tol = self.m_pips * self.point
        slope = self.frama_slope_series(self.frama).abs()
        # rolling max over the last `window` bars (includes current and previous window-1)
        # need min_periods=window to mimic MQL conservative behavior
        rolling_max = slope.rolling(window=window, min_periods=window).max()
        return rolling_max <= tol

    def far_above_series(self, mult: float) -> pd.Series:
        """
        Vectorized FarAboveFrama for every row:
        dist = abs(close - frama)
        atr = high.shift(1) - low.shift(1)   (previous bar's range, matching MQL's ind+1)
        condition: close > frama AND dist > mult * point * atr / 4
        """
        dist = (self.close - self.frama).abs()
        atr = (self.high.shift(1) - self.low.shift(1))
        # avoid divide-by-zero; treat atr<=0 as False
        cond = (self.close > self.frama) & (atr > 0) & (dist > (mult * self.point * atr / 4.0))
        # fill NaNs with False
        return cond.fillna(False)

    def far_below_series(self, mult: float) -> pd.Series:
        """
        Vectorized FarBelowFrama for every row:
        condition: close < frama AND dist > mult * point * atr / 4
        """
        dist = (self.close - self.frama).abs()
        atr = (self.high.shift(1) - self.low.shift(1))
        cond = (self.close < self.frama) & (atr > 0) & (dist > (mult * self.point * atr / 4.0))
        return cond.fillna(False)

    # ------------------------
    # Vectorized divergence detection
    # ------------------------
  
    # Trimmed code...

Bei den Signalmustern, auf die wir uns in den letzten Artikeln und auch in diesem Artikel bezogen haben, helfen die Hilfsfunktionen „flat FrAMA series“ und „FrAMA slope series“ bei der Ermittlung der Bereiche für Muster 5 bzw. der Steigungen für Muster 9.

Archetypen des Marktes

Die von den Märkten gezeigten Verhaltensweisen lassen sich in eine Vielzahl von Taxonomien einteilen. In den letzten beiden Artikeln und in diesem Artikel haben wir uns im Prinzip nur auf drei konzentriert. Trend vs. Rückkehr zum Mittelwert, Autokorreliert vs. Entkoppelt und Hohe vs. Niedrige Volatilität. Marktregimes, die sich in einem Trend befinden, können anhaltende Richtungsbewegungen aufweisen, bei denen Indikatoren wie die positive Steigung des FrAMA ein dominantes Merkmal sind, was mit den Spielregeln für das Momentum übereinstimmt, aber falsche Umkehrsignale der Stochastik nicht berücksichtigt. Auf der anderen Seite fluktuieren Marktphasen mit Mittelwertumkehr um einen Gleichgewichtspunkt, und dies begünstigt die überkauften/überverkauften Ausschläge des Stochastik-Oszillators, insbesondere wenn der FrAMA im Wesentlichen flach ist.

Korrelationen zeigen die Interdependenz von Vermögenswerten auf. So wird zum Beispiel viel über die unheimliche Korrelation zwischen Aktien und vermeintlichen Absicherungen wie Bitcoin gesprochen. Die beiden bewegen sich stark parallel zueinander, entgegen dem akademischen Argument, dass Bitcoin eine Absicherung gegen die US-Wirtschaft und die „fiskalische Verantwortungslosigkeit“ ist. Wären die beiden wirklich entkoppelt, würde das Halten von beiden eine effektive Form der Diversifizierung darstellen. Innerhalb des SPX 500 gibt es gelegentlich Sektoren, die negative Korrelationen aufweisen könnten, und diese Veränderungen waren das Argument für unsere Verwendung dieses Vermögenswerts in den letzten Artikeln für die Autokorrelationsmuster 2, 3 und 9.  

Diese Vielfalt an Markttypen spricht für ein „breites Testuniversum“, um das Musterlernen unseres Beta-VAE zu testen und zu validieren. Wir argumentierten, dass diese Markttypen jeweils für bestimmte Vermögenswerte geeignet sind, und so wählten wir drei Vermögenswerte aus jeweils einer etablierten Anlageklasse aus. Wir haben XAUUSD, SPX 500 und USDJPY ausgewählt. Gold wurde aus dem Rohstoffkorb ausgewählt und verkörpert in hohem Maße die Volatilität von Rohstoffen, die in der Regel durch Ströme aus sicheren Häfen, geopolitische Spannungen, hohe Inflation usw. verursacht wird. Die Gedächtniseffekte, die verlängert werden können, sind ein Test für die latente Erfassung der Regimepersistenz durch die Beta-VAE. 

Der SPX 500 wurde als bewährter Indikator für das Geschehen im Aktienmarkt gewählt. Er weist eine korrelierte Trendfolge auf, die von der Risikostimmung abhängt. Sie trug dazu bei, ein Hinterherhinken der Stochastik in den Trendphasen aufzudecken, in denen das Muster 9 ins Wanken geriet. USDJPY schließlich war der Vertreter aus dem Devisenbereich, der die Volatilität an den Märkten ausnutzen sollte, die durch Renditedifferenzen und Interventionen der Zentralbanken beeinflusst wird. Diese Auswahl diente der Untersuchung von „Flat-FrAMA“-Filtern, insbesondere in Muster-5.

Für unser VAE-Modell implementieren wir die drei Nachzügler-Muster gleichzeitig, indem wir ein latentes Modell entwickeln, das die zugrundeliegenden Muster über die Signalmuster 5, 6 und 9 hinweg erfasst oder erlernt. Wir testen nach wie vor jeden Vermögenswert unabhängig, wobei jeder getestete Vermögenswert gleichzeitig die drei Nachzügler-Muster untersucht. Die Tests mehrerer Muster können problematisch sein, wenn wir ihre Signale nicht richtig aggregieren, wie bei dem maschinellen Lernansatz, den wir in diesem Artikel verwenden. In früheren Artikeln haben wir bereits auf die Gefahr hingewiesen, dass sich die Positionen verschiedener Muster gegenseitig aufheben, sodass jedes Training oft auf eine Kurvenanpassung hinausläuft. Mit dem hier vorgestellten Ansatz werden alle Signale vereinheitlicht und Käufe/Verkäufe als ein einziges generiert. Nicht unabhängig voneinander, sodass diese Kombination der Muster zu einem Beta-VAE-Modell ein Fall sein könnte, in dem die Summe größer ist als die Teile.

Das beta-VAE-Modell

Das Herzstück unseres Signal-Umbrella-Modells ist der Beta Variational Auto Encoder, ein generatives Modell, das unbeaufsichtigt ist und eine Verbesserung des Standard-VAE darstellt, indem es sich auf unentwirrte Repräsentationen konzentriert. Seine Struktur besteht aus einem Encoder-Decoder-Paar mit einem verborgenen Raum, der in der Regel hochdimensional ist, um ein Vielfaches mehr als die Eingabe. Der Encoder ist ein neuronales Netz, das im Vorwärtsdurchlauf von einem niedrigdimensionalen Eingaberaum zu einem hochdimensionalen latenten Raum dient.

In diesem Artikel hat unsere Eingabe 6 Dimensionen, um einen latenten Raum mit 2048 Dimensionen zu erhalten. Die 6 Eingangsdimensionen sind für die 3 Signalmuster 5, 6 und 9. Zusammenfassend gibt jedes Muster einen zweidimensionalen Vektor aus, bei dem jeder Index so normiert ist, dass er den Wert 1 oder 0 ausgibt. Die beiden Indizes zeigen jeweils an, ob ein bestimmtes Signalmuster auf oder abwärts zeigt. Wir implementieren das Beta-VAE-Modell in Python wie folgt:

# ----------------------------- β-VAE (inference simplified to VAE-only) -----------------------------
class BetaVAEUnsupervised(nn.Module):
    """
    Encoder: features -> (mu, logvar)
    Decoder: z -> x_hat
    **Inference (now VAE-only):** latent z is mapped to y via an internal head.
    All former infer modes (ridge/knn/kernel/lwlr/mlp) are bypassed.
    """
    def __init__(self, feature_dim, latent_dim, k_neighbors=5, beta=4.0, recon='bce',
                 infer_mode='vae', ridge_alpha=1e-2, kernel_bandwidth=1.0):
        super().__init__()
        self.latent_dim = latent_dim
        self.k_neighbors = k_neighbors
        self.beta = beta
        self.recon = recon
        self.infer_mode = 'vae'  # force VAE-only
        self.ridge_alpha = float(ridge_alpha)
        self.kernel_bandwidth = float(kernel_bandwidth)

        # Encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256), nn.ReLU(),
            nn.Linear(256, 128), nn.ReLU(),
            nn.Linear(128, latent_dim * 2)
        )
        # Decoder
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 256), nn.ReLU(),
            nn.Linear(256, feature_dim)
        )
        # New: latent→y head (supervised head trained with MSE)
        self.y_head = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 1)
        )

    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar

    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std

    def decode(self, z):
        return self.decoder(z)

    def predict_from_latent(self, z):
        # VAE-only mapping
        return self.y_head(z)

    def forward(self, features, y=None):
        mu, logvar = self.encode(features)
        z = self.reparameterize(mu, logvar)
        x_logits = self.decode(z)
        y_hat = self.predict_from_latent(z)
        if y is not None:
            return {'z': z, 'z_mean': mu, 'z_logvar': logvar, 'x_logits': x_logits, 'y_hat': y_hat}
        else:
            return {'y': y_hat}

Die Abbildung der 6D-Binäreingabe auf eine 2048D-Latentschicht erfolgt über lineare ReLU-Schichten in der Konfiguration 6⇾256⇾128⇾4096.  Wir haben 4096 am Ende, weil es zwei Sätze von 2048 darstellt. Wir haben eine Aufteilung mit einer Verzweigung zum Mittelwert und einer weiteren zum Logarithmus der Varianz, jeweils in der Größe 2048. Die Neuparametrisierung wird von dieser probabilistischen Kodierung verwendet, um z, die regenerierte Eingabe, abzutasten, die dann in die Netzausgabe eingespeist wird, was dann Backpropagation ermöglicht. Die Dekodierung erfolgt in umgekehrter Reihenfolge wie die angegebene Konfiguration, nämlich 2048⇾128⇾256⇾6. Diese Rekonstruktion der binären Eingabe liefert Logits, die dann einer sigmoidalen Aktivierung unterzogen werden, um Wahrscheinlichkeiten zu erzeugen. 

Bei einer früheren Beta-VAE-Implementierung verließen wir uns ausschließlich auf den dualen Modus eines Vorwärtsdurchlauf, um die prognostizierte Preisentwicklung abzuleiten, da dieser beim Training mit Indikator-Eingabewerten gepaart worden war. Die eingespeisten Daten zur Erstellung dieser Prognose hätten dann die angestrebten, zukünftigen Preisänderungen als neutrale Platzhalterwerte. Da unsere Spanne für Preisänderungen also von 0,0 bis 1,0 reichte, war der neutrale Platzhalterwert 0,5. Unser implementierter Beta-VAE hat eine ähnliche flexible Vorwärtsdurchlauf-Funktion, allerdings haben wir eine neuartige latente y-Kopfgröße hinzugefügt, die auf 2048⇾128⇾1 konfiguriert ist und die nächste Preisaktion als Werte im Bereich von -1 bis +1 prognostiziert, was jeweils einen Aufwärtstrend bedeutet. Dies geschieht durch die Eingabe von z und bedeutet, dass wir unüberwachtes Lernen mit überwachtem Lernen mischen. 

Der Beta-Parameter, den wir in dieser VAE verwenden, legt fest, wie stark ein Modell die Einfachheit und Unabhängigkeit der Variablen in seinem verborgenen Raum, dem so genannten latenten Raum, erzwingt. In einem Autoencoder, der „variational“ ist, müssen zwei Dinge ausgeglichen werden. Die Rekonstruktionsgenauigkeit der Eingabedaten und die Regularisierung oder ein Maß für die Übereinstimmung des latenten Raums mit einem etablierten metrischen System, z. B. einer Standardnormalverteilung.

Wenn Beta 1 ist, spricht man von einer „normalen“ VAE. Der Name leitet sich, wie zu vermuten ist, von der Normalverteilung ab, und in diesem Fall würde die Kullback-Leibler-Divergenz die Werte im latenten Raum so anpassen, dass sie in etwa einer Gauß-Verteilung folgen. Sobald wir jedoch beginnen, Beta zu erhöhen und es zum Beispiel auf 4 setzen, beginnen wir, der Regularisierung mehr Bedeutung oder „Gewicht“ zuzuweisen. Im Wesentlichen würde man versuchen, die Werte im latenten Raum so spärlich wie möglich zu halten, mit vielen Werten nahe bei Null, sowie viel Unabhängigkeit und weniger Korrelationen. Dies dient in der Praxis dazu, dass das Modell die verschiedenen verborgenen Merkmale und Muster im latenten Raum besser trennen und „entwirren“ kann.

Ein besser unterschiedener verborgener Raum soll der VAE helfen, zu verallgemeinern und Muster in Situationen außerhalb der Stichprobe besser zu erkennen. Unsere beta-VAE-Loss Funktion ist Fleisch, um den Kullback-Leibler zu berechnen und wir implementieren sie in Python wie folgt:

def beta_vae_loss(features, x_logits, mu, logvar, beta=4.0, recon='bce'):
    if recon == 'bce':
        recon_loss = F.binary_cross_entropy_with_logits(x_logits, features, reduction='sum') / features.size(0)
    else:
        recon_loss = F.mse_loss(torch.sigmoid(x_logits), features, reduction='mean') * features.size(1)
    kl = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) / features.size(0)
    loss = recon_loss + beta * kl
    return loss, recon_loss.detach(), kl.detach()

KL wird als -0,5 ∑(1 + logvar – μ² – exp(logvar)) berechnet und dann pro Charge gemittelt und mit Beta gewichtet. Dadurch wird, wie oben dargelegt, die Rekonstruktionsgenauigkeit gegen die Variabilität des latenten Raums ausgetauscht, wodurch verborgene Indikatorhierarchien aufgedeckt werden. Die Verlustzerlegung ist ein mehrstufiger Prozess, bei dem wir die Eingabedaten mithilfe der binären Kreuzentropie mit Logits rekonstruieren können. Der Gesamtverlust ist ein hybrides Ziel, das garantiert, dass das Modell nicht nur in der Lage ist, Eingabemuster zu rekonstruieren, sondern dass der latente Raum in der Lage ist, sich zu „spezialisieren“ und verschiedene Facetten der Eingabemerkmale zu erfassen, wobei beispielsweise einige Werte die Kreuzungsstärke protokollieren, andere die Neigungsrichtung usw. Die Fähigkeit, eine Vielzahl dieser Merkmale zu protokollieren, wird, wie wir oben dargelegt haben, wiederum durch den Beta-Faktor gesteuert.

MQL5-Implementierung

Um das Ökosystem des maschinellen Lernens von Python mit dem Handelsrahmen von MQL5 zu verbinden, decken wir die wichtigsten Schritte in Python ab, die zum Exportieren einer ONNX-Datei zur Verwendung in MQL5 führen. Diese Schritte, wie oben beschrieben, laufen auf die Schaffung einer nahtlosen Pipeline für die Datenverarbeitung, die Modellschulung und den Einsatz hinaus. Wir initialisieren die exportierten ONNX-Modelle, eines für jeden Vermögenswert, und erinnern daran, dass jedes Modell alle drei Muster synergetisch nutzt, ohne dass es zu Überschneidungen kommt. Während die ONNX-Modelle in früheren Artikeln musterspezifisch waren, sind diese hier anlagespezifisch. Unser Klassenkonstruktor und die Validierung sehen daher wie folgt aus:

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CSignalIL_Stochastic_FrAMA::CSignalIL_Stochastic_FrAMA(void) : m_pattern_6(50),
   m_pattern_9(50),
   m_pattern_5(50),
   m_model_type(0)
//m_patterns_usage(255)
{
//--- initialization of protected data
   m_used_series = USE_SERIES_CLOSE + USE_SERIES_TIME;
   PatternsUsage(m_patterns_usage);
//--- create model from static buffer
   m_handles[0] = OnnxCreateFromBuffer(__84_USDJPY, ONNX_DEFAULT);
   m_handles[1] = OnnxCreateFromBuffer(__84_XAU, ONNX_DEFAULT);
   m_handles[2] = OnnxCreateFromBuffer(__84_SPY, ONNX_DEFAULT);
}

//+------------------------------------------------------------------+
//| Validation settings protected data.                              |
//+------------------------------------------------------------------+
bool CSignalIL_Stochastic_FrAMA::ValidationSettings(void)
{
//--- validation settings of additional filters
   if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   // Set input shapes
   const long _in_shape[] = {1, 6};
   const long _out_shape[] = {1, 1};
   if(!OnnxSetInputShape(m_handles[m_model_type], ONNX_DEFAULT, _in_shape))
   {  Print("OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   // Set output shapes
   if(!OnnxSetOutputShape(m_handles[m_model_type], 0, _out_shape))
   {  Print("OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//--- ok
   return(true);
}

Die Tests wurden für die verschiedenen „Modelltypen“ durchgeführt, wobei dieser Parameter ein Akronym für die drei verschiedenen Vermögenswerte ist, die wir testen, während wir alle drei Signalmuster auf einmal ausführen. Wenn dieser Ganzzahlwert also 0 zugewiesen wird, bedeutet das, dass wir USDJPY testen, wenn er 1 ist, testen wir XAUUSD, und wenn er 2 ist, testen wir SPX 500. Unsere Tests zielten darauf ab, zu untersuchen, ob die Leistung der Signalmuster 5, 6 und 9 umgedreht werden kann. Normalerweise geschieht dies eher durch das Testen eines Musters nach dem anderen, aber in diesem Fall vereinen wir alle drei Muster um die drei verschiedenen getesteten Vermögenswerte. Die Verwendung verschiedener Testanlagen, die jeweils auf bestimmte Markttypen ausgerichtet sind, bildet unser Testuniversum.

Wir haben mit ähnlichen Testfenstern trainiert/optimiert, die wir im letzten Artikel von Juli 2023 bis Juli 2024 verwendet haben. Die Kriterien, die wir angepasst haben, waren die Schwellenwerte für die Eröffnungs- und Schlusskurse des nutzerdefinierten Signals, die Einstiegspreis-Pips, die den Abstand unserer Limit-Orders festlegen, und die Schwellenwerte für die Signalmuster, die für jedes Muster akkumuliert werden, wenn es vorhanden ist, da es bei jedem neuen Balken geprüft wird. Die Ergebnisse der Vorwärtstest waren wie folgt:

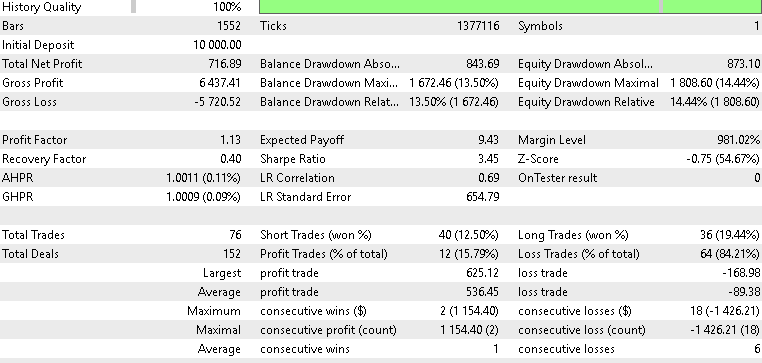
Für XAUUSD

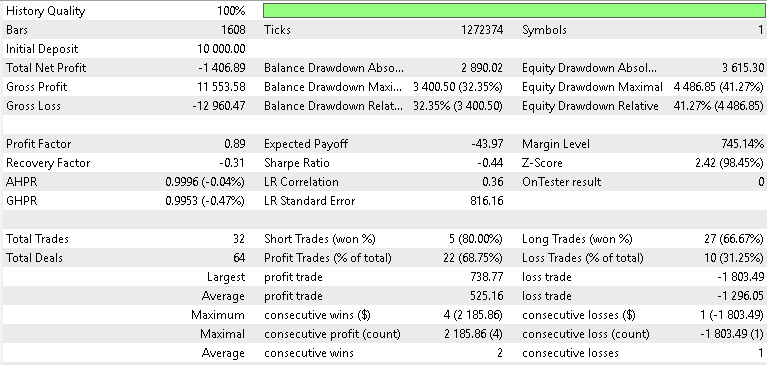
Für USDJPY

Für SPX 500

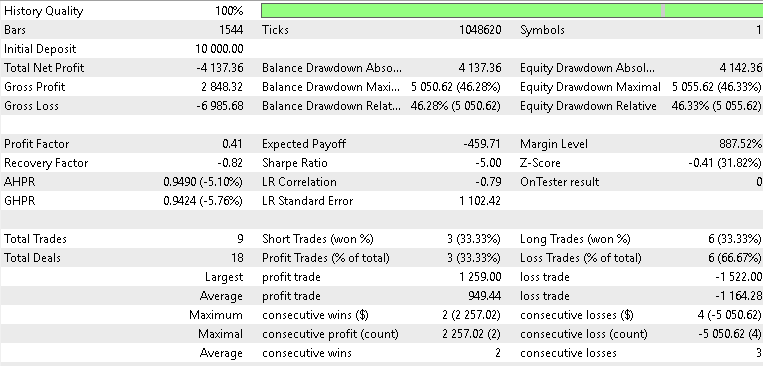
Die Ergebnisse unseres Vorwärtstests waren gemischt, aber dennoch aufschlussreich. Beim Test mit Gold verzeichnete unser Beta-VAE-Modell eine kleine Rendite von 2,1 Prozent über das Jahr auf dem 4-Stunden-Zeitfenster. Wir können die Variablen der latenten Schicht nicht auseinandernehmen und nicht genau bestimmen, welche Variablen sich auf welche Signalmuster spezialisieren. Wir können jedoch vermuten, dass die Einbettungen von flach und kreuzen des Musters 5 in der Lage waren, volatilitätsbedingte Umkehrungen inmitten der Goldspikes zu erkennen. Wir haben auch einen Test mit dem SPX 500 durchgeführt, und die Rendite des Vorwärtstests für das Jahr war negativ mit 0,8 Prozent. Auch der USDJPY schnitt nicht besser ab, sondern schnitt mit einer Rendite von -1,4 Prozent am schlechtesten von den drei ab. Im Großen und Ganzen war also nur XAU in der Lage, die Gewinnschwelle zu überschreiten, was bedeutet, dass die Ergebnisse dieses Tests im Großen und Ganzen denen des letzten Artikels, Teil 84, entsprechen, da die VAE uns nur einen bescheidenen Auftrieb gegeben hat, wenn wir mit XAUUSD testen.

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass die Kombination des Beta-VAE-Inferenzmodells mit der Indikatorpaarung des Stochastik-Oszillators und der Paarung des Fractal Adaptive Moving Average versteckte Merkmale liefert, die bis zu einem gewissen Grad eine gewisse Anwendbarkeit gezeigt haben. Unsere „Pipeline“ von ONNX zu MQL5 hat seit dem letzten Artikel einige Zuwächse gezeigt, vor allem bei XAUUSD; sie hat aber auch einige Grenzen aufgezeigt. Der Vorwärtstest für USD, JPY und SPX 500 war glanzlos bis bestenfalls mittelmäßig. Dies erfordert ein sorgfältiges Feature-Engineering, regelbasierte Tests und eine konservative Implementierung. Alle hier vorgestellten Ergebnisse sind wie immer experimentell und bedürfen vor einer weiteren Betrachtung unabhängiger Tests und einer sorgfältigen Prüfung.

Name	Beschreibung
WZ-84.mq5	Assistent Assemblierter Expert Advisor, in dessen Kopfzeile Name und Ort der referenzierten Dateien aufgeführt sind
SignalWZ-84.mqh	Datei der nutzerdefinierte Signalklassen
84-XAU.onnx	Mit Gold trainiertes ONNX Modell
84-USDJPY.onnx	Mit dem Dollar-Yen trainiertes ONNX-Modell
84-SPY.onnx	Mit dem SPX 500 trainiertes Modell