
MetaTrader 5 Machine Learning Blueprint (Teil 2): Kennzeichnung von Finanzdaten für maschinelles Lernen
Inhaltsverzeichnis
- Einführung
- Überblick über die Kennzeichnungsmethoden
- Umsetzung: Dreifach-Barriere-Kennzeichnungsmethode
- Berichte der Meta-Kennzeichen: Bollinger Band Strategie
- Schlussfolgerung
Einführung
Stellen Sie sich Folgendes vor: Sie trainieren, um ein Elitescharfschütze zu werden. Möchten Sie lieber üben, auf perfekte Kreise auf einer Papierscheibe zu schießen, oder mit menschlichen Silhouetten trainieren, die reale Kampfszenarien imitieren? Die Antwort liegt auf der Hand: Sie brauchen Ziele, die die Realität widerspiegeln, mit der Sie konfrontiert werden.
Das gleiche Prinzip gilt für das maschinelle Lernen im Finanzwesen. Die meisten akademischen Forschungen verwenden das so genannte „Fixed-Time Horizon Labeling“, was dem Schießen auf diese perfekten Kreise entspricht. Bei diesem Ansatz wird eine einfache Frage gestellt: „Wird der Preis in genau X Tagen höher oder niedriger sein?“ Aber hier liegt das Problem: Echte Händler interessieren sich nicht nur dafür, wo der Preis am Ende steht. Sie interessieren sich für die Reise, d. h., wann ihr Stop-Loss erreicht wird, wann sie Gewinne mitnehmen sollten und wie sich der Kurs auf dem Weg dahin entwickelt.
Willkommen zurück zu unserer Serie über MetaTrader 5 Machine Learning Blueprint. In Teil 1 haben wir die kritische „Zeitstempelfalle“ gelöst, die die meisten Handelsalgorithmen zum Scheitern bringt. Jetzt nehmen wir eine ebenso wichtige Herausforderung in Angriff: Wie können wir Etiketten erstellen, die tatsächlich widerspiegeln, wie Sie in der realen Welt handeln.
Stellen Sie sich das so vor: Wenn Sie ein Modell erstellen, mit dem Sie vorhersagen können, ob jemand einen Herzinfarkt erleiden wird, würden Sie nicht nur darauf achten, ob er in genau 365 Tagen noch lebt oder tot ist. Sie möchten über Warnzeichen, Frühinterventionen und die Abfolge von Ereignissen Bescheid wissen, die für medizinische Entscheidungen relevant sind. Die Finanzmärkte funktionieren auf die gleiche Weise.
In diesem Artikel wird davon ausgegangen, dass Sie sich bereits mit Python auskennen und ein Grundverständnis für Konzepte des maschinellen Lernens haben. Wir werden tief in praktischen Code und reale Anwendungen eintauchen, die Sie sofort implementieren können.
Rekapitulation von Teil 1: Behebung von Datenlecks und Zeitstempeln
Im ersten Teil der Serie haben wir uns mit einem kritischen, aber oft übersehenen Problem befasst, das maschinelle Lernmodelle auf den Finanzmärkten untergraben kann: die „Zeitstempel-Falle“ und Datenlecks in der Standard-Datenstruktur des MetaTrader 5. Wir haben die entscheidende Grundlage geschaffen, indem wir uns mit der Datenintegrität befasst und die Notwendigkeit betont haben, saubere, unverzerrte Balken aus rohen Tickdaten zu erstellen. Diese Grundlage ist für die Entwicklung zuverlässiger Modelle für maschinelles Lernen im Finanzbereich unverzichtbar. Wenn Sie Teil 1 noch nicht gelesen haben, empfehlen wir Ihnen dringend, dies zu tun, bevor Sie fortfahren.
Die dort gelegte Grundlage gewährleistet:
- Integrität der Daten: Alle Zeitstempel geben an, wann die Informationen tatsächlich verfügbar waren.
- Statistische Solidität: Aktivitätsgesteuerte Balken bieten bessere statistische Eigenschaften für ML-Modelle.
- Ausrichtung auf die reale Welt: Die Konstruktion der Balken entspricht dem tatsächlichen Informationsfluss auf dem Markt.
Nachdem wir diese grundlegenden Probleme mit der Datenqualität gelöst haben, verfügen wir nun über saubere, unverfälschte Datensätze, die für den nächsten entscheidenden Schritt in unserer Pipeline für maschinelles Lernen bereit sind – Techniken der Kennzeichnung, die die Marktdynamik wirklich erfassen.
Überblick über die Kennzeichnungsmethoden
Die meisten Modelle des maschinellen Lernens im Finanzbereich scheitern aus einem überraschend banalen Grund – nicht wegen schlechter Algorithmen oder unzureichender Rechenleistung, sondern wegen schlechter Kennzeichnungen. Als ich mit der Entwicklung von Handelsmodellen begann, verbrachte ich Monate damit, Merkmale zu optimieren und verschiedene neuronale Netzwerkarchitekturen auszuprobieren, nur um dann festzustellen, dass mein Kennzeichnungsschema grundlegend fehlerhaft war. Ich habe meinem Modell im Wesentlichen beigebracht, ins Schwarze zu treffen, obwohl ich es eigentlich brauchte, um ein bewegliches Ziel in einem Wirbelsturm zu treffen.
Die Finanzmärkte haben ein unerbittliches Rauschen. Jeder Tick enthält eine Mischung aus echter Information und zufälligem Chaos, und unsere Aufgabe ist es, das Signal zu extrahieren und dabei zu berücksichtigen, dass die meisten Kursbewegungen nur darauf zurückzuführen sind, dass Marktteilnehmer ihre Meinung ändern oder Algorithmen auf Schwankungen im Mikrosekundenbereich reagieren. Eine gute Kennzeichnung sagt uns nicht nur, was passiert ist, sondern hilft uns zu verstehen, worauf es bei tatsächlichen Handelsentscheidungen ankommt.
Der einfachste Ansatz, mit dem die meisten Menschen beginnen, ist die Kennzeichnung mit einem festen Zeithorizont. Sie wählen einen Zeitraum – z. B. fünf Tage – und fragen, ob der Preis am Ende dieses Zeitraums höher oder niedriger sein wird. Wenn Apple am Montag bei 150 $ schließt und bis Freitag 155 $ erreicht, wird der Montag als Kaufsignal gewertet. Es ist sauber, intuitiv und entspricht nicht der Realität des Handels. Wann haben Sie das letzte Mal eine Aktie mit dem Gedanken gekauft: „Ich schaue in genau fünf Tagen wieder rein, egal was passiert?“ Wenn die Aktie am Dienstag um 20 % einbricht, warten Sie nicht bis Freitag, um sie neu zu bewerten. Wenn der Kurs am Mittwoch um 15 % steigt, könnten Sie sofort Gewinne mitnehmen.
Dies bringt uns zur Triple-Barrier-Methode, die die Denkweise seriöser Praktiker über ML verändert hat. Anstelle von willkürlichen Zeithorizonten setzen Sie drei Barrieren um jeden potenziellen Handel, genau wie ein professioneller Händler es tun würde. Das ist Ihr Gewinnziel – vielleicht 5 % über Ihrem Einstiegskurs. Das ist Ihr Stop-Loss – vielleicht 3 % unter dem Kaufkurs. Und es gibt ein Zeitlimit, denn Sie wollen nicht ewig an Verlustpositionen festhalten. Ihr Etikett hängt davon ab, welches Hindernis zuerst getroffen wird. Plötzlich lernt Ihr Modell keine abstrakten Kursbewegungen mehr, sondern es lernt, ob bestimmte Handelssetups wahrscheinlich Gewinnziele erreichen werden, bevor sie Stop-Loss-Werte erreichen.
Das Schöne an diesem Ansatz ist, dass er die tatsächliche Handelspsychologie widerspiegelt. Echten Händlern ist es egal, ob eine Aktie letztendlich steigt, wenn sie zunächst so weit fällt, dass ihre Risikomanagementregeln ausgelöst werden. Der Weg ist ebenso wichtig wie das Ziel, und die Methode der dreifachen Schranke erfasst diese Pfadabhängigkeit auf natürliche Weise. Sie können die Barrieren sogar dynamisch gestalten – breitere Stops in volatilen Zeiten, engere Stops in ruhigen Marktphasen.
Für Märkte, auf denen die Länge der Trends stark variiert, bieten Trend-Scanning-Methoden eine elegante Lösung. Anstatt einen festen Zeitrahmen festzulegen, testen diese Algorithmen die Prognose mehrere Zeitrahmen und ermitteln den statistisch signifikantesten Trend. Vielleicht ist der 5-Tage-Trend schwach, der 10-Tage-Trend stark und der 15-Tage-Trend moderat. Die Methode wählt das stärkste Signal aus und kennzeichnet es entsprechend. Es ist, als würde der Algorithmus selbst den optimalen Prognosehorizont für jede Marktbedingung bestimmen.
Dann gibt es noch die Meta-Kennzeichen, die ein ganz anderes Problem angeht. Anstatt die Marktrichtung vorherzusagen, werden Fragen gestellt: „Wann sollte ich meinen anderen Vorhersagen vertrauen?“ Stellen Sie sich vor, Sie haben bereits eine Handelsstrategie, die Kauf- und Verkaufssignale erzeugt. Beim der Meta-Kennzeichnung wird ein zweites Modell erstellt, das bewertet, ob die einzelnen Signale wahrscheinlich profitabel sind. Ihre Hauptstrategie könnte „Kaufen“ lauten, aber das Metamodell berücksichtigt zusätzliche Faktoren – die jüngste Performance, die Marktvolatilität, die Zeit seit dem letzten großen Nachrichtenereignis – und gibt einen Vertrauenswert aus. Hohes Vertrauen bedeutet, dass Sie in die Position aggressiv einsteigen. Geringes Vertrauen bedeutet, dass Sie passen oder wenig setzen.
Dieser Ansatz berücksichtigt eine wichtige Erkenntnis: Zu wissen, wann man wahrscheinlich Recht hat, ist oft wertvoller als zu versuchen, öfter Recht zu haben. Das ist der Unterschied zwischen einem guten Prognostiker und einem profitablen Händler. Viele Strategien scheitern nicht, weil ihre Richtungsprognosen schlecht sind, sondern weil sie den gleichen Betrag auf Signale mit hohem und niedrigem Vertrauen setzen.
Mit jeder Kennzeichnungsmethode lernt Ihr Modell etwas anderes. Methoden mit festem Zeithorizont konzentrieren sich auf die reine Kursrichtung. Triple-Barrier-Methoden beinhalten Risikomanagement und Pfadabhängigkeit. Trend-Scanning passt sich an wechselnde Marktbedingungen an. Meta-Kennzeichnung optimiert die Überzeugung und die Positionsbestimmung. Die von Ihnen gewählte Methode beeinflusst grundlegend, was Ihr Modell lernt und wie es sich im Live-Handel verhält.
Wichtige Überlegungen bei der Arbeit mit Finanzdaten
- Vermeiden Sie Einseitigkeit: Stellen Sie sicher, dass Ihre Kennzeichnungen nur auf Informationen basieren, die bis zum Zeitpunkt der Entscheidung verfügbar sind. Wenn Sie z. B. einen Datenpunkt für „heute“ beschriften, können Sie nur Informationen von „heute“ oder früher zur Bestimmung der Merkmale und Informationen aus der „Zukunft“ (relativ zu „heute“) zur Bestimmung der Kennzeichnung verwenden.
- Balance Your Classes: Wenn Sie für „Kaufen“, „Verkaufen“ und „Halten“ kennzeichnen, werden Sie feststellen, dass „Halten“-Signale (oder kleine Bewegungen) viel häufiger vorkommen. Stark unausgewogene Klassen können es ML-Modellen erschweren, die Minderheitsklassen zu lernen. Es gibt Techniken, um damit umzugehen (z. B. Oversampling, Subsampling oder die Verwendung geeigneter Bewertungsmetriken).
- Volatilität ist der Schlüssel: Die Finanzmärkte unterliegen einer wechselnden Volatilität. Ein Kursanstieg von 2 % kann in einem ruhigen Markt enorm sein, in einer volatilen Phase jedoch unbedeutend. Erwägen Sie die Verwendung von volatilitätsangepassten Schwellenwerten für Ihre Etiketten (wie bei der Triple-Barrier-Methode).
- Stationarität: Finanzielle Zeitreihen sind oft nicht stationär (ihre statistischen Eigenschaften wie Mittelwert und Varianz ändern sich im Laufe der Zeit). Während die Kennzeichnung selbst die Daten nicht direkt stationär macht, sind die Wahl der Kennzeichnung (z. B. die Kennzeichnung von Renditen, die oft stationärer sind als Preise) und die anschließende Merkmalstechnik entscheidend.
- Iterieren und verfeinern: Ihr erster Kennzeichnungsansatz ist vielleicht nicht der beste. Seien Sie bereit, mit verschiedenen Methoden, Zeithorizonten und Schwellenwerten zu experimentieren, um herauszufinden, was für Ihre spezifischen Ziele und die von Ihnen analysierten Vermögenswerte am besten geeignet ist.
Umsetzung: Dreifach-Barriere-Kennzeichnungsmethode
Dynamische Schranken setzen
Wie im vorigen Abschnitt dargelegt, wollen wir in der Praxis Gewinnmitnahme- und Stop-Loss-Limits festlegen, die von den mit einer Wette verbundenen Risiken abhängen. Andernfalls werden wir in Anbetracht der herrschenden Volatilität manchmal zu hoch (𝜏 ≫ 𝜎ti,0) und manchmal zu niedrig (𝜏 ≪ 𝜎ti,0) zielen.
Der nachstehende Code berechnet die tägliche Volatilität zu Intraday-Schätzzeitpunkten und wendet eine Spanne von Rückblickstagen auf eine exponentiell gewichtete gleitende Standardabweichung an. Diese Volatilität wird für die Festlegung der Gewinnmitnahme- und Stop-Loss-Barrieren verwendet.
def get_daily_vol(close, lookback=100): """ Advances in Financial Machine Learning, Snippet 3.1, page 44. Daily Volatility Estimates Computes the daily volatility at intraday estimation points. In practice we want to set profit taking and stop-loss limits that are a function of the risks involved in a bet. Otherwise, sometimes we will be aiming too high (tao ≫ sigma_t_i,0), and sometimes too low (tao ≪ sigma_t_i,0), considering the prevailing volatility. Snippet 3.1 computes the daily volatility at intraday estimation points, applying a span of lookback days to an exponentially weighted moving standard deviation. See the pandas documentation for details on the pandas.Series.ewm function. Note: This function is used to compute dynamic thresholds for profit taking and stop loss limits. :param close: (pd.Series) Closing prices :param lookback: (int) Lookback period to compute volatility :return: (pd.Series) Daily volatility value """ # Find previous valid trading day for each date prev_idx = close.index.searchsorted(close.index - pd.Timedelta(days=1)) prev_idx = prev_idx[prev_idx > 0] # Drop indices before the start # Align current and previous closes curr_idx = close.index[close.shape[0] - prev_idx.shape[0] :] prev_close = close.iloc[prev_idx - 1].values # Previous day's close ret = close.loc[curr_idx] / prev_close - 1 vol = ret.ewm(span=lookback).std() return vol
Vertikale Barrieren setzen
Zur Einstellung der vertikalen Schranken verwenden wir die folgende Funktion. Bei der Verwendung von aktivitätsgesteuerten Balken ist es sinnvoller, die Barrieren auf der Grundlage der Anzahl der Stäbe bis zum Verfall festzulegen als auf der Grundlage eines festen Zeitraums, da innerhalb eines Zeithorizonts extreme Schwankungen auftreten können.
# Snippet 3.4 page 49, Adding a Vertical Barrier def add_vertical_barrier(t_events, close, num_bars=0, **time_delta_kwargs): """ Advances in Financial Machine Learning, Enhanced Implementation. Adding a Vertical Barrier For each event in t_events, finds the timestamp of the next price bar at or immediately after: - A fixed number of bars (for activity-based sampling), OR - A time delta (for time-based sampling) This function creates a series of vertical barrier timestamps aligned with the original events index. Out-of-bound barriers are marked with NaT for downstream handling. :param t_events: (pd.Series) Series of event timestamps (e.g., from symmetric CUSUM filter) :param close: (pd.Series) Close price series with DateTimeIndex :param num_bars: (int) Number of bars for vertical barrier (activity-based mode). Takes precedence over time delta parameters when > 0. :param time_delta_kwargs: Time components for time-based barrier (mutually exclusive with num_bars): :param days: (int) Number of days :param hours: (int) Number of hours :param minutes: (int) Number of minutes :param seconds: (int) Number of seconds :return: (pd.Series) Vertical barrier timestamps with same index as t_events. Out-of-bound events return pd.NaT. Example: # Activity-bar mode (tick/volume/dollar bars) vertical_barriers = add_vertical_barrier(t_events, close, num_bars=10) # Time-based mode vertical_barriers = add_vertical_barrier(t_events, close, days=1, hours=3) """ # Validate inputs if num_bars and time_delta_kwargs: raise ValueError("Use either num_bars OR time deltas, not both") # BAR-BASED VERTICAL BARRIERS if num_bars > 0: indices = close.index.get_indexer(t_events, method="nearest") t1 = [] for i in indices: if i == -1: # Event not found t1.append(pd.NaT) else: end_loc = i + num_bars t1.append(close.index[end_loc] if end_loc < len(close) else pd.NaT) return pd.Series(t1, index=t_events) # TIME-BASED VERTICAL BARRIERS td = pd.Timedelta(**time_delta_kwargs) if time_delta_kwargs else pd.Timedelta(0) barrier_times = t_events + td # Find next index positions t1_indices = np.searchsorted(close.index, barrier_times, side="left") t1 = [] for idx in t1_indices: if idx < len(close): t1.append(close.index[idx]) else: t1.append(pd.NaT) # Mark out-of-bound for downstream return pd.Series(t1, index=t_events)
Anwendung der Dreifach-Barriere-Etikettierung
Die Triple-Barrier-Methode ist von Natur aus pfadabhängig, d. h. wir können nicht nur den Endpreis betrachten, um unsere Kennzeichnung zu bestimmen. Stattdessen müssen wir den gesamten Kursverlauf vom Einstieg in eine Position bis zum Ausstieg verfolgen, unabhängig davon, ob wir ein Gewinnziel, einen Stop-Loss oder ein Zeitlimit erreicht haben.
Wenn wir die Methode der dreifachen Barriere anwenden, stellen wir im Wesentlichen die Frage: „Ausgehend vom Zeitpunkt ti,0, was wird zuerst passieren, wenn wir uns in der Zeit vorwärts bewegen?“ Der Prozess wird fortgesetzt, bis ti,1 erreicht ist, was den Moment darstellt, in dem die erste Barriere berührt wird. Dies könnte unser Gewinnziel, unser Stop-Loss oder unsere maximale Haltedauer sein (die vertikale Barriere, die bei ti,0 + h). Die Rendite, die wir für die Kennzeichnung verwenden, wird ab unserem Einstiegspunkt ti,0 bis zu diesem ersten Berührungszeitpunkt ti,1.
Die Funktion apply_pt_sl_on_t1() implementiert diese Logik und benötigt mehrere Eingänge, um richtig zu funktionieren. Zunächst benötigt es die Zeitreihe der Schlusskurse, um den tatsächlichen Kursverlauf verfolgen zu können. Der Ereignisdatenrahmen enthält die wesentlichen Informationen für jeden potenziellen Handel: Die Spalte t1 gibt an, wann jeder Handel auslaufen soll (die vertikale Barriere), während die Spalte trgt definiert, wie breit unsere horizontalen Barrieren sein sollen.
Der Parameter pt_sl ist besonders wichtig. Es handelt sich um eine Liste mit zwei Elementen, die die Schrankenbreiten steuert. Das erste Element (pt_sl[0]) legt fest, wie viele Vielfache des Zielabstands für die Barriere der Gewinnmitnahme zu verwenden sind, während das zweite Element (pt_sl[1]) dasselbe für die Stop-Loss-Barriere tut. Ist einer der beiden Werte gleich Null, ist die betreffende Barriere deaktiviert. Diese Flexibilität ermöglicht es Ihnen, asymmetrische Risiko-Ertrags-Setups zu erstellen. Sie können zum Beispiel einen engen Stop-Loss setzen, aber die Gewinne weiter laufen lassen.
Die Funktion verarbeitet diese Barrieren systematisch, indem sie die Kursbewegungen Balken für Balken verfolgt, bis eine der Barrieren durchbrochen wird, was uns die genauen Zeit- und Renditeinformationen liefert, die wir für eine genaue Kennzeichnung benötigen.
# Snippet 3.2, page 45, Triple Barrier Labeling Method def apply_pt_sl_on_t1(close, events, pt_sl, molecule): """ Advances in Financial Machine Learning, Snippet 3.2, page 45. Triple Barrier Labeling Method This function applies the triple-barrier labeling method. It works on a set of datetime index values (molecule). This allows the program to parallelize the processing. Mainly it returns a DataFrame of timestamps regarding the time when the first barriers were reached. :param close: (pd.Series) Close prices :param events: (pd.Series) Indices that signify "events" (see cusum_filter function for more details) :param pt_sl: (np.array) Element 0, indicates the profit taking level; Element 1 is stop loss level :param molecule: (an array) A set of datetime index values for processing :return: (pd.DataFrame) Timestamps of when first barrier was touched """ # Apply stop loss/profit taking, if it takes place before t1 (end of event) events = events.loc[molecule].copy() out = events[["t1"]].copy(deep=True) profit_taking_multiple = pt_sl[0] stop_loss_multiple = pt_sl[1] # Profit taking active if profit_taking_multiple > 0: profit_taking = np.log(1 + profit_taking_multiple * events["trgt"]) else: profit_taking = pd.Series(index=events.index) # NaNs # Stop loss active if stop_loss_multiple > 0: stop_loss = np.log(1 - stop_loss_multiple * events["trgt"]) else: stop_loss = pd.Series(index=events.index) # NaNs # Use dictionary to collect barrier hit times barrier_dict = {"sl": {}, "pt": {}} # Get events for loc, vertical_barrier in events["t1"].fillna(close.index[-1]).items(): closing_prices = close[loc:vertical_barrier] # Path prices for a given trade cum_returns = np.log(closing_prices / close[loc]) * events.at[loc, "side"] # Path returns barrier_dict["sl"][loc] = cum_returns[ cum_returns < stop_loss[loc] ].index.min() # Earliest stop loss date barrier_dict["pt"][loc] = cum_returns[ cum_returns > profit_taking[loc] ].index.min() # Earliest profit taking date # Convert dictionary to DataFrame and join to `out` barrier_df = pd.DataFrame(barrier_dict) out = out.join(barrier_df) # Join on index (loc) return out
Die Triple-Barrier-Method bietet acht mögliche Konfigurationen, je nachdem, welche Barrieren Sie aktivieren. Stellen Sie sich jedes Setup als [profit_target, stop_loss, time_limit] vor, wobei 1 für aktiv und 0 für deaktiviert steht.
- Die meisten praktischen Handelsstrategien verwenden eine von drei Konfigurationen:
- [1,1,1] – Die vollständige Einrichtung: Alle drei Barrieren aktiv. Sie wollen Gewinne erzielen und gleichzeitig das Abwärtsrisiko und die Haltedauer kontrollieren. Dies spiegelt wider, wie die meisten professionellen Händler tatsächlich arbeiten.
- [0,1,1] – Gewinner laufen lassen: Kein Gewinnziel, aber Sie steigen nach X Perioden aus, wenn Sie nicht vorher ausgestoppt werden. Perfekt für Momentum-Strategien, bei denen Sie auf Trends setzen wollen.
- [1,1,0] – Kein Zeitdruck: Gewinnziel und Stop-Loss aktiv, aber kein Zeitlimit. Sie halten so lange, bis eine der Preisbarrieren erreicht ist, egal wie lange das dauert.
- Drei technisch mögliche, aber weniger realistische Konfigurationen:
- [0,0,1] – Fester Horizont: Nur zeitabhängige Ausgänge. Dies ist im Wesentlichen eine Kennzeichnung mit festem Zeithorizont, obwohl sie auch mit aktivitätsgesteuerten Balken funktionieren kann.
- [1,0,1] – Verluste ignorieren: Halten, bis die Gewinne erzielt wurden oder die Zeit abgelaufen ist, ohne Rücksicht auf zwischenzeitliche Verluste. Gefährlich für das Risikomanagement.
- [1,0,0] – Für immer halten: Kein Stop-Loss oder Zeitlimit. Halten der Verlustpositionen so lange, bis sie schließlich profitabel werden – ein Rezept für die Zerstörung des Portfolios.
- Zwei im Wesentlichen nutzlose Konfigurationen:
- [0,1,0] – Erwartetes Scheitern: Halten der Positionen, bis sie den Stop-Loss erreichen. Warum sollte man Handelsgeschäfte eingehen, bei denen man nur Verluste erwartet?
- [0,0,0] – Kein Ausstieg: Alle Barrieren deaktiviert. Positionen werden nie geschlossen und es werden keine Kennzeichnungen erzeugt.
Im Folgenden werden zwei mögliche Konfigurationen der Dreifachschrankenmethode vorgestellt.
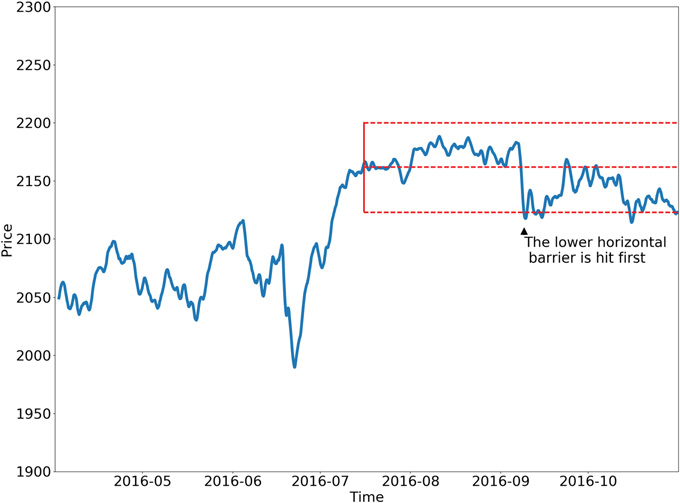
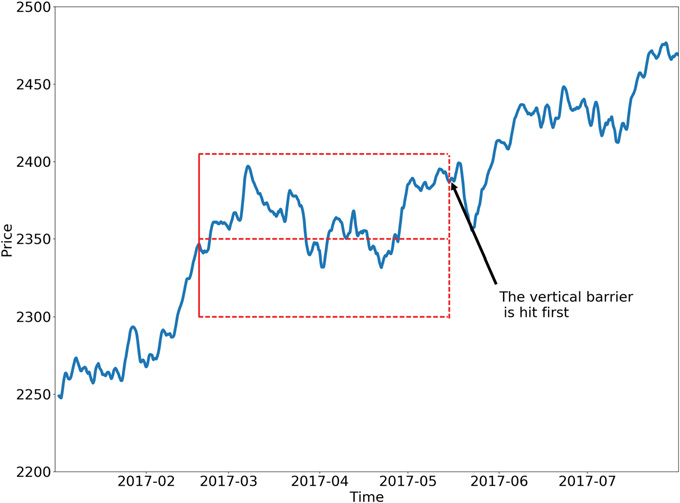
Lernen von Seite und Größe
Die Funktionen in diesem Abschnitt nutzen die Triple-Barrier-Methode, um entweder die Seite {1, 0, -1} zu lernen, wenn side_prediction=None in get_events(), oder um die Größe aus den meta-etikettierten Daten zu lernen, wenn die Seite bekannt ist. Die Kenntnis der Seite für die Wette setzt voraus, dass es keine horizontalen Schranken gibt oder dass die horizontalen Schranken symmetrisch sind. Dies liegt daran, dass wir zu diesem Zeitpunkt nicht zwischen Gewinnmitnahme- und Stop-Loss-Barrieren unterscheiden können. Sobald die Seite bekannt ist, können wir die Barrieren optimieren, um herauszufinden, welche Kombination das leistungsfähigste Modell ergibt. Wir erhalten die Daten der ersten berührten Barriere, indem wir get_events() ausführen.
# Snippet 3.3 -> 3.6 page 50, Getting the Time of the First Touch, with Meta Labels def get_events(close, t_events, pt_sl, target, min_ret, num_threads, vertical_barrier_times=False, side_prediction=None, verbose=True): """ Advances in Financial Machine Learning, Snippet 3.6 page 50. Getting the Time of the First Touch, with Meta Labels This function is orchestrator to meta-label the data, in conjunction with the Triple Barrier Method. :param close: (pd.Series) Close prices :param t_events: (pd.Series) of t_events. These are timestamps that will seed every triple barrier. These are the timestamps selected by the sampling procedures discussed in Chapter 2, Section 2.5. E.g.: CUSUM Filter :param pt_sl: (list) Element 0, indicates the profit taking level; Element 1 is stop loss level. A non-negative float that sets the width of the two barriers. A 0 value means that the respective horizontal barrier (profit taking and/or stop loss) will be disabled. :param target: (pd.Series) of values that are used (in conjunction with pt_sl) to determine the width of the barrier. In this program this is daily volatility series. :param min_ret: (float) The minimum target return required for running a triple barrier search. :param num_threads: (int) The number of threads concurrently used by the function. :param vertical_barrier_times: (pd.Series) A pandas series with the timestamps of the vertical barriers. We pass a False when we want to disable vertical barriers. :param side_prediction: (pd.Series) Side of the bet (long/short) as decided by the primary model :param verbose: (bool) Flag to report progress on asynch jobs :return: (pd.DataFrame) Events -events.index is event's starttime -events['t1'] is event's endtime -events['trgt'] is event's target -events['side'] (optional) implies the algo's position side -events['pt'] is profit taking multiple -events['sl'] is stop loss multiple """ # 1) Get target target = target.reindex(t_events) target = target[target > min_ret] # min_ret # 2) Get vertical barrier (max holding period) if vertical_barrier_times is False: vertical_barrier_times = pd.Series(pd.NaT, index=t_events, dtype=t_events.dtype) # 3) Form events object, apply stop loss on vertical barrier if side_prediction is None: side_ = pd.Series(1.0, index=target.index) pt_sl_ = [pt_sl[0], pt_sl[0]] else: side_ = side_prediction.reindex(target.index) # Subset side_prediction on target index. pt_sl_ = pt_sl[:2] # Create a new df with [v_barrier, target, side] and drop rows that are NA in target events = pd.concat({'t1': vertical_barrier_times, 'trgt': target, 'side': side_}, axis=1) events = events.dropna(subset=['trgt']) # Apply Triple Barrier first_touch_dates = mp_pandas_obj(func=apply_pt_sl_on_t1, pd_obj=('molecule', events.index), num_threads=num_threads, close=close, events=events, pt_sl=pt_sl_, verbose=verbose) for ind in events.index: events.at[ind, 't1'] = first_touch_dates.loc[ind, :].dropna().min() if side_prediction is None: events = events.drop('side', axis=1) # Add profit taking and stop loss multiples for vertical barrier calculations events['pt'] = pt_sl[0] events['sl'] = pt_sl[1] return events
Wir verwenden get_bins(), um einen Datenrahmen mit Ereignissen zurückzugeben:
- events.index ist die Startzeit des Ereignisses
- events['t1'] ist die Endzeit des Ereignisses
- events['trgt'] ist das Ziel des Ereignisses
- events['side'] (optional) impliziert die Positionsseite der Strategie
- Fall 1: Wenn „side“ nicht in Ereignissen → bin ∈ {-1, 1} (Kennzeichnung durch Preisaktion)
- Fall 2: Wenn „side“ vorhanden ist → bin ∈ {0, 1} (Kennzeichnung durch PnL – Meta-Kennzeichnung)
# Snippet 3.4 -> 3.7, page 51, Labeling for Side & Size with Meta Labels def get_bins(triple_barrier_events, close, vertical_barrier_zero=False, pt_sl=[1, 1]): """ Advances in Financial Machine Learning, Snippet 3.7, page 51. Labeling for Side & Size with Meta Labels Compute event's outcome (including side information, if provided). events is a DataFrame where: Now the possible values for labels in out['bin'] are {0,1}, as opposed to whether to take the bet or pass, a purely binary prediction. When the predicted label the previous feasible values {−1,0,1}. The ML algorithm will be trained to decide is 1, we can use the probability of this secondary prediction to derive the size of the bet, where the side (sign) of the position has been set by the primary model. :param triple_barrier_events: (pd.DataFrame) Events DataFrame with the following structure: - **index**: pd.DatetimeIndex of event start times - **t1**: (pd.Series) Event end times - **trgt**: (pd.Series) Target returns - **side**: (pd.Series, optional) Algo's position side Labeling behavior depends on the presence of 'side': - Case 1: If 'side' not in events → `bin ∈ {-1, 1}` (label by price action) - Case 2: If 'side' is present → `bin ∈ {0, 1}` (label by PnL — meta-labeling) :param close: (pd.Series) Close prices :param vertical_barrier_zero: (bool) If True, set bin to 0 for events that touch vertical barrier, else bin is the sign of the return. :param pt_sl: (list) Take-profit and stop-loss multiples :return: (pd.DataFrame) Meta-labeled events :returns index: Event start times :returns t1: Event end times :returns trgt: Target returns :returns side: Optional. Algo's position side :returns ret: Returns of the event :returns bin: Labels for the event, where 1 is a positive return, -1 is a negative return, and 0 is a vertical barrier hit """ # 1. Align prices with their respective events events = triple_barrier_events.dropna(subset=["t1"]) all_dates = events.index.union(other=events["t1"].array).drop_duplicates() prices = close.reindex(all_dates, method="bfill") # 2. Create out DataFrame out_df = events[["t1"]].copy() out_df["ret"] = np.log(prices.loc[events["t1"].array].array / prices.loc[events.index]) out_df["trgt"] = events["trgt"] # Meta labeling: Events that were correct will have pos returns if "side" in events: out_df["ret"] *= events["side"] # meta-labeling if vertical_barrier_zero: # Label 0 when vertical barrier reached out_df["bin"] = barrier_touched( out_df["ret"].values, out_df["trgt"].values, np.array(pt_sl, dtype=float), ) else: # Label is the sign of the return out_df["bin"] = np.where(out_df["ret"] > 0, 1, -1).astype("int8") # Meta labeling: label incorrect events with a 0 if "side" in events: out_df.loc[out_df["ret"] <= 0, "bin"] = 0 # Add the side to the output. This is useful for when a meta label model must be fit if "side" in triple_barrier_events.columns: out_df["side"] = triple_barrier_events["side"].astype("int8") out_df["ret"] = np.exp(out_df["ret"]) - 1 # Convert log returns to simple returns return out_df
HINWEIS: mp_pandas_obj() , wie oben verwendet, ist eine Hilfsfunktion, die die parallele Verarbeitung bei der Arbeit mit Pandas-Objekten erleichtert (Pandas läuft immer auf einer einzigen CPU). Das Attachment multiprocess.py enthält diese Funktion und andere Multiprocessing-Hilfsfunktionen.
Um die Kennzeichnung auf Null zu setzen, wenn eine vertikale Barriere berührt wird, rufen wir barrier_touched() inget_bins() auf.
# Snippet 3.9, page 55, Question 3.3 def barrier_touched(ret, target, pt_sl): """ Advances in Financial Machine Learning, Snippet 3.9, page 55, Question 3.3. Adjust the getBins function (Snippet 3.7) to return a 0 whenever the vertical barrier is the one touched first. Top horizontal barrier: 1 Bottom horizontal barrier: -1 Vertical barrier: 0 :param ret: (np.array) Log-returns :param target: (np.array) Volatility target :param pt_sl: (ArrayLike) Take-profit and stop-loss multiples :return: (np.array) Labels """ N = ret.shape[0] # Number of events store = np.empty(N, dtype=np.int8) # Store labels in an array profit_taking_multiple = pt_sl[0] stop_loss_multiple = pt_sl[1] # Iterate through the DataFrame and check if the vertical barrier was reached for i in range(N): pt_level_reached = ret[i] > np.log(1 + profit_taking_multiple * target[i]) sl_level_reached = ret[i] < np.log(1 - stop_loss_multiple * target[i]) if ret[i] > 0.0 and pt_level_reached: # Top barrier reached store[i] = 1 elif ret[i] < 0.0 and sl_level_reached: # Bottom barrier reached store[i] = -1 else: # Vertical barrier reached store[i] = 0 return store
Wann es als Null oder als Signal des Rückgabewerts zu kennzeichnen ist
Die Kennzeichnung eines Nichtberührungsereignisses als Null ist sinnvoll, wenn sich Ihr Modell strikt auf eindeutige risikogesteuerte Ergebnisse konzentrieren soll, während die Verwendung des Vorzeichens der Rendite am Horizont alle Richtungsdifferenzen erfasst, selbst wenn Ihre Risikoschwellen nicht überschritten werden.
Als Null kennzeichnen, wenn:
- Sie bauen einen Drei-Klassen-Klassifikator auf (aufwärts, abwärts, neutral) und wollen, dass „neutral“ „keine entscheidende Bewegung“ innerhalb Ihrer Risikogrenzen bedeutet.
- Sie ziehen es vor, zweideutige Signale – kleine Abweichungen, die keine der beiden Grenzen berühren – aus dem Training herauszufiltern.
- Sie wollen den Erfolg eines Ereignisses ausschließlich daran messen, ob Sie Ihre vordefinierten Gewinn- oder Verlustschwellen erreichen, und alle anderen Fälle ignorieren.
Kennzeichnung als Signal des Rückgabewertes, wenn:
- Bei einem Zwei-Klassen-Problem muss jede Stichprobe eine binäre Richtung (aufwärts/abwärts) tragen, und man möchte ein Übermaß an neutralen Bezeichnungen vermeiden.
- Sie modellieren eher Momentum- oder Zeithorizont-Renditen als streng risikokontrollierte Ausstiege.
- Sie sind der Meinung, dass Preisbewegungen – egal wie gering – informativ sind und Ihren Schätzer beeinflussen sollten.
Beachten Sie darüber hinaus, wie sich diese Wahl auf die Klassenbalance und das Etikettenrauschen auswirkt. Wenn Sie zu viele Nullen sehen, könnten Sie die Neutralen unterbewerten oder die horizontalen Schranken erhöhen, und wenn Ihre Vorzeichen-Kennzeichen zu verrauscht sind, könnten Sie einen Mindestrückgabe-Schwellenwert anwenden, bevor Sie +1/-1 zuweisen.
Ereignisbezogene Probenahme
Als Händler entscheiden wir nicht einfach zufällig, wann wir Wertpapiere kaufen oder verkaufen. Stattdessen warten wir darauf, dass sich bestimmte Dinge auf dem Markt ereignen, bevor wir selbst aktiv werden. Zu diesen „auslösenden Ereignissen“ können gehören:
- Wenn wichtige Wirtschaftsdaten veröffentlicht werden (wie Beschäftigungszahlen oder Inflationsberichte)
- Wenn die Marktpreise plötzlich sehr unbeständig werden
- Wenn sich der Preisunterschied zwischen verwandten Investitionen weit von dem entfernt, was man normalerweise erwartet
Sobald eines dieser Ereignisse eintritt, betrachten wir es als ein Signal dafür, dass sich etwas Wichtiges auf dem Markt ereignen könnte. Wir können dann unsere ML-Algorithmen herausfinden lassen, ob es unter diesen Umständen eine genaue Vorhersagefunktion gibt.
Der Kerngedanke ist, herauszufinden, ob es eine genaue Möglichkeit gibt, Marktbewegungen genau dann vorherzusagen, wenn diese Ereignisse eintreten. Wenn der Algorithmus zeigt, dass ein bestimmter Ereignistyp nicht zu genauen Vorhersagen führt, müssen wir entweder die Definition dessen, was als signifikantes Ereignis gilt, ändern oder es mit anderen Merkmalen als Input für das Modell erneut versuchen.
Der CUSUM-Filter
Eine leistungsstarke Technik für ereignisbasierte Stichproben ist der CUSUM-Filter, eine Qualitätskontrollmethode, die zur Erkennung von Verschiebungen des Mittelwerts einer Messgröße verwendet wird. In der Finanzwelt können wir diesen Filter so anpassen, dass er immer dann Datenpunkte abgreift, wenn eine signifikante Abweichung bei einer Marktvariablen, wie dem Preis, auftritt. Der CUSUM-Filter funktioniert, indem er Abweichungen von einem erwarteten Wert akkumuliert und ein Stichprobenereignis auslöst, wenn diese Akkumulation einen bestimmten Schwellenwert überschreitet.
Der symmetrische CUSUM-Filter ist wie folgt definiert:
-
S⁺ = max(0, S⁺ + ΔP)
-
S- = min(0, S- + ΔP)
Dabei ist ΔP die Preisänderung. Ein Ereignis wird ausgelöst, wenn entweder S⁺ einen positiven Schwellenwert h überschreitet oder S⁻ einen negativen Schwellenwert -h unterschreitet. Wenn ein Ereignis ausgelöst wird, wird der entsprechende Akkumulator zurückgesetzt. Mit dieser Methode wird vermieden, dass mehrere Ereignisse ausgelöst werden, wenn sich der Preis um einen Schwellenwert herum bewegt, was bei gängigen Marktsignalen wie Bollinger-Bändern häufig der Fall ist. Durch die Verwendung eines CUSUM-Filters können wir eine Merkmalsmatrix X erstellen, die in Momenten signifikanter Marktaktivität abgetastet wird und somit relevantere Daten für unsere ML-Modelle liefert.
# Snippet 2.4, page 39, The Symmetric CUSUM Filter. def cusum_filter(raw_time_series, threshold, time_stamps=True): """ Advances in Financial Machine Learning, Snippet 2.4, page 39. The Symmetric Dynamic/Fixed CUSUM Filter. The CUSUM filter is a quality-control method, designed to detect a shift in the mean value of a measured quantity away from a target value. The filter is set up to identify a sequence of upside or downside divergences from any reset level zero. We sample a bar t if and only if S_t >= threshold, at which point S_t is reset to 0. One practical aspect that makes CUSUM filters appealing is that multiple events are not triggered by raw_time_series hovering around a threshold level, which is a flaw suffered by popular market signals such as Bollinger Bands. It will require a full run of length threshold for raw_time_series to trigger an event. Once we have obtained this subset of event-driven bars, we will let the ML algorithm determine whether the occurrence of such events constitutes actionable intelligence. Below is an implementation of the Symmetric CUSUM filter. Note: As per the book this filter is applied to closing prices but we extended it to also work on other time series such as volatility. :param raw_time_series: (pd.Series) Close prices (or other time series, e.g. volatility). :param threshold: (float or pd.Series) When the abs(change) is larger than the threshold, the function captures it as an event, can be dynamic if threshold is pd.Series :param time_stamps: (bool) Default is to return a DateTimeIndex, change to false to have it return a list. :return: (datetime index vector) Vector of datetimes when the events occurred. This is used later to sample. """ t_events = [] s_pos = 0 s_neg = 0 # log returns raw_time_series = pd.DataFrame(raw_time_series) # Convert to DataFrame raw_time_series.columns = ['price'] raw_time_series['log_ret'] = raw_time_series.price.apply(np.log).diff() if isinstance(threshold, (float, int)): raw_time_series['threshold'] = threshold elif isinstance(threshold, pd.Series): raw_time_series.loc[threshold.index, 'threshold'] = threshold else: raise ValueError('threshold is neither float nor pd.Series!') raw_time_series = raw_time_series.iloc[1:] # Drop first na values # Get event time stamps for the entire series for tup in raw_time_series.itertuples(): thresh = tup.threshold pos = float(s_pos + tup.log_ret) neg = float(s_neg + tup.log_ret) s_pos = max(0.0, pos) s_neg = min(0.0, neg) if s_neg < -thresh: s_neg = 0 t_events.append(tup.Index) elif s_pos > thresh: s_pos = 0 t_events.append(tup.Index) # Return DatetimeIndex or list if time_stamps: event_timestamps = pd.DatetimeIndex(t_events) return event_timestamps return t_events
Lassen Sie uns analysieren, wie eine Mean-Reverting-Bollinger-Band-Strategie abschneidet, wenn wir ungefilterte und CUSUM-gefilterte Einstiegssignale verwenden. Wir verwenden EURUSD 5-Minuten-Zeitbalken vom 2018-01-01 bis 2021-12-31 für Training und Validierung und Daten vom 2022-01-01 bis 2024-12-31 für Out-of-Sample-Tests.
Für diese Demonstration verwenden wir eine bewusst sensible Bollinger-Band-Konfiguration (20 Perioden, 1,5 Standardabweichungen), um eine große Anzahl von Handelssignalen zu erzeugen, die das Meta-Modell auswerten kann. Während dies für eine eigenständige Strategie zu laut wäre, bietet es einen idealen Stresstest für unsere Kennzeichnungs- und Filterungspipeline.
Um die Konsistenz und Interoperabilität aller Strategien zu gewährleisten, ziehe ich es vor, sie mit dem objektorientierten Design von Python zu strukturieren, insbesondere durch eine gemeinsame Schnittstelle oder Basisklasse. Dieser Ansatz ermöglicht es, dass jede Strategie dieselbe Kernfunktionalität aufweist (z. B. Signalerzeugung, Ereignisfilterung), was es einfacher macht, sie zu vergleichen, zu erweitern und in umfassendere Arbeitsabläufe zu integrieren. Die Verwendung von TA-Lib und Pandas TA für die Generierung häufig verwendeter Signale ist vorteilhaft, da es branchenübliche Formeln implementiert, auf einem hoch optimierten C-Backend aufbaut und damit 2-4x schneller ist als entsprechende Python-Implementierungen. Außerdem wird sichergestellt, dass die Ausgaben standardisiert sind und Randfälle einheitlich behandelt werden, was nachgelagerte Aufgaben wie Kennzeichnung, Filterung oder Visualisierung vereinfacht. Diese Bibliothek kann manchmal schwierig zu installieren sein, daher empfehle ich, die Anweisungen in diesem Artikle zu befolgen.
import pandas as pd from typing import Tuple, Union import logging from abc import ABC, abstractmethod from typing import Dict, Tuple, Union import numpy as np import pandas as pd import talib from loguru import logger class BaseStrategy(ABC): """Abstract base class for trading strategies""" @abstractmethod def generate_signals(self, data: pd.DataFrame) -> pd.Series: """Generate trading signals (1 for long, -1 for short, 0 for no position)""" pass @abstractmethod def get_strategy_name(self) -> str: """Return strategy name""" pass @abstractmethod def get_objective(self) -> str: """Return strategy objective""" pass class BollingerMeanReversionStrategy(BaseStrategy): """Bollinger Bands mean reversion strategy""" def __init__(self, window: int = 20, num_std: float = 2.0, objective: str = "mean_reversion"): self.window = window self.num_std = num_std self.objective = objective def generate_signals(self, data: pd.DataFrame) -> pd.Series: """Generate mean-reversion signals using Bollinger Bands""" close = data["close"] # Calculate Bollinger Bands upper_band, _, lower_band = talib.BBANDS( close, timeperiod=self.window, nbdevup=self.num_std, nbdevdn=self.num_std ) # Generate signals signals = pd.Series(0, index=data.index, dtype="int8", name="side") signals[(close >= upper_band)] = -1 # Sell signal (mean reversion) signals[(close <= lower_band)] = 1 # Buy signal (mean reversion) return signals def get_strategy_name(self) -> str: return f"Bollinger_w{self.window}_std{self.num_std}" def get_objective(self) -> str: return self.objective def get_entries( strategy: 'BaseStrategy', data: pd.DataFrame, filter_events: bool = False, filter_threshold: Union[float, pd.Series] = None, on_crossover: bool = True, ) -> Tuple[pd.Series, pd.DatetimeIndex]: """Get timestamps and position information for entry events. This function processes signals from a given `BaseStrategy` to identify trade entry points. It can apply a CUSUM filter to isolate significant events or, by default, detect entries at signal crossover points. Args: strategy (BaseStrategy): The trading strategy object that generates the primary signals. data (pd.DataFrame): A pandas DataFrame containing the input data, expected to have a 'close' column if `filter_events` is True. filter_events (bool, optional): If True, a CUSUM filter is applied to the signals to identify significant events. Defaults to False. filter_threshold (Union[float, pd.Series], optional): The threshold for the CUSUM filter. Must be a float or a pandas Series. Defaults to None. on_crossover (bool, optional): If True, only events where the signal changes from the previous period are considered entry points. Defaults to True. Raises: ValueError: If `filter_events` is True and `filter_threshold` is not a `float` or `pd.Series`. Returns: Tuple[pd.Series, pd.DatetimeIndex]: A tuple containing: side (pd.Series): A Series with the same index as the input data, where each value represents the trading position (-1 for short, 1 for long, 0 for no position). t_events (pd.DatetimeIndex): A DatetimeIndex of the timestamps for each detected entry event. """ primary_signals = strategy.generate_signals(data) signal_mask = primary_signals != 0 # Vectorized CUSUM filter application if filter_events: try: close = data.close except AttributeError as e: logger.error(f"Dataframe must have a 'close' column: {e}") raise e if not isinstance(filter_threshold, (pd.Series, float)): raise ValueError("filter_threshold must be a Series or a float") elif isinstance(filter_threshold, pd.Series): filter_threshold = filter_threshold.copy().dropna() close = close.reindex(filter_threshold.index) # Assuming cusum_filter is a function that takes a Series and a threshold filtered_events = cusum_filter(close, filter_threshold) signal_mask &= primary_signals.index.isin(filtered_events) else: # Vectorized signal change detection if on_crossover: signal_mask &= primary_signals != primary_signals.shift() t_events = primary_signals.index[signal_mask] side = pd.Series(index=data.index, name="side") side.loc[t_events] = primary_signals.loc[t_events] side = side.ffill().fillna(0).astype("int8") if filter_events: s = " generated by CUSUM filter" elif on_crossover: s = " generated by crossover" else: s = "" logger.info(f"Generated {len(t_events):,} trade events{s}.") return side, t_events
Merkmalstechnik für Meta-Kennzeichen
Um die nuancierte Dynamik von Finanzzeitreihen zu erfassen, haben wir einen umfangreichen Funktionssatz entwickelt, der statistische Strenge mit bereichsspezifischen Erkenntnissen verbindet. Dazu gehören volatilitätsbereinigte Momentum-Indikatoren, Autokorrelationsstrukturen und Renditemomente höherer Ordnung (Schiefe und Kurtosis) sowie von Bollinger abgeleitete Metriken und normalisierte gleitende Durchschnittsdifferenzen. Technische Signale wie RSI, MACD, ADX und ATR wurden mit TA-Lib und pandas-ta extrahiert, um Konsistenz und Reproduzierbarkeit zu gewährleisten. Durch die Einbeziehung sowohl kurzfristiger als auch langfristiger Merkmale – verzögerte Renditen, Yang-Zhang-Volatilitätsschätzungen und Trendfolgeindikatoren – ist das Modell in der Lage, subtile Verschiebungen im Marktverhalten zu erkennen und auf sich entwickelnde Handelsbedingungen zu reagieren. Der Code findet sich im Anhang features.py.
Um die Effektivität des CUSUM-Filters zu veranschaulichen, habe ich einen Random Forest mit ungefilterten und gefilterten Signalen auf unseren EURUSD M5-Daten trainiert. Meine horizontalen Barrieren wurden anhand der exponentiell gewichteten, täglichen Volatilität über 100 Tage als Ziel festgelegt, wobei die Gewinnmitnahme-Barriere auf 1 und die Stop-Loss-Barriere auf 2 gesetzt wurde. Meine vertikale Barriere war auf 50 Balken eingestellt.
target = get_daily_vol(close, lookback=100)
cusum_filter_threshold = target.mean()
Auswirkungen des Filterns von Daten
Bevor wir uns den Modellvergleichen zuwenden, hier eine kurze Einführung in die wichtigsten Kennzahlen, die in jeder Klassifizierungstabelle aufgeführt sind:- Precision: Prozentualer Anteil der richtigen positiven Vorhersagen an allen positiven Aufrufen. Hohe Präzision bedeutet wenige Fehlalarme.
- Recall: Prozentualer Anteil der korrekt identifizierten Positivmeldungen. Ein hoher Recall bedeutet wenige verpasste Ereignisse.
- F1-Score: Die Genauigkeit ist möglicherweise kein angemessener Klassifizierungswert für Meta-Kennzeichnung-Anwendungen. Nehmen wir an, dass es nach der Anwendung des Meta-Kennzeichnung viel mehr negative Fälle (Kennzeichen „0“) als positive Fälle (Kennzeichen „1“) gibt. In diesem Szenario wird ein Klassifikator, der jeden Fall als negativ vorhersagt, eine hohe Genauigkeit erreichen, auch wenn recall=0 und precision undefiniert ist. Der F1-Score korrigiert diesen Fehler, indem er den Klassifikator anhand des (gleich gewichteten) harmonischen Mittelwerts von Precision und Recall bewertet.
- Unterstützung: Die Anzahl der Instanzen für jede Klasse in der Validierungsmenge.
- Genauigkeit: Gesamtanteil der richtigen Vorhersagen über alle Klassen hinweg.
Eine ausführliche Beschreibung dieser Metriken finden Sie unter „How to Interpret the Classification Report in sklearn“.
Bevor wir die Ergebnisse vergleichen, sollten wir beachten, dass der CUSUM-Filter die Stichprobengröße um 76,1 % reduziert.
| Ungefilterte Signale | Gefilterte Signale | Rückgang % |
|---|---|---|
| 32828 | 7825 | 76.1 |
TABELLE 0: Signalanzahl – Gefiltert vs. Ungefiltert
Der CUSUM-Filter zielt darauf ab, „Rauschen“ zu verwerfen, das untrennbar mit der Klasse-0-Dynamik verbunden ist. Das ideale Ergebnis ist eine Verbesserung von F1 für Klasse 1 (bessere Erfassung von Ereignissen) bei gleichzeitiger Beibehaltung von F1 für Klasse 0 (keine zusätzlichen falschen Signale). Unser gefiltertes primäres Modell ist ideal, aber unser gefiltertes Metamodell hat einen Rückgang von 5,8 % beim F1-Wert für Klasse 0. Um dies abzumildern, könnten wir die im Modell verwendeten Hyperparameter anpassen oder unseren Merkmalsatz ändern.
| Kennzahl | Ungefiltert | Gefiltert | Δ |
|---|---|---|---|
| Recall (1) | 1.00. | 1.00. | 0% |
| Precision (1) | 0.33 | 0.38 | +15.2% |
| F1 (1) | 0.49 | 0.55 | +11.0% |
| Kennzahl | Ungefiltert | Gefiltert | Δ |
|---|---|---|---|
| F1 (0) | 0.69 | 0.65 | -5.8% |
| F1 (1) | 0.57 | 0.60 | +5.3% |
| Accuracy | 0.64 | 0.63 | -1.6% |
Tabelle 4: Vergleich von gefilterten und ungefilterten Meta-Modellen
Der Kompromiss zwischen Datenreduzierung und Modellleistung kann wie folgt berechnet werden:
- Leistungserhalt = gefilterte Leistung / ungefilterte Leistung * 100
- Nettonutzen = Leistungserhalt – Datenreduzierung
Wenn wir einen positiven Nettonutzen erhalten, dann ist der Filter effizient und sollte verwendet werden.
| Modell | Datenreduzierung | Leistungserhalt | Nettovorteil |
|---|---|---|---|
| Primäre | 76.1% | 112.2% | +36.1% |
| Meta | 76.1% | 98.5% | +22.4% |
Tabelle 5: Analyse der Kompromisse
Aus dem Vergleich der ungefilterten und gefilterten Signale ergeben sich folgende Erkenntnisse:
- Mit dem CUSUM-Filter wurden 76,1 % der Ereignisse erfolgreich als Rauschen aussortiert.
- Die Filterung verbesserte die Präzision sowohl im Primärmodell als auch im Metamodell.
- Die Filterung verschlechterte die Gesamtleistung des Metamodells trotz 76 % weniger Daten nur geringfügig. Es gab einen Gewinn von 5,3 % für die Klasse 1 und einen Rückgang von 5,6 % für die Klasse 0. Trotz des Rückgangs in der Klasse 0 F1 erzielten wir immer noch einen Nettovorteil durch die Verwendung des CUSUM-Filters.
Meta-Kennzeichnung-Berichte: Bollinger Band Strategie
Die nachstehenden Klassifizierungsberichte und ROC-Kurven unterstreichen eine wichtige Erkenntnis: Meta-Kennzeichnung gedeiht, wenn es mit realistischen, risikobewussten Kennzeichnungsschemata kombiniert wird.
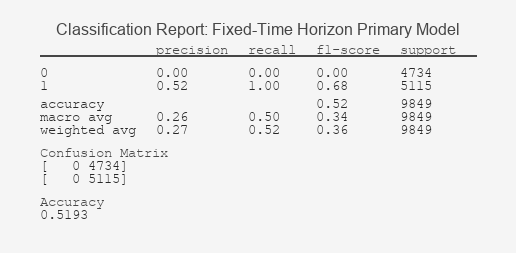
Abbildung 1: Fester Zeithorizont Primäres Modell Klassifizierungsbericht
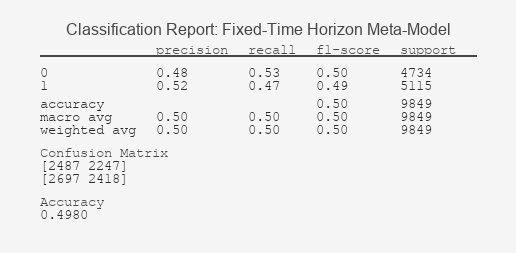
Abbildung 2: Fester Zeithorizont Metamodell Klassifizierungsbericht
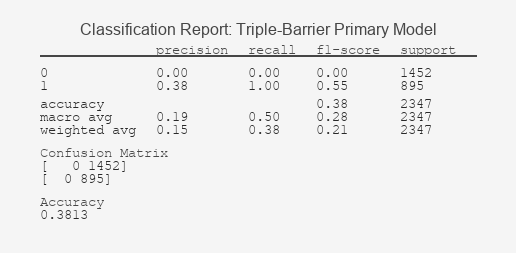
Abbildung 3: Dreifach-Barriere Bericht zur Klassifizierung des primären Modells
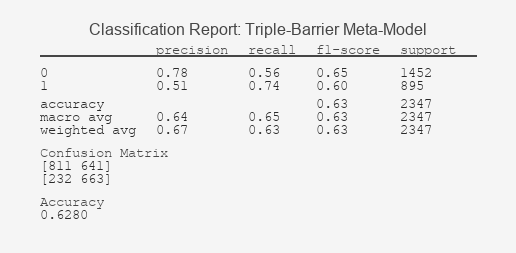
Abbildung 4: Dreifach-Barriere Metamodell Klassifizierungsbericht
Kurve der Receiver Operating Characteristic (ROC)
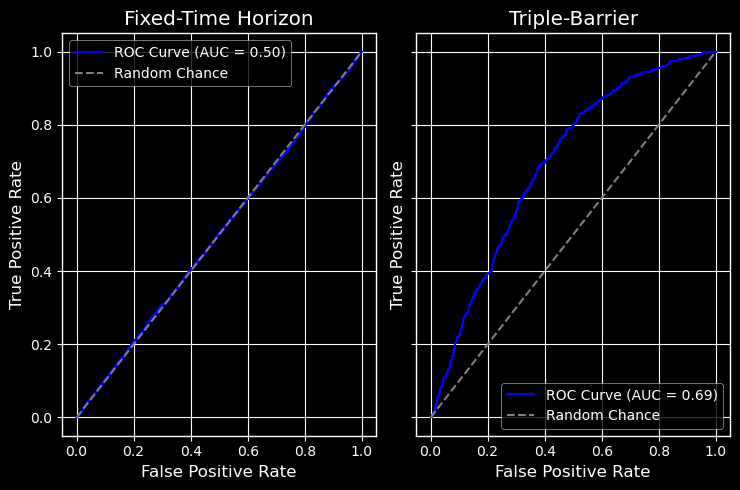
Abbildung 5: ROC für fester Zeithorizont und Triple-Barrier-Metamodelle
Interpretation der Ergebnisse: Entschlüsselung der Leistung des Modells
Der starke Kontrast zwischen diesen Ergebnissen bestätigt die Kernthese: Die Kennzeichnung definiert den Erfolg. Der Klassifizierungsbericht des Modells mit festem Zeithorizont offenbart ein grundlegendes Versagen beim Lernen; seine Unfähigkeit, Signale von Zufallsereignissen zu unterscheiden, wird grafisch durch seine ROC-Kurve bestätigt, die sich an die Diagonale klammert, ein Kennzeichen für einen unbrauchbaren Klassifizierer. Im Gegensatz dazu zeigt der Bericht der Triple-Barrier-Methode ein Modell, das erfolgreich prädiktive Muster identifiziert hat, was durch die ausgeprägte Krümmung der ROC-Kurve in Richtung der oberen linken Ecke unterstrichen wird, die auf einen signifikanten Kompromiss zwischen wahrer und falscher Positivrate hinweist. Dieser ROC-AUC-Wert, der deutlich über 0,5 liegt, beweist die greifbare Vorhersagekraft des Modells.
Noch wichtiger ist, dass sich die Präzisionsmetriken direkt auf die Handelsrealität übertragen lassen: Eine höhere Präzision für die Klasse „1“ bedeutet, dass ein größerer Anteil der von uns vorhergesagten profitablen Trades (Meta-Labels) wahrscheinlich richtig ist, was die potenzielle Rentabilität der Strategie erhöht und eine konkrete statistische Grundlage für die vertrauensbasierte Positionsgrößenbestimmung bietet.
Wirtschaftliche Bedeutung: Leistung außerhalb der Stichprobe
Während das Triple-Barrier-Modell eine statistisch signifikante Verbesserung der AUC aufweist, zeigt sich sein wahrer Wert in der simulierten Kapitalkurve. Abbildung 7 zeigt, dass die Strategie, die unsere neue Kennzeichnungsmethode nutzt, eine Rendite von -0,03 % bei einem maximalen Drawdown von 36,9 % erzielt und damit die Benchmark-Strategie mit festem Zeithorizont, die eine Rendite von -0,71 % bei einem maximalen Drawdown von 76 % erzielt, deutlich übertrifft.
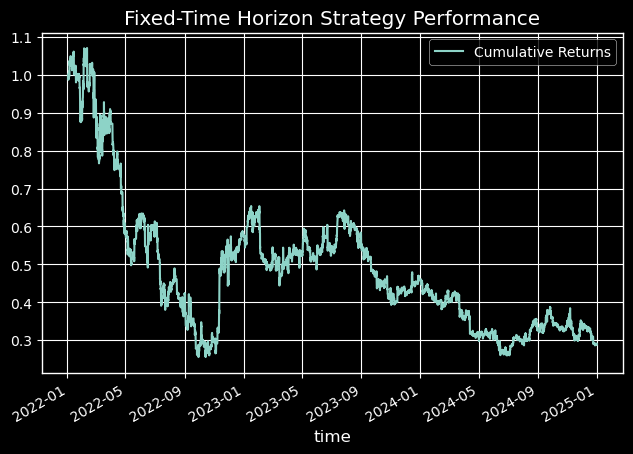
Abbildung 6: Fester Zeithorizont Leistung Kapitalkurve
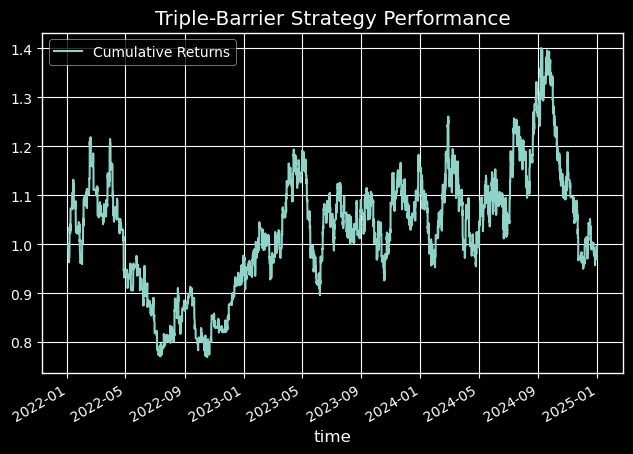
Abbildung 7: Triple-Barrier-Strategie Performance Kapitalkurve
Nachfolgend finden Sie eine umfassende Tabelle mit den Leistungskennzahlen für jede Kennzeichnungsmethode:
| Metriken | Fester Zeithorizont | Triple-Barriere |
|---|---|---|
| total_return | -0.709771 | -0.028839 |
| annualized_return | -0.338102 | -0.009714 |
| volatility | 0.483111 | 0.37613 |
| downside_volatility | 0.336945 | 0.231413 |
| sharpe_ratio | -4.778646 | -0.021566 |
| sortino_ratio | -6.851611 | -0.035053 |
| var_95 | -0.002864 | -0.00215 |
| cvar_95 | -0.004164 | -0.002992 |
| skewness | -0.014451 | 0.034745 |
| kurtosis | 3.857222 | 2.507046 |
| max_drawdown | 0.761708 | 0.368585 |
| avg_drawdown | 0.08375 | 0.039945 |
| drawdown_duration | 84 days 01:18:50 | 32 days 03:17:12 |
| ulcer_index | 0.217503 | 0.098507 |
| calmar_ratio | -0.443874 | -0.026354 |
| bet_frequency | 3901 | 3969 |
| bets_per_year | 1300.040115 | 1322.701671 |
| num_trades | 37691 | 27426 |
| trades_per_year | 12560.83363 | 9139.93853 |
| win_rate | 0.497546 | 0.504339 |
| avg_win | 0.001266 | 0.001081 |
| avg_loss | -0.001322 | -0.001105 |
| best_trade | 0.014599 | 0.01451 |
| worst_trade | -0.013828 | -0.010548 |
| profit_factor | 0.952754 | 0.999799 |
| expectancy | -0.000034 | -0.000002 |
| kelly_criterion | -0.027194 | -0.002226 |
| consecutive_wins | 77 | 92 |
| consecutive_losses | 66 | 90 |
| avg_trade_duration | 0 days 00:39:18 | 0 days 06:22:15 |
Tabelle 6: Leistungsmetriken außerhalb der Stichprobe
Schlussfolgerung
In diesem zweiten Teil des MetaTrader 5 Machine Learning Blueprints haben wir untersucht, wie die Wahl der Kennzeichnung das Verhalten und die Zuverlässigkeit von Finanzmodellen beeinflusst. Indem wir über feste Zeithorizonte hinausgehen und pfadabhängige Techniken wie die Triple-Barrier-Methode einsetzen, haben wir gezeigt, wie Risikobewusstsein und realistische Handelsdynamik direkt in den Lernprozess integriert werden können.
Die Meta-Kennzeichnung hat sich als strategisches Overlay erwiesen, das Signale mit geringer Überzeugungskraft herausfiltert und die Präzision erhöht – vor allem, wenn sie mit robusten Kennzeichnungsschemata kombiniert wird. Die Klassifizierungsberichte und ROC-Kurven zeigen, wie dieser mehrschichtige Ansatz die Signalqualität verbessert, selbst bei aggressiver Filterung.
Aber unsere Reise ist noch lange nicht zu Ende.
Im nächsten Artikel werden wir die Trend-Scanning-Methode implementieren, die es den Modellen ermöglicht, ihren Prognosehorizont auf der Grundlage statistisch signifikanter Kursbewegungen dynamisch auszuwählen. Dies ermöglicht ein neues Maß an Anpassungsfähigkeit in volatilen Märkten.
Wir werden auch die Herausforderung der Gleichzeitigkeit in den Finanzdaten angehen – wenn sich mehrere Signale zeitlich überschneiden – indem wir Stichprobengewichte einführen, die die Einzigartigkeit und Relevanz jeder Beobachtung widerspiegeln. Dadurch wird sichergestellt, dass unsere Modelle von wirklich unabhängigen Signalen lernen und nicht von redundantem Rauschen.
Schließlich werden wir untersuchen, wie die durch Meta-Kennzeichnung generierten Wahrscheinlichkeiten genutzt werden können, um Wetten intelligenter zu gestalten. Anstelle der binären Ausführung verwenden wir probabilistisches Vertrauen, um die Positionsgrößen zu skalieren und so die Modellüberzeugung mit der Kapitalallokation in Einklang zu bringen.
Zusammen bringen uns diese Verbesserungen näher an eine produktionsreife Pipeline für maschinelles Lernen für die Finanzmärkte heran – eine Pipeline, die nicht nur technisch solide ist, sondern auch strategisch auf das reale Handelsverhalten abgestimmt ist.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18864
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Statistische Arbitrage durch kointegrierte Aktien (Teil 3): Datenbank-Einrichtung
Statistische Arbitrage durch kointegrierte Aktien (Teil 3): Datenbank-Einrichtung
 Beherrschung von Protokollaufzeichnungen (Teil 10): Vermeidung von Log Replay durch Implementierung einer Unterdrückung
Beherrschung von Protokollaufzeichnungen (Teil 10): Vermeidung von Log Replay durch Implementierung einer Unterdrückung
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 79): Verwendung von Gator-Oszillator und Akkumulations-/Distributions-Oszillator mit überwachtem Lernen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 79): Verwendung von Gator-Oszillator und Akkumulations-/Distributions-Oszillator mit überwachtem Lernen
 Statistische Arbitrage durch kointegrierte Aktien (Teil 2): Expert Advisor, Backtests und Optimierung
Statistische Arbitrage durch kointegrierte Aktien (Teil 2): Expert Advisor, Backtests und Optimierung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Etwas, das ich nicht verstehe:
Wenn Sie Modelle nicht mit den rohen Tick-Daten, sondern mit erstellten Balken (Zeit, Tick usw.) trainieren, müssen Sie dann während des Live-Handels Balken erstellen?