
共和分株式による統計的裁定取引(第2回):エキスパートアドバイザー、バックテスト、最適化
はじめに
私たちは、平均的な個人トレーダーでも利用できる統計的裁定取引(Statistical Arbitrage)のフレームワークを開発するという課題に取り組むことにしました。核心となる考え方は、統計的関数や分析手法をまとめ、一般的なノートパソコンと通常の証券口座を持つ個人トレーダーが、FX、株式、ETF、商品などで統計的裁定取引を始められるようにすることです。
最初は単純な相関に基づくペアトレードから始めました。バックテストでは非常に良好な結果を示しましたが、デモ口座ではまったくうまくいきませんでした。ここから分かるのは、注文執行レベルで取引が失敗していたという点です。戦略は注文執行の速度に非常に依存していましたが、私たちのインフラ(一般的なノートパソコン、低速インターネット接続、プロトタイプコード)は、この種の裁定取引に必要な品質には程遠いものでした。エントリーとエグジットのルールはタイミングに強く依存しており、裁定機会は私たちの注文がブローカーサーバーに届く前に閉じてしまっていました。
この注文執行のタイミング問題を解決、最小化、あるいは回避する方法としては、VPNを設定する(これは将来的におこなう予定です)、最大許容スリッページを設定したプロフェッショナル口座を開設する、またはプロトタイプコードを改善する、といった手段があります。これらの明白で比較的安価な手段はいずれも一定の効果があります。両方を組み合わせれば戦略を確実に軌道に戻すことができるでしょう。しかし、私たちは「平均的な個人トレーダーが最小限のリソースで利用できる」という初期の制約を維持したいため、注文執行速度にあまり依存しない戦略の開発を目標としました。以下に示す実装は、その目標に対する1つの回答です。
前回の記事では、エングル=グレンジャー共和分検定とジョハンセン共和分検定を紹介し、トレーダーの視点からの理論的背景と基本的な解釈について解説しました。今回は、それらの手法を用いて共和分ポートフォリオを構築していきます。
共和分関係に基づく株式ポートフォリオの構築
酔っ払い、犬、そしてランダムウォーク*
共和分を研究する際、共和分時系列、ここでは共和分株価の本質的な特徴をうまく説明する比喩に出会うことはよくあります。その比喩によれば、共和分関係にない2つの時系列は、酔っ払った男性が犬と一緒に歩いているようなものです。男性と犬の進む道はランダムにずれ、内在的にも、観測可能な意味でも、測定可能な論理でも統一されていません。男性と犬は別々の道を通って家にたどり着くこともありますし、犬が永遠に迷子になることさえあります。
しかし、共和分関係にある2つの時系列は、犬が首輪で導かれているような関係に例えられます。男性は依然として酔っ払っていて足取りはふらついていますが、それでも男性と犬は常に一緒に進みます。共和分関係にある株式は、まるで価格が「目に見えない首輪」で結ばれているかのようです。長期的には、男性と犬は一緒に家にたどり着く傾向があります。この「家」は共通の平均、すなわちスプレッドの平均値を指します。
では、数千銘柄ある中から、どのようにして共和分関係にある株式を見つければよいのでしょうか。幸いにも、同じセクターや業界の銘柄は一緒に動く傾向があることが既に知られています。この知識により、初期候補はより扱いやすい数に絞られますが、それでもまだ多くの銘柄が残ります。
図1: MetaQuotesデモサーバーで利用可能な銘柄の数
図2:商用ブローカーデモサーバーで国別に利用可能な株式銘柄の数
ペアトレーディングの候補銘柄をフィルタリングするための古典的・新規の方法はいくつか学術文献でレビューされていますが、結局のところ、いずれも共和分関係に勝る結果は得られていません [Brunetti & De Luca, 2023]。
ここでの目的は学術的なレビューではなく、サンプル実装をバックテストして説明することなので、小規模ポートフォリオを構築するためにシンプルなヒューリスティックを採用しました。
「ヒューリスティックとは、問題解決において、完全に最適化されたり、洗練されたり、理論的に合理化された方法ではないものの、それでもなお『十分に良い』近似解として機能する実用的な手法のことを指します」(ウィキペディア)
- ナスダック上場銘柄の中から、まずは高い流動性を持つ半導体関連企業を数十銘柄ほど抽出します。
- その中から、過去6か月以内の日足においてNVIDIAとの相関が最も高い銘柄を選定します。市場環境はAIおよび半導体分野を中心に非常に動的であるため、より長い期間のデータは使用しない方が望ましいと考えています。また、今後はモデルを毎月あるいは毎週更新していくため、初期段階として6か月以内のデータでフィルタリングすることが適切な方向性につながります。
- 次に、NVDAと高相関となった少数の銘柄群について、共和分関係を検定します。
- 少なくとも1つの有意なジョハンセンベクトルが見つかった場合、その共和分スプレッドが定常であるかどうかを確認します。
- 少なくとも1つの有意なジョハンセンベクトルを持ち、スプレッドが定常的である小さな銘柄グループが得られたら、最初のジョハンセン固有ベクトルを用いて相対的なポートフォリオの重みを算出します。
- 重みが得られた後は、その共和分関係を持つ銘柄バスケットのバックテストをおこないいます。
前回の記事で紹介したピアソン相関法を使用して、相関を用いる手法により、最終的に次の3銘柄に絞り込みました。いずれもAIハードウェア需要の恩恵を受けており、直接または隣接市場を通じてNVIDIAのサプライチェーンに関わっています。
Microchip Technology, Inc.(MCHP):MCHPはNVIDIA GPUと直接的な結びつきこそ弱いものの、ロボティクスや産業用AIなど、NVIDIAベースのシステムを導入するOEMやシステムインテグレーターを通じて、AIインフラ需要が高まる際に半導体セクター全体として恩恵を受けます。
Monolithic Power System Inc (MPWR):MPWRはサーバーやデータセンター向けの電源管理IC (PMIC)を提供しています。これらのPMICは、高負荷環境で熱的・電気的安定性が求められる高性能NVIDIA GPUにも使用されています。同社はNVIDIAのデータセンター事業や推論向け事業の拡大による恩恵を受けています。
Micron Technology Inc.(MU):MUはHBM (High-Bandwidth Memory)を含むメモリ製品を供給しており、これはNVIDIAのH100をはじめとするAIアクセラレータに不可欠です。同社のメモリ製品はNVIDIA GPUやデータセンターソリューションに組み込まれており、NVIDIAのAIチップ販売が増えるほどMicronの高性能メモリ需要も増加します。Micronは2024〜2025年にかけてAI需要を背景とした強い見通しを発表しており、その成長見込みはNVIDIAのパフォーマンスに密接に結びついています。
なお、今回選定した銘柄そのものが最も重要というわけではありません。重要なのは、仮説の基準となる銘柄、今回で言えばNVDAに対して最も相関の高い銘柄を選別するという点です。私たちの場合はNVDAでしたが、仮説に適合する任意の銘柄を使用できます。
また、NVDAに対して非常に高い相関を持ちながら、銘柄同士の相関が低いものは避ける必要があります。求めているのは、NVDAと高相関であると同時に、銘柄同士の相関もある程度高いグループです。つまり、リファレンス銘柄を中心に相関構造が形成されるバスケットを探すことが、今回の仮説に適した「銘柄の選別」プロセスとなります。
そのため、目指すべきは次のようなピアソン相関行列です。
| NVDA | MCHP | MPWR | MU | |
|---|---|---|---|---|
| NVDA | 1.000000 | 0.916887 | 0.894362 | 0.897219 |
| MCHP | 0.916887 | 1.000000 | 0.877042 | 0.941977 |
| MPWR | 0.894362 | 0.877042 | 1.000000 | 0.852675 |
| MU | 0.897219 | 0.941977 | 0.852675 | 1.000000 |
表1:NVDA、MCHP、MPWR、MU間のピアソン相関行列
このデータは、Seabornヒートマップとしてより簡単に表示できます。
import seaborn as sns sns.heatmap(corr_matrix, annot=True, cmap="coolwarm")
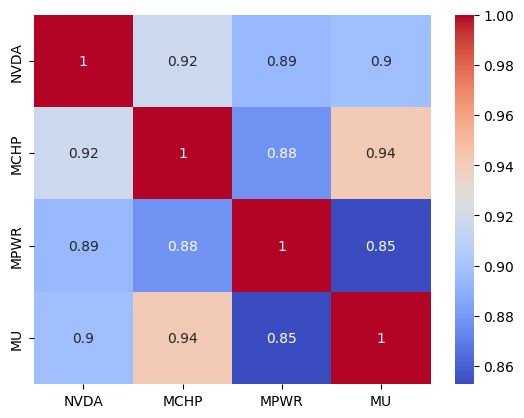
図3:NVDA、MCHP、MPWR、MUのピアソン相関行列(Seabornヒートマップによる可視化)
MCHP、MPWR、MUはいずれもNVDAとの相関が特別高いわけではありませんが、互いに適度な相関を持っている点にご注意ください。
また、実際の取引においては、スプレッドの計算をおこない、その結果によってエントリーとエグジットのポイントを決定するために、4つの資産すべてのティックデータが必要になります。これが、最初に高流動性の資産を選別した主な理由です。流動性の低い資産では、同期が崩れたり、OnTickイベントハンドラから数秒以上遅延してしまう可能性があるため避けたいのです(後述のとおりです)。
このようにして相関バスケットが定義できたら、まずエングル=グレンジャー共和分検定を用いて各ペアの共和の度合いを評価し、さらにジョハンセン共和分検定を用いて、バスケット全体、つまり資産グループとしての共和分レベルを調べます。これら2つの検定については、前回の記事により詳細な説明がありますのでそちらをご参照ください。
その後、ジョハンセン固有ベクトルからポートフォリオのヘッジ比率を取得します。
🧮 ポートフォリオの重み(ジョハンセン固有ベクトル):
MCHP-2.505294
ジョハンセン固有ベクトルとは、グループ内の各銘柄に対応した数値のリストであり、ジョハンセン検定によって特定された安定した関係を維持するために、各銘柄がどの程度の重み(重要度)を持つかを示すものです。これらの重みによって、特定の比率で銘柄を売買した際に、それらを組み合わせた価格変動がある程度予測可能で、結果として比較的安定した価格関係が維持されます。
これらの値は、注文数量のバランスを取るため、そして市場へのエクスポージャーを最小化するために使用します。統計的裁定戦略では、常にマーケットニュートラルを目指す点が重要です。重み付きポートフォリオは、「各銘柄を1単位ずつ同時に売買する」という単純なペアトレード手法を発展させたものと考えることができます。
これらのポートフォリオの重みは、サンプルEAのグローバル変数の中に含まれています。
// Global variables string symbols[] = {"MU", "NVDA", "MPWR", "MCHP"}; // Asset symbols double weights[] = {2.699439, 1.000000, -1.877447, -2.505294}; // Johansen eigenvector
NVDAの値が1.0になっているのは、Pythonコード(添付)において銘柄リストの最初の資産であるNVDAを基準として正規化したためです。正規化をおこなうことで、他の値を相対的に解釈できるようになります。Pythonリストの中にあるどの銘柄を基準として正規化しても問題ありません。これは任意のリファレンスにすぎません。
# === FIRST COINTEGRATION VECTOR === v = johansen_result.evec[:, 0] # v = v / v[-1] # Normalize on symbols list last asset v = v / v[0] # Normalize on symbols list first asset
これで、多変量スプレッドの定常性をテストできるようになります。
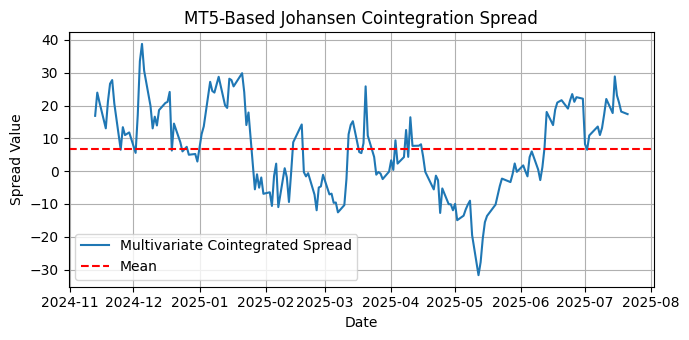
図4:NVDA、MCHP、MPWR、MUに対する多変量共和分スプレッドのプロット
多変量スプレッドを視覚的に確認することは、そのスプレッドが平均回帰戦略に適しているかどうかを評価する有効な方法です。視覚的な確認によって、スプレッドが平均周辺にどのように分布しているか、平均へ戻る動きが存在するか、そして定常性が期待できるかどうかを素早く推定できます。明確なトレンドが見られないことは定常性を示唆する強いサインであり、また季節性がないことも同様です。
しかし、視覚的な確認だけでは十分とは言えず、自動化されたモデルやポートフォリオ更新には使用できません。幸い、拡張ディッキー–フラー(ADF)検定とKPSS (Kwiatkowski-Phillips-Schmidt-Shin)検定があるので、これらを用いて客観的に判断することができます。
ADFとKPSSの両検定を使用して、スプレッドが平均回帰性を持っていることを確認します。
# Augmented Dickey-Fuller Test from statsmodels.tsa.stattools import adfuller adf_result = adfuller(spread, regression='c') # 'ct' for trend and constant print("ADF Test on Spread:") print(f" ADF Statistic : {adf_result[0]:.4f}") print(f" p-value : {adf_result[1]:.4f}") print(f" Critical Values:") for key, value in adf_result[4].items(): print(f" {key}: {value:.4f}") if adf_result[1] < 0.05: print("\n✅ The cointegrated spread is stationary (reject the null hypothesis).") else: print("\n❌ The cointegrated spread is NOT stationary (fail to reject the null hypothesis).")
ADF Test on Spread:
Critical Values:
10%: -2.5761
✅ The cointegrated spread is stationary (reject the null hypothesis).
# KPSS Test from statsmodels.tsa.stattools import kpss def run_kpss(series, regression='c'): statistic, p_value, lags, crit_values = kpss(series, regression=regression, nlags='auto') print("KPSS Test on Spread:")
KPSS Test on Spread:
Critical Values:
1%:0.739
✅ The cointegrated spread is stationary (fail to reject null of stationarity).
このステップは極めて重要です。スプレッドが定常でなければ、平均回帰という私たちの仮説は根本から崩れてしまいます。スプレッドが定常でない場合、価格は乖離し続ける可能性があり、平均回帰によって適切にクローズされないポジションを抱えたままになってしまう恐れがあります。この種の戦略において、スプレッドが定常であることを確認する作業は不可欠です。
今後、統計的裁定のフレームワークが進化するにつれて、ポートフォリオを自動的にローテーションさせる仕組みを導入していきます。そのため、視覚的なプロット確認だけに依存することはできず、定常性を検証するテストをツールキットとして備えておくことが極めて重要になります。
サンプル実装
サンプル実装では、まず平均からの標準偏差を用いてエントリー/エグジットポイントの閾値を定義します。
// Input parameters input double EntryThreshold = 2.0; // Entry threshold (standard deviations) input double ExitThreshold = 0.3; // Exit threshold (standard deviations) input double LotSize = 10.0; // Fixed lot size per leg input int LookbackPeriod = 252; // Lookback for moving average/standard deviation input int Slippage = 3; // Max allowed slippage
デフォルトのロットサイズである10.0単位は、バックテスト中に注文内のポートフォリオの重みを確認しやすくするための設定です。
最大許容スリッページは、ここではほぼ飾りのようなものです。というのも、私たちは一般的なリテールトレーダー向けに開発しており、最大スリッページ設定は通常、プロ向け口座でのみ利用可能な機能だからです。しかし、将来的な改良のためにこのパラメータを残しておくことは害になりません。この機能が無効化されている取引口座では、ブローカーサーバーによって単に無視されるだけです。
移動平均や標準偏差の計算に使用するルックバック(遡及)期間は、相関や共和分検定に使用した期間と同じでもよいですが、必須ではありません。たとえば、過去6か月の日足データで共和分を確認できた場合、1時間足で2週間のルックバック期間を使って運用することにも問題はありません。システムは十分に柔軟であり、その柔軟性の中に多くの機会が広がっています。以下では、特定のコード関数についていくつか説明します。
OnInit()
// Check if all symbols are available for(int i = 0; i < ArraySize(symbols); i++) { if(!SymbolSelect(symbols[i], true)) { Print("Error: Symbol ", symbols[i], " not found!"); return(INIT_FAILED); } }
バスケット内のすべての銘柄が、クオート取得のために気配値表示上で利用可能かどうかを確認します。
// Set a timer for spread, mean, and stdev calculations EventSetTimer(1); // one second
スプレッド、平均、標準偏差の計算のために、OnTick()関数の外側でタイマーを設定します。これは、すでにご存じのとおり、OnTickイベントハンドラがEAを起動したチャート/銘柄に依存しているためです。この銘柄に更新がない場合、OnTickは発生しません。私たちはこの更新依存に左右されることを避けたいのです。そのため、今回のように1秒のタイマーを使用することで、この間隔で確実に新しいクオートを確認できます。これは、受動的なクオート更新から、能動的なクオート更新への移行といえます。
OnTimer()
void OnTimer(void) { // Calculate current spread value currentSpread = CalculateSpread(); // Update spread buffer (rolling window) static int barCount = 0; if(barCount < LookbackPeriod) { spreadBuffer[barCount] = currentSpread; barCount++; return; // Wait until buffer is filled } // Shift buffer (remove oldest value, add newest) for(int i = 0; i < LookbackPeriod - 1; i++) spreadBuffer[i] = spreadBuffer[i + 1]; spreadBuffer[LookbackPeriod - 1] = currentSpread; // Calculate mean and standard deviation using custom functions spreadMean = CalculateMA(spreadBuffer, LookbackPeriod); spreadStdDev = CalculateStdDev(spreadBuffer, LookbackPeriod, spreadMean); }
OnTimerイベントハンドラ内では、チャートのルックバック期間を順次参照しながら、スプレッド、平均、および標準偏差を計算します。
OnTick()
void OnTick() { // Trading logic if(!tradeOpen) { // Check for entry signal (spread deviates from mean) if(currentSpread > spreadMean + EntryThreshold * spreadStdDev) { // Short spread (sell MU/NVDA, buy MPWR/MCHP) ExecuteTrade(ORDER_TYPE_SELL); tradeOpen = true; } else if(currentSpread < spreadMean - EntryThreshold * spreadStdDev) { // Buy spread (buy MU/NVDA, sell MPWR/MCHP) ExecuteTrade(ORDER_TYPE_BUY); tradeOpen = true; } } else { // Check for exit signal (spread reverts to mean) if((currentSpread <= spreadMean + ExitThreshold * spreadStdDev) && (currentSpread >= spreadMean - ExitThreshold * spreadStdDev)) { CloseAllTrades(); tradeOpen = false; } } // Display spread in chart Comment(StringFormat("Spread: %.2f | Mean: %.2f | StdDev: %.2f", currentSpread, spreadMean, spreadStdDev)); }
OnTick()イベントハンドラには、取引ロジックのみを実装しています。市場にポジションがない場合(!tradeOpen())、取引シグナルが発生していれば、ジョハンセン固有ベクトルから得られたポートフォリオの重みに従って、買いまたは売りをおこないます。
ExecuteTrade(ENUM_ORDER_TYPE orderType)
//+------------------------------------------------------------------+ //| Execute trade with normalized integer lots | //+------------------------------------------------------------------+ void ExecuteTrade(ENUM_ORDER_TYPE orderType) { double volumeArray[]; ArrayResize(volumeArray, ArraySize(symbols)); if(!NormalizeVolumeToIntegerLots(volumeArray, symbols, weights, LotSize)) { Print("Volume normalization failed!"); return; } for(int i = 0; i < ArraySize(symbols); i++) { ENUM_ORDER_TYPE legType = (weights[i] > 0) ? orderType : (orderType == ORDER_TYPE_BUY ? ORDER_TYPE_SELL : ORDER_TYPE_BUY); trade.PositionOpen(symbols[i], legType, volumeArray[i], 0, 0, 0, "NVDA Coint"); } } (...) //+------------------------------------------------------------------+ //| Normalize volumes to integer lots | //+------------------------------------------------------------------+ bool NormalizeVolumeToIntegerLots(double &volumeArray[], const string &symbols_arr[], const double &weights_arr[], double baseLotSize) { MqlTick tick; // Structure to store bid/ask prices double totalDollarExposure = 0.0; double dollarExposures[]; ArrayResize(dollarExposures, ArraySize(symbols_arr)); // Step 1: Calculate dollar exposure for each leg for(int i = 0; i < ArraySize(symbols_arr); i++) { if(!SymbolInfoTick(symbols_arr[i], tick)) // Get latest bid/ask { Print("Failed to get price for ", symbols_arr[i]); return false; } // Use bid price for short legs, ask for long legs double price = (weights_arr[i] > 0) ? tick.ask : tick.bid; dollarExposures[i] = MathAbs(weights_arr[i]) * price * baseLotSize; totalDollarExposure += dollarExposures[i]; } // Step 2: Convert dollar exposure to integer lots for(int i = 0; i < ArraySize(symbols_arr); i++) { double ratio = dollarExposures[i] / totalDollarExposure; double targetDollarExposure = ratio * totalDollarExposure; // Get min/max lot size and step for the symbol double minLot = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_MIN); double maxLot = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_MAX); double lotStep = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_STEP); // Get current price again (for lot calculation) if(!SymbolInfoTick(symbols_arr[i], tick)) return false; double price = (weights_arr[i] > 0) ? tick.ask : tick.bid; double lots = targetDollarExposure / price; lots = MathFloor(lots / lotStep) * lotStep; // Round down to nearest step // Clamp to broker constraints using custom Clamp() volumeArray[i] = Clamp(lots, minLot, maxLot); } return true; }
バックテスト
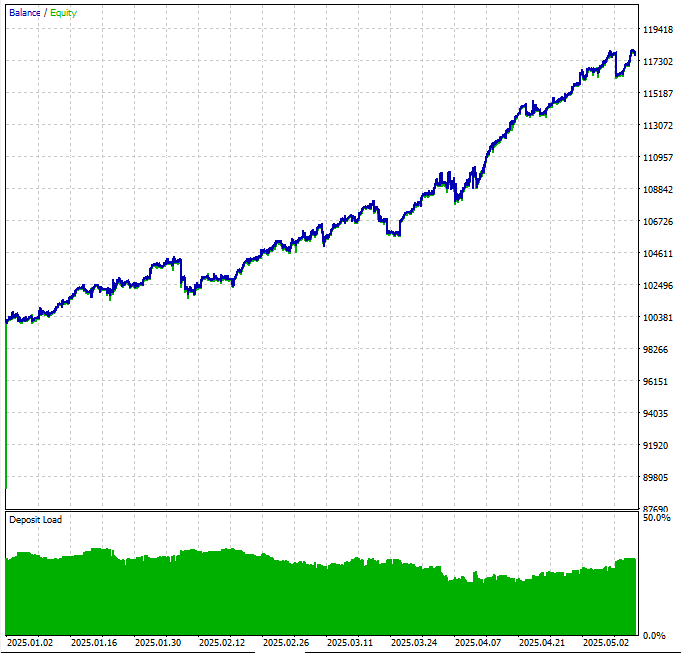
図5:2025年前半の日足データを用いたナスダック共和分バスケットのバックテストにおける資産曲線
資産曲線は、私たちの仮説が有効であることを示しています。ただし、一部の大きなドローダウンを回避するためには、まだ実装されていないマネーマネジメント戦略が必要です。
図6:2025年前半の日足データを用いたナスダック共和分バスケットのバックテスト概要
ご覧のとおり、今回使用している価格データの品質は非常に低いものです。しかし、これら4銘柄について無料で入手できるデータはこれしかないため、手元にあるもので運用しています。実際の資金でこの戦略を運用する際には、より高品質な価格履歴を使用することを強く推奨します。
図7:2025年前半の日足データを用いたナスダック共和分バスケットのバックテストにおける期間別エントリー数
図8:2025年前半の日足データを用いたナスダック共和分バスケットのバックテストにおける保有期間
平均ポジション保有時間がおよそ20分であることは好ましいといえます。これは、記事の前半で述べた最初の(そして失敗した)試みで発生していた、1〜2秒の極端に短いポジション保有を回避できているためです。
図9:2025年前半の日足データを用いたナスダック共和分バスケットのバックテストにおけるMFE(最大利益幅)およびMAE(最大損失幅)
株式を超えた共和分
これは、私たちが構築した初めての同一セクター内の共和分株式バスケットとしては、まずまず満足のいく結果です。切なマネーマネジメントや、最適化のためのより高品質なデータなどの改善を加えれば、数週間デモ口座でテストできる妥当な候補を得られる可能性があります。
しかし、すでにお気づきの通り、これは非常に一般的なアプローチであり、ナスダック銘柄のごく一部しか使用しておらず、さらに共和分検定の遡及期間や時間足の組み合わせも非常に限られています。つまり、過去6か月の日足データで共和分検定をおこなった4銘柄のみを使用しています。これらのパラメータを組み合わせていくと、注目に値する機会が数十件見つかる可能性があります。
さらに、対象はナスダック銘柄に限定されるわけではなく、株式自体に限定される必要もありません。株式とETF、あるいはセクター指数との間で、多資産の共和分検定を試すこともできます。
いくつかの例
以下は、過去6か月(180日)の日足データで検定した共和分の例です。
金関連ETF
symbols = ['AAAU', 'USGO', 'BGLD']
1. AAAU – Goldman Sachs Physical Gold ETF
「AAAUは金地金価格の動きを反映することを目的とした上場投資信託です。ファンドは安全な保管庫に保管された金の地金を保有しており、投資家は条件付きで株式を実際の金に換金することができます。AAAUは、追跡誤差を最小限に抑えつつ、デリバティブを使用せずに金価格への直接的なエクスポージャーを提供するよう設計されています。」
2. USGO – Abrdn Physical Gold Shares ETF
「USGOはAberdeen Investmentsが運用する物理的に裏付けられた金ETFです。AAAUと同様に、安全な保管庫に保管された割当金地金を保持することで金価格に連動することを目指しています。投資家は物理的に金を受け取ることなく、簡単かつ低コストで金へのエクスポージャーを得ることができます。」
3. BGLD – FT Vest Gold Strategy Target Income ETF
「BGLDはアクティブ運用の金戦略ETFで、収益と金へのエクスポージャーを提供することを目的としています。AAAUやUSGOとは異なり、BGLDは直接金地金を保有しません。その代わり、金関連デリバティブ(先物やオプションなど)と収益生成戦略を組み合わせることで、金の動きに類似したパフォーマンスと月次収益の獲得を目指します。」
Index(['AAAU', 'USGO', 'BGLD'], dtype='object')
エングル=グレンジャー共和分検定の結果:
USGO and BGLD | p-value:0.0144
最も強い共和分関係にあるペア(エングル=グレンジャー):USGO and BGLD | p-value:0.0144
エングル=グレンジャー共和分検定は、あくまでペアごとの関係性のみを評価する点に注意してください。この検定では、ジョハンセン共和分検定が捉えるような、バスケット全体の相互作用を示すことはできません。
Johansen Test Results (Trace Statistic):
Number of observations:119Number of variables:3
Rank 2:Trace Stat = 4.25 | 5% CV = 3.84 | Significant
ジョハンセン共和分検定を用いることで、バスケット全体における各ランクでの共和関係の数を確認できます。
ランク0では、トレース統計量(30.21)が5%の臨界値(29.80)を上回っており、少なくとも1つの共和分ベクトルが存在することを示しています。ランク1では検定は有意ではありませんが、ランク2では再び有意となっており(4.25 > 3.84)、これは2つ目の共和分関係が存在することを示唆しています。
エングル=グレンジャー共和分検定の結果を見ると、AAAU-BGLD (p = 0.0209)およびUSGO-BGLD (p = 0.0144)は、AAAU-USGO (p = 0.1322)よりも有意に「より共和的」であることが分かります。これは、3つの資産の間に2つの独立した共和分ベクトルが存在すること、そしておそらくバスケット内に強固で安定した長期均衡関係があることを示しています。
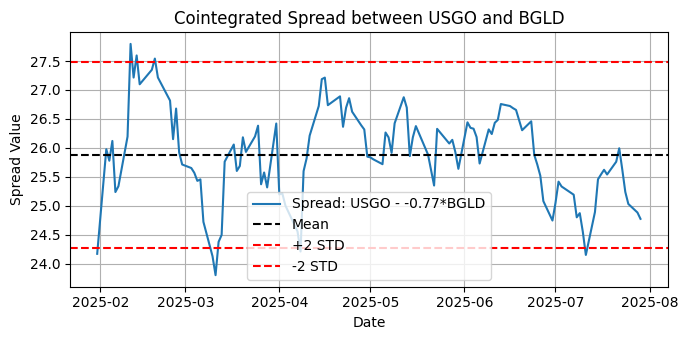
図10:過去6か月の日足における、USGOとBGLD間の共和分スプレッドのプロット
ADF Test on Spread:
Critical Values:
10%: -2.5800
✅ The spread is stationary (reject the null hypothesis).
KPSS Test on Spread:
Critical Values:
1%:0.739
✅ The spread is stationary (fail to reject null of stationarity).
BGLDはAAAUおよびUSGOの両方と強い共和分関係を持っており、USGO-BGLD間のスプレッドが定常であることが確認できたことで、これらの資産は金関連の共和分バスケットの有力な候補であることが強く示唆されます。
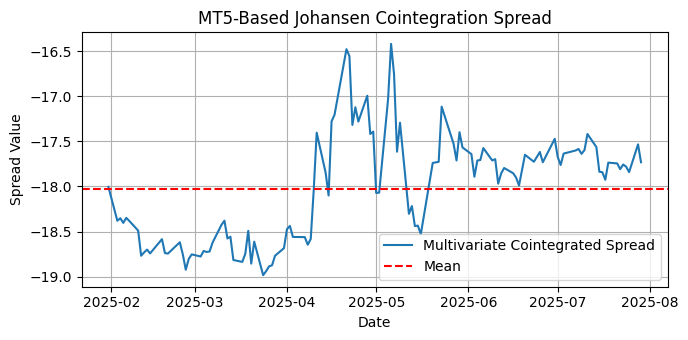
図11:過去6か月の日足における、AAAU、USGO、BGLD間の多変量共和分スプレッドのプロット
しかしながら、この期間および時間足では、多変量共和分スプレッドは定常ではありません。
ADF Test on Spread:
Critical Values:
10%: -2.5800
❌ The cointegrated spread is NOT stationary (fail to reject the null hypothesis).
KPSS Test on Spread:
Critical Values:
1%:0.739
❌ The cointegrated spread is NOT stationary (reject null of stationarity).
銀関連ETF
symbols = ['CEF', 'SLV', 'SIVR']
1. CEF – Sprott Physical Gold and Silver Trust
「金および銀の地金を両方保有するクローズドエンド型トラストです。純資産価値に対してプレミアムまたはディスカウントで取引され、純粋な銀ETFではないため、SLVやSIVRとは構造的に異なります。」
2. SLV – iShares Silver Trust
「銀地金価格の動きを反映することを目的とした、物理的に裏付けられた銀ETFです。最大かつ流動性の高い銀ETFの1つです。」
3. SIVR – Aberdeen Physical Silver Shares ETF
「SLVと同様に物理的に裏付けられた銀ETFですが、通常は経費率が低く、コスト意識の高い投資家にとって魅力的です。」
Index(['CEF', 'SLV', 'SIVR'], dtype='object')
エングル=グレンジャー共和分検定の結果:
CEF and SLV | p-value:0.6092
CEF and SIVR | p-value:0.6109SLV and SIVR | p-value:0.0000
最も強い共和分関係にあるペア(エングル=グレンジャー):SLV and SIVR | p-value:0.0000
Johansen Test Results (Trace Statistic):
Number of observations:121Number of variables:3
Rank 2:Trace Stat = 1.95 | 5% CV = 3.84 | Not significant
ランク0(62.67 > 29.80)では、トレース統計量が有意であり、3つの銀関連ETFの間に少なくとも1つの共和分ベクトルが存在することを示しています。しかし、ランク1およびランク2では有意ではなく、このバスケットには安定した長期的関係は1つしか存在しないことが分かります。
共和分検定の結果を見ると、SLVとSIVRのペアは強い共和分シグナル(p = 0.0000)を示しています。一方、CEFはSLVまたはSIVRのいずれとも共和分関係があるとは言えません(p > 0.6)。ジョハンセン結果を改めて見ると、共和分はほぼ完全な代替関係にあるSLVとSIVRの密接な関係に由来していると推測できます。両者は物理的に裏付けられた銀ETFであり、その共和分関係は妥当です。CEFは銀にエクスポージャーを持つ一方で金にも投資しており、かつクローズドエンド型ファンドであるため、挙動が異なります。
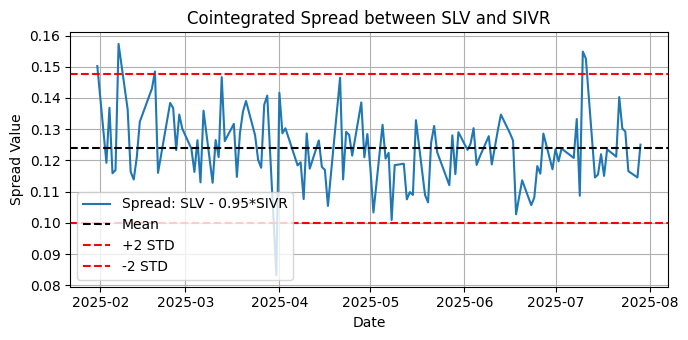
図12:過去6か月の日足における、SLVとSIVR間の共和分スプレッドのプロット
ADF Test on Spread:
Critical Values:
10%: -2.5798
✅ The spread is stationary (reject the null hypothesis).
KPSS Test on Spread:
Critical Values:
1%:0.739
❌ The spread is NOT stationary (reject null of stationarity).
ここでは、SLVとSIVR間の共和分スプレッドがADF検定では定常であると判断されましたが、KPSS検定では非定常と判断されました。 前回の記事でも同様の例を示しており、 statsmodelsライブラリのドキュメントにある対応する解説を参照すると、このような矛盾した結果の解釈方法が分かります。
「ケース1:ADFとKPSSの両方が「非定常」と結論した場合 → 非定常系列
ケース2:ADFとKPSSの両方が「定常」と結論した場合 → 定常系列
ケース3:KPSSが「定常」、ADFが「非定常」と結論した場合 → トレンド定常系列。トレンドを除去すれば厳密な定常系列になる。除去後の系列で定常性を再確認する。
ケース4:KPSSが「非定常」、ADFが「定常」と結論した場合 → 差分定常系列。差分を取ることで定常系列になる。差分系列で定常性を確認する。
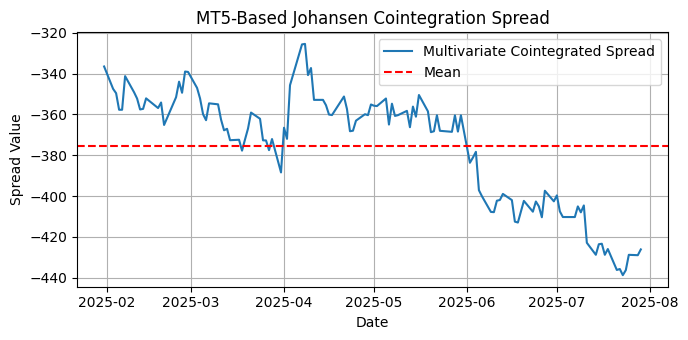
図13:過去6か月の日足における、CEF、SLV、SIVR間の多変量共和分スプレッドのプロット
多変量共和分スプレッド、つまりバスケット全体については、プロットを見る限り、この期間および時間足ではスプレッドは平均回帰していません。定常性の検定によってこれが確認されます。
ADF Test on Spread:
Critical Values:
10%: -2.5799
❌ The cointegrated spread is NOT stationary (fail to reject the null hypothesis).
KPSS Test on Spread:
Lags Used:6
Critical Values:
1%:0.739
❌ The cointegrated spread is NOT stationary (reject null of stationarity).
これは何を意味するのでしょうか。確かに、ここで銀関連ETFの適切なバスケットは得られていません。しかし、SLVとSIVRという、非常に共和分関係にある2つのETFが存在しており、ペアトレードの対象として注目に値する可能性があります。ペアトレードは、本連載の最初の記事の主題でもあります。
これら 2 つの例は、統計的裁定取引の機会を探す際には、実験とリサーチが重要であることを示しています。また、統計的手法だけに依存せず、セクターや市場の理解と知識を併せて考慮することが重要である点も忘れてはなりません。
結論
本記事では、共和分株式の小規模グループを対象にバックテストしたサンプルEAについて説明しました。本記事は、統計的裁定取引のポートフォリオ構築における最も一般的な統計的指標である相関係数および共和分評価、さらにスプレッド定常性検定について述べた2部構成の記事の第2弾です。
なお、この種の戦略は、複数の通貨ペア間で共和分関係が成立する条件が非常に稀なため、FX(通貨)にはほぼ適用不可能ですが、指数、ETF、コモディティなどには適用可能です。
共和分に基づくポートフォリオ構築の基本ツールが揃った今、次の論理的ステップとしては、リアルタイムでのポートフォリオローテーションの実装が考えられ、最終的に機械学習アプローチへ発展させることも可能です。
参照文献
Marianna Brunetti & Roberta De Luca, 2023."Pre-selection in cointegration-based pairs trading," Statistical Methods & Applications, Springer; Società Italiana di Statistica, vol. 32(5), pages 1611-1640, December.
備考
* このアナロジーはおそらくそこから派生していますが、ここでいうランダムウォークは、英国の数学者によって定義・命名された確率過程であるピアソンのランダムウォークとは混同しないでください。
| 添付ファイル | 説明 |
|---|---|
| corr_pearson.ypng | Pythonコードを含むJupyter Notebook。スクリプトはピアソン相関テストを実行。 |
| coint_stocks_ETFs.ypnb | Pythonコードを含むJupyter Notebook。スクリプトは、エングル=グレンジャーおよびジョハンセン共和分検定、ADFおよびKPSS定常性検定を実行。 |
| Nasdaq_NVDA_Coint.mql5 | バックテストで使用されるサンプルEA |
| Nasdaq_NVDA_Coint.ini | バックテストで使用されるパラメータを含む構成設定ファイル(.ini) |
| Nasdaq_NVDA_Coint.NVDA.Daily.20250101_20250515.021.ini | バックテストで使用される最適化パラメータを含む構成設定ファイル(.ini) |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/19052
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 MQL5取引ツール(第8回):ドラッグ&最小化可能な拡張情報ダッシュボード
MQL5取引ツール(第8回):ドラッグ&最小化可能な拡張情報ダッシュボード
 ログレコードをマスターする(第10回):抑制機能を実装してログの再表示を防ぐ
ログレコードをマスターする(第10回):抑制機能を実装してログの再表示を防ぐ
 取引システムの構築(第2回):ポジションサイズ管理の科学
取引システムの構築(第2回):ポジションサイズ管理の科学
 初心者からエキスパートへ:MQL5を使用したアニメーションニュースヘッドライン(III) - ニュース取引のためのクイック取引ボタン
初心者からエキスパートへ:MQL5を使用したアニメーションニュースヘッドライン(III) - ニュース取引のためのクイック取引ボタン
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索