通过配对交易中的均值回归进行统计套利:用数学战胜市场
引言
“我能计算天体的运行,却无法计算人们的疯狂。”(艾萨克·牛顿爵士,在他九十多岁时,因投资股市几乎损失了所有退休储蓄后所说。)
去年5月10日,世界失去了有史以来最成功的对冲基金经理——吉姆·西蒙斯。
吉姆·西蒙斯是一位公认的数学家,在微分几何和密码学领域拥有多项荣誉和学术成就。然而,他在量化金融分析领域的角色,使他的名声甚至在那些对数学或金融不感兴趣的人群中也广为人知。
他是数本传记的主人公,有数十本关于他生活和职业生涯的书籍,数百个电视节目,以及全世界成千上万的文章和博客帖子都曾报道过他。《战胜市场的人:吉姆·西蒙斯如何发起量化革命》 是他最著名的传记。
在八十年代初,西蒙斯创立了文艺复兴科技公司,并开始聚集一支由高度熟练的“数学家、物理学家、信号处理专家和统计学家”组成的团队。他们合作了数十年,证明了只要有足够的数据和计算能力来发现其中的统计模式和异常,市场就可以“被数学战胜”。
“1988年,该公司建立了其最盈利的投资组合——大奖章基金,该基金使用了伦纳德·鲍姆的数学模型的改进和扩展形式,由代数学家詹姆斯·阿克斯改进,以探索可以从中获利的关联性。”(维基百科)
大奖章基金在1988年至2018年间平均每年回报率为66%,在这三十年里创造了超过1040亿美元的交易利润。文艺复兴科技的大奖章基金至今仍在活跃运营,并赚取着大量资金。正如你可能预料到的,许多人都想知道他们的运作方式、细节、秘密算法、作弊代码……凡此种种。但是,就凡人所知,他们的秘密配方被作为最高级别的企业机密保存着。当被其传记作者问及大奖章基金的运作策略时,西蒙斯用他在未来几年中给多位采访者的同样简洁的回答作答:投资组合层面的统计套利。他还透露,他们从一开始就在使用“一种机器学习”来寻找市场异常。
统计套利本身就是一个庞大的研究领域。当我们把机器学习加入其中时,没有强大数学和统计学背景的普通散户交易者就被排除在外了。更不用说新手交易者。但是,如果说在没有所有这些知识的情况下,要实现一个功能齐全的、由机器学习驱动的投资组合层面统计套利确实非常困难且需要大量资源,那么同样真实的是,完全有可能理解什么是投资组合层面的统计套利、它是如何工作的,以及更重要的是:完全有可能从小处着手,通过耐心、努力和时间来逐步发展壮大。
本文绝不是试图复现,或者更糟地,“揭示”文艺复兴科技/吉姆·西蒙斯的“秘密代码”。如上所述,对于任何没有直接参与他们运作的人来说,这都是不可能的。这是为了与您分享我对驱动他们模型的通用原理的理解。这些原理可以为最卑微的散户交易者的交易系统提供信息。不同之处在于结果的规模,这将与投入到系统和运营中的资源数量成正比。
因此,您接下来将读到的内容,是我在书籍、视频纪录片和专业互联网社区中研究的成果,并结合了我在金融领域(更多是在业务层面而非开发者层面)几年的个人经验。文艺复兴科技运行的规模是巨大的,但我们在这里将看到的是一个微缩版,可以说,是一个超级英雄的玩具人偶,一座摩天大楼的比例模型。
其目标是贡献一种低成本、轻量级且易于开发的分析方法,普通散户交易者可以使用消费级笔记本电脑(可能是低端笔记本)上运行的 MetaTrader 5 平台中已有的工具进行测试和改进。该方法应该对算法交易者和自主交易者都有用。我们将从最直接的设置开始,仅足以描述整个过程。
在理解了模型背后的通用概念后,我们将为最简单形式的统计套利构建一个最小的投资组合,通过一个智能交易系统以自动化模式进行交易,记录一些关于结果的笔记,最后思考必要的后续步骤。我希望这次经验能帮助您开始使用这种强大的交易技术,并能够在以后扩展这些知识,将其他品种引入投资组合,并测试这里描述之外的其他算法,从而逐步构建适合您资源和目标的、功能齐全的统计套利策略。
模型背后的通用概念
在创立文艺复兴科技之前,吉姆·西蒙斯曾在冷战期间为美国情报部门担任密码破译员。当他开始交易金融市场时,他试图预测股票和大宗商品价格,但失败了。然后他改变了他的方法。他假设他将永远无法预测市场的未来。他明白他必须接受市场是一个谜题。这是模型背后的第一个相关概念。
另一个概念是市场处于持续的变化状态。也就是说,不存在所谓的牛市或熊市、K线/棒线形态,或者“协同良好的相关股票”。一切都在此刻和永远地变化着。
如果你思考一秒钟,你就会发现这两个概念都被忽视了。
市场是一个谜题市场是一个谜题,但与那个由艾伦·图灵及其团队破译了密码的二战时期的“谜”型机不同,市场谜题没有可以逆向工程和破解的确定性算法。在输入和输出之间,可能会发生意外事件。虽然央行加息具有使该国货币走强的预期效果,但另一个遥远国家政治冲突的爆发可能产生相反的效果,通过减少其影响来抵消加息,使其失效,甚至使该货币走弱。
市场是一个谜题,因为在输入和输出之间,存在着经济代理的非理性、政治的不可预见性,以及驱动它的各种力量之间相互作用的混沌特性。在长达一年的黄金牛市与其下周的一个月暴跌之间,存在着人类行为。心理学家丹尼尔·卡尼曼获得诺贝尔经济学奖,并非出于其他原因。因为他恰好解决了这个问题。尽管市场是一个由非理性经济代理在混沌环境中统治的谜题,但投资银行仍然基于金融模型买卖股票,对冲基金使用布莱克-斯科尔斯模型来评估期权,几乎所有最大的市场参与者都花费数百万美元开发量化交易策略。为什么呢?当然是因为它有效。如果市场是不可预见、不可预测、非理性和混沌的,为什么它仍然有效?
吉姆·西蒙斯,连同成千上万其他成功的量化、算法和自主交易者,对这个问题给出了最坦诚的答案。这是任何有志成为交易者的人都应该在每天进入市场前像念咒语一样背诵的一课:
但是,无论是否使用金融模型,任何交易策略都可能在一段时间内运作良好,一段未知长度的时间。它可能盈利一天、一个月、一年……我们不知道。唯一的保证是它在过去是有效的,并且在那些品种、时间周期和回测中使用的参数值下是盈利的。它可能在下一分钟、在第一次运行时就停止盈利,也可能永远有效。再说一次,我们不知道。我们无法知道,因为市场是一个谜题。我们无法解开这个谜题。没有可以被破解的密码。只有一个持续的变化状态。
市场处于持续的变化状态
市场一直在变化。市场中唯一不变的就是变化本身。我们参数值的被选中,不是因为它们最适合特定的市场状态,而是因为它们最适合特定的市场变化。在我们下了一张盈利订单和该订单被平仓的时刻之间,市场以我们预期的方式发生了变化。相反,在我们下了一张亏损订单和该订单被平仓的时刻之间,市场以我们没有预期的方式发生了变化。即使我们无法说出是哪个变化对最终结果贡献最大,这也是事实。
明确地说:我们将永远无法精确定位是将一个盈利策略变成亏损策略(或反之)的确切变化。为了改进交易策略,我们要做的是寻找一种模式,以便在未来面临类似的市场状态变化时,增加重复正确选择的概率。发现、学习和理解这些模式,正是经验丰富的交易者在数月或数年交易同一资产或一组资产时所做的事情。我们之所以有交易日记,并非出于其他原因。它是为了记录我们对预期市场变化的假设,并能够稍后审查它们以改进我们的假设。
感谢当今海量的可用数据和强大的计算机来处理这些数据,我们可以将寻找模式的这些学习年限缩短到几小时甚至几分钟。我们可以自动化数据收集、分析和交易执行。我们可以自动化测试和报告。我们甚至可以通过训练一个全面的机器学习模型来学习这些模式,从而自动化对要交易的品种/资产以及要使用的策略的选择。只要有足够的资金、合格的人和时间,是的,我们可以做到。
但是,如上所述,这些笔记的重点是普通散户交易者。让我们牢记这两个简单但被忽视的原则,看看我们如何开始理解统计套利是什么以及它是如何工作的。
构建投资组合
因为市场是一个处于持续变化状态的谜题,我们将不带任何先入为主的观念来构建我们的投资组合,我们不会对我们认为正确的事情做任何假设,并且我们会定期更新它。更新间隔将由交易策略决定,并受到计算能力的限制。
我们必须考虑到,投资组合构建或投资组合管理本身就是一个庞大的研究领域。根据一项全面的学术文献回顾,十年前至少有四种构建配对交易统计套利投资组合的主要方法:距离法、协整法、时间序列法和随机控制法。除了这四种主要方法外,作者还确定了其他方法,包括机器学习、组合预测、copula(连接函数)和主成分分析。
为了保持我们对简单和基础的关注,让我们从一个简单的配对交易投资组合开始。对一些作者来说,配对交易是统计套利的一个子集,而对另一些作者来说,“配对交易被广泛认为是统计套利的‘祖先’”,区别在于投资组合规模和统计算法的复杂性。顾名思义,配对交易仅限于两种证券,而统计套利可能涉及几十个甚至上百个需要被跟踪并最终交易的品种。
配对交易,正如你可能已经知道的,无非是,给定两个具有相关或协整历史价格的证券,当它们之间的历史价差扩大到超过一个选定的阈值时,同时卖出趋势向上的证券并买入趋势向下的证券。其基本假设是价格将“回归均值”,围绕历史价差收敛。
在一个功能齐全的统计套利中,我们不仅限于价格之间的相关性或协整性。由于我们在本文中的主要目标是简化统计套利的复杂性,使其适用于普通散户交易者,我们将开始收集历史数据,为外汇市场构建一个最小的配对交易投资组合。稍后,您可以扩展到其他市场以及价格相关性之外的其他统计关系。
选择一组证券作为开始在撰写本文时,我的 MetaTrader 5 终端账户报告有超过一万个可用品种。我们将在分析中使用针对 Metatrader 5 的 Python 集成。
print("Total symbols =",mt5.symbols_total()) # display all symbols Total symbols = 10563因此,出于现实原因,首先我们需要从所有可用品种中选择一个子集。让我们从XAU相关货币对开始。
# get symbols containing XAU in their names xau_symbols=mt5.symbols_get("*XAU*") print('len(*XAU*): ', len(xau_symbols)) for s in xau_symbols: print(s.name) len(*XAU*): 6 XAUUSD XAUEUR XAUAUD * XAUG XAUCHF XAUGBP
* XAUG 是一个ETF(交易所交易基金),所以我们可以暂时将其排除,专注于其他五个货币对。让我们看看它们各自与XAUUSD的相关性。
现在我们需要计算它们的历史价格相关性。在真实场景中,我们可能希望探索所选品种之间所有可能的排列组合,可能是数百个股票品种,因为我们假设对它们没有任何先验知识。但在这里,我们将进行筛选,只查看以美元计价的黄金(XAUUSD)与以欧元、澳元、瑞士法郎和英镑计价的黄金报价之间的价格相关性。我们需要获取从当前日期起过去一年的每日收盘价数据,对于外汇市场来说,这大约是250个交易日。
# get 250 D1 bars from the current day xauusd_rates = mt5.copy_rates_from_pos("XAUUSD", mt5.TIMEFRAME_D1, 0, 250) xaueur_rates = mt5.copy_rates_from_pos("XAUEUR", mt5.TIMEFRAME_D1, 0, 250) xauaud_rates = mt5.copy_rates_from_pos("XAUAUD", mt5.TIMEFRAME_D1, 0, 250) xauchf_rates = mt5.copy_rates_from_pos("XAUCHF", mt5.TIMEFRAME_D1, 0, 250) xaugbp_rates = mt5.copy_rates_from_pos("XAUGBP", mt5.TIMEFRAME_D1, 0, 250) (...) # calculate correlation coefficients import numpy as np usd_eur_corr = np.corrcoef(xauusd_close['close'], xaueur_close['close']) usd_aud_corr = np.corrcoef(xauusd_close['close'], xauaud_close['close']) usd_chf_corr = np.corrcoef(xauusd_close['close'], xauchf_close['close']) usd_gbp_corr = np.corrcoef(xauusd_close['close'], xaugbp_close['close'])
这将给我们带来以下结果:
| XAUUSD 皮尔逊相关系数 | |
|---|---|
| XAUEUR | 0.9692368 |
| XAUAUD | 0.96677962 |
| XAUCHF | 0.8418827 |
| XAUGBP | 0.90490282 |
表 1 - 2024年4月9日至2025年3月26日期间,以美元(XAUUSD)和以欧元、澳元、瑞士法郎及英镑计价的黄金的每日收盘价相关性。
我们可以在下图中直观地判断出接近0.97的价格相关性是什么样子。
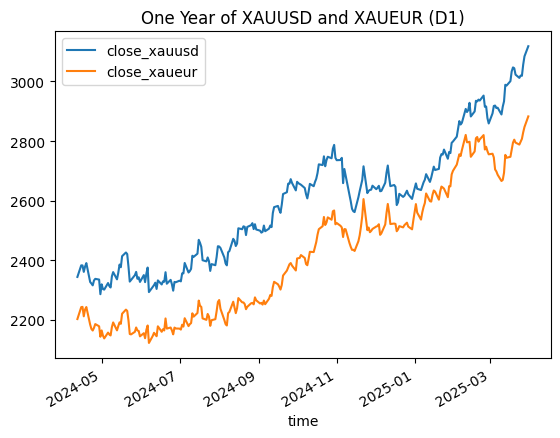
图 1 - 以美元和欧元计价的黄金一年期每日收盘价
请注意,上图可能具有误导性。我们可能会倾向于“交易这对货币对之间的价差”,但这并非真正的价差(如果存在价差的话)。让我们根据当天的汇率将XAUEUR转换为美元。adjusted_for_dollars = pd.concat([xauusd_close, xaueur_close['close'], eurusd_close['close']], join='inner', axis=1) adjusted_for_dollars.columns = ['time', 'xauusd', 'xaueur', 'eurusd'] adjusted_for_dollars['xaueur_dollars'] = adjusted_for_dollars['xaueur'] * adjusted_for_dollars['eurusd'] adjusted_for_dollars['diff'] = abs(adjusted_for_dollars['xauusd'] - adjusted_for_dollars['xaueur_dollars']) print(adjusted_for_dollars) time xauusd xaueur eurusd xaueur_dollars diff 0 2024-04-12 2344.22 2202.92 1.06237 2340.316120 3.903880 1 2024-04-15 2383.10 2242.90 1.06181 2381.533649 1.566351 2 2024-04-16 2382.85 2243.81 1.06720 2394.594032 11.744032 3 2024-04-17 2361.16 2212.14 1.06425 2354.269995 6.890005 4 2024-04-18 2378.86 2234.79 1.06557 2381.325180 2.465180 .. ... ... ... ... ... ... 245 2025-03-25 3019.81 2797.81 1.07918 3019.340596 0.469404 246 2025-03-26 3018.85 2807.50 1.07370 3014.412750 4.437250 247 2025-03-27 3056.42 2829.26 1.07975 3054.893485 1.526515 248 2025-03-28 3084.20 2847.12 1.08276 3082.747651 1.452349 249 2025-03-31 3118.19 2882.78 1.08152 3117.784226 0.405774 [250 rows x 6 columns]
adjusted_for_dollars.plot(title = 'One Year of XAUUSD and XAUEUR in US Dollars (D1)', x='time', y=['xauusd', 'xaueur_dollars']) plt.show()
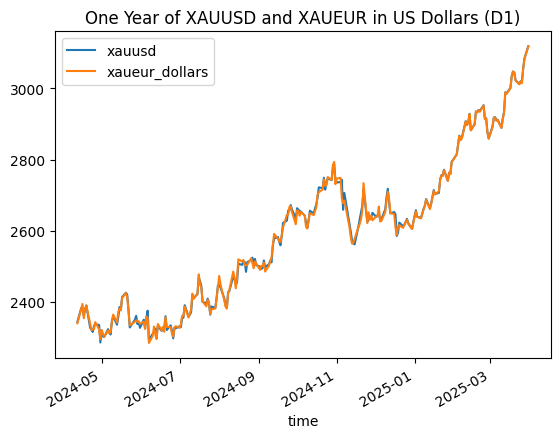
图 2 - 以美元计价的黄金和以欧元计价并调整为美元的黄金一年期每日收盘价
通过观察以美元计价的黄金报价和以欧元计价的黄金报价之间的差异……
print("median: ", adjusted_for_dollars['diff'].median()) adjusted_for_dollars['diff'].describe() median: 4.052404150000029 count 250.000000 mean 5.894673 std 6.238511 min 0.050646 25% 1.279615 50% 4.052404 75% 8.587763 max 51.483719 median: 4.052404150000029
……我们会注意到,在这一年期间,真实的平均价差约为5.9美元,标准差约为6.2美元。如果我们过度简化,并假设在按当前汇率转换后,两种报价之间的差异(价差)应接近于零,那么我们可以将任何高于平均值的价差视为市场中可交易的异常。
选择要寻找的统计关系
然后,我们选择基于在上一个交易年度(约250天)发现的XAUUSD和XAUEUR之间的高度相关性,开始构建我们的统计套利投资组合。但是,价格相关性是构建统计套利投资组合时正确的、甚至是更好的统计关系吗?
当我们谈论历史价格中的相关性时,我们可能会被该术语的通俗用法与其正确的统计含义之间的差异所误导。这个事实在外汇社区中更为明显。简单搜索“外汇相关性货币对”会指向许多资源,这些资源列出了最/最不相关的货币对,并提供了如何交易它们的技巧。我们的目的不是说这个或那个资源、列表或交易技巧是对是错。我们必须牢记的是,我们正在为投资组合层面的统计套利奠定基础,其目的不应仅限于外汇货币对。相反,我们的系统必须能够泛化到任何资产类别、任何市场和时间周期,只需满足市场中性且可测试的要求。
根据统计学家的观点,皮尔逊相关系数函数预期应用于平稳序列,而价格时间序列是非平稳的。通过在非平稳时间序列中计算相关性,我们可能会得到他们所谓的“伪相关性”。
“非平稳数据,通常来说,是不可预测的,也无法建模或预测。使用非平稳时间序列获得的结果可能是伪的,因为它们可能指示出两个变量之间存在一个实际不存在的关系。为了获得一致、可靠的结果,需要将非平稳数据转换为平稳数据。” (Nason, G. P. (2006). 平稳和非平稳时间序列。Investopedia)
那么,作为寻求构建统计套利投资组合的交易者,我们必须做出一个决定:这种“伪相关性”是否足够,还是我们需要统计学意义上的真正相关性?目前,我们接受第一个不完美的度量,作为我们简化模型的足够条件。但我们绝不能忘记,相关的货币对在长期内可能持续扩大价差,同时上涨或下跌,也就是说,它们可能在很长一段时间内不回归均值,然而统计相关性仍然适用。在处理货币时,这种情况是例外,但在处理大宗商品、期货或股票价格时间序列时则非常普遍。因此,在处理“预期回归均值”策略时,止损水平和仓位时机是强制性的。
选择作为交易触发器的统计度量为什么选择均值或中位数作为我们历史价差的度量?根据统计学家的观点,当我们的数据异常值较少时,我们应该使用均值;而当数据集存在极端峰值时,我们应该使用中位数,因为中位数受这些峰值的影响较小。例如,如果你想过滤掉由高影响力新闻引起的巨大价差,你可以选择中位数。相反,如果你想考虑这些高影响力新闻对价差的影响,你可能想选择均值。
所以,这里没有“食谱”。你必须根据自己的数据和良好的判断力自行决定。你甚至可能选择既不使用均值也不使用中位数。相反,你可以研究并决定另一种关系更适合你的用例。
我将选择均值,并根据均值的扩大为我们的交易策略设置一个参数。比方说,当XAUUSD和XAUEUR之间的价差扩大超过均值的50%时,我们触发交易,买入在竞争中落后的品种,同时卖出上涨更快的品种。
我们如何确定哪个品种在上涨,哪个在下跌?对于我们这里的特定情况,由于我们假设两种黄金报价在转换后应该相同,我们可以简单地获取价格较高的品种作为上涨的货币对,另一个作为下跌的货币对。如果我们处理的是回归均值的股票价差,我们可以使用周期非常短的指数移动平均线,并假设在EMA上方交易的品种正在上涨,反之亦然。
bool IsRising(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is rising? ", quotes_base[0] > ema_base[0]); return quotes_base[0] > ema_base[0]; case CORR_PAIR: //Print("Corr pair is rising? ", quotes_corr[0] > ema_corr[0]); return quotes_corr[0] > ema_corr[0]; default: return false; } } bool IsFalling(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is falling? ", quotes_base[0] < ema_base[0]); return quotes_base[0] < ema_base[0]; case CORR_PAIR: //Print("Corr pair is falling? ", quotes_corr[0] < ema_corr[0]); return quotes_corr[0] < ema_corr[0]; default: return false; } }或者我们可以使用斜率。
void CalculateSlopes(double & slope_b[], double & slope_c[]) { slope_b[0] = MathAbs((quotes_base[0] - quotes_base[SlopePeriod]) / SlopePeriod); slope_c[0] = MathAbs((quotes_corr[0] - quotes_corr[SlopePeriod]) / SlopePeriod); }在我们的案例中,我们只是简单地使用价格最高的品种。
if(quotes_base[0] > quotes_corr[0])
交易投资组合
我们已经构建了一个简单的EA来在回测中检验我们的假设。
我们在 OnInit() 函数中获取初始报价,并在 OnTimer() 函数中更新它们。这是因为我们不能依赖 OnTick 事件处理器来更新非当前工作图表的货币对报价,因为 OnTick() 仅针对当前品种/图表被调用。请参阅多货币或多品种智能交易系统。
int OnInit() { ArrayResize(quotes_base, CountQuotes); ArrayResize(quotes_corr, CountQuotes); ArrayResize(quotes_conv, CountQuotes); //--- Get start quotes for both pairs GetQuotes(); //--- EMA indicators EMA_Handle_Base = iMA(BasePair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); EMA_Handle_Corr = iMA(CorrPair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); if(EMA_Handle_Base == INVALID_HANDLE || EMA_Handle_Corr == INVALID_HANDLE) { printf(__FUNCTION__ + ": EMA initialization failed"); return(INIT_FAILED); } //--- create timer EventSetTimer(5); // seconds //--- return(INIT_SUCCEEDED); } bool GetQuotes() { if(CopyClose(BasePair, _Period, 0, CountQuotes, quotes_base) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes base pair %i ", ArraySize(quotes_base)); return false; } if(CopyClose(CorrPair, _Period, 0, CountQuotes, quotes_corr) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes corr pair %i ", ArraySize(quotes_corr)); return false; } if(CheckMode == PRICE) { if(CopyClose(ConvPair, _Period, 0, CountQuotes, quotes_conv) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes conv pair %i ", ArraySize(quotes_conv)); return false; } //--- for(int i = 0; i < CountQuotes; i++) { quotes_corr[i] *= quotes_conv[i]; } } return true; } void OnTimer() { UpdateQuotes(); CalculateMeanSpread(); if(CheckMode == EMA) { GetEMAs(); } } void UpdateQuotes() { ArrayRemove(quotes_base, ArraySize(quotes_base) - 1); double new_quote_base[1]; CopyClose(BasePair, _Period, 0, 1, new_quote_base); ArrayInsert(quotes_base, new_quote_base, 0, 0); //--- ArrayRemove(quotes_corr, ArraySize(quotes_corr) - 1); double new_quote_corr[1]; CopyClose(CorrPair, _Period, 0, 1, new_quote_corr); ArrayInsert(quotes_corr, new_quote_corr, 0, 0); //--- if(CheckMode == PRICE) { ArrayRemove(quotes_conv, ArraySize(quotes_conv) - 1); double new_quote_conv[1]; CopyClose(ConvPair, _Period, 0, 1, new_quote_conv); ArrayInsert(quotes_conv, new_quote_conv, 0, 0); quotes_corr[0] *= quotes_conv[0]; } }
计算平均价差
bool CalculateMeanSpread() { int sz_base_p = ArraySize(quotes_base); int sz_corr_p = ArraySize(quotes_corr); int sz_conv_p = ArraySize(quotes_conv); if(sz_base_p != sz_corr_p || sz_corr_p != sz_conv_p) { Print(__FUNCTION__ + " Failed: Arrays must be of same size"); return false; } //--- ArrayResize(pairs_spread, CountQuotes); for(int i = 0; i < sz_base_p; i++) { pairs_spread[i] = MathAbs(quotes_base[i] - quotes_corr[i]); } double max_spread = pairs_spread[ArrayMaximum(pairs_spread)]; double min_spread = pairs_spread[ArrayMinimum(pairs_spread)]; mean_spread = MathMean(pairs_spread); //--- //printf("Last quote XAUUSD %f ", quotes_base[0]); //printf("Last quote XAUEUR %f ", quotes_corr[0]); //printf("Last spread %f ", pairs_spread[0]); //printf("Max spread %f ", max_spread); //printf("Min spread %f ", min_spread); //printf("Mean spread %f ", mean_spread); return true; }
我们在 OnTick 中检查交易信号。
void OnTick() { //--- CheckForClose(); CheckForOpen(); }
价差至少比我们设定的百分比高出均值时
bool HasSpreadTrigger() { double trigger_spread = mean_spread + (mean_spread * (PercentTrigger / 100.0)); //printf(" trigger spread %f ", trigger_spread); double current_spread = pairs_spread[0]; //printf(" current spread %f ", current_spread); return current_spread >= trigger_spread; }
我们买入价格较低的品种,并卖出价格较高的品种。在我们的示例中,这个切换是通过 CheckMode 枚举来执行的。
void CheckForOpen()
{
if(PositionsTotal() == 0 && HasSpreadTrigger())
{
switch(CheckMode)
{
case EMA:
if(IsRising(BASE_PAIR) && IsFalling(CORR_PAIR))
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
if(IsFalling(BASE_PAIR) && IsRising(CORR_PAIR))
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case SLOPE:
CalculateSlopes(slope_base, slope_corr);
if(slope_base[0] > slope_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case PRICE:
if(quotes_base[0] > quotes_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
}
}
}
持仓将通过止损/止盈或在 CheckForClose() 函数中的均值回归来平仓。
void CheckForClose() { int total = PositionsTotal(); ulong ticket = 0; if(total > 0) { if(PositionSelect(BasePair) || PositionSelect(CorrPair)) { for(int i = 0; i < total; i++) { ticket = PositionGetTicket(i); if(ticket == 0) continue; if(pairs_spread[0] <= mean_spread) { ExtTrade.PositionClose(ticket); } } } } }
回测证实了均值回归策略对于配对交易是可行的。
图 3. 回测资金曲线图
尽管回测验证了我们的假设,但您可以看到,这个特定的算法需要改进以使资金曲线更加平滑。也许需要一个动态的订单大小(此处的交易量固定为最小的0.01 - 微手),以及对止损/止盈比的优化。但盈利能力并非本文在此的主要关注点。话虽如此,让我们来看一些有趣的结果——根据一些作者的说法,这些结果似乎在统计套利操作中很常见。
图 4. 回测结果
交易数量众多,盈利与亏损的比率很小(约55/45),且最大余额回撤相对较低。
图 5. 回测交易时间
交易集中在特定时段(小时、一周中的某几天等)。在我们的案例中,交易集中在美国开盘时段,并在2024年4月达到峰值。
图 6. 回测持仓时间与盈利的关系
大量的极短时间操作表明,我们的系统通过在盈利交易后重新入场,探索了市场不稳定的时刻。
可以如何改进?
现在,我想提请您注意这样一个事实:交易策略或设置的卖家会试图向您展示尽可能好的过往结果,以激发您对其产品的兴趣。最终,他们会在仔细优化后,精心挑选表现最佳的参数,以强调潜在的收益,同时降低亏损的风险。
但是,除了让您理解这些原则并从小规模开始统计套利的想法之外,我在此并非向您“推销”任何东西。相反,我想说,回测显示我们正在处理一个需要改进的算法,我对此感到高兴。因为这是每个统计套利系统的基石。
也就是说,到目前为止,对于这个简化的自动化程序,我们一直局限于使用任意选择的参数来管理风险。相反,我们需要的是:
- 根据每个时间点的评估风险来控制要开仓的数量
- 拥有一个考虑到波动率的浮动触发价差百分比
- 开发一个动态的止损/止盈策略,该策略从触发价差值及可能的其它变量中推导出盈利的概率
这些是该EA未来改进的一些可能方向。
简化模型总结
1. 从一个假设开始
相关货币对之间的价差倾向于回归均值。这就是我们此处的假设。
从交易者的角度来看,均值回归的概念简单而直观:当当前价格低于平均价格时,可以预期价格会上涨;当当前价格高于平均价格时,可以预期价格会下跌。俗话说,价格总是在“寻找均值”。
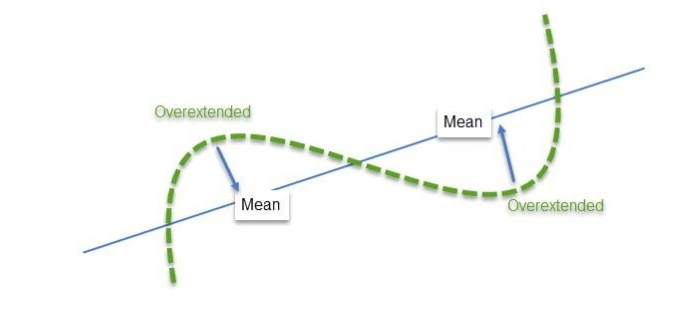
图 7. 超买或超卖的证券倾向于回归到平均价格 (来源: ResearchGate CC BY 4.0)
在趋势市场中,均值对于牛市趋势转变为动态支撑,对于熊市趋势转变为动态阻力。在盘整市场中,均值倾向于在通道内运行,即最高点和最低点之间的中点。
这一特征在货币汇率的短时间框架上更为明显,因为虽然任何其他资产价格至少在理论上可以无限上涨或下跌,但货币汇率受到国家间贸易规则的“限制”。
例如:“苹果公司于1980年12月12日上市,每股价格为22.00美元。自首次公开募股以来,该股票已拆分五次,因此,在拆分调整的基础上,IPO的股价为0.10美元。”
在撰写本文时,苹果的报价为192.00美元(约875倍)。而且它仍在上涨。没有理论上的限制。
另一方面,你不能期望两种货币之间的汇率出现50%的升值或贬值,而不同时考虑极端因素,如恶性通货膨胀甚至大规模战争。在正常情况下,定义外汇交易中货币对“价格”的汇率应该会更早地回归均值。
2. 在数据中搜索模式以检验假设
XAUUSD和XAUEUR之间0.97的皮尔逊相关性代表了我们的模式:这两种证券的价格倾向于同时上涨或下跌。
3. 监控模式中的异常
XAUUSD和XAUEUR之间的平均价差远高于均值,就是我们的异常。在市场模式中寻找异常,是投资组合层面统计套利的核心,正如西蒙斯团队的操作所使用的那样。
4. 开发自动化程序来交易这些异常
这个简化的EA代表了我们的自动化程序,但如上所述,该算法需要许多改进,它只是一个帮助我们更好地理解原理的工具。除此之外,EA本身也需要所有常规的错误检查。
结论
对于普通散户交易者来说,像大玩家那样进行投资组合层面的统计套利几乎是不可能的。因为我们需要在高频交易(HFT)中操作,拥有高技能的团队、高质量的大数据和雄厚的资金。要将我们的简化模型变成类似或接近吉姆·西蒙斯对冲基金的操作,我想说,带点开玩笑的口吻,我们所需要的是能够做到:
- 对每个投资组合中的数百个资产品种进行亚秒级粒度的实时市场分析。(在某个时期,西蒙斯的团队处理着超过八千只不同的股票,遍布十几个市场和地区。)
- 发送百万美元级别的订单,并在百万分之一秒内成交
- 定期更新模型
嗯,我想我们可以从定期更新模型开始。🙂
但严肃地说,上文艾萨克·牛顿的名言教导我们,仅靠数学不足以在金融市场中取得成功。许多数学家在西蒙斯成功的地方失败了。但西蒙斯并非只带着数学就上了战场。他的金融生涯始于像其他任何交易者一样进行交易,寻找趋势,依赖技术分析和直觉,赚钱也亏钱。他尝试了多种方法,学习了交战规则,与专业交易者交流、合作,并共同工作,同时努力寻找一种可持续的交易方式。
尽管如此,他的概念框架对任何愿意付出必要努力去选择正确投资组合、选择要研究的正确特征、寻找模式和异常、使用免费数据进行原型设计、并在原型足够有希望时购买高质量数据以获得特定投资组合最平衡模型的人来说,都是可以接触到的。可能世界上许多散户交易者正在通过日常的认真工作为这种努力付出代价。他们中的大多数人没有成为亿万富翁,但当然,他们中的许多人已经将他们的交易活动转变为了一项可持续的业务。
我们甚至可以遵循机器学习的路径来发现这些模式和异常。它对凡人是可及的,并且似乎已是未来,就在此时此地。有数百篇关于在MetaTrader 5环境中使用机器学习的高质量文章。今天,我们不需要了解底层数学知识就可以在我们的交易系统中使用机器学习。我们可以使用MQL5或Python,两者都自带电池,意味着都包含高级机器学习库。
总之,本文为资源有限的散户交易者提出了一种图解方式,以理解投资组合层面统计套利背后的基本原理。
俗话说,过往结果并不保证未来结果。但如果我们用正确的工具和客观数据来分析那些过往结果,我们就可以做出更明智的决策。
| 附件 | 说明 |
|---|---|
| pairs-trading.mq5 | 此文件包含用于重现实验的示例EA代码。它需要(#include)文件 PairsTradingFunctions.mqh。 |
| PairsTradingFunctions.mqh | 此文件是列表中前一个文件所需的包含文件,目前仅包含一个EA用于识别配对中上涨/下跌品种的检查模式的枚举。 |
| pairs-trading.ipynb | 此文件是一个Jupyter notebook文件,包含用于运行统计分析的Python代码。 |
| stat_arb_pairs_trading_GOLD_XAUEUR.ini | 此文件是一个Metratrader 5策略测试器配置设置文件,用于重现实验。 |
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/17735
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 从基础到中级:模板和类型名称(三)
从基础到中级:模板和类型名称(三)
 价格行为分析工具包开发(第19部分):ZigZag分析器
价格行为分析工具包开发(第19部分):ZigZag分析器
 MQL5 交易工具包(第 7 部分):使用最近取消的挂单函数扩展历史管理 EX5 库
MQL5 交易工具包(第 7 部分):使用最近取消的挂单函数扩展历史管理 EX5 库
 MQL5 简介(第 11 部分):MQL5 中使用内置指标的初学者指南(二)
MQL5 简介(第 11 部分):MQL5 中使用内置指标的初学者指南(二)
与文章问题无关,但非常有趣....
为什么这篇文章是今天(9 月 16 日)发表的,而第一篇评论的日期却是 4 月 11 日?
与文章主题无关,但非常有趣....
为什么这篇文章是今天(9 月 16 日)发表的,而第一篇评论的日期却是 4 月 11 日?
我意识到这是从另一种论坛语言翻译过来的.....。这篇文章的母语显然是早些时候发表的.....已发表
> 艾萨克-牛顿爵士九十岁 时...
牛顿活了84岁(俄语翻译有误?)
感谢您的文章。3、4、6 个字符的旋转方法!!您的解析代码。再次感谢您的精彩内容!
获取的 pairs_spread[0]数组超出范围;