Die Grenzen des maschinellen Lernens überwinden (Teil 3): Eine neue Perspektive auf irreduzible Fehler

In diesem Artikel wird der Leser mit den fortgeschrittenen Einschränkungen aktueller Modelle für maschinelles Lernen vertraut gemacht, die den Lehrkräften nicht ausdrücklich vermittelt werden, bevor sie diese Modelle einsetzen. Der Bereich des maschinellen Lernens wird von mathematischer Notation und Literatur dominiert. Und da es viele Abstraktionsebenen gibt, von denen aus ein Praktiker lernen kann, ist der Ansatz oft unterschiedlich. So studieren manche Praktiker maschinelles Lernen einfach mit Hilfe von High-Level-Bibliotheken wie scikit-learn, die einen einfachen und intuitiven Rahmen für die Verwendung von Modellen bieten, während sie von den mathematischen Konzepten, die ihnen zugrunde liegen, abstrahieren.

Je nach dem Grad der Beherrschung und dem Ausmaß an Kontrolle, das der Praktizierende wünscht, müssen diese Abstraktionen jedoch manchmal entfernt werden, um zu sehen, was wirklich unter der Haube vor sich geht. Daher ist bei jedem Projekt, das Modelle des maschinellen Lernens beinhaltet, der irreduzible Fehler immer vorhanden, auch wenn er selten direkt erwähnt wird.

Betrachten wir die Formel für eine einfache lineare Regression. Normalerweise kann man sich das Ziel, das wir vorhersagen wollen, Y, als eine Funktion, f, einiger Eingaben vorstellen, die wir messen können, X, die durch eine Reihe von Koeffizienten, B, transformiert werden, um das Ziel, Y, zu erzeugen, wenn ein gewisses Maß an zufälligem Rauschen vorliegt, das wir nicht beobachten oder kontrollieren können, e. Unsere heutige Diskussion konzentriert sich auf diesen Fehlerterm, e, der in allen Modellen für maschinelles Lernen vorkommt. Unser Ziel ist es, dem Leser zu zeigen, dass dieser Fehlerterm nicht ganz so zufällig ist, wie uns die klassische Literatur glauben machen möchte. Die Annahme, dass dieser Fehlerterm zufällig und völlig irreduzibel ist, scheint der Wahrheit zu widersprechen.

Abbildung 1: Mathematische Erklärungen der gewöhnlichen Regression nach der Methode der kleinsten Quadrate enthalten nur wenige Details zu den irreduziblen Fehlertermen und deren Ursachen

Unser einziges Ziel ist es, dem Leser eine neue Perspektive auf den irreduziblen Fehler zu geben, indem wir zeigen, dass das, was gemeinhin als eine einzige Größe, der „irreduzible Fehler“, bezeichnet wird, möglicherweise in ein Spektrum unabhängiger Fehlerquellen zerlegt werden kann. Die ersten beiden sind in der wissenschaftlichen Gemeinschaft wohlbekannt:

1. Die inhärente Variabilität oder natürliche Zufälligkeit des zugrunde liegenden Prozesses.
   
2. Die Verzerrung des Modells selbst.

Unsere heutige Diskussion zielt daher darauf ab, eine dritte, weniger bekannte Komponente des irreduziblen Fehlers einzuführen. Die wichtigste Erkenntnis aus diesem Punkt ist, dass wir diese dritte Fehlerquelle kontrollieren können, um unsere Handelsleistung zu verbessern.

Modelle des maschinellen Lernens können aus verschiedenen Blickwinkeln betrachtet werden, sodass es für jeden Leser schwierig ist, sie alle zu beherrschen. Wir lernen diese Modelle oft aus einer statistischen Perspektive kennen. Nur wenige Leser erforschen sie jedoch aus einer geometrischen Perspektive – und genau hier lebt und versteckt sich die dritte Quelle irreduzibler Fehler, die für Praktiker, die auf höheren Abstraktionsebenen bleiben, nicht sichtbar ist.

Diese dritte Art von Fehler ist nicht nur schwer zu beheben – daher der Begriff „irreduzibel“ -, sondern auch schwer zu bemerken, wenn er überhaupt auftritt. Sie ist oft hinter einer knappen mathematischen Notation versteckt, die für jeden von uns gleichermaßen schwer zu erkennen ist.

Unser Artikel erhebt nicht den Anspruch, diesen Fehler auf Null zu reduzieren. Vielmehr wird gezeigt, wie wir Modelle des maschinellen Lernens intelligenter und angemessener einsetzen können, wenn wir diesen Fehler erkennen.

Aus einer geometrischen Perspektive betrachtet, sollte der Leser verstehen, dass Modelle des maschinellen Lernens die Funktion, die Eingaben auf Ausgaben abbildet, nicht wirklich „lernen“. Tatsächlich unternimmt das Modell keinen wirklichen Versuch, die Funktion, die das Ziel erzeugt, direkt zu approximieren. 

Stellen Sie sich einen menschlichen Künstler vor, der ein Bild auf Papier zeichnet. Das Papier dient dem Künstler als Leinwand, auf der er ein Bild seiner Muse einfängt. In ähnlicher Weise verwenden die Modelle des maschinellen Lernens die von uns bereitgestellten Eingaben, um eine neue „Leinwand“ (canvas) zu erstellen, die als mannigfaltig (manifold) bezeichnet wird. Stellen Sie sich nun vor, wir würden eine Münze so halten, dass sie einen Schatten auf die „Leinwand“ wirft, die unser maschinelles Lernmodell aus den von uns eingegebenen Daten erstellt. Der Punkt, an dem der Schatten auf die Leinwand trifft, ist die Vorhersage, die unser Modell macht. Aber unser eigentliches Ziel ist die echte Münze. Der Punkt, den der Leser verstehen soll, ist, dass unsere maschinellen Lernmodelle im Wesentlichen Bilder des Ziels in eine Kombination/Mannigfaltigkeit der ihm gegebenen Eingaben einbetten.

Aber das Ziel, das Sie vorhersagen wollen, befindet sich nicht unbedingt in der Vielfalt, die wir aus den Eingaben erstellen können, sondern in seinem eigenen mannigfaltigen Raum. Daher besteht immer ein gewisser irreduzibler Abstand zwischen dem durch Ihre Eingaben erzeugten Mannigfaltigkeit und der Mannigfaltigkeit, in dem das wahre Ziel lebt. Dies ist eine Fehlerquelle. Wenn man dann noch die natürliche Zufälligkeit des Prozesses (die zweite Quelle) und die Verzerrung des Modells (die dritte Quelle) hinzunimmt, ergibt sich ein vollständiges Bild.

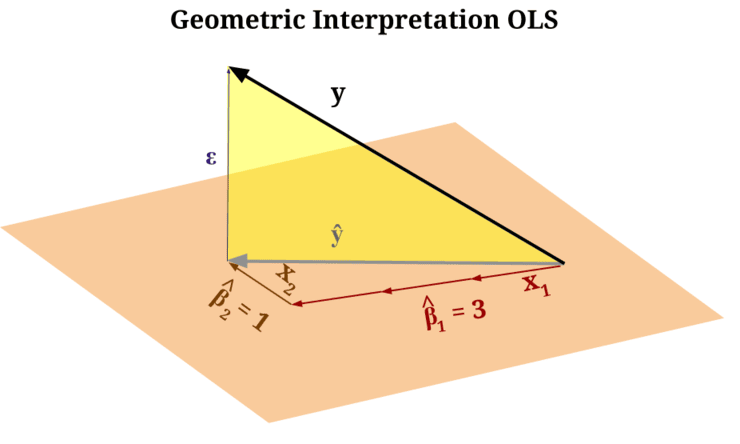
Abbildung 2: Die „orangefarbene Ebene“ stellt die „Leinwand“ dar, die das Modell aus den von Ihnen eingegebenen Daten erstellt hat, während das „gelbe Dreieck“ den irreduziblen Fehler zwischen der Leinwand und dem tatsächlichen Ziel darstellt.

Leser, die bereits mit analytischer Geometrie vertraut sind, werden erkennen, dass die Spanne der Eingaben, die einem Modell für maschinelles Lernen gegeben werden, ein neues Koordinatensystem definiert. Das Modell versucht dann, das Ziel mithilfe dieses neuen Koordinatensystems zu beschreiben, das es aus den Eingabedaten gelernt hat. Aber denken Sie daran: Das Ziel lebt in seinem eigenen Koordinatensystem, unabhängig von dem, das durch die Eingaben definiert ist!

Fortgeschrittene Leser, die mit dieser geometrischen Perspektive des maschinellen Lernens bereits vertraut sind, werden die folgende Diskussion vielleicht als selbstverständlich empfinden und können überlegen, ob sie nicht doch lieber weiterblättern wollen. Für diejenigen, die noch nicht auf diese Weise auf das Problem gestoßen sind, ist der Rest des Artikels gedacht.

Die wichtigste Erkenntnis ist, dass wir diesen Fehler bei unseren Handelsaktivitäten bis zu einem gewissen Grad kontrollieren können, indem wir die Modelle des maschinellen Lernens bewusster, gezielter und intelligenter einsetzen.

Wir beginnen unser Gespräch mit dem grundlegenden Leistungsniveau, das wir in unserer früheren Diskussion über Feedback-Controller festgelegt haben; den Link dazu finden Sie hier. Unser Feedback-Controller hat die Leistung im Vergleich zum Ausgangspunkt des Gesprächs deutlich verbessert. Nachdem wir die in diesem Artikel vorgeschlagenen Anpassungen vorgenommen hatten, übertrafen wir die Leistung des alten Feedback-Controllers, der schon fast akzeptabel war.

Bei unserer Methodik haben wir uns von direkten Punkt-zu-Punkt-Vergleichen verabschiedet. Anstatt das Modell zu bitten, ein zukünftiges Preisniveau vorherzusagen und es mit dem aktuellen Preis zu vergleichen, haben wir die Preisniveaus über zwei Zeitintervalle modelliert und den erwarteten Anstieg/Trend gehandelt. Mit anderen Worten, wir haben die vom Modell vorhergesagte Steigung über zwei Intervalle hinweg gehandelt, anstatt einen direkten Vergleich zwischen vorhergesagten und tatsächlichen Preisen anzustellen.

Wir haben einen Fünf-Jahres-Backtest für das Währungspaar EUR/USD mit identischen Strategien durchgeführt, wobei der einzige Unterschied darin bestand, wie wir unsere Modelle angewiesen haben, den Preis zu modellieren. Die Ergebnisse zeigen ein Wachstum in den folgenden Leistungsbereichen:

Rentabilität im Handel
Unser Gesamtnettogewinn stieg von 245 $ auf 253 $, was einer Verbesserung der Rentabilität um 3 % entspricht, während gleichzeitig unsere Sharpe Ratio von 0,68 auf 0,84 anstieg. Eine Verbesserung der Sharpe Ratio um 23 % ist bemerkenswert, wenn man mit einem so schwierigen Finanzmarkt wie dem EUR/USD-Paar handelt.

Handelsrisiko
Noch erstaunlicher war, dass der Bruttoverlust über den 5-Jahres-Backtest von 838 $ auf 721 $ sank; dies entspricht einer Reduzierung des Gesamtrisikos unserer Handelsanwendung um 13 %. Darüber hinaus sank unsere kumulative Handelsaktivität von 152 auf 139 Abschlüsse, was einem Rückgang der Gesamtzahl der erforderlichen Abschlüsse um 8 % entspricht. Das bedeutet, dass unsere Anwendung größere Gewinnspannen bei geringerem Risiko erzielt.

Handelsgenauigkeit

Schließlich stieg der Anteil der Handelsgeschäfte mit Gewinn um 4 %, von 57,24 % im ursprünglichen Benchmark unseres Feedback-Controllers auf 59,71 % nach den von uns vorgeschlagenen Anpassungen.  Das bedeutet, dass unser System insgesamt profitabler wurde, während es weniger Risiken einging – eine ideale Eigenschaft für jede Handelsanwendung.

Diese Änderungen sollten von allen Praktikern unbedingt berücksichtigt werden. Aber lassen Sie uns zunächst die alten Leistungswerte des ersten Feedback-Controllers überprüfen, den wir in unserer vorherigen Ausarbeitung verwendet haben.

Der erste Backtest wurde vom 01. Januar 2020 bis zum 01. Mai 2025 durchgeführt. Wir werden diese Daten auch bei diesem zweiten Test beibehalten.

Abbildung 3: Die in der Eröffnungsdiskussion ermittelten Basisleistungsniveaus werden erneut überprüft

Der alte Feedback-Controller lieferte Ergebnisse, die durchaus akzeptabel sind, aber wir können immer noch besser abschneiden als dieser. Wir haben diese alten Ergebnisse hier beibehalten, damit der Leser die neuen Ergebnisse, die wir jetzt produzieren werden, vergleichen kann; daher wurde die folgende Abbildung 4 von unserem alten Feedback-Controller übernommen. Sie dient uns als Benchmark, die wir heute übertreffen müssen.

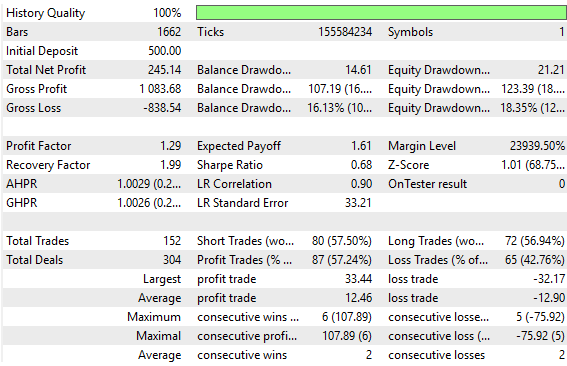
Abbildung 4: Die alten Leistungswerte, die bei unserem ersten Versuch, einen Feedback-Controller zu bauen, ermittelt wurden

Die von unserem alten Feedback-Controller erzeugte Kapitalkurve war vielversprechend. Es ist uns gelungen, mehr Gewinn aus der Strategie zu erzielen, indem wir einige Anpassungen an der ursprünglichen Strategie vorgenommen haben, die sich letztendlich deutlich auf die Rentabilität unseres gesamten Systems ausgewirkt haben. In Abbildung 5 ist zu sehen, dass der alte Feedback-Controller erst im Jahr 2023 die Gewinnschwelle von 700 $ erreicht. Wie wir jedoch bald sehen werden, hat unser überarbeiteter Feedback-Controller im Jahr 2021 die Gewinnschwelle von 700 Dollar erreicht. Zwar erlitt das Unternehmen kurz nach 2021 einen Rentabilitätsschock, doch die Verbesserungen sind unübersehbar.

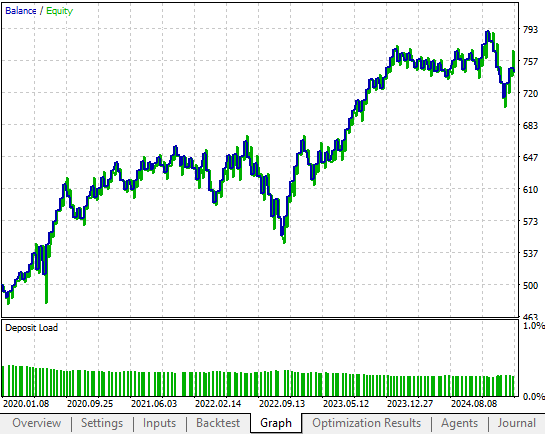
Abbildung 5: Die Gewinn- und Kapitalkurve, die sich aus der Benchmark-Version unserer Handelsstrategie ergibt

Erste Schritte in MQL5

Wie bei allen unseren Handelsanwendungen beginnen wir mit der Definition wichtiger Systemdefinitionen, die ohne Änderungen aus der ursprünglichen Version unserer Handelsstrategie übernommen wurden. Diese Definitionen sind wichtig, weil sie uns helfen, unsere Tests fair und unsere Vergleiche konsistent zu halten.

//+------------------------------------------------------------------+
//|                                     Closed Loop Feedback 1.2.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System definitions                                               |
//+------------------------------------------------------------------+
#define MA_PERIOD    10
#define FEATURES     12
#define TARGETS      15
#define HORIZON      10
#define OBSERVATIONS 90
#define ACCOUNT_STATES 3

Als Nächstes definieren wir wichtige globale Variablen, die in der Handelsstrategie verwendet werden. Diese Variablen verfolgen die technischen Indikatoren, den Zustand und den Status unseres Handelskontos, die Breite unseres Stop-Loss und ob die Strategie ohne Vorhersage handeln soll oder erst eine Vorhersage machen soll, bevor sie handelt. Globale Variablen ermöglichen es uns, das Verhalten unserer Anwendung in einer Weise zu definieren und zu steuern, die sowohl vorhersehbar als auch wiederholbar ist.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int    ma_h_handler,ma_l_handler,atr_handler,scenes,b_matrix_scenes;
double ma_h[],ma_l[],atr[];
double padding;
matrix snapshots,OB_SIGMA,OB_VT,OB_U,b_vector,b_matrix;
vector S,prediction;
vector account_state;
bool predict,permission;

Alle Handelsanwendungen haben auch Abhängigkeiten, die dazu beitragen, dass nicht immer derselbe Standardcode geschrieben werden muss. Daher laden wir wichtige Bibliotheken wie die Handelsbibliothek (zum Öffnen und Schließen von Positionen) sowie zwei speziell für diese Diskussionen entwickelte Bibliotheken: die Zeitbibliothek und die Handelsinformationsbibliothek. Die Zeitbibliothek hilft uns festzustellen, wann sich eine neue Kerze gebildet hat, während die Handelsinformationsbibliothek wichtige Details wie die zulässige Mindestlosgröße und den aktuellen Geld- und Briefkurs liefert.

//+------------------------------------------------------------------+
//| Dependencies                                                     |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
#include <VolatilityDoctor\Time\Time.mqh>
#include <VolatilityDoctor\Trade\TradeInfo.mqh>

CTrade      Trade;

Time        *DailyTimeHandler;
TradeInfo   *TradeInfoHandler;

Bei der Initialisierung erstellen wir neue Instanzen aller nutzerdefinierten Klassen, die wir bisher erstellt haben. Wir definieren auch technische Indikatoren, wie den gleitenden Durchschnitt und den ATR-Indikator, sowie die wichtigen Matrizen und Vektoren, die wir benötigen. Boolesche Flags werden initialisiert, und der Zähler für abgelaufene Szenen wird bei jedem Start der Anwendung auf Null zurückgesetzt. 

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   DailyTimeHandler  = new Time(Symbol(),PERIOD_D1);
   TradeInfoHandler  = new TradeInfo(Symbol(),PERIOD_D1);
   ma_h_handler      = iMA(Symbol(),PERIOD_D1,MA_PERIOD,0,MODE_EMA,PRICE_HIGH);
   ma_l_handler      = iMA(Symbol(),PERIOD_D1,MA_PERIOD,0,MODE_EMA,PRICE_LOW);
   atr_handler       = iATR(Symbol(),PERIOD_D1,14);
   snapshots         = matrix::Ones(FEATURES,OBSERVATIONS);
   scenes            = 0;
   b_matrix_scenes   = 0;
   account_state     = vector::Zeros(3);
   b_matrix          = matrix::Zeros(1,1);
   prediction        = vector::Zeros(2);
   predict           = false;
   permission        = true;
//---
   return(INIT_SUCCEEDED);
  }

Wenn die Anwendung nicht mehr nutzt wird, ist es in MQL5 eine gute Praxis, eine angemessene Speicherverwaltung zu praktizieren. Daher löschen wir nutzerdefinierte Objektinstanzen und geben alle technischen Indikatoren frei, die nicht mehr verwendet werden.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   delete DailyTimeHandler;
   delete TradeInfoHandler;
   IndicatorRelease(ma_h_handler);
   IndicatorRelease(ma_l_handler);
   IndicatorRelease(atr_handler);
  }

Wenn neue Preisniveaus vom Handelsserver empfangen werden, ruft unser Expert Advisor auch seine OnTick-Funktion auf. Bei diesem Setup wird zunächst geprüft, ob sich eine neue Kerze gebildet hat. Dies gewährleistet, dass unsere Backtests schneller ablaufen, da die Aktionen nur einmal pro Kerze ausgeführt werden.

Sobald dies bestätigt ist, aktualisieren wir die Werte der technischen Indikatoren und unsere Variable Pageant, die uns sagt, wie hoch unser Stop-Loss sein sollte. Wir verfolgen dann den letzten geschlossenen Kurs. Wenn es eine oder mehrere offene Positionen gibt, wählen wir die Tickets der offenen Positionen aus und ändern ihre Stop-Losses so, dass sie mit steigender Rentabilität nachgeben.

Um einen Trailing Stop einzurichten, erfassen wir zunächst die aktuellen Werte von Stop Loss und Take Profit. Durch den Vergleich dieser Werte mit den vorgeschlagenen aktualisierten Werten entscheiden wir, ob eine Aktualisierung erforderlich ist. Wenn der vorgeschlagene Wert rentabler ist, wird die Aktualisierung vorgenommen; andernfalls wird keine Änderung vorgenommen. Bevor wir diese Aktualisierung durchführen, müssen wir bestätigen, welche Art von Position wir ändern.

Wenn keine Positionen offen sind, initialisieren wir den Kontostandsvektor. Erinnern Sie sich daran, dass dieser Vektor festhält, welche Art von Position wir zu eröffnen beabsichtigen. Wenn der Schlusskurs über dem hohen gleitenden Durchschnitt liegt, eröffnen wir eine Kaufposition. Wenn er unter dem unteren gleitenden Durchschnitt liegt, eröffnen wir eine Verkaufsaktion.

Handelsgeschäfte werden direkt eröffnet, wenn das boolesche Flag für die Vorhersage auf false und das boolesche Flag für die Erlaubnis auf true gesetzt ist. Andernfalls zeichnet das System alle Variablen auf und erstellt eine Vorhersage, bevor es den Handel eröffnet.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(DailyTimeHandler.NewCandle())
     {
      CopyBuffer(ma_h_handler,0,0,1,ma_h);
      CopyBuffer(ma_l_handler,0,0,1,ma_l);
      CopyBuffer(atr_handler,0,0,1,atr);
      padding = atr[0]*2;
      double c = iClose(Symbol(),PERIOD_D1,0);

      if(PositionsTotal() > 0)
        {
         ulong ticket = PositionSelectByTicket(PositionGetTicket(0));
         if(ticket)
           {
            double sl,tp;

            sl = PositionGetDouble(POSITION_SL);
            tp = PositionGetDouble(POSITION_TP);

            if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
              {
               double new_sl = TradeInfoHandler.GetBid()-padding;
               double new_tp = TradeInfoHandler.GetBid()+padding;

               if(new_sl > sl)
                  Trade.PositionModify(ticket,new_sl,new_tp);
              }

            else
               if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
                 {
                  double new_sl = TradeInfoHandler.GetAsk()+padding;
                  double new_tp = TradeInfoHandler.GetAsk()-padding;

                  if(new_sl < sl)
                     Trade.PositionModify(ticket,new_sl,new_tp);
                 }
           }
        }

      if(PositionsTotal() == 0)
        {
         account_state = vector::Zeros(ACCOUNT_STATES);

         if(c > ma_h[0])
           {
            if(!predict)
              {
               if(permission)
                  Trade.Buy(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetAsk(),(TradeInfoHandler.GetBid()-(padding)),(TradeInfoHandler.GetBid()+(padding)),"");
              }

            account_state[0] = 1;
           }

         else
            if(c < ma_l[0])
              {
               if(!predict)
                 {
                  if(permission)
                     Trade.Sell(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetBid(),(TradeInfoHandler.GetAsk()+(padding)),(TradeInfoHandler.GetAsk()-(padding)),"");
                 }

               account_state[1] = 1;
              }

            else
              {
               account_state[2] = 1;
              }
        }

      if(scenes < OBSERVATIONS)
        {
         take_snapshots();
        }

      else
        {
         matrix temp;
         temp.Assign(snapshots);
         snapshots = matrix::Ones(FEATURES,scenes+1);

         //--- The first row is the intercept and must be full of ones
         for(int i=0;i<FEATURES;i++)
            snapshots.Row(temp.Row(i),i);

         take_snapshots();
         fit_snapshots();

         predict = true;
         permission = false;
        }
      scenes++;
     }
  }

Die Methode, mit der wir einen Schnappschuss machen, ist ganz einfach. Es zeichnet wichtige Marktinformationen in einer Matrix auf, die wir Snapshot nennen. Dazu gehören der Eröffnungs-, Höchst-, Tiefst- und Schlusskurs sowie das Kapital des Kontos. Leser, die frühere Diskussionen verfolgt haben, werden diesen Code wiedererkennen, da er derselbe ist, den wir zu Beginn der Serie verwendet haben.

//+------------------------------------------------------------------+
//| Record the current state of our system                           |
//+------------------------------------------------------------------+
void take_snapshots(void)
  {
   snapshots[1,scenes] = iOpen(Symbol(),PERIOD_D1,1);
   snapshots[2,scenes] = iHigh(Symbol(),PERIOD_D1,1);
   snapshots[3,scenes] = iLow(Symbol(),PERIOD_D1,1);
   snapshots[4,scenes] = iClose(Symbol(),PERIOD_D1,1);
   snapshots[5,scenes] = AccountInfoDouble(ACCOUNT_BALANCE);
   snapshots[6,scenes] = AccountInfoDouble(ACCOUNT_EQUITY);
   snapshots[7,scenes] = ma_h[0];
   snapshots[8,scenes] = ma_l[0];
   snapshots[9,scenes] = account_state[0];
   snapshots[10,scenes] = account_state[1];
   snapshots[11,scenes] = account_state[2];
  }

Jetzt aber sehen wir die Verbesserungen, die gegenüber dieser ersten Version vorgenommen wurden. Bis zu diesem Punkt sollte den Lesern alles vertraut sein. Wir bereiten jetzt die Eingaben und Ausgaben des Systems vor, das die Entwicklung unserer Schnappschüsse modelliert. Erinnern Sie sich daran, dass Snapshots wichtige Details darüber aufzeichnen, wie unsere Strategie mit dem Markt interagiert – zum Beispiel, wie sich unser Kontostand und unser Kapital im Laufe der Zeit verändern.

Die X-Matrix speichert die Eingabedaten, während die Y-Matrix die Ausgabedaten speichert. Wenn der Leser die Y-Matrix genau betrachtet, wird er feststellen, dass die Zeilen 4, 5, 6 und 7 von Y aus den Zeilen 5, 6, 7 und 8 von X kopiert werden. Das bedeutet, dass wir unser Modell nicht nur bitten, den Kontostand in einem Schritt in die Zukunft vorherzusagen, sondern auch in zehn Schritten in die Zukunft.

Je nach dem über diese beiden Zeithorizonte vorhergesagten Trend entscheiden wir, ob wir einen Handel eröffnen. Sobald die optimale Lösung mit Hilfe der Pseudo-Inverse-Methode (siehe oben) gefunden ist, gibt unser Modell zwei Vorhersagen aus:

1. Der erwartete Saldo bei der nächsten Kerze (Vorhersage 4).
   
2. Der erwartete Saldo nach zehn Kerzen (Vorhersage 8).

Das Modell trifft dann auf der Grundlage dieser Vorhersagen Handelsentscheidungen. Wenn er ein Wachstum des Kontos erwartet, ist der Handel erlaubt. Erwartet es einen Rückgang, wird die Genehmigung verweigert.

Dies ist eine erhebliche Verbesserung gegenüber der bisherigen Methode. In früheren Diskussionen haben wir den vom Modell vorhergesagten Kontostand direkt mit dem aktuellen realen Saldo verglichen, so als ob die beiden gleich wären. Bei diesem Ansatz vermeiden wir diesen Fehler.

//+------------------------------------------------------------------+
//| Fit our linear model to our collected snapshots                  |
//+------------------------------------------------------------------+
void fit_snapshots(void)
  {
   matrix X,y;
   X.Reshape(FEATURES,scenes);
   y.Reshape(TARGETS,scenes);

   for(int i=0;i<scenes-HORIZON;i++)
     {
      X[0,i] = snapshots[0,i];
      X[1,i] = snapshots[1,i];
      X[2,i] = snapshots[2,i];
      X[3,i] = snapshots[3,i];
      X[4,i] = snapshots[4,i];
      X[5,i] = snapshots[5,i];
      X[6,i] = snapshots[6,i];
      X[7,i] = snapshots[7,i];
      X[8,i] = snapshots[8,i];
      X[9,i] = snapshots[9,i];
      X[10,i] = snapshots[10,i];
      X[11,i] = snapshots[11,i];

      y[0,i] = snapshots[1,i+1];
      y[1,i] = snapshots[2,i+1];
      y[2,i] = snapshots[3,i+1];
      y[3,i] = snapshots[4,i+1];
      y[4,i] = snapshots[5,i+1];
      y[5,i] = snapshots[6,i+1];
      y[6,i] = snapshots[7,i+1];
      y[7,i] = snapshots[8,i+1];
      y[8,i] = snapshots[5,i+HORIZON];
      y[9,i] = snapshots[6,i+HORIZON];
      y[10,i] = snapshots[7,i+HORIZON];
      y[11,i] = snapshots[8,i+HORIZON];
      y[12,i] = snapshots[9,i+1];
      y[13,i] = snapshots[10,i+1];
      y[14,i] = snapshots[11,i+1];
     }

   if(PositionsTotal() == 0)
     {
      //--- Find optimal solutions
      b_vector = y.MatMul(X.PInv());
      Print("Day Number: ",scenes+1);
      Print("Snapshot");
      Print(snapshots);
      Print("Input");
      Print(X);
      Print("Target");
      Print(y);
      Print("Coefficients");
      Print(b_vector);
      Print("Prediciton");
      prediction = b_vector.MatMul(snapshots.Col(scenes-1));
      Print("Expected Balance at next candle: ",prediction[4],". Expected Balance after 10 candles: ",prediction[8]);

      permission = false;

      if(prediction[4] < prediction[8])
        {
         Print("Account size expected to grow, permission granted");
         permission = true;
        }

      else
         permission = false;

      if(permission)
        {
         if(PositionsTotal() == 0)
           {
            if(account_state[0] == 1)
               Trade.Buy(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetAsk(),(TradeInfoHandler.GetBid()-(atr[0]*2)),(TradeInfoHandler.GetBid()+(atr[0]*2)),"");

            else
               if(account_state[1] == 1)
                  Trade.Sell(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetBid(),(TradeInfoHandler.GetAsk()+(atr[0]*2)),(TradeInfoHandler.GetAsk()-(atr[0]*2)),"");
           }
        }
     }
  }
//+------------------------------------------------------------------+

Wie bei unserem vorangegangenen Gespräch müssen wir die Daten der Tests gleich halten, um sicherzustellen, dass wir jederzeit faire Vergleiche anstellen können.

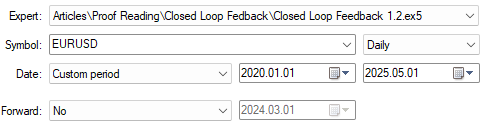
Abbildung 6: Backtest der verbesserten Version unseres Feedback-Controllers über denselben Zeitraum

Unsere detaillierten Statistiken zeigen ein deutliches und messbares Wachstum gegenüber der ersten Version der Handelsstrategie. Mit dieser verbesserten Version der Strategie sind wir insgesamt einem geringeren Risiko ausgesetzt als mit der ursprünglichen Version der Handelsstrategie. Interessant ist auch, dass sich der Anteil der profitablen Short-Trades deutlich verbessert hat und fast 70 % erreicht.

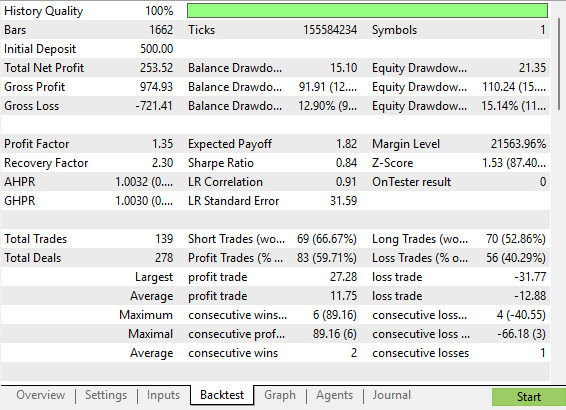
Abbildung 7: Eine detaillierte Analyse der Verbesserungen, die wir an unserem Handelssystem vorgenommen haben

Unsere neue Strategie führte zu einer Kapitalkurve, die im Vergleich zur ursprünglichen Strategie weniger Perioden des Drawdowns aufwies. Diese Strategie zeigt ein stetiges Wachstum, das weniger volatil, aber immer noch schneller ist als die ursprüngliche riskante Version unserer Handelsstrategie.

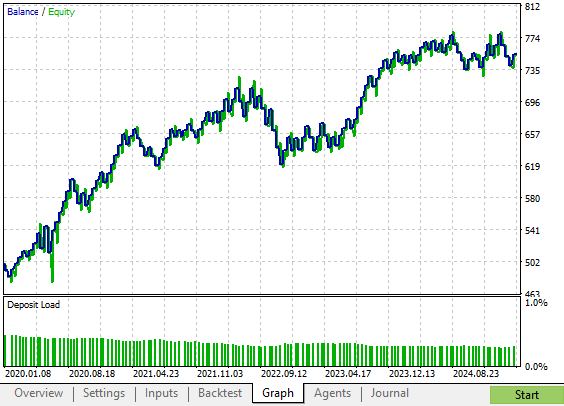
Abbildung 8: Die von unserer verbesserten Version der Handelsstrategie erzeugte Kapitalkurve zeigt uns ein beschleunigtes Wachstum im Vergleich zur ursprünglichen Strategie

Schlussfolgerung

Stellen Sie sich vor, Sie halten einen Golfball in Armeslänge gegen den Himmel und bitten Ihr KI-Modell, dessen Größe mit dem Mond zu vergleichen. An manchen Tagen würde das Modell entscheiden, dass der Mond etwas größer als der Golfball ist, und an anderen Tagen könnte es behaupten, dass der Golfball etwas größer als der Mond ist. Als Menschen wissen wir, dass eine solche Tätigkeit grundsätzlich fehlerhaft und bis zu einem gewissen Grad auch lustig ist, aber hier hört der Spaß auf.

Im Prinzip könnten unsere maschinellen Lernmodelle beim Handel an den Finanzmärkten stillschweigend denselben Fehler machen. Bei dem Gedankenexperiment besteht der Fehler darin, dass das Modell nicht verstanden hat, dass es nicht direkt mit dem Mond arbeitet, sondern ein Bild des Mondes vergleicht, das am Himmel projiziert wird.

Und auf den Märkten sagen unsere Modelle des maschinellen Lernens nicht den „echten“ zukünftigen Kurswert voraus, sondern sie erstellen Bilder des Ziels auf die Merkmale. Daher sollten wir die Vorhersagen unseres Modells nicht direkt mit den realen Preisen vergleichen, als ob sie identisch wären. Stattdessen müssen wir erkennen, dass unsere Modelle des maschinellen Lernens versuchen, ein Bild des Ziels zu zeichnen, indem sie ein aus den Eingaben erlerntes Koordinatensystem verwenden, und Bilder sind immer durch einen nicht reduzierbaren Abstand von der Realität getrennt. Dieses Bild kann durch viele Faktoren verzerrt werden, weshalb wir uns nicht auf direkte Vorhersagen verlassen sollten.

Stattdessen geht der Leser nach der Lektüre dieses Artikels gestärkt aus der Lektüre hervor, weil er weiß, warum wir mehrere Prognosehorizonte verwenden sollten, um die Auswirkungen dieses Fehlers zu verringern, der normalerweise nicht hinterfragt wird.