Matrix-Faktorisierung: Ein praktikables Modell

Einführung

Hallo Leute und willkommen zu meinem neuen Artikel, der wieder didaktische Inhalte enthält.

In dem vorherigen Artikel „Matrixfaktorisierung: Die Grundlagen“, habe ich ein wenig darüber gesprochen, wie Sie, liebe Leserinnen und Leser, Matrizen in Ihren allgemeinen Berechnungen verwenden können. Damals wollte ich jedoch, dass Sie verstehen, wie die Berechnungen durchgeführt wurden, daher habe ich nicht so sehr darauf geachtet, das richtige Modell der Matrizen zu erstellen.

Sie haben vielleicht nicht bemerkt, dass die Matrixmodellierung etwas seltsam war, da nur Spalten und nicht Zeilen und Spalten angegeben wurden. Das sieht sehr seltsam aus, wenn man den Code liest, der die Matrixfaktorisierung durchführt. Wenn Sie erwartet haben, die Zeilen und Spalten aufgelistet zu sehen, könnten Sie beim Versuch, zu faktorisieren, verwirrt werden.

Außerdem ist diese Matrixmodellierungsmethode nicht die beste. Denn wenn wir Matrizen auf diese Weise modellieren, stoßen wir auf einige Einschränkungen, die uns zwingen, andere Methoden oder Funktionen zu verwenden, die nicht notwendig wären, wenn die Modellierung auf eine angemessenere Weise erfolgen würde.

Da das Verfahren zwar nicht kompliziert ist, aber ein gutes Verständnis voraussetzt, um es richtig anzuwenden, habe ich mich entschlossen, im vorherigen Artikel nicht ins Detail zu gehen. In diesem Artikel werden wir alles in Ruhe und ohne Eile betrachten, um falsche Vorstellungen über die Modellierung von Matrizen zu vermeiden und ihre korrekte Faktorisierung zu gewährleisten.

Matrizen sind von Natur aus besser geeignet, um bestimmte Berechnungen durchzuführen, da sie nur minimale zusätzliche Implementierungsarbeit von unserer Seite erfordern. Aus genau demselben Grund sollten Sie jedoch sehr vorsichtig sein, wenn Sie etwas in Matrizen implementieren. Anders als bei der konventionellen Modellierung erhalten wir bei der Modellierung von Matrizen, wenn wir etwas falsch modellieren, eher merkwürdige Ergebnisse oder haben bestenfalls große Schwierigkeiten bei der Wartung des entwickelten Codes.

Vorsicht bei der Modellierung einer Matrix

Sie werden sich vielleicht fragen, warum ich die Modellierung im vorigen Artikel als seltsam bezeichnet habe, denn sie macht ja durchaus Sinn. Vielleicht haben Sie alles verstanden, was in diesem Artikel beschrieben wurde. Schauen wir uns das Codefragment aus dem vorherigen Artikel an, in dem Matrizen modelliert wurden. Vielleicht wird dadurch ein wenig deutlicher, was ich Ihnen zeigen möchte. Hier ist dieser Code.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2] = {
24.                            cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                           -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                         },
27.            M_2[][2]  =  {
28.                            0.0,  0.0,
29.                            1.5, -.75,
30.                            1.0,  0.0,
31.                            1.5,  .75
32.                         },
33.            M_3[M_2.Size() / 2][2];

Obwohl es funktioniert, wie Sie aus dem Fragment ersehen können, ist das Problem ziemlich verwirrend. Das ist schwer zu verstehen. Wenn wir ein mehrdimensionales Array in Code schreiben, verwenden wir die folgende Konfiguration:

Label[Dimension_01][Dimension_02]....[Dimension_N];

Obwohl der Code im Allgemeinen einfach erscheinen mag, ist diese Art von Notation schwer zu verstehen, wenn sie auf das Gebiet der Matrixfaktorisierung angewendet wird. Der Grund dafür ist, dass bei der Arbeit mit Matrizen diese Art des Ausdrucks in einem mehrdimensionalen Array Verwirrung stiftet. Sie werden den Grund dafür bald verstehen. Der Einfachheit halber werden wir dieses Konzept auf ein zweidimensionales System reduzieren, d. h. nur auf Zeilen und Spalten. Matrizen können jedoch eine beliebige Anzahl von Dimensionen haben. Vereinfacht auf eine zweidimensionale Matrix sieht die Notation wie folgt aus:

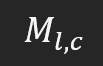
Was bedeutet das? Der Buchstabe „M“ steht für den Namen der Matrix, „l“ steht für die Anzahl der Zeilen und „c“ für die Anzahl der Spalten. Wenn wir uns auf ein Matrixelement beziehen, verwenden wir im Allgemeinen die gleiche Notation, die wie folgt aussieht:

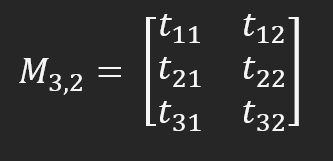
Man beachte, dass die Matrix M nun aus sechs Elementen besteht, auf die über das Zeilen- und Spaltensystem zugegriffen werden kann. Aber sehen Sie sich das vorherige Bild genau an: Wie sieht sie aus? Je nach Ihrer Erfahrung kann das anders aussehen. Aber was wäre das in der Programmiersprache? Es handelt sich also um ein zweidimensionales Array. Bei diesem Ansatz erscheint die Matrix jedoch statisch. Eine Matrix ist ein dynamisches Gebilde; sie kann auf unterschiedliche Weise gelesen werden, je nachdem, was wir gerade berechnen. In einigen Fällen müssen wir sie diagonal lesen, in anderen spaltenweise und in wieder anderen zeilenweise. Wenn man sich also eine Matrix als mehrdimensionales Array vorstellt, wird etwas Dynamisches zu etwas Statischem. Dies erschwert die Durchführung einiger Matrixberechnungen.

Wir sind jedoch nicht hier, um die Grundlagen des Programmierens zu erlernen. Ich möchte Ihnen, liebe Leserinnen und Leser, zeigen, wie man eine Matrix am besten visualisiert und gleichzeitig dafür sorgt, dass sie die dynamische Einheit bleibt, die sie sein soll.

Die Vorstellung, dass eine Matrix ein Array ist, ist also nicht falsch. Das Problem tritt auf, wenn man es als mehrdimensionales Array betrachtet. Idealerweise sollten Sie sich eine Matrix als eindimensionales Array vorstellen, jedoch ohne eine feste Anzahl von Dimensionen. Dieser Punkt mag seltsam klingen, aber das Problem liegt in der Sprache. Es gibt derzeit keine geeigneten Begriffe oder Ausdrücke zur Beschreibung einiger Konzepte.

Erinnern Sie sich an die Schwierigkeiten, mit denen Isaac Newton konfrontiert war, als er seine Berechnungen erstmals erläuterte. Es muss ziemlich schwierig gewesen sein, weil es für einige Begriffe keine passenden Bezeichnungen gab. Aber kommen wir zurück zu unserer Frage.

Wir haben bereits eine Möglichkeit, eine Matrix als Array darzustellen. Doch nun stellt sich das erste Problem: Wie kann man die Elemente in einem Array sortieren? Wenn Sie nicht verstehen, warum das ein Problem ist, dann verstehen Sie auch andere Dinge nicht, die mit der Matrixfaktorisierung zusammenhängen. Die Art und Weise, wie die Elemente angeordnet sind, bestimmt weitgehend, wie der Faktorisierungscode implementiert wird. Obwohl die Ergebnisse in beiden Fällen gleich sind, benötigen wir möglicherweise mehr oder weniger Übergänge innerhalb des Feldes, um das richtige Ergebnis zu erhalten. Dies ist darauf zurückzuführen, dass der Computerspeicher linear ist. Wenn wir die Elemente als t11, t12, t21, t22, t31 und t32 anordnen, was in vielen Fällen in Ordnung ist, müssen wir Sprünge erzwingen, um auf die Elemente in einer anderen Reihenfolge zuzugreifen, um eine bestimmte Berechnung durchzuführen. Das wird auf jeden Fall passieren, egal was wir tun.

Normalerweise sortieren wir die Elemente eines Arrays, indem wir Zeile für Zeile lesen. Sie können sie jedoch auch anders anordnen, z. B. spaltenweise lesen oder auf eine andere Art und Weise, die Sie selbst bestimmen können. Fühlen Sie sich frei, es so zu tun, wie Sie es für richtig halten.

Sobald dies geschehen ist, ergibt sich ein weiteres kleines Problem, das nicht mit der Programmierung, sondern mit der Durchführung der Matrixfaktorisierung zusammenhängt. In diesem Fall werde ich nicht ins Detail gehen. Der Grund dafür ist einfach: Wie wir damit umgehen, hängt davon ab, wie wir die Matrix implementiert haben oder welche Art von Matrix wir verwenden. Ich empfehle, Bücher oder mathematische Literatur zu studieren, um zu verstehen, wie man Lösungen für eventuell auftretende Probleme implementiert und die Faktorisierung korrekt durchführt. Die Implementierung des Codes ist jedoch nie schwierig, denn der Code ist der einfachste Teil der Entwicklung. Der schwierigste Teil besteht darin, zu verstehen, wie die Faktorisierung durchgeführt wird. Ein Beispiel ist die Berechnung der Matrixdeterminante, die in der vorherigen Abbildung dargestellt ist. Beachten Sie, dass es sich hier nicht um eine quadratische Matrix handelt und die Konstruktion der Determinante in diesem Fall etwas anders abläuft als im Falle einer quadratischen Matrix. Wie bereits erwähnt, ist es notwendig, den mathematischen Teil zu studieren, da jeder spezifische Fall einen besonderen Ansatz erfordern kann.

Eine Verwirrung

Nun, da alles erklärt ist, können wir mit der Codierung beginnen. Bleiben wir bei dem im vorigen Artikel besprochenen Beispiel, da es recht praktisch und leicht zu verstehen ist. Außerdem zeigt dieses Beispiel leicht einen weiteren Vorteil der Verwendung von Matrixberechnungen in einigen Situationen. Erinnern wir uns daran, wie der Code aussah. Also, hier ist dieser Code:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

Da dieser Code bereits im vorangegangenen Artikel beschrieben wurde und auch im Anhang zu diesem Artikel zu finden ist, werden wir ihn hier nicht wiederholen. Konzentrieren wir uns nur auf die Prozeduren Arrow und MatrixA_x_MatrixB, die in unserem Democode tatsächlich etwas tun.

Zunächst müssen wir die Art und Weise ändern, wie Arrays erstellt werden. Die Änderungen werden einfacher und subtiler sein, als es den Anschein hat, aber sie werden dennoch die Art und Weise verändern, wie wir anfangen müssen.

Beginnen wir mit dem Array M_1 aus dem obigen Code. Studieren Sie es, um zu verstehen, worum es geht.

Hier gibt es etwas Interessantes, das genau mit dem im vorigen Abschnitt behandelten Thema zusammenhängt. Zeile 23 deklariert ein Array oder eine Matrix M_1 mit zwei Zeilen und zwei Spalten. In diesem Fall ist das ganz einfach. Das Gleiche gilt für ein Array oder eine Matrix M_2, die keine Definition der Anzahl der Zeilen, aber eine Definition der Anzahl der Spalten hat, deren Anzahl gleich zwei ist. Bis zu diesem Punkt gibt es keine Zweifel oder Probleme; es ist recht einfach zu verstehen, was wir tun, da jede neue Zeile im Code einer neuen Zeile in der Matrix entspricht, und jede neue Spalte in dieser Zeile eine neue Spalte in der Matrix sein wird. Es ist alles ganz einfach. Es gibt jedoch ein Problem, das im Code der Prozedur MatrixA_x_MatrixB liegt. Können Sie das Problem erkennen? Nein? Oder ja? Vielleicht sehen Sie es, aber Sie verstehen es nicht.

Tatsächlich liegt das Problem in der Prozedur MatrixA_x_MatrixB, die für die Matrixmultiplikation zuständig ist. Da es sich hier um eine recht einfache Aufgabe handelt, wird die Implementierung des Codes nicht beeinträchtigt. Dennoch müssen wir das Problem lösen, denn es existiert und bremst unseren Fortschritt. Sobald wir eine komplexere Multiplikation durchführen müssen, wird dies zu einem echten Hindernis.

Wenn Sie das Problem nicht bemerkt haben, achten Sie auf die Variable B. Es handelt sich um eine Matrix, die eine andere Matrix multipliziert. Um das Problem besser zu veranschaulichen, reduzieren wir die Matrix B auf eine Spalte, aber mit zwei Zeilen, da die Matrix A zwei Spalten hat. Um eine Multiplikation durchzuführen, müssen Sie wie in der folgenden Abbildung dargestellt vorgehen.

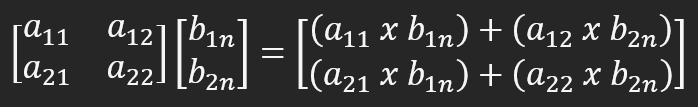
So erhalten wir das richtige Ergebnis. Genau das passiert, wenn Sie eine Matrix multiplizieren oder faktorisieren. Für genauere Informationen empfehle ich Ihnen, diese Ausgabe zu lesen. In beiden Fällen wird die Multiplikation zeilenweise in der Spalte durchgeführt und ergibt den Wert, der in der Spalte verbleibt. Dies geschieht, weil der zweite Faktor eine Spalte ist. Wird die Multiplikation spaltenweise durchgeführt, muss der resultierende Wert in Form von Zeilen angegeben werden.

Auch wenn es scheint, dass alles, was gesagt wurde, Sie nur verwirren kann, ist dies tatsächlich genau die Regel für die Durchführung der Matrixmultiplikation. Wenn ein anderer Programmierer den Code analysiert, wird er nicht sehen, dass alles richtig gemacht wurde. Dies ist das Problem, das in den Zeilen 16 und 17 zu sehen ist, wo die in der obigen Abbildung dargestellte Berechnung durchgeführt werden muss. Aber in Matrix A verwenden wir die zeilenweise Berechnung, und in Matrix B verwenden wir ebenfalls die zeilenweise Berechnung. Das verwirrt uns, obwohl es in diesem einfachen Beispiel die richtigen Daten liefert.

Sie könnten denken: Na und? Wenn alles funktioniert, lassen Sie es so, wie es ist. Aber das ist nicht der Punkt. Wenn Sie irgendwann den Code verbessern müssen, um eine größere Matrix zu handhaben oder einen etwas anderen Fall abzudecken, dann machen wir das Problem viel komplizierter, indem wir versuchen, etwas relativ Einfaches zum Laufen zu bringen. Solche Dinge sollten also richtig gemacht werden, um Verwirrung zu vermeiden. Um dieses Problem zu lösen, müssen wir dieses Modell durch ein etwas anderes ersetzen. Auch wenn es auf den ersten Blick verwirrend erscheinen mag, ist es genau so, wie in der Abbildung oben gezeigt.

Um Verwirrung zu vermeiden, schauen wir uns an, wie man das in einem neuen Thema macht.

Die Dinge einfacher machen

Was wir hier tun werden, mag zwar kompliziert erscheinen, ist es aber nicht, wenn es richtig und mit der nötigen Sorgfalt gemacht wird. Dies könnte etwas mühsamer sein, aber wir werden dies auf eine recht einfache Weise tun. Sehen Sie sich die folgende Abbildung an.

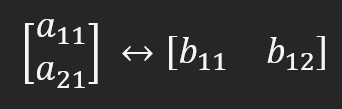
Diese Darstellung zeigt, dass beide Matrizen gleichwertig sind. Das liegt daran, dass die Matrix mit den Elementen A auf der linken Seite eine Zeilenmatrix ist. Bei der Umwandlung in eine Matrix mit B-Elementen auf der rechten Seite, die in diesem Fall eine Spaltenmatrix ist, müssen wir nicht viele Änderungen vornehmen, vielleicht nur eine Drehung oder eine Änderung des Index in einigen Fällen. Es kann jedoch sein, dass wir dies mehr als einmal tun müssen: um eine Zeilenmatrix in eine Spaltenmatrix umzuwandeln und umgekehrt, um Matrizen zu faktorisieren. Aber damit dieses Beispiel richtig ist, muss a11 gleich b11 und a21 gleich b12 sein.

In einigen Fällen werden Sie feststellen, dass keine größeren Änderungen erforderlich sind, sondern nur eine Änderung des Index, die es uns ermöglicht, die Zeilenstruktur in eine der Spalten umzuwandeln. Wie man das richtig macht, hängt jedoch vom jeweiligen Einzelfall ab. Daher ist es wichtig, in den einschlägigen Mathematikbüchern zu lernen, wie die Matrixfaktorisierung durchgeführt wird.

Kehren wir nun zu unserem Code zurück, den wir uns im vorherigen Thema angeschaut haben. Lassen Sie uns zunächst die Darstellung korrigieren. Ändern wir den Code wie unten gezeigt.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double  M_1[]= {
24.                        cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                        -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                    },
27.             M_2[]= {
28.                        0.0,  0.0,
29.                        1.5, -.75,
30.                        1.0,  0.0,
31.                        1.5,  .75
32.                    },
33.            M_3[M_2.Size()];

Beachten Sie, dass wir in den Arrays keine Indizes mehr haben. Die Matrixstruktur wird wie im Code dargestellt erstellt, d. h. Zeilen sind Zeilen und Spalten sind Spalten. Achten Sie jedoch auf dynamische Arrays wie M_3. Wir müssen die zugewiesene Länge korrekt definieren, um RUN-TIME-Fehler beim Zugriff auf die Elemente dieser Matrizen zu vermeiden.

Dies ist der erste Teil. Danach ist die Prozedur MatrixA_x_MatrixB nicht mehr in der Lage zu verstehen, wie man Berechnungen durchführt. Außerdem kann die Schleife in Zeile 42 (siehe Code im vorherigen Thema) die Daten nicht korrekt dekodieren.

Zunächst korrigieren wir die Berechnungen, die in der Prozedur MatrixA_x_MatrixB durchgeführt wurden, und dann korrigieren wir die Darstellung. Bevor wir jedoch fortfahren, sei darauf hingewiesen, dass die Matrix M_1 praktisch unverändert ist, da sie symmetrisch und quadratisch ist. Dies ist einer der Fälle, in denen wir sie sowohl in Zeilen als auch in Spalten lesen können.

Da sich der größte Teil des Codes ändern wird, sehen wir uns den neuen Teil des Codes an. Ich denke, das wird es einfacher machen, zu erklären, wie das Ganze funktionieren wird.

09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[], const ushort Rows, const double &B[], double &R[])
13. {
14.     uint Lines = (uint)(A.Size() / Rows);
15. 
16.     for (uint cbl = 0; cbl < B.Size(); cbl += Rows)
17.         for (uint car = 0; car < Rows; car++)
18.         {
19.             R[car + cbl] = 0;
20.             for (uint cal = 0; cal < Lines; cal++)
21.                 R[car + cbl] += (A[(cal * Rows) + car] * B[cal + cbl]);
22.         }
23. }
24. //+------------------------------------------------------------------+
25. void Plot(const int x, const int y, const double &A[])
26. {
27.     int dx[], dy[];
28. 
29.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
30.     {
31.         ArrayResize(dx, c0 + 1, A.Size());
32.         ArrayResize(dy, c0 + 1, A.Size());
33.         dx[c0] = x + (int)(A[c1++]);
34.         dy[c0] = y + (int)(A[c1++]);
35.     }
36. 
37.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
38.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
39. 
40.     ArrayFree(dx);
41.     ArrayFree(dy);
42. }
43. //+------------------------------------------------------------------+
44. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
45. {
46.     double  M_1[]={
47.                      cos(_ToRadians(angle)), sin(_ToRadians(angle)),
48.                      -sin(_ToRadians(angle)), cos(_ToRadians(angle))
49.                   },
50.             M_2[]={
51.                      0.0,  0.0,
52.                      1.5, -.75,
53.                      1.0,  0.0,
54.                      1.5,  .75
55.                   },
56.            M_3[M_2.Size()];
57.     
58.     MatrixA_x_MatrixB(M_1, 2, M_2, M_3);
59.     ZeroMemory(M_1);
60.     M_1[0] = M_1[3] = size;
61.     MatrixA_x_MatrixB(M_1, 2, M_3, M_2);
62.     Plot(x, y, M_2);
63. }
64. //+------------------------------------------------------------------+

Es scheint, als ob alles viel komplizierter geworden ist. Brauchen wir wirklich diese ganze Verwirrung? Beruhigen Sie sich, lieber Leser. Dieser Code ist weder kompliziert noch verwirrend. Es ist eigentlich sehr einfach und klar. Außerdem ist sie sehr flexibel. Ich werde erklären, warum ich so denke.

In diesem Fragment wird die Multiplikation zwischen zwei Matrizen korrekt durchgeführt. In diesem Fall haben wir ein Spalte-in-Zeile-Modell implementiert, was dazu führte, dass eine neue Zeile als Produkt der Multiplikation entstand. Die Multiplikation erfolgt genau in Zeile 21. Ich weiß, dass das in Zeile 12 beschriebene Verfahren sehr kompliziert erscheinen mag, aber das ist es nicht. Alle diese Variablen dienen dazu, den korrekten Zugriff auf einen bestimmten Index im Array zu gewährleisten.

Da es keine Tests gibt, die sicherstellen, dass die Anzahl der Zeilen in der einen Matrix gleich der Anzahl der Spalten in der anderen ist, müssen wir bei der Verwendung dieses Verfahrens vorsichtig sein, um RUN-TIME-Fehler zu vermeiden.

Nun, da die Matrix A, die in Spalten organisiert sein muss, die Matrix B multipliziert, die in Zeilen organisiert sein muss, und das Ergebnis in die Matrix R eingefügt wird, die in Zeilen organisiert ist, können wir sehen, wie die Aufrufe gemacht werden. Dies geschieht in den Zeilen 58 und 61. Schauen wir uns zunächst die Zeile 58 an. Die erste Matrix, die übergeben wird, ist die Spaltenmatrix M_1. Als zweite Matrix übergeben wir die Matrix M_2, die dynamisch und nach Zeilen organisiert ist. Wenn wir diese Reihenfolge in Zeile 58 ändern, erhalten wir einen Fehler in den berechneten Werten. Ich weiß, es mag seltsam erscheinen, dass 2 x 3 anders ist als 3 x 2, aber bei Matrizen beeinflusst die Reihenfolge der Faktoren das Ergebnis. Beachten Sie jedoch, dass dies ähnlich wie bei der vorherigen Vorgehensweise ist. Natürlich gibt das zweite Argument des Aufrufs die Anzahl der Spalten in der ersten Matrix an. Da unser Ziel hier didaktisch ist, werde ich nicht prüfen, ob es möglich ist, die Matrix B (in diesem Fall M_2) mit der Matrix A (M_1) zu multiplizieren. Ich gehe davon aus, dass Sie die Struktur nicht ändern werden, vielleicht nur die Anzahl der Zeilen in der Matrix M_2 erhöhen, was die Faktorisierung in MatrixA_x_MatrixB nicht beeinflussen wird.

Gut. Die Zeilen 59 und 60 wurden bereits im vorangegangenen Artikel erklärt, und was in Zeile 61 geschieht, entspricht dem, was in Zeile 58 geschieht, sodass wir davon ausgehen können, dass die Erklärung bereits gegeben wurde. In Zeile 62 haben wir jedoch einen neuen Aufruf, der die Prozedur in Zeile 25 aufruft. Mit der Zeile 25 können Sie andere Objekte oder Bilder direkt auf dem Bildschirm darstellen. Alles, was wir tun müssen, ist, dieser Prozedur eine zeilenartige Matrix zu übergeben, wobei jede Zeile einen Scheitelpunkt des zu zeichnenden Bildes darstellt. Die Punkte, die in der Matrix enthalten sein sollten, sollten in der folgenden Reihenfolge angeordnet sein: X in der ersten Spalte und Y in der zweiten, da wir auf einem zweidimensionalen Bildschirm zeichnen. Selbst wenn wir also etwas in 3D zeichnen, müssen wir einige Berechnungen in der Matrix durchführen, damit der Scheitelpunkt in der Z-Dimension auf die XY-Ebene projiziert wird. Wir müssen uns keine Gedanken über die Trennung von Dingen oder die Größe der Matrix machen. Die Methode „Plot“ wird dies tun. Beachten Sie, dass wir in Zeile 27 zwei dynamische Arrays deklarieren. In Zeile 29 erstellen wir eine interessante for-Schleife, die sich von der Art und Weise unterscheidet, wie viele Menschen Schleifen zu schreiben gewohnt sind. In dieser Schleife gibt es zwei Variablen: eine wird von der Schleife gesteuert und die andere befindet sich innerhalb des Codes. Die Variable c0 wird von einer Schleife verwaltet, die versucht, den Index für dx und dy korrekt zu instanziieren und bei Bedarf mehr Speicher zuzuweisen. Dies geschieht in den Zeilen 31 und 32. Dies mag zwar ineffizient erscheinen, aber ein Blick in die MQL5-Dokumentation zeigt, dass dies überhaupt nicht der Fall ist.

Andererseits wird die Variable c1 innerhalb des Codes verwaltet. Um dies zu verstehen, sehen wir uns an, was mit c1 in den Zeilen 33 und 34 geschieht. Jede Iteration erhöht sich um eins. Es ist jedoch c1, das bestimmt, wann die for-Schleife beendet werden soll. Die Bedingung für den Abbruch der Schleife finden Sie in Zeile 29.

Hier wird nicht geprüft, ob das Array oder die Matrix A korrekt strukturiert ist. Wenn wir nicht zwei Spalten in einer Reihe haben, wird an einem bestimmten Punkt in dieser for-Schleife ein RUN-TIME-Fehler erzeugt, der anzeigt, dass versucht wurde, auf eine Position zuzugreifen, die außerhalb des Bereichs liegt. Daher sollten Sie bei der Erstellung der Matrix A vorsichtig sein.

Zum Schluss rufen wir in Zeile 37 eine Methode aus der CCanvas-Klasse auf. Dies geschieht, um die Matrixform auf dem Chart darzustellen. Zeile 38 zeigt die Position des Punktes an, an dem die Aufzeichnung beginnt. Wenn alles gut geht, werden wir das folgende Bild sehen.

Und natürlich geben wir in den Zeilen 40 und 41 den zugewiesenen Speicher an das Betriebssystem zurück, wodurch die zugewiesene Ressource freigegeben wird.

Abschließende Überlegungen

In den letzten beiden Artikeln habe ich versucht, etwas zu behandeln, das vielen Menschen schwerfällt: die Matrixfaktorisierung. Ich weiß, dass das hier vorgestellte Material nicht alle Aspekte und Vorteile der Verwendung von Matrizen in Berechnungen abdeckt. Ich möchte jedoch betonen, dass es sehr wichtig ist, zu verstehen, wie man Methoden zur Berechnung von Matrizen entwickelt. 3D-Programme, einschließlich Spiele und Vektorgrafik-Editoren, verwenden diese Art der Faktorisierung. Selbst scheinbar einfache Programme (z. B. Rasterbildprogramme) verwenden ebenfalls Matrixberechnungen, um die Systemleistung zu optimieren.

In diesen beiden Artikeln habe ich versucht, dies so einfach wie möglich darzustellen, weil ich festgestellt habe, dass viele Neulinge in der Welt des Programmierens einfach ignorieren, dass sie bestimmte Dinge lernen müssen. Oft verwenden sie Bibliotheken oder andere ausgefallene Software, ohne zu wissen, was hinter den Kulissen vor sich geht.

Hier habe ich versucht, den Prozess so weit wie möglich zu vereinfachen. Ich habe mich auf eine Operation konzentriert: die Multiplikation zweier Matrizen. Und um zu zeigen, wie einfach es ist, habe ich nicht gezeigt, wie man die GPU für die Arbeit verwendet, die in der MatrixA_x_MatrixB-Prozedur erledigt wird, was in vielen Fällen der Fall ist. Hier verwenden wir nur die CPU. Im Allgemeinen wird die Matrixfaktorisierung jedoch nicht auf der CPU, sondern auf der GPU durchgeführt, wobei OpenCL für die korrekte Programmierung verwendet wird.

Ich denke, ich habe in gewisser Weise gezeigt, dass wir viel mehr tun können, als manche Leute für möglich halten. Studieren Sie das in den Artikeln vorgestellte Material, denn bald werde ich über ein Thema sprechen, bei dem die Matrixfaktorisierung von grundlegender Bedeutung ist.

Und das letzte Detail, das ich hinzufügen möchte, ist, dass die Multiplikation von zwei Matrizen auf die Lösung eines bestimmten Problems abzielt. Dies ist weit entfernt von der Methode, die traditionell in Büchern oder in der Schule gelehrt wird. Erwarten Sie nicht, dass Sie dieses Faktorisierungsmodell im Allgemeinen verwenden können, denn es wird nicht funktionieren. Es eignet sich nur für die Lösung des vorgeschlagenen Problems, d. h. die Drehung eines Objekts.