Модель глубокого обучения GRU на Python с использованием ONNX в советнике, GRU vs LSTM

Введение

Это продолжение Прогнозирование на основе глубокого обучения и открытие ордеров с помощью пакета MetaTrader 5 python и файла модели ONNX, Если вы не читали эту статью, ничего страшного. Все необходимые моменты буду описаны в текущей. Также все файлы, о которых идет речь, будут прикреплены к статье. Мы с вами шаг за шагом рассмотрим процесс разработки модели GRU, создадим советник для торговли по этой модели и протестируем его.

Машинное обучение — это подраздел искусственного интеллекта, который использует алгоритмы и статистические модели, позволяющие компьютерам выполнять задачи без явного их программирования. Основная цель машинного обучения — дать возможность компьютерам учиться на данных и со временем повышать свою производительность.

Как работают модели

Воспользуемся основными принципами, лежащими в основе работы и применения моделей машинного обучения. Тем, у кого уже есть опыт статистического моделирования или машинного обучения, данный материал может показаться элементарным. Не переживайте, мы быстро перейдем к разработке сложных и надежных моделей.

Для дальнейшей работы возьмем модель дерева решений. Конечно, существуют более сложные модели, обеспечивающие более высокую точность прогнозирования. Однако деревья решений — определенная доступная точка входа, ведь они просты и при этом играют фундаментальную роль в построении даже некоторых продвинутых моделей в области машинного обучения.

Чтобы упростить задачу, давайте начнем с самой элементарной формы дерева решений.

Здесь мы разделяем дома всего на две группы. Ожидаемая цена каждого дома, отвечающего требованиям, рассчитывается на основе исторической средней цены домов той же категории.

Здесь используются данные для определения оптимального метода классификации домов на эти две группы, а затем определяется ожидаемая цена для каждой группы. Этот важный шаг, на котором модель извлекает закономерности из данных, называется обучением модели. Используемый для этого набор данных называется обучающими данными.

Тонкости подбора модели, включая решения по сегментации данных, достаточно сложны. Их мы рассмотрим позже. После настройки модели ее можно применить к новым данным для прогнозирования цен на новые дома.

Улучшение дерева решений

Какое из двух показанных ниже деревьев решений с большей вероятностью появится в результате корректировки обучающих данных при работе с недвижимостью?

Дерево решений слева, очевидно, больше соответствует действительности, поскольку оно отражает корреляцию между количеством спален и более высокими ценами на дома. Однако его главный недостаток заключается в том, что он не учитывает множество других факторов, влияющих на стоимость жилья, таких как количество ванных комнат, размер участка, расположение и т. д.

Чтобы учесть более широкий диапазон факторов, можно использовать дерево с дополнительными «разветвлениями», то есть более глубокое дерево. Например, дерево решений, учитывающее общий размер участка каждого дома, может выглядеть следующим образом:

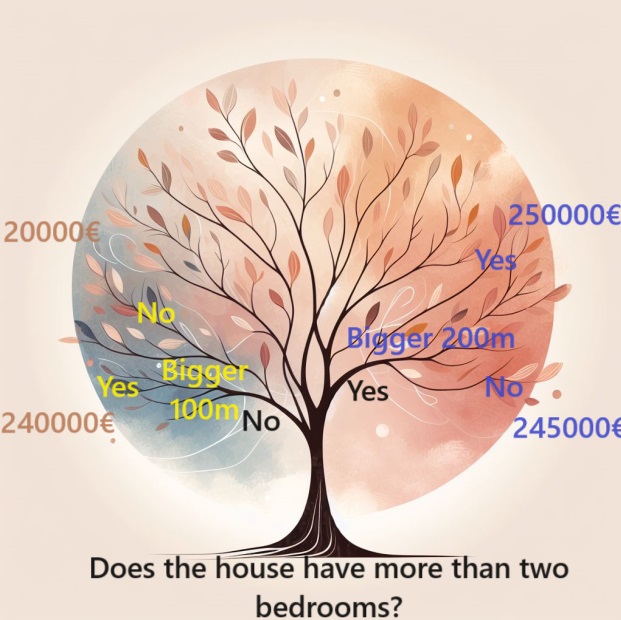
Чтобы оценить цену дома, следуем ветвям дерева решений, всегда выбирая путь в зависимости от конкретных характеристик дома. Прогнозируемая цена дома находится в конце дерева. Эта конкретная точка, где делается прогноз, называется листом.

Разделения и значения на этих листах зависят от данных. В связи с этим, стоит взглянуть на набор данных, с которым мы работаем.

Использование Pandas для данных

На начальном этапе любого проекта машинного обучения вам необходимо ознакомиться с набором данных. Для этого нам просто необходима библиотека Pandas. Специалисты по обработке данных обычно используют Pandas в качестве основного инструмента для изучения и обработки данных. В коде она обычно встречается как pd.

import pandas as pd

Выбор данных для моделирования

Набор данных содержит огромное количество переменных, которые затрудняют понимание основных моментов. Как организовать этот огромный объем данных в более управляемую форму, чтобы лучше понять их?

Первый вариант — выбрать подмножество переменных на основе интуиции. В дальнейшем мы представим статистические методы, которые позволят автоматически расставлять приоритеты переменных.

Чтобы определить переменные или столбцы, которые будут использоваться, сначала необходимо изучить полный список всех столбцов в наборе данных.

Мы импортируем такие данные отсюда:

mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, start_date, end_date)

Построение модели

Лучшим ресурсом для создания моделей является библиотека scikit-learn (sklearn). Scikit-learn часто выбирают для моделирования типов данных, обычно хранящихся в DataFrames.

Вот ключевые этапы создания и использования модели:

• Определяем тип модели, который нужно создать. Будет это дерево решений или другая модель? Вы также определяете конкретные параметры для выбранного типа модели.
• Настраиваем модель. Этот этап является основным, здесь ваша модель изучает и фиксирует закономерности на основе предоставленных данных. Сюда входит обучение модели на вашей выборке.
• Прогнозирование новых или незнакомых данных построенной вами моделью. На этом этапе ваша модель обобщает то, чему научилась, чтобы делать новые обоснованные прогнозы.
• Оценка точности прогнозов вашей модели. На этом важном этапе выходные данные модели сравниваются с фактическими результатами, что позволяет вам оценить, насколько хорошо модель справилась с задачей.

Если вы используете библиотеку scikit-learn, эти шаги создают структурированную основу для эффективного построения, обучения и оценки моделей, адаптированных к различным данным, обычно содержащимся в DataFrames.

Закрытый рекуррентный блок GRU

Wikipedia:

Управляемые рекуррентные блоки(GRU) — механизм ворот для рекуррентных нейронных сетей, представленный в 2014 году Кёнхёном Чо. GRU похожи на модель длинной кратковременной памяти LSTM с механизмом пропускания для ввода или забывания определенных функций, но они не имеют вектора контекста или выходных ворот, благодаря чему они используют меньшее количество параметров, чем LSTM. Было установлено, что эффективность GRU при решении задач моделирования музыки, речевых сигналов и обработки естественного языка аналогична производительности LSTM. Механизм GRU показал, что пропуски в целом действительно полезны. При этом команда Бенджио не пришла к конкретному выводу, какой из двух механизмов лучше.

GRU представляет собой вариант архитектуры рекуррентной нейронной сети (RNN), похожей на LSTM (длинная краткосрочная память).

Как и LSTM, механизм GRU создан для моделирования последовательных данных, обеспечивая выборочное сохранение или пропуск информации во времени. При этом GRU имеет более простую архитектуру по сравнению с LSTM и меньшее количество параметров. Эта особенность повышает простоту обучения и эффективность вычислений.

Основное различие между GRU и LSTM заключается в способе обработке состояния ячейки памяти. В LSTM состояние ячейки памяти отличается от скрытого состояния и обновляется через три типа ворот: входные, выходные и забывания. А GRU заменяет состояние ячейки памяти вектором активации-кандидатом, обновляемым через два типа ворот: сброса и обновления.

Таким образом, GRU может быть более удобной альтернативой LSTM для последовательного моделирования данных, особенно когда имеем дело с вычислительными ограничениями или требуется более простая архитектура.

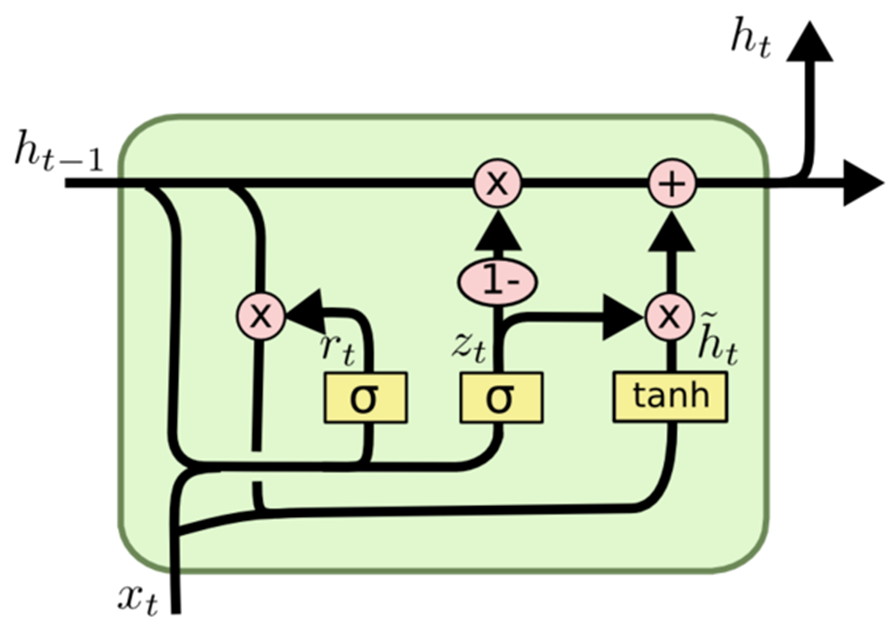
Как работает GRU:

Подобно другим архитектурам рекуррентных нейронных сетей, GRU поэлементно обрабатывает последовательные данные, корректируя свое скрытое состояние на основе текущего ввода и предыдущего скрытого состояния. На каждом временном шаге GRU вычисляет вектор-кандидат, объединяя информацию из входных данных и предыдущего скрытого состояния. Затем этот вектор обновляет скрытое состояние для последующего временного шага.

Вектор-кандидат вычисляется с использованием двух ворот: сброса и обновления. Ворота сброса определяют степень забывания предыдущего скрытого состояния, а ворота обновления влияют на интеграцию вектора активации кандидата в новое скрытое состояние.

Именно эту модель (GRU) мы будем использовать для этой статьи.

model.add(Dense(128, activation='relu', input_shape=(inp_history_size,1), kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(1, activation='linear'))

Сначала выбираем входные данные в функциях и целевую переменную.

if 'Close' in data.columns:
    data['target'] = data['Close']
else:
    data['target'] = data.iloc[:, 0]

# Extract OHLC columns
x_features = data[[0]]
# Target variable
y_target = data['target']

Запускаем данные в обучающие и тестовые выборки.

x_train, x_test, y_train, y_test = train_test_split(x_features, y_target, test_size=0.2, shuffle=False)

Здесь размер тестовой выборки равен 20%, обычно для тестирования тестов выбирают не более 30% (чтобы не переобучать)

Последовательная инициализация модели:

model = Sequential()

Эта строка создает пустую последовательную модель, которая позволяет добавлять слои пошагово.

Добавление плотных слоев:

model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))

Плотный слой — это полностью связный слой нейронной сети.

Цифры в скобках указывают количество нейронов в каждом слое. Таким образом, первый слой состоит из 128 нейронов, второй — из 256, третий — из 128, а четвертый — из 64.

Функция активации relu (Rectified Linear Unit) используется для введения нелинейности после каждого слоя, что помогает модели изучать сложные закономерности.

Параметр input_shape указывается только в первом слое и определяет форму входных данных. В данном случае он равен количеству признаков во входных данных.

kernel_regularizer=l2(k_reg) применяет регуляризацию L2 к весам слоя и помогает предотвратить переобучение, накладывая штраф на большие значения веса.

Выходной слой:

model.add(Dense(1, activation='linear'))

• Последний слой состоит из одного нейрона, что типично для задачи регрессии (прогнозирование непрерывного значения).
• Используется линейная функция активации: выход представляет собой линейную комбинацию входов без дальнейшего преобразования.
• То есть эта модель состоит из нескольких плотных слоев с выпрямленными функциями активации линейной единицы, за которыми следует линейный выходной слой. Для регуляризации к весам применяется L2. Такая архитектура обычно используется для задач регрессии, целью которых является прогнозирование числового значения.

Теперь компилируем модель

# Compile the model[]
model.compile(optimizer='adam', loss='mean_squared_error')

Оптимизатор:

Оптимизатор — важнейший компонент процесса обучения. Он определяет, как обновляются веса модели во время обучения, чтобы минимизировать функцию потерь. Адам — популярный алгоритм оптимизации, достаточно эффективный при обучении нейронных сетей. Он подстраивает скорость обучения для каждого параметра индивидуально и поэтому подходит для широкого круга задач.

Функция потерь:

Параметр потерь определяет цель, которую модель пытается минимизировать во время обучения. В нашем случае в качестве функции потерь используется mean_squared_error. Среднеквадратическая ошибка (MSE) часто используется для задач регрессии. Целью при этом является минимизация среднеквадратической разницы между прогнозируемыми значениями и фактическими значениями. Она подходит для задач, где выходной сигнал представляет собой непрерывное значение. MAE вычисляет среднее значение абсолютных разностей между прогнозируемыми значениями и фактическими значениями.

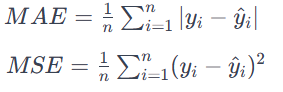
Все ошибки рассматриваются с одинаковой значимостью независимо от их направления. Более низкое значение MAE также означает лучшую эффективность модели.

Итак, оператор model.compile настраивает модель нейронной сети для обучения. Он определяет оптимизатор (Adam) для обновления весов во время обучения и функцию потерь (mean_squared_error). Этот этап компиляции является необходимым предварительным этапом для обучения модели данными.

И мы обучаем ранее определенную модель нейронной сети.

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2, verbose=1)

Обучающие данные:

X_train_scaled — входные данные объекта для обучения, предположительно масштабированные или предварительно обработанные для обеспечения числовой стабильности.

y_train — соответствующие целевые значения или метки для обучающих данных.

Конфигурация обучения:

epochs=int(epoch) — параметр указывает, сколько раз весь набор обучающих данных проводится в прямых и обратных проходах через нейронную сеть.

int(epoch) — указывает, что количество эпох определяется переменной epoch.

batch_size=256 — во время каждой эпохи обучающие данные делятся на пакеты, а веса модели обновляются после обработки каждого пакета. Здесь каждый пакет состоит из 256 точек данных.

Данные для валидации:

validation_split=0.2 — параметр указывает, что 20% обучающих данных используется в качестве набора для тестирования. Эффективность модели на этом наборе отслеживается во время обучения, но не используется для обновления весов.

Визуализация:
verbose=1 — параметр управляет выводом результатов обучения. Значение 1 означает, что прогресс обучения отображается в консоли.

В процессе обучения модель учится делать прогнозы, корректируя свои веса на основе предоставленных входных данных (X_train_scaled) и целевых значений (y_train). Отделение валидационной выборки позволяет оценить эффективность модели на незнакомых данных, при этом ход обучения отображается на основе настроек.

Линейный блок

При работе с нейронными сетями правильно начать изучать их с основного строительного блока — нейрона. Схематически нейрон выглядит так, если он настроен на один входной параметр:

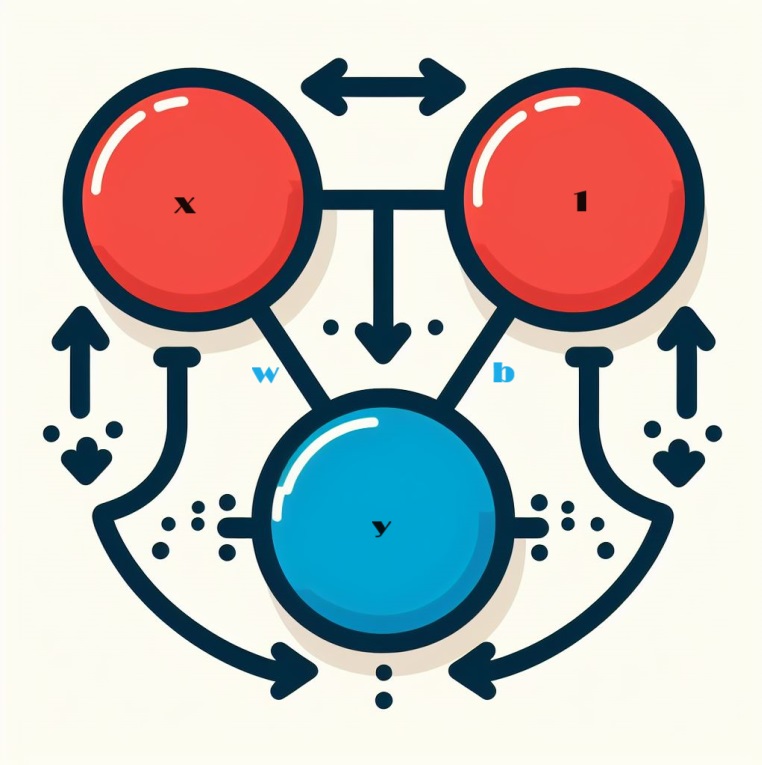
Механика линейного блока

Давайте рассмотрим основной компонент нейронной сети: нейрон. Визуально нейрон с одним входом x представляется следующим образом:

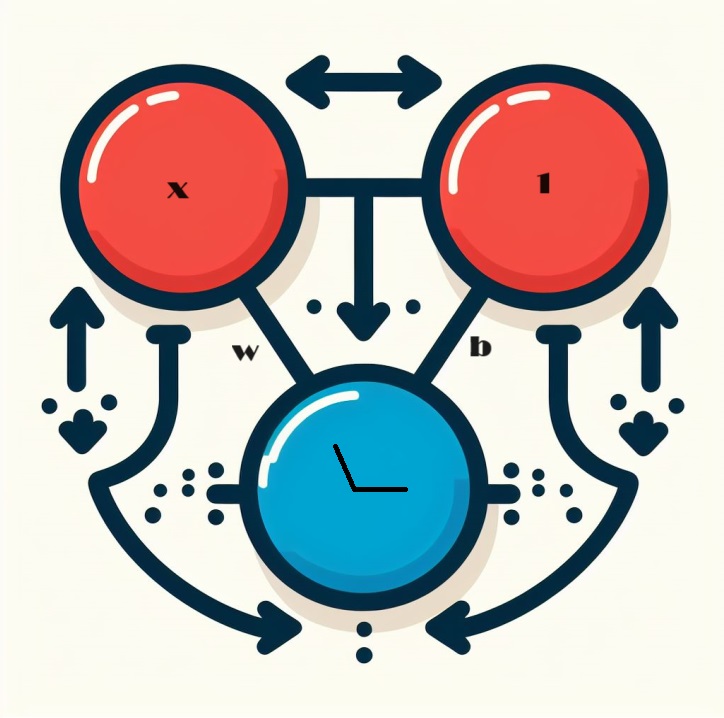
Входной параметр, обозначенный x, образует соединение с нейроном, и этому соединению назначен вес, обозначенный w. Когда информация проходит через это соединение, значение умножается на вес, присвоенный соединению. Если вход это x то, то в конечном итоге до нейрона доходит произведение w * x. Регулируя эти веса, нейронная сеть со временем обучается.

Теперь мы вводим b, особую форму взвешивания, называемую смещением. В отличие от других весов, смещение не имеет связанных с ним входных данных. Здесь в график вставляется значение 1, чтобы гарантировать, что значение, достигающее нейрона, равно просто b (поскольку 1 * b равно b). Вводя смещение, нейрон получает возможность изменять свой выходной сигнал независимо от входных данных.

Y = X*W + b*1

Использование нескольких множества входных данных

А если нам нужно включить больше факторов? Это также довольно легко сделать. Расширив нашу модель, мы можем легко добавлять к нейрону дополнительные входные соединения, каждое из которых соответствует определенной функции.

Чтобы получить результат, выполним несколько простых шагов. Каждый входной параметр умножается на соответствующий вес соединения, а результаты объединяются. В результате получается целостное представление, в котором нейрон умело обрабатывает множество входных данных. Это делает модель более детальной и отражает сложное взаимодействие различных функций. Этот метод позволяет нашей нейронной сети захватывать более широкий спектр информации, повышая ее способность всесторонне распознавать закономерности.

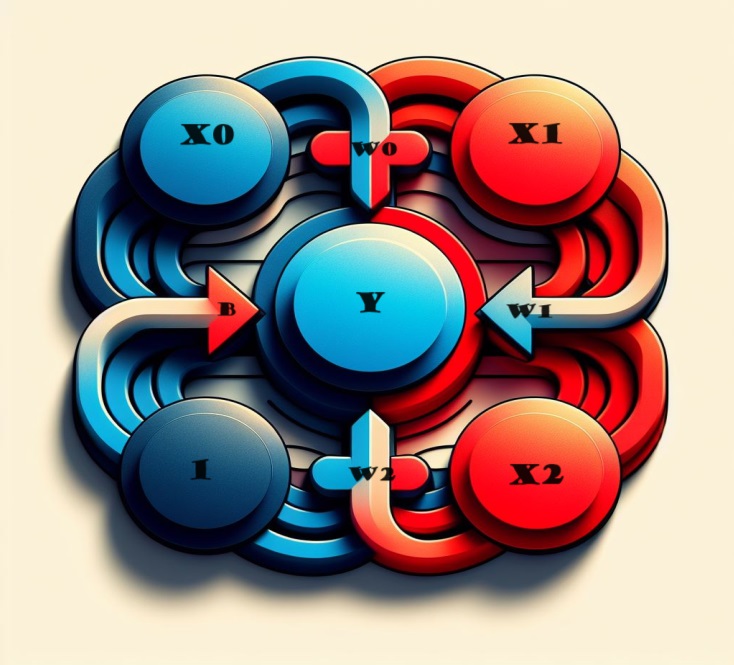
Математически работа этого нейрона кратко описывается формулой:

y = w 0 ⋅ x 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 + b =  y=w0​⋅x0​+w1​⋅x1​+w2​⋅x2​+b

Где:

• y представляет выход нейрона.
• w 0 , w 1 , w 2 обозначают веса, связанные с соответствующими входными данными x 0 , x 1 , x 2.
• b означает смещение.

Этот линейный блок с двумя входами обладает возможностью моделирования плоскости в трехмерном пространстве. Когда количество входных данных превышает два, модуль становится способным подгонять гиперплоскости — многомерные поверхности, которые сложным образом отражают взаимосвязи между несколькими входными объектами. Эта гибкость позволяет нейронной сети ориентироваться и понимать сложные закономерности в данных, выходящие за рамки простых линейных отношений.

Линейные блоки в Keras

Нейронную сеть в Keras можно создать с помощью утилиты `keras.Sequential()`. Она собирает нейронную сеть путем наложения слоев. Это простой и удобный способ создать модель. Архитектура нейронной сети предполагает наличие слоев. Модели, которые мы с вами рассмотрели, строятся из так называемых плотных слоев.

model = Sequential()

В дальнейшем мы углубимся в детали плотного слоя, рассмотрим его возможности и роль в построении архитектур нейронных сетей.

Глубокие нейронные сети

Глубина нейронной сети увеличивается за счет интеграции скрытых слоев. Эти скрытые слои позволяют охватить и выявить сложные взаимосвязи внутри данных, благодаря чему нейросеть может различать и фиксировать сложные закономерности. При добавлении скрытых слоев в модель у нее появляется способность изучать и представлять детализированные функции для более полных и точных прогнозов.

Построение сложных нейронных сетей

Теперь мы переходим к созданию нейронных сетей, способных понимать сложные взаимосвязи. Это относится к глубоким нейронным сетям.

Центральное место здесь занимает концепция модульности — стратегия, которая предполагает объединение сложной сети из элементарных функциональных блоков. Ранее мы увидели, как линейный блок вычисляет линейную функцию. Следующим шагом мы должны перейти к комбинации и адаптации этих отдельных блоков. Комбинируя и модифицируя базовые блоки, сложные нейросети могут понимать более сложные и многогранные отношения, присущие сложным выборкам. Создание нейронных сетей, способных выявлять понимать сложные и тонкие закономерности, относится к сфере глубокого обучения.

Слои нейронных сетей

В сложной архитектуре нейронных сетей нейроны организованы в слои. В этой связи рассматриваемая нами конфигурация плотного слоя представляет собой объединение линейных блоков, имеющих общий набор входных данных.

Такое расположение обеспечивает взаимосвязанную структуру, позволяющую нейронам внутри слоя коллективно обрабатывать и интерпретировать информацию. Конструкция плотного слоя иллюстрирует, как нейроны могут совместно вносить вклад в способность сети понимать и изучать сложные взаимосвязи внутри данных.

 

Слои в Keras

В парадигме библиотеки Keras слой представляет собой довольно универсальную сущность. По сути, он проявляется в любой форме преобразования данных. Есть целый ряд слоев, такие как сверточные и рекуррентные слои, которые используют нейроны для метаморфизации данных, отличающихся главным образом сложными моделями связей, которые они создают. Также есть другие уровни, которые служат различным целям, от проектирования признаков до элементарной арифметики. Таким образом в рамках модульной структуры нейронной сети можно организовать широкий спектр. Многообразие слоев подчеркивает адаптивность и широкие возможности, которые способствуют богатому разнообразию архитектур нейронных сетей.

Расширение возможностей нейронных сетей с помощью функций активации

Удивительно, но объединение двух плотных слоев, лишенных каких-либо промежуточных элементов, не эффективнее, чем одиночный плотный слой. Плотные слои изолированно ограничиваются линейными структурами, которые не могут выйти за границы линий и плоскостей. Чтобы избавиться от этой линейности, мы вводим логичный элемент — нелинейность. Для этого используются функции активации.

При добавлении функции активации в нейронную сеть привносится нелинейность. Такое усложнение модели позволяет ей различать сложные закономерности и взаимосвязи в данных. По сути, функции активации являются катализаторами, которые помогают нейронным сетям улавливать нюансы, присущие различным наборам данных.

Например, если объединить выпрямитель (функция активации) с линейным блоком, в результате получается огромная сущность, известная как выпрямленная линейная единица или ReLU. В целом саму функцию выпрямителя часто называют «функцией ReLU». Применение функции активации ReLU к линейному блоку преобразует выходные данные в max(0, w * x + b). Схематично это можно изобразить так:

Многоуровневое распределение с плотными сетями

Используя вновь изученную нелинейностью, давайте рассмотрим возможности наложения слоев для организации сложных преобразований данных.

Скрытые слои в нейронных сетях

Промежуточные слои, предшествующие выходному слою, часто называют скрытыми слоями, поскольку их выходные данные остаются скрытыми от прямого наблюдения.

Обратите внимание, что конечный (выходной) слой принимает вид линейного блока, не имеющего какой-либо функции активации. Такая архитектура соответствует задачам регрессионного характера, целью которых является прогнозирование числового значения. Однако такие задачи, как классификация, могут потребовать включения функции активации в выходной слой.

Построение последовательных моделей

Последовательная модель, которую мы используем, связывает ряд слоев последовательным образом — от начального до конечного. В этой структуре первый уровень служит получателем входных данных, а последний уровень завершается созданием желаемого результата. Эта последовательная сборка отражает модель, изображенную на иллюстрации выше:

model = keras.Sequential([
    # the hidden ReLU layers
    layers.Dense(units=4, activation='relu', input_shape=[2]),
    layers.Dense(units=3, activation='relu'),
    # the linear output layer 
    layers.Dense(units=1),
])

Для связи слоев нужно представить все слои вместе в списке, например [слой, слой, слой, ...], а не перечислять их по отдельности. Чтобы включить функцию активации в слой, просто укажите ее имя в аргументе активации. Такой подход обеспечивает краткое и организованное представление архитектуры нейронной сети.

Выбор количества блоков в плотном слое

Решение относительно количества блоков в слое Layers.Dense (например, Layers.Dense(units=4, ...) ) зависит от конкретных характеристик рассматриваемой задачи и сложности закономерностей, которые нужно обнаружить в данных. Учитываются следующие факторы:

Сложность задачи:

• Для более простых задач с менее сложными взаимосвязями в данных подходящей отправной точкой может быть меньшее количество блоков, например 4.
• В более сложных сценариях, характеризующихся тонкими и многогранными отношениями, зачастую нужно выбирать больше блоков.

Размер данных:

• Важен размер выборки: большие выборки могут вместить большее количество блоков, на которых модель может учиться.
• Меньшие наборы данных требуют более осторожного подхода, чтобы предотвратить переобучение и потенциальный шум обучения модели.

Емкость модели:

• Количество блоков влияет на способность модели улавливать сложные закономерности, при этом увеличение блоков обычно улучшает такие способности.
• Рекомендуется при этом быть осторожным и избегать чрезмерной параметризации, особенно при работе с ограниченными данными, поскольку это может привести к переобучению.

Эксперименты:

• Экспериментируйте с различными конфигурациями, начиная с небольшого количества блоков обучая модель и уточняя ее на основе эффективности и наблюдений.
• Такие методы, как перекрестная проверка, дают представление об эффективности обобщения модели для различных наборов данных.

Помните, что выбор количества блоков не является универсальным, иногда нудно использовать метод проб и ошибок. Мониторинг производительности модели на валидационной выборке и итеративная корректировка архитектуры также являются неотъемлемыми частями процесса разработки модели.

Мы с вами используем следующий вариант:

model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(1, activation='linear'))

Первый слой (Входной слой):

Блоки (128) — относительно большее количество единиц, 128, в первом слое позволяет модели улавливать разнообразные и сложные закономерности во входных данных. Такое вариант может быть полезным для извлечения сложных признаков на начальных этапах работы сети. Активация — функция активации ReLU вводит нелинейность, позволяя модели учиться на сложных взаимосвязях и закономерностях. Регуляризация (L2) — L2 (kernel_regularizer=l2(k_reg)) помогает предотвратить переобучение, налагая штраф на большие веса в слое.

Второй и третий слои:

Блоки (256 и 128) — поддержание большего количества блоков в последующих слоях (256 и 128) по-прежнему позволяет модели собирать и обрабатывать сложную информацию. Постепенное сокращение количества блоков помогает создать иерархию функций. Активация — также используем ReLU для обеспечения нелинейности на каждом уровне. Регуляризация (L2) — последовательное применение регуляризации L2 на разных уровнях помогает предотвратить переобучение.

Четвертый слой: 

Блоки (64) — сокращение единиц еще больше улучшает представление функций, помогая выделить важную информацию, сохраняя при этом баланс между сложностью и простотой. Активация — снова активация ReLU, сохраняет нелинейные свойства. Регуляризация (L2) — применяется для обеспечения стабильности.

Пятый уровень (выходной уровень):

Блоки (1) — последний слой с одной единицей хорошо подходит для задач регрессии, целью которых является прогнозирование непрерывного числового значения. Активация (linear) — такая активация подходит для регрессии, позволяя модели напрямую выводить прогнозируемое значение без каких-либо дополнительных преобразований.

В целом выбранная архитектура кажется адаптированной для задачи регрессии с продуманным балансом между выразительными возможностями и регуляризацией, чтобы предотвратить переобучение. Постепенное сокращение количества блоков облегчает извлечение иерархических признаков. Такая архитектура предполагает всестороннее понимание сложности задачи и попытку построить модель, которая сможет хорошо обобщать невидимые данные.

Таким образом, постепенное уменьшение количества модулей в скрытых слоях, а также конкретный выбор для каждого слоя предполагает структуру, направленную на сбор иерархических и абстрактных представлений входных данных. Архитектура уравновешивает сложность модели, связанную с необходимостью бороться с переобучением, а выбор количества блоков соответствует характеру текущей задачи регрессии. Конкретные цифры можно определить, поэкспериментировав с настройками на основе эффективности модели на валидационных данных.

Компиляция модели

# Compile the model[]
model.compile(optimizer='adam', loss='mean_squared_error')

Мы рассмотрели создание полностью связанных сетей с использованием стеков плотных слоев. На начальном этапе создания веса сети задаются случайным образом. Это означает, что сети не хватает каких-либо предварительных знаний. Теперь перейдем к процессу обучения нейронной сети.

Как это принято в области машинного обучения, начинаем с тщательно подобранной выборки обучающих данных. Каждый пример в этом наборе данных включает в себя признаки (входные данные) и ожидаемую цель (выходные данные). Суть обучения сети заключается в корректировке ее весов для преобразования входных признаков в точные прогнозы целевых выходных данных.

Обучение сети для такой задачи подразумевает, что ее веса в некоторой степени инкапсулируют взаимосвязь между этими признаками и целью.

Помимо данных обучения, здесь в игру вступают два важнейших компонента:

1. Функция потерь, которая измеряет эффективность прогнозов сети.
2. Оптимизатор, которому поручено говорить сети, как итеративно корректировать ее веса для повышения производительности.

Основная уели при создании нейронной сети — развить ее способности обобщать и делать точные прогнозы на основе незнакомых данных.

Функция потерь

Мы уже рассмотрели архитектурное проектирование сети. Но нам еще предстоит изучить, как же сеть узнает о конкретной проблеме, которую она должна решить. Эта ответственность ложится на функцию потерь.

По сути, функция потерь количественно определяет разницу между истинным значением цели и значением, предсказанным моделью. Она служит критерием оценки того, насколько эффективно прогнозы модели согласуются с фактическими результатами.

Часто используемой функцией потерь в задачах регрессии является средняя абсолютная ошибка (MAE). В контексте каждого прогноза, обозначаемого как y_pred, MAE оценивает отличие от истинного целевого значения y_true путем расчета абсолютной разницы abs(y_true - y_pred).

Совокупная ошибка MAE в выборке рассчитывается как среднее значение всех этих абсолютных различий. Этот показатель обеспечивает комплексную оценку средней величины ошибок прогнозирования, направляя модель к минимизации общего несоответствия между ее прогнозами и истинными целями.

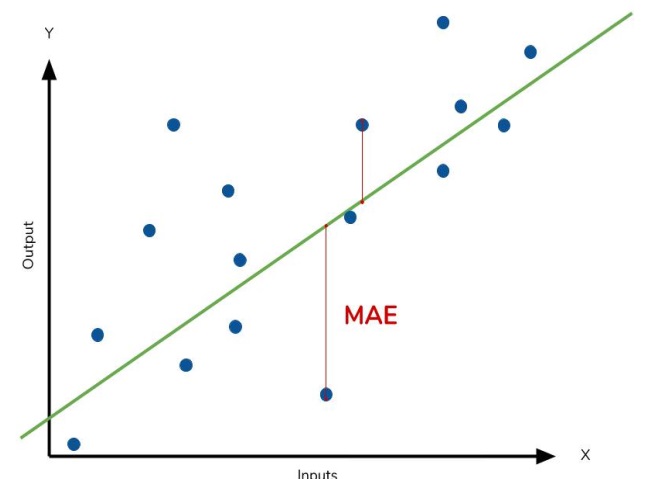
Средняя абсолютная ошибка MAE представляет собой среднее расстояние между подобранной кривой и фактическими точками данных.

Кроме MAE, часто используются и альтернативные функции потерь, например среднеквадратическая ошибка (MSE) и функция потерь Хубера. Они доступны в библиотеке Keras.

На протяжении всего процесса обучения модель использует функцию потерь в качестве ориентира для определения оптимальных значений весов, стремясь к минимально возможным потерям. По сути, функция потерь сообщает о цели сети, направляя ее к обучению и уточнению ее параметров для повышения точности прогнозирования.

Оптимизатор — стохастический градиентный спуск

Следующий шаг, после того как мы определили задачу, которую должна решить сеть, — это определение способа ее решения. Для этого используется оптимизатор — алгоритм, предназначенный для точной настройки весов с целью минимизации потерь.

В области глубокого обучения большинство алгоритмов оптимизации подпадают под действие стохастического градиентного спуска. Это итеративные алгоритмы, которые постепенно обучают сеть. Каждый этап обучения следует такой последовательности:

1. Берем некоторые обучающие данные и вводим их в сеть для генерации прогнозов.
2. Оцениваем потери, сравнив прогнозы с истинными значениями.
3. Корректируем веса в направлении уменьшения потери.

Этот процесс повторяется итеративно до тех пор, пока не будет достигнут желаемый уровень снижения потерь или пока дальнейшее снижение не станет нецелесообразным. По сути, оптимизатор проводит сеть через настройки весов, направляя ее к конфигурации, которая минимизирует потери и повышает точность прогнозирования.

Каждый набор обучающих данных, выбранный в каждой итерации, называется мини-пакетом или просто пакетом. Полный же набор обучающих данных называется эпохой. Указанное количество эпох определяет, сколько раз сеть обрабатывает каждый обучающий пример.

Скорость обучения и размер пакета

На каждом пакете мы видим лишь небольшой сдвиг, а не полную смену данных. Величина этих сдвигов определяется скоростью обучения. Меньшая скорость обучения означает, что сети требуется воздействие большего количества пакетов, прежде чем ее веса установятся на оптимальные значения.

Скорость обучения и размер пакетов влияют на траекторию обучения SGD. Понимание их взаимодействия может быть тонким, и оптимальный выбор не всегда очевиден.

К счастью, для большинства задач исчерпывающий поиск оптимальных гиперпараметров не является обязательным для достижения удовлетворительных результатов. Например, со стохастическим алгоритмом Adam нет необходимости в расширенной настройке параметров. Его способность к самонастраиванию делает его отличным универсальным оптимизатором, подходящим для решения широкого круга задач.

В этом примере мы выбрали ADAM в качестве стохастического градиентного спуска и MSE в качестве функции потерь.

model.compile(optimizer='adam', loss='mean_squared_error')

При обучении

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2, verbose=1)

получим примерно такое:

44241/44241 [==============================] - 247s 6ms/step - loss: 0.0021 - val_loss: 8.0975e-04
Epoch 2/30
44241/44241 [==============================] - 247s 6ms/step - loss: 2.3062e-04 - val_loss: 0.0010
Epoch 3/30
44241/44241 [==============================] - 288s 7ms/step - loss: 2.3019e-04 - val_loss: 8.5903e-04
Epoch 4/30
44241/44241 [==============================] - 248s 6ms/step - loss: 2.3003e-04 - val_loss: 7.6378e-04
Epoch 5/30
44241/44241 [==============================] - 257s 6ms/step - loss: 2.2993e-04 - val_loss: 9.5630e-04
Epoch 6/30
44241/44241 [==============================] - 247s 6ms/step - loss: 2.2988e-04 - val_loss: 7.3110e-04
Epoch 7/30
44241/44241 [==============================] - 224s 5ms/step - loss: 2.2985e-04 - val_loss: 8.7191e-04

Подгонка и недостаточное обучение

Keras ведет учет потерь при обучении и проверке на протяжении всех эпох, пока модель обучается. Мы с вами рассмотрим интерпретацию этих кривых обучения и выясним, как их использовать для улучшения разработки моделей. В частности, мы проанализируем кривые обучения, чтобы выявить признаки недостаточного обучения и переобучения, а также рассмотрим несколько стратегий для решения этих проблем.

Интерпретация кривых обучения:

Информацию в обучающих данных можно разделить на два компонента: сигнал и шум. Сигнал представляет собой обобщающую часть, помогающую нашей модели делать прогнозы на основе новых данных. Шум включает в себя случайные колебания, возникающие на основе реальных данных, и неинформативные закономерности, которые не способствуют прогнозирующим возможностям модели. Очень важно уметь выявлять и понимать шум.

Во время обучения модели мы стремимся выбрать веса или параметры, которые минимизируют потери в обучающем наборе. Но для комплексной оценки эффективности модели необходимо оценить ее на новом наборе данных — валидационной выборке.

Поэтому важно анализировать такие кривые для успешного обучения моделей глубокого обучения.

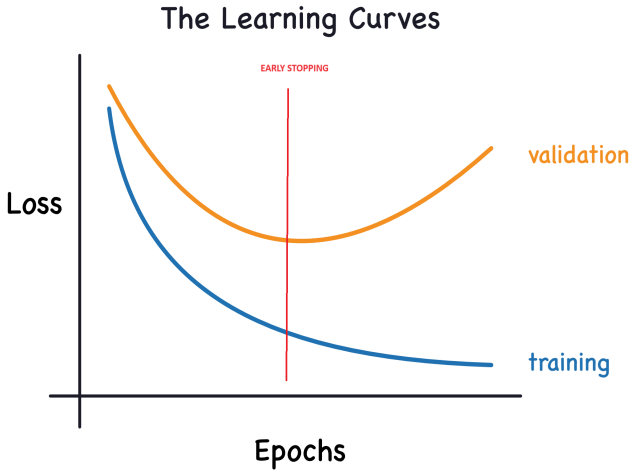
Ошибка на обучении уменьшается, когда модель получает либо сигнал, либо шум. Но на валидационной выборке ошибка уменьшается только тогда, когда модель изучает сигнал, поскольку любой шум, полученный из обучающей выборки, не может быть обобщен на новые данные. Следовательно, когда модель изучает сигнал, обе кривые идут вниз, а шум обучения создает разрыв между ними. Величина этого разрыва указывает на степень шума, полученного моделью.

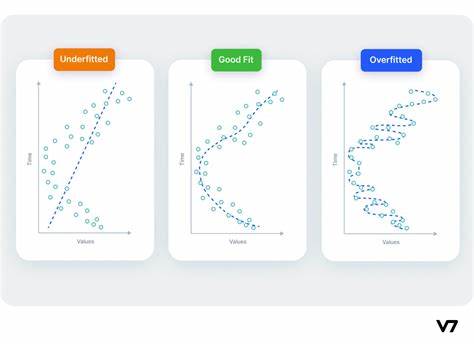
В идеальном мире мы бы стремились построить модель, которая изучает все сигналы и не учитывают шум. Но в реальном мире это практически невозможно. Поэтому мы идем на компромисс. Мы можем побудить модель изучить больше сигналов за счет получения большего количества шума. Пока этот компромисс нам выгоден, ошибка на валидации будет продолжать уменьшаться. Затем наступает момент, когда компромисс становится невыгодным, затраты перевешивают выгоду, и ошибки на валидационной выборке начинают увеличиваться.

Этот компромисс подчеркивает две потенциальные проблемы при обучении модели: недостаточный сигнал и чрезмерный шум. Недообучение происходит, когда потери нет минимизации ошибки из-за того, что модель не усвоила достаточно сигнала. Переобучение происходит, когда ошибка не уменьшается из-за того, что модель поглотила слишком много шума. Поэтому наша цель — найти оптимальный баланс между этими двумя вариантами.

График теперь будет выглядеть так:

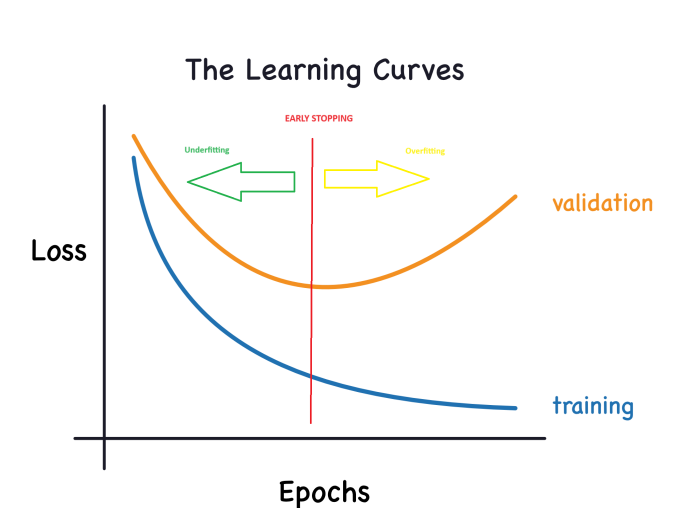
Емкость модели:

Емкость модели влияет на ее способность модели улавливать и понимать сложные закономерности. В контексте нейронных сетей на это преимущественно влияет количество нейронов и их взаимосвязанность. Если кажется, что ваша сеть неадекватно улавливает сложность данных (недообучена), рассмотрите возможность увеличения ее емкости.

Возможности сети можно увеличить либо за счет ее расширения (добавление дополнительных устройств к существующим уровням), либо за счет ее углубления (включение большего количества слоев). Более широкие сети превосходно справляются с изучением более линейных отношений, тогда как более глубокие сети склонны улавливать больше нелинейных закономерностей. Выбор зависит от характера выборки.

Ранняя остановка:

Как обсуждалось ранее, когда модель включает много шума во время обучения, ошибка при валидации может начать расти. Чтобы обойти эту проблему, можно добавить раннюю остановку — метод, при котором мы останавливаем процесс обучения, как только становится очевидно, что ошибка на валидационных данных больше не уменьшается. Такое вмешательство помогает предотвратить переобучение и гарантирует, что модель хорошо обобщается на новые данные.

Как только заметили рост ошибки при валидации, можно сбросить веса до точки, где был зафиксирован минимум. Таким образом, что модель не будет постоянно обучаться шуму. Это способ избежать переобучения.

Реализация обучения с ранней остановкой также снижает риск преждевременной остановки процесса обучения до того, как сеть полностью уловит сигнал. Помимо борьбы переобучением из-за чрезмерно длительного обучения, ранняя остановка служит защитой от недостаточной подготовки, вызванной недостаточной продолжительностью периода обучения. Можно установить довольно большое количество эпох обучения (больше, чем требуется), а ранняя остановка позволит управлять завершением на основе изменения ошибки при валидации.

Интеграция ранней остановки:

В Keras включение ранней остановки в наше обучение осуществляется посредством callback-вызова. Callback — это, по сути, функция, которая выполняется через регулярные промежутки времени в процессе обучения сети. Такая функция для раннего обучения срабатывает после каждой эпохи. В Keras есть ряд предопределенных callback-вызовов, а также вы можете создавать собственные запросы для конкретных требований.

Код с использованием Keras:

from tensorflow import keras
from tensorflow.keras import layers, callbacks

early_stopping = callbacks.EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2,callbacks=[early_stopping], verbose=1)

А также мы добавили больше блоков и еще один скрытый слой (после настройки модель в .py становится более сложной).

model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(1, activation='linear'))

Эти параметры содержат следующую инструкцию: «Если ошибка при валидации не улучшатся хотя бы на 0,001 за предыдущие 20 эпох, останавливаем обучение и сохраняем наиболее эффективную модель, найденную к данному моменту». Определить, увеличивается ли ошибка при валидации из-за переобучения или просто случайных изменений в пакете, иногда может быть непросто. Указанные параметры позволяют устанавливать определенные допуски, указывая системе, когда следует остановить процесс обучения.

У нас установлено количество эпох 300 в надежде на более раннее завершение процесса обучения.

Работа с пропусками

Различные обстоятельства могут привести к наличию пропусков в выборке.

При работе с библиотеками машинного обучения, такими как scikit-learn, попытка построить модель с использованием данных с пропусками обычно приводит к ошибке. Следовательно, для решения этой проблемы необходимо принять одну из следующих стратегий.

Три подхода

1. Оптимизированное решение (отбросить nan) — исключить столбцы с пропущенными значениями. Несложный подход предполагает удаление столбцов, содержащих пропущенные значения.

df2 = df2.dropna()

Однако, если значительная часть значений в отброшенных столбцах отсутствует, выбор этого подхода приводит к тому, что модель теряет доступ к значительному объему потенциально ценной информации. Для иллюстрации представьте себе набор данных из 10 000 строк, в котором в важном столбце отсутствует только одна запись. По этой стратегии у нас будет удаление всего столбца.

2) Улучшенная альтернатива: импутация

Импутация включает заполнение пропущенных значений конкретными числовыми значениями. Например, можно указать среднее значение по каждому столбцу.

Хотя в большинстве случаев добавленное значение может быть неточным, этот метод обычно дает более точные модели по сравнению с полным отбрасыванием строки.

3) Развитие методов импутации

Этот традиционный подход часто оказывается эффективным. Тем не менее условно исчисленные значения могут систематически отклоняться от истинных значений (отсутствующих в наборе данных). Кроме того, строки с пропущенными значениями могут иметь разные характеристики. В таких случаях улучшение вашей модели с учетом оригинальности пропущенных значений может повысить точность прогноза.

В этой методологии мы продолжаем добавлять пропущенные значения, как описано ранее. Дополнительно для каждого столбца с отсутствующими записями в исходном наборе данных мы вводим новый столбец, указывающий позиции добавленных записей.

Хотя этот метод может значительно улучшить результаты в определенных сценариях, его эффективность может быть разной, а в некоторых случаях он может не дать никакого улучшения.

Вывод модели ONNX

1 Загрузка данных.

У нас есть базовое представление о файле .py, который мы создали для обучения модели. Теперь приступим к его обучению. 

Записываем пути:

# get rates
eurusd_rates = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, start_date, end_date)

# create dataframe
df = pd.DataFrame(eurusd_rates)

Вот как в итоге выглядит код (GRU_create_model.py):

При обучении получаем такие результаты:

Mean Squared Error: 0.0031695919830203693

Mean Absolute Error: 0.05063149001883482

R2 Score: 0.9263800140852619
Baseline MSE: 0.0430534174061265
Baseline MAE: 0.18048216851868318
Baseline R2 Score: 0.0

Как и в статье Прогнозирование курса валют Форекс с использованием глубоких рекуррентных нейронных сетей, результаты для GRU и LTSM аналогичны. 

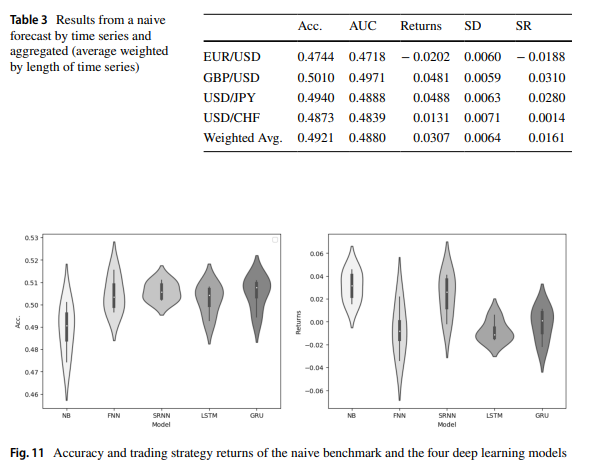
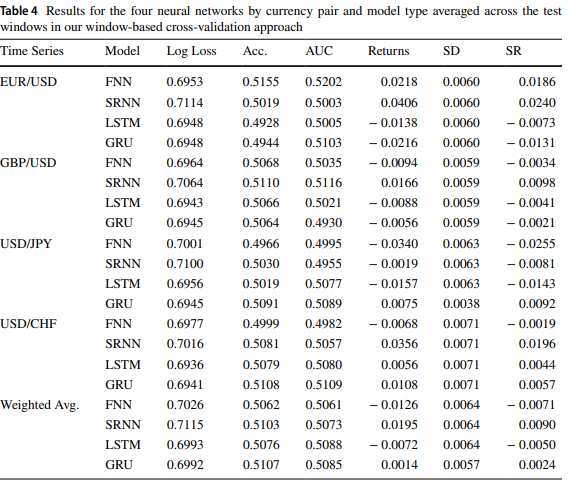
После запуска ONNX_GRU.py мы получим модель ONNX в той же папке, где находится файл Python для обучения (ONNX_GRU.py). Эту модель ONNX необходимо сохранить в папке MQL5 Files, чтобы можно было вызывать ее из советника.

Советник доступен в приложениях к статье.

Так можно протестировать модель с помощью тестера стратегий или даже использовать ее в торговле.

Сравнения LSTM и GRU

Ячейка LSTM поддерживает состояние ячейки, из которого она одновременно считывает и записывает. Механизм включает в себя четыре типа ворот, которые управляют процессами чтения, записи и вывода значений в состояние ячейки и обратно в зависимости от входных значений и значений состояния ячейки. Начальные ворота определяют информацию, которую скрытое состояние должно забыть. Последующие ворота отвечают за идентификацию записываемого сегмента состояния ячейки. Третьи ворота определяют содержимое, которое необходимо записать. Наконец, последние ворота извлекают информацию из состояния ячейки для генерации выходных данных.

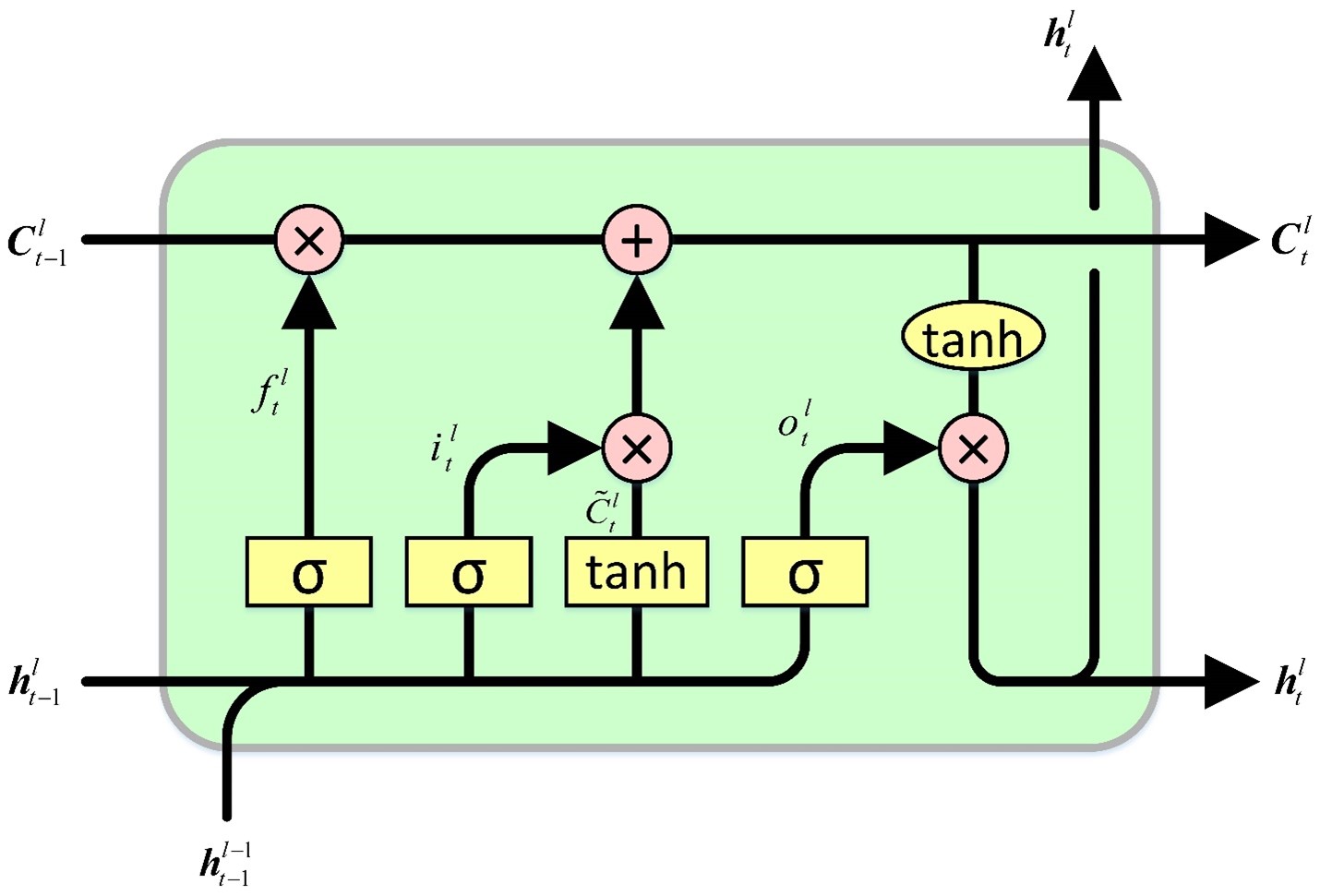
Ячейка GRU имеет сходство с ячейкой LSTM, но имеет несколько существенных отличий. Во-первых, в нем отсутствует скрытое состояние, поскольку функциональность скрытого состояния в конструкции ячейки LSTM предполагается состоянием ячейки. Поэтому процессы принятия решения о том, что забывает состояние ячейки и в какую часть состояния ячейки записывается, объединяются в единые ворота. Затем записывается только та часть состояния ячейки, которая была стерта. Наконец, все состояние ячейки служит выходными данными, в отличие от ячейки LSTM, которая выборочно считывает состояние ячейки для генерации выходных данных. Так получается более простая конструкция с меньшим количеством параметров по сравнению с LSTM. Однако снижение параметров потенциально может привести к снижению выразительных способностей.

Экспериментальное сравнение

GRU

# Split the data into training and testing sets
x_train, x_test, y_train, y_test = train_test_split(x_features, y_target, test_size=0.2, shuffle=False)


# Standardize the features StandardScaler()
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(x_train)
X_test_scaled = scaler.transform(x_test)

scaler_y = StandardScaler()
y_train_scaled = scaler_y.fit_transform(np.array(y_train).reshape(-1, 1))
y_test_scaled = scaler_y.transform(np.array(y_test).reshape(-1, 1))

# Define parameters

learning_rate = 0.001
dropout_rate = 0.5
batch_size = 1024
layer_1 = 256
epochs = 1000
k_reg = 0.001
patience = 10
factor = 0.5
n_splits = 5  # Number of K-fold Splits
window_size = days  # Adjust this according to your needs

def create_windows(data, window_size):
    return [data[i:i + window_size] for i in range(len(data) - window_size + 1)]

custom_optimizer = Adam(learning_rate=learning_rate)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=factor, patience=patience, min_lr=1e-26)

def build_model(input_shape, k_reg):
    model = Sequential()
    
    layer_sizes = [ 512,1024,512, 256, 128, 64]
    model.add(Dense(layer_1, kernel_regularizer=l2(k_reg), input_shape=input_shape))
    for size in layer_sizes:
        model.add(Dense(size, kernel_regularizer=l2(k_reg)))
        model.add(BatchNormalization())
        model.add(Activation('relu'))
        model.add(Dropout(dropout_rate))

    model.add(Dense(1, activation='linear'))
    model.add(BatchNormalization())
    model.compile(optimizer=custom_optimizer, loss='mse', metrics=[rmse()])
    
    return model



# Define EarlyStopping callback
early_stopping = EarlyStopping(monitor='val_loss', patience=patience, restore_best_weights=True)

# KFold Cross Validation
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=42)
history = []
loss_per_epoch = []
val_loss_per_epoch = []

for train, val in kfold.split(X_train_scaled, y_train_scaled):
    x_train_fold, x_val_fold = X_train_scaled[train], X_train_scaled[val]
    y_train_fold, y_val_fold = y_train_scaled[train], y_train_scaled[val]
    
    # Flatten the input data
    x_train_fold_flat = x_train_fold.flatten()
    x_val_fold_flat = x_val_fold.flatten()

    # Create windows for training and validation
    x_train_windows = create_windows(x_train_fold_flat, window_size)
    x_val_windows = create_windows(x_val_fold_flat, window_size)

    # Rebuild the model
    model = build_model((window_size, 1), k_reg)

    # Create a new optimizer
    custom_optimizer = Adam(learning_rate=learning_rate)
    
    # Recompile the model
    model.compile(optimizer=custom_optimizer, loss='mse', metrics=[rmse()])
    
    hist = model.fit(
        np.array(x_train_windows), y_train_fold[window_size - 1:],
        epochs=epochs,
        validation_data=(np.array(x_val_windows), y_val_fold[window_size - 1:]),
        batch_size=batch_size,
        callbacks=[reduce_lr, early_stopping]
    )
    history.append(hist)
    loss_per_epoch.append(hist.history['loss'])
    val_loss_per_epoch.append(hist.history['val_loss'])




mean_loss_per_epoch = [np.mean(loss) for loss in loss_per_epoch]
val_mean_loss_per_epoch = [np.mean(val_loss) for val_loss in val_loss_per_epoch]

print("mean_loss_per_epoch", mean_loss_per_epoch)
print("unique_min_val_loss_per_epoch", val_loss_per_epoch)

# Create a DataFrame to display the mean loss values
epoch_df = pd.DataFrame({
    'Epoch': range(1, len(mean_loss_per_epoch) + 1),
    'Train Loss': mean_loss_per_epoch,
    'Validation Loss': val_loss_per_epoch
})

LSTM

model = Sequential()
model.add(Conv1D(filters=256, kernel_size=2, activation='relu',padding = 'same',input_shape=(inp_history_size,1)))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100, return_sequences = True))
model.add(Dropout(0.3))
model.add(LSTM(100, return_sequences = False))
model.add(Dropout(0.3))
model.add(Dense(units=1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss= 'mse' , metrics = [rmse()])

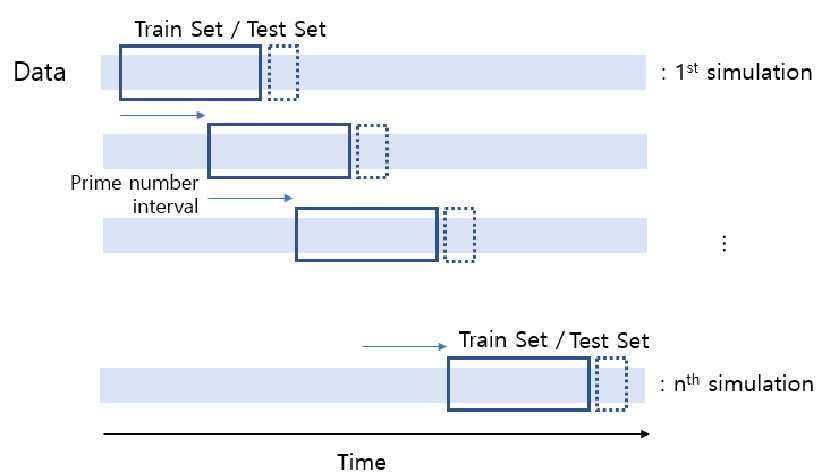
К статье прикреплен файл .py для сравнения LSTM и GRU, а также cross validation.py.

Также есть GRU simple.py для создания моделей ONNX.

Используя простую модель GRU, получаем такие результаты за январь 2024 года.

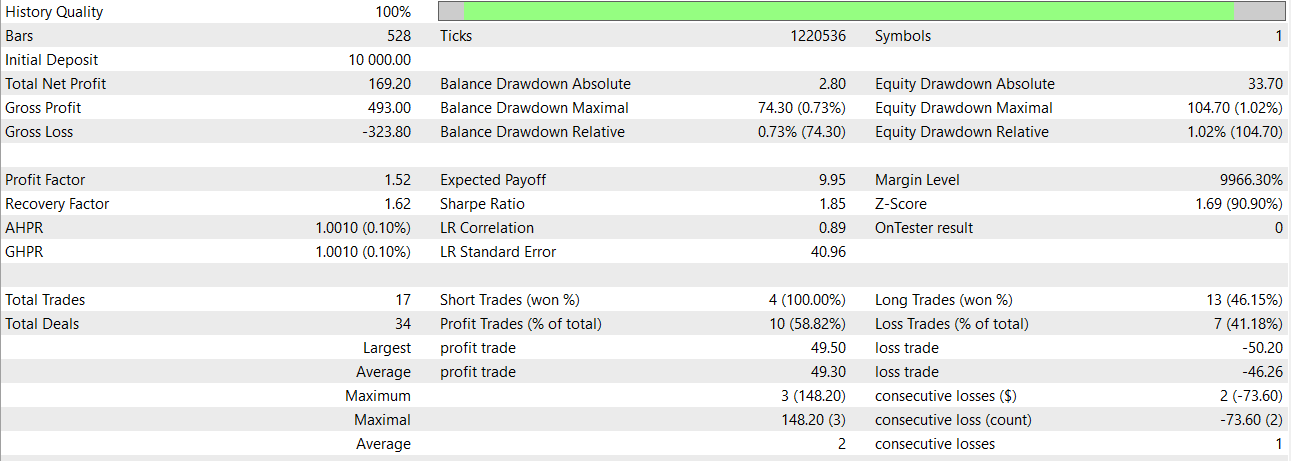
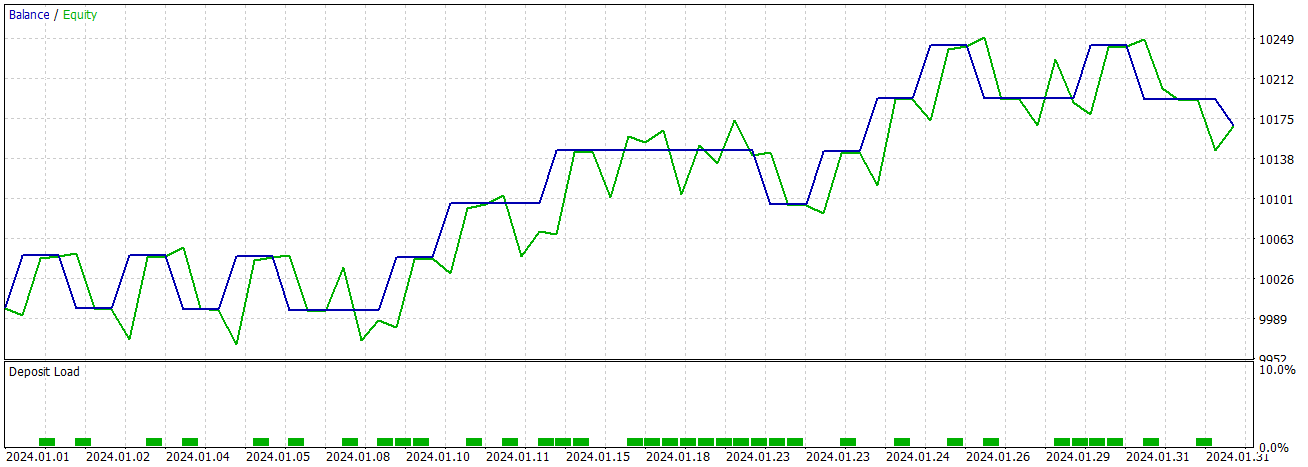
Заключение и будущая работа

Это сравнение поможет определить, какую модель использовать в том или ином случае. Мы также можем рассмотреть возможность использования обеих моделей. Этот подход позволяет извлекать важную информацию из моделей, несмотря на присущие различия в размерах пакетов и конфигурациях слоев. При одинаковых условиях модель GRU работает быстрее.

В рамках будущей работы было бы полезно изучить различные ядра и рекуррентные инициализаторы, адаптированные к каждому типу ячеек, для потенциального повышения производительности.

Хорошим подходом к торговле моделями ONNX будет интеграция обеих моделей в один советник. Рекомендую прочесть статью: Пример ансамбля ONNX-моделей в MQL5.

Заключение

Модели вроде GRU способны давать хорошие результаты и выглядят вполне надежными. Надеюсь, вам понравилась эта статья. В статье представлено сравнение моделей GRU и LSTM. Также добавлен код на питоне, который поможет остановить эпохи (принимая во внимание количество входных данных).

Примечание

Прошлые результаты не гарантируют будущих результатов.