MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
在 MQL5 中实现增广迪基–富勒检验

在 MQL5 中实现增广迪基–富勒检验

MetaTrader 5 — 示例 | 6 八月 2024, 09:30
465 0
Francis Dube
Francis Dube

概述

增广迪基–富勒（ADF）检验是评估时间序列是否静止的常用程序。  尽管众所周知，金融时间序列本质上是非平稳的。许多受益于平稳性的统计方法通常要求在分析非平稳数据集之前以某种方式进行转换。ADF 检验可用于评估这些转换在诱导平稳性方面的功效。或者，评估序列的协整性也利用了平稳性检验。可用于开发利用相关金融工具定价差异的交易策略。在本文中，我们将介绍使用纯 MQL5 实现 ADF 检验，并通过在 MetaTrader 5 中识别协整交易品种来演示其应用。


理解 ADF 检验

简单地说，ADF检验是一种假设检验，它使我们能够确定观察到的数据的特定特征是否具有统计学意义。在这种情况下，所要确定的特征是序列的平稳性。  统计假设是对样本所代表的数据集所做的假设。我们只能通过处理整个数据集来了解真正的真相，但出于某些原因，这通常是不可能的。因此，对数据集的一个样本进行测试，是为了对整个数据集进行假设。这里需要记住的重要一点是，在使用样本时，统计假设的真实性永远无法确定。我们得到的是一个假设，可能是真的也可能是假的。

有趋势的非平稳数列

在 ADF 检验中，我们考虑了两种情况：

  • 时间序列中存在单位根的零假设。
  • 时间序列中不存在单位根的备择假设。

在时间序列分析中，单位根是序列数据集的一个特殊特征。想象一下，一个人牵着狗走在街上。这个人可能会沿着一条相当直的直线向目的地走去。虽然狗狗经常会走来走去，去嗅一些东西或追逐一些吸引它注意的小动物，但它最终还是会跟着主人走。如果绘制出狗的运动轨迹，我们就能观察到某种振荡。狗四处游荡，但最终又回到了人所遵循的预期大方向。

狗路径上的任意点代表变量在特定时间的值。如果我们对这些值进行评估，它们很可能会保持在中心趋势附近的一定范围内。统计特性不会随时间发生显著变化。这样的序列不会有单位根。现在再想象一下，如果这个人在同一条街上遛他那只没有受过训练的狗。狗很可能会跑掉，再也不会回到主人身边。与这只狗所走路径相关的数值会发生不可预知的变化。这样的序列会有单位根。

有水平变化的序列

单位根的概念来自随机过程的特征方程。随机过程是以时间为索引的变量序列，描述了一个随机演变的系统。随机过程的特征方程就是捕捉系统特性的方程。单位根是特征方程等于 1 的解。如果一个过程有单位根，就意味着冲击或随机效应对该过程有持续影响。这种系统采用随机效应和滞后值建模。这意味着它具有自回归的性质。

因此，ADF 检验使用回归模型来检验单位根。该模型最常见的形式如以下公式所示。

自回归公式

其中：

  • "Y" 时间序列的第一个差值
  •  "a" 一个常数项
  •  "b" 时间序列的滞后水平系数
  •  "x" 时间趋势系数 (t)
  •  "V" 滞后第一差异系数
  •  "E" 误差项

测试的重点是系数 "b"。如果 "b"=0，则存在单位根；如果 "b"<0，则时间序列是平稳的。ADF 统计量是根据 "b" 的估计值及其标准误差计算得出的。它与 Dickey-Fuller 分布的临界值进行了比较。如果ADF统计量在特定显著性水平上比临界值更负，则单位根的零假设被拒绝。这意味着序列是平稳的。


实现

为了确保我们的实现是准确的，我们将使用现有的 Python ADF 检验实现作为参考。在 'statsmodels' Python 软件包中，'adfuller' 函数用于执行 ADF 检验。

adfuller(x, maxlag: 'int | None' = None, regression='c', autolag='AIC', store=False, regresults=False)


该函数首先使用普通最小二乘法估计输入序列的自回归模型的参数。然后根据估计参数计算检验统计量，它用于计算 p 值。再从代表置信度的分布表中得出三个临界值。最后，可以将检验统计量与这些值中的任何一个进行比较，以确定序列是否平稳。

根据上述概述，我们必须实现三个重要组成部分。首先是普通最小二乘回归模型。这可能是最重要的部分，因为这里的任何误差都会传播到检验的其他阶段。这将用于确定所分析序列的最合适的自回归模型。除了模型参数，我们还需要计算模型的各种属性，如 Akaike 信息准则和贝叶斯信息准则。

第二部分是关于 p 值计算的。p 值由最优自回归模型的 t 统计量得出的检验统计量决定。t 统计量是用来确定两组平均值之间是否存在显著差异的指标。计算方法是取样本平均值之间的差值除以差值的标准差。在这种情况下，t 统计量的计算方法是用模型参数除以模型的标准差。计算 p 值的方法是由 J.G.MacKinnon 提出的 ，因此称为 MacKinnon 近似 p 值法。它提供了与统计检验临界值相关的 p 值近似值。

完成 ADF 检验的最后一个组件是计算临界值。这些数值是根据 MacKinnon 撰写的一篇工程论文中的近似值得出的。

//+------------------------------------------------------------------+
//| Ordinary least squares class                                     |
//+------------------------------------------------------------------+
class OLS
  {
private:
   matrix m_exog,               //design matrix
          m_pinv,               //pseudo-inverse of matrix
          m_cov_params,         //covariance of matrix
          m_m_error,            //error matrix
          m_norm_cov_params;    //normalized covariance matrix
   vector m_endog,              //dependent variables
          m_weights,            //weights
          m_singularvalues,     //singular values of solution
          m_params,             //coefficients of regression model(solution)
          m_tvalues,            //test statistics of model
          m_bse,                //standard errors of model
          m_resid;              //residuals of model
   ulong  m_obs,                //number of observations
          m_model_dof,          //degrees of freedom of model
          m_resid_dof,          //degrees of freedom of residuals
          m_kconstant,          //number of constants
          m_rank;               //rank of design matrix
   double m_aic,                //Akiake information criteria
          m_bic,                //Bayesian information criteria
          m_scale,              //scale of model
          m_llf,                //loglikelihood of model
          m_sse,                //sum of squared errors
          m_rsqe,               //r-squared of model
          m_centeredtss,        //centered sum of squares
          m_uncenteredtss;      //uncentered sum of squares
   uint              m_error;              //error flag
   // private methods
   ulong             countconstants(void);
   void              scale(void);
   void              sse(void);
   void              rsqe(void);
   void              centeredtss(void);
   void              uncenteredtss(void);
   void              aic(void);
   void              bic(void);
   void              bse(void);
   void              llf(void);
   void              tvalues(void);
   void              covariance_matrix(void);


public:
   //constructor
                     OLS(void);
   //destructor
                    ~OLS(void);
   //public methods
   bool              Fit(vector &y_vars,matrix &x_vars);
   double            Predict(vector &inputs);
   double            Predict(double _input);
   //get properties of OLS model
   ulong             ModelDOF(void) { if(m_error) return 0; else return m_model_dof;}
   ulong             ResidDOF(void) { if(m_error) return 0; else return m_resid_dof;}
   double            Scale(void)  { if(m_error) return EMPTY_VALUE; else return m_scale;    }
   double            Aic(void)    { if(m_error) return EMPTY_VALUE; else return m_aic;      }
   double            Bic(void)    { if(m_error) return EMPTY_VALUE; else return m_bic;    }
   double            Sse(void)    { if(m_error) return EMPTY_VALUE; else return m_sse;    }
   double            Rsqe(void)   { if(m_error) return EMPTY_VALUE; else return m_rsqe;   }
   double            C_tss(void)  { if(m_error) return EMPTY_VALUE; else return m_centeredtss;}
   double            Loglikelihood(void) { if(m_error) return EMPTY_VALUE; return m_llf; }
   vector            Tvalues(void) { if(m_error) return m_m_error.Col(0); return m_tvalues; }
   vector            Residuals(void) { if(m_error) return m_m_error.Col(0); return m_resid; }
   vector            ModelParameters(void) { if(m_error) return m_m_error.Col(0); return m_params; }
   vector            Bse(void) { if(m_error) return m_m_error.Col(0);  return m_bse; }
   matrix            CovarianceMatrix(void) { if(m_error) return m_m_error; return m_cov_params; }
  };

OLS.mqh 包含 OLS 类的定义，代表普通最小二乘法回归模型。该类有几个公有方法。第一个方法是 "Fit()"，这是用户在创建该类实例后应该调用的第一个方法。它需要输入一个向量和一个矩阵。向量 "y_vars" 应填入依赖值，"x_vars" 是设计矩阵。"Fit()" 执行成功后将返回 true，此时可以调用任何其他公有方法。所有这些方法都会返回计算模型的特定属性。下表概述了这些属性。

返回数据类型
 错误时返回的值 方法
 描述
ulong
0
 ModelDOF()
 模型的自由度
ulong
 0
 ResidDOF()
 模型残差的自由度
double
 EMPTY_VALUE
 Scale()
 这是误差项的方差，表示自变量无法解释的因变量的可变性
double
 EMPTY_VALUE
Aic()
 Akaike 信息标准
double
EMPTY_VALUE
 Bic()
 贝叶斯信息标准
double
 EMPTY_VALUE
Sse()
 模型的平方差之和
double
 EMPTY_VALUE
Rsqe()
 这是模型的 R 方指标，即决定系数
double
 EMPTY_VALUE
C_tss()
 即以平均值为中心的平方差总和
double
 EMPTY_VALUE
Loglikelihood()
 OLS 模型的似然函数
vector
 空值向量
Tvalues()
 提供模型各参数估计的 t 统计量
vector
 空值向量
Residuals()
 模型的残差，即预测值与实际值之差
vector
 空值向量
Bse()
 参数估计的标准误差
matrix
 空值矩阵
CovarianceMatrix()
 显示变量方差和变量间协方差的矩阵

 "Predict()" 有两个重载，它们的输入数据类型各不相同。其中要么是一个向量，要么是一个 double 类型的标量值。两者都是在给定新的自变量的情况下，返回单一的预测值。

我们的下一部分实现工作将转移到 ADF.mqh 文件。该文件将包含一系列与 ADF 检验相关的函数定义。其中一个函数将是 "adfuller()"。我们要包含 OLS 类的 OLS.mqh、标准库中的 Math.mqh，以及 Alglib 库中的 specialfunctions.mqh。

//+------------------------------------------------------------------+
//|                                                          ADF.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\specialfunctions.mqh>
#include<OLS.mqh>

我们的下一部分实现工作将转移到 ADF.mqh 文件。该文件将包含一系列函数定义以及 CAdf 类的函数定义。我们要包含 OLS 类的 OLS.mqh、标准库中的 Math.mqh，以及 Alglib 库中的 specialfunctions.mqh。ADF.mqh 首先定义了一些枚举。ENUM_INFO_CRIT 表示在确定特定序列的最佳回归模型时的可用选项。它定义了用于选择正确模型的指标。ENUM_TRIM、ENUM_ORIGINAL、ENUM_HAS_CONST 和 ENUM_TREND 用于构建设计矩阵。  

//+------------------------------------------------------------------+
//| Information criterion                                            |
//+------------------------------------------------------------------+
enum ENUM_INFO_CRIT
  {
   INFO_NONE=0,
   INFO_AIC,
   INFO_BIC
  };
//+------------------------------------------------------------------+
//| Options for  trimming invalid observations                       |
//+------------------------------------------------------------------+
enum ENUM_TRIM
  {
   TRIM_NONE=0,
   TRIM_FORWARD,
   TRIM_BACKWARD,
   TRIM_BOTH
  };
//+------------------------------------------------------------------+
//| options for how to handle original data set                      |
//+------------------------------------------------------------------+

enum ENUM_ORIGINAL
  {
   ORIGINAL_EX=0,
   ORIGINAL_IN,
   ORIGINAL_SEP
  };
//+------------------------------------------------------------------+
//| Constant and trend used in regression model                      |
//+------------------------------------------------------------------+

enum ENUM_TREND
  {
   TREND_NONE=0,
   TREND_CONST_ONLY,
   TREND_LINEAR_ONLY,
   TREND_LINEAR_CONST,
   TREND_QUAD_LINEAR_CONST
  };
//+------------------------------------------------------------------+
//| Options for how to handle existing constants                     |
//+------------------------------------------------------------------+

enum ENUM_HAS_CONST
  {
   HAS_CONST_RAISE=0,
   HAS_CONST_SKIP,
   HAS_CONST_ADD
  };


CAdf 的 "Adfuller()" 方法返回一个布尔值，表示测试执行成功，而不是序列的平稳性。如果返回 false，则一定是发生了错误。任何错误都会在终端日志中输出详细信息。它的输入参数是一个待分析序列的数组。  函数的其他参数为可选参数。在大多数情况下，用户无需关注这些参数，使用上述参数调用函数就足够了。

//+---------------------------------------------------------------------+
//|Class CAdf                                                           |
//|   encapsulates the the Augmented Dickey Fuller Test for Stationarity|
//+---------------------------------------------------------------------+

class CAdf
{
 private:
  double m_adf_stat,  //adf statistic
         m_bestic,    //optimal bic or aic
         m_pvalue;    //p-value
  ulong  m_usedlag;   //lag used for optimal reg model
  vector m_critvals;  //estimated critical values
  OLS    *m_ols;      //internal ordinary least squares reg model
   // private methods
 bool   gridsearch(vector &LHS, matrix &RHS, ulong f_lag, ulong l_lag,ENUM_INFO_CRIT crit, double &b_ic, ulong &best_lag);
 bool   lagmat(matrix &in,matrix &out[],ulong mlag,ENUM_TRIM trim=TRIM_BOTH,ENUM_ORIGINAL original=ORIGINAL_IN);
 bool   prepare_lhs_rhs(vector &lhs, matrix &rhs, double &in[], double &in_diff[],ulong lag);
 
 
 public:
  CAdf(void);
  ~CAdf(void);
  
 bool Adfuller(double &array[],ulong max_lag = 0,ENUM_TREND trend = TREND_CONST_ONLY, ENUM_INFO_CRIT autolag=INFO_AIC);
 vector CriticalValues(void) {  return m_critvals; }
 double AdfStatistic(void)   {  return m_adf_stat; }
 double Pvalue(void)         {  return m_pvalue;   }
};

"max_lag" 定义回归模型的最大滞后期数。"trend" 是一个枚举，允许指定回归模型的趋势和常数配置。"autolag" 决定使用什么指标来选择最能描述输入序列的最优模型。在 "Adfuller()" 中，首先要检查函数参数，然后才能用于构建回归模型的因变量和自变量。

对这一初始设计矩阵的多个变体进行采样，以确定哪一个最适合输入序列。得出最佳模型的标准取决于 "autolag" 参数的值。搜索由 "gridsearch()" 函数完成。

一旦找到最佳模型，该模型的滞后属性（指初始设计矩阵中包含的列数）将用于定义最佳模型。其参数将用于评估序列的平稳性。最优 OLS 模型的第一个 t 统计量定义了 ADF 检验的 ADF 统计量。p 值由 "mackinnop()" 函数计算。调用 CAdf 的 "Pvalue()" 方法会返回相应的 p 值。

//+----------------------------------------------------------------------+
//| calculates MacKinnon's approximate p-value for a given test statistic|
//+----------------------------------------------------------------------+
double mackinnonp(double teststat, ENUM_TREND trend = TREND_CONST_ONLY,ulong nseries = 1, uint lags =0)
  {
   vector small_scaling =  {1, 1, 1e-2};
   vector large_scaling =  {1, 1e-1, 1e-1, 1e-2};

   double tau_star_nc []= {-1.04, -1.53, -2.68, -3.09, -3.07, -3.77};
   double tau_min_nc []= {-19.04, -19.62, -21.21, -23.25, -21.63, -25.74};
   double tau_max_nc []= {double("inf"), 1.51, 0.86, 0.88, 1.05, 1.24};
   double tau_star_c []= {-1.61, -2.62, -3.13, -3.47, -3.78, -3.93};
   double tau_min_c []= {-18.83, -18.86, -23.48, -28.07, -25.96, -23.27};
   double tau_max_c []= {2.74, 0.92, 0.55, 0.61, 0.79, 1};
   double tau_star_ct []= {-2.89, -3.19, -3.50, -3.65, -3.80, -4.36};
   double tau_min_ct []= {-16.18, -21.15, -25.37, -26.63, -26.53, -26.18};
   double tau_max_ct []= {0.7, 0.63, 0.71, 0.93, 1.19, 1.42};
   double tau_star_ctt []= {-3.21, -3.51, -3.81, -3.83, -4.12, -4.63};
   double tau_min_ctt []= {-17.17, -21.1, -24.33, -24.03, -24.33, -28.22};
   double tau_max_ctt []= {0.54, 0.79, 1.08, 1.43, 3.49, 1.92};

   double tau_nc_smallp [][3]=
     {
        {0.6344, 1.2378, 3.2496},
        {1.9129, 1.3857, 3.5322},
        {2.7648, 1.4502, 3.4186},
        {3.4336, 1.4835, 3.19},
        {4.0999, 1.5533, 3.59},
        {4.5388, 1.5344, 2.9807}
     };

   double tau_c_smallp [][3]=
     {
        {2.1659, 1.4412, 3.8269},
        {2.92, 1.5012, 3.9796},
        {3.4699, 1.4856, 3.164},
        {3.9673, 1.4777, 2.6315},
        {4.5509, 1.5338, 2.9545},
        {5.1399, 1.6036, 3.4445}
     };

   double tau_ct_smallp [][3]=
     {
        {3.2512, 1.6047, 4.9588},
        {3.6646, 1.5419, 3.6448},
        {4.0983, 1.5173, 2.9898},
        {4.5844, 1.5338, 2.8796},
        {5.0722, 1.5634, 2.9472},
        {5.53, 1.5914, 3.0392}
     };

   double tau_ctt_smallp [][3]=
     {
        {4.0003, 1.658, 4.8288},
        {4.3534, 1.6016, 3.7947},
        {4.7343, 1.5768, 3.2396},
        {5.214, 1.6077, 3.3449},
        {5.6481, 1.6274, 3.3455},
        {5.9296, 1.5929, 2.8223}
     };



   double tau_nc_largep [][4]=
     {
        {0.4797, 9.3557, -0.6999, 3.3066},
        {1.5578, 8.558, -2.083, -3.3549},
        {2.2268, 6.8093, -3.2362, -5.4448},
        {2.7654, 6.4502, -3.0811, -4.4946},
        {3.2684, 6.8051, -2.6778, -3.4972},
        {3.7268, 7.167, -2.3648, -2.8288}
     };

   double tau_c_largep [][4]=
     {
        {1.7339, 9.3202, -1.2745, -1.0368},
        {2.1945, 6.4695, -2.9198, -4.2377},
        {2.5893, 4.5168, -3.6529, -5.0074},
        {3.0387, 4.5452, -3.3666, -4.1921},
        {3.5049, 5.2098, -2.9158, -3.3468},
        {3.9489, 5.8933, -2.5359, -2.721}
     };

   double tau_ct_largep [][4]=
     {
        {2.5261, 6.1654, -3.7956, -6.0285},
        {2.85, 5.272, -3.6622, -5.1695},
        {3.221, 5.255, -3.2685, -4.1501},
        {3.652, 5.9758, -2.7483, -3.2081},
        {4.0712, 6.6428, -2.3464, -2.546},
        {4.4735, 7.1757, -2.0681, -2.1196}
     };

   double tau_ctt_largep [][4]=
     {
        {3.0778, 4.9529, -4.1477, -5.9359},
        {3.4713, 5.967, -3.2507, -4.2286},
        {3.8637, 6.7852, -2.6286, -3.1381},
        {4.2736, 7.6199, -2.1534, -2.4026},
        {4.6679, 8.2618, -1.822, -1.9147},
        {5.0009, 8.3735, -1.6994, -1.6928}
     };


   vector maxstat,minstat,starstat;
   matrix tau_smallps, tau_largeps;

   switch(trend)
     {
      case TREND_NONE:
         if(!maxstat.Assign(tau_max_nc) ||
            !minstat.Assign(tau_min_nc) ||
            !starstat.Assign(tau_star_nc)||
            !tau_smallps.Assign(tau_nc_smallp)||
            !tau_largeps.Assign(tau_nc_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_CONST_ONLY:
         if(!maxstat.Assign(tau_max_c) ||
            !minstat.Assign(tau_min_c) ||
            !starstat.Assign(tau_star_c)||
            !tau_smallps.Assign(tau_c_smallp)||
            !tau_largeps.Assign(tau_c_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ct) ||
            !minstat.Assign(tau_min_ct) ||
            !starstat.Assign(tau_star_ct)||
            !tau_smallps.Assign(tau_ct_smallp)||
            !tau_largeps.Assign(tau_ct_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_QUAD_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ctt) ||
            !minstat.Assign(tau_min_ctt) ||
            !starstat.Assign(tau_star_ctt)||
            !tau_smallps.Assign(tau_ctt_smallp)||
            !tau_largeps.Assign(tau_ctt_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      default:
         Print(__FUNCTION__," Error invalid input for trend argument");
         return double("nan");
     }

   if(teststat>maxstat[nseries-1])
      return 1.0;
   else
      if(teststat<minstat[nseries-1])
         return 0.0;


   vector tau_coef;

   if(teststat<=starstat[nseries-1])
      tau_coef = small_scaling*(tau_smallps.Row(nseries-1));
   else
      tau_coef = large_scaling*(tau_largeps.Row(nseries-1));


   double rv,tau[];

   ArrayResize(tau,int(tau_coef.Size()));

   for(ulong i=0; i<tau_coef.Size(); i++)
      tau[i]=tau_coef[tau_coef.Size()-1-i];

   rv=polyval(tau,teststat);

   return CNormalDistr::NormalCDF(rv);
  }
而临界值是由 "mackinnoncrit()" 计算得出的。其结果可通过 CAdf 的 "CriticalValues()" 方法获取。
//+------------------------------------------------------------------+
//|Computes critical values                                          |
//+------------------------------------------------------------------+
vector mackinnoncrit(ulong nseries = 1,ENUM_TREND trend = TREND_CONST_ONLY, ulong num_obs=ULONG_MAX)
  {
   matrix tau_nc_2010 [] = {{
           {-2.56574, -2.2358, -3.627, 0},  // N [] = 1
           {-1.94100, -0.2686, -3.365, 31.223},
           {-1.61682, 0.2656, -2.714, 25.364}
        }
     };

   matrix tau_c_2010 [] =
     {
        {  {-3.43035, -6.5393, -16.786, -79.433},  // N [] = 1, 1%
           {-2.86154, -2.8903, -4.234, -40.040},   // 5 %
           {-2.56677, -1.5384, -2.809, 0}
        },        // 10 %
        {  {-3.89644, -10.9519, -33.527, 0},       // N [] = 2
           {-3.33613, -6.1101, -6.823, 0},
           {-3.04445, -4.2412, -2.720, 0}
        },
        {  {-4.29374, -14.4354, -33.195, 47.433},  // N [] = 3
           {-3.74066, -8.5632, -10.852, 27.982},
           {-3.45218, -6.2143, -3.718, 0}
        },
        {  {-4.64332, -18.1031, -37.972, 0},       // N [] = 4
           {-4.09600, -11.2349, -11.175, 0},
           {-3.81020, -8.3931, -4.137, 0}
        },
        {  {-4.95756, -21.8883, -45.142, 0},       // N [] = 5
           {-4.41519, -14.0405, -12.575, 0},
           {-4.13157, -10.7417, -3.784, 0}
        },
        {  {-5.24568, -25.6688, -57.737, 88.639},  // N [] = 6
           {-4.70693, -16.9178, -17.492, 60.007},
           {-4.42501, -13.1875, -5.104, 27.877}
        },
        {  {-5.51233, -29.5760, -69.398, 164.295},  // N [] = 7
           {-4.97684, -19.9021, -22.045, 110.761},
           {-4.69648, -15.7315, -5.104, 27.877}
        },
        {  {-5.76202, -33.5258, -82.189, 256.289},  // N [] = 8
           {-5.22924, -23.0023, -24.646, 144.479},
           {-4.95007, -18.3959, -7.344, 94.872}
        },
        {  {-5.99742, -37.6572, -87.365, 248.316},  // N [] = 9
           {-5.46697, -26.2057, -26.627, 176.382},
           {-5.18897, -21.1377, -9.484, 172.704}
        },
        {  {-6.22103, -41.7154, -102.680, 389.33},  // N [] = 10
           {-5.69244, -29.4521, -30.994, 251.016},
           {-5.41533, -24.0006, -7.514, 163.049}
        },
        {  {-6.43377, -46.0084, -106.809, 352.752},  // N [] = 11
           {-5.90714, -32.8336, -30.275, 249.994},
           {-5.63086, -26.9693, -4.083, 151.427}
        },
        {  {-6.63790, -50.2095, -124.156, 579.622},  // N [] = 12
           {-6.11279, -36.2681, -32.505, 314.802},
           {-5.83724, -29.9864, -2.686, 184.116}
        }
     };

   matrix tau_ct_2010 [] =
     {
        {  {-3.95877, -9.0531, -28.428, -134.155},   // N [] = 1
           {-3.41049, -4.3904, -9.036, -45.374},
           {-3.12705, -2.5856, -3.925, -22.380}
        },
        {  {-4.32762, -15.4387, -35.679, 0},         // N [] = 2
           {-3.78057, -9.5106, -12.074, 0},
           {-3.49631, -7.0815, -7.538, 21.892}
        },
        {  {-4.66305, -18.7688, -49.793, 104.244},   // N [] = 3
           {-4.11890, -11.8922, -19.031, 77.332},
           {-3.83511, -9.0723, -8.504, 35.403}
        },
        {  {-4.96940, -22.4694, -52.599, 51.314},    // N [] = 4
           {-4.42871, -14.5876, -18.228, 39.647},
           {-4.14633, -11.2500, -9.873, 54.109}
        },
        {  {-5.25276, -26.2183, -59.631, 50.646},    // N [] = 5
           {-4.71537, -17.3569, -22.660, 91.359},
           {-4.43422, -13.6078, -10.238, 76.781}
        },
        {  {-5.51727, -29.9760, -75.222, 202.253},   // N [] = 6
           {-4.98228, -20.3050, -25.224, 132.03},
           {-4.70233, -16.1253, -9.836, 94.272}
        },
        {  {-5.76537, -33.9165, -84.312, 245.394},   // N [] = 7
           {-5.23299, -23.3328, -28.955, 182.342},
           {-4.95405, -18.7352, -10.168, 120.575}
        },
        {  {-6.00003, -37.8892, -96.428, 335.92},    // N [] = 8
           {-5.46971, -26.4771, -31.034, 220.165},
           {-5.19183, -21.4328, -10.726, 157.955}
        },
        {  {-6.22288, -41.9496, -109.881, 466.068},  // N [] = 9
           {-5.69447, -29.7152, -33.784, 273.002},
           {-5.41738, -24.2882, -8.584, 169.891}
        },
        {  {-6.43551, -46.1151, -120.814, 566.823},  // N [] = 10
           {-5.90887, -33.0251, -37.208, 346.189},
           {-5.63255, -27.2042, -6.792, 177.666}
        },
        {  {-6.63894, -50.4287, -128.997, 642.781},  // N [] = 11
           {-6.11404, -36.4610, -36.246, 348.554},
           {-5.83850, -30.1995, -5.163, 210.338}
        },
        {  {-6.83488, -54.7119, -139.800, 736.376},  // N [] = 12
           {-6.31127, -39.9676, -37.021, 406.051},
           {-6.03650, -33.2381, -6.606, 317.776}
        }
     };

   matrix tau_ctt_2010 [] =
     {
        {  {-4.37113, -11.5882, -35.819, -334.047},  // N [] = 1
           {-3.83239, -5.9057, -12.490, -118.284},
           {-3.55326, -3.6596, -5.293, -63.559}
        },
        {  {-4.69276, -20.2284, -64.919, 88.884},    // N [] =2
           {-4.15387, -13.3114, -28.402, 72.741},
           {-3.87346, -10.4637, -17.408, 66.313}
        },
        {  {-4.99071, -23.5873, -76.924, 184.782},   // N [] = 3
           {-4.45311, -15.7732, -32.316, 122.705},
           {-4.17280, -12.4909, -17.912, 83.285}
        },
        {  {-5.26780, -27.2836, -78.971, 137.871},   // N [] = 4
           {-4.73244, -18.4833, -31.875, 111.817},
           {-4.45268, -14.7199, -17.969, 101.92}
        },
        {  {-5.52826, -30.9051, -92.490, 248.096},   // N [] = 5
           {-4.99491, -21.2360, -37.685, 194.208},
           {-4.71587, -17.0820, -18.631, 136.672}
        },
        {  {-5.77379, -34.7010, -105.937, 393.991},  // N [] = 6
           {-5.24217, -24.2177, -39.153, 232.528},
           {-4.96397, -19.6064, -18.858, 174.919}
        },
        {  {-6.00609, -38.7383, -108.605, 365.208},  // N [] = 7
           {-5.47664, -27.3005, -39.498, 246.918},
           {-5.19921, -22.2617, -17.910, 208.494}
        },
        {  {-6.22758, -42.7154, -119.622, 421.395},  // N [] = 8
           {-5.69983, -30.4365, -44.300, 345.48},
           {-5.42320, -24.9686, -19.688, 274.462}
        },
        {  {-6.43933, -46.7581, -136.691, 651.38},   // N [] = 9
           {-5.91298, -33.7584, -42.686, 346.629},
           {-5.63704, -27.8965, -13.880, 236.975}
        },
        {  {-6.64235, -50.9783, -145.462, 752.228},  // N [] = 10
           {-6.11753, -37.056, -48.719, 473.905},
           {-5.84215, -30.8119, -14.938, 316.006}
        },
        {  {-6.83743, -55.2861, -152.651, 792.577},  // N [] = 11
           {-6.31396, -40.5507, -46.771, 487.185},
           {-6.03921, -33.8950, -9.122, 285.164}
        },
        {  {-7.02582, -59.6037, -166.368, 989.879},  // N [] = 12
           {-6.50353, -44.0797, -47.242, 543.889},
           {-6.22941, -36.9673, -10.868, 418.414}
        }
     };

   vector ret_vector = {0,0,0};

   switch(trend)
     {
      case TREND_CONST_ONLY:
         process(tau_c_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_NONE:
         process(tau_nc_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_LINEAR_CONST:
         process(tau_ct_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_QUAD_LINEAR_CONST:
         process(tau_ctt_2010,ret_vector,num_obs,nseries);
         break;
      default:
         Print("Invalid input for trend argument");
         return ret_vector;
     }

   return ret_vector;
  }


测试和验证

为了验证我们的实现是否运行正确，我们将首先在 Python 中对随机序列进行 ADF 测试。然后，我们将在 Metatrader 5 中对同一序列运行 ADF 检验，并比较输出结果。

Python 中的 ADF 检验代码如下。

import numpy as np
from statsmodels.tsa.stattools import adfuller

#initialize array with 100 elements
x = np.array([0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
              0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
              0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
              0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
              0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
              0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
              0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
              0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
              0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
              0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
              0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
              0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
              0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
              0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
              0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
              0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
              0.20684364,0.29630613,0.65178447,0.86559185])
   
#perform ADF test on array 
result = adfuller(x)

#print ADF statistic and p-value
print(f"ADF statistic: {result[0]}, p-value:{result[1]}")

#print critical values
print(f"Critical values:{result[4]}")
  

接下来，我们在同一个数组上运行 MQL5 版本的 ADF 测试，脚本程序代码如下所示。

//+------------------------------------------------------------------+
//|                                                     ADF_test.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<ADF.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---series
   double rand_array[] =
     {
      0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
      0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
      0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
      0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
      0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
      0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
      0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
      0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
      0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
      0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
      0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
      0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
      0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
      0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
      0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
      0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
      0.20684364,0.29630613,0.65178447,0.86559185
     };

//---variables that will be used to store test results
   CAdf adf;
//--- Do ADF test
   if(adf.Adfuller(rand_array))
      Print("ADF test statistic: ", adf.AdfStatistic(), " P-value:", adf.Pvalue(),"\nCritical values \n",adf.CriticalValues());
   else
      Print("ADF test failed");
  }
//+------------------------------------------------------------------+

首先运行 python 脚本：

LD      0       18:30:22.912    Test_adfuller (NFLX_us,Daily)   ADF statistic: -8.495443215534635, p-value:1.2796318143567197e-13
GJ      0       18:30:22.913    Test_adfuller (NFLX_us,Daily)   Critical values:{'1%': -3.4989097606014496, '5%': -2.891516256916761, '10%': -2.5827604414827157}

接着是 MetaTrader 5 脚本，我们可以看到结果是一样的。

DO      0       18:30:48.460    ADF_test (NFLX_us,D1)   ADF test statistic: -8.495443215534634 P-value:1.2796318143567197e-13
ND      0       18:30:48.460    ADF_test (NFLX_us,D1)   Critical values 
OL      0       18:30:48.460    ADF_test (NFLX_us,D1)   [-3.49890976060145,-2.891516256916761,-2.582760441482716]


协整

相关性和协整是用来衡量变量之间关系的统计概念，尤其是在时间序列数据中。虽然两者都能衡量关系，但目的不同，应用场景也不同。相关性是指对两个变量之间线性关系的强度和方向的统计测量。

协整序列



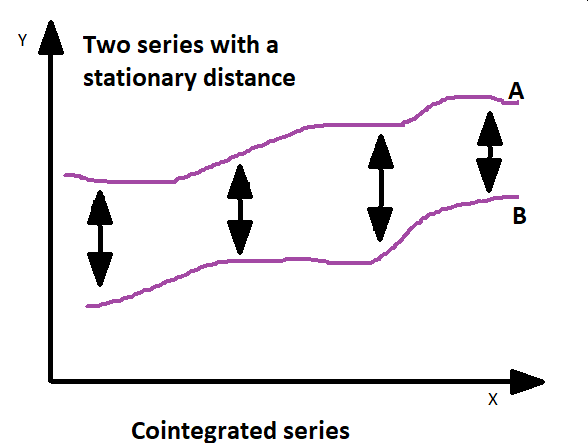
另一方面，协整处理的是具有长期均衡或稳定关系的非平稳时间序列变量之间的关系。更简单地说，它确定是否存在两个或多个非平稳变量的组合，这些变量在一起考虑时具有稳定的长期关系。协整在确定一对变量时非常有用，这对变量尽管有短期波动，但随着时间的推移会一起变化。这意味着变量之间存在长期联系，可以利用这种关系制定交易策略或建立模型。

协整关系通常通过 Engle-Granger 检验或 Johansen 检验等统计检验进行评估。这些测试检验非平稳变量的线性组合是否会产生一个平稳序列，从而表明一种长期关系。Engle-Granger 检验是在时间序列设置中检验两个变量之间协整关系的两步程序。它包括估计回归模型，然后对残差进行检验，以确定是否存在协整关系。如果发现回归模型的残差是平稳的，则表明两个变量之间存在协整关系。在这种情况下，它表明尽管变量不是单独平稳的，但它们的线性组合是平稳的。

Engle-Granger 检验的局限性在于它无法同时处理多个序列。Johansen 检验法解决了这一局限性。这实质上是 Engle-Granger 方法的延伸，用于检验向量自回归模型中多个序列之间的协整关系。在本文中，我们不会研究 Johansen 检验，因为我们每次只处理两个序列。


CointegrationTest.mqh 包含 CCoint 类函数。它借助 CAdf 类实现了增强的 Engle-Granger 检验。测试通过调用 CCoint 的 "Aeg()" 方法进行。需要两个包含待测系列的输入数组。可选输入参数 "trend"、"max_lag" 和 "autolag" 与 CAdf 中 "Adfuller()" 方法的参数类似。同样，对于大多数测试，默认值就足够了。下一节将对此进行演示。  协整检验的结果是通过调用 CCoint 的三个方法得出的。第一个 "CointStatistic" 返回内部 ADF 检验的 ADF 统计量。"CriticalValues()" 返回测试临界值的向量。调用 "Pvalue()" 可获得 p 值。

//+------------------------------------------------------------------+
//|                                            CointegrationTest.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<ADF.mqh>

//+------------------------------------------------------------------+
//|Class CCoint                                                      |
//|    implements cointegration test of two series                   |
//+------------------------------------------------------------------+
class CCoint
{
 private:
  double m_coint_stat;       //ADF test statistic
  double m_coint_pvalue;     //cointegration p-value
  vector m_coint_critvalues; //Cointegration critical values
  CAdf   *m_adf;             //CAdf object pointer
 public:
  CCoint(void);
  ~CCoint(void);
  
  bool Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC);
  
  double CointStatistic(void){ return m_coint_stat; }
  double Pvalue(void)        { return m_coint_pvalue;}
  vector CriticalValues(void){ return m_coint_critvalues;}
};
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CCoint::CCoint(void)
{
 m_adf = new CAdf();
 
 m_coint_critvalues = vector::Zeros(3);
 
 m_coint_stat=m_coint_pvalue=EMPTY_VALUE;
}
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CCoint::~CCoint(void)
{
 if(CheckPointer(m_adf)==POINTER_DYNAMIC)
     delete m_adf;
}
//+------------------------------------------------------------------+
//| Test for cointegration                                           |
//+------------------------------------------------------------------+
bool CCoint::Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC)
  {
//---  
   if(CheckPointer(m_adf)==POINTER_INVALID)
    {
     Print("Critical Internal error: Invalid CAdf pointer");
     return false;
    }
//---    
   if(in_one.Size()<1 || in_two.Size()<1 || in_one.Size()!=in_two.Size())
     {
      Print(__FUNCTION__," Invalid input for one or both arrays");
      return false;
     }

   vector y1,temp;
   matrix y2;

   if(!y1.Assign(in_one) || !temp.Assign(in_two) || !y2.Resize(temp.Size(),1) || !y2.Col(temp,0))
     {
      Print(__FUNCTION__," Assignment error: ", GetLastError());
      return false;
     }


   ulong obs,kvars=1;
   obs = y2.Rows();
   kvars++;
   matrix xx;

   if(trend==TREND_NONE)
     {
      if(!xx.Copy(y2))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }
     }
   else
    if(!addtrend(y2,xx,trend,false))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }

   OLS ols;

   if(!ols.Fit(y1,xx))
      return false;

   if(ols.Rsqe()< 1 - 100*SQRTEPS)
     {
      double resid[];

      vector resd = ols.Residuals();

      ArrayResize(resid,int(resd.Size()));

      for(uint i = 0; i<resid.Size(); i++)
         resid[i]=resd[i];

      if(!m_adf.Adfuller(resid,max_lag,TREND_NONE,autolag))
         return false;

      m_coint_stat = m_adf.AdfStatistic();
     }
   else
     {
      Print("They are (almost) perfectly collinear.\nCointegration test is not reliable in this case");
      m_coint_stat=double("nan");
     }

   if(trend==TREND_NONE)
      m_coint_critvalues.Fill(double("nan"));
   else
      m_coint_critvalues = mackinnoncrit(kvars,trend,obs-1);

   m_coint_pvalue = mackinnonp(m_coint_stat,trend,kvars);

   return true;
  }    


协整检验交易品种

在最后的演示中，我们将创建一个 MQL5 脚本，使用 CCoint 测试一系列交易品种的协整关系。用户输入一个交易品种列表，以逗号分隔。设置要研究的收盘价的开始日期和历史长度。"ConfidenceLevel" 可让用户选择所需的显著性水平。这决定了最终结果与 ADF 统计量比较的临界值。

//+------------------------------------------------------------------+
//|                                    SymbolCointegrationTester.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <CointegrationTest.mqh>
//+------------------------------------------------------------------+
//| enumeration maps to confidence levels of 99%,95%, and 90%        |
//+------------------------------------------------------------------+
enum ENUM_CONFIDENCE_LEVEL
  {
   CONF_99=0,//99%
   CONF_95,//95%
   CONF_90 //90%
  };
//--- input parameters
input string   Symbols = "FB_us,GOOG_us,MSFT_us,NFLX_us,NVDA_us,AAPL_us,TSLA_us";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2022.01.01 00:00:01';
input int Size = 250;//History length
input ENUM_CONFIDENCE_LEVEL ConfidenceLevel=CONF_90;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(Size<100)
     {
      Print("Invalid input for Size");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;

//---in case there are less than two symbols specified
   if(num_symbols<2)
     {
      Print("Invalid input. Please list at least two symbols");
      return;
     }
//---output matrix of indices
   matrix sym_combos;
//---fill sym_combos with index values of symbols array
   PairedCombinations(symbols,sym_combos,num_symbols);
//---price arrays for pair of symbols
   double symA_prices [], symB_prices[];
//---output vectors holding results of cointegration test
   vector stats, critvals;
//---symbol pairs and result output
   string symA,symB,result;
//---CCoint object
   CCoint coint;
//---loop through all paired combinations from list
   for(ulong i=0; i<sym_combos.Rows(); i++)
     {
      //--- get symbol pair for current combination
      symA = symbols[int(sym_combos[i][0])];
      symB = symbols[int(sym_combos[i][1])];
      //--- get prices for the pair of symbols
      if(CopyClose(symA,TimeFrame,StartDate,Size,symA_prices)<Size||
         CopyClose(symB,TimeFrame,StartDate,Size,symB_prices)<Size)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //--- test the pair for cointegreation
      if(!coint.Aeg(symA_prices,symB_prices))
        {
         Print("Cointegration test failed ", ::GetLastError());
         return;
        }
      //---
      vector critvals = coint.CriticalValues();
      //--- prepare results output for a test
      if(coint.CointStatistic()<critvals[ConfidenceLevel])
         result="likely cointegrated.";
      else
         result="likely not cointegrated.";
      //--- output the result from cointegration test
      Print(symA," and ",symB, " are ", result);
     }
  }
//+------------------------------------------------------------------+
//| Combinations: generates paired combinations                      |
//+------------------------------------------------------------------+
bool PairedCombinations(string &in[], matrix &out,int count = 0)
  {
//---check input array
   if(in.Size()<1)
     {
      Print(__FUNCTION__," input array is empty");
      return false;
     }
//---set value for upto equal to the number of elements that should be
//---considered in the input array
   int upto = (count>1 && count<ArraySize(in))?count:ArraySize(in);
//--- calculate the number of rows equivalent to number of combinations
   ulong rows = ulong(MathFactorial(upto)/(MathFactorial(2)*MathFactorial(upto-2)));
//---resize output matrix accordingly
   out.Resize(rows,2);
//---fill output matrix with indexes of input array
   for(uint i=0,z=0; i<in.Size(); i++)
     {
      for(uint k = i+1; k<in.Size(); k++,z++)
        {
         out[z][0]=i;
         out[z][1]=k;
        }
     }
//---return
   return true;
  }
//+------------------------------------------------------------------+


在我们的示例中，我们将测试 Google、Facebook、Microsoft、NetFlix、Nvidia、Apple 和 Tesla 等交易品种。运行脚本的结果如下所示。

HN      0       18:37:31.239    SymbolCointegrationTester (NFLX_us,D1)  FB_us and GOOG_us are likely not cointegrated.
PQ      0       18:37:31.280    SymbolCointegrationTester (NFLX_us,D1)  FB_us and MSFT_us are likely not cointegrated.
IE      0       18:37:31.322    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NFLX_us are likely not cointegrated.
MG      0       18:37:31.365    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NVDA_us are likely not cointegrated.
PH      0       18:37:31.411    SymbolCointegrationTester (NFLX_us,D1)  FB_us and AAPL_us are likely not cointegrated.
NL      0       18:37:31.453    SymbolCointegrationTester (NFLX_us,D1)  FB_us and TSLA_us are likely not cointegrated.
EO      0       18:37:31.496    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and MSFT_us are likely not cointegrated.
ES      0       18:37:31.540    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NFLX_us are likely not cointegrated.
FE      0       18:37:31.582    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NVDA_us are likely not cointegrated.
CF      0       18:37:31.623    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and AAPL_us are likely not cointegrated.
EJ      0       18:37:31.665    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and TSLA_us are likely not cointegrated.
HM      0       18:37:31.705    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NFLX_us are likely not cointegrated.
RN      0       18:37:31.744    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NVDA_us are likely not cointegrated.
LP      0       18:37:31.785    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and AAPL_us are likely not cointegrated.
OD      0       18:37:31.825    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and TSLA_us are likely not cointegrated.
IG      0       18:37:31.866    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and NVDA_us are likely not cointegrated.
QI      0       18:37:31.906    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and AAPL_us are likely not cointegrated.
FP      0       18:37:31.946    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and TSLA_us are likely cointegrated.
EO      0       18:37:31.987    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and AAPL_us are likely not cointegrated.
RS      0       18:37:32.026    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and TSLA_us are likely not cointegrated.
DE      0       18:37:32.072    SymbolCointegrationTester (NFLX_us,D1)  AAPL_us and TSLA_us are likely not cointegrated.

他们的研究表明，NetFlix 和特斯拉很可能存在协整关系，置信度为 90%。

下面是用 Python 进行相同测试的代码，以及测试结果。

"""
 Script demonstrates use of coint() from statsmodels
 to test symbols for cointegration
"""
# imports 
from statsmodels.tsa.stattools import coint
from itertools import combinations
from datetime import datetime
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import pytz

#initialize connection to mt5
if not mt5.initialize():
    print("initialize() failed ")
    mt5.shutdown()
 
#set up timezone infomation   
tz=pytz.timezone("Etc/UTC")

#use time zone to set correct date for history data extraction
startdate = datetime(2022,1,1,hour=0,minute=0,second=1,tzinfo=tz)

#list the symbols 
Symbols = ["FB_us","GOOG_us","MSFT_us","NFLX_us","NVDA_us","AAPL_us","TSLA_us"]

#set length of data history
num_bars = 250

#set up the shape of the data structure to store prices 
data = np.zeros((num_bars,len(Symbols)))
prices = pd.DataFrame(data,columns=Symbols)

#fill prices dataframe with close prices
for symbol in Symbols:
    prices[symbol]=[rate[4]  for rate in mt5.copy_rates_from(symbol,mt5.TIMEFRAME_D1,startdate,num_bars)]
    
#we donot need mt5 from here 
mt5.shutdown()

#generate pairs from Symbols list 
pairs = list(combinations(prices.columns,2))

#set our desired significance level, 0.01->99%, 0.05->95%, 0.1->90%
confidence_level = 0.1

#do the test for cointegration on each pair and print results
for pair in pairs:
    df=prices[list(pair)]
    adf_stat,pvalue,critvalues=coint(df.values[:,0],df.values[:,1])
    if pvalue < confidence_level:
        print(pair[0]," and ",pair[1], " are likely cointegrated")
    else:
        print(pair[0]," and ",pair[1], " are likely not cointegrated")  

Python 结果

MR      0       18:35:17.835    SymbolCointegration (NFLX_us,Daily)     FB_us  and  GOOG_us  are likely not cointegrated
GE      0       18:35:17.851    SymbolCointegration (NFLX_us,Daily)     FB_us  and  MSFT_us  are likely not cointegrated
DI      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NFLX_us  are likely not cointegrated
CJ      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NVDA_us  are likely not cointegrated
MO      0       18:35:17.882    SymbolCointegration (NFLX_us,Daily)     FB_us  and  AAPL_us  are likely not cointegrated
JQ      0       18:35:17.898    SymbolCointegration (NFLX_us,Daily)     FB_us  and  TSLA_us  are likely not cointegrated
CD      0       18:35:17.914    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  MSFT_us  are likely not cointegrated
MF      0       18:35:17.930    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NFLX_us  are likely not cointegrated
QK      0       18:35:17.946    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NVDA_us  are likely not cointegrated
HM      0       18:35:17.962    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  AAPL_us  are likely not cointegrated
OO      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  TSLA_us  are likely not cointegrated
MS      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NFLX_us  are likely not cointegrated
PD      0       18:35:17.994    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NVDA_us  are likely not cointegrated
MF      0       18:35:18.010    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  AAPL_us  are likely not cointegrated
RJ      0       18:35:18.042    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  TSLA_us  are likely not cointegrated
RM      0       18:35:18.058    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  NVDA_us  are likely not cointegrated
GP      0       18:35:18.074    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  AAPL_us  are likely not cointegrated
LN      0       18:35:18.089    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  TSLA_us  are likely cointegrated
EF      0       18:35:18.105    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  AAPL_us  are likely not cointegrated
QI      0       18:35:18.121    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  TSLA_us  are likely not cointegrated
OJ      0       18:35:18.137    SymbolCointegration (NFLX_us,Daily)     AAPL_us  and  TSLA_us  are likely not cointegrated

结论

到目前为止，我们已经研究了使用 MQL5 实现的增广 Dickey-Fuller 检验，并用它实现了 Engle-Granger 的协整检验。对于那些有兴趣探索配对交易策略或统计套利的人来说，ADF 检验是一个重要工具。  文章中描述的所有代码都包含在压缩文件中。下表列出了该文件的所有内容。

文件
描述
Mql5\include\OLS.mqh
 包含实现普通最小二乘法回归的 OLS 类的定义
Mql5\include\ADF.mqh
 包含各种函数的定义和实现 ADF 检验的 CAdf 类
Mql5\include\CointegrationTest.mqh
  定义 CCoint 类，利用增强 Engle-Granger 技术进行协整检验
Mql5\scripts\ADF_test.mq5
 这是用于测试 ADF 检验的 MQL5 实现的 MQL5 脚本
Mql5\scripts\SymbolCointegrationTester.mq5
 在 MetaTrader 5 中测试交易品种协整的脚本
Mql5\scripts\Test_adfuller.py
 这是一个使用 statsmodels 实现 ADF 检验的 python 脚本，用于验证我们的 MQL5 实现
Mql5\scripts\SymbolCointegration.py
 SymbolCointegrationTester 的 Python 版本


本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/13991

附加的文件 |
下载ZIP
SymbolCointegration.py (1.71 KB)
Test_adfuller.py (1.71 KB)
ADF.mqh (30.73 KB)
OLS.mqh (13.36 KB)
CointegrationTest.mqh (4.13 KB)
ADF_test.mq5 (2.34 KB)
SymbolCointegrationTester.mq5 (4.6 KB)
Mql5.zip (17.2 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
用于时间序列挖掘的数据标签（第 5 部分）：使用 Socket 在 EA 中进行应用和测试 用于时间序列挖掘的数据标签（第 5 部分）：使用 Socket 在 EA 中进行应用和测试
本系列文章介绍了几种时间序列标注方法，可以创建符合大多数人工智能模型的数据，根据需求有针对性地进行数据标注，可以使训练出来的人工智能模型更符合预期设计，提高我们模型的准确性，甚至帮助模型实现质的飞跃！
数据科学和机器学习（第 16 部分）：全新面貌的决策树 数据科学和机器学习（第 16 部分）：全新面貌的决策树
在我们的数据科学和机器学习系列的最新一期中，深入到错综复杂的决策树世界。本文专为寻求策略洞察的交易者量身定制，全面回顾了决策树在分析市场趋势中所发挥的强大作用。探索这些算法树的根和分支，解锁它们的潜力，从而强化您的交易决策。加入我们，以全新的视角审视决策树，并探索它们如何在复杂的金融市场航行中成为您的盟友。
数据科学和机器学习（第 17 部分）：摇钱树？外汇交易中随机森林的艺术与科学 数据科学和机器学习（第 17 部分）：摇钱树？外汇交易中随机森林的艺术与科学
探索算法炼金术的秘密，我们将引导您融会贯通如何在解码金融领域时将艺术性和精确性相结合。揭示随机森林如何将数据转化为预测能力，为驾驭股票市场的复杂场景提供独特的视角。加入我们的旅程，进入金融魔法的心脏地带，此处我们会揭开随机森林在塑造市场命运、及解锁赚钱机会之门方面之角色的神秘面纱
MQL5 简介（第 2 部分）：浏览预定义变量、通用函数和控制流语句 MQL5 简介（第 2 部分）：浏览预定义变量、通用函数和控制流语句
通过我们的 MQL5 系列第二部分，开启一段启迪心灵的旅程。这些文章不仅是教程，还是通往魔法世界的大门，在那里，编程新手和魔法师将团结在一起。是什么让这段旅程变得如此神奇？我们的 MQL5 系列第二部分以令人耳目一新的简洁性脱颖而出，使复杂的概念变得通俗易懂。与我们互动，我们会回答您的问题，确保您获得丰富和个性化的学习体验。让我们建立一个社区，让理解 MQL5 成为每个人的冒险。欢迎来到魔法世界！