Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (Энкодер)

MetaTrader 5 — Торговые системы | 16 января 2026, 14:04

Введение

Продолжаем работу над фреймворком, предложенным в статье "Perturbed State Space Feature Encoders for Optical Flow with Event Cameras". Но вначале остановимся на мгновение и ещё раз чётко обозначим, с какой проблемой мы вообще имеем дело, работая с финансовыми рынками, и почему стандартные инструменты анализа здесь раз за разом упираются в естественные ограничения.

Рынок — это не аккуратный временной ряд, заботливо разложенный по барам, это поток событий — неравномерный, прерывистый, насыщенный микродвижениями, которые либо теряются при агрегации, либо маскируются под шум. Мы привыкли называть этот шум случайным, но именно в нём чаще всего и прячется информация. Классические модели, будь то линейная авторегрессия или более современные рекуррентные сети, по сути, работают с усреднённой историей. Они хорошо чувствуют инерцию, хуже — резкие переходы, совсем плохо — структурные сдвиги, когда рынок на коротком интервале меняет характер своего поведения.

Финансовый рынок разумнее рассматривать как динамическую систему с внутренним состоянием, которое эволюционирует под воздействием внешних и внутренних возмущений. Цена в этой картине — лишь наблюдаемая проекция. Следствие, а не причина. Такой взгляд сам по себе не нов. Модели пространства состояний существуют десятилетиями. Новизна появляется в момент, когда мы перестаём трактовать возмущения как неизбежное зло и начинаем рассматривать их как полноценный источник сигнала. Именно здесь идеи фреймворка Perturbed State Space Feature Encoder оказываются неожиданно близки к реалиям рынка, несмотря на их происхождение из области компьютерного зрения.

P-SSE изначально проектировался для работы с потоками событий. В них данные приходят неравномерно, а ключевая информация скрыта в локальных изменениях динамики. Это удивительно точное описание того, что происходит внутри торгового потока. Сделки возникают не по расписанию, импульсы ликвидности появляются и исчезают, краткосрочные дисбалансы могут радикально менять поведение цены, не оставляя при этом заметного следа в стандартных агрегированных данных. В такой среде попытка сгладить шум часто приводит к потере самого ценного.

Архитектурно P-SSE опирается на компактную, но выразительную модель пространства состояний. Текущее состояние системы обновляется рекурсивно, а возмущения встроены непосредственно в динамику перехода. Это принципиальный момент. Возмущение не добавляется постфактум и не интерпретируется как ошибка аппроксимации, оно параметризовано, обучаемо и влияет на эволюцию состояния наравне с основной динамикой. Для финансовых рынков это означает следующее: модель получает возможность отличать пустой шум от значимого микрособытия, даже если внешне они выглядят похоже.

Ещё одно важное преимущество фреймворка — устойчивость при работе с длинными последовательностями. Классические рекуррентные архитектуры, особенно в их наивной реализации, либо теряют чувствительность к далёкому прошлому, либо становятся нестабильными при обучении. P-SSE решает эту проблему за счёт строгой структуры обновления состояния и контролируемого распространения возмущений. Градиенты не взрываются и не исчезают, линамика остаётся управляемой. Для прикладных торговых моделей это критично, поскольку реальный рынок не позволяет роскоши переобучения на коротком окне с постоянным ручным вмешательством.

Не менее важно и то, что P-SSE не навязывает жёсткую привязку к конкретному виду входных данных. В исходной работе речь идёт о событийных камерах, но сама архитектура оперирует абстрактным потоком признаков. В финансовом контексте такими признаками могут быть цены, объёмы, производные величины, индикаторы микроструктуры. Все они рассматриваются как разные проявления одного и того же скрытого состояния рынка. Это позволяет строить модели, которые отслеживают эволюцию рыночной среды в целом.

Важный момент, который стоит подчеркнуть отдельно, — это баланс между выразительностью и вычислительной сложностью. P-SSE сохраняет линейную сложность по длине последовательности. Для практической реализации в торговых системах это означает возможность работы в реальном времени без экзотического аппаратного ускорения. Архитектура не требует массивных трансформеров и не полагается на глобальное внимание. Она аккуратно и последовательно накапливает информацию в состоянии, позволяя модели оставаться быстрой и предсказуемой с точки зрения ресурсов.

Преимущества предложенного фреймворка очевидны: устойчивость, чувствительность к локальным импульсам, явная работа с возмущениями и компактная архитектура. Остаётся самый интересный этап — показать, как эти идеи реализуются на практике, какие инженерные решения приходится принимать при адаптации P-SSE к финансовым данным и какие компромиссы оказываются неизбежными.

Авторская визуализация фреймворка представлена ниже.

E-TROF E-MOP

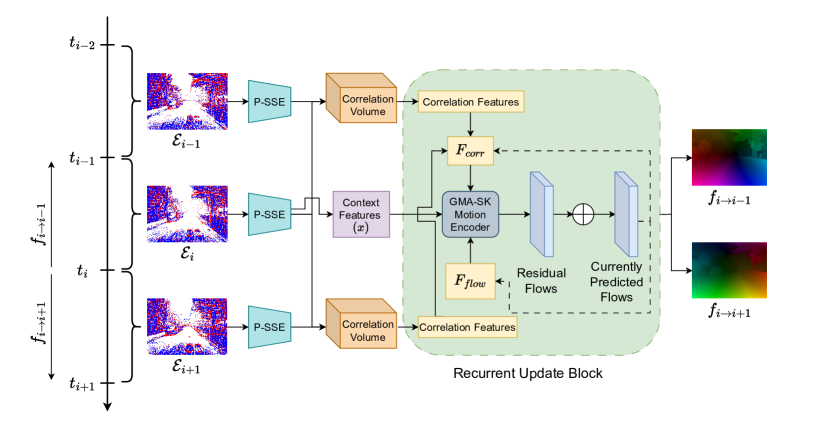
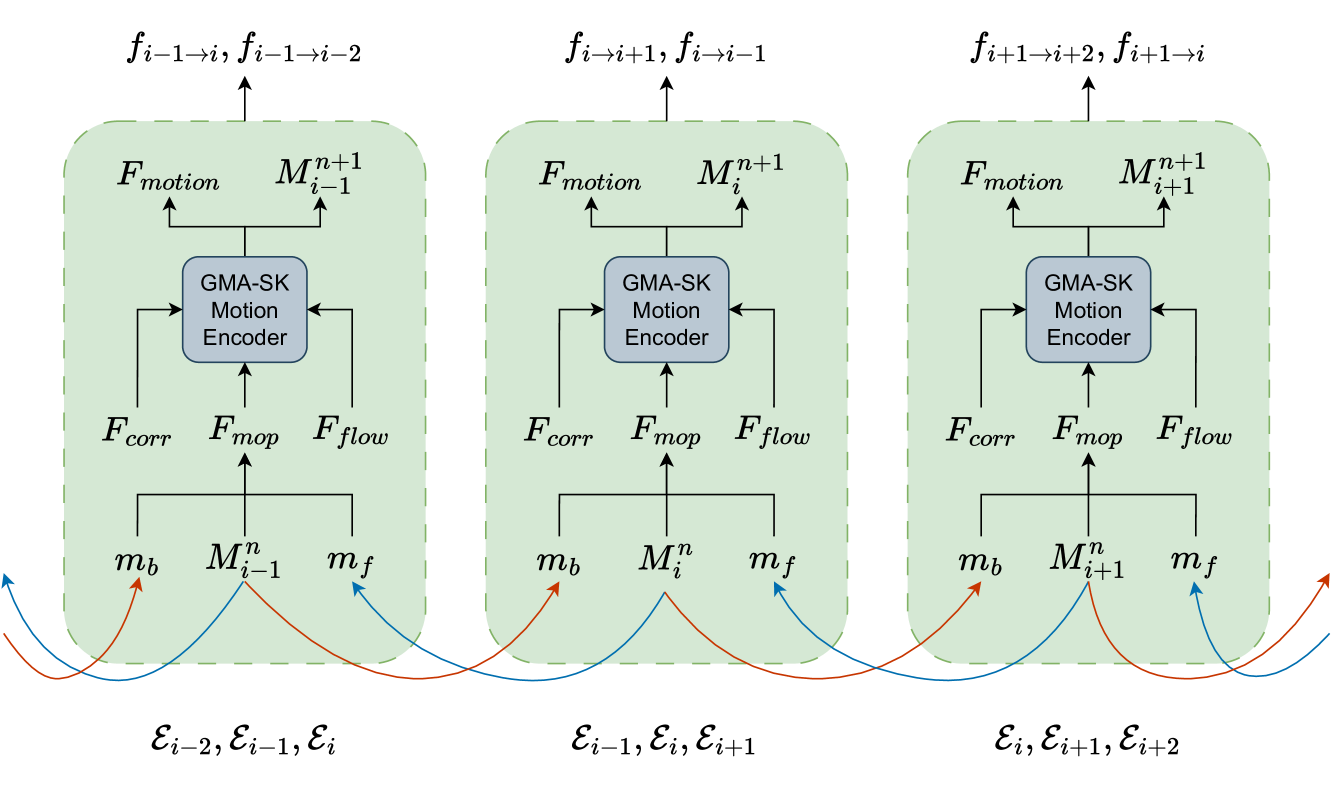
Принципы построения

Прежде чем перейти к практической реализации, важно зафиксировать один принципиальный момент, без которого дальнейшее изложение легко увести в неверную сторону. Предложенный авторами фреймворка модуль P-SSE — это не модель пространства состояний в её классическом понимании. Формально он опирается на State-Space представление, использует рекуррентное обновление состояния и наследует многие свойства традиционных SSM, но по своей роли в архитектуре и по функциональному назначению это уже иной класс объектов.

P-SSE — это полноценный энкодер признаков, построенный на базе моделей пространства состояний, а не их прямое воплощение. Он не ограничивается задачей фильтрации или прогнозирования наблюдаемой величины. Его цель шире: сформировать устойчивое, информативное и контекстно насыщенное представление анализируемого потока данных, пригодное для дальнейшей обработки. Состояние здесь — не конечный результат модели, а внутренний носитель информации, в нем энкодер аккумулирует динамику, локальные изменения и структурные сдвиги во входных данных.

Именно поэтому архитектура P-SSE выходит за рамки классических SSM. В традиционной постановке модель пространства состояний стремится как можно точнее описать скрытую динамику системы и восстановить наблюдения, в P-SSE же состояние используется как активный механизм кодирования признаков. Здесь возмущения, параметры перехода и структура обновления работают совместно, формируя представление, чувствительное к микроизменениям, но устойчивое на длинных интервалах. Это тонкое, но крайне важное различие, особенно в контексте финансовых рынков.

Для практики это означает, что мы строим инструмент извлечения признаков. Он использует строгую математику пространства состояний как каркас, но при этом остаётся гибким, обучаемым и ориентированным на последующую интеграцию в торговую логику. Такой энкодер можно рассматривать как промежуточный слой между сырыми рыночными данными и прикладной моделью принятия решений.

Осознание этой роли P-SSE существенно упрощает дальнейшую работу. Оно снимает ложные ожидания, связанные с классическими SSM, и сразу задаёт правильный фокус. Нас интересует качество и стабильность представления рыночной динамики. Всё остальное — следствие.

Есть ещё один тонкий, но принципиально важный момент, на котором стоит остановиться отдельно, прежде чем двигаться дальше. В оригинальной архитектуре фреймворка авторы используют обработку перекрывающихся троек состояний. Такой подход логичен в исходной постановке задачи и хорошо работает в офлайн-режиме, когда весь поток данных доступен заранее и стоимость повторных вычислений не критична. Каждая тройка формирует локальный контекст, позволяя модулю P-SSE учитывать взаимное расположение состояний во времени и усиливать чувствительность к динамическим переходам.

Однако в контексте финансовых рынков мы имеем иную постановку задачи. Нас интересует анализ текущего состояния рынка в реальном времени, где каждое новое наблюдение должно обрабатываться быстро и без избыточных операций. Поток данных обновляется последовательно. На каждой итерации изменяется лишь одно состояние — последнее. Два предыдущих не несут новой информации, они лишь смещаются во временной позиции. Тем не менее при прямом следовании авторской схеме эти состояния снова и снова проходят через модуль P-SSE, что приводит к очевидному дублированию вычислений.

С инженерной точки зрения это избыточно. Мы фактически повторно обрабатываем уже известные данные, расходуя вычислительные ресурсы без какого-либо прироста информации. В условиях онлайн-анализа, особенно при работе с высокочастотными потоками, такой подход быстро становится узким местом. Рынок не ждёт, пока мы красиво пересчитаем прошлое, он идёт дальше.

Чтобы устранить этот эффект и одновременно сохранить логику оригинального фреймворка, мы вводим стек эмбеддингов, в котором сохраняем результаты работы модуля P-SSE для каждого отдельного состояния. Идея простая и, в некотором смысле, классическая. Каждое состояние проходит через P-SSE ровно один раз, полученное закодированное представление помещается в стек и далее используется повторно при формировании последующих контекстов. Историческая последовательность при этом полностью сохраняется, но повторные вычисления исключаются.

В результате алгоритм естественным образом переходит от обработки перекрывающихся троек к потоковой схеме, оптимальной для реального времени. При этом мы не нарушаем архитектурную идею P-SSE и не искажаем его функционал, мы лишь приводим реализацию в соответствие с требованиями практического трейдинга, где скорость и предсказуемость вычислений имеют не меньшую ценность, чем выразительность модели.

Такой шаг выглядит небольшим, но на практике он сильно меняет характер системы. Модель становится более аккуратной, более экономной и, что особенно важно, лучше приспособленной к непрерывному онлайн-анализу.

Объект P-SSE

Практическая реализация всех описанных выше соображений аккуратно сведена в новый объект CNeuronPSSE, который становится центральным элементом всей дальнейшей архитектуры. Его структура уже на уровне интерфейса хорошо отражает тот сдвиг, о котором мы говорили ранее. Перед нами не классическая модель пространства состояний и не отдельный вычислительный слой, а самостоятельный энкодер признаков, рассчитанный на потоковую работу и интеграцию со стеком состояний.

class CNeuronPSSE :  public CNeuronAddToStack
  {
protected:
   CLayer                  cPrepare;
   //---
   CParams                 cA;
   CNeuronSpikeConvBlock   cBCDxE;
   //---
   CNeuronBaseOCL          cB;
   CNeuronBaseOCL          cC;
   CNeuronBaseOCL          cDx;
   CNeuronBaseOCL          cE;
   CNeuronBaseOCL          cH;
   //---
   CNeuronBaseOCL          cAE;
   CNeuronTransposeVRCOCL  cAET;
   CNeuronBaseOCL          cAED;
   //---
   CNeuronBaseOCL          cAH;
   CNeuronBaseOCL          cBX;
   CNeuronBaseOCL          cHc;
   CNeuronBaseOCL          cCHc;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPSSE(void) {};
                    ~CNeuronPSSE(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint stack_size, uint dimension,
                          uint patch_dimension, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   override const   {  return defNeuronPSSE;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj)   override;
   virtual void      TrainMode(bool flag) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual bool      Clear(void) override;
  };

Наследование от CNeuronAddToStack здесь не случайно и не декоративно. Оно сразу фиксирует ключевую идею реализации — каждое состояние рынка проходит через P-SSE один раз, после чего результат сохраняется и используется повторно. Таким образом, логика хранения и последовательного смещения состояний вынесена на уровень базового механизма. Сам же CNeuronPSSE может сосредоточиться на вычислении представления, а не на управлении историей.

Внутренняя композиция объекта выглядит достаточно насыщенной, но за этим нет избыточности. Блок cPrepare отвечает за предварительное приведение исходных данных к форме, удобной для дальнейшей обработки, и первичное извлечение признаков. Это важный этап, особенно в финансовом контексте, где размерности, масштабы и структура входных признаков могут сильно различаться. Подготовка данных здесь — не формальность, а способ стабилизировать поведение всей цепочки.

Параметры динамики инкапсулированы в cA, что подчёркивает их особый статус. Это не вспомогательные коэффициенты, а обучаемая часть модели, напрямую влияющая на эволюцию состояния. Связка cBCDxE реализует компактный, но выразительный блок обработки, в котором сочетаются свёрточные операции и спайковая логика, позволяющая параллельно сформировать каркас SSM в зависимости от анализируемого состояния системы.

Набор базовых нейронных объектов cB, cC, cDx, cE, cH формирует буферы хранения промежуточных данных, соответствующих внутренней структуре P-SSE. Здесь нет попытки спрятать математику за абстракциями. Каждый компонент отвечает за свой участок преобразований, что упрощает контроль над вычислениями и делает поведение модели более прозрачным при отладке и анализе.

Отдельного внимания заслуживает блок, связанный с обработкой матрицы переходов и её производных: cAE, cAET, cAED. Использование явного транспонирования и раздельной обработки здесь продиктовано практикой работы в OpenCL. Такой подход позволяет более эффективно распределять вычисления на устройстве и избегать лишних преобразований данных при обучении.

Компоненты cAH, cBX, cHc, cCHc завершают цепочку, формируя итоговое представление состояния и обеспечивая корректное распространение градиентов. В совокупности они превращают P-SSE в замкнутый, самодостаточный энкодер, который можно обучать, сохранять, загружать и использовать в составе более крупной архитектуры без дополнительных костылей.

За инициализацию всей внутренней архитектуры отвечает метод Init. Его структура очень показательная — в ней уже зашита логика того, как именно P-SSE преобразуется в потоковый энкодер состояния рынка.

bool CNeuronPSSE::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint stack_size, uint dimension, uint patch_dimension,
                       uint variables, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(CNeuronAddToStack::Init(numOutputs, myIndex, open_cl, stack_size,
                              patch_dimension, variables, optimization_type, batch))
      ReturnFalse;

Первое, с чего начинается метод, — это передача управления одноименному методу родительского класса. Тем самым мы сразу встраиваем модуль в стековую механику. Архитектура P-SSE с этого момента изначально ориентирована на последовательную обработку состояний с сохранением истории, а не на изолированные вызовы. Это важная отправная точка. Вся последующая инициализация происходит уже в контексте потоковой модели.

Далее следует подготовительный блок cPrepare. Его очистка и привязка к OpenCL — не формальность, а аккуратная точка входа для анализируемых данных.

   cPrepare.Clear();
   cPrepare.SetOpenCL(OpenCL);
   CNeuronBatchNormOCL* norm = NULL;
   CNeuronSpikeQKAttention* att = NULL;
   CNeuronSpikeConvBlock* conv = NULL;
   uint index = 0;
   uint units = MathMax(dimension - 2, 1);

Сама последовательность внутри cPrepare выстроена достаточно элегантно. Сначала используется батч-нормализация без нелинейности. Это подчёркивает, что на данном этапе нас интересует не выразительность, а стабилизация распределений.

   norm = new CNeuronBatchNormOCL();
   if(!norm ||
      !norm.Init(0, index, OpenCL, dimension * variables, iBatch, optimization) ||
      !cPrepare.Add(norm))
      ReturnFalse;
   norm.SetActivationFunction(None);

В нашей реализации P-SSE на каждом шаге работает только с одним состоянием рынка, то есть с одним срезом данных. Временного измерения внутри этого шага просто нет. История учитывается исключительно через стек уже закодированных состояний и через рекуррентную динамику самого пространства состояний, но не через входной тензор текущего шага.

Создаваемый далее свёрточный блок работает исключительно в пространстве признаков. Он не анализирует временные зависимости и не ищет паттерны во времени. Его задача иная и гораздо более приземлённая — выделение локальных контекстов внутри набора признаков одного состояния. По сути, он исследует, какие группы признаков ведут себя согласованно, какие комбинации усиливают друг друга и где возникают локальные структуры, характерные для текущего рыночного режима.

   index++;
   conv = new CNeuronSpikeConvBlock();
   if(!conv ||
      !conv.Init(0, index, OpenCL, MathMin(dimension, 3), 1, patch_dimension, units,
                                                 variables, optimization, iBatch) ||
      !cPrepare.Add(conv))
      ReturnFalse;

Однако мы уже не раз говорили, что близость признаков в тензоре описания состояния окружающей среды далеко не всегда ассоциируется с их зависимостью. Поэтому далее мы добавляем механизм QK-attention в спайковом исполнении. Модуль внимания выполняет выравнивание локальных представлений в рамках одного состояния.

Attention здесь выступает как механизм согласования. Он позволяет модели сопоставить локальные контексты между собой и выделить те из них, которые действительно имеют значение для текущей динамики рынка. Иначе говоря, внимание отвечает на простой, но важный вопрос — какие фрагменты текущего состояния заслуживают быть усиленными при формировании итогового представления.

   index++;
   att = new CNeuronSpikeQKAttention();
   if(!att ||
      !att.Init(0, index, OpenCL, units * variables, patch_dimension, 4,
                     (patch_dimension + 3) / 4, optimization, iBatch) ||
      !cPrepare.Add(att))
      ReturnFalse;

В результате связка свёртка + внимание работает как аккуратный фильтр текущего среза рынка. Сначала выявляются локальные структуры в пространстве признаков, затем они приводятся к единому, взвешенному представлению состояния.

Завершается подготовка ещё одним свёрточным блоком, уже работающим с более плотным представлением.

   index++;
   conv = new CNeuronSpikeConvBlock();
   if(!conv ||
      !conv.Init(0, index, OpenCL, patch_dimension * units, patch_dimension * units,
                             patch_dimension, variables, 1, optimization, iBatch) ||
      !cPrepare.Add(conv))
      ReturnFalse;

В сумме этот каскад формирует компактное, но насыщенное описание текущего состояния рынка.

После подготовки данных инициализируется параметрический блок cA. Это ядро динамики, отвечающее за структуру переходов и возмущений.

   index++;
   if(!cA.Init(0, index, OpenCL, patch_dimension * (patch_dimension + 3) / 4 * variables, optimization, iBatch))
      ReturnFalse;
   cA.SetActivationFunction(None);
   CBufferFloat* temp = cA.getWeightsParams();
   if(!temp ||
      !temp.Fill(0))
      ReturnFalse;

Характерный момент — явная инициализация весов нулями. Тем самым модель стартует из нейтрального состояния, без навязанных априорных предпочтений. Динамика не зашита заранее, она формируется исключительно в процессе обучения. Для рынка это принципиально. Мы не предполагаем форму движения, мы позволяем модели её выучить.

Блок cBCDxE объединяет несколько вычислительных путей в единую конструкцию, он подготавливает данные для дальнейшего разветвления на компоненты, соответствующие разным аспектам состояния и возмущений.

   index++;
   if(!cBCDxE.Init(0, index, OpenCL, patch_dimension, patch_dimension,
                   patch_dimension * (2 * patch_dimension + 1 + (patch_dimension + 3) / 4),
                   variables, 1, optimization, iBatch))
      ReturnFalse;

Следующие за ним объекты cB, cC, cDx, cE и cH формируют классическую, но расширенную схему внутренней динамики. При этом все они работают без активационных функций, что подчёркивает линейный характер базовой эволюции состояния. Нелинейность уже была внесена ранее, на этапе кодирования признаков.

   index++;
   if(!cB.Init(0, index, OpenCL, patch_dimension * patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cB.SetActivationFunction(None);
   index++;
   if(!cC.Init(0, index, OpenCL, patch_dimension * patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cC.SetActivationFunction(None);
   index++;
   if(!cDx.Init(0, index, OpenCL, patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cDx.SetActivationFunction(None);
   index++;
   if(!cE.Init(0, index, OpenCL, cA.Neurons(), optimization, iBatch))
      ReturnFalse;
   cE.SetActivationFunction(None);
   index++;
   if(!cH.Init(0, index, OpenCL, patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cH.SetActivationFunction(None);
   if(!cH.Clear())
      ReturnFalse;
   index++;

Отдельного внимания заслуживает инициализация cH. Его явная очистка сразу после создания — это не просто забота о корректности. Это прямое указание на то, что состояние в P-SSE — объект живой, накапливающий историю, и его начальное значение должно быть строго контролируемым. Иначе модель начинает помнить то, чего никогда не было.

Далее следует группа cAE, cAET, cAED. Именно в cAE происходит суммирование детерминированной динамики состояния и параметризованного возмущения. Иначе говоря, это точка, в которой базовая эволюция состояния рынка объединяется с тем самым perturbation-сигналом. Здесь формируется расширенный оператор перехода, отражающий текущее напряжение рыночной среды.

   if(!cAE.Init(0, index, OpenCL, cA.Neurons(), optimization, iBatch))
      ReturnFalse;
   cAE.SetActivationFunction(None);
   index++;

Блок cAET при этом выполняет строго техническую, но крайне важную функцию — транспонирование результата cAE. Это не побочный шаг и не оптимизация ради оптимизации. Явное хранение транспонированной копии позволяет дальше работать с матрицей перехода без неявных преобразований и без дополнительных проходов по памяти, что особенно критично в OpenCL-реализации и в режиме онлайн-анализа.

   if(!cAET.Init(0, index, OpenCL, variables, patch_dimension, (patch_dimension + 3) / 4, optimization, iBatch))
      ReturnFalse;
   index++;

А вот cAED — это уже следующий логический уровень. Здесь формируется симметричная матрица перехода, получаемая прямым умножением cAE на её транспонированную копию cAET.

   if(!cAED.Init(0, index, OpenCL, patch_dimension * patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cAED.SetActivationFunction(None);
   index++;

Такой приём хорошо известен в классических моделях пространства состояний и в численных методах в целом. Он решает сразу две задачи. Во-первых, обеспечивает симметричность и положительную полуопределённость оператора, что напрямую влияет на устойчивость динамики. Во-вторых, позволяет интерпретировать полученную матрицу как энергетическую или корреляционную форму перехода, а не как произвольное линейное преобразование.

В контексте финансовых рынков это имеет вполне прикладной смысл. Мы не хотим, чтобы динамика состояния разгонялась случайным образом под действием локальных импульсов. Возмущения должны усиливать чувствительность модели, но не разрушать её устойчивость. Конструкция вида AE · AEᵀ аккуратно решает эту задачу. Модель остаётся отзывчивой к новым событиям, но её состояние эволюционирует в контролируемом, симметричном пространстве.

Таким образом, связка cAE → cAET → cAED — это ядро механизма Perturbed State Transition. Здесь сначала объединяется динамика и возмущение. Затем обеспечивается корректная геометрия оператора перехода. Именно здесь P-SSE окончательно перестаёт быть обычной SSM и превращается в устойчивый энкодер состояния, способный работать с реальным рынком, а не с лабораторными данными.

Финальный блок, включающий cAH, cBX, cHc и cCHc, завершает формирование выходного представления состояния и замыкает цепочку.

   if(!cAH.Init(0, index, OpenCL, patch_dimension * variables, optimization, iBatch))
      ReturnFalse;
   cAH.SetActivationFunction(None);
   if(!cBX.Init(0, index, OpenCL, cAH.Neurons(), optimization, iBatch))
      ReturnFalse;
   cBX.SetActivationFunction(None);
   index++;
   if(!cHc.Init(0, index, OpenCL, cAH.Neurons(), optimization, iBatch))
      ReturnFalse;
   cHc.SetActivationFunction(None);
   index++;
   if(!cCHc.Init(0, index, OpenCL, cAH.Neurons(), optimization, iBatch))
      ReturnFalse;
   cCHc.SetActivationFunction(None);
//---
   return true;
  }

Все эти компоненты также работают без активаций, сохраняя строгую, контролируемую динамику. В результате на выходе мы получаем чистое, структурированное представление состояния рынка, готовое к использованию в последующих модулях.

В целом метод инициализации хорошо иллюстрирует философию всей реализации. Здесь нет случайных элементов. Каждый объект появляется в строго определённом месте и решает конкретную задачу. Архитектура сложная, но не перегруженная: она остаётся дисциплинированной, как и положено модели, предназначенной для работы с рынком в реальном времени. Именно такая аккуратная, почти консервативная инженерия и позволяет теоретически сильному фреймворку уверенно чувствовать себя в прикладной торговой среде.

Алгоритм прямого прохода в P-SSE предстает как логичная, пошаговая эволюция представления текущего состояния рынка. На каждом шаге мы работаем исключительно с одним срезом, одним состоянием, и вся дальнейшая динамика строится вокруг него. Такой подход отражает суть потокового анализа: рынок меняется постоянно, и нам необходимо обрабатывать каждый новый импульс быстро и без лишних операций.

bool CNeuronPSSE::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cA.FeedForward())
         ReturnFalse;
     }

Первым этапом в прямом проходе идет работа с блоком cA, который при обучении аккуратно обновляет внутренние параметры динамики. Обновление матрицы переходов осуществляется только в процессе обучения. В режиме прогнозирования этот шаг пропускается. Используется ранее сформированная матрица переходов, что обеспечивает мгновенный отклик модели на новые данные без повторной подстройки.

Далее данные проходят через каскад подготовки признаков — cPrepare. Здесь происходит последовательная обработка: батч-нормализация выравнивает распределение признаков, свёрточные блоки выявляют локальные структуры, а спайковый attention аккуратно сопоставляет их внутри состояния, подчеркивая наиболее значимые паттерны.

   CNeuronBaseOCL* prev = NeuronOCL;
   CNeuronBaseOCL* curr = NULL;
   for(int i = 0; i < cPrepare.Total(); i++)
     {
      curr = cPrepare[i];
      if(!curr ||
         !curr.FeedForward(prev))
         ReturnFalse;
      prev = curr;
     }

Важно, что свёртка работает только в пространстве признаков. Внимание не добавляет временного измерения, а лишь упорядочивает локальные контексты, формируя целостное, согласованное представление текущего состояния.

Следующий этап — разложение выходов cBCDxE на отдельные каналы cB, cC, cDx и cE, каждая часть которых несет информацию о специфических аспектах состояния или возмущения.

   if(!cBCDxE.FeedForward(prev))
      ReturnFalse;
   if(!DeConcat(cB.getOutput(), cC.getOutput(), cDx.getOutput(), cE.getOutput(), cBCDxE.getOutput(),
                cB.Neurons() / iVariables, cC.Neurons() / iVariables,
                cDx.Neurons() / iVariables, cE.Neurons() / iVariables, iVariables))
      ReturnFalse;

Блок cAE объединяет динамику и возмущение в единый оператор перехода, а cAET обеспечивает его транспонирование для дальнейших линейных операций.

   if(!PerturbedMatrix(cA.AsObject(), cE.AsObject(), cAE.AsObject(), 0.01f,
                                    cE.Neurons() / iVariables, iVariables))
      ReturnFalse;
   uint AE_dimension = cAE.Neurons() / (iDimension * iVariables);
   if(!Normilize(cAE.getOutput(), AE_dimension))
      ReturnFalse;
   if(!cAET.FeedForward(cAE.AsObject()))
      ReturnFalse;
   if(!MatMul(cAE.getOutput(), cAET.getOutput(), cAED.getOutput(), iDimension,
                                  AE_dimension, iDimension, iVariables, true))
      ReturnFalse;

Симметричная матрица cAED, формируемая через произведение cAE · cAET, гарантирует устойчивость и корректность эволюции, сохраняя положительную полуопределённость оператора.

После этого формируется окончательное представление состояния через серию линейных и нормализующих операций: комбинация выходов cAH, контекста входных признаков через cBX, корректировка через остаточные пути cCHc и локальная интеграция с cDx.

//---
   if(!cH.SwapOutputs())
      ReturnFalse;
   if(!MatMul(cAED.getOutput(), cH.getPrevOutput(), cAH.getOutput(), iDimension, iDimension, 1, iVariables, true))
      ReturnFalse;
   if(!MatMul(cB.getOutput(), prev.getOutput(), cBX.getOutput(), iDimension, iDimension, 1, iVariables, true))
      ReturnFalse;
   if(!SumAndNormilize(cAH.getOutput(), cBX.getOutput(), cHc.getOutput(), iDimension, false, 0, 0, 0, 1))
      ReturnFalse;
   if(!MatMul(cC.getOutput(), cHc.getOutput(), cCHc.getOutput(), iDimension, iDimension, 1, iVariables, true))
      return false;
   if(!SumAndNormilize(cCHc.getOutput(), cDx.getOutput(), cH.getOutput(), iDimension, true, 0, 0, 0, 1))
      ReturnFalse;

В сумме это обеспечивает сбалансированное, информативное и устойчивое кодирование одного состояния рынка, готовое для сохранения и дальнейшего использования.

И наконец, вызов одноименного метода родительского класса сохраняет результат в стек.

   if(!CNeuronAddToStack::feedForward(cH.AsObject()))
      ReturnFalse;
//---
   return true;
  }

Каждый срез проходит через P-SSE только один раз, а стек обеспечивает доступ к прошлым состояниям без повторной обработки. Такой механизм исключает излишние вычисления и позволяет поддерживать высокую скорость онлайн-анализа, что особенно важно для рыночных потоков с высокой частотой событий.

В результате алгоритм прямого прохода в P-SSE аккуратно формирует структурированное, согласованное и стабильное представление текущего состояния рынка, которое учитывает как локальные признаки, так и глобальную динамику через perturbation. Это превращает P-SSE в полноценный энкодер, оптимизированный для реального времени, способный работать с финансовыми потоками так, чтобы каждый новый импульс обрабатывался эффективно и без потери информации.

Метод calcInputGradients — это сердцевина механизма обратного распространения ошибки. Он демонстрирует, как аккуратно распределяется градиент по сложной, многоканальной архитектуре P-SSE, сохраняя при этом физический смысл каждого блока и обеспечивая стабильное обучение в онлайн-режиме.

bool CNeuronPSSE::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      ReturnFalse;
   if(!CNeuronAddToStack::calcInputGradients(cH.AsObject()))
      ReturnFalse;

Сначала метод передаёт управление родительскому классу. Это отражает фундаментальный принцип P-SSE: текущее скрытое состояние cH сохраняется в стек, и градиент распространяется сначала по накопленной истории, а затем — по текущему срезу. Таким образом, модель корректно учитывает влияние прошлых состояний на ошибку без дублирования вычислений.

Далее идёт последовательная работа с выходными каналами последних слоёв. Вызовы DeActivation для cCHc и cDx аккуратно снимают эффекты активации, перенося градиенты к исходным линейным представлениям.

   if(!DeActivation(cCHc.getOutput(), cCHc.getGradient(), cH.getGradient(), cCHc.Activation()))
      ReturnFalse;
   if(!DeActivation(cDx.getOutput(), cDx.getGradient(), cH.getGradient(), cDx.Activation()))
      ReturnFalse;

После этого MatMulGrad распределяет градиенты через линейные связи каналов cC, cHc и cCHc. Каждое вычисление учитывает как размерность признаков, так и количество переменных, что критично для многоканальных финансовых данных.

   if(!MatMulGrad(cC.getOutput(), cC.getGradient(), cHc.getOutput(), cHc.getGradient(),
                  cCHc.getGradient(), iDimension, iDimension, 1, iVariables, true))
      return false;
   Deactivation(cC);
   Deactivation(cHc);

Обработка блоков cAH и cBX аналогична. Сначала снимается активация, затем градиенты аккуратно передаются к предыдущим слоям. Для блока cB через MatMulGrad градиент передаётся дальше в подготовительный каскад cPrepare, обеспечивая корректное распределение ошибок по всем компонентам, участвующим в формировании выходного состояния.

   if(!DeActivation(cAH.getOutput(), cAH.getGradient(), cHc.getGradient(), cAH.Activation()))
      ReturnFalse;
   if(!DeActivation(cBX.getOutput(), cBX.getGradient(), cHc.getGradient(), cBX.Activation()))
      ReturnFalse;
//---
   CNeuronBaseOCL* next = cPrepare[-1];
   CNeuronBaseOCL* curr = NULL;
   if(!next ||
      !MatMulGrad(cB.getOutput(), cB.getGradient(), next.getOutput(), cBX.getPrevOutput(),
                  cBX.getGradient(), iDimension, iDimension, 1, iVariables, true))
      ReturnFalse;

Особое внимание уделено блокам динамики и возмущения: cAED и cAE. Градиенты проходят через умножение матриц и транспонирование.

   if(!MatMulGrad(cAED.getOutput(), cAED.getGradient(), cH.getPrevOutput(), cAH.getPrevOutput(),
                  cAH.getGradient(), iDimension, iDimension, 1, iVariables, true))
      ReturnFalse;
   uint AE_dimension = cAE.Neurons() / (iDimension * iVariables);
   if(!MatMulGrad(cAE.getOutput(), cAE.getPrevOutput(), cAET.getOutput(), cAET.getGradient(),
                  cAED.getGradient(), iDimension, AE_dimension, iDimension, iVariables, true))
      ReturnFalse;
   if(!cAE.CalcHiddenGradients(cAET.AsObject()) ||
      !SumAndNormilize(cAE.getGradient(), cAE.getPrevOutput(), cAE.getGradient(), AE_dimension,
                                                                            false, 0, 0, 0, 1))
      ReturnFalse;

Затем аккуратно вычисляем скрытые градиенты, а последующее суммирование гарантирует учет градиентов от двух информационных потоков.

Метод PerturbedMatrixGrad обеспечивает корректное распространение ошибки через объединение динамики и возмущения, сохраняя смысл оператора Perturbed State Transition. Это ключевой момент: градиенты распределяются не хаотично, а в точности повторяют структуру прямого прохода.

   if(!PerturbedMatrixGrad(cA.AsObject(), cE.AsObject(), cAE.AsObject(), 0.01f,
                                       cE.Neurons() / iVariables, iVariables))
      ReturnFalse;
   Deactivation(cA);
   Deactivation(cE);

После этого отдельные каналы конкатенируются, чтобы восстановить совместное представление, готовое к передаче в подготовительный каскад.

   if(!Concat(cB.getGradient(), cC.getGradient(), cDx.getGradient(), cE.getGradient(), cBCDxE.getGradient(),
              cB.Neurons() / iVariables, cC.Neurons() / iVariables,
              cDx.Neurons() / iVariables, cE.Neurons() / iVariables, iVariables))
      ReturnFalse;

Далее градиенты проходят обратно через все слои cPrepare в обратном порядке, с учётом активаций, нормализаций и специфической структуры внимания и свёртки.

   if(!next.CalcHiddenGradients(cBCDxE.AsObject()))
      ReturnFalse;
   if(!next.Activation() != None)
      if(!DeActivation(next.getOutput(), next.getPrevOutput(), next.getPrevOutput(), next.Activation()))
         ReturnFalse;
   if(!SumAndNormilize(next.getGradient(), next.getPrevOutput(), next.getGradient(), iDimension, false, 0, 0, 0, 1))
      ReturnFalse;
//---
   for(int i = cPrepare.Total() - 2; i >= 0; i++)
     {
      curr = cPrepare[i];
      if(!curr ||
         !curr.CalcHiddenGradients(next))
         ReturnFalse;
      next = curr;
     }

Это обеспечивает полное и корректное распространение ошибки по всем компонентам текущего среза, без потери информации и без нарушения структурной логики P-SSE.

В завершение метод передаёт градиенты на уровень объекта исходных данных, замыкая цепочку обратного распространения.

   if(!NeuronOCL.CalcHiddenGradients(next))
      ReturnFalse;
//---
   return true;
  }

В совокупности весь метод формирует стабильный, аккуратный и контролируемый поток градиентов, который точно повторяет структуру прямого прохода, обеспечивает устойчивое обучение и позволяет P-SSE корректно накапливать знания о динамике рынка без избыточных вычислений.

В итоге CNeuronPSSE становится тем самым связующим звеном между теорией и практикой. Он аккуратно переносит идеи авторской работы в среду реального трейдинга, учитывая требования онлайн-анализа, ограничения по скорости и необходимость строгого контроля вычислений. Архитектура получилась плотной, но логичной. Без лишней экзотики. Полный код объекта и всех его методов представлен во вложении.

Заключение

Подводя итог, можно с уверенностью сказать, что предложенная реализация модуля P-SSE представляет собой полноценный энкодер признаков, способный работать с потоками рыночных данных в реальном времени. Архитектура аккуратно сочетает локальный анализ признаков через свёртку, механизм внимания для выделения значимых паттернов, интеграцию динамики и возмущений, а также аккуратное хранение и использование исторических состояний в стеке.

Прямой проход алгоритма обеспечивает эффективное формирование структурированного представления текущего состояния рынка, а распределение градиентов ошибки реализовано с высокой точностью, позволяя корректно обучать все элементы модели без дублирования вычислений. Такой подход делает систему одновременно выразительной и стабильной, способной быстро реагировать на новые рыночные импульсы, не теряя накопленной информации.

В практическом контексте финансовых рынков это означает возможность анализа микроимпульсов, прогнозирования краткосрочной динамики и построения предсказательных моделей с высокой скоростью и точностью. Представленная архитектура демонстрирует, как идеи пространства состояний могут быть переосмыслены для современного трейдинга, сохраняя строгую математическую основу и одновременно адаптируясь к требованиям онлайн-анализа.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (3551.22 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Особенности написания Пользовательских Индикаторов

Написание пользовательских индикаторов в торговой системе MetaTrader 4

Знакомство с языком MQL5 (Часть 25): Создание советника для торговли по графическим объектам (II)

В этой статье объясняется, как создать советник, который взаимодействует с графическими объектами, особенно с трендовыми линиями, чтобы выявлять потенциальные пробои и развороты и торговать по ним. Вы узнаете, как советник подтверждает действительность сигналов, управляет частотой торговли и поддерживает согласованность с выбранными пользователем стратегиями.

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Двунаправленная LSTM и квантовые вычисления для предсказания направления движения

Статья представляет воспроизводимую реализацию гибридной квантово-нейросетевой модели для алгоритмической торговли на Forex без использования реального квантового оборудования. Фиксированная трёхкубитная схема в IBM Qiskit преобразует статистики скользящего окна (средняя доходность, волатильность, размах) в распределение вероятностей, из которого вычисляются 7 квантовых метрик. Эти признаки интегрируются в архитектуру двунаправленной LSTM с регуляризацией и механизмами борьбы с дисбалансом классов (в т.ч. focal loss и sampler).