Торгуем опционы без опционов (Часть 4): Более сложные опционные стратегии

Введение

Теория торговли опционами основана на формуле Блэка-Шоулза, которая, в свою очередь, основана на предположении, что движение базового актива подчиняется случайному закону с нормальным распределением приращений цены. Данное предположение уверенно опровергается практикой (см. рис. 1), а значит и теория в целом — ошибочна.

Для сравнения на рис.1 приведены графики распределения изменений цены для нормального распределения  (Normal distribution — темно-синяя линия) и реального усредненного распределения с "толстыми хвостами" ("Fat tail" distribution — темно-зеленая линия) для некоего произвольного базового актива. Видна принципиальная разница между ними — главным образом в области больших изменений цены. По оси ординат отложена частота появления соответствующих ценовых приращений в указанном на оси абсцисс интервале.

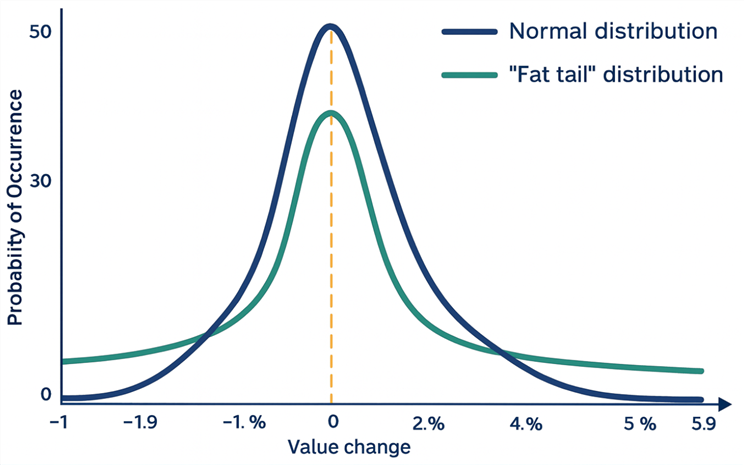
Рис.1 Сравнение графиков нормального распределения приращений цены и реального распределения с "толстыми хвостами".

Кроме того, рыночные данные обладают свойством фрактальности (самоподобия). Это значит, что графики за день, неделю или месяц выглядят структурно похоже. Это свойство однозначно не укладывается в рамки простого случайного блуждания.

И наконец, существует такое явление как кластеризация исторической волатильности. Это явление не описывается самим распределением на одном временном интервале, но важно для понимания динамики. Историческая волатильность непостоянна: периоды высокой волатильности имеют тенденцию группироваться вместе. Также как и периоды низкой. После сильного движения обычно следует череда других сильных движений. Это полностью противоречит гипотезе о независимости приращений цен активов.

Это явление (кластеризация исторической волатильности) мы попытаемся проверить и использовать в торговле опционами в следующей статье данного цикла.

Ошибочность теории не означает, что ее нельзя использовать в практическом применении. Хотя бы частично.Так называемые "толстые хвосты" в подавляющем большинстве случаев обусловлены новостным фоном, который заранее предсказать не всегда возможно, а вернее — почти всегда невозможно. Поэтому, если учитывать их в расчете, например, исторической волатильности HV, получится занижение средней прибыли, которая может уже не компенсировать потери от "толстых хвостов". Поэтому, более правильно ограничивать такие риски. Об этом пойдет речь дальше.

Экспирация опционной конструкции по уровню для стратегий, основанных на купленных опционах

В предыдущей статье мы рассмотрели наряду с другими опционные стратегии, основанные на покупке опционов. При практической проверке выяснилось, что было бы неплохо досрочно экспирировать опционную конструкцию при достижении ценой базового актива статистически обоснованного уровня (здесь и далее речь идет об уровнях ребалансировки опционной конструкции).

В реальной опционной торговле не всегда возможно это сделать из-за ограниченной ликвидности в таких случаях (особенно актуально на бирже MOEX). При эмуляции опционов, с досрочной экспирацией проблем из-за ликвидности, как правило, нет. Добавим в наш эксперт эту возможность.

Для начала, добавим внешний задаваемый параметр в виде номера опционного уровня, при достижении которого опционная конструкция должна экспирироваться. Это целое число, большее нуля. Также, добавим флаг управления включением/выключением режима экспирации по уровню. С приведенными ниже настройками опционная конструкция закроется на седьмом опционном уровне.

// ---------------------------------------------------------------------
input bool      UseExpirationPriceLevel = true;                       // Use Expiration Price Level
input int       ExpirationPriceLevel = 7;                             // Expiration Price Level
// ---------------------------------------------------------------------

Теперь модернизируем наш эксперт. Если включена экспирация по уровню, то при увеличении опционного уровня ребалансировки, проверяем его номер и, если достигли заданного для экспирации значения, закрываем позиции и переходим в режим остановки торговли до следующего дня. Данный алгоритм представлен в коде ниже (полный код находится в файле Article4-OptionTrader.mq5).

// ---------------------------------------------------------------------
//      Проверка необходимости экспирации опционов:
// ---------------------------------------------------------------------
bool  CheckExpiration(const datetime _curr_time, const double _bid_price, const double _ask_price)
{
  //  Если включена экспирация по УРОВНЮ:
  if(UseExpirationPriceLevel == true)
  {
    //  Проверим необходимость экспирации по УРОВНЮ:
    if(OptionConstruction == ENUM_OPTION_CONSTRUCTION_RISING || OptionConstruction == ENUM_OPTION_CONSTRUCTION_STRADDLE_LONG || OptionConstruction == ENUM_OPTION_CONSTRUCTION_STRANGLE_LONG)
    {
      if(live_option_level_sign == 1)
      {
        price_auto_expiration = UpPriceLevel_Array[ExpirationPriceLevel - 1];
        if(_bid_price >= price_auto_expiration)
        {
          return(true);
        }
      }
      else if(live_option_level_sign == -1)
      {
        price_auto_expiration = DnPriceLevel_Array[ExpirationPriceLevel - 1];
        if(_ask_price <= price_auto_expiration)
        {
          return(true);
        }
      }
    }
  }

  return(false);
}

Прежде чем проводить экспирацию по уровню, проверяем тип опционной конструкции. Напомним, что стратегия должна быть основана на купленных опционах. Далее, сравниваем текущие значения цен Bid/Ask с ценой опционного уровня экспирации, номер которого задан во внешнем параметре ExpirationPriceLevel.

Теперь проверим работу экспирации по уровню в торговле. На рис. 2 представлен результат работы нашего эксперта. В данном случае был задан уровень экспирации равный четырем. Мы видим, что отработав три уровння ребалансировки опционной конструкции, все позиции были закрыты на четвертом уровне (с точностью до текущего спреда инструмента).

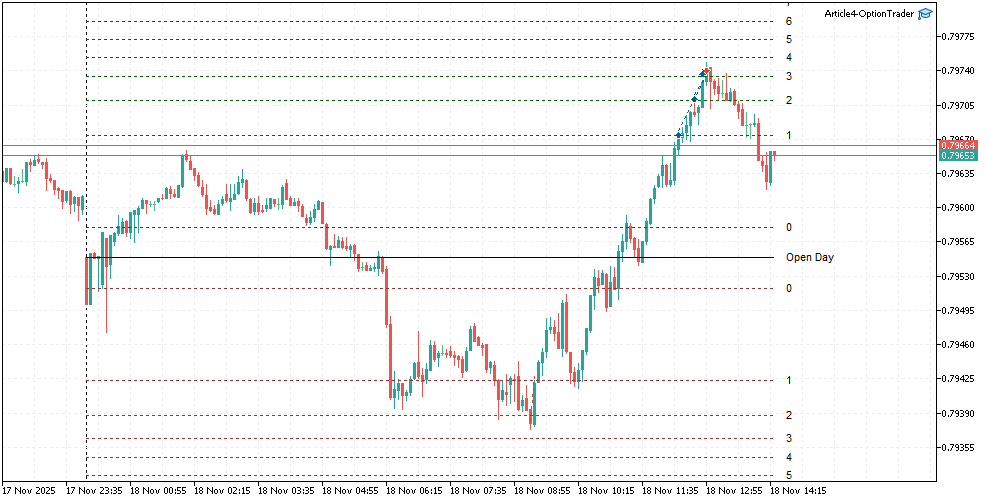
Рис.2 Экспирация опционной конструкции Long Straddle по уровню

Номер уровня для экспирации рекомендуется определять на основе статистики по исторической волатильности базового актива. Также, для определения оптимального уровня экмпирации возможно использование встроенного тестера в терминале Meta Trader 5.

Адаптивный расчет исторической волатильности HV

Прежде чем двигаться дальше, усовершенствуем алгоритм расчета исторической волатильности HV. Вместо жесткого задания длины окна во входных параметрах, будем подбирать число дней для расчета адаптивно. Меняя длину окна от трех до сорока (диапазон оптимизации выбран эмпирически), подбираем окно с минимальным средним разбросом от реальных значений.

Добавим в наш эксперт параметры для задания пределов при оптимизации окна расчета исторической волатильности HV:

// ---------------------------------------------------------------------
input int  OptimizeDayNumberMin = 3;    // Optimize Days Number Min
input int  OptimizeDayNumberMax = 40;   // Optimize Days Number Max
// ---------------------------------------------------------------------

Задается минимальное и максимальное число завершенных дней, среди которых ищется оптимальное (с точки зрения ошибки) окно для расчета исторической волатильности HV.

Будем использовать для расчетов стандартную библиотеку статистики, поставляемую в составе терминала Meta Trader 5. Для каждой длины окна проводим следующую последовательность расчетов:

1. Рассчитываем медианное значение волатильности HV для текущего окна wnd  — получаем значение MedianHV(wnd).
2. Вычисляем массив абсолютных разностей между полученным на предыдущем шаге медианным значением MedianHV(wnd) и истинным диапазоном для каждого дня в массиве цен базового актива — получаем массив ошибок (по абсолютному значению) Error[i] = |HV[i] - MedianHV(wnd)|.
3. Рассчитываем медианное значение в полученном массиве ошибок — получаем ошибку определения HV для данной длины окна по сравнения с реальностью — MedianErr = Median(Error[]).

Повторим расчеты п.1-3 для каждого окна wnd из заданного диапазона оптимизации и получим массив ошибок MedianErr[]. Минимальной ошибке будет соответствовать оптимальное (из рассчитанных по предыдущим волатильностям) окно для текущего дня. Его и используем для расчета HV.

ПРИМЕЧАНИЕ:

Медианные значения используем для того, чтобы отбросить из расчетов экстремально высокие и экстремально низкие значения исторической волатильности. Это уменьшит влияние "толстых хвостов" реального распределения приращений цен на расчет значения HV.

Полный код адаптивного расчета исторической волатильности HV находится в файле HistoryVolatilityA4.mqh, приложенном к данной статье. Рассмотрим основную часть кода, представленную ниже:

#include  <Object.mqh>
#include  <Arrays\List.mqh>
// ---------------------------------------------------------------------
#include  <Math\Stat\Stat.mqh>
// --------------------------------------------------------------------

// =====================================================================
//  Расчет средне-дневной волатильности (СДД):
// =====================================================================
class ResultVolatility : public CObject
{
private:
  int     days_number;
  double  volatility_error;
  double  volatility;

public:
  // --------------------------------------------------------------------
  //  Конструктор:
  // --------------------------------------------------------------------
  ResultVolatility(const int _days_number, const double _volatility_error, const double _volatility)
  :
  days_number(_days_number),
  volatility_error(_volatility_error),
  volatility(_volatility),
  CObject()
  {
  }
  // --------------------------------------------------------------------
  int     DaysNumber()
  {
    return(this.days_number);
  }
  // --------------------------------------------------------------------
  double  VolatilityError()
  {
    return(this.volatility_error);
  }
  // --------------------------------------------------------------------
  double  Volatility()
  {
    return(this.volatility);
  }
};
// --------------------------------------------------------------------
class TDailyVolatility
{
protected:
  string    data_symbol;
  datetime  data_start_time;
  datetime  data_end_time;

  int       min_days_number;
  int       max_days_number;

  MqlRates  daily_data_rates_Array[ ];
  double    daily_range_Array[];
  double    daily_errors_Array[];
  CList*    results_List;

  int       optimal_days_number;
  double    optimal_volatility;
  double    optimal_volatility_error;

  bool      data_prepared_flag;
  bool      volatility_calculated_flag;

public:
  // --------------------------------------------------------------------
  //  Конструктор:
  // --------------------------------------------------------------------
  TDailyVolatility(const string _symbol, const int _min_days, const int _max_days)
  :
  data_symbol(_symbol),
  min_days_number(_min_days),
  max_days_number(_max_days),
  data_prepared_flag(false),
  volatility_calculated_flag(false)
  {
    this.results_List = new CList();
    this.results_List.FreeMode(true);
  }

protected:
  // ---------------------------------------------------------------------
  //  Получение данных временного ряда в заданном временном диапазоне:
  // ---------------------------------------------------------------------
  bool  PrepareData(const datetime _start_time, const int _days_number)
  {
    if(CopyRates(this.data_symbol, PERIOD_D1, _start_time, _days_number, this.daily_data_rates_Array) <= 0)
    {
      this.data_prepared_flag = false;
    }
    else
    {
      this.data_prepared_flag = true;
      this.data_start_time = this.daily_data_rates_Array[0].time;
      this.data_end_time = this.daily_data_rates_Array[ArraySize(this.daily_data_rates_Array) - 1].time;
    }
   
    return(this.data_prepared_flag);
  }

protected:
  // ---------------------------------------------------------------------
  //  Волатильность суток в указанном диапазоне дней:
  // ---------------------------------------------------------------------
  bool  CalcDayRange(const int _day_start_index, const int _days_number)
  {
    if(this.data_prepared_flag != true)
    {
      return(false);
    }

    int   max_day_index = MathMin(_days_number, ArraySize(this.daily_data_rates_Array));
    ArrayResize(this.daily_range_Array, _days_number);

    for(int i = 0; i < max_day_index; i++)
    {
      this.daily_range_Array[i] = this.daily_data_rates_Array[i + _day_start_index].high - this.daily_data_rates_Array[i + _day_start_index].low;
    }

    return(true);
  }
  // ---------------------------------------------------------------------

public:
  // ---------------------------------------------------------------------
  //  Расчет ADR:
  // ---------------------------------------------------------------------
  bool  CalculateADR(const datetime _current_time)
  {
    this.volatility_calculated_flag = false;

    //  Получим данные временного ряда:
    if(this.PrepareData(_current_time, max_days_number - min_days_number + 1) != true)
    {
      return(false);
    }

    ArrayResize(daily_errors_Array, max_days_number - min_days_number + 1);
    if(CalcDayRange(0, max_days_number - min_days_number + 1) != true)
    {
      return(false);
    }

    double  curr_volatitlity_Arr[];
    double  curr_volatitlity_error_Arr[];
    double  curr_median_volatility;
    double  curr_median_volatility_error;

    this.results_List.Clear();
    for(int wnd_length = min_days_number; wnd_length < max_days_number; wnd_length++)
    {
      ArrayResize(curr_volatitlity_Arr, wnd_length);
      ArrayResize(curr_volatitlity_error_Arr, wnd_length);

      ArrayCopy(curr_volatitlity_Arr, this.daily_range_Array, 0, max_days_number - min_days_number - wnd_length, wnd_length);

      curr_median_volatility = MathMedian(curr_volatitlity_Arr);
      for(int i = 0; i < wnd_length; i++)
      {
        curr_volatitlity_error_Arr[i] = MathAbs(curr_volatitlity_Arr[i] - curr_median_volatility);
      }
      curr_median_volatility_error = MathMedian(curr_volatitlity_error_Arr);
      this.results_List.Add(new ResultVolatility(wnd_length, curr_median_volatility_error, curr_median_volatility));
    }

    if(this.results_List.Total() <= 0)
    {
      return(false);
    }

    this.optimal_volatility_error = DBL_MAX;

    ResultVolatility* curr_result = this.results_List.GetFirstNode();
    while(true)
    {
      if(curr_result.VolatilityError() < this.optimal_volatility_error)
      {
        this.optimal_days_number = curr_result.DaysNumber();
        this.optimal_volatility_error = curr_result.VolatilityError();
        this.optimal_volatility = curr_result.Volatility();
      }
      curr_result = this.results_List.GetNextNode();
      if(CheckPointer(curr_result) == POINTER_INVALID)
      {
        break;
      }
    }
  
    this.volatility_calculated_flag = true;
    return(true);
  }
};

Класс для хранения результатов ResultVolatility унаследован от класса CObject из стандартной библиотеки терминала Meta Trader 5. Это сделано для того, чтобы можно было использовать стандартные списки CList для манипуляции результатами. Объект класса ResultVolatility содержит результаты расчетов на одном шаге (одном значении окна) адаптивного вычисления волатильности. Это члены-данные со значениями: длина окна, ошибка расчета волатильности и рассчитанная волатильность.

Конструктор класса для расчета волатильности TDailyVolatility(const string symbol, const int min_days, const int max_days) принимает в качестве аргументов следующие значения:

• symbol  — имя рабочего символа (может отличаться от символа графика, на котором установлен эксперт,
• min_days  — минимальное значение окна при оптимизации для расчета исторической волатильности HV (по умолчанию, принято равным трем),
• max_days  — максимальное значение окна при оптимизации для расчета исторической волатильности HV (по умолчанию, принято равным сорока).

Основной метод, который вызывается для расчета исторической волатильности HV:

bool  CalculateADR(const datetime _current_time)

В качестве аргумента передается текущее время — например, время открытия нового бара на графике, на который установлен эксперт. Данный метод проводит всю цепочку адаптивного вычисления исторической волатильности: загружает временной ряд с историческими данными, расчитывает волатильности по дням, медианное значение и оптимальное окно.

После успешного вызова метода TDailyVolatility::CalculateADR (в этом случае он возвращает true) можно получать рассчитанные оптимальные параметры с помощью простых методов:

double  GetOptimalVolatility();    // получить рассчитанную волатильность
double  GetOptimalVolatilityVar(); // получить рассчитанную ошибку волатильности
int     GetOptimalDaysNumber();    // получить рассчитанное значение оптимального окна - число дней

Повторный расчет волатильности в эксперте происходит раз в сутки с открытием нового дня и при рестарте эксперта для текущих незавершенных суток. После расчета обновляются опционные уровни и визуализация их на графике.

Контроль рисков для стратегий, основанных на проданных опционах

Как было показано в предыдущей статье, опционные стратегии, основанные на проданных опционах, имеют неограниченный риск. Оказывается, есть способ, усложнив опционную конструкцию, ограничить этот риск. Это можно сделать добавлением еще двух опционов в конструкцию — Long Put и Long Call.

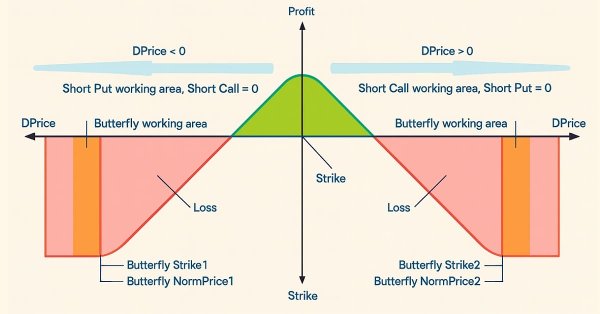
Страйки этих опционов должны быть больше максимального опционного уровня в положительной и отрицательной области значений DPrice (см. рис.7 в предыдущей статье). Тогда результирующий график зависимости значения PnL (профит/убыток) от относительного изменения цены DPrice примет вид, показанный на рис.5 и рис.7.

Как видно на рисунках, получился грфик с характерным изломом справа и слева от нуля, который (график) называют "бабочкой" (или "кондором", в зависимости от ориентации графика вверх/вниз). По-английски такую конструкцию будем называть Butterfly  — добавляем это слово в конце общего названия опционной конструкции.

Если помотреть график зависимости дельты опционной конструкции (Delta) от относительного изменения цены (DPrice) на рис.4, то мы увидим, как после достижения высшей точки со значением дельты около единицы (или минус единицы), кривая дельты на графике устремляется к нулевому значению. Это результат работы купленных опционов Put/Call с соответствующими настройками.

Таким образом, позиции плавно закрываются и, при дальнейшем движении базового актива в неблагоприятную для нас сторону, нарастания убытков не происходит. При обратном движении цены из убыточной области в рабочий диапазон по волатильности HV, опционная позиция восстанавливается до исходного уровня в соответствии с кривой изменения дельты.

Нормирующие цены и страйки для этих дополнительных опционов Long Put / Long Call выбираем, исходя из приемлемого риска. Эти значения (страйк и нормирующий уровень) будем задавать во внешних параметрах эксперта. Между страйком и нормирующей ценой в "зоне Butterfly" ("Butterfly working area" на рис.5 и рис.7) будет происходить плавное сокращение опционной позиции вплоть до полного закрытия. Тем самым ограничивается максимальный риск. "Зону Butterfly" также добавим в визуализатор уровней нашего эксперта.

Реальный график с визуализацией опционных уроыней изображен на рис.3. Параметры опционов для "зоны Butterfly" подобраны таким образом, чтобы закрытие позиций происходило примерно на четверти диапазона волатильности HV. Это позволяет сбалансировать соотношение риск/прибыль для таких или подобных опционных конструкций.

Дополним наш список опционных конструкций новыми стратегиями:

// ---------------------------------------------------------------------
//  Опционная конструкция:
// ---------------------------------------------------------------------
enum ENUM_OPTION_CONSTRUCTION
{
  ENUM_OPTION_CONSTRUCTION_STRADDLE_BUTTERFLY_SHORT = 10,      // Short STRADDLE + Butterfly
  ENUM_OPTION_CONSTRUCTION_STRANGLE_BUTTERFLY_SHORT = 12,      // Short STRANGLE + Butterfly
};
// ---------------------------------------------------------------------

Для расчета опционных уровней в "зоне Short Straddle/Strangle" можно использовать такие же методы как и в стратегии Short Straddle/Strangle из предыдущей статьи. Поскольку функция для зависимости значения дельты "Delta" от относительного изменения цены "DPrice" перестала быть монотонной, то для правильного расчета опционных уровней во всем диапазоне ребалансировки опционной конструкции нам придется разделить область определения функции на два участка: рабочую область и "зону Butterfly". В соответствие с этим участкам добавим отдельные методы расчета:

void CalculateUpPriceLevels(const double _norm_zero_level, double& _strike_price[], double& _norm_price[], double& _limit_price[]) override
void CalculateDnPriceLevels(const double _norm_zero_level, double& _strike_price[], double& _norm_price[], double& _limit_price[]) override
void CalculateButterflyUpPriceLevels(const double _norm_zero_level, double& _strike_price[], double& _norm_price[], double& _limit_price[])
void CalculateButterflyDnPriceLevels(const double _norm_zero_level, double& _strike_price[], double& _norm_price[], double& _limit_price[])

Первые два метода полностью аналогичны методам для конструкции Short Straddle / Short Strangle, а третий и четвертый методы добавлены для расчета опционных уровней в "зоне Butterfly". Они декларированы в классах-потомках от базового класса опционной конструкции ShortStraddleButterflyOptionConstruction и ShortStrangleButterflyOptionConstruction. Сам алгоритм расчета последних двух методов ничем не отличается — это метод деления отрезка пополам (метод дихотомии).

Также добавим внешние параметры для настройки визуализации опционных уровней в "зоне Butterfly":

// ---------------------------------------------------------------------
input color     OptionButterflyUpLevelsTextColor = clrLightYellow;    // Option Butterfly Up Levels Text Color
input color     OptionButterflyUpLevelsColor = clrGreen;              // Option Butterfly Up Levels Color
input ENUM_LINE_STYLE OptionButterflyUpLevelsStyle = STYLE_DOT;       // Option Butterfly Up Levels Line Style
// ---------------------------------------------------------------------
input color     OptionButterflyDnLevelsTextColor = clrLightYellow;    // Option Butterfly Dn Levels Text Color
input color     OptionButterflyDnLevelsColor = clrRed;                // Option Butterfly Dn Levels Color
input ENUM_LINE_STYLE OptionButterflyDnLevelsStyle = STYLE_DOT;       // Option Butterfly Dn Levels Line Style
// ---------------------------------------------------------------------

Пример визуализации рассчитанных уровней для конструкции Short Strangle Butterfly приведен ниже на рис.3. Левая половина показывает верхние (выше цены открытия) опционные уровни, а правая — нижние (ниже цены открыиия) опционные уровни. Уровни рабочей зоны и  "зоны Butterfly" расчитаны для значений, указанных ниже.

input double    StrangleKoeffStrike = 0.1;                            // Strangle Koeff for Strike (0.01...0.90)
input double    ButterflyKoeffStrike = 0.94;                          // Butterfly Koeff for Strike (0.60...2.00)
input double    ButterflyKoeffNorm = 1.345;                           // Butterfly Koeff for Strike (1.00...2.00)

Значение параметра ButterflyKoeffStrike задает положение цены страйка для "зоны Butterfly" — это страйк для опционов Long Put и Long Call. Задается в виде коэффициента, на который умножается значение исторической волатильности HV. В этой зоне дельта опционов Short Put и Short Call равна плюс-минус единице и уже не меняется при дальнейшем росте/падении цены базового актива. Значение дельты опционов "зоны Butterfly" напротив — отрывается от нуля и начинает уменьшать общее значение опционной позиции при дальнейшем росте/падении цены базового актива, вплоть до нуля.

Чем меньше значение параметра ButterflyKoeffStrike, тем раньше начинается уменьшение объема опционной позиции.

Значение параметра ButterflyKoeffNorm задает положение нормировки по HV для опционов Long Put и Long Call. Задается также в виде коэффициента, на который умножается значение исторической волатильности HV для текущего дня. Увеличение значения ButterflyKoeffNorm приводит к растяжению "зоны Butterfly", внутри которой происходит закрытие опционной позиции, то есть получаем более плавное закрытие.

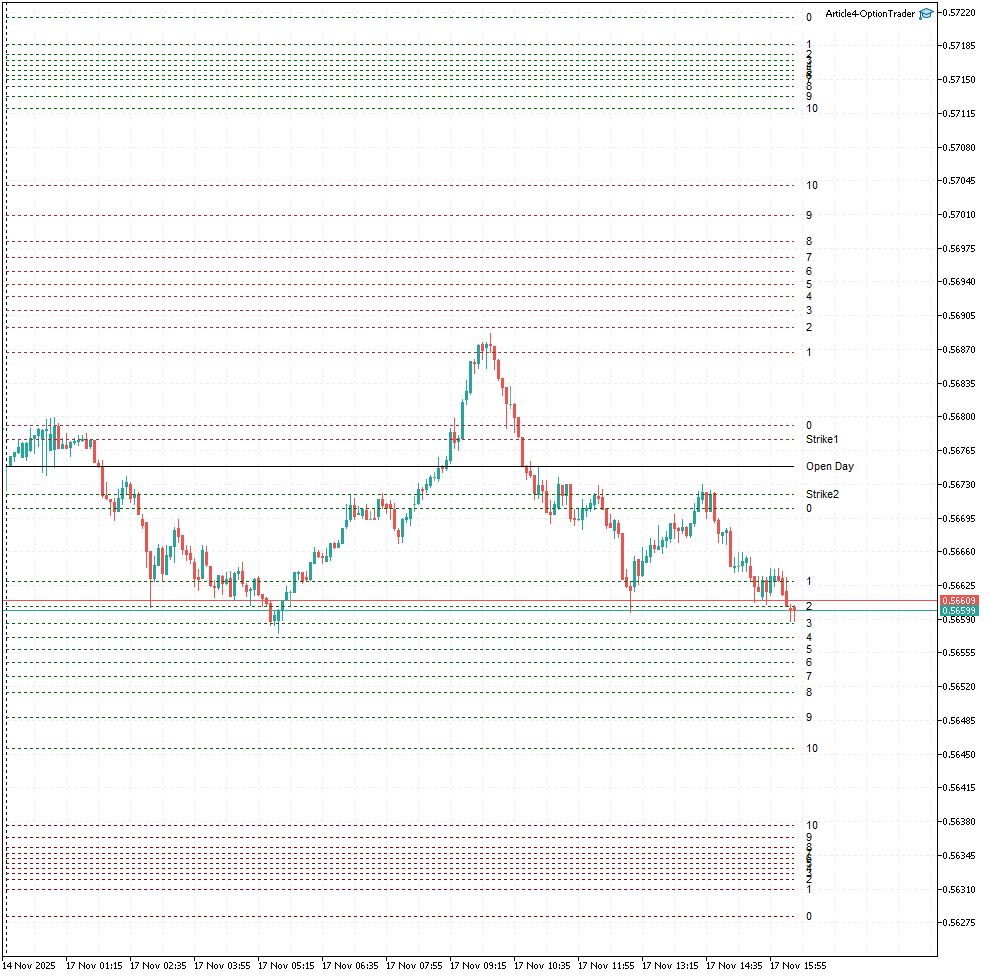
Рис.3 Опционные уровни, рассчитанные для конструкции Short Strangle Butterfly.

Рассмотрим смысл и условия использования Butterfly-конструкций, перечисленных выше.

Продажа стрэдла с "бабочкой" — Short Straddle Butterfly

• Смысл: одновременная продажа опционов колл и пут с одинаковыми страйками;
• Условие использования: если есть уверенность в том, что цена базового актива останется в среднем диапазоне исторической волатильности HV, а направление ее не имеет значения;
• Прибыль: премия, которую платит покупатель за два опциона (при эмуляции отсутствует) + прибыль, накапливающаяся при колебаниях цены внутри диапазона (есть только при эмуляции);
• Риск: ограничен параметрами опционов "бабочки".

Использование стрэдла с "бабочкой" аналогично использованию простого стрэдла, описанного в предыдущей статье.  Пример работы опционной конструкции Short Straddle Butterfly показан на рис.6.

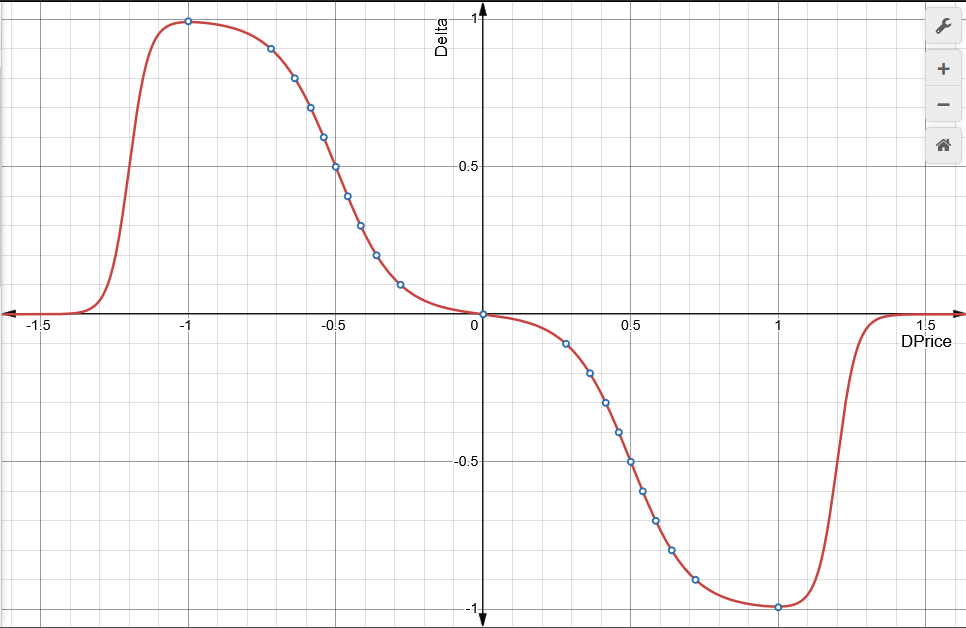
Рис.4 Зависимость значения дельты "Delta" от относительного изменения цены "DPrice" для эмулируемой опционной конструкции Short Straddle Butterfly

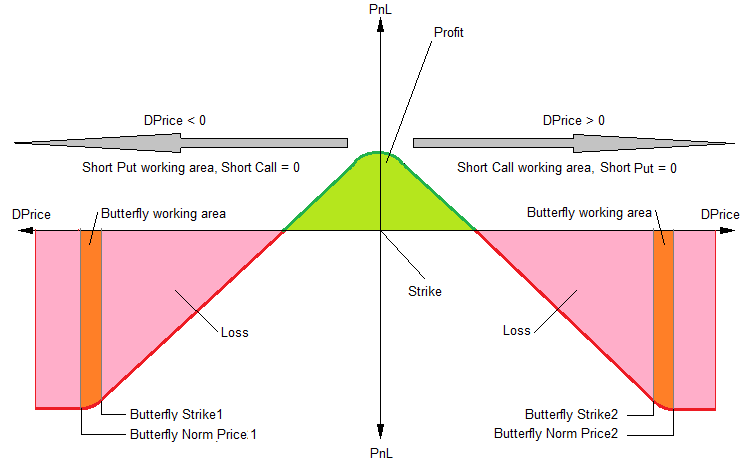
Рис.5 Зависимость значения PnL (профит/убыток) от относительного изменения цены "DPrice" для эмулируемой опционной конструкции Short Straddle Butterfly

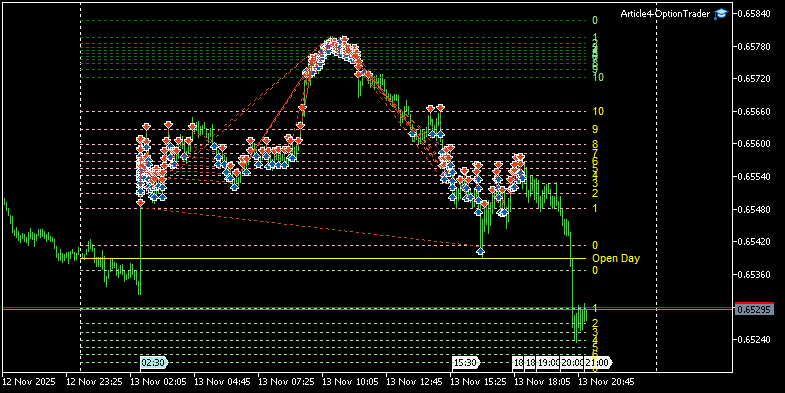
Рис.6 Пример работы опционной конструкции Short Straddle Butterfly

Продажа стрэнгла — Short Strangle Butterfly

• Смысл: одновременная продажа опционов колл и пут с разными страйками, лежащими внутри диапазона исторической волатильности HV;
• Условие использования: если есть уверенность в том, что цена базового актива останется в широком диапазоне, а направление ее не имеет значения;
• Прибыль: премия, которую платит покупатель за два опциона (при эмуляции отсутствует) + прибыль, накапливающаяся при колебаниях цены внутри широкого диапазона;
• Риск: ограничен параметрами опционов "бабочки".

Использование стрэнгла с "бабочкой" аналогично использованию простого стрэнгла, описанного в предыдущей статье.  Пример работы опционной конструкции Short Strangle Butterfly показан на рис.8. В данном случае дальнейшего движения вниз не произошло, но мы предотвратили возможный большой убыток.

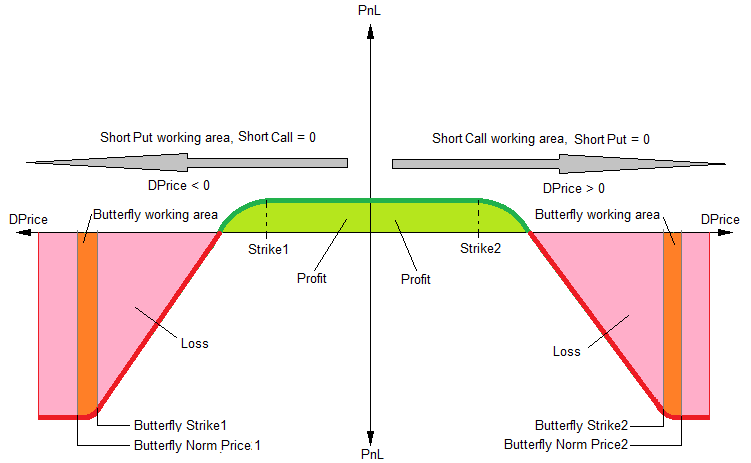
Рис.7 Зависимость значения PnL (профит/убыток) от относительного изменения цены "DPrice" для эмулируемой опционной конструкции Short Strangle Butterfly

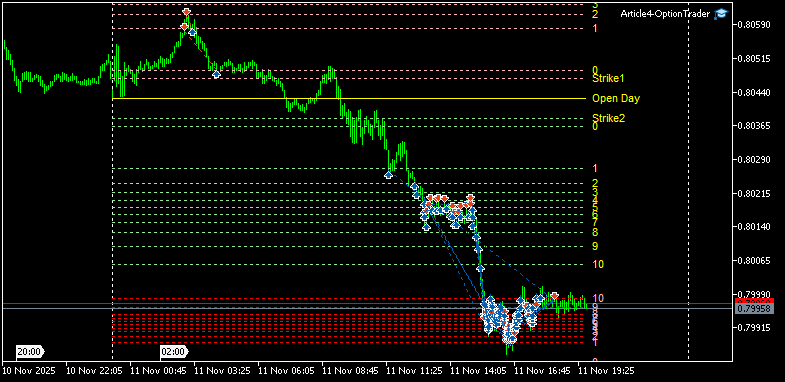
Рис.8 Пример работы опционной конструкции Short Strangle Butterfly

Выбор параметров "бабочки" для стратегий, основанных на продаже опционов, лучше всего проводить по результатам статистического анализа исторической волатильности базового актива. Определяем величину и частоту появления "толстых хвостов", затем тестируем стратегию встроенным тестером Meta Trader'a 5 на предмет получения минимальных потерь на этих участках — оптимизируем параметры "бабочки".

Заключение

В данной статье мы рассмотрели возможные способы снижения риска и увеличения прибыльности для сложных опционных стратегий. В следующей статье цикла рассмотрим еще несколько вариантов использования опционов на практике. В частности, рассмотрим торговлю синтетическими инструментами. А также добавим в наш эксперт новые возможности — торговлю на неттинговых счетах, интерактивное управление некоторыми параметрами и другие.

Кроме того, проведем некоторые статистические исследования для определения оптимальных параметров торговли.

ЗАМЕЧАНИЕ:

Следует также понимать, что торговля опционами (как и другими инструментами) предполагает участие трейдера на всех этапах реализации стратегии — от разработки системы управления средствами и до контроля хода торгов в реальном времени.

В таблице представлены файлы, приложенные к статье:

Название файла	Описание
Article4-OpionTrader.mq5	Файл, содержащий код эксперта, торгующего опционными конструкциями, описанными в статье, используя эмуляцию опционов
CheckNewBar.mqh	Файл, содержащий код класса для проверки появления нового бара на графике терминала Meta Trader 5
OptionEmulatorA4.mqh	Файл, содержащий код классов для эмуляции опционов и опционных конструкций, описанных в статье
PriceLevelsA4.mqh	Файл, содержащий код классов для визуализации опционных уровней на графике терминала Meta Trader 5
HistoryVolatilityA4.mqh	Файл, содержащий код классов для адаптивного расчета исторической волатильности HV