Самоорганизующиеся карты Кохонена в советнике MQL5

Введение: в поисках невидимого порядка

Представьте, что вы смотрите на график валютной пары. Тысячи свечей, миллионы точек данных, бесконечный поток цифр. Где-то в этом хаосе скрыты паттерны, закономерности, повторяющиеся структуры. Но человеческий мозг не может держать в голове одновременно тысячи свечей и находить между ними связи. Нам нужна карта этого хаоса. Нам нужна структура, которая покажет, где похожие рыночные ситуации группируются вместе, а где начинается что-то принципиально новое.

Именно для этого финский ученый Тейво Кохонен в 1982 году изобрел самоорганизующиеся карты — Self-Organizing Maps или SOM. Это не просто очередная нейронная сеть. Это способ заставить компьютер увидеть невидимую структуру данных, найти порядок в хаосе, создать двумерную карту многомерного пространства. И что самое интересное — эта технология, придуманная сорок лет назад для анализа речи, оказалась идеально подходящей для анализа финансовых рынков.

Что такое самоорганизующиеся карты: география рыночного хаоса

Давайте начнем с простой аналогии. Представьте, что вы географ и перед вами стоит задача создать карту неизвестной местности. У вас есть координаты тысяч точек, измерения высот, температур, влажности — множество параметров для каждой точки. Как превратить эту груду чисел в понятную двумерную карту, где похожие места будут рядом, а разные — далеко друг от друга?

Самоорганизующаяся карта Кохонена делает именно это, но с рыночными данными. У нас есть многомерное пространство признаков — цены, объемы, волатильность, изменения за разные периоды, технические индикаторы. Каждая свеча на графике — это точка в этом многомерном пространстве. SOM берет все эти точки и проецирует их на двумерную сетку нейронов, сохраняя при этом топологию — похожие рыночные ситуации оказываются в соседних нейронах карты.

Магия начинается в процессе обучения. Сеть состоит из двумерной решетки нейронов, например двадцать на двадцать — четыреста нейронов. Каждый нейрон имеет вектор весов той же размерности, что и входные данные. Когда мы показываем сети новый паттерн с рынка, она находит нейрон с наиболее похожими весами — это называется Best Matching Unit или BMU. Затем происходит волшебство: не только BMU обновляет свои веса, чтобы стать еще более похожим на входной паттерн, но и его соседи на карте тоже сдвигаются в том же направлении. Чем дальше от BMU, тем слабее влияние.

После обучения на тысячах рыночных ситуаций, карта самоорганизуется. Нейроны в одном углу карты могут отвечать за сильные бычьи тренды, в другом углу — за медвежьи падения, посередине — за флэты и неопределенность. Карта создает своего рода географию рыночных состояний, где расстояние между нейронами отражает степень различия между паттернами.

Почему SOM идеальны для трейдинга: преимущества топологии

Традиционные нейронные сети для классификации, такие как многослойный персептрон или сверточные сети, работают по принципу "черного ящика". Вы скармливаете им данные, они выдают предсказание, но что происходит внутри — загадка. SOM другие. Они дают вам визуализацию, понимание, структуру. Вы можете посмотреть на карту и увидеть, в какой области пространства паттернов находится текущая рыночная ситуация. Вы можете отследить, как рынок мигрирует по карте от одного состояния к другому.

Еще важнее то, что SOM сохраняют топологию. Если два рыночных паттерна похожи, они окажутся в соседних нейронах. Это означает, что сеть не просто классифицирует — она кластеризует, группирует, находит естественные границы между разными типами рыночного поведения. Это unsupervised learning — обучение без учителя. Вам не нужно заранее размечать данные на классы "бычий тренд", "медвежий тренд", "флэт". Сеть сама найдет эти классы, сама определит границы между ними.

SOM также устойчивы к шуму. Рыночные данные зашумлены по определению — случайные выбросы, гэпы, манипуляции, новостные всплески. Обычные нейронные сети могут переобучиться на этом шуме. SOM, благодаря обновлению окрестностей нейронов, усредняют шум и выделяют устойчивые паттерны.

Архитектура SOM в MQL5: создание нейронной карты

Давайте посмотрим, как реализована самоорганизующаяся карта в коде торгового советника. Начнем с базовых параметров:

#define SOM_WIDTH 20
#define SOM_HEIGHT 20
#define SOM_NEURONS (SOM_WIDTH * SOM_HEIGHT)

struct QuantumProcessor {
    matrix som_weights;           // Веса SOM [SOM_NEURONS x input_dim]
    double learning_rate_som;
    double neighborhood_radius;
    
    void Init() {
        learning_rate_som = 0.1;
        neighborhood_radius = 5.0;
        som_weights = matrix::Zeros(SOM_NEURONS, FEATURES_COUNT);
        InitializeRandomMatrix(som_weights, -0.5, 0.5);
    }

Карта размером двадцать на двадцать нейронов дает нам четыреста точек в пространстве классификации. Каждый нейрон имеет вектор весов размерности FEATURES_COUNT — четыреста признаков, извлеченных из рыночных данных. Инициализация весов случайными значениями от минус половины до плюс половины создает начальное разнообразие в карте.

Ключевые параметры обучения — скорость обучения 0.1 и радиус окрестности 5.0. Радиус окрестности определяет, как далеко от Best Matching Unit распространяется влияние при обновлении весов. Большой радиус в начале обучения позволяет карте грубо организоваться. По мере обучения радиус можно уменьшать для тонкой настройки.

Поиск Best Matching Unit: сердце алгоритма

Самая важная операция в SOM — поиск нейрона, наиболее похожего на входной паттерн:

int FindBestMatchingUnit(const vector &_input) {
    int bmu = 0;
    double min_distance = DBL_MAX;
    
    for(int i = 0; i < SOM_NEURONS; i++) {
        vector neuron_weights = som_weights.Row(i);
        double distance = 0.0;
        
        for(ulong j = 0; j < MathMin(_input.Size(), neuron_weights.Size()); j++) {
            double diff = _input[j] - neuron_weights[j];
            distance += diff * diff;
        }
        
        if(distance < min_distance) {
            min_distance = distance;
            bmu = i;
        }
    }
    return bmu;
}

Алгоритм прост и элегантен. Проходим по всем четыремстам нейронам карты, для каждого вычисляем евклидово расстояние между весами нейрона и входным вектором. Квадратичное расстояние считается быстрее, чем с извлечением корня, и для сравнения этого достаточно. Нейрон с минимальным расстоянием становится победителем — BMU.

Это операция линейной сложности от количества нейронов. Для карты двадцать на двадцать и четырехсот признаков одна итерация поиска BMU требует ста шестидесяти тысяч операций умножения и сложения. На современных процессорах это выполняется за микросекунды. Важно, что эта операция детерминированная — для одного и того же входа всегда найдется один и тот же BMU (если веса не изменились).

Обновление весов: танец нейронов

После нахождения BMU начинается самое интересное — обновление весов окрестности:

void UpdateSOMWeights(const vector &_input, int bmu) {
    int bmu_x = bmu % SOM_WIDTH;
    int bmu_y = bmu / SOM_WIDTH;
    
    for(int i = 0; i < SOM_NEURONS; i++) {
        int neuron_x = i % SOM_WIDTH;
        int neuron_y = i / SOM_WIDTH;
        
        double distance = MathSqrt((neuron_x - bmu_x) * (neuron_x - bmu_x) + 
                                 (neuron_y - bmu_y) * (neuron_y - bmu_y));
        
        if(distance <= neighborhood_radius) {
            double influence = MathExp(-(distance * distance) / 
                              (2.0 * neighborhood_radius * neighborhood_radius));
            
            for(ulong j = 0; j < MathMin(_input.Size(), som_weights.Cols()); j++) {
                som_weights[i][j] += learning_rate_som * influence * 
                                   (_input[j] - som_weights[i][j]);
            }
        }
    }
}

Код реализует классическую функцию соседства с гауссовым ядром. Сначала вычисляем координаты BMU на двумерной карте — индекс по модулю ширины дает x-координату, целочисленное деление на ширину дает y-координату. Затем, для каждого нейрона вычисляем евклидово расстояние до BMU в координатах карты (не в пространстве признаков!).

Если расстояние меньше радиуса окрестности, нейрон попадает под влияние. Степень влияния определяется гауссовой функцией — экспонентой от минус квадрата расстояния. В центре (сам BMU) влияние максимально и равно единице. На границе радиуса влияние падает почти до нуля. Эта плавная функция создает гладкую топологию — нейроны обновляются пропорционально близости к победителю.

Финальное правило обучения — классическое дельта-правило. Новый вес равен старому весу плюс скорость обучения, умноженная на влияние, умноженная на разность между входом и текущим весом. Это правило притягивает вектор весов нейрона к входному вектору. Чем ближе нейрон к BMU, тем сильнее притяжение. Чем дальше — тем слабее.

Интеграция SOM в торговую систему: квантовые эффекты

Особенность реализации в советнике — интеграция SOM в составе "квантового процессора", который добавляет дополнительные эффекты поверх базовой SOM:

matrix ApplyQuantumEffects(const matrix &input_data, const matrix &context_data) {
    matrix result = matrix::Zeros(input_data.Rows(), input_data.Cols());
    
    for(ulong i = 0; i < input_data.Rows(); i++) {
        vector input_row = input_data.Row(i);
        
        // Находим BMU для текущего входа
        int bmu = FindBestMatchingUnit(input_row);
        
        // Обновляем веса SOM
        UpdateSOMWeights(input_row, bmu);
        
        // Получаем активацию от BMU
        vector bmu_weights = som_weights.Row(bmu);
        
        // Применяем классические эффекты + SOM активацию
        for(ulong j = 0; j < input_data.Cols(); j++) {
            double input_val = input_data[i][j];
            double context_val = (i < context_data.Rows() && j < context_data.Cols()) ? 
                                context_data[i][j] : 0.0;
            
            // SOM эффект
            double som_factor = 1.0;
            if(j < bmu_weights.Size()) {
                som_factor += (bmu_weights[j] - input_val) * coherence * 0.1;
            }
            
            // Классические эффекты
            double resonance = 1.0 + resonance_strength * 
                             MathCos(input_val * context_val * M_PI);
            double interference = interference_amplitude * 
                                MathSin(input_val * context_val * 2.0 * M_PI);
            double coherent_factor = coherence + (1.0 - coherence) * 
                                   MathExp(-decoherence_rate * i);
            
            result[i][j] = input_val * resonance * coherent_factor * 
                         som_factor + interference;
        }
    }
    
    return result;
}

Название "квантовые эффекты" — это, конечно, метафора. Никаких настоящих квантовых вычислений здесь нет. Но идея интересная: к выходу SOM применяются дополнительные трансформации, моделирующие резонанс, интерференцию и когерентность. SOM находит похожие паттерны и группирует их, а дополнительные эффекты добавляют нелинейность и контекстную зависимость.

SOM эффект вычисляет разность между весами BMU и входными данными, умножает на параметр когерентности и добавляет к базовому коэффициенту. Это создает обратную связь — если текущий паттерн далек от центра кластера (от весов BMU), выход усиливается или ослабляется. Резонанс моделируется через косинус произведения входа и контекста. Интерференция добавляется как синусоидальная компонента. Когерентный фактор экспоненциально затухает с индексом, моделируя потерю памяти.

Обучение на исторических данных: от баров к паттернам

Процесс обучения советника начинается при инициализации эксперта:

void TrainSOMNetwork() {
    matrix training_data = matrix::Zeros(TrainingBars, FEATURES_COUNT);
    vector targets = vector::Zeros(TrainingBars);
    
    MqlRates rates[];
    ArraySetAsSeries(rates, true);
    
    if(CopyRates(Symbol(), Period(), 0, TrainingBars + 50, rates) < TrainingBars + 50) {
        Print("Failed to copy rates for training");
        return;
    }
    
    for(int i = 0; i < TrainingBars; i++) {
        vector features = vector::Zeros(FEATURES_COUNT);
        
        // Базовые признаки
        double price_change = (rates[i].close - rates[i].open) / rates[i].open;
        double volatility = 0.0;
        for(int j = i; j < i + 10 && j < ArraySize(rates); j++) {
            double change = (rates[j].close - rates[j].open) / rates[j].open;
            volatility += change * change;
        }
        volatility = MathSqrt(volatility / 10.0);
        
        double volume_ratio = (rates[i].tick_volume > 0) ? 
            MathLog(1.0 + rates[i].tick_volume / 1000.0) : 0.0;
        
        features[0] = MathMax(-1.0, MathMin(1.0, price_change * 100));
        features[1] = MathMax(0.0, MathMin(1.0, volatility * 100));
        features[2] = MathMax(0.0, MathMin(1.0, volume_ratio / 10.0));

Первые три признака — базовые. Изменение цены текущего бара, нормализованное в диапазон от минус единицы до плюс единицы. Волатильность за последние десять баров, вычисленная как среднеквадратичное отклонение изменений, нормализованная от нуля до единицы. Объем в логарифмической шкале, также нормализованный.

Затем добавляются дополнительные признаки — изменения цен и диапазоны для предыдущих двадцати баров, создавая временное окно для анализа краткосрочной истории. Всего четыреста признаков на каждый бар. Это многомерное представление рыночного состояния, которое SOM научится кластеризовать.

Создание таргетов: предсказание будущего

Ключевой момент обучения — определение целевой переменной. Что мы хотим предсказать?

// НОВЫЙ ТАРГЕТ: изменение цены через N баров (по умолчанию 24)
if(i + TargetBarsLookahead < ArraySize(rates)) {
    double current_price = rates[i].close;
    double future_price = rates[i + TargetBarsLookahead].close;
    double price_change_percent = (current_price - future_price) / future_price * 100.0;
    
    // Определяем таргет на основе настраиваемых порогов
    if(price_change_percent > BullishThreshold) {        // Рост больше порога
        targets[i] = 0.8;
    }
    else if(price_change_percent < BearishThreshold) {   // Падение больше порога
        targets[i] = 0.2;
    }
    else {                                               // Боковое движение
        targets[i] = 0.5;
    }
}

Система смотрит вперед на настраиваемое количество баров (по умолчанию двадцать четыре) и вычисляет изменение цены в процентах. Если изменение превышает порог роста (по умолчанию 0.5 процента), таргет устанавливается в 0.8 — сильный бычий сигнал. Если падение превышает порог (по умолчанию минус 0.5 процента), таргет 0.2 — сильный медвежий сигнал. Все остальное классифицируется как боковик с таргетом 0.5.

Такая трехклассовая классификация дает сети четкие цели обучения. SOM группирует рыночные ситуации, которые ведут к росту, в одной области карты, ситуации перед падением — в другой области, неопределенность — в третьей. После обучения на тысячах примеров карта становится предсказательным инструментом.

Процесс предсказания: от признаков к сигналу

Когда советник получает новый тик, он извлекает признаки и делает предсказание:

double GetSOMPrediction(double &confidence) {
    vector feature_data = vector::Zeros(FEATURES_COUNT);
    
    MqlRates rates[];
    ArraySetAsSeries(rates, true);
    
    if(CopyRates(Symbol(), Period(), 0, 50, rates) < 50) {
        Print("Failed to copy rates");
        return -1;
    }
    
    // Заполняем признаки
    double price_change = (rates[0].close - rates[1].close) / rates[1].close;
    double volatility = 0.0;
    for(int i = 0; i < 10; i++) {
        double change = (rates[i].close - rates[i].open) / rates[i].open;
        volatility += change * change;
    }
    volatility = MathSqrt(volatility / 10.0);
    
    double volume_ratio = (rates[0].tick_volume > 0) ? 
        MathLog(1.0 + rates[0].tick_volume / 1000.0) : 0.0;
    
    feature_data[0] = MathMax(-1.0, MathMin(1.0, price_change * 100));
    feature_data[1] = MathMax(0.0, MathMin(1.0, volatility * 100));
    feature_data[2] = MathMax(0.0, MathMin(1.0, volume_ratio / 10.0));
    
    return g_som_net.Predict(feature_data, confidence);
}

Извлечение признаков идентично тому, что делалось при обучении — изменение цены, волатильность, объем, плюс исторические значения. Вектор признаков передается в метод Predict нейронной сети, который проходит через всю архитектуру: SOM находит BMU, применяются квантовые эффекты, данные обрабатываются трансформерными блоками, на выходе получается предсказание от нуля до единицы.

Значение близкое к 0.8 означает, что текущая рыночная ситуация похожа на те ситуации в обучающей выборке, после которых следовал рост. Значение близкое к 0.2 сигнализирует о вероятном падении. Значение около 0.5 говорит о неопределенности — рынок в боковике или на грани перелома.

Обработка сигналов и открытие позиций

Логика принятия торговых решений основана на предсказании и уверенности модели:

void ProcessSignals(double prediction, double confidence) {
    if(TimeCurrent() - g_last_signal_time < PeriodSeconds(Period())) return;
    
    int positions = CountPositions();
    
    if(confidence >= MinConfidence && prediction >= 0.6 && positions == 0) {
        if(OpenPosition(ORDER_TYPE_BUY)) {
            g_last_signal_time = TimeCurrent();
            Print("SOM BUY: Prediction=", DoubleToString(prediction*100,1), 
                  "%, Confidence=", DoubleToString(confidence*100,1), "%");
        }
    }
    else if(confidence >= MinConfidence && prediction <= 0.4 && positions == 0) {
        if(OpenPosition(ORDER_TYPE_SELL)) {
            g_last_signal_time = TimeCurrent();
            Print("SOM SELL: Prediction=", DoubleToString(prediction*100,1), 
                  "%, Confidence=", DoubleToString(confidence*100,1), "%");
        }
    }
}

Советник открывает позицию только если выполнены три условия: уверенность модели выше минимального порога (по умолчанию 65 процентов), предсказание достаточно сильное (выше 0.6 для покупки или ниже 0.4 для продажи), и нет открытых позиций. Такая осторожная логика минимизирует ложные входы.

Параметр уверенности вычисляется мета-моделью, которая оценивает, насколько надежно текущее предсказание, основываясь на исторической точности модели и характеристиках текущего паттерна. Низкая уверенность может означать, что паттерн не похож ни на что из обучающей выборки — модель в неизвестной территории и лучше воздержаться от торговли.

Непрерывное обучение: адаптация к рынку

Рынки меняются. Паттерны, которые работали год назад, могут устареть. Поэтому советник поддерживает непрерывное обучение:

input bool     ContinuousLearning = true; // Retrain periodically
input int      RetrainHours = 12;        // Retrain every N hours

void OnTick() {
    if(!g_net_initialized) return;
    if(!IsNewBar()) return;
    
    if(ContinuousLearning && ShouldRetrain()) {
        Print("Retraining SOM...");
        TrainSOMNetwork();
        g_last_retrain_time = TimeCurrent();
        Print("SOM retrained!");
    }

Каждые двенадцать часов (параметр настраивается) советник запускает переобучение на свежих исторических данных. SOM карта обновляется, адаптируясь к новым рыночным условиям. Старые паттерны не забываются полностью — веса нейронов изменяются постепенно, сохраняя накопленную структуру, но добавляя новую информацию.

Этот механизм критически важен для долгосрочной стабильности торговой системы. Статическая модель, обученная один раз, рано или поздно деградирует. Адаптивная модель, постоянно учащаяся на свежих данных, остается релевантной.

Визуализация SOM карты: увидеть невидимое

Одно из главных преимуществ SOM — возможность визуализации. После обучения можно построить U-матрицу (unified distance matrix), которая показывает расстояния между соседними нейронами. Темные области на U-матрице — это границы между кластерами, светлые области — однородные регионы со схожими паттернам.

Можно также раскрасить карту по средним значениям таргетов, которые попали в каждый нейрон. Красные нейроны — это область медвежьих паттернов, зеленые — бычьих, серые — боковика. Такая карта становится инструментом для трейдера: посмотрев, в какой нейрон попадает текущая ситуация, можно сразу оценить вероятное направление движения. 

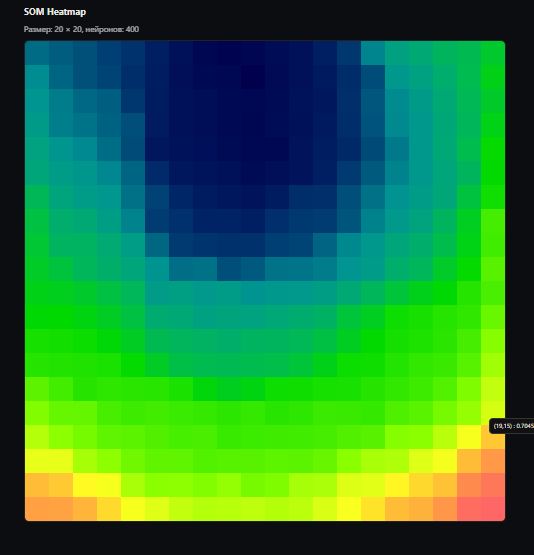
В реализации советника визуализация реализована через экспорт интерактивной HTML-карты — тепловой карты SOM с hover-подсказками и масштабированием. Это автономная веб-страница, генерируемая на MQL5 без внешних библиотек. После обучения (или по горячей клавише 'H' на графике) метод ExportSOMHTML вычисляет L2-норму весов каждого нейрона (как меру "силы" или структурной плотности кластера), нормализует значения в [0..1] и записывает HTML-файл в общий каталог терминала (Common\Files\SOM_map.html).

Код экспорта прост и эффективен:

bool ExportSOMHTML(const string filename = "SOM_map.html") {
    // Проверка инициализации
    if(input_quantum_proc.som_weights.Rows() != SOM_NEURONS) {
        Print("ExportSOMHTML: som_weights not initialized");
        return false;
    }
    
    // Вычисление L2-норм для тепловой карты
    vector vals = vector::Zeros(SOM_NEURONS);
    double vmin = DBL_MAX, vmax = -DBL_MAX;
    for(int i = 0; i < SOM_NEURONS; i++) {
        double s = 0.0;
        for(ulong j = 0; j < input_quantum_proc.som_weights.Cols(); j++) {
            double w = input_quantum_proc.som_weights[i][j];
            s += w * w;
        }
        s = MathSqrt(s);
        vals[i] = s;
        if(s < vmin) vmin = s;
        if(s > vmax) vmax = s;
    }
    
    // Нормализация и запись HTML
    double range = (vmax > vmin) ? (vmax - vmin) : 1.0;
    int h = FileOpen(filename, FILE_WRITE | FILE_TXT | FILE_COMMON, CP_UTF8);
    if(h == INVALID_HANDLE) {
        Print("ExportSOMHTML: cannot open file: ", filename);
        return false;
    }
    
    // Генерация HTML с Canvas и JS для рендера
    // ... (полный HTML-код с HSL-палитрой от синего к красному, hover и resize)
    
    FileClose(h);
    Print("SOM map exported to Common\\Files\\", filename);
    return true;
}

Файл открывается двойным кликом в терминале MT5 или в любом браузере. Карта 20×20 клеток раскрашивается от "холодного" синего (низкая норма весов — слабые/пустые кластеры) к "горячему" красному (высокая норма — плотные, активные паттерны). Наведите курсор на клетку — увидите координаты (x, y) и нормализованную интенсивность (0.0000–1.0000). Масштабирование адаптивно: на большом экране клетки крупнее, на мобильном — компактнее.

Эта визуализация — ключ к интерпретации модели. Например, если текущий BMU попадает в "горячую" красную зону с высокой нормой, это сигнал сильного кластера паттернов (бычий или медвежий). Если в синюю — рынок в редкой, неопределенной зоне, где лучше не торговать.  

Сравнение с другими методами: где SOM выигрывает

Классический технический анализ работает с предопределенными индикаторами — RSI, MACD, полосы Боллинджера. Эти индикаторы придуманы людьми на основе гипотез о рыночном поведении. SOM ничего не предполагает заранее. Она учится на данных и находит паттерны, которые реально работают, а не те, которые мы думаем, что работают.

Простые нейронные сети прямого распространения (feedforward networks) требуют размеченных данных — для каждого примера нужно указать правильный ответ. SOM — это unsupervised learning, обучение без учителя. Она может работать и в supervised режиме (как в нашем советнике), но ее главная сила — способность находить структуру в данных самостоятельно.

Глубокие нейронные сети (LSTM, GRU, трансформеры) требуют огромных объемов данных и вычислительных ресурсов. SOM компактна, быстра, и может обучаться даже на небольших выборках. Четыреста нейронов карты тренируются за минуты на обычном компьютере, а предсказание выполняется за миллисекунды.

Random Forest и градиентный бустинг отлично работают для табличных данных, но плохо сохраняют топологию. Они создают деревья решений, которые делят пространство признаков на прямоугольные области. SOM создает плавную, непрерывную карту, где похожие паттерны находятся рядом. Это свойство критически важно для финансовых данных, где небольшие изменения в признаках не должны приводить к резким скачкам в предсказаниях.

Ограничения и проблемы: реальность против теории

Как и любая технология, SOM не панацея. Первая проблема — размер карты. Слишком маленькая карта (например, десять на десять нейронов) не сможет захватить всю сложность рыночных паттернов. Слишком большая карта (скажем, сто на сто) будет переобучаться и медленно обучаться. Оптимальный размер подбирается экспериментально.

Вторая проблема — количество эпох обучения. Слишком мало эпох — карта не успеет организоваться, слишком много — возникнет переобучение. В нашем советнике используется всего три эпохи при непрерывном обучении, что является компромиссом между адаптацией и стабильностью.

Третья проблема — нормализация признаков. SOM чувствительна к масштабу данных. Если один признак имеет значения от нуля до ста, а другой от нуля до единицы, первый признак будет доминировать при вычислении расстояний. Необходима тщательная нормализация всех признаков в одинаковый диапазон.

Четвертая проблема – временная зависимость. Классическая SOM не учитывает временной порядок данных — каждый паттерн обрабатывается независимо. Для финансовых временных рядов это ограничение. Наш советник частично решает проблему, добавляя исторические лаги в признаки и интегрируя SOM с трансформерными блоками, которые обрабатывают последовательности.

Будущие направления: куда двигаться дальше

Самоорганизующиеся карты — это только начало. Существуют модификации классического алгоритма Кохонена, которые можно интегрировать в советник. Например, Growing Neural Gas — алгоритм, который динамически добавляет и удаляет нейроны в процессе обучения, автоматически подстраивая размер карты под сложность данных.

Temporal Kohonen Maps добавляют временные связи между нейронами, позволяя карте запоминать не только паттерны, но и последовательности паттернов. Это критически важно для предсказания рыночных трендов, где важна не только текущая ситуация, но и траектория, по которой рынок к ней пришел.

Hierarchical SOM создают несколько уровней карт, где верхний уровень группирует нейроны нижнего уровня в мета-кластеры. Это позволяет захватить структуру рынка на разных временных масштабах — от минутных колебаний до недельных трендов.

Интеграция SOM с другими техниками глубокого обучения открывает еще больше возможностей. Можно использовать SOM как первый слой feature extraction перед LSTM сетью. Можно обучать ансамбли SOM карт на разных временных фреймах и комбинировать их предсказания. Можно применять reinforcement learning поверх SOM, где агент учится торговым стратегиям, используя состояния рынка, классифицированные картой.

Практические рекомендации: как использовать советника

Если вы решите тестировать или использовать SOM-советника, начните с тщательной настройки параметров обучения. Параметр TrainingBars определяет, сколько исторических баров использовать для обучения: две тысячи — это минимум, четыре тысячи — лучше. TargetBarsLookahead определяет горизонт предсказания — двадцать четыре бара для часового графика означает прогноз на один день вперед.

Пороги BullishThreshold и BearishThreshold критичны. Слишком низкие пороги (например, 0.1 процента) приведут к множеству слабых сигналов. Слишком высокие (например, 2 процента) сделают сигналы редкими. Оптимальные значения зависят от волатильности инструмента и временного фрейма.

Параметр MinConfidence фильтрует слабые предсказания. Значение 0.65 означает, что советник будет торговать, только когда уверенность модели выше 65 процентов. Это снижает количество сделок, но повышает их качество. При тестировании на истории смотрите на соотношение win rate и profit factor при разных значениях этого параметра.

Обязательно используйте непрерывное обучение (ContinuousLearning = true) при работе на реальном счете. Рынки эволюционируют, и статическая модель быстро устареет. Параметр RetrainHours = 12 означает переобучение два раза в сутки, что является разумным балансом между адаптацией и стабильностью.

Рассмотрим же тест нашей системы:

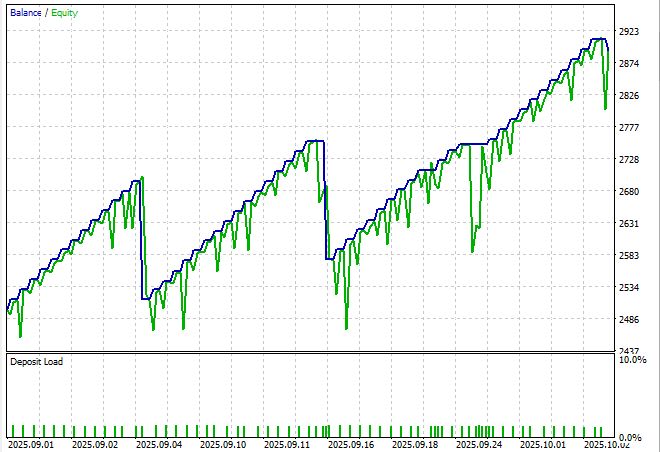
График не то чтобы очень красив, но ведь это без какой-либо оптимизации, с параметрами выставленными наобум. И тем не менее — Шарп почти выбил значение 4:

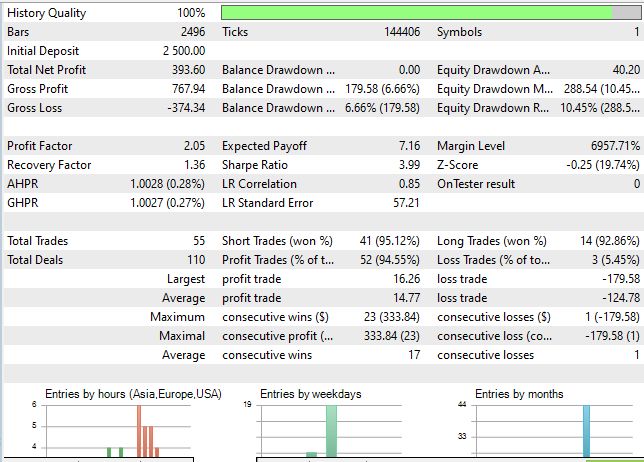
Заключение: нейронная картография финансов

Самоорганизующиеся карты Кохонена — это элегантный инструмент для анализа сложных, многомерных данных. Придуманные сорок лет назад для распознавания речи, они нашли применение в сотнях областей — от биоинформатики до социологии. И как оказалось, отлично подходят для анализа финансовых рынков.

Советник, код которого мы разобрали, показывает один из способов применения SOM в алгоритмическом трейдинге. Это не готовая торговая система, а исследовательская платформа, демонстрирующая возможности технологии. Реальная торговля потребует дополнительной работы —тестирования на исторических данных, оптимизации параметров, интеграции с системой управления рисками, психологической готовности к просадкам.

Но главное — это концепция. Идея о том, что рынок можно картографировать, что хаос свечей на графике скрывает упорядоченную структуру, которую можно найти и использовать. SOM дает нам инструмент для создания этой карты. Карты, которая показывает, где мы находимся в пространстве рыночных состояний, и куда, вероятно, движемся дальше.

Код открыт. Технология доступна. Осталось только применить ее с умом, терпением и должной осторожностью. Рынки не прощают самоуверенности, но награждают тех, кто использует правильные инструменты правильным образом. Может быть, самоорганизующиеся карты станут вашим инструментом для навигации в океане финансовых данных.