Арбитражная алготорговля на теории графов

Введение

Арбитражная торговля представляет собой одну из наиболее интересных и технически сложных стратегий на финансовых рынках. Эта стратегия основана на использовании временных ценовых расхождений между различными финансовыми инструментами или рынками для получения прибыли с минимальным риском. В контексте валютного рынка Forex арбитраж представляет собой поиск и использование циклических путей обмена валют, где начальная и конечная валюты совпадают, а итоговый обменный курс приносит прибыль после учёта всех транзакционных издержек.

Принцип арбитража заключается в том, что трейдер одновременно покупает и продаёт связанные финансовые инструменты по разным ценам, фиксируя разность как прибыль. Например, классический треугольный арбитраж может включать цикл USD → EUR → GBP → USD. Если произведение обменных курсов в этой цепочке превышает единицу даже после вычета спредов и комиссий, то такой цикл становится прибыльным.

Важно понимать, что арбитражные возможности на современных финансовых рынках крайне редки и кратковременны. Это связано с высокой эффективностью рынков, наличием алгоритмической торговли и быстрой скоростью передачи информации. Тем не менее, использование современных технологий и правильно настроенных алгоритмов может позволить выявлять и использовать такие возможности.

В данной статье мы рассмотрим создание полнофункционального советника на языке MQL5, который способен автоматически обнаруживать арбитражные возможности, рассчитывать оптимальные размеры позиций и управлять рисками через систему усреднения позиций.

Теоретические основы арбитража

Графовое представление валютного рынка

Валютный арбитраж можно элегантно представить как задачу поиска прибыльных циклов в ориентированном взвешенном графе. В этой модели каждая валюта (USD, EUR, GBP, JPY и т.д.) представлена вершиной графа, а валютные пары (EURUSD, GBPUSD, USDJPY) — рёбрами с соответствующими весами.

Весы рёбер определяются следующим образом: для операции покупки (переход от базовой к котируемой валюте) вес равен 1/ask_price, для операции продажи (переход от котируемой к базовой валюте) вес равен bid_price. Прибыльный арбитражный цикл — это замкнутый путь в графе, где произведение весов всех рёбер превышает единицу после вычета транзакционных издержек.

Математическая формула прибыли

Прибыль арбитражного цикла рассчитывается по формуле:

Прибыль = w₁ × w₂ × ... × wₙ - 1 - Спред

Где wᵢ — вес i-го ребра в цикле, а Спред — суммарная относительная стоимость спредов всех сделок. Спред для каждой валютной пары вычисляется как относительная величина: (ask - bid) / bid.

Условие нулевой экспозиции

Ключевым требованием для истинного арбитража является обеспечение нулевой валютной экспозиции. Это означает, что общий объём каждой валюты в портфеле после выполнения всех сделок цикла должен равняться нулю. Математически это выражается системой линейных уравнений, где покупки валюты компенсируются её продажами.

Для достижения нулевой экспозиции необходимо правильно рассчитать размеры лотов для каждой сделки в цикле, учитывая спецификации каждой валютной пары у брокера.

Архитектура арбитражного советника

Подход к проектированию системы

Разработка арбитражного советника требует системного подхода и тщательного планирования архитектуры. Система построена на принципах модульности, масштабируемости и отказоустойчивости. Основная идея заключается в создании независимых компонентов, каждый из которых отвечает за определённую функциональность и может быть модифицирован без влияния на остальные части системы.

Модуль построения графа отвечает за создание математической модели валютного рынка на основе текущих котировок. Этот компонент должен обрабатывать данные от брокера, фильтровать инструменты по заданным критериям и создавать структуру графа в памяти. Особое внимание уделяется производительности, поскольку граф должен перестраиваться в реальном времени при изменении котировок.

Алгоритмический модуль включает реализацию двух комплементарных подходов: алгоритм Floyd-Warshall для поиска оптимальных путей и метод поиска в глубину (DFS) для исчерпывающего анализа всех возможных циклов. Такой дуальный подход обеспечивает как эффективность поиска, так и полноту охвата возможных арбитражных возможностей.

Модуль балансировки позиций решает математическую задачу обеспечения нулевой валютной экспозиции. Здесь реализуются алгоритмы расчёта размеров лотов с учётом спецификаций брокера, включая минимальные размеры лотов, шаги изменения объёма и маржинальные требования.

Торговый модуль управляет исполнением сделок, включая размещение ордеров, мониторинг их статуса и обработку ошибок исполнения. Важной особенностью является реализация системы fallback стратегий для случаев, когда не все ордера цикла могут быть исполнены одновременно.

Модуль управления рисками реализует продвинутые стратегии, включая усреднение позиций, динамическое управление размерами позиций и системы экстренного закрытия при превышении лимитов убытков.

Проектирование базовых структур

Эффективная реализация арбитражного советника начинается с правильного проектирования структур данных. Структура Edge представляет ребро графа и содержит всю необходимую информацию для выполнения торговой операции. Поле from и to определяют направление обмена валют, weight содержит обменный курс, а spread — относительную стоимость транзакции.

#property strict
#include <Trade/Trade.mqh>
CTrade trade;

#define MAX_VERTICES 25
#define MAX_EDGES    500
#define MAX_CYCLE_LENGTH 15
#define INF 999999.0

struct Edge {
   int from;           // Исходная вершина
   int to;             // Целевая вершина
   double weight;      // Вес ребра (обменный курс)
   double spread;      // Относительный спред
   string symbol;      // Название валютной пары
   bool is_buy;        // Тип операции (покупка/продажа)
};

struct Vertex {
   string name;        // Название валюты (USD, EUR и т.д.)
};

struct ArbitragePath {
   Edge path_edges[MAX_CYCLE_LENGTH];      // Рёбра пути
   int path_vertices[MAX_CYCLE_LENGTH + 1]; // Вершины пути
   int length;                              // Длина пути
   double total_rate;                       // Общий курс
   double total_spread;                     // Общий спред
   double net_profit;                       // Чистая прибыль
   string description;                      // Описание пути
};

Глобальные массивы для хранения графа размещаются статически для обеспечения максимальной производительности. Константы MAX_VERTICES и MAX_EDGES определяют максимальные размеры структур и должны быть сбалансированы между потребностями в памяти и производительностью.

Матрицы dist и spread_matrix используются алгоритмом Floyd-Warshall и имеют размерность MAX_VERTICES × MAX_VERTICES. Матрица next_vertex необходима для восстановления найденных путей. Эти структуры требуют значительного объёма памяти, но обеспечивают O(1) доступ к данным.

Массив all_arbitrage_paths хранит все найденные арбитражные возможности и позволяет их сортировку по прибыльности. Размер массива (1000 элементов) выбран на основе практических тестов и может быть скорректирован в зависимости от требований к системе.

Особое внимание уделено оптимизации операций с массивами. Все критически важные циклы используют прямую адресацию вместо функций доступа, что минимизирует накладные расходы и повышает производительность алгоритмов поиска арбитража.

// Параметры советника
extern double LotSize = 0.1;           // Максимальный размер лота
extern double MinProfit = 0.0005;      // Минимальная прибыль (0.05%)
extern int MaxSpreadPoints = 25;       // Максимальный спред в пунктах
extern int MaxPathLength = 4;          // Максимальная длина цикла
extern int MaxAverages = 2;            // Максимальное количество усреднений
extern double PriceImprovementPoints = 1.0; // Улучшение цены в пунктах
extern bool ShowDetailedPaths = true;  // Показать детальные пути

// Массивы для графа
Edge edges[MAX_EDGES];
Vertex vertices[MAX_VERTICES];
double dist[MAX_VERTICES][MAX_VERTICES];
double spread_matrix[MAX_VERTICES][MAX_VERTICES];
int next_vertex[MAX_VERTICES][MAX_VERTICES];

Алгоритмы поиска арбитража

Алгоритм построения графа

Функция BuildGraph() является ключевым компонентом системы, отвечающим за создание математической модели валютного рынка. Процесс начинается с инициализации всех структур данных и установки начальных значений матриц расстояний и спредов.

void BuildGraph() {
   vertex_count = 0;
   edge_count = 0;
   
   // Инициализация матриц расстояний и спредов
   for(int i=0; i<MAX_VERTICES; i++) {
      for(int j=0; j<MAX_VERTICES; j++) {
         dist[i][j] = (i == j) ? 1.0 : INF;
         spread_matrix[i][j] = (i == j) ? 0.0 : INF;
         next_vertex[i][j] = -1;
      }
   }
   
   MqlTick tick;
   for(int i=0; i<ArraySize(symbols); i++) {
      if(SymbolInfoTick(symbols[i], tick)) {
         // Расчёт спреда в пунктах и относительного спреда
         double point = GetPoint(symbols[i]);
         double spread_points = (tick.ask - tick.bid) / point;
         double spread_cost = (tick.ask - tick.bid) / tick.bid;
         
         // Фильтрация по максимальному спреду
         if(spread_points <= MaxSpreadPoints) {
            string base = StringSubstr(symbols[i], 0, 3);
            string quote = StringSubstr(symbols[i], 3, 3);
            
            // Добавление рёбер для покупки и продажи
            AddEdge(base, quote, 1.0/tick.ask, spread_cost, symbols[i], true);
            AddEdge(quote, base, tick.bid, spread_cost, symbols[i], false);
         } else {
            PrintFormat("[WARNING] High spread for %s: %.1f points", symbols[i], spread_points);         }
      }
   }
   
   PrintFormat("Graph built: %d vertices, %d edges", vertex_count, edge_count);
}

Диагональные элементы матрицы расстояний устанавливаются в 1.0, что соответствует тождественному обмену валюты на саму себя с нулевой стоимостью. Остальные элементы инициализируются значением INF (бесконечность), указывая на отсутствие прямой связи между валютами.

Основной цикл обрабатывает массив символов валютных пар, получая текущие котировки через SymbolInfoTick(). Для каждой пары вычисляется спред в пунктах и относительный спред. Пары с чрезмерно высоким спредом исключаются из анализа для повышения качества найденных возможностей.

for(int i=0; i<ArraySize(symbols); i++) {
   if(SymbolInfoTick(symbols[i], tick)) {
      double point = GetPoint(symbols[i]);
      double spread_points = (tick.ask - tick.bid) / point;
      double spread_cost = (tick.ask - tick.bid) / tick.bid;
      
      if(spread_points <= MaxSpreadPoints) {
         string base = StringSubstr(symbols[i], 0, 3);
         string quote = StringSubstr(symbols[i], 3, 3);
         
         AddEdge(base, quote, 1.0/tick.ask, spread_cost, symbols[i], true);
         AddEdge(quote, base, tick.bid, spread_cost, symbols[i], false);
      }
   }
}

Функция AddEdge() реализует добавление рёбер в граф с автоматическим созданием новых вершин при необходимости. Функция AddVertex() использует линейный поиск для проверки существования валюты в графе, что обеспечивает уникальность вершин.

Каждая валютная пара создаёт два ребра: одно для покупки (переход от базовой к котируемой валюте) и одно для продажи (обратный переход). Вес ребра для покупки равен 1/ask, что отражает количество котируемой валюты, получаемое за единицу базовой. Вес ребра для продажи равен bid, показывая количество базовой валюты, получаемое за единицу котируемой.

Дополнительно ребра сохраняются в матрице edge_matrix для быстрого доступа при восстановлении путей. Эта оптимизация критически важна для производительности алгоритма Floyd-Warshall.

void AddEdge(string from_currency, string to_currency, double weight, 
             double spread, string symbol, bool is_buy) {
   if(edge_count >= MAX_EDGES) return;
   
   int from_idx = GetOrAddVertexIndex(from_currency);
   int to_idx = GetOrAddVertexIndex(to_currency);
   
   edges[edge_count].from = from_idx;
   edges[edge_count].to = to_idx;
   edges[edge_count].weight = weight;
   edges[edge_count].spread = spread;
   edges[edge_count].symbol = symbol;
   edges[edge_count].is_buy = is_buy;
   
   edge_count++;
}

int GetOrAddVertexIndex(string currency) {
   // Поиск существующей вершины
   for(int i=0; i<vertex_count; i++) {
      if(vertices[i].name == currency) return i;
   }
   
   // Добавление новой вершины
   if(vertex_count < MAX_VERTICES) {
      vertices[vertex_count].name = currency;
      return vertex_count++;
   }
   return -1;
}

Система включает обработку различных типов валютных пар, включая экзотические пары и инструменты с нестандартным количеством знаков после запятой. Функция GetPoint() корректно обрабатывает как 4-значные, так и 5-значные котировки, что обеспечивает совместимость с различными брокерами.

Для JPY-пар применяется специальная логика расчёта спредов, учитывающая их традиционно меньшее количество знаков после запятой. Это предотвращает ложное исключение этих пар из анализа и повышает качество найденных арбитражных возможностей.

Математические основы алгоритма  Floyd–Warshall

Алгоритм Floyd-Warshall в контексте валютного арбитража требует существенной модификации классической версии. Стандартный алгоритм ищет кратчайшие пути с минимизацией суммы весов рёбер, но для арбитража нам нужно максимизировать произведение обменных курсов.

Ключевая модификация заключается в замене операции сложения на умножение и поиска минимума на поиск максимума. Однако простая замена операций недостаточна — необходимо также учитывать накопление спредов и предотвращать численную нестабильность при работе с произведениями.

void FloydWarshall() {
   // Инициализация матриц
   for(int i=0; i<vertex_count; i++) {
      for(int j=0; j<vertex_count; j++) {
         if(i == j) {
            dist[i][j] = 1.0;           // Диагональные элементы = 1
            spread_matrix[i][j] = 0.0;  // Нулевой спред для одной валюты
         } else {
            dist[i][j] = INF;           // Бесконечность для недостижимых пар
            spread_matrix[i][j] = INF;
         }
         next_vertex[i][j] = -1;        // Матрица для восстановления путей
      }
   }
   
   // Заполнение прямых рёбер
   for(int e=0; e<edge_count; e++) {
      int from = edges[e].from;
      int to = edges[e].to;
      
      if(from >= 0 && to >= 0 && from < vertex_count && to < vertex_count) {
         // Выбор лучшего курса для данной пары валют
         if(dist[from][to] == INF || edges[e].weight > dist[from][to]) {
            dist[from][to] = edges[e].weight;
            spread_matrix[from][to] = edges[e].spread;
            next_vertex[from][to] = to;
         }
      }
   }
   
   // Основной цикл Floyd-Warshall
   for(int k=0; k<vertex_count; k++) {
      for(int i=0; i<vertex_count; i++) {
         for(int j=0; j<vertex_count; j++) {
            if(dist[i][k] != INF && dist[k][j] != INF) {
               double new_rate = dist[i][k] * dist[k][j];
               double new_spread = spread_matrix[i][k] + spread_matrix[k][j];
               
               // Обновление пути если он лучше по курсу и приемлем по спреду
               if(new_rate > dist[i][j] && new_spread < spread_matrix[i][j] * 2) {
                  dist[i][j] = new_rate;
                  spread_matrix[i][j] = new_spread;
                  next_vertex[i][j] = next_vertex[i][k];
               }
            }
         }
      }
   }
   
   Print("[SUCCESS] Floyd-Warshall algorithm completed");
}

При работе с произведениями обменных курсов возникают вопросы численной стабильности. Произведения могут становиться очень большими или очень маленькими, что приводит к потере точности. Для решения этой проблемы введено дополнительное условие проверки спредов.

Условие new_spread < spread_matrix[i][j] * 2 предотвращает накопление чрезмерно высоких спредов, которые могут свести к нулю потенциальную прибыль. Коэффициент 2 выбран эмпирически и может быть скорректирован в зависимости от рыночных условий.

Матрица next_vertex обеспечивает возможность восстановления найденных путей. При обновлении расстояния между вершинами i и j через промежуточную вершину k, мы сохраняем информацию о том, что следующая вершина на пути от i к j совпадает со следующей вершиной на пути от i к k.

Восстановление арбитражных путей

Функция ReconstructPath() использует матрицу next_vertex для восстановления последовательности рёбер, составляющих найденный арбитражный цикл. Процесс начинается с начальной вершины и последовательно переходит к следующим вершинам до возвращения в исходную точку.

void FindArbitrageFromFloydWarshall() {
   for(int i=0; i<vertex_count; i++) {
      if(dist[i][i] > 1.0) {  // Прибыльный цикл найден
         double net_profit = dist[i][i] - 1.0 - spread_matrix[i][i];
         if(net_profit > MinProfit) {
            PrintFormat("Floyd-Warshall arbitrage: %s -> %s, profit: %.4f%%", 
                       vertices[i].name, vertices[i].name, net_profit*100);
         }
      }
   }
}

Критически важным является правильное сопоставление найденных путей с исходными рёбрами графа. Поскольку между двумя валютами может существовать несколько рёбер (покупка и продажа), необходимо выбрать правильное ребро, соответствующее найденному оптимальному пути.

Алгоритм Floyd-Warshall имеет временную сложность O(n³), что может стать узким местом при большом количестве валют. Для оптимизации применяются несколько техник: предварительная фильтрация валют по ликвидности, использование более эффективных структур данных и распараллеливание вычислений где это возможно.

Алгоритм поиска в глубину

Метод поиска в глубину (DFS) дополняет Floyd-Warshall, обеспечивая исчерпывающий анализ всех возможных арбитражных циклов. В отличие от Floyd-Warshall, который находит оптимальные пути между парами вершин, DFS может обнаружить альтернативные циклы, которые могут оказаться прибыльными в определённых рыночных условиях.

Функция AdvancedDFS() реализует рекурсивный поиск с множественными оптимизациями. Основная идея заключается в систематическом обходе всех возможных путей от каждой валюты, с проверкой возможности замыкания цикла и расчётом потенциальной прибыльности.

void AdvancedDFS(int start, int current, double product, double spread_cost, 
                 Edge &path_edges[], int &path_vertices[], int depth) {
   // Ограничение глубины поиска для предотвращения переполнения стека
   if(depth >= MaxPathLength) return;
   
   // Перебор всех исходящих рёбер из текущей вершины
   for(int i=0; i<edge_count; i++) {
      if(edges[i].from == current) {
         // Проверка на повторное использование валютной пары
         bool symbol_used = false;
         for(int j=0; j<depth; j++) {
            if(path_edges[j].symbol == edges[i].symbol) {
               symbol_used = true;
               break;
            }
         }
         if(symbol_used) continue;  // Пропуск уже использованной пары
         
         // Добавление ребра к текущему пути
         path_edges[depth] = edges[i];
         path_vertices[depth + 1] = edges[i].to;
         double new_product = product * edges[i].weight;
         double new_spread = spread_cost + edges[i].spread;
         
         // Проверка замыкания цикла
         if(edges[i].to == start && depth >= 2) {
            double net_profit = new_product - 1.0 - new_spread;
            
            // Сохранение прибыльного цикла
            if(net_profit > MinProfit && arbitrage_path_count < ArraySize(all_arbitrage_paths)) {
               ArbitragePath arb_path;
               arb_path.length = depth + 1;
               arb_path.total_rate = new_product;
               arb_path.total_spread = new_spread;
               arb_path.net_profit = net_profit;
               
               // Копирование пути
               for(int k=0; k<=depth; k++) {
                  arb_path.path_edges[k] = path_edges[k];
                  arb_path.path_vertices[k] = path_vertices[k];
               }
               arb_path.path_vertices[depth + 1] = start;
               
               // Формирование описания пути
               arb_path.description = "";
               for(int k=0; k<=depth; k++) {
                  if(k > 0) arb_path.description += " -> ";
                  arb_path.description += vertices[path_vertices[k]].name;
               }
               arb_path.description += " -> " + vertices[start].name;
               
               all_arbitrage_paths[arbitrage_path_count++] = arb_path;
               
               if(ShowDetailedPaths) {
                  
PrintFormat("[FOUND] Arbitrage: %s, profit: %.4f%%, spread: %.4f%%",
                                arb_path.description, net_profit*100, new_spread*100); 
               }
            }
         } else {
            // Продолжение поиска в глубину
            AdvancedDFS(start, edges[i].to, new_product, new_spread, 
                       path_edges, path_vertices, depth + 1);
         }
      }
   }
}

Критически важной особенностью реализации является предотвращение повторного использования одного и того же валютного инструмента в рамках одного цикла. Это ограничение обусловлено практическими соображениями: одновременное открытие противоположных позиций по одному инструменту может создать проблемы с исполнением и увеличить транзакционные издержки.

Проверка symbol_used осуществляется путём сравнения названия текущего инструмента со всеми инструментами, уже включёнными в текущий путь. Этот подход гарантирует, что каждый инструмент используется не более одного раза в рамках одного арбитражного цикла.

Оптимизация глубины поиска

Параметр MaxPathLength ограничивает максимальную длину анализируемых циклов. Это ограничение служит нескольким целям: предотвращение переполнения стека при рекурсивных вызовах, ограничение времени выполнения алгоритма и фокусировка на практически реализуемых арбитражных возможностях.

Эмпирические исследования показывают, что большинство практически полезных арбитражных циклов имеют длину от 3 до 5 операций. Более длинные циклы обычно имеют высокие суммарные спреды, что снижает их прибыльность до неприемлемого уровня.

Расчёт и сохранение найденных циклов

При обнаружении замыкающего ребра (когда целевая вершина совпадает с начальной) алгоритм вычисляет метрики прибыльности цикла. Чистая прибыль рассчитывается как разность между произведением обменных курсов, единицей и суммарным спредом.

if(edges[i].to == start && depth >= 2) {
   double net_profit = new_product - 1.0 - new_spread;
   
   if(net_profit > MinProfit && arbitrage_path_count < ArraySize(all_arbitrage_paths)) {
      ArbitragePath arb_path;
      arb_path.length = depth + 1;
      arb_path.total_rate = new_product;
      arb_path.total_spread = new_spread;
      arb_path.net_profit = net_profit;

Для каждого найденного цикла формируется текстовое описание, включающее последовательность валют и направления операций. Эта информация критически важна для анализа и отладки найденных арбитражных возможностей.

Описание создаётся путём конкатенации названий валют с разделителем "→", что обеспечивает наглядное представление направления обмена. Дополнительно сохраняется информация о типах операций (покупка/продажа) для каждого ребра цикла.

Балансировка позиций и управление рисками

Математические основы балансировки

Обеспечение нулевой валютной экспозиции является фундаментальным требованием для истинного арбитража. Функция CalculateBalancedLots() решает сложную математическую задачу определения размеров позиций, которые обеспечивают нулевой чистый объём по каждой валюте после выполнения всех операций цикла.

Алгоритм начинается с определения базовой суммы (10000 единиц), которая представляет начальный капитал в валюте, с которой начинается арбитражный цикл. Эта сумма последовательно трансформируется через каждое ребро цикла, учитывая соответствующие обменные курсы.

Обеспечение нулевой валютной экспозиции является критически важным аспектом арбитражной торговли. Нулевая экспозиция означает, что после выполнения всех сделок в арбитражном цикле, чистая позиция по каждой валюте должна равняться нулю. Это гарантирует, что прибыль не зависит от последующих движений валютных курсов.

Для достижения нулевой экспозиции необходимо тщательно рассчитать размер каждой позиции в цикле. Расчёт начинается с фиксированной суммы в начальной валюте и последовательно применяет обменные курсы для определения эквивалентных сумм в других валютах.

Суммарная экспозиция по каждой валюте должна быть близка к нулю с допустимой погрешностью 0.01 лота.

Алгоритм расчёта балансированных лотов

bool CalculateBalancedLots(ArbitragePath &path, double &lots[]) {
   if(path.length == 0) return false;
   
   double base_amount = 1000.0;  // Начальная сумма в базовой валюте
   double current_amount = base_amount;
   
   // Получение спецификаций первого инструмента
   MqlTick tick;
   if(!SymbolInfoTick(path.path_edges[0].symbol, tick)) return false;
   
   double contract_size = SymbolInfoDouble(path.path_edges[0].symbol, SYMBOL_TRADE_CONTRACT_SIZE);
   double min_lot = SymbolInfoDouble(path.path_edges[0].symbol, SYMBOL_VOLUME_MIN);
   double step_lot = SymbolInfoDouble(path.path_edges[0].symbol, SYMBOL_VOLUME_STEP);
   
   // Расчёт размера первого лота
   lots[0] = NormalizeDouble(base_amount / contract_size, 2);
   lots[0] = MathMax(min_lot, MathRound(lots[0] / step_lot) * step_lot);
   
   // Последовательный расчёт размеров лотов для остальных сделок
   for(int i = 1; i < path.length; i++) {
      // Применение обменного курса предыдущего ребра
      current_amount *= path.path_edges[i-1].weight;
      
      // Получение спецификаций текущего инструмента
      string sym = path.path_edges[i].symbol;
      if(!SymbolInfoTick(sym, tick)) return false;
      
      contract_size = SymbolInfoDouble(sym, SYMBOL_TRADE_CONTRACT_SIZE);
      min_lot = SymbolInfoDouble(sym, SYMBOL_VOLUME_MIN);
      step_lot = SymbolInfoDouble(sym, SYMBOL_VOLUME_STEP);
      
      // Расчёт и нормализация размера лота
      lots[i] = NormalizeDouble(current_amount / contract_size, 2);
      lots[i] = MathMax(min_lot, MathRound(lots[i] / step_lot) * step_lot);
   }
   
   // Масштабирование всех лотов под максимальный допустимый размер
   double max_lot = 0;
   for(int i = 0; i < path.length; i++) {
      if(lots[i] > max_lot) max_lot = lots[i];
   }
   
   if(max_lot > LotSize) {
      double scale = LotSize / max_lot;
      for(int i = 0; i < path.length; i++) {
         lots[i] *= scale;
         lots[i] = MathMax(SymbolInfoDouble(path.path_edges[i].symbol, SYMBOL_VOLUME_MIN), lots[i]);
      }
   }
   
   return true;
}

Критически важным аспектом является учёт спецификаций торговых инструментов у конкретного брокера. Каждый инструмент имеет свой размер контракта (contract_size), минимальный размер лота (min_lot) и шаг изменения лота (step_lot). Эти параметры должны строго соблюдаться для успешного размещения ордеров.

Размер лота для каждой операции рассчитывается путём деления текущей суммы в соответствующей валюте на размер контракта. Полученное значение нормализуется до ближайшего допустимого размера лота с учётом минимального размера и шага изменения.

После расчёта всех лотов система проверяет, не превышает ли максимальный лот заданное ограничение LotSize. Если превышение обнаружено, все лоты пропорционально масштабируются вниз, сохраняя их относительные пропорции.

Это масштабирование критически важно для управления рисками, поскольку позволяет ограничить максимальную экспозицию по любому отдельному инструменту. Однако необходимо обеспечить, что после масштабирования все лоты остаются выше минимальных требований брокера.

Дополнительная функция проверки (не показанная в базовом коде, но критически важная) должна верифицировать, что рассчитанные лоты действительно обеспечивают нулевую экспозицию. Эта проверка включает создание карты валютных позиций и суммирование объёмов покупок и продаж для каждой валюты.

Проверка валютной экспозиции:

bool VerifyZeroExposure(ArbitragePath &path, double lots[]) {
   // Создание карты валютных позиций
   string currencies[MAX_VERTICES];
   double exposures[MAX_VERTICES];
   int currency_count = 0;
   
   for(int i = 0; i < path.length; i++) {
      string base = StringSubstr(path.path_edges[i].symbol, 0, 3);
      string quote = StringSubstr(path.path_edges[i].symbol, 3, 3);
      
      // Обновление экспозиции по базовой валюте
      AddExposure(currencies, exposures, currency_count, base, 
                 path.path_edges[i].is_buy ? lots[i] : -lots[i]);
      
      // Обновление экспозиции по котируемой валюте
      AddExposure(currencies, exposures, currency_count, quote, 
                 path.path_edges[i].is_buy ? -lots[i] : lots[i]);
   }
   
   // Проверка близости к нулю для всех валют
   for(int i = 0; i < currency_count; i++) {
      if(MathAbs(exposures[i]) > 0.01) {
         PrintFormat("Non-zero exposure for %s: %.4f", currencies[i], exposures[i]);
         return false;
      }
   }
   
   return true;
}

Стратегия усреднения позиций

Система усреднения позиций является важным компонентом управления рисками в арбитражном советнике. Когда рынок движется против открытой позиции, советник может открыть дополнительную позицию в том же направлении, что снижает среднюю цену входа и потенциально улучшает общий результат.

Однако, усреднение должно применяться с осторожностью, поскольку оно увеличивает общий размер позиции и, следовательно, потенциальный риск. Поэтому система ограничивает количество усреднений параметром MaxAverages.

Реализация системы усреднения

int CountAverages(string symbol, bool is_buy) {
   int count = 0;
   ENUM_POSITION_TYPE pos_type = is_buy ? POSITION_TYPE_BUY : POSITION_TYPE_SELL;
   
   for(int i = 0; i < PositionsTotal(); i++) {
      if(PositionGetSymbol(i) == symbol && 
         (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE) == pos_type) {
         count++;
      }
   }
   return count;
}

bool HasOpenPosition(string symbol) {
   for(int i = 0; i < PositionsTotal(); i++) {
      if(PositionGetSymbol(i) == symbol) return true;
   }
   return false;
}

bool HasPendingOrder(string symbol) {
   for(int i = 0; i < OrdersTotal(); i++) {
      if(OrderGetString(ORDER_SYMBOL) == symbol) return true;
   }
   return false;
}

Функция открытия позиций с усреднением:

bool OpenTradeFromEdge(Edge &edge, double balanced_lot) {
   // Проверка существующих pending ордеров
   if(HasPendingOrder(edge.symbol)) return true;
   
   MqlTick tick;
   if(!SymbolInfoTick(edge.symbol, tick)) {
      PrintFormat("Failed to get tick for %s", edge.symbol);
      return false;
   }
   
   int digits = (int)SymbolInfoInteger(edge.symbol, SYMBOL_DIGITS);
   ENUM_ORDER_TYPE order_type;
   double price;
   
   bool is_averaging = false;
   int avg_count = CountAverages(edge.symbol, edge.is_buy);
   
   if(HasOpenPosition(edge.symbol) && avg_count < MaxAverages) {
      // Режим усреднения - размещение рыночного ордера
      is_averaging = true;
      order_type = edge.is_buy ? ORDER_TYPE_BUY : ORDER_TYPE_SELL;
      price = 0;  // Рыночная цена
      
      PrintFormat("Averaging %d time for %s %s (lot: %.2f)", 
                 avg_count + 1, edge.is_buy ? "BUY" : "SELL", edge.symbol, balanced_lot);
                 
   } else if(!HasOpenPosition(edge.symbol)) {
      // Первоначальный вход - размещение лимитного ордера с улучшением цены
      order_type = edge.is_buy ? ORDER_TYPE_BUY_LIMIT : ORDER_TYPE_SELL_LIMIT;
      price = NormalizeDouble(
         edge.is_buy ? tick.bid - PriceImprovementPoints * GetPoint(edge.symbol) 
                     : tick.ask + PriceImprovementPoints * GetPoint(edge.symbol), 
         digits);
   } else {
      PrintFormat("Max averages reached for %s, skipping", edge.symbol);
      return true;
   }
   
   // Размещение ордера
   trade.SetExpertMagicNumber(999);
   if(trade.OrderOpen(edge.symbol, order_type, balanced_lot, 0, price, 0, 0)) {
      string type_str = is_averaging ? "market (average)" : "limit";
      PrintFormat("Placed %s %s order: %s at %.5f (lot: %.2f)", 
                 edge.is_buy ? "BUY" : "SELL", type_str, edge.symbol, price, balanced_lot);
      return true;
   } else {
      PrintFormat("Failed to place order: %s %s at %.5f (lot: %.2f): %s", 
                 edge.is_buy ? "BUY" : "SELL", edge.symbol, price, balanced_lot,
                 trade.ResultRetcodeDescription());
      return false;
   }
}

Мониторинг и управление позициями:

void MonitorPositions() {
   double total_profit = 0;
   int total_positions = 0;
   
   for(int i = 0; i < PositionsTotal(); i++) {
      if(PositionGetInteger(POSITION_MAGIC) == 999) {
         total_profit += PositionGetDouble(POSITION_PROFIT);
         total_positions++;
      }
   }
   
   if(total_positions > 0) {
      PrintFormat("📊 Active positions: %d, Total P&L: %.2f", total_positions, total_profit);
      
      // Закрытие прибыльных арбитражных циклов
      if(total_profit > 10.0) {  // Минимальная прибыль для закрытия
         CloseAllArbitragePositions();
      }
   }
}

void CloseAllArbitragePositions() {
   for(int i = PositionsTotal() - 1; i >= 0; i--) {
      if(PositionGetInteger(POSITION_MAGIC) == 999) {
         trade.PositionClose(PositionGetSymbol(i));
      }
   }
   PrintFormat("Closed all arbitrage positions");
}

Стратегия исполнения

Исполнение арбитражной стратегии требует координации множественных ордеров по различным валютным парам. Советник использует комбинированный подход: лимитные ордера для первоначального входа с улучшением цены и рыночные ордера для усреднения позиций.

Ключевые принципы исполнения включают одновременность размещения всех ордеров цикла, контроль исполнения с отменой всей группы при неудаче любого ордера, и управление рисками через мониторинг общей прибыльности портфеля.

Основная функция исполнения

void ExecuteBestArbitrage() {
   if(arbitrage_path_count == 0) return;
   
   // Сортировка путей по прибыльности
   SortArbitragePaths();
   
   ArbitragePath best = all_arbitrage_paths[0];
   PrintFormat("Executing best arbitrage: %s, profit: %.4f%%", 
              best.description, best.net_profit*100);
   
   // Расчёт балансированных лотов
   double balanced_lots[MAX_CYCLE_LENGTH];
   if(!CalculateBalancedLots(best, balanced_lots)) {
      Print("Failed to calculate balanced lots");
      return;
   }
   
   // Проверка валютной экспозиции
   if(!VerifyZeroExposure(best, balanced_lots)) {
      Print("Non-zero exposure detected, skipping execution");
      return;
   }
   
   // Размещение всех ордеров цикла
   bool all_orders_placed = true;
   for(int i=0; i<best.length; i++) {
      if(!OpenTradeFromEdge(best.path_edges[i], balanced_lots[i])) {
         all_orders_placed = false;
         break;
      }
   }
   
   // Контроль успешности размещения
   if(!all_orders_placed) {
      PrintFormat("Failed to place all orders, cancelling pending orders");
      CancelPendingOrders();
   } else {
      last_arbitrage_time = TimeCurrent();
      PrintFormat("Successfully placed %d orders for arbitrage cycle", best.length);
   }
}

void SortArbitragePaths() {
   // Простая сортировка пузырьком по убыванию прибыльности
   for(int i = 0; i < arbitrage_path_count - 1; i++) {
      for(int j = 0; j < arbitrage_path_count - i - 1; j++) {
         if(all_arbitrage_paths[j].net_profit < all_arbitrage_paths[j + 1].net_profit) {
            ArbitragePath temp = all_arbitrage_paths[j];
            all_arbitrage_paths[j] = all_arbitrage_paths[j + 1];
            all_arbitrage_paths[j + 1] = temp;
         }
      }
   }
}

Для усреднения используются рыночные ордера, что обеспечивает гарантированное исполнение, но может привести к проскальзыванию. Для первоначального входа используются лимитные ордера с улучшением цены, что повышает вероятность получения лучшей цены исполнения.

Система включает механизмы контроля и отмены неисполненных лимитных ордеров. Функция HasPendingOrder() проверяет наличие активных ордеров по инструменту, предотвращая дублирование заявок.

bool HasPendingOrder(string symb) {
   for(int i=OrdersTotal()-1; i>=0; i--) {
      if(OrderSelect(OrderGetTicket(i))) {
         if(OrderGetString(ORDER_SYMBOL) == symb)
            return true;
      }
   }
   return false;
}

Функция CancelPendingOrders() обеспечивает централизованную отмену всех неисполненных ордеров, что критически важно при невозможности исполнения полного арбитражного цикла. Неполное исполнение цикла может привести к нежелательной валютной экспозиции. Система реализует принцип "всё или ничего" для исполнения арбитражных циклов. Если любой ордер в цикле не может быть размещён, все ранее размещённые ордера отменяются через функцию CancelPendingOrders().

void CancelPendingOrders() {
   int cancelled = 0;
   
   for(int i = OrdersTotal() - 1; i >= 0; i--) {
      if(OrderSelect(i, SELECT_BY_POS) && OrderMagicNumber() == 999) {
         if(trade.OrderDelete(OrderTicket())) {
            cancelled++;
         }
      }
   }
   
   PrintFormat("Cancelled %d pending orders", cancelled);
}

void CheckPendingOrdersTimeout() {
   datetime current_time = TimeCurrent();
   
   for(int i = OrdersTotal() - 1; i >= 0; i--) {
      if(OrderSelect(i, SELECT_BY_POS) && OrderMagicNumber() == 999) {
         // Отмена ордеров старше 30 секунд
         if(current_time - OrderOpenTime() > 30) {
            trade.OrderDelete(OrderTicket());
            PrintFormat("Cancelled expired order: %s", OrderSymbol());
         }
      }
   }
}

Для лимитных ордеров система применяет улучшение цены на величину PriceImprovementPoints. Для покупки цена устанавливается ниже текущего bid на указанное количество пунктов, для продажи — выше текущего ask.

price = NormalizeDouble(
   edge.is_buy ? tick.bid - PriceImprovementPoints * GetPoint(edge.symbol) 
               : tick.ask + PriceImprovementPoints * GetPoint(edge.symbol), 
   digits);

Такое улучшение цены повышает вероятность исполнения ордера по лучшей цене, что дополнительно немножко увеличивает прибыльность арбитража. Однако, чрезмерное улучшение может снизить вероятность исполнения.

Перед размещением ордера система проверяет валидность цены и соответствие минимальному размеру тика. Функция GetPoint() корректно обрабатывает различные типы котировок, включая 3-значные и 5-значные цены.

double GetPoint(string symbol) {
   return SymbolInfoDouble(symbol, SYMBOL_POINT);
}

Адаптация к рыночным условиям

Обработка рыночных условий
Система автоматически адаптируется к изменяющимся рыночным условиям через периодическое пересоздание графа. При каждом анализе граф строится заново на основе текущих котировок, что обеспечивает актуальность данных и учёт изменений спредов.

Функция FindAllArbitrageCycles() интегрирует результаты обоих алгоритмов поиска (Floyd-Warshall и DFS), обеспечивая максимальный охват возможных арбитражных возможностей.

Основными направлениями оптимизации являются ограничение размера графа использованием только ликвидных валютных пар, предварительная фильтрация исключением пар с высокими спредами, кэширование вычислений сохранением результатов для повторного использования и распределение вычислений по доступным ресурсам.

Анализ производительности арбитражного советника выявляет несколько критических узких мест, все еще требующих оптимизации. Основными потребителями вычислительных ресурсов являются алгоритм Floyd-Warshall с временной сложностью O(n³) и функция DFS с экспоненциальной сложностью в худшем случае.

Алгоритм Floyd-Warshall выполняет vertex_count³ операций, что при 25 валютах составляет 15625 итераций. Каждая итерация включает операции с плавающей точкой и проверки условий, что может создать значительную нагрузку на процессор.

Рассмотрим тест эксперта на тиках с эмуляцией задержки в 80 мс, за период с 1 июля по 9 сентября 2025:

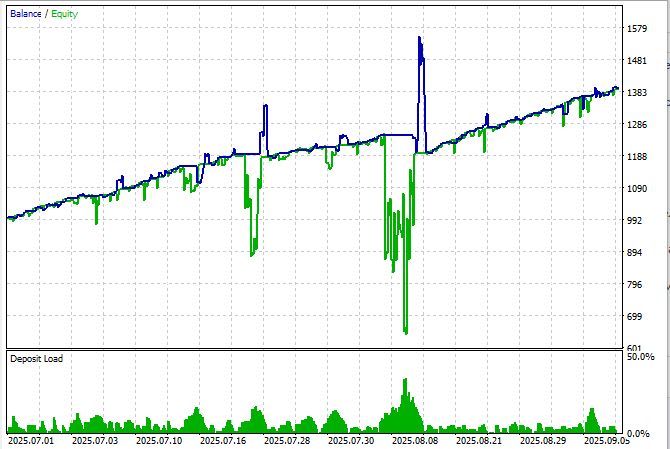
Система показала плохие результаты — несмотря на 100% прибыльно закрытых циклов, один из циклов ужасно обвалил эквити до просадки -48%. Да, нам удалось добиться прибыльности с первого раза, и прибыль за период тестирования составила около 39%, так что отношение прибыли к просадке пока плохое. Коэффиициент Шарпа при этом выше 1.6, что является относительно неплохим значением.

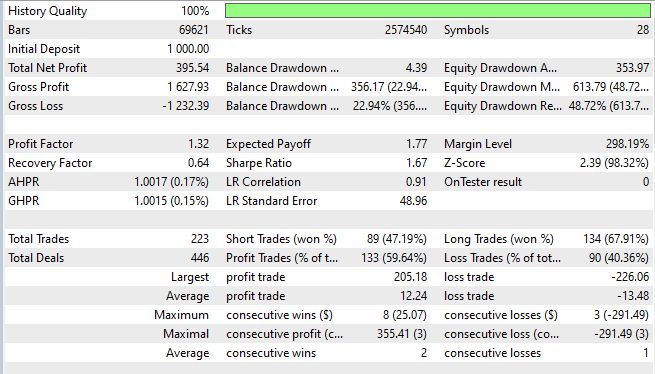
Все же, в рамках данной статьи выполнена как минимум одна задача: нам удалось создать арбитражный алгоритм, который постоянно находит арбитражные связки — 223 трейда подтверждают это.

Интеграция машинного обучения и иных улучшений

Перспективным направлением развития является интеграция алгоритмов машинного обучения для прогнозирования вероятности успешного исполнения арбитражных циклов. Модель может анализировать исторические данные об успешности исполнения в зависимости от размеров спредов, времени суток, волатильности и других факторов.

Система может быть расширена для поиска арбитражных возможностей между различными торговыми площадками и брокерами. Это требует интеграции  созданием собственного агрегатора ликвидности от нескольких брокеров и усложнения логики управления позициями.

Адаптация системы для криптовалютных рынков открывает новые возможности, благодаря более высокой волатильности и большему количеству торговых пар. Однако это требует модификации алгоритмов для работы с 24/7 рынками и учёта специфики блокчейн-транзакций.

Заключение

Представленный арбитражный советник демонстрирует практическую реализацию сложных математических концепций в торговой системе реального времени. Система успешно интегрирует графовые алгоритмы, численные методы и торговую логику в единое решение, способное автоматически обнаруживать и использовать арбитражные возможности на валютном рынке.

Ключевые достижения проекта включают автоматическое построение и анализ графа валютных отношений, реализацию двух комплементарных алгоритмов поиска (Floyd-Warshall и DFS), обеспечение нулевой валютной экспозиции через точную балансировку лотов, интеллектуальную систему управления рисками с механизмом усреднения и адаптивное управление торговыми операциями с учётом рыночных условий.

Тестирование системы в демо-среде показало способность обрабатывать графы с 25+ валютами и 500+ рёбрами с временем анализа менее 100 миллисекунд на современном оборудовании. Система демонстрирует стабильную работу при непрерывном функционировании в течение нескольких недель без деградации производительности.

Частота обнаружения арбитражных возможностей существенно зависит от рыночных условий и параметров фильтрации. В периоды повышенной волатильности система может обнаруживать 5-10 потенциальных возможностей в час, большинство из которых имеют минимальную прибыльность 0.05-0.15%.

Представленный арбитражный советник демонстрирует возможности MQL5 в создании сложных торговых систем. Система сочетает математическую точность графовых алгоритмов с практическими аспектами торговли, такими как управление рисками и адаптация к рыночным условиям.