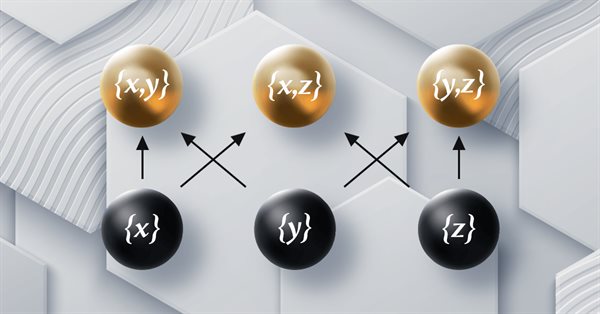
Теория категорий в MQL5 (Часть 12): Порядок
Введение
В предыдущей статье мы рассмотрели графы, вершины и стрелки взаимосвязанной системы в рамках теории категорий и изучили, как различные пути с их атрибутами могут использоваться для определения различных методов трейлинг-стопа в типичной торговой системе.
В этой статье мы рассмотрим порядок (orders) в рамках теории категорий и как он может дополнить торговые установки с помощью трейлинг-стопов. Говоря по-простому, порядок связан с ранжированием "величины" различных элементов, обычно встречающихся в множестве. Он реализует идею о том, что элементы определенного набора могут ранжироваться по нескольким критериям. Теория категорий добавляет этой идее новое измерение, вводя понятие множества множеств и даже множества множества множеств и т. д. Поэтому в этой статье мы остановимся на рангах множеств (set ranks).
В частности, мы сосредоточимся на закономерностях (паттернах) в упорядоченных множествах как средстве генерации выходов из сделок. В рамках этой работы можно рассмотреть довольно много множеств, поскольку наш список может варьироваться от паттернов ценового действия до паттернов индикаторов или даже распространенных паттернов индексов с несколькими активами. Однако, следуя шагам базовой торговой системы, которые мы рассмотрели в предыдущих статьях, мы разобьем три внутренних шага между первым и последним шагами нашего пятишагового процесса на подмножества, чтобы получить наши упорядоченные наборы паттернов.
Понимание порядка в теории категорий
Согласно отношению порядка, существует три основных типа порядка - предпорядок (pre-orders), нестрогий порядок (partial orders) и линейный порядок (linear или total orders). Предпорядок — это ранжирование элементов множества, при котором каждый элемент множества сравнивается со всеми другими элементами (рефлексивность), и результаты каждого сравнения имеют логическое значение для сравнения других элементов (транзитивность). Предпорядок учитывает неоднозначность: если какие-либо два элемента имеют одинаковую величину в соответствии с бинарной операцией, оба могут быть включены в выходное множество. Кроме того, множества предпорядка учитывают неопределенные результаты, которые возникают в том случае, если два элемента не могут быть сопоставлены из-за, скажем, фундаментального различия. Нестрогий порядок — это тип предпорядка, который вводит дополнительную концепцию антисимметрии. Это означает, что если в результате двоичной операции сравнения обнаружено, что какие-либо два элемента имеют одинаковую величину, то только один из них включается в выходное множество. Таким образом, определение "нестрогий" используется, поскольку выводится только один из любых равных элементов. Наконец, линейный порядок представляют собой специализированную форму нестрогого порядка, при которой нет неопределенных результатов. Это означает, что все элементы сопоставимы. Как и в случае с предпорядком, некоторые элементы могут быть несравнимыми, что означает, что бинарная операция выдает неопределенный результат. Это не учитывается линейным порядком.
Таким образом, формально для множества S с бинарным отношением R
R ⊆ S x S
R будет считаться предпорядком, если для всех:
s, s’, s” ∈ S
мы имеем рефлексивность, которая формально представляется как:
s ≦ s
а также транзитивность, которая подразумевается следующим образом:
s ≦ s’ and s’ ≦ s”, что означает s ≦ s”
Нестрогий порядок, как упоминалось выше, добавляет антисимметрии предпорядку, так что если:
s ≦ s’ и s’ ≦ s, то s = s’,
подразумевая, что в выходных данных представлен только один из s или s'.
Линейный порядок добавит сопоставимости нестрогому порядку, так что для любых двух элементов существует определенная связь:
s ≦ s’ или s’ ≦ s,
что означает, что неопределенные выходные данные не учитываются.
Как уже упоминалось, эти форматы порядка полезны для обозначения моделей, которые могут помочь в принятии решений в любой торговой системе. В этой статье мы воссоздадим внутришаговые моноидные множества, использованные в предыдущих статьях, для периода ретроспективного анализа, применяемой цены и индикатора, сохраняя при этом для простоты конечные множества таймфрейма и торгового действия. Как и в предыдущей статье, основным тестируемым параметром будет порядок принятия решения, однако, поскольку мы будем рассматривать нестрогий порядок, существует вероятность неопределенных результатов. Это означает, что наш выходной порядок множеств моноидов, представляющих точки принятия решения, может быть меньше входного 3. Он может быть равен 2 или даже 1. Это означает, что в определенных ситуациях нам, возможно, придется принять только 3 или 4 решения, а не 5 по умолчанию при оценке того, следует ли изменять наш стоп-лосс.
Применение отношения порядка в MQL5
В этой статье мы не будем рассматривать предпорядок, так как в этом случае статья окажется слишком длинной. Вместо этого мы сосредоточимся на нестрогом и линейном порядках. Поскольку у нас уже есть структуры данных, определяющие наши пять торговых шагов согласно предыдущей статье, главное, что ожидается от реализации отношения порядка, — это бинарные функции, которые обрабатывают наши структуры данных и выводят множество (обычно подмножество входных данных). Поскольку мы рассматриваем нестрогий и линейный порядок, для каждого из них будет своя функция.
Возможно, будет полезно подчеркнуть различия и относительные преимущества двух форм порядка, которые мы рассматриваем в этой статье. Как упоминалось выше, нестрогий порядок допускает неопределенную классификацию результатов в отличие от линейного. Это может быть полезно в ряде случаев. Давайте рассмотрим простой случай классификации ценовых баров на графике как бычьих или медвежьих. В этом процессе вы обязательно встретите длинноногую свечу Доджи, которая, строго говоря, не является ни бычьей, ни медвежьей. При классификации линейного порядка эту точку данных придется опустить, поскольку это нарушит аксиому сопоставимости.
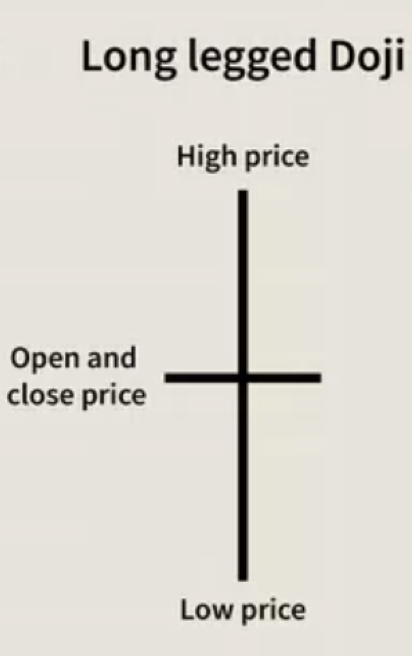
Однако при нестрогом порядке, включение этой точки данных и, следовательно, ее результата сделает выходное множество более полным и репрезентативным для набора данных. Чтобы показать, почему это важно, свечи Доджи с длинными ногами и другие подобные свечи, в том числе Доджи Надгробие и Доджи Стрекоза, как правило, появляются в основных областях ценовой поддержки и сопротивления. Таким образом, если в вашей классификации отсутствует какая-либо из этих моделей, ваш анализ и, следовательно, прогнозы будут менее точными, поскольку для большинства торговых систем в долгосрочной перспективе области ценовой поддержки и сопротивления играют решающую роль в определении торговых установок. Таким образом, добавление свойства антисимметрии при нестрогом порядке можно использовать для лучшей фильтрации торговых сигналов.
Рассмотрение торговой системы, которое отличается от нашего пятиэтапного процесса, рассмотренного в предыдущих статьях, может включать в себя векторизацию ценовых баров. Отображая каждый ценовой бар в виде вектора, который представляет собой просто массив весов, мы можем сравнивать, насколько похожи различные модели. Если мы обучаемся в течение достаточного периода времени и идентифицируем возможные ценовые формирования для значительного числа векторизованных моделей, мы можем сравнить любую новую модель с той, которая была обучена, и на основе евклидова расстояния от этих обученных моделей, модель, наиболее близкая к нашей новой модели, может рассматривать его "постценовое" формирование как наиболее вероятный результат новой модели.
Линейный порядок может быть предпочтительнее нестрогого в случаях анализа портфеля. Если мы сталкиваемся с широким спектром активов, которые необходимо оценить или включить в портфель, то линейная упорядоченность со строгими требованиями одинакового взвешивания (сопоставимость) является обязательной. Это происходит по ряду причин, некоторые из которых считаются само собой разумеющимися. Линейный порядок позволяет оценивать активы последовательным образом, что обеспечивает оптимизированный процесс. Независимо от количества активов, приоритеты уже определены посредством взвешивания активов, которое может представлять собой величину, выражающую в количественном выражении все - от прошлой реализованной стоимости до будущего потенциального риска. Это не только приводит к повышению эффективности, но и позволяет трейдеру не распылять внимание на все возможные активы.
Такая расстановка приоритетов означает, что инвестиционные решения по активам, которые имеют наибольшее значение, рассматриваются в первую очередь, что приводит к критическому вопросу распределения активов. Как будет определяться размер каждого актива в портфеле? При линейном порядке вес каждого актива часто может выступать в качестве справедливого показателя того, сколько капитала следует использовать для покупки актива, что было бы труднее последовательно делать при нестрогом порядке.
Пример: Разработка торговой системы с разными форматами порядка
Выбранная торговая стратегия основана на системе, которую мы рассматривали в предыдущих статьях, и будет включать в себя выбор промежуточных шагов со 2 по 4 нашего 5-шагового метода. Мы выберем их методом нестрогого порядка в одной торговой системе, а также методом линейного порядка в другой системе.
Для немедленного выбора нестрогого ордера все наши множества моноидов несравнимы, потому что у нас есть период просмотра, который является целочисленным типом. Мы применяем цену, которая представляет собой строковое перечисление, и, наконец, тип индикатора, который также, строго говоря, является выбором строки. Итак, чтобы ввести возможность использовать бинарный оператор:
≦
Мы нормализуем только пару множеств, оставив третье в формате по умолчанию. Входные данные функции, обеспечивающей нестрогий порядок, по своей сути будут ценовым действием. Ценовые параметры, которые мы будем рассматривать в качестве входных данных для нашей функции нестрогого порядка, будут индексироваться автокорреляцией. Мы просто назначим индексы различным паттернам автокорреляции, и для каждого индекса у нас будет определенная нормализованная пара множеств, которые затем будут информировать выбранный нами порядок для нашей торговой системы. При нестрогом порядке, как указано выше, наличие неопределенных множеств означает, что будут выбраны только два множества, а это означает, что мы почти наверняка всегда будем иметь 4-шаговый процесс, а не 5-шаговый, который мы использовали.
Однако для линейного порядка все моноидные множества будут нормализованы. Это должно дать нам полные 5 шагов, которые мы рассматривали, и, как и в случае с нестрогим порядком, входными данными для функции линейного порядка будет наш индекс автокорреляции. Назначение индекса автокорреляции будет очень простым, как видно из листинга ниже.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CTrailingCT::Ordering(int Lookback) { m_low.Refresh(-1); m_high.Refresh(-1); m_close.Refresh(-1); double _c[],_l[],_h[]; ArrayResize(_c,Lookback);ArrayInitialize(_c,0.0); ArrayResize(_l,Lookback);ArrayInitialize(_l,0.0); ArrayResize(_h,Lookback);ArrayInitialize(_h,0.0); for(int i=0;i<Lookback;i++) { _c[i]=m_close.GetData(i); _l[i]=m_low.GetData(Lookback+i); _h[i]=m_high.GetData(Lookback+i); } double _r_h=0.0,_r_l=0.0; if(MathCorrelationSpearman(_c,_l,_r_l) && MathCorrelationSpearman(_c,_h,_r_h)) { if(_r_l>=__PHI){ LongIndex(5); } else if(_r_l>=1.0-__PHI){ LongIndex(4); } else if(_r_l>=0.0){ LongIndex(3); } else if(_r_l>=(-1.0+__PHI)){ LongIndex(2); } else if(_r_l>=(-__PHI)){ LongIndex(1); } else{ LongIndex(0);} if(_r_h>=__PHI){ ShortIndex(5); } else if(_r_h>=1.0-__PHI){ ShortIndex(4); } else if(_r_h>=0.0){ ShortIndex(3); } else if(_r_h>=(-1.0+__PHI)){ ShortIndex(2); } else if(_r_h>=(-__PHI)){ ShortIndex(1); } else{ ShortIndex(0);} return(true); } return(false); }
Для обработки нестрогого порядка код будет встроен в функции обработки длинного и короткого трейлинг-стопа, как указано в приложении к статье ниже. Здесь примечательно то, что, по сути, каждый присвоенный индекс отображает только два множества, поскольку третий не определен. Порядок, определенный каждым возможным индексом, подразумевает, что первое назначенное множество имеет более высокий вес, чем последнее. Таким образом, необходимость в создании нормализующей функции, придающей физический вес каждому из них, отменяется, поскольку она не окажет существенного влияния на конечный результат.
Аналогично, функция линейного порядка будет выглядеть следующим образом:
ENUM_TIMEFRAMES _timeframe=GetTimeframe(m_timeframe,__TIMEFRAMES); int _lookback=m_default_lookback; ENUM_APPLIED_PRICE _appliedprice=__APPLIEDPRICES[m_default_appliedprice]; double _indicator=m_default_indicator; if(m_long_index==0) { _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,_appliedprice); } else if(m_long_index==1) { _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,_appliedprice); } else if(m_long_index==2) { _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe); _indicator=GetIndicator(m_default_lookback,_timeframe,_appliedprice); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); } else if(m_long_index==3) { _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,m_default_lookback,_timeframe); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); } else if(m_long_index==4) { _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); } else if(m_long_index==5) { _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); } // int _trade_decision=GetTradeDecision(_timeframe,_lookback,_appliedprice,_indicator);
Здесь примечательно то, что каждый индекс обеспечивает исчерпывающий перечень всех множеств, поскольку сопоставимость является требованием для всех множеств. И, как упоминалось выше, процедура присвоения весовых чисел каждому множеству, которые затем используются при сортировке, избегается, поскольку используемая индексация подразумевает порядок взвешивания, который реализуется, как показано выше.
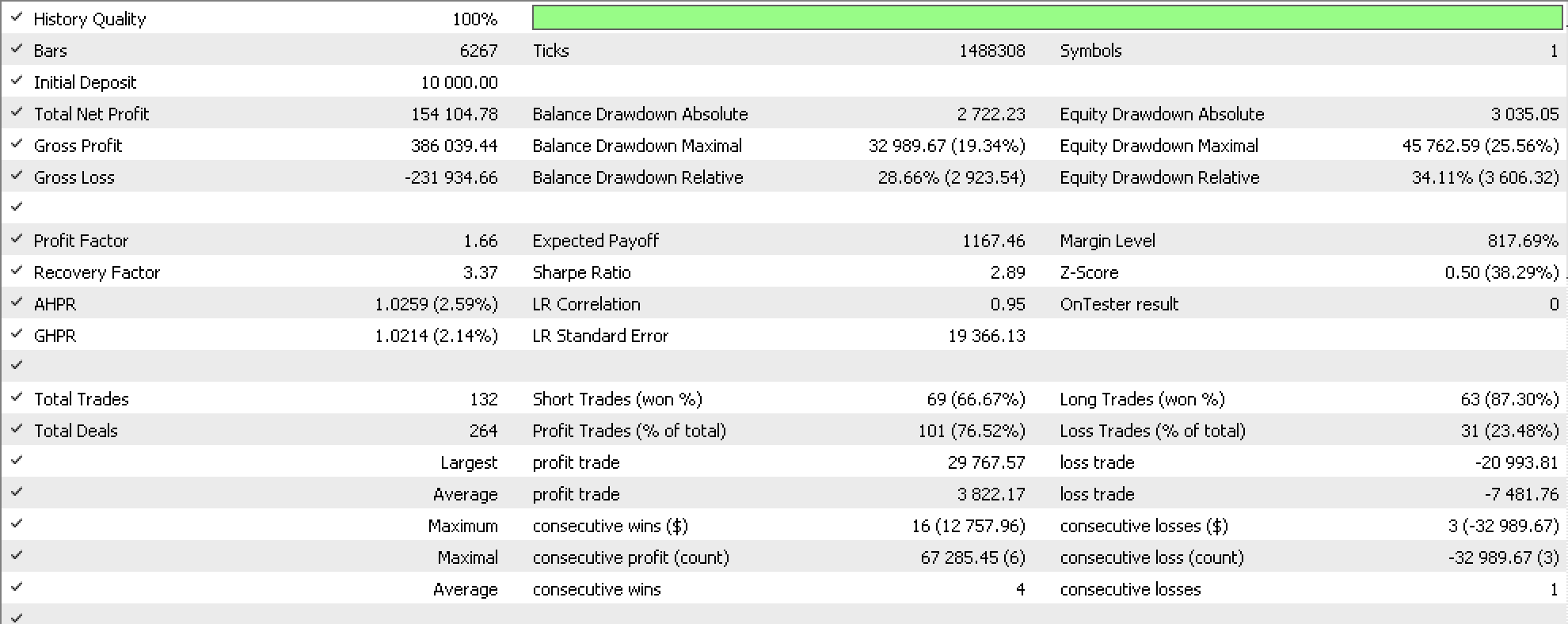
Если мы проведем тесты с использованием наших новых трейлинг-классов, на классе сигналов библиотечного Awesome Oscillator с использованием фиксированной маржи для символа USDJPY за последние 12 месяцев, мы получим следующие отчеты для каждого из методов порядка. Метод нестрогого порядка:
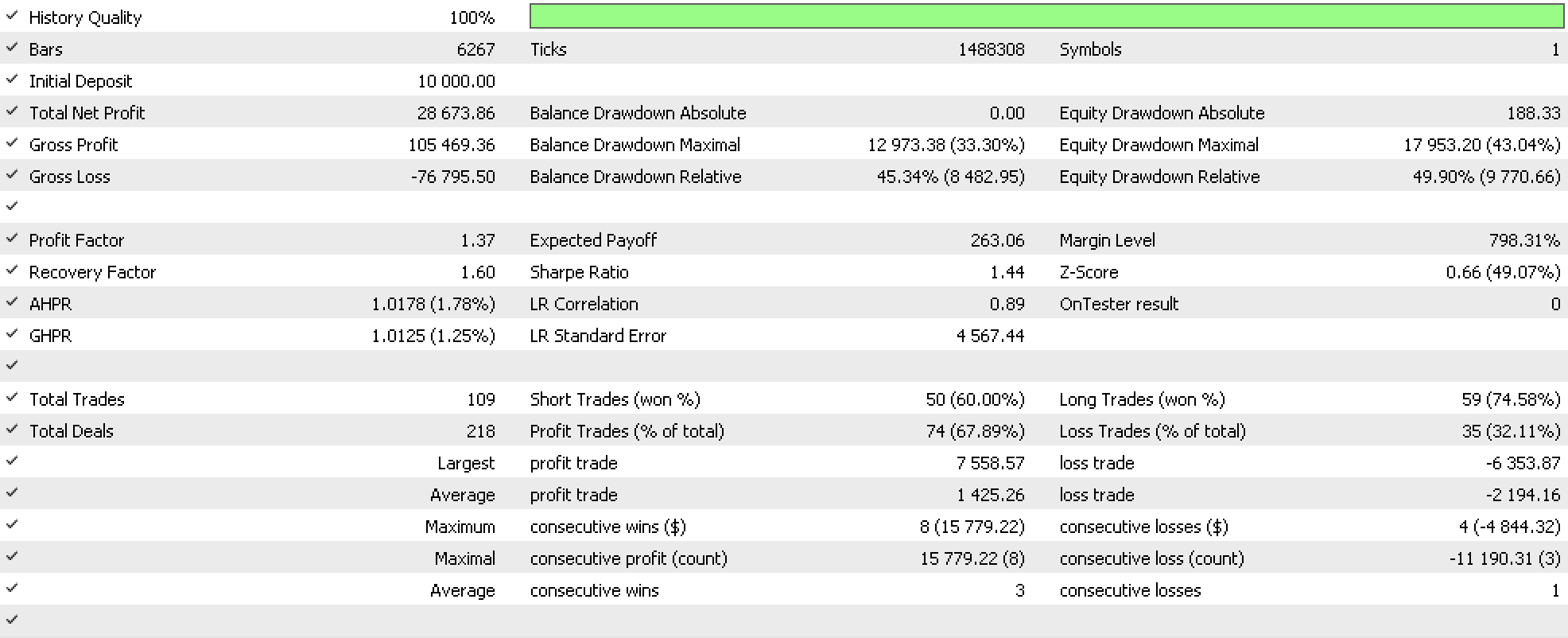
Наш советник заработал более 100 тысяч, как это всегда бывает в этой серии статей, если не использовать целевые цены для тейк-профита или стоп-лосса, а удерживать позиции только до тех пор, пока сигнальный индикатор не сочтет, что их следует закрыть. Кроме того, поскольку мы улучшаем наш трейлинг-стоп, большинство прибыльных закрытых позиций на самом деле были связаны с нашим трейлинг-стопом, что говорит о преимуществе нестрогого порядка в создании надежных индикаторов установки трейлинг-стопа. Мы также протестировали трейлинг-стопы на основе линейного порядка. Результаты приведены ниже.
Прибыль здесь на удивление ниже той, что была получена при нестрогом («неоднозначном», приспосабливающемся) порядке. Как ни странно, просадка капитала становится еще выше при меньшем количестве сделок. Для получения каких-либо окончательных выводов необходимо тестирование на более длительных периодах и на нескольких символах, но можно с уверенностью сказать, что нестрогий порядок более перспективен, чем линейный.
Заключение
Мы рассмотрели эффективность нестрогого порядка по сравнению с линейным при установке и изменении трейлинг-стопа для типичного советника. До этого мы рассматривали относительные преимущества этих двух принципов упорядочения и не рассматривали принцип привязки обоих, а именно предпорядок, поскольку это сделало бы статью слишком длинной, при этом мало что добавив по сути. Помните, что нестрогий порядок — это специализированная форма предпорядка, а линейный порядок — это также специализированная форма нестрогого порядка. Поскольку основные определения этих типов упорядочения во многом совпадают, мы сосредоточились на последних двух.
Нестрогие и линейные методы отношения порядка использовались ради их конкретных преимуществ. Нестрогий порядок обеспечивает большую гибкость в классификации множеств необработанных данных, что может привести к более богатому и точному анализу. И наоборот, более строгий линейный порядок, как правило, требует нормализации необработанных данных для обеспечения сопоставимости, что приводит к общей расстановке приоритетов и эффективности принятия решений.
Эти методы упорядочивания имеют потенциал для дальнейшего изучения и совершенствования по мере того, как мы начнем интегрировать прошлые концепции в новые.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/12873
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Это разочаровывает, снова нет советника, который бы выдавал показанные результаты тестирования. :(
Пожалуйста, предоставьте здесь советник(и) с настройками, чтобы мы могли воспроизвести результаты.