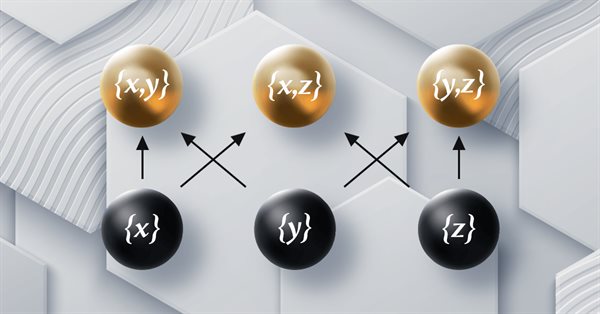
MQL5における圏論（第12回）：順序

はじめに

前回の記事では、圏論の中で、相互接続されたシステムの頂点と矢印であるグラフに注目し、その属性を持つ様々なパスが、典型的な取引システムに様々なトレーリングストップ手法を定義するためにどのように使用できるかを検討しました。

この記事では、圏論における順序について考え、前回の記事と同様に、トレーリングストップを通じた取引設定をどのように補うことができるかを考えます。順序とは、わかりやすく言えば、一般的に集合の中にある様々な要素の「大きさ」をランク付けすることです。これらは、特定の集合が複数の基準に従ってその要素をランク付けすることができるという考えをもたらします。圏論は、集合の集合や集合の集合の集合（など）の概念を導入することで、これに次元を加えています。そこで今回は、集合のランク付けについて取り上げます。

具体的には、取引の出口を生み出す手段として、順序集合のパターンに注目します。リストはプライスアクションパターンから指標パターン、さらには一般的なマルチア集合インデックスパターンにまで及ぶ可能性があるため、この取り組みで考慮できる集合は多数あります。しかし、以前の記事で見てきた基本的な取引システムのステップにならって、5つのステップのプロセスの最初と最後のステップの間にある3つのステップを部分集合に再構成して、順序集合パターンを導き出すことにします。

圏論における順序について

順序論によれば、順序には主に3つのタイプがあります。前順序（英語）、半順序、全順序です。全順序は線型順序とも呼ばれます。前順序とは、集合の各要素が他のすべての要素と比較され（反射性）、各比較の結果が他の要素の比較に論理的に関係する（推移性）、集合要素のランク付けです。前順序は、二項演算によって2つの要素が同じ大きさを持つ場合、両方を出力集合に含めることができるという曖昧さに対応します。また、前順序集合は、例えば基本的な非類似性のために2つの要素を比較できない場合に起こる未定義の結果に対応します。半順序は前順序の一種であり、非対称性という新たな概念を導入しています。これが意味するのは、二項演算の比較によって同じ大きさを持つ2つの要素が見つかった場合、そのうちの1つだけが出力集合に含まれるということです。このように、等しい要素のうち1つだけが出力されるため、「半」が名前に入っています。最後に、線型順序はこのトレンドに沿ったもので、未定義の結果がない半順序の特殊な形式です。つまり、すべての要素が比較可能です。上述した前順序のように、いくつかの要素は二項演算が未定義の結果を出力することを意味する、比較できない可能性があることを思い出してください。これは全順序では対応できません。

したがって、正式には、二項関係Rを持つ集合S

R ⊆ S x S

があった場合、すべての

s, s', s" ∈ S

について、正式には

s ≦ s

として表現される反射性があり、かつ、

s ≦ s’ かつ s’ ≦ s” よって s ≦ s”

によって暗示される推移性もある場合、Rは、前順序とみなされます。前述の半順序は、前順序に

s ≦ s' かつ s' ≦ s ならば s = s'

という非対称性を加えることになります。つまり、sかs'のどちらか一方だけが出力されます。

線形順序は、半順序に比較可能性を追加するもので、2つの要素に対して

s ≦ s' または s' ≦ s

のどちらかの明確な関係があります。つまり、未定義の出力には対応できません。

前述したように、これらの順序形式は、あらゆる取引システムで意思決定をおこなう際に役立つパターンをマークするのに便利です。この記事では、前回の記事で使用した、振り返り期間、適用価格、指標のステップ内モノイド集合を再構成しますが、簡略化するために時間枠と取引アクションの最終セットは保持します。主なテストパラメータは、前回の記事と同様に決定順ですが、今回は半順序を考慮するため、未定義の結果が出る可能性があります。つまり、決定点を表すモノイド集合の出力順序は、入力の3より小さくなる可能性があるということです。時には2だったり、1だったりすることもあります。つまり、ストップロスを変更するかどうかを判断する際に、デフォルトの5回ではなく、3回だけ、あるいは4回だけ判断しなければならない状況もあるということです。

MQL5における順序論の適用

記事が長くなりすぎるので、今回は前順序については触れません。むしろ、半順序と線形順序に焦点を当てます。前回の記事に続き、5つの取引ステップを定義するデータ構造はすでに持っているので、順序論の実装に必要な主なものは、データ構造を処理して集合（通常は入力の部分集合）を出力する二項関数です。ここでは半順序と線形順序に焦点を当てるので、それぞれの関数は1つになります。

この記事で考えている2つの順序付けの形態の違いと相対的な利点を強調しておくことは有益かもしれません。前述のように半順序は、線形順序とは異なり、出力に未定義の分類を許容します。これは様々な場面で役に立ちます。チャート上の価格バーを強気か弱気かに分類する単純なケースを考えてみましょう。この過程で、厳密には強気でも弱気でもない、足の長い同時ローソク足に出くわすことになります。線形順序分類では、このデータポイントは比較可能性の公理に反するため、省略せざるを得ません。

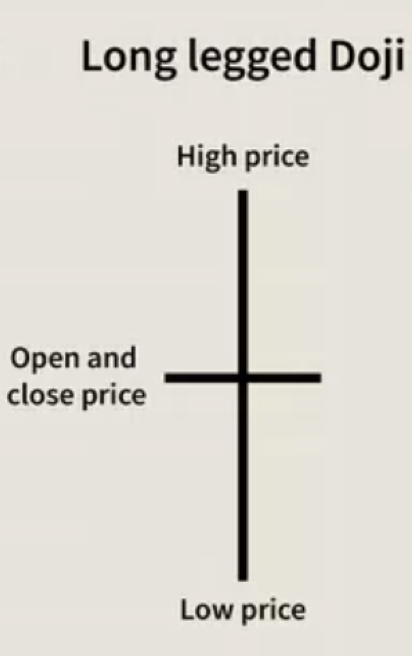
しかし、半順序では、このデータ点とその結果を含めることで、出力集合はより完全で、データ集合を代表するものになります。これがなぜ重要なのかを示すために、足長、塔婆、トンボなどの他の同時足は、主要な価格の支持と抵抗の領域で特徴づけられる傾向があります。したがって、分類でこれらのパターンのいずれかを省略している場合、分析と予測の精度が低下することは間違いありません。これは、ほとんどの取引システムでは、長期にわたる価格の支持と抵抗の領域が取引設定を定義する上で重要な役割を果たすためです。このように、半順序を作成する際に非対称性を追加することで、取引シグナルをより適切にフィルタリングすることができます。

これまでの記事で見てきた5ステップのプロセスとは異なる取引システムのケーススタディでは、価格バーのパターンをベクトル化することができます。各価格バーの形成を単純な重みの配列であるベクトルとして持つことで、様々なパターンがどれだけ似ているかを比較することができます。適切な期間にわたって訓練し、かなりの数のベクトル化されたパターンの最終的な価格形成を特定すれば、新しいパターンを訓練済みのものと比較することができます。これらの訓練済みパターンからのユークリッド距離に基づいて、新しいパターンに最も近いパターンが、新しいパターンの最も可能性の高い結果として、その後の価格形成を提供することができます。

線形順序は、ポートフォリオ分析の例では半順序よりも好ましくなります。もし、鑑定が必要な、あるいはポートフォリオに組み入れる必要のある様々な資産に直面した場合、厳格な一様な重み要件（比較可能性）を持つ線形順序を使用するのは当然のｌことでしょう。これにはいくつかの理由があります。線型順序は、順次に資産を評価することを可能にし、合理的なプロセスを提供します。資産の数に関係なく、優先順位はすでに資産の重みによって定義されています。この重みは、過去の実現価値から将来の潜在的リスクまで、あらゆるものを数値化したものです。これは効率化につながるだけでなく、集中力を高めることによって、トレーダーがあらゆる可能性のある資産を考慮しないことを可能にします。

この優先順位付けは、最も重要な資産が最初に投資決定されることを意味し、資産配分の重要な問題につながります。各資産はポートフォリオ内でどのようにサイズ分けされるでしょうか。線形順序では、各資産の重み付けは、しばしば、半順序では一貫しておこなうことが困難であるような資産の購入に使用されるべき資本の公正な代理として機能することができます。

ケーススタディ順序による取引システムの開発

当連載でこれまで見てきたシステムをベースに、5ステップのうち2～4の中間ステップを選択する取引戦略を選択します。取引システムの1つでは半順序方式から、あと１つのシステムでは線形順序方式から選択します。

最初から半順序を選択する場合、すべてのモノイド 集合は比較できません。なぜなら、整数型である振り返り期間があり、文字列列挙型である価格を適用し、最後に、これも厳密に言えば文字列選択である指標型を適用しているからです。そこで、二項演算子

≦

を使う能力を導入します。2組の集合だけを正規化し、3組目はデフォルトの形式のままにします。半順序を実行する関数の入力は、本来プライスアクションです。半順序関数の入力として考慮する価格パラメータは、自己相関インデックスです。インデックスをさまざまな自己相関パターンに割り当てるだけで、インデックスごとに特定の集合の対が正規化され、これが取引システム用に選択した集合の順序を通知します。上で指摘したように、半順序では、未定義の集合が存在すると、2つの集合しか選択されないことになります。つまり、ほぼ確実に、これまで使用してきた5ステップではなく、4ステップのプロセスを使用することになります。

線形順序の場合、すべてのモノイド集合は正規化されます。これによって、これまで検討してきた5ステップの全ステップが得られるはずで、半順序の場合と同様に、線形順序関数の入力は自己相関指数となります。自己相関指数の割り当ては、以下のコードからわかるように初歩的なものです。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CTrailingCT::Ordering(int Lookback)
   {
      m_low.Refresh(-1);
      m_high.Refresh(-1);
      m_close.Refresh(-1);
      
      double _c[],_l[],_h[];
      
      ArrayResize(_c,Lookback);ArrayInitialize(_c,0.0);
      ArrayResize(_l,Lookback);ArrayInitialize(_l,0.0);
      ArrayResize(_h,Lookback);ArrayInitialize(_h,0.0);
      
      for(int i=0;i<Lookback;i++)
      {
         _c[i]=m_close.GetData(i);
         _l[i]=m_low.GetData(Lookback+i);
         _h[i]=m_high.GetData(Lookback+i);
      }
      
      double _r_h=0.0,_r_l=0.0;
      
      if(MathCorrelationSpearman(_c,_l,_r_l) && MathCorrelationSpearman(_c,_h,_r_h))
      {
         if(_r_l>=__PHI){ LongIndex(5); }
         else if(_r_l>=1.0-__PHI){ LongIndex(4); }
         else if(_r_l>=0.0){ LongIndex(3); }
         else if(_r_l>=(-1.0+__PHI)){ LongIndex(2); }
         else if(_r_l>=(-__PHI)){ LongIndex(1); }
         else{ LongIndex(0);}
         
         if(_r_h>=__PHI){ ShortIndex(5); }
         else if(_r_h>=1.0-__PHI){ ShortIndex(4); }
         else if(_r_h>=0.0){ ShortIndex(3); }
         else if(_r_h>=(-1.0+__PHI)){ ShortIndex(2); }
         else if(_r_h>=(-__PHI)){ ShortIndex(1); }
         else{ ShortIndex(0);}
         
         return(true);
      }
      
      return(false);
   }

まず始めに、記事末尾の添付ファイルにあるように、半順序処理コードをロングとショートのトレイリングストップ処理関数に組み込みます。ここで注目すべき点は、3番目の集合が未定義であるため、割り当てられた各インデックスは本質的に2つの集合のみを写像するということです。各インデックスで定義される順位は、最初に割り当てられた集合が最後に割り当てられた集合よりも高い重み付けを持つことを意味します。従って、それぞれに物理的な重みを与える正規化関数を実際に考え出す必要性は、最終結果に意味のある影響を与えないため否定されます。

同様に、線形順序関数は以下のようになります。

	ENUM_TIMEFRAMES _timeframe=GetTimeframe(m_timeframe,__TIMEFRAMES);
         
         int _lookback=m_default_lookback;
         ENUM_APPLIED_PRICE _appliedprice=__APPLIEDPRICES[m_default_appliedprice];
         double _indicator=m_default_indicator;
         
         if(m_long_index==0)
         {
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,_appliedprice);
         }
         else if(m_long_index==1)
         {
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,_appliedprice);
         }
         else if(m_long_index==2)
         {
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe);
            _indicator=GetIndicator(m_default_lookback,_timeframe,_appliedprice);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
         }
         else if(m_long_index==3)
         {
            _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,m_default_lookback,_timeframe);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
         }
         else if(m_long_index==4)
         {
            _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
         }
         else if(m_long_index==5)
         {
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
         }
         //
         int _trade_decision=GetTradeDecision(_timeframe,_lookback,_appliedprice,_indicator);

ここで注目するべき点は、比較可能性がすべての集合の要件であるため、各インデックスがすべての集合を網羅的に列挙していることです。上述したように、各集合に重みの数値を割り当て、それを並び替えに使用するという作業は、使用されるインデックスが上記のように実装される重み付け順序を意味するため、敬遠されます。

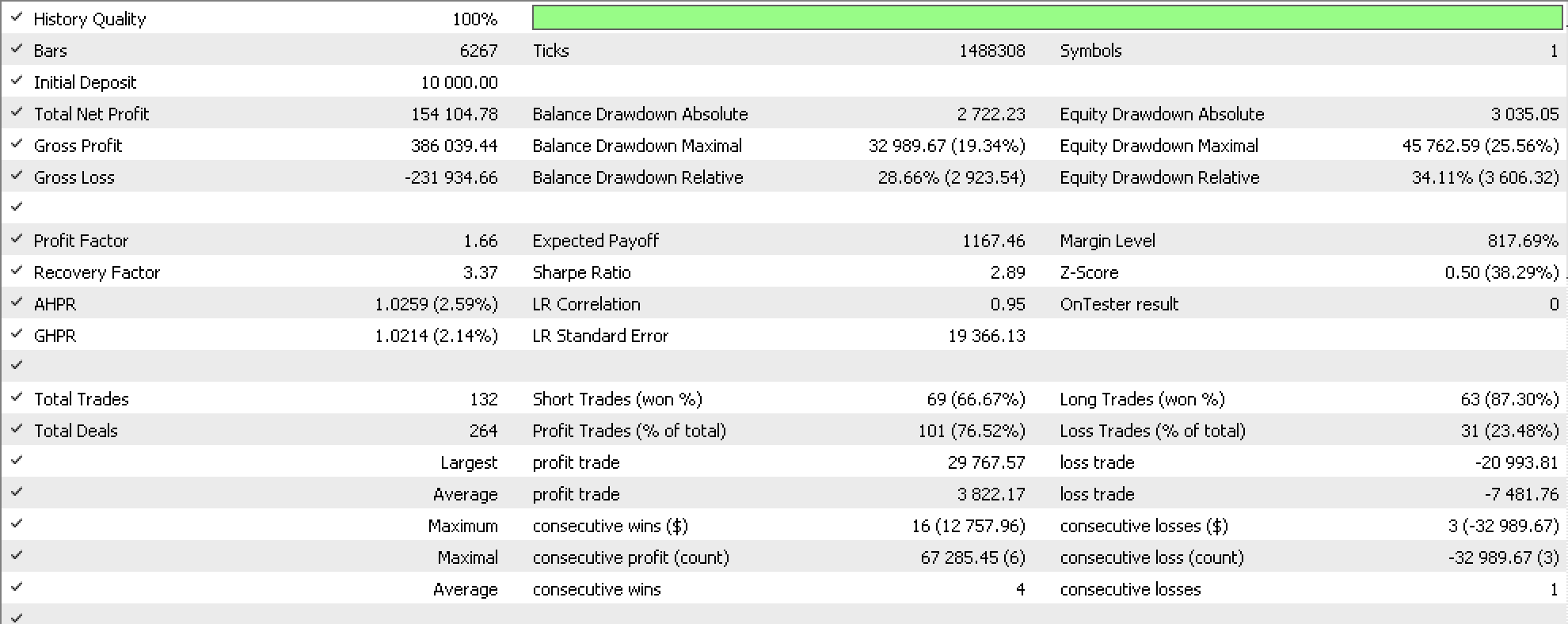
新しいトレーリングクラスを使ってテストを実行すると、シンボルUSDJPYの固定証拠金を使ったライブラリawesome oscillatorのシグナルクラスで過去12ヶ月間、各順序方法について以下のようなレポートが得られます。まずは半順序方式のレポートです。

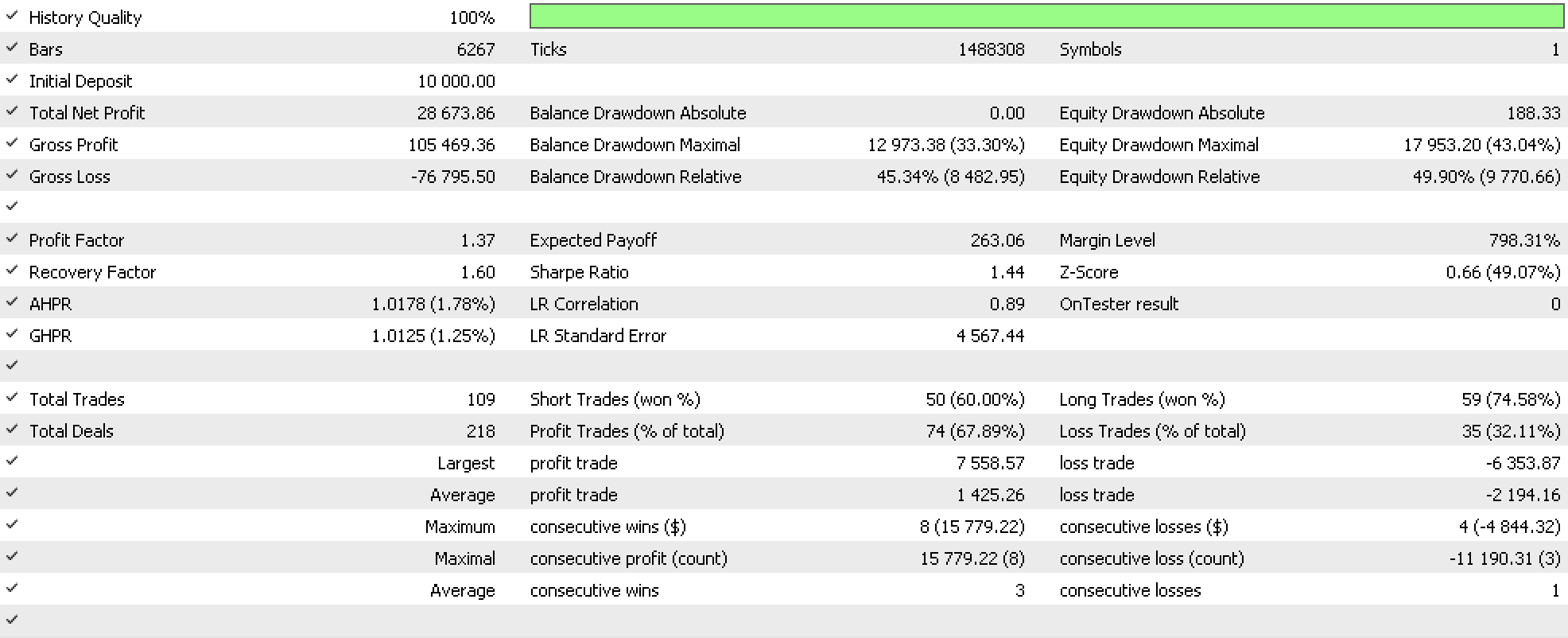
これらの連載ではいつもそうであるように、私たちのエキスパートアドバイザー(EA)は、利益確定や損切りに目標株価を利用せず、シグナル指標が決済すべきと判断するまでポジションを保有する設定で、10万以上の収益を記録しています。さらに、トレーリングストップに磨きをかけているので、もちろん、利益を上げたポジション決済のほとんどは、実際にトレーリングストップによるものです。これは、信頼できるトレーリングストップセットの指標を生成する際の部分注文のメリットを物語っていると主張できます。また、線型順序に基づくトレーリングストップもテストし、以下のレポートを得ました。

意外なことに、この結果は、（曖昧さを含む）半順序の場合ほど有益ではありません。奇妙なことに、取引回数が少ないと株式のドローダウンはさらに悪化します。決定的な結論を出すには、より長い期間と複数の銘柄でのテストが必要だが、線型順序よりも半順序の方が有望だと言ってもいいかもしれません。

結論

この記事では、典型的なEAのトレーリングストップの設定と変更における、半順序と線形順序の有効性について考察しました。その前に、これら 2 つの順序付け原則の相対的な利点を検討しましたが、両方のアンカー順序付け原則、つまり前順序については検討しませんでした。コンテンツに意味のある追加をせずに記事が長くなりすぎてしまうためです。半順序は前順序の特殊な形態であり、線形順序も半順序の特殊な形態であることを忘れてはいけません。これらの順序タイプの基本的な定義には重複が多いため、最後の2つに焦点を当てました。

半順序と線形順序の理論の方法は、その特有の利点のために利用されました。半順序は、生データ集合の分類をより柔軟にし、より豊かで正確な分析につなげることができます。逆に、線形順序付けはより厳格であるため、比較可能性を確保するために生データの正規化を必要とする傾向があり、これは全体的な優先順位付けと意思決定の効率化につながります。

これらの順序法は、過去に取り上げたコンセプトを、これから取り上げるいくつかの新しいコンセプトに統合し始めるので、この順序の連載でさらに探求し、洗練させる可能性があります。