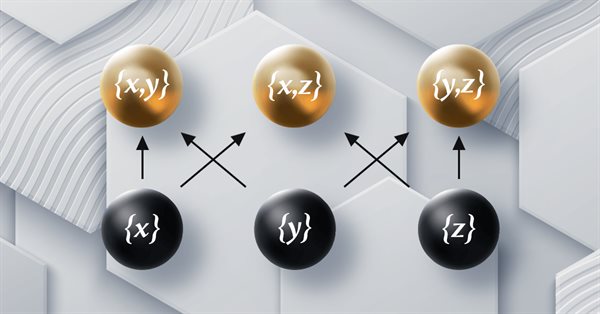
MQL5 中的范畴论 (第 12 部分):秩序(Orders)
概述
在上一篇文章中,我们见识了范畴论中的图论,其为相互连接的顶点和箭头系统,并实证了如何利用具有自身属性的各种路径来定义典型交易系统的各种尾随停止方法。
在本文中,我们将研究范畴论中的秩序,以及它们如何如同我们之前的文章一样,通过尾随停止来补充交易设置。秩序,坦率地说,关注的是各种元素“量级”的排位,典型情况下是在一个集合中查找。它们引发出思想亮点,即一个特定的集合能依据多个准则对其元素进行排位。范畴论通过引入集合之集合,甚至集合之集合之集合(等等)观念来增加维度。由此,在本文中,我们就唠唠集合排位。
具体来说,我们将聚焦在有序集合中的形态,作为产生交易离场的一种手段。在这项工作中有许多集合应当参考,因为我们的列表范围从价格动作形态,到指标形态,甚或是常见的多资产指数形态。然而,与我们在前几篇文章中研究的基本交易系统的步骤保持一致,我们将把五步过程的第一步和最后一步之间的三个内部步骤重组为子集,以便推导出我们的有序集合形态。
理解范畴论中的秩序
根据秩序论,主要有三种秩序类型。预序、偏序,和线性序。线性序也称为总序。预序是集合元素排位,其中集合中的每个元素都与所有其它元素进行比较(反身性),且每次比较的结果会对其它元素的比较(传递性)具有逻辑影响。预序确实可以容纳歧义,如果任何两个元素经二元运算得到相同的量级,则两者都可以包含在输出集合之中。此外,预序集还适用于无法比较两个元素相异性时发生的未定义结果。偏序是一种预序类型,它引入了一个额外的抗对称概念。这意味着,如果发现任何两个元素经二元运算比较得到相同的量级,则输出集中仅包含其中一个元素。因此,名之“偏”,因为只任意输出相等元素中的一个。最后,与这一趋势保持一致的线性序是一种特殊的偏序形式,其中没有未定义结果。这意味着所有元素都是可比的。回想一下,如上所述,对于预序,某些元素可能是无法比较的,这意味着二元操作输出未定义结果。这不适用于线性序。
因此,形式上,给定一个具有二元关系 R 的集合 S,
R ⊆ S x S
如果 R 符合以下条件,则被视为预序:
s ≦ s’ 或 s’ ≦ s
我们有反身性,其形式表示为:
s ≦ s
以及传递性,这将由以下方面所隐含:
s ≦ s’ 且 s’ ≦ s” 意即 s ≦ s”
如上所述的偏序会给预序增加抗对称性,那么如果:
s ≦ s’ 且 s’ ≦ s 那么 s = s’
这意味着在输出中仅表示 s 或 s' 中的一个。
线性序将为偏序增加可比性,因此对于任何两个元素,都存在以下任一元素的确定关系:
s ≦ s’ 或 s’ ≦ s
这意味着无法容纳未定义输出。
如前所述,这些秩序格式可用于标记形态,这些形态可有助于在任何交易系统中制定决策。在本文中,我们将重构前几篇文章中使用的步骤内幺半群集,包括回溯期、应用价格和指标,同时为简单起见,保留时间帧和交易动作的最终集合。与上一篇文章一样,主要测试参数将是决策序,不过,由于我们将考虑偏序,因此可能会出现未定义结果。这意味着我们的输出序,即表示决策点的幺半群集,也许小于输入 3。有时也许是 2,甚至 1。这意味着在某些情况下,在评估是否修改止损时,我们也许只需做出 3 次决定,或 4 次决定,而非默认的 5 次决定。
在 MQL5 中应用秩序论
对于本文,我们不会研讨预序,因为这样的话文章就太长了。相反,我们将专注于偏序和线性序。由于在上一篇文章之后,我们已经有了定义五个交易步骤的数据结构,故实现秩序论的待定要事即为处理数据结构并输出集合(通常是输入的子集)的二元函数。由于我们专注于偏序和线性序,因此每个都有一个对应函数。
也许强调一下我们在本文中考虑的两种排序形式的差异和相对优势会有所帮助。与线性序不同,如上所述,偏序允许在其输出中含有未定义分类。这在许多情况下都很实用。我们研究一个简单的案例,将图表上的价格柱线按看涨或看跌分类。在这个过程中,您一定会遇到长影线十字星蜡烛,严格来说,它既非看涨也非看跌。依据线性序分类,必须省略该数据点,因为它违反了可比性公理。
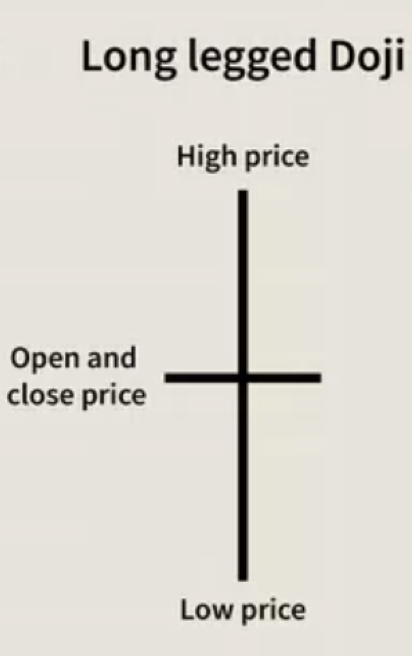
不过,依据偏序,包含该数据点及其结果,则输出集能更加完整地代表数据集。为了说明为什么这很重要,长影线十字星蜡烛,以及其它类似的蜡烛,包括墓碑十字星和蜻蜓十字星,都往往出现在主要的价格支撑和阻力区域。因此,如果您的分类省略了这些形态中的任何一种,那么您的分析和预测必然会不太准确,因为对于大多数交易系统来说,长期价格支撑和阻力区域在定义交易设置方面起着至关重要的作用。因此,在创建偏序时添加的抗对称属性可用来更好地过滤交易信号。
一个关于交易系统的案例研究,与我们在之前的文章中看到的 5-步骤过程不同,可以将价格柱线形态矢量化。把每根价格柱线制式当成一个向量,其为一个简单的权重数组,我们可以比较各种形态的相似程度。如果我们训练覆盖相当长的一段区间,并辨别出大量矢量化心态的最终价格制式,我们可以取任何新形态与训练过的形态进行比较,并基于这些已训练形态的欧几里得距离,那么与我们新形态最接近的形态其价格制式可当作我们新形态最可能的结果。
在投资组合分析的实例中,线性序可能比偏序更可取。如果我们面临需要评估算在投资组合中包含的大量资产,那么具有严格统一权重要求(可比性)的线性序就是不二之选。之所以如此,原因有很多,其中一些被认为是理所当然的。线性序允许按顺序方式估算资产,从而提供了一条简化的流程。无论资产数量如何,优先级已经由资产权重定义,资产权重可以是任何一个从过去实际价值到未来潜在风险的量化值。这不仅可以提高效率,而且令交易者不必通过增加关注来考虑所有可能的资产。
这种优先级意味着首先要参考最重要资产的投资决策,这导致了资产配置的关键问题。投资组合中的每项资产应如何调整规模?在线性序中,每种资产的权重通常能公正的作为购置该资产时动用多少资本的代表,而偏序则很难始终如一地做到这一点。
案例研究:开发带有秩序的交易系统
所选择的交易策略是基于我们之前文章中研究过的系统基础之上构建,将涉及从我们的 5-步骤方法的第 2 到第 4 步骤中选择临时步骤。在其中一个交易系统中,我们将从偏序方法选择这些,而另一个系统则从线性序中选择。
对于偏序选择,我们所有的幺半群集合都是不可比的,因为我们有整数类型的回溯周期,我们所应用的价格是字符串枚举,且最后的指标类型严格来说也是由字符串选择。因此,为了引入一些使用二元运算符的能力:
≦
我们将只对一对集合进行常规化,而第三个集合则保留为默认格式。执行偏序的函数输入本质上是价格动作。我们考虑作为偏序函数输入的价格参数将是自相关索引。我们将简单地将索引分配给各种自相关形态,对于每个索引,我们得到一对常规化的集合,然后针对我们的交易系统通知选择的集合序。如上所述,对于偏序,未定义集合的存在意味着只有两个集合可供选择,这意味着我们最终几乎肯定会得到一个 4-步骤过程,而非我们曾一直在用的 5-步骤。
对于线性序,所有幺半群集都将被常规化。这应为我们给予我们一直研究的完整 5-步骤,并且与偏序一样,线性序函数的输入将是我们的自相关索引。自相关索引的分配将是基本的,可从下面的列表中看出。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CTrailingCT::Ordering(int Lookback) { m_low.Refresh(-1); m_high.Refresh(-1); m_close.Refresh(-1); double _c[],_l[],_h[]; ArrayResize(_c,Lookback);ArrayInitialize(_c,0.0); ArrayResize(_l,Lookback);ArrayInitialize(_l,0.0); ArrayResize(_h,Lookback);ArrayInitialize(_h,0.0); for(int i=0;i<Lookback;i++) { _c[i]=m_close.GetData(i); _l[i]=m_low.GetData(Lookback+i); _h[i]=m_high.GetData(Lookback+i); } double _r_h=0.0,_r_l=0.0; if(MathCorrelationSpearman(_c,_l,_r_l) && MathCorrelationSpearman(_c,_h,_r_h)) { if(_r_l>=__PHI){ LongIndex(5); } else if(_r_l>=1.0-__PHI){ LongIndex(4); } else if(_r_l>=0.0){ LongIndex(3); } else if(_r_l>=(-1.0+__PHI)){ LongIndex(2); } else if(_r_l>=(-__PHI)){ LongIndex(1); } else{ LongIndex(0);} if(_r_h>=__PHI){ ShortIndex(5); } else if(_r_h>=1.0-__PHI){ ShortIndex(4); } else if(_r_h>=0.0){ ShortIndex(3); } else if(_r_h>=(-1.0+__PHI)){ ShortIndex(2); } else if(_r_h>=(-__PHI)){ ShortIndex(1); } else{ ShortIndex(0);} return(true); } return(false); }
首先,我们在多头和空头尾随停止处理函数中嵌入偏序处理代码,如本文末尾的附件。此处值得注意的是,从本质上讲,每个分配的索引只映射两个集合,因为第三个集合是未定义的。由每个可能的索引定义的顺序意味着第一个分配的集合比后一个分配的集合具有更高的权重。因此,不再需要提出一个实际的常规化函数来为每个索引赋予一个物理权重,因为它不会对最终结果产生有意义的影响。
同样,线性序函数如下所列:
ENUM_TIMEFRAMES _timeframe=GetTimeframe(m_timeframe,__TIMEFRAMES); int _lookback=m_default_lookback; ENUM_APPLIED_PRICE _appliedprice=__APPLIEDPRICES[m_default_appliedprice]; double _indicator=m_default_indicator; if(m_long_index==0) { _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,_appliedprice); } else if(m_long_index==1) { _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,_appliedprice); } else if(m_long_index==2) { _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe); _indicator=GetIndicator(m_default_lookback,_timeframe,_appliedprice); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); } else if(m_long_index==3) { _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,m_default_lookback,_timeframe); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); } else if(m_long_index==4) { _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); } else if(m_long_index==5) { _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe); _indicator=GetIndicator(_lookback,_timeframe,__APPLIEDPRICES[m_default_appliedprice]); _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe); } // int _trade_decision=GetTradeDecision(_timeframe,_lookback,_appliedprice,_indicator);
此处值得留意的是,每个索引都提供了所有集合的详尽枚举,因为可比性是所有集合的需求。如上所述,避免了为每个集合分配权重数字而进行的排序,因为所用索引含义等同上面所示实现的权重顺序。
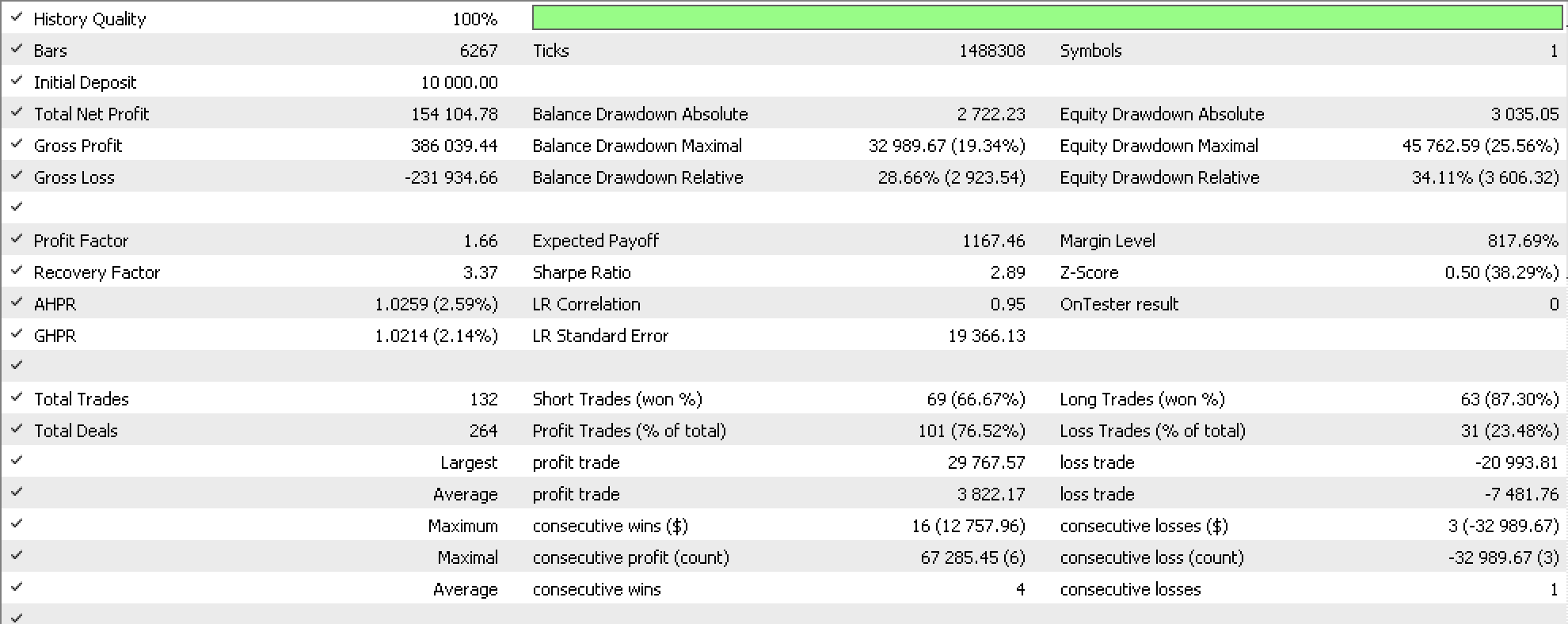
如果我们使用新的尾随类运行测试,在过去 12 个月中,依据函数库动量震荡指标信号类,使用固定保证金,交易品种 USDJPY,我们会得到每种排序方法的以下报告。首先是关于偏序方法的报告。
我们的智能系统按设置测得超过十万的收益,就像这些文章系列中的情况一样,这些设置没有利用价格目标来设置止盈或止损,而是一直持仓,直到信号指标认为它们应该平仓。此外,当然,由于我们正在磨合我们的尾随停止,大多数盈利平仓实际上是由于我们的尾随停止,而这说明了偏序在生成可靠尾随停止指示方面的优点。我们还测试了基于线性序的尾随停止,并得到以下报告。
令人惊讶的是,这个结果并不像我们在偏序(“模棱两可”的、通融的)中那样有利可图。奇怪的是,在交易较少的情况下,净值回撤甚至更糟。为了得出任何明确的结论,需要在更长的时间段和多个交易品种上进行测试,但可以肯定地说,偏序比线性序更有前途。
结束语
本文研究了偏序与线性序在典型智能交易系统里设置和修改尾随停止方面的有效性。在此之前,我们研究过这两种秩序原理的相对益处,我们没有探讨两种秩序原理的锚点,即预序,因为这会令文章太长,且内容并无太多意义。请记住,偏序是预序的一种特殊形式,而线性序也是偏序的一种特殊形式。如此,由于这些秩序类型的基本定义有很多重叠,我们专注于最后两种。
秩序论中偏序和线性序方法因其具备特殊益处而被利用。偏序允许对原始数据集进行更灵活的分类,从而实现更丰富、更准确的分析。相反,线性序更严格,往往需要原始数据的规范化,以便确保可比性,从而导出决策制定的整体优先级和效率。
在秩序论系列中这些方法有进一步探索和完善的潜力,故我们开始将过去涵盖的概念整合到我们即将研究的一些新概念之中。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/12873
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
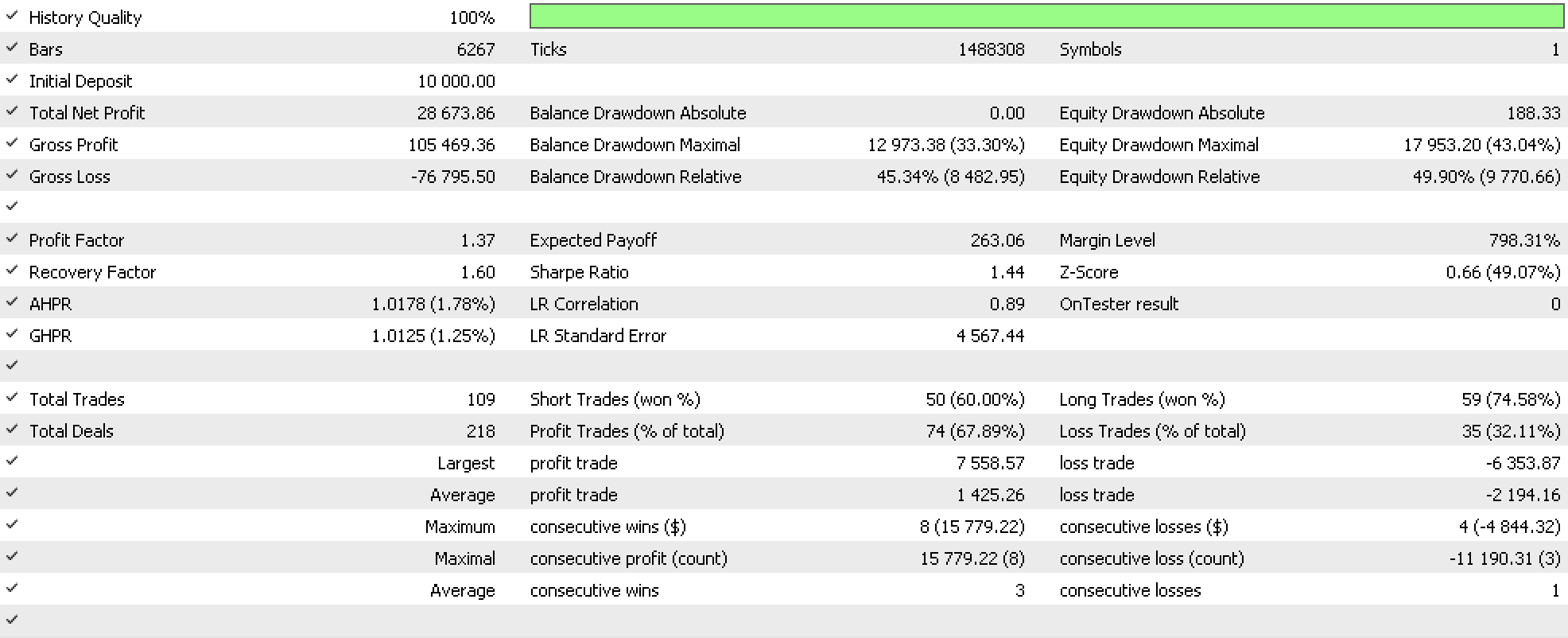
令人失望的是,同样没有 EA 能够产生所示的测试结果。
请在此提供 EA 设置,以便我们重现结果。