Популяционные алгоритмы оптимизации: Поиск косяком рыб (Fish School Search — FSS)

MetaTrader 5 — Примеры | 15 декабря 2022, 10:23

2 167

Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Скопление рыбы — это общий термин для любой группы рыб, собравшейся в каком-либо месте. Скопления рыб бывают структурированными или неструктурированными. Неструктурированные скопления могут состоять из особей смешанных видов и размеров, собравшихся случайно у локальных ресурсов, например, корма или гнездовья.

Между тем, группа рыб, которая держится коллективно по социальным причинам, представляют собой уже стаю. Большинство из них находится в одинаковой фазе жизненного цикла, активно контактирует друг с другом и в любой момент могут проявить биологически активную и полезную для членов группы организованную деятельность.
В отличие от индивидуального стайный образ жизни является компромиссом между преимуществом жизни в группе в плане большей защищённости от хищников и усилением конкуренции в добывании пищи.

Рыбы образуют стаи в природе по нескольким параметрам. Как правило, они предпочитают более крупные косяки, состоящие из особей только своего вида. Любой член стаи, который выделяется своим внешним видом, либо имеет какие-то отличия, станет преимущественной мишенью для хищников. Этот факт объясняет, почему рыбы предпочитают стаи идентично похожих на себя особей. Таким образом, обусловливается полная гомогенность стаи.

Стая бывает организована достаточно жёстко, когда рыбы плавают синхронно с одинаковой скоростью и в одном направлении, это обусловлено рыбами не только одного вида, но одного возраста и размера, двигающимися на некотором расстоянии друг от друга. Косяки рыб способны производить сложные манёвры, так будто обладают групповым интеллектом и общим разумом.
Тонкости формирования стаи изучены далеко не полностью, особенно аспекты движения и способы питания рыб.

Для объяснения стайного поведения выдвинуто множество гипотез, в том числе лучшая ориентация, синхронизация охоты, запутывание хищника и снижение риска быть схваченным. Рыбы в косяках как бы делятся между собой информацией, контролируя поведение друг друга с близкого расстояния. Кормовое поведение одной рыбы быстро стимулирует активный поиск пищи и у других особой. Стайные рыбы плывут стройными фалангами, зачастую совершая стремительные подъемы и спуски, и крутясь вокруг своей оси, при этом они меняют форму стаи, минуя столкновений между собой. Для осуществления подобных манёвров необходима очень быстрая система реагирования. Стайный образ жизни подразумевает наличие у рыб сенсорных систем, способных мгновенно реагировать на небольшие изменения в их положении по отношению к своему соседу.

Для создания более полной картины используется математическое моделирование такого стайного поведения. Наиболее распространенные математические модели предполагают, что отдельные животные в стае следуют трём основным правилам:

Двигаться в одном направлении с соседом
Оставаться рядом с соседними сородичами
Избегать столкновений с соседними особями

Остаётся неразрешённым вопрос относительно того, как стайные рыбы выбирают направление, в котором плыть. При совершении миграций складывается впечатление, что большинство членов стаи знают, куда им двигаться. Если все члены стаи одинаково осведомлены относительно наличия корма, в группе всё равно присутствуют определенные лидеры, которые смелее своих остальных сородичей. Данное стайное поведение сподвигло многих исследователей на создание не только математической модели, но и алгоритмической для решения различных задач оптимизации.

2. Описание алгоритма

Поиск косяком рыб (FSS) — это подсемейство алгоритмов роевого интеллекта, относящихся к классу метаэвристических алгоритмов, предложено Бастосом Филью и Лимой Нето в 2008 г. и впервые было опубликовано в 2009 г. В FSS простые агенты называются рыбами, и каждая рыба имеет вес, который представляет "успех", достигнутый во время поиска. Значения и вариации весов влияют на индивидуальные и коллективные движения. Встроенные механизмы кормления и скоординированных действий заставляют косяк двигаться в направлении положительного градиента, чтобы набирать вес и находить лучшие места на местном и глобальном уровнях. FSS был разработан для задач непрерывной оптимизации в мультимодальных пространствах поиска. Это также побудило других исследователей предложить варианты решения других задач, таких как оптимизация в бинарных задачах, многокритериальная оптимизация.

В алгоритме FSS упрощенно можно представить, что рыбы плавают в условном аквариуме, стенки которого являются границами области определения исследуемой функции. Рыб характеризует их вес как мера успешности в поиске пищи (решения) и играет роль памяти рыбы. Наличие веса у рыб является основной идеей алгоритма и отличием от роя частиц. Эта особенность алгоритма FSS позволяет отказаться от необходимости отыскивать и фиксировать глобально лучшие решения, как это происходит в рое частиц.

Операторы алгоритма FSS объединены в две группы:
-оператор кормления формализует успешность исследования областей
-операторы плавания реализуют алгоритмы миграции отдельных рыб и косяка в целом

Оператор кормления представляет собой расчет веса рыбы. Основная идея состоит в том, чтобы заставить рыб "плыть" к положительному градиенту, чтобы "есть" и "набирать вес". В совокупности более тяжелые рыбы оказывают большее влияние на процесс поиска в целом, что заставляет цент масс косяка рыб перемещаться в сторону лучших мест в пространстве поиска в течение итераций. Приращение веса на данной итерации пропорционально нормализованной разности значений фитнесс - функции, то есть:

fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);

где:

weight - вес рыбы
delta_fitness - разность значений фитнесс - функции
max_delta_fitness - максимальное значение разности фитнесс - функции среди всех рыб

Операторы плавания подразделяются по виду перемещений на три типа:

-индивидуальное;

-инстинктивно - коллективное;

-коллективно - волевое;

Индивидуальное плавание можно интерпретировать как локальный поиск в окрестностях текущего положения рыбы. Вектор движения каждой особи направлен рандомно и имеет разную величину.

fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;

где:

new_position - новая позиция по соответствующей координате
current_position - текущая позиция по соответствующей координате
step_ind - шаг индивидуального перемещения, рассчитывается как

initial_step_ind * (rangeMax [d] - rangeMin [d]);

где:

initial_step_ind - параметр алгоритма для индивидуального перемещения
rangeMax и rangeMin - диапазоны значений оптимизируемых аргументов
r - случайное число [-1.0;1.0]

Схематично индивидуальное плавание представлено на рисунке 1.

individual

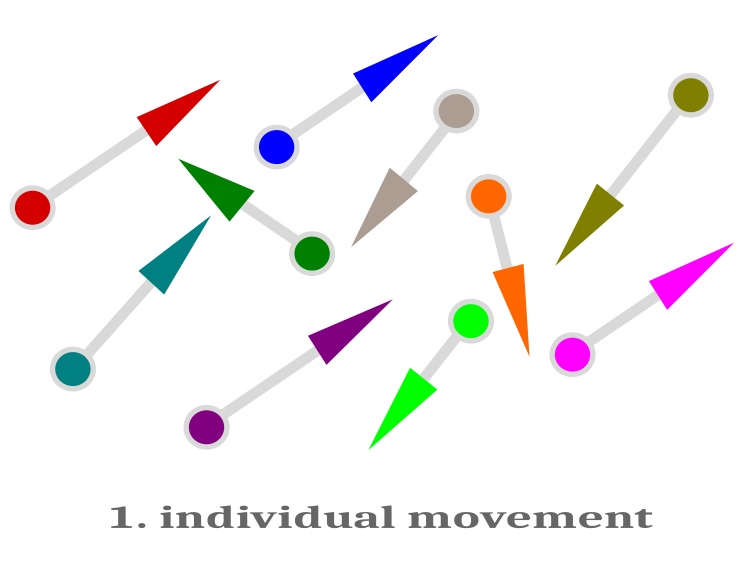
Рисунок 1. Индивидуальное плавание. Вектор перемещения каждой рыбы направлен в случайном направлении и имеет разную скалярную величину.

После индивидуального плавания происходит замер фитнес - функции. Если в результате индивидуального движения улучшение позиции рыбы не произошло, то считаем что движения у этой конкретной рыбы не было и она остаётся на месте. То есть переместятся на новое положение только те рыбы, у которых произошло улучшение фитнес - функции.

После завершения индивидуального плавания выполняется оператор инстинктивно - коллективного перемещения. Сначала посмотрим на рисунок 2.

collect

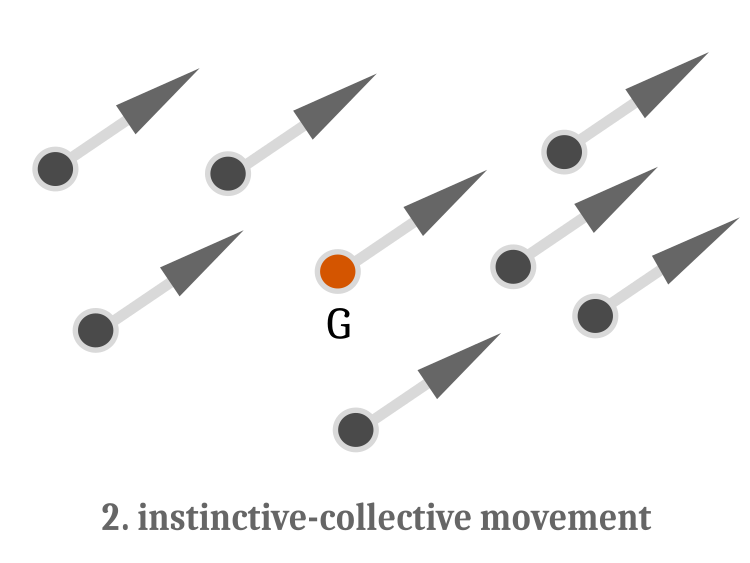
Рисунок 2. Инстинктивно - коллективное плавание. Перемещение характеризуется для всех рыб одинаковым вектором направления и величины относительно центра масс G.

Инстинктивно - коллективное перемещение служит для корректировки общего положения косяка рыб с учетом изменения фитнес - функции каждой рыбы на предыдущей итерации. Новые координаты рассчитываются так:

fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];

где:

new_position - новая позиция рыбы по соответствующей координате
current_position - текущая позиция рыбы по соответствующей координате
collective_instinct - величина перемещения по соответствующей координате, рассчитывается как:

collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

где:

delta_position - разность координат текущей и предыдущей, полученной на этапе индивидуального плавания
delta_fitness - изменение фитнесс - функции текущего положения и предыдущего на этапе индивидуального плавания

Инстинктивно-коллективное плавание формализует групповое синхронное перемещение косяка рыб на новое место, обеспечивая поиск новых мест корма, тогда как индивидуальное перемещение позволяет улучшать положение локально.

Далее рассмотрим коллективно - волевое плавание. Оно в свою очередь делится на два вида:

- от центра масс - если улучшение положения косяка в целом не произошло по сравнению с предыдущим положением, при этом рыбы расплываются в стороны, символизируя дальнейший поиск корма (рисунок 3)

- движение к центру масс, если улучшение произошло. Тогда рыбы перемещаются к центру масс, сжимая кольцо и символизируя нападение на добычу. Алгоритмически это означает уточнение решения задачи оптимизации (рисунок 4).

col vol out

Рисунок 3. Коллективно - волевое плавание. Векторы направления направлены от центра масс G.

col vol in

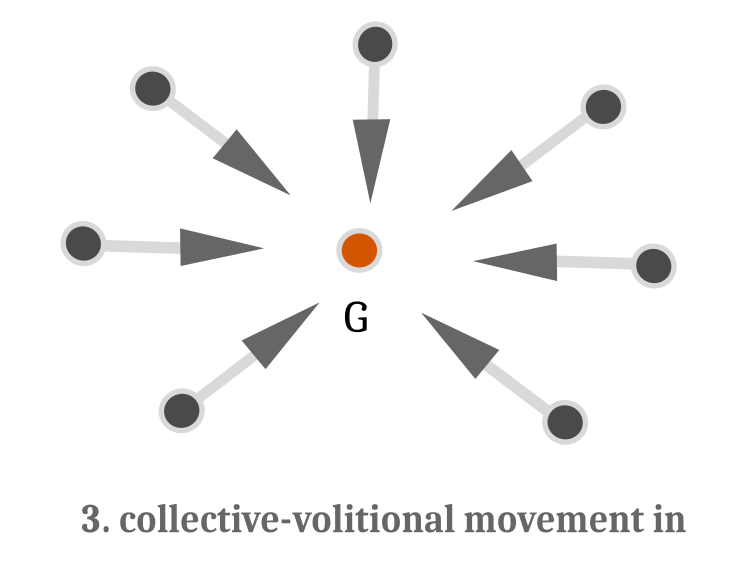
Рисунок 4. Коллективно - волевое плавание. Векторы направления направлены к центру масс G.

Для расчета коллективно - волевого плавания вводится понятие центра масс. Отсюда формула расчета коллективно - волевого плавания будет выглядеть так:

fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);

где:

pos - это тот же current_position
search_operator - 1 если предыдущее перемещение дало улучшение позиции, и -1 если нет
step_vol [d] - шаг коллективного перемещения, рассчитывается как:

step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);

где:

initial_step_vol - параметр алгоритма для коллективного перемещения
barycenter [d] - центр масс, которые рассчитывается как сумма весов рыб помноженных на координату:

barycenter [d] += fishes [f].weight * fishes [f].current_position [d];

и поделённого на общий вес косяка рыб:

barycenter [d] /= current_total_weight;

Псевдо код алгоритма выглядит так:

1) инициализировать случайными числами позиции рыб

2) индивидуальные перемещения

3) расчет фитнес - функции

4) переопределение весов для каждой рыбы

5) инстинктивно-коллективное движение

6) коллективно-волевое движение

7) пересчитать общий вес

8) расчет фитнес - функции

9) повторить с пункта 2) до выполнения критерия останова

Schema FSS

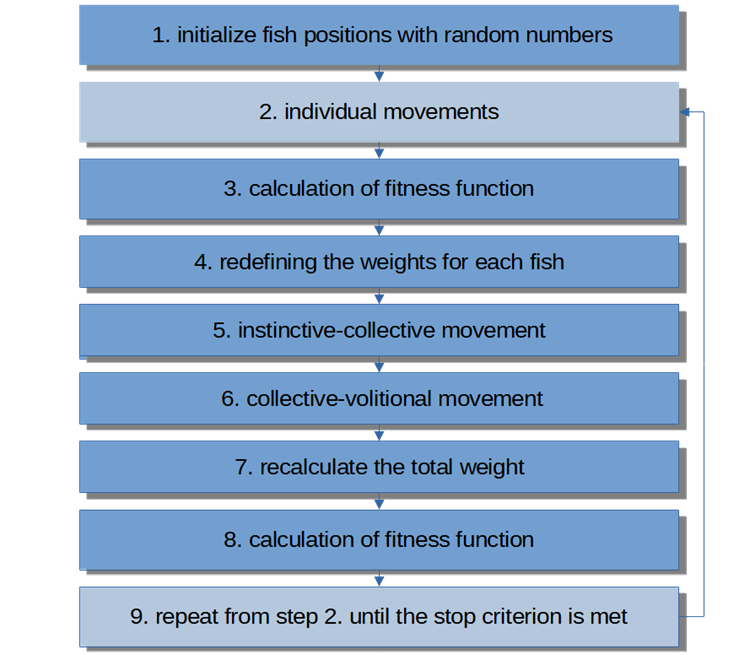
Рисунок 5. Блок-схема алгоритма FSS.

Приступим к описанию кода.

Простейшей логической единицей алгоритма, как несложно догадаться, является структура, описывающая рыбу. Поскольку рыбу нам придется инициализировать несколько раз, то эту структуру, из-за своего сравнительно большого размера, целесообразно "обнулять" в специальном методе Init (), что позволит немного оптимизировать код. Включает в себя массивы координат текущего положения, нового положения и разницу координат после последнего перемещения. Переменная вес, которая по умолчанию применяется равной 1000 условных единиц, в принципе эта цифра можно быть любой. Рыбу также характеризует значение текущего фитнесс, предыдущего и разницы между ними. В методе Init () фитнесс инициализируем числом, минимально возможным double, соответственно разница фитнесс равна нулю, поскольку никаких еще перемещений у рыбы не было.

//——————————————————————————————————————————————————————————————————————————————
struct S_Fish
{
  void Init (int dimensions)
  {
    ArrayResize (current_position, dimensions);
    ArrayResize (new_position,     dimensions);
    ArrayResize (delta_position,   dimensions);
    weight        = 1000.0;
    fitness       = -DBL_MAX;
    delta_fitness = 0.0;
  }

  double current_position [];
  double new_position     [];
  double delta_position   [];
  double weight;
  double fitness;
  double new_fitness;
  double delta_fitness;
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс C_AO_FSS - косяк рыб, математически представляя модель природного сообщества. Здесь нет ничего необычного, есть также два открытых метода, необходимых для взаимодействия с программой пользователя, диапазоны значений оптимизируемой функции, необходимые для учета координат рыб и взаимодействие в стае, массивы.

В открытом методе класса инициализации Init () необходимо сбросить переменные в первоначальные значения, распределить память под массивы. Особенно стоит уделить внимание переменной init и swimmingRegime. Дело в том, что согласно псевдо коду, который мы видели, вычисление фитнесс - функции производится два раза, первый раз после индивидуального движения, второй раз после двух видов коллективного, это противоречит принятой нами схеме построения связки алгоритм - приложение, при которой на каждой итерации должна быть последовательность: первый_метод -> вычисление_фитнесc_функции -> второй_метод. Для того, чтобы исправить это и изменить последовательность действий в каноническом алгоритме, как раз и служат эти две переменные. Переменная init в начале работы алгоритма должна быть false. Это флаг, который укажет, что необходимо инициализировать рыб, вычислить фитнесс - функцию и сделать снова перемещение, поскольку вся логика алгоритма использует разницу между текущим и предыдущим значением координат и фитнесс - функции, если бы этого не сделали, нам не было бы возможности получить разность значений. Второй важный флаг - swimmingRegime, он позволяет нам переопределить очередность вызова методов, описывающих передвижение рыб так, чтобы это соответствовало нашей схеме. Значение 1 соответствует вызову "индивидуального" плавания, иначе последовательность групповых движений, которые мы рассмотрели выше.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Init (const int    dimensionsP,
                     const int    fishSchSizeP,
                     const double initial_step_indP,
                     const double initial_step_volP)
{
  MathSrand (GetTickCount ());
  init = false;
  swimmingRegime = 1;

  dimensions     = dimensionsP;

  ArrayResize (rangeMax,  dimensions);
  ArrayResize (rangeMin,  dimensions);
  ArrayResize (rangeStep, dimensions);

  num_of_individuos = fishSchSizeP;

  ArrayResize (fishes, num_of_individuos);

  for (int i = 0; i < num_of_individuos; i++)
  {
    fishes [i].Init (dimensions);
  }

  global_best = -DBL_MAX;
  ArrayResize (global_best_position, dimensions);

  total_weight     = num_of_individuos;

  initial_step_ind = initial_step_indP;
  ArrayResize (step_ind, dimensions);

  initial_step_vol = initial_step_volP;
  ArrayResize (step_vol, dimensions);

  ArrayResize (collective_instinct, dimensions);
  ArrayResize (barycenter, dimensions);
}
//——————————————————————————————————————————————————————————————————————————————

Первый открытый метод, вызываемый на каждой итерации, Swimming () определяет последовательность вызовов индивидуального и групповых движений рыб. Если метод вызывается первый раз, тогда инициализируются шаги индивидуального и группового движений как часть возможного диапазона по соответствующей координате посредством двух параметров алгоритма initial_step_ind и initial_step_vol. Некоторые авторы рекомендуют устанавливать значения 0.01 и 0.001 соответственно. Однако я не получил хороших результатов при этих значениях и использую 0.1 и 0.8. Также при первом запуске алгоритма текущее значение координат позиции рыб инициализируем случайными числами в диапазоне оптимизируемых параметров. При последующих вызовах метода в соответствии с флагом swimmingRegime будут вызываться соответствующие виды перемещений.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Swimming (int i)
{
  //----------------------------------------------------------------------------
  if (!init)
  {
    global_best    = -DBL_MAX;
    swimmingRegime = 1;

    for (int d = 0; d < dimensions; d++)
    {
      step_ind [d] = initial_step_ind * (rangeMax [d] - rangeMin [d]);
      step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      fishes [f].Init (dimensions);

      for (int d = 0; d < dimensions; d++)
      {
        fishes [f].new_position [d] = RNDfromCI (rangeMin [d], rangeMax [d]);
        fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
      }
    }
  }
  //----------------------------------------------------------------------------
  else
  {
    switch (swimmingRegime)
    {
    case 1:
      apply_individual_movement ();            //individual movement
      break;
    default:
      apply_instintive_collective_movement (); //instinctively-collective movement
      apply_collective_volitive_movement ();   //collective-volitional movement
      update_total_weight ();                  //recalculate the total weight
      break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Второй открытый метод, вызываемый на каждой итерации - Regrouping (), предназначен в первую очередь для определения порядка вызовов методов плавания индивидуальное, коллективно - инстинктивное, коллективно - волевое. Дополнительную функциональность метода для обеспечения порядка вызовов служит флаг swimmingRegime, который принимает значение 1 и 2. Это необходимо для переопределения порядка вызова методов перемещения рыб в классическом варианте для схемы принятой нами: первый_открытый_метод -> расчет_фитнесс_функции -> второй_открытый_метод. В зависимости от флага Init, если алгоритм находится на первой итерации, мы сохраним текущее положение координат и значение фитнесс - функции для дальнейших вычислений их разностей, поскольку предполагается, что метод вызван после расчета фитнесс - функции. Если же флаг Init указывает, что алгоритм находится на второй и последующих итерациях, то необходимо после индивидуального перемещения получить разность текущего и предыдущего значения фитнесс - функции, а так же разность координат текущей и предыдущей позиции. Разности вычисляются при условии, что позиция улучшилась, в противном случае считаем, что перемещения не было, сбрасываем значения веса рыбы в исходное состояние, а разности перемещений и фитнесс - функции принимаем равным нулю. Мы тут же выполняем обновление наилучшего решения, если оно достигнуто, вызывая метод updates_optimal_solution () и применяем кормление рыб методом apply_feeding (). Если флаг swimmingRegime не равен 1, значит, были применены коллективно - инстинктивное и коллективно - волевое движения, после их выполнения назначим swimmingRegime равным 1 и следующим будет индивидуальное движение.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Regrouping ()
{
  //----------------------------------------------------------------------------
  if (swimmingRegime == 1
  {
    if (!init)
    {
      for (int f = 0; f < num_of_individuos; f++)
      {
        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
        ArrayInitialize (fishes [f].delta_position, 0.0);

        fishes [f].fitness = fishes [f].new_fitness;
        fishes [f].delta_fitness = 0.0;
      }

      init = true;
      return;
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      //remember the best position for the fish
      if (fishes [f].new_fitness > fishes [f].fitness)
      {
        fishes [f].delta_fitness = fishes [f].new_fitness - fishes [f].fitness; //fabs
        fishes [f].fitness = fishes [f].new_fitness;

        for (int d = 0; d < dimensions; d++)
        {
          fishes [f].delta_position [d] = fishes [f].new_position [d] - fishes [f].current_position [d];
        }

        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        ArrayInitialize (fishes [f].delta_position, 0.0);
        fishes [f].delta_fitness = 0.0;
      }
    }

    swimmingRegime = 2;
    updates_optimal_solution ();
    apply_feeding ();
    return;
  }

  //----------------------------------------------------------------------------
  swimmingRegime = 1;
  updates_optimal_solution ();
}
//——————————————————————————————————————————————————————————————————————————————

Следующий простой приватный метод, служит для обновления наилучших результатов алгоритма, если они достигнуты. Для этого просто значения фитнесс - функции каждой рыбы сравниваем с глобальными. Если оно лучше, тогда сохраняем.

//——————————————————————————————————————————————————————————————————————————————
//обновить лучшее общее решение
void C_AO_FSS::updates_optimal_solution ()
{
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].fitness > global_best)
    {
      global_best = fishes [f].fitness;
      ArrayCopy (global_best_position, fishes [f].current_position, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Приватный метод, обеспечивающий индивидуальное плавание, в принципе формулу мы рассмотрели выше и здесь все просто: к текущим координатам каждой рыбы прибавляем индивидуальный шаг, помноженный на случайное число в диапазоне от -1.0 до 1.0, что дает приращение как в положительную, так и отрицательную сторону. Если произошел выход за пределы диапазона значений оптимизируемых параметров, тогда координате назначаем значение границы.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_individual_movement ()
{
  //передвинем рыб на новые места-----------------------------------------------
  double r = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (-1.0, 1.0);

      fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод кормления не должен вызывать трудности с пониманием, вес рыбы, по сути, определяется как частное от разности фитнесс - функции самой рыбы и максимальное значение разности среди всего косяка рыб. Однако может так случиться, что максимальная разность среди всех рыб будет равна нулю. В описании классического варианта алгоритма говорится, что вес рыб всегда должен быть положительным и вообще рассматриваются только случаи, когда фитнесс - функция принимает только положительные значения, но я не нашел практического смысла в этом требовании и допускаю, что вес рыб может принимать отрицательные значения, поэтому, если максимальная разность фитнесс - функции (на это значение мы должны нормировать вес каждой рыбы) равно нулю среди всех рыб, тогда вес рыбы принимаем равным 1.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_feeding ()
{
  double max_delta_fitness = -DBL_MAX;

  //find the maximum weight among fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].delta_fitness > max_delta_fitness) max_delta_fitness = fishes [f].delta_fitness;
  }

  //feed the fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (max_delta_fitness != 0.0)
    {
      fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);
    }
    else fishes [f].weight = 1;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Приватный метод инстинктивно - коллективного движения заключается в изменении координаты каждой рыбы путем приращения на значение коллективного инстинкта, что в свою очередь есть ни что иное как произведение разности позиций на текущей и предыдущей итерациях на разность фитнесс - функции, достигнутое на предыдущих перемещениях. Здесь также при выходе за пределы границ оптимизируемых параметров назначаем значения границ.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_instintive_collective_movement ()
{
  double sum_delta_fitness = 0.0;
  for (int f = 0; f < num_of_individuos; f++)
  {
    sum_delta_fitness += fishes [f].delta_fitness;
  }

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

      if (sum_delta_fitness != 0.0)
      {
        collective_instinct [d] /= sum_delta_fitness;
      }

      fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Приватный метод коллективно - волевого плавания, в котором рассчитывается центр масс косяка рыб, а также текущий общий вес. Если общий вес стаи увеличился, тогда рыбы начинают двигаться к центру масс, в противном случае от центра. Детально формула была рассмотрена ранее. Общий вес косяка рыб обновляется в специальном для этого методе, который рассмотрим далее.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_collective_volitive_movement ()
{
  //----------------------------------------------------------------------------
  double current_total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    current_total_weight += fishes [f].weight;
  }

  ArrayInitialize (barycenter, 0.0);

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      barycenter [d] += fishes [f].weight * fishes [f].current_position [d];
    }
  }

  for (int d = 0; d < dimensions; d++)
  {
    barycenter [d] /= current_total_weight;
  }

  //----------------------------------------------------------------------------
  double search_operator = current_total_weight > total_weight ? 1.0 : -1.0;
  double r   = 0.0;
  double pos = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (0.0, 1.0);
      pos = fishes [f].current_position [d];

      fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Собственно, вот и тот самый метод обновления общего веса рыб. Здесь все просто, берем вес каждой рыбы и суммируем.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::update_total_weight ()
{
  total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    total_weight += fishes [f].weight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Переходим к заключительной и самой интересной части - результатам. Интересные приемы, используемые в этом алгоритме, такие как отсутствие необходимости учитывать глобальный оптимум, введение понятий центра масс и инстинктивно - волевого перемещения, подразумевающего схождение или разбегание от центра косяка в зависимости от того, было ли улучшено положение в целом, давало надежду на оригинальное поведение алгоритма на исследуемых функциях.

В принципе оригинальность в поведении в поисковой области пространства присутствует, наблюдаются рассредоточения рыб на отдельные участки пространства, так как это наблюдалось у пчелиного алгоритма, хотя детальное рассмотрение формул и принципа действия FSS не предполагают рассредоточение косяка на отдельные группы. В целом алгоритм показал себя слабо, лишь немного опередив алгоритм PSO в общем результате.

Если же рассматривать отдельные тесты, в некоторых FSS все же смог отличиться. Так на гладкой функции Skin алгоритм FSS обогнал даже волчий алгоритм, показав неплохие (но не лучшие) результаты, что в принципе легко объяснить, в алгоритме используется градиент поверхности исследуемой функции, учитываемый в приращении по каждой из координат и изменение фитнесс - функции на каждой итерации. Поскольку функция Skin гладкая, то алгоритм хорошо "цепляется" за изменения поверхности.

Что касается функции Forest, то алгоритм показал результаты ниже среднего по таблице, гладкие изменения тестовой функции в какой-то мере помогали ориентироваться алгоритму в пространстве, однако он так и не смог найти глобальный максимум. А если рассмотреть результаты работы на Megacity, то становятся ещё более заметны недостатки FSS, алгоритм очень "не любит", когда исследуемая функция не изменяется в окрестностях текущего положения отдельных агентов, а дальние прыжки для выявления новых потенциально лучших мест алгоритм делать не в состоянии. Поэтому происходит застревание в любых локальных экстремумах, которые не имеют приращения в окрестностях.

Хотя тест Megacity очень сложный для любых алгоритмов оптимизации и другие участники сравнительной таблицы не намного в целом опередили FSS, всё же нужно признать слабые способности алгоритма на дискретных задачах, в отдельных тестах случайный поиск показал лучший результат. Как мы можем увидеть на анимации и в виду вышесказанного, ожидаемо, что "кластеризации" в работе алгоритма не наблюдается. Напомню, что в предыдущей статье, было описано явление "кристаллизации" у алгоритмов оптимизации.

Распечатка работы алгоритма FSS:

2022.12.08 13:14:06.033    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.892861444841324
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    Score: 0.99391
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.11410005347766
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    Score: 0.56920
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.20519552002827
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    Score: 0.11341
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.5057381856551146
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    Score: 0.85172
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.21468156279781656
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    Score: 0.12143
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.056970068652984526
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    Score: 0.03223
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 11.0
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    Score: 0.91667
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.03
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    Score: 0.08583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.31
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    Score: 0.02583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    All score for C_AO_FSS: 0.4122477188979048

Skin

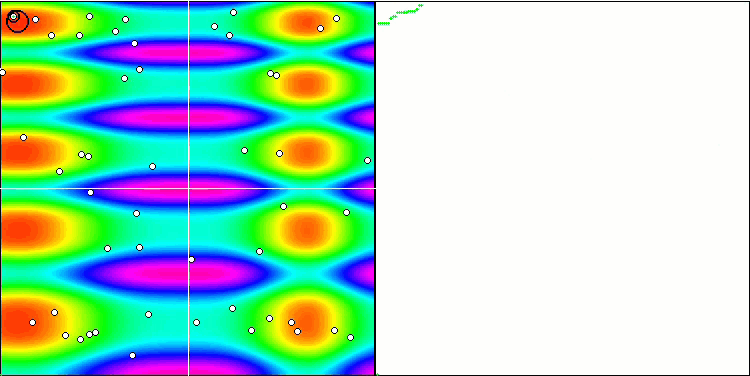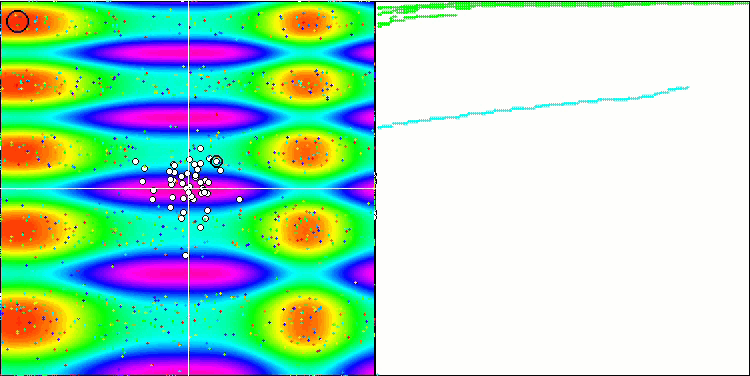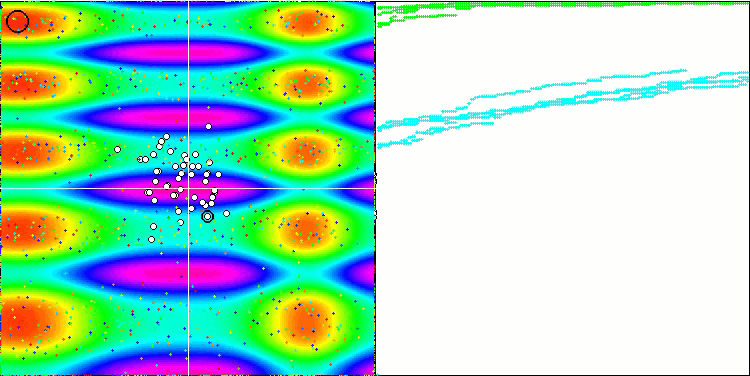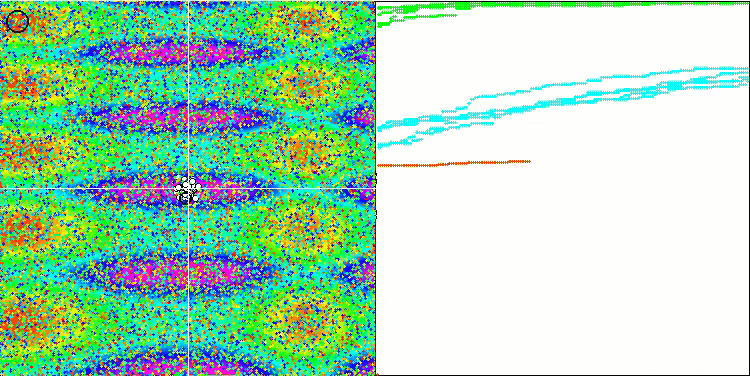
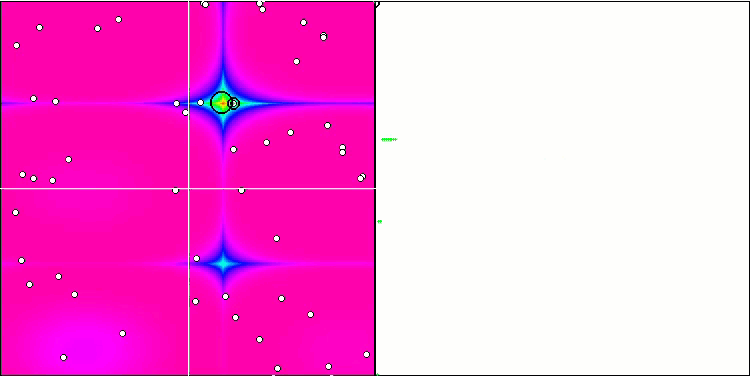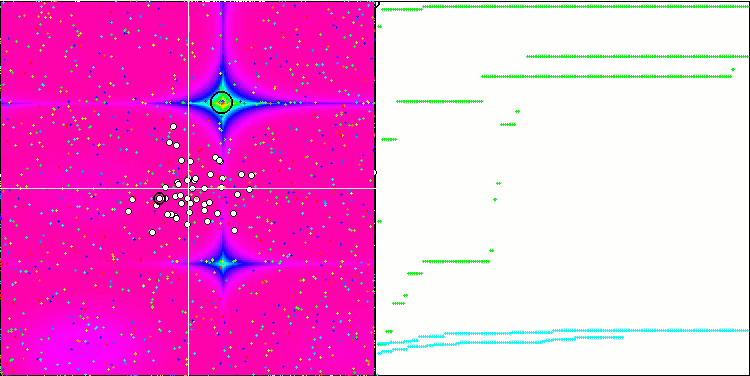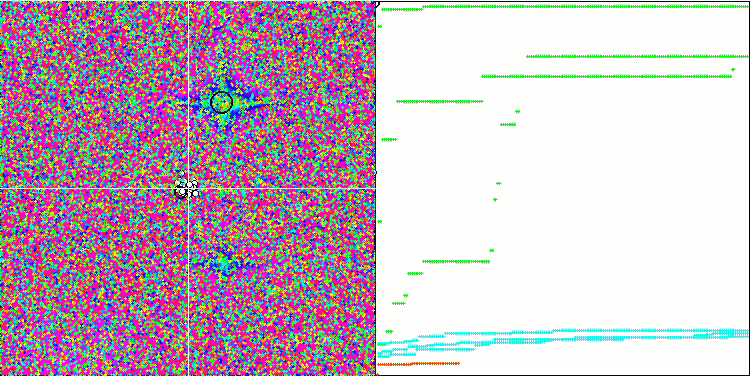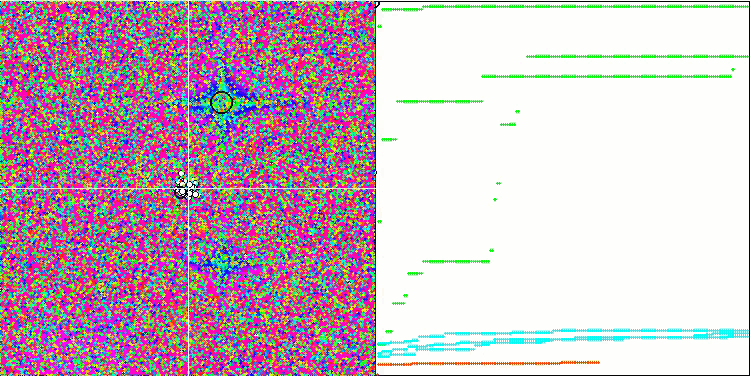
FSS на тестовой функции Skin.

Forest

FSS на тестовой функции Forest.

Megacity

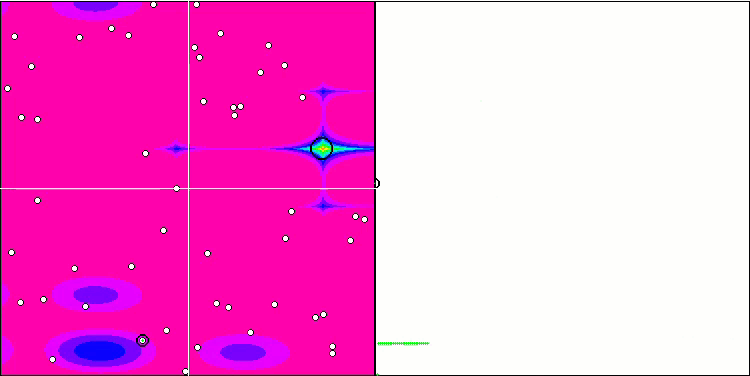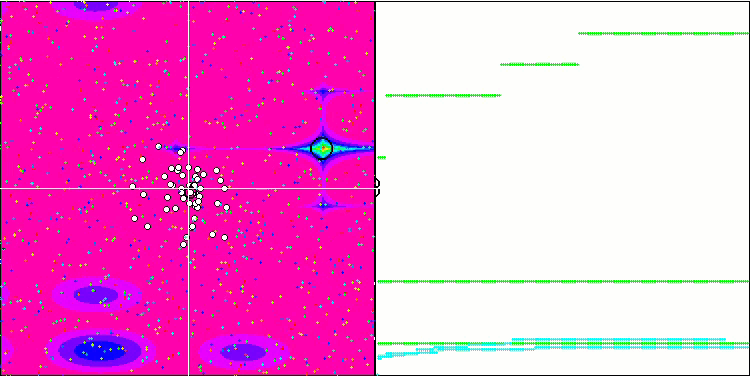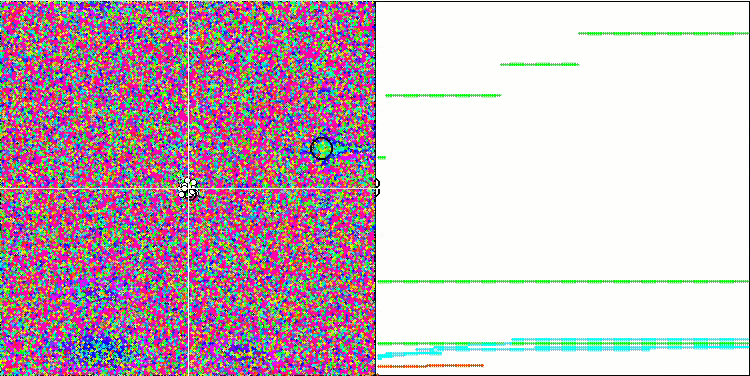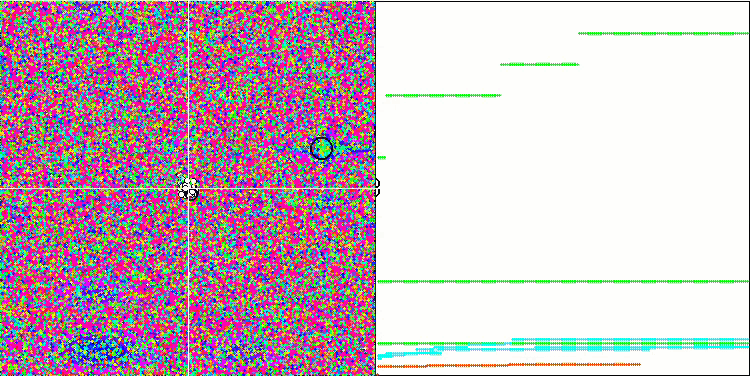
FSS на тестовой функции Megacity.

Вот и финальная таблица. В неё я добавил дополнительные столбцы, что бы было удобнее оценивать алгоритмы по каждой тестовой функции по отдельности, что позволяет более справедливо рассуждать на тему применимости каждого алгоритма для тех или иных задач.

AO	Description	Skin			Skin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
AO	Description	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Skin final	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Forest final	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Megacity final	Final result
COAm	cuckoo optimization algorithm	1,00000	0,85911	0,14316	0,66742	0,99283	0,28787	0,04551	0,44207	1,00000	0,24917	0,03537	0,42818	0,51255778
ACOm	ant colony optimization	0,98229	0,79108	0,12602	0,63313	1,00000	0,62077	0,11521	0,57866	0,38333	0,44000	0,02377	0,28237	0,49805222
ABCm	artificial bee colony M	1,00000	0,63922	0,08076	0,57333	0,99908	0,20112	0,03785	0,41268	1,00000	0,16333	0,02823	0,39719	0,46106556
ABC	artificial bee colony	0,99339	0,73381	0,11118	0,61279	0,99934	0,21437	0,04215	0,41862	0,85000	0,16833	0,03130	0,34988	0,46043000
GWO	grey wolf optimizer	0,99900	0,48033	0,18924	0,55619	0,83844	0,08755	0,02555	0,31718	1,00000	0,10000	0,02187	0,37396	0,41577556
FSS	fish school search	0,99391	0,5692	0,11341	0,55884	0,85172	0,12143	0,03223	0,33513	0,91667	0,08583	0,02583	0,34278	0,41224778
PSO	particle swarm optimisation	0,99627	0,38080	0,05089	0,47599	0,93772	0,14540	0,04856	0,37723	1,00000	0,09333	0,02233	0,37189	0,40836667
RND	random	0,99932	0,44276	0,06827	0,50345	0,83126	0,11524	0,03048	0,32566	0,83333	0,09000	0,02403	0,31579	0,38163222

Стохастические (рандомизированные) эвристические методы не гарантируют получение точного решения, но они, как правило, позволяют находить достаточно близкие для практического использования решения за приемлемое время. Однако, с практикой можем признать, что некоторые алгоритмы способны демонстрировать превосходные способности к сходимости, но это не про FSS. Вообще, алгоритм поиска косяком рыб является частным случаем алгоритмов на основе роя частиц, поэтому унаследовал как плюсы так и минусы, всё же проявились уникальные именно для этого алгоритма по сравнению со своими "предками" особенности - разделения косяка рыб (роя) на отдельные группы, что в рое частиц не наблюдается. Отдельно стоит подчеркнуть достоинства - алгоритм относительно неплохо справляется с гладкими функциями, хотя уверенности, что FSS хорошо справится с функциями со многими переменными, нет.

Плюсы:
1. Достаточно хорошо справляется с гладкими функциями.
2. Способность косяка рыб разделяться на отдельные группы, что позволяет алгоритму дополнительно исследовать другие локальные потенциально хорошие экстремумы.

Минусы:
1. Большой разброс результатов в отдельных тестах указывает на нестабильность алгоритма.
2. Очень слабая сходимость на дискретных и функциях и с изломами. Для дискретных функций практически не применим.
3. Слабая масштабируемость.

Прикрепленные файлы |

Загрузить ZIP

7_The_world_of_AO_yFSSa.ZIP (65.23 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Разработка торгового советника с нуля (Часть 31): Навстречу будущему (IV)

Мы продолжаем удалять разные вещи внутри советника. Это будет последняя статья в этой серии. Последнее, что будет удалено в данной серии статей - это звуковая система. Это может сбить читателя с толку, если он не следил за этими статьями.

Рецепты MQL5 — Сервисы

В статье описаны разносторонние возможности сервисов — таких MQL5-программ, для которых не нужен график привязки. Приводятся отличия сервисов от других MQL5-программ, подчёркиваются нюансы работы разработчика с сервисами. В качестве примеров читателю предложены различные задачи, охватывающие широкий спектр функционала, который может быть реализован в виде cервиса.

DoEasy. Элементы управления (Часть 30): Оживляем элемент управления "ScrollBar"

В статье продолжим разрабатывать элемент управления ScrollBar и начнём делать функционал взаимодействия с мышкой. Помимо этого расширим списки флагов состояния и событий мышки.

DoEasy. Элементы управления (Часть 29): Вспомогательный элемент управления "ScrollBar"

В статье начнём разработку элемента вспомогательного управления ScrollBar и его производных объектов — вертикальной и горизонтальной полос прокрутки. ScrollBar (полоса прокрутки) используется для прокручивания содержимого формы, если оно выходит за пределы контейнера. Полосы прокрутки обычно расположены снизу и справа формы. Горизонтальная, расположенная снизу, служит для прокрутки содержимого влево-вправо, а вертикальная — для прокрутки вверх-вниз.