Popülasyon optimizasyon algoritmaları: Balık sürüsü arama (Fish School Search, FSS)

MetaTrader 5 — Örnekler | 5 Ekim 2023, 09:36

321

Andrey Dik

İçindekiler

1. Giriş
2. Algoritma tanımı
3. Test sonuçları

1. Giriş

Balık kümesi, bir bölgede bir araya gelmiş herhangi bir balık topluluğu için kullanılan genel bir terimdir. Balık kümeleri yapılandırılmış veya yapılandırılmamış olabilir. Yapılandırılmamış bir küme, yiyecek veya yuvalama alanları gibi bazı yerel kaynakların yakınında rastgele toplanmış karışık tür ve büyüklükteki bir grup olabilir.

Buna ek olarak, eğer küme etkileşimli, sosyal bir şekilde bir araya geliyorsa, sürü halinde oldukları söylenebilir. Çoğu yaşam döngülerinin aynı evresindedir, birbirleriyle aktif olarak temas halindedirler ve her an grup üyeleri için yararlı olan biyolojik olarak aktif ve organize faaliyetler sergileyebilirler.

Bireysel yaşamın aksine, sürü yaşamı, grup halinde yaşamanın avcılardan daha fazla korunma avantajı ile yiyecek elde etmede artan rekabet arasındaki bir uzlaşmadır.

Balıklar doğada çeşitli şekillerde sürü oluştururlar. Kural olarak, yalnızca kendi türlerinden bireylerden oluşan daha büyük sürüleri tercih ederler. Sürünün görünüşüyle öne çıkan veya bir tür farklılığa sahip olan herhangi bir üyesi, avcılar için birincil hedef haline gelir. Bu gerçek, balıkların neden aynı bireylerden oluşan sürüleri tercih ettiğini açıklar. Bu şekilde tüm sürünün homojenliği sağlanır.

Bir sürü, balıklar aynı hızda ve aynı yönde senkronize olarak yüzdüğünde oldukça katı bir şekilde organize olur. Bunun nedeni balıkların aynı tür, yaş ve büyüklükte olup birbirlerinden belirli bir mesafede hareket etmeleridir. Balık sürüleri, sanki grup zekasına ve ortak bir akla sahiplermiş gibi karmaşık manevralar yapabilirler.

Sürü oluşumunun incelikleri, özellikle de hareket ve beslenme şekilleri tam olarak anlaşılabilmiş değildir.

Sürü davranışını açıklamak için daha iyi yön bulma, avlanma senkronizasyonu, avcıların kafasını karıştırma ve yakalanma riskini azaltma gibi birçok hipotez ortaya atılmıştır. Sürüdeki balıklar, birbirlerinin davranışlarını yakın mesafeden kontrol eden bazı bilgiler paylaşıyor gibi görünmektedir. Bir balığın beslenme davranışı, diğerlerinde aktif bir yiyecek arayışını hızla tetikler. Sürü halindeki balıklar, birbirleriyle çarpışmaktan kaçınmak amacıyla sürünün şeklini değiştirirken, genellikle hızlı yükseliş ve inişler yaparak ve kendi eksenleri etrafında dönerek ince falankslar halinde yüzerler. Bu tür manevralar çok hızlı bir tepki sistemi gerektirir. Sürü halindeki yaşam tarzı, balıkların komşularına göre konumlarındaki küçük değişikliklere anında yanıt verebilecek duyu sistemlerine sahip olduğu anlamına gelir.

Daha eksiksiz bir resim oluşturmak için, bu tür davranışların matematiksel modellemesi kullanılır. En yaygın matematiksel modeller, sürüdeki her bir hayvanın şu üç temel kurala uyduğunu varsayar:

Komşularla aynı yönde hareket etme
Komşulara yakın durma
Komşularla çarpışmalardan kaçınma

Sürü halindeki balıkların yüzecekleri yönü nasıl seçtikleri sorusu hala çözülememiştir. Göç sırasında, sürünün çoğu üyesi nereye gideceğini biliyor gibi görünmektedir. Sürünün tüm üyeleri yiyecek mevcudiyetinin eşit derecede farkında olsa da, grupta diğer türdeşlerinden daha cesur olan bazı liderler vardır. Bu sürü davranışı, birçok araştırmacıyı sadece matematiksel bir model değil, aynı zamanda çeşitli optimizasyon problemlerini çözmek için algoritmik bir model oluşturmaya teşvik etmiştir.

2. Algoritma tanımı

Balık sürüsü arama algoritması, metasezgisel algoritmalar sınıfına ait sürü zekası algoritmalarının bir alt ailesidir. Bastos Filho ve Lima Neto tarafından 2008 yılında ortaya çıkarılmış ve ilk olarak 2009 yılında yayınlanmıştır. FSS'de basit temsilciler balıklardır ve her balığın arama sırasında elde edilen "başarı"yı temsil eden bir ağırlığı vardır. Ağırlıkların değerleri ve varyasyonları bireysel ve kolektif hareketleri etkiler. Yerleşik beslenme ve koordineli eylem mekanizmaları, sürüyü ağırlık kazanmak ve yerel ve global olarak en iyi konumları bulmak için pozitif bir gradyana doğru yönlendirir. FSS, çok modlu arama uzaylarında sürekli optimizasyon problemleri için geliştirilmiştir. Bu durum, diğer araştırmacıları da ‘ikili problemlerde optimizasyon’ ve ‘çok amaçlı optimizasyon’ gibi diğer problemleri çözmeye yönelik seçenekler ortaya çıkarmaya sevk etmiştir.

FSS algoritmasında balıklar, duvarları çalışılan fonksiyonun tanım kümesinin sınırları olan koşullu bir akvaryumda yüzüyor gibi düşünülebilir. Balık ağırlığı, yiyecek (çözümler) bulmadaki başarının bir ölçüsüdür. Aynı zamanda bu, balığın hafızası rolünü de oynar. Ağırlığın varlığı algoritmanın ana fikridir ve parçacık sürüsünden farkıdır. FSS algoritmasının bu özelliği, parçacık sürüsünde olduğu gibi global olarak en iyi çözümleri bulma ve sabitleme ihtiyacını ortadan kaldırır.

FSS algoritması operatörleri iki gruba ayrılır:
- beslenme operatörü alan araştırmasının başarısını tescil eder
- yüzme operatörleri bireysel balıklar ve bir bütün olarak sürü için göç algoritmaları uygular

Beslenme operatörü, balığın ağırlığının hesaplamasıdır. Temel fikir, balığın "yemek" ve "kilo almak" için pozitif bir gradyana doğru "yüzmesini" sağlamaktır. Toplu olarak, daha ağır balıkların genel arama süreci üzerinde daha büyük bir etkisi vardır, bu da balık sürüsünün kütle merkezinin yinelemeler boyunca arama uzayında daha iyi konumlara doğru hareket etmesine neden olur. Belirli bir yinelemedeki ağırlık artışı, uygunluk fonksiyonunun değerlerindeki normalleştirilmiş farkla orantılıdır:

fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness)

Tanımlamalar:

weight - balık ağırlığı
delta_fitness - uygunluk fonksiyonu değerleri arasındaki fark
max_delta_fitness - tüm balıklar arasındaki uygunluk fonksiyonu farkının maksimum değeri

Yüzme operatörleri hareket türüne göre üç türe ayrılır:

- bireysel

- içgüdüsel-kolektif

- kolektif-iradeli

Bireysel yüzme, balığın mevcut konumunun çevresinde yerel bir arama olarak yorumlanabilir. Her bireyin hareket vektörü rastgele yönlendirilir ve farklı bir değere sahiptir.

fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r

Tanımlamalar:

new_position - ilgili koordinattaki yeni konum
current_position - ilgili koordinattaki mevcut konum
step_ind - bireysel hareket adımı, şu şekilde hesaplanır:

initial_step_ind * (rangeMax [d] - rangeMin [d])

Tanımlamalar:

initial_step_ind - bireysel hareket için algoritma parametresi
rangeMax ve rangeMin - optimize edilen argümanların değer aralıkları
r - rastgele sayı [-1.0; 1.0]

Bireysel yüzme şematik olarak Şekil 1'de gösterilmektedir.

individual

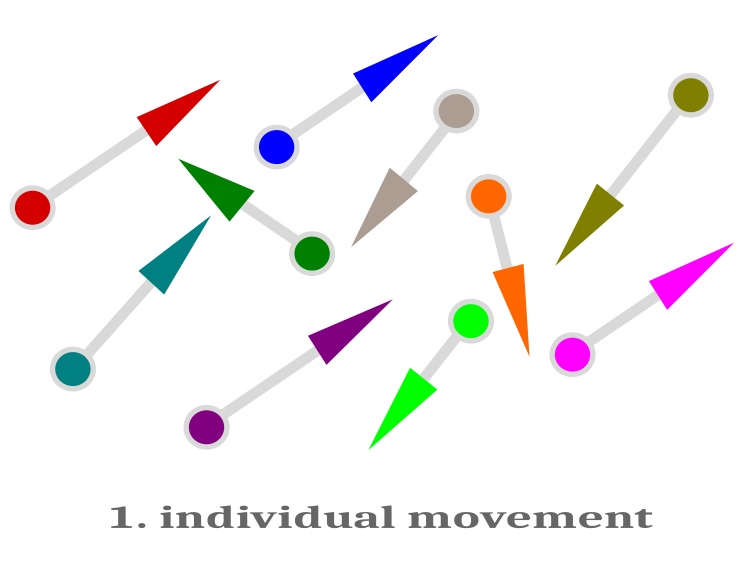
Şekil 1. Bireysel yüzme. Her balığın hareket vektörü rastgele bir yöne yönlendirilir ve farklı bir skaler değere sahiptir

Bireysel yüzmeden sonra uygunluk fonksiyonu ölçülür. Eğer balığın sonuçtaki konumu iyileşmediyse, o zaman bu balığın herhangi bir hareketi olmadığını ve yerinde kaldığını düşünürüz. Sadece uygunluk fonksiyonlarını geliştiren balıklar yeni bir konuma geçecektir.

Bireysel yüzmenin tamamlanmasının ardından içgüdüsel-kolektif hareket operatörü yürütülür. Önce Şekil 2'ye bakalım.

collect

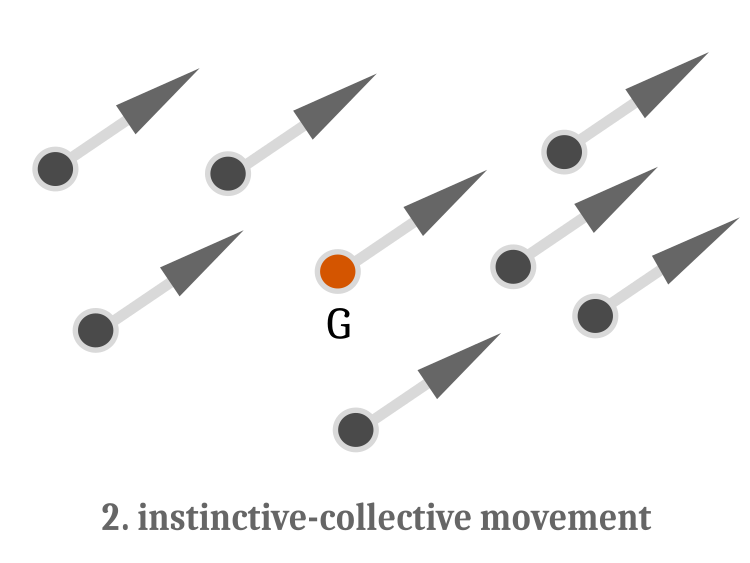
Şekil 2. İçgüdüsel-kolektif yüzme. Hareket, tüm balıklar için G kütle merkezine göre aynı yön ve büyüklük vektörü ile karakterize edilir

İçgüdüsel-kolektif hareket, bir önceki yinelemedeki her bir balığın uygunluk fonksiyonundaki değişikliği dikkate alarak balık sürüsünün genel konumunu düzeltmeye yarar. Yeni koordinatlar aşağıdaki gibi hesaplanır:

fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d]

Tanımlamalar:

new_position - ilgili koordinattaki yeni konum
current_position - ilgili koordinattaki mevcut konum
collective_instinct - ilgili koordinat boyunca hareket miktarı, şu şekilde hesaplanır:

collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness

Tanımlamalar:

delta_position - mevcut konumun koordinatı ile bireysel yüzme aşamasındaki bir önceki konumun koordinatı arasındaki fark
delta_fitness - mevcut konumun uygunluk fonksiyonu ile bireysel yüzme aşamasındaki bir önceki konumun uygunluk fonksiyonu arasındaki fark

İçgüdüsel-kolektif yüzme, balık sürüsünün yeni bir yere senkronize grup hareketini gerçekleştirerek yeni yiyecek yerleri arayışını sağlarken, bireysel hareket yerel olarak durumun iyileştirilmesine olanak tanır.

Şimdi de kolektif-iradeli yüzmeyi inceleyelim. İki türe ayrılır:

- kütle merkezinden dışarıya hareket - eğer bir bütün olarak sürünün konumunda önceki konuma kıyasla bir iyileşme meydana gelmemişse, balıklar yanlara doğru yayılır (bu, daha fazla yiyecek arayışını sembolize eder) (Şekil 3)

- İyileşme meydana gelmişse kütle merkezine doğru hareket. Balıklar kütlenin merkezine doğru hareket ederek halkayı sıkıştırır (bu da ava saldırıyı sembolize eder). Algoritmik olarak bu, optimizasyon probleminin çözümünün iyileştirilmesi anlamına gelir (Şekil 4)

col vol out

Şekil 3. Kolektif-iradeli yüzme. Yön vektörleri kütle merkezi G'den dışarıya yönlendirilir

col vol in

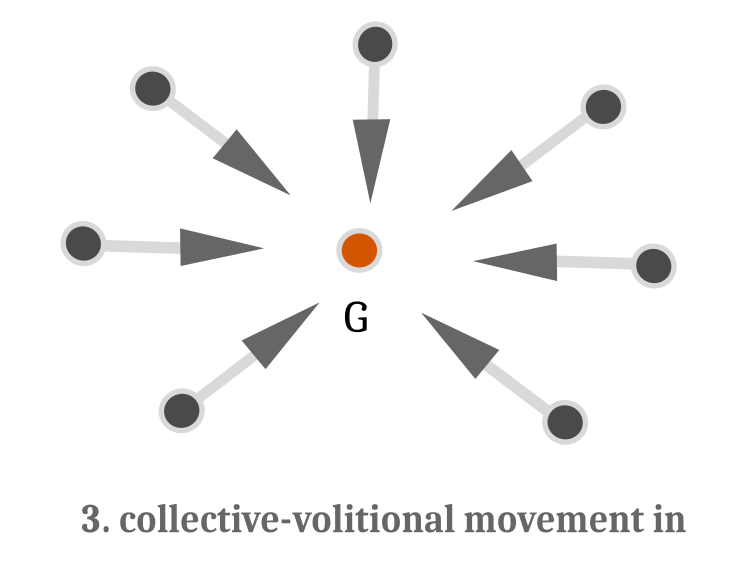
Şekil 4. Kolektif-iradeli yüzme. Yön vektörleri kütle merkezi G'ye doğru yönlendirilir

Kütle merkezi kavramı, kolektif-iradeli yüzmenin hesaplanması için tanıtılmıştır. Böylece, kolektif-iradeli yüzme denklemi şu şekilde görünecektir:

fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator)

Tanımlamalar:

pos - current_position ile aynıdır
search_operator - önceki hareket, konumun iyileşmesiyle sonuçlandıysa 1, sonuçlanmadıysa -1
step_vol [d] - kolektif hareket adımı, şu şekilde hesaplanır:

step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d])

Tanımlamalar:

initial_step_vol - kolektif hareket için algoritma parametresi
barycenter [d] - balık ağırlıklarının toplamının koordinat ile çarpımı olarak hesaplanan kütle merkezi:

barycenter [d] += fishes [f].weight * fishes [f].current_position [d]

ve balık sürüsünün toplam ağırlığına bölünür:

barycenter [d] /= current_total_weight

Algoritmanın yalancı kodu şu şekildedir:

1) Balık konumlarının rastgele sayılarla başlatılması

2) Bireysel hareketler

3) Uygunluk fonksiyonunun hesaplanması

4) Her balık için ağırlıkların yeniden tanımlanması

5) İçgüdüsel-kolektif hareket

6) Kolektif-iradeli hareket

7) Toplam ağırlığın yeniden hesaplanması

8) Uygunluk fonksiyonun hesaplanması

9) Durma kriteri karşılanana kadar 2. adımdan itibaren tekrarlanır

Schema FSS

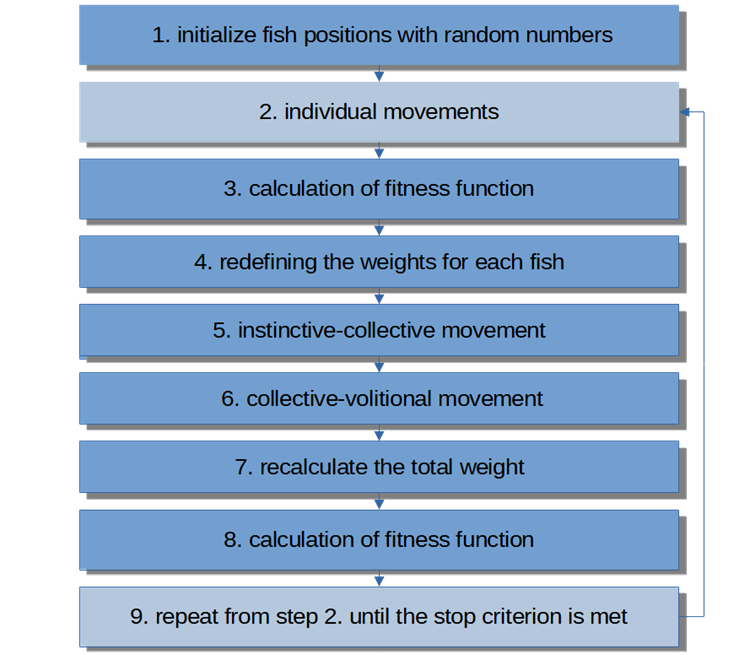
Şekil 5. FSS algoritmasının blok diyagramı

Kodu açıklamaya başlayalım.

Tahmin edebileceğiniz gibi, algoritmanın en basit mantıksal birimi balığı tanımlayan yapıdır. Balığı birkaç kez başlatmamız gerekeceğinden, özel Init () metodunda nispeten büyük boyutu nedeniyle bu yapıyı "sıfırlamamız" tavsiye edilir, bu da kodu biraz optimize etmemizi sağlayacaktır. Yapı, mevcut konum, yeni konum ve son hareketten bu yana koordinatlardaki fark için koordinat dizilerini içerir. Varsayılan ağırlık 1000 standart birime eşittir ve herhangi bir değere sahip olabilir. Balık ayrıca mevcut uygunluk fonksiyonunun değeri, bir öncekinin değeri ve aralarındaki fark ile karakterize edilir. Init () metodunda, uygunluk fonksiyonu mümkün olan en düşük 'double' değeri ile başlatılır. Dolayısıyla, balık henüz hareket etmediği için uygunluk farkı sıfırdır.

//——————————————————————————————————————————————————————————————————————————————
struct S_Fish
{
  void Init (int dimensions)
  {
    ArrayResize (current_position, dimensions);
    ArrayResize (new_position,     dimensions);
    ArrayResize (delta_position,   dimensions);
    weight        = 1000.0;
    fitness       = -DBL_MAX;
    delta_fitness = 0.0;
  }

  double current_position [];
  double new_position     [];
  double delta_position   [];
  double weight;
  double fitness;
  double new_fitness;
  double delta_fitness;
};
//——————————————————————————————————————————————————————————————————————————————

Doğal topluluk modelini matematiksel olarak temsil eden bir balık sürüsü olan C_AO_FSS sınıfını bildirelim. Burada olağandışı bir şey yoktur. Ayrıca kullanıcı programı (balıkların koordinatlarını, sürüdeki etkileşimi ve dizileri dikkate almak için gerekli optimize edilen fonksiyonun değer aralıkları) ile etkileşim için gerekli iki public metot vardır.

Init () başlatma sınıfının public metodunda, değişkenleri orijinal değerlerine sıfırlamak ve diziler için bellek ayırmak gerekir. init ve swimmingRegime değişkenleri özellikle dikkat etmeye değerdir. Gördüğümüz yalancı koda göre, uygunluk fonksiyonunun hesaplanması iki kez gerçekleştirilir: ilk kez - bireysel hareketten sonra, ikinci kez - iki tür toplu hareketten sonra. Bu durum, bizim tarafımızdan benimsenen ve her yinelemenin bir sıralama içerdiğini belirten algoritma-uygulama bağlantı şemasıyla çelişmektedir: birinci metot -> uygunluk fonksiyonunun hesaplanması -> ikinci metot. Bu iki değişken, bunu düzeltmek ve kanonik algoritmadaki eylem sırasını değiştirmek için uygulanır. Algoritmanın başında init değişkeni 'false' olmalıdır. Bu, balığın başlatılması, uygunluk fonksiyonunun hesaplanması ve hareketin tekrar yapılması gerektiğini gösteren bir bayraktır, çünkü algoritmanın tüm mantığı koordinatların ve uygunluk fonksiyonunun mevcut ve önceki değeri arasındaki farkı kullanır. Bu olmasaydı, değer farkını elde edemezdik. İkinci önemli bayrak ise swimmingRegime’dir. Balıkların hareketini tanımlayan metotları çağırma sırasını yapımıza uyacak şekilde yeniden tanımlamamızı sağlar. 1 değeri "bireysel" yüzme çağrısına karşılık gelir, aksi takdirde yukarıda ele aldığımız grup hareketleri sırasını kullanırız.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Init (const int    dimensionsP,
                     const int    fishSchSizeP,
                     const double initial_step_indP,
                     const double initial_step_volP)
{
  MathSrand (GetTickCount ());
  init = false;
  swimmingRegime = 1;

  dimensions     = dimensionsP;

  ArrayResize (rangeMax,  dimensions);
  ArrayResize (rangeMin,  dimensions);
  ArrayResize (rangeStep, dimensions);

  num_of_individuos = fishSchSizeP;

  ArrayResize (fishes, num_of_individuos);

  for (int i = 0; i < num_of_individuos; i++)
  {
    fishes [i].Init (dimensions);
  }

  global_best = -DBL_MAX;
  ArrayResize (global_best_position, dimensions);

  total_weight     = num_of_individuos;

  initial_step_ind = initial_step_indP;
  ArrayResize (step_ind, dimensions);

  initial_step_vol = initial_step_volP;
  ArrayResize (step_vol, dimensions);

  ArrayResize (collective_instinct, dimensions);
  ArrayResize (barycenter, dimensions);
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çağrılan ilk public metot olan Swimming (), bireysel ve grup balık hareketlerine yapılan çağrıların sırasını belirler. Metot ilk kez çağrılırsa, bireysel ve grup hareket adımları, iki initial_step_ind ve initial_step_vol algoritma parametresi aracılığıyla ilgili koordinat boyunca olası aralığın bir parçası olarak başlatılır. Bazı yazarlar bu değerlerin sırasıyla 0.01 ve 0.001 olarak ayarlanmasını önermektedir. Ancak bu değerlerle iyi sonuçlar alamadım. Bu yüzden 0.1 ve 0.8 değerlerini kullanıyorum. Ayrıca, algoritmanın ilk çalıştırılmasında, balık konumu koordinatlarının mevcut değeri, optimize edilen parametreler aralığında rastgele sayılarla başlatılır. Uygun hareket türleri, swimmingRegime bayrağına uygun olarak sonraki metot çağrıları sırasında çağrılacaktır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Swimming (int i)
{
  //----------------------------------------------------------------------------
  if (!init)
  {
    global_best    = -DBL_MAX;
    swimmingRegime = 1;

    for (int d = 0; d < dimensions; d++)
    {
      step_ind [d] = initial_step_ind * (rangeMax [d] - rangeMin [d]);
      step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      fishes [f].Init (dimensions);

      for (int d = 0; d < dimensions; d++)
      {
        fishes [f].new_position [d] = RNDfromCI (rangeMin [d], rangeMax [d]);
        fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
      }
    }
  }
  //----------------------------------------------------------------------------
  else
  {
    switch (swimmingRegime)
    {
    case 1:
      apply_individual_movement ();            //individual movement
      break;
    default:
      apply_instintive_collective_movement (); //instinctively-collective movement
      apply_collective_volitive_movement ();   //collective-volitional movement
      update_total_weight ();                  //recalculate the total weight
      break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çağrılan ikinci public metot olan Regrouping (), öncelikle bireysel, kolektif-içgüdüsel, kolektif-iradeli yüzme metotlarına yapılan çağrıların sırasını belirlemeyi amaçlar. Çağrıların sırasını ayarlamak için metodun ek işlevselliği, 1 ve 2 değerlerini alan swimmingRegime bayrağı tarafından sağlanır. Bu, bizim benimsediğimiz şema için klasik versiyondaki balık hareketi metotlarını çağırma sırasını yeniden tanımlamak için gereklidir: birinci public metot -> uygunluk fonksiyonunun hesaplanması -> ikinci public metot. Init bayrağına bağlı olarak, algoritma ilk yinelemede ise, metodun uygunluk fonksiyonunun hesaplanmasından sonra çağrıldığı varsayıldığından, mevcut koordinat konumunu ve uygunluk fonksiyonu değerini, farklarının sonraki hesaplamaları için saklayacağız. Init bayrağı algoritmanın ikinci ve sonraki yinelemelerde olduğunu gösteriyorsa, bireysel hareketten sonra, uygunluk fonksiyonunun mevcut ve önceki değerleri arasındaki farkın yanı sıra mevcut ve önceki konumların koordinatları arasındaki farkın elde edilmesi gerekir. Farklar, pozisyonun iyileştiği koşulda hesaplanır, aksi takdirde hareket olmadığı kabul edilir. Bu nedenle, balık ağırlığı değerlerini başlangıç durumuna sıfırlıyoruz ve hareketlerdeki ve uygunluk fonksiyonlarındaki farkları sıfıra eşit alıyoruz. En iyi çözüme ulaşılırsa, updates_optimal_solution () metodunu çağırarak hemen güncelleriz ve apply_feeding () metoduyla balık beslemesi uygularız. Eğer swimmingRegime bayrağı 1'e eşit değilse, o zaman kolektif-içgüdüsel ve kolektif-iradeli hareketler uygulanmıştır. Tamamlanmalarının ardından swimmingRegime 1 olarak ayarlanır. Sırada bireysel hareket vardır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Regrouping ()
{
  //----------------------------------------------------------------------------
  if (swimmingRegime == 1
  {
    if (!init)
    {
      for (int f = 0; f < num_of_individuos; f++)
      {
        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
        ArrayInitialize (fishes [f].delta_position, 0.0);

        fishes [f].fitness = fishes [f].new_fitness;
        fishes [f].delta_fitness = 0.0;
      }

      init = true;
      return;
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      //remember the best position for the fish
      if (fishes [f].new_fitness > fishes [f].fitness)
      {
        fishes [f].delta_fitness = fishes [f].new_fitness - fishes [f].fitness; //fabs
        fishes [f].fitness = fishes [f].new_fitness;

        for (int d = 0; d < dimensions; d++)
        {
          fishes [f].delta_position [d] = fishes [f].new_position [d] - fishes [f].current_position [d];
        }

        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        ArrayInitialize (fishes [f].delta_position, 0.0);
        fishes [f].delta_fitness = 0.0;
      }
    }

    swimmingRegime = 2;
    updates_optimal_solution ();
    apply_feeding ();
    return;
  }

  //----------------------------------------------------------------------------
  swimmingRegime = 1;
  updates_optimal_solution ();
}
//——————————————————————————————————————————————————————————————————————————————

Aşağıdaki basit private metot, algoritmanın en iyi sonuçlarına ulaşıldığında onları güncellemek için kullanılır. Bunu yapmak için, her bir balığın uygunluk fonksiyonunun değerlerini global olanlarla karşılaştırırız. Eğer daha iyilerse, onları koruruz.

//——————————————————————————————————————————————————————————————————————————————
// update the best overall solution
void C_AO_FSS::updates_optimal_solution ()
{
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].fitness > global_best)
    {
      global_best = fishes [f].fitness;
      ArrayCopy (global_best_position, fishes [f].current_position, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Bireysel yüzme sağlayan bu private metodun denklemini yukarıda zaten ele almıştık. Yani, burada her şey basittir: her balığın mevcut koordinatlarına -1.0 ila 1.0 aralığında rastgele bir sayı ile çarpılan bireysel bir adım ekliyoruz, bu da hem pozitif hem de negatif yönde bir artış sağlar. Optimize edilen parametrelerin değer aralığı aşılırsa, koordinat için sınır değeri ayarlanır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_individual_movement ()
{
  // move the fish to new places-----------------------------------------------
  double r = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (-1.0, 1.0);

      fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Beslenme metodu anlamada zorluklara neden olmamalıdır. Balığın ağırlığı, aslında, balığın kendi uygunluk fonksiyonundaki fark ile tüm balık sürüsü arasındaki farkın maksimum değerinin bölümü olarak belirlenir. Ancak, tüm balıklar arasındaki maksimum fark sıfıra eşit olabilir. Algoritmanın klasik versiyonunun tanımı, balık ağırlığının her zaman pozitif olması gerektiğini söyler. Genellikle sadece uygunluk fonksiyonunun pozitif değerler aldığı durumlar dikkate alınır, ancak bu gereklilikte pratik bir anlam bulamadım. Balık ağırlığının negatif değerler alabileceğini kabul ediyorum, bu nedenle uygunluk fonksiyonunun maksimum farkı (bu değere göre her balığın ağırlığını normalize etmemiz gerekir) tüm balıklar arasında sıfırsa, balığın ağırlığını 1 olarak alırız.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_feeding ()
{
  double max_delta_fitness = -DBL_MAX;

  //find the maximum weight among fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].delta_fitness > max_delta_fitness) max_delta_fitness = fishes [f].delta_fitness;
  }

  //feed the fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (max_delta_fitness != 0.0)
    {
      fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);
    }
    else fishes [f].weight = 1;
  }
}
//——————————————————————————————————————————————————————————————————————————————

İçgüdüsel-kolektif hareketin private metodu, her balığın koordinatlarını kolektif içgüdünün değeri kadar artırarak değiştirmekten ibarettir; bu da mevcut ve önceki yinelemelerdeki konum farkının önceki hareketlerde elde edilen uygunluk fonksiyonu farkıyla çarpımından başka bir şey değildir. Burada da, sınırları aşmaları halinde optimize edilecek parametreler için sınır değerler atıyoruz.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_instintive_collective_movement ()
{
  double sum_delta_fitness = 0.0;
  for (int f = 0; f < num_of_individuos; f++)
  {
    sum_delta_fitness += fishes [f].delta_fitness;
  }

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

      if (sum_delta_fitness != 0.0)
      {
        collective_instinct [d] /= sum_delta_fitness;
      }

      fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Balık sürüsünün kütle merkezinin yanı sıra mevcut toplam ağırlığının hesaplandığı private kolektif-iradeli yüzme metodu. Sürünün toplam ağırlığı arttıysa, balıklar kütle merkezine doğru hareket etmeye başlar, aksi takdirde merkezden uzaklaşır. Denklem daha önce ayrıntılı olarak tartışılmıştı. Balık sürüsünün toplam ağırlığı aşağıdaki private metotla güncellenir.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_collective_volitive_movement ()
{
  //----------------------------------------------------------------------------
  double current_total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    current_total_weight += fishes [f].weight;
  }

  ArrayInitialize (barycenter, 0.0);

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      barycenter [d] += fishes [f].weight * fishes [f].current_position [d];
    }
  }

  for (int d = 0; d < dimensions; d++)
  {
    barycenter [d] /= current_total_weight;
  }

  //----------------------------------------------------------------------------
  double search_operator = current_total_weight > total_weight ? 1.0 : -1.0;
  double r   = 0.0;
  double pos = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (0.0, 1.0);
      pos = fishes [f].current_position [d];

      fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Burası toplam ağırlığın güncellendiği metottur. Burada her şey basittir. Her balığın ağırlığını alıp topluyoruz.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::update_total_weight ()
{
  total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    total_weight += fishes [f].weight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test sonuçları

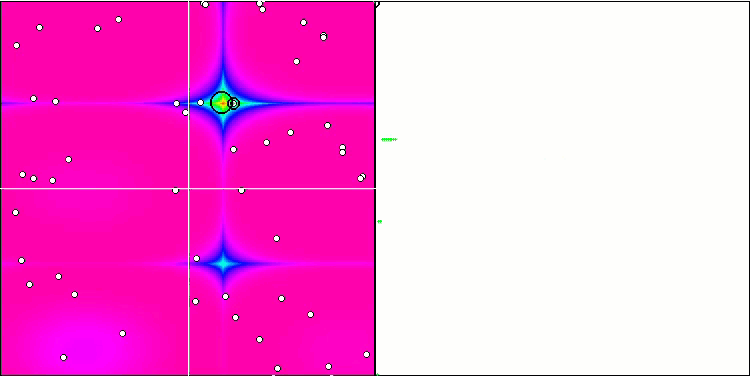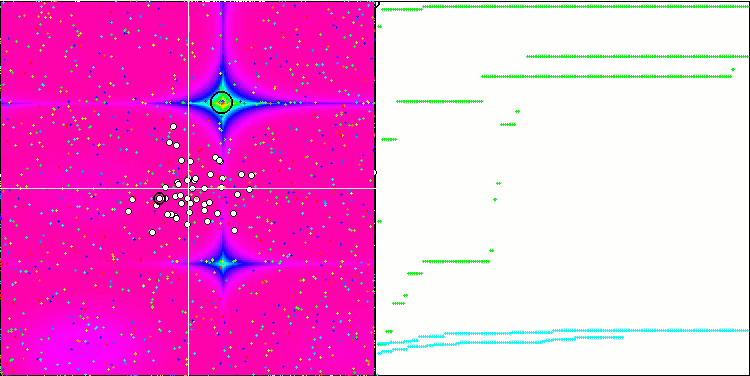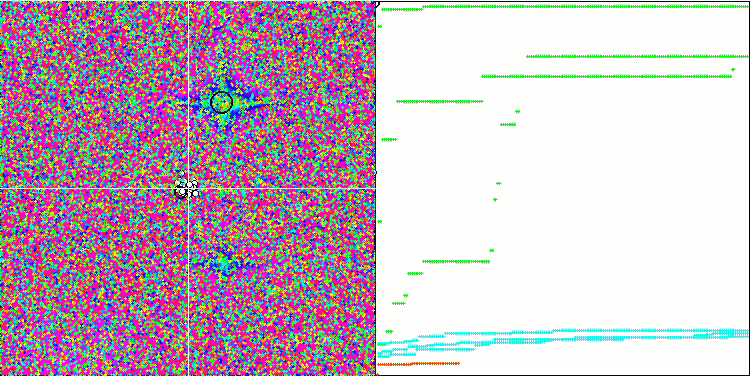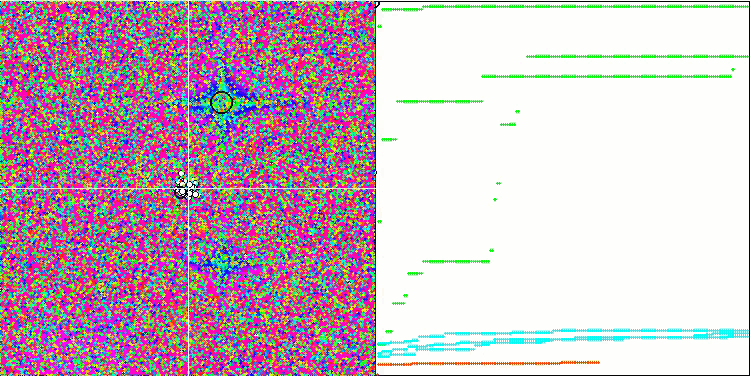
Son ve en ilginç kısma geçelim - sonuçlar. Algoritma, global optimumun dikkate alınmasına gerek olmaması ve bir bütün olarak konumun iyileşip iyileşmediğine göre sürünün merkezine yakınsama veya oradan dağılma anlamına gelen içgüdüsel-iradeli hareket ve kütle merkezi kavramlarının tanıtılması gibi ilginç teknikler içermektedir. Tüm bunlar, algoritmanın çalışılan fonksiyonlar üzerindeki orijinal davranışı için umut vermiştir.

Genel olarak, uzayın arama alanındaki davranışta özgünlük vardır, yani arı algoritmasında gözlemlenene benzer şekilde balıkların uzayın ayrı bölümlerine dağılması söz konusudur, ancak FSS'nin denklemlerinin ve çalışma prensibinin ayrıntılı bir değerlendirmesi, sürünün ayrı gruplara dağılmasını ima etmemektedir. Genel olarak, algoritma kötü performans göstermiştir. Genel sonuç açısından PSO algoritmasından sadece biraz daha iyidir.

Tek tek testleri ele alırsak, FSS yine de bazılarında üstünlük sağlamayı başarmıştır. Özellikle, düzgün Skin fonksiyonunda, FSS algoritmasının kurt algoritmasından daha iyi olduğu ortaya çıkmıştır ve açıklaması kolay olan iyi (ancak en iyi değil) sonuçlar göstermiştir. Algoritma, incelenen fonksiyon yüzeyinin gradyanını kullanır (her yinelemede her koordinat için artışlar halinde ve uygunluk fonksiyonundaki değişimi dikkate alarak). Skin fonksiyonu düzgün olduğundan, algoritma yüzey değişikliklerine iyi "tutunmaktadır".

Forest fonksiyonuna gelince, algoritma ortalamanın altında sonuçlar göstermiştir. Test fonksiyonundaki yumuşak değişiklikler algoritmanın uzayda gezinmesine bir dereceye kadar yardımcı olmuştur, ancak global maksimum değeri bulamamıştır. Megacity’e bakıldığında, FSS'nin eksiklikleri daha da belirgin hale gelmektedir. Algoritma, incelenen fonksiyonun bireysel temsilcilerin mevcut konumlarının yakınında değişmemesini gerçekten "sevmemektedir" ve algoritma potansiyel olarak daha iyi yeni yerleri belirlemek için uzun atlamalar yapamamaktadır. Bu nedenle, çevresinde bir artış olmayan herhangi bir yerel ekstremumda takılıp kalmaktadır.

Megacity testi herhangi bir optimizasyon algoritması için çok zor olsa ve karşılaştırma tablosundaki diğer katılımcılar genel olarak FSS'nin çok önünde olmasa da, yine de algoritmanın ayrık problemler üzerindeki zayıf yeteneklerini kabul etmek gerekir. Bazı testlerde rastgele arama en iyi sonucu vermiştir. Animasyonda da görebileceğimiz gibi algoritma işleyişinde herhangi bir "kümelenme" gözlemlenememektedir. Bir önceki makalede açıklanan optimizasyon algoritmalarındaki "kristalleşme" olgusunu hatırlayabilirsiniz.

FSS algoritması sonuçları:

2022.12.08 13:14:06.033    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.892861444841324
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    Score: 0.99391
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.11410005347766
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    Score: 0.56920
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.20519552002827
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    Score: 0.11341
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.5057381856551146
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    Score: 0.85172
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.21468156279781656
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    Score: 0.12143
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.056970068652984526
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    Score: 0.03223
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 11.0
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    Score: 0.91667
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.03
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    Score: 0.08583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.31
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    Score: 0.02583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    All score for C_AO_FSS: 0.4122477188979048

Skin

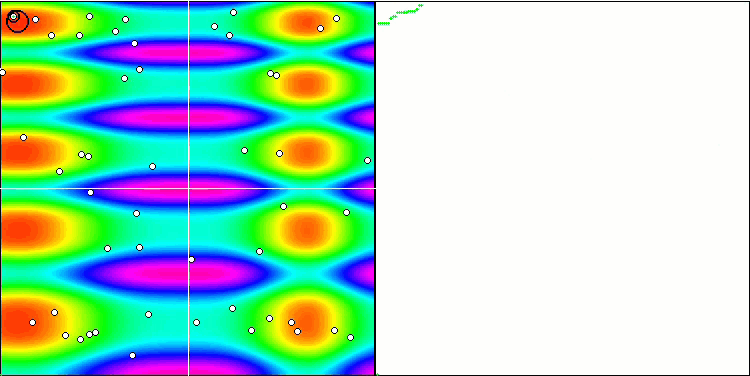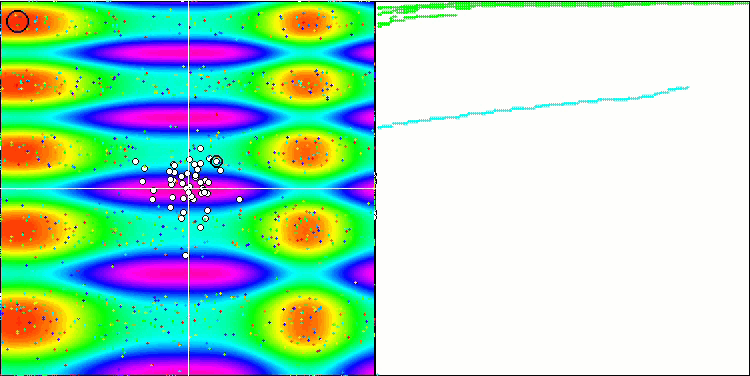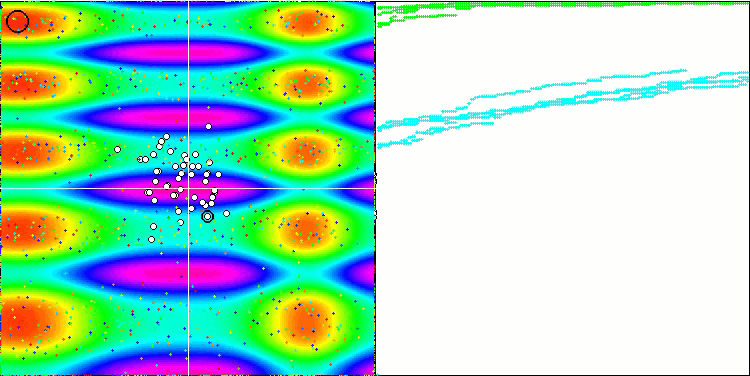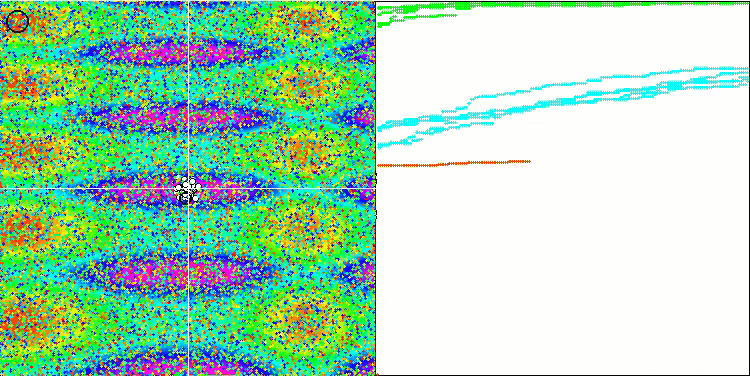
Skin test fonksiyonu üzerinde FSS

Forest

Forest test fonksiyonu üzerinde FSS

Megacity

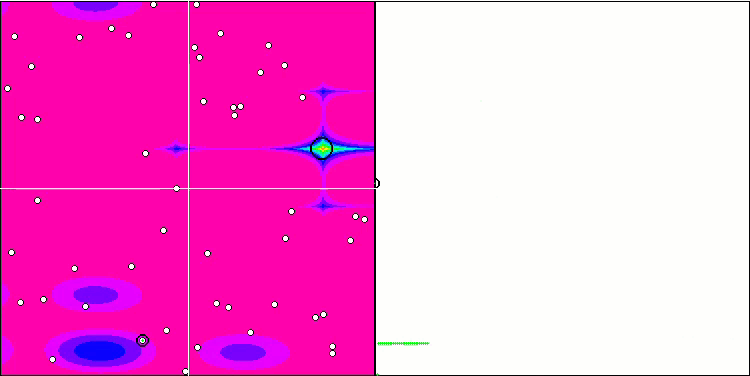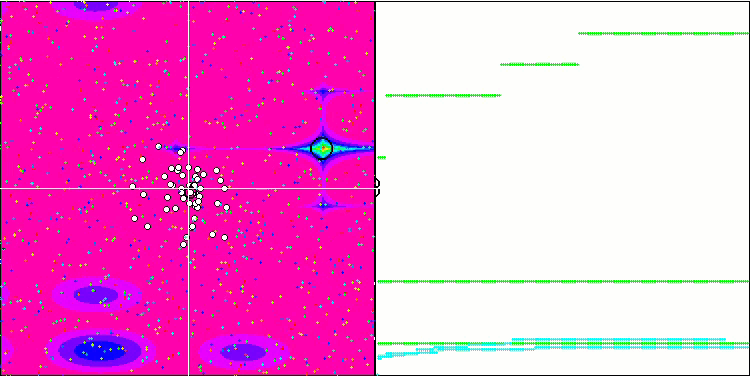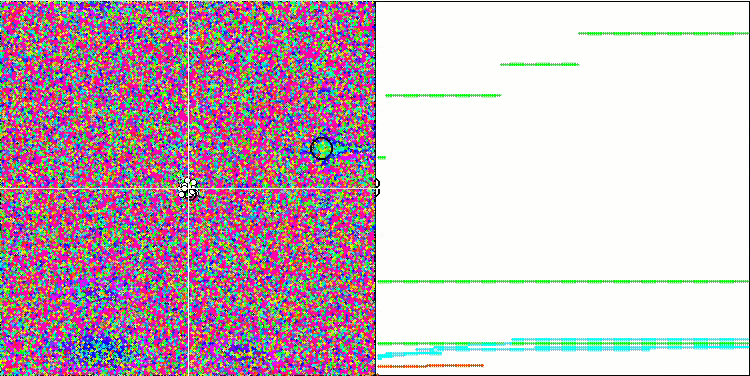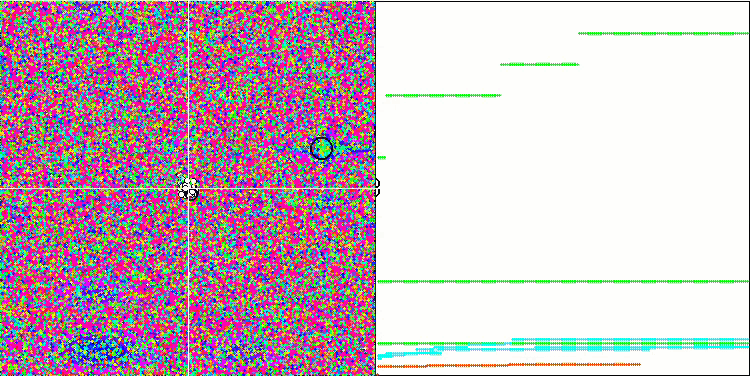
Megacity test fonksiyonu üzerinde FSS

İşte nihai tablo. Her bir test fonksiyonu için algoritmaları ayrı ayrı değerlendirmede daha fazla kolaylık sağlamak adına tabloya ek sütunlar ekledim, bu da her bir algoritmanın belirli görevler için uygulanabilirliği hakkında daha adil bir yargıya varmamıza olanak tanır.

AO	Açıklama	Skin			Skin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
AO	Açıklama	2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)	Skin için nihai sonuç	2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)	Forest için nihai sonuç	2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)	Megacity için nihai sonuç	Nihai sonuç
COAm	Guguk kuşu optimizasyon algoritması	1.00000	0.85911	0.14316	0.66742	0.99283	0.28787	0.04551	0.44207	1.00000	0.24917	0.03537	0.42818	0.51255778
ACOm	Karınca kolonisi optimizasyonu	0.98229	0.79108	0.12602	0.63313	1.00000	0.62077	0.11521	0.57866	0.38333	0.44000	0.02377	0.28237	0.49805222
ABCm	Yapay arı kolonisi (m)	1.00000	0.63922	0.08076	0.57333	0.99908	0.20112	0.03785	0.41268	1.00000	0.16333	0.02823	0.39719	0.46106556
ABC	Yapay arı kolonisi	0.99339	0.73381	0.11118	0.61279	0.99934	0.21437	0.04215	0.41862	0.85000	0.16833	0.03130	0.34988	0.46043000
GWO	Gri kurt optimizasyonu	0.99900	0.48033	0.18924	0.55619	0.83844	0.08755	0.02555	0.31718	1.00000	0.10000	0.02187	0.37396	0.41577556
FSS	Balık sürüsü arama	0.99391	0.5692	0.11341	0.55884	0.85172	0.12143	0.03223	0.33513	0.91667	0.08583	0.02583	0.34278	0.41224778
PSO	Parçacık sürüsü optimizasyonu	0.99627	0.38080	0.05089	0.47599	0.93772	0.14540	0.04856	0.37723	1.00000	0.09333	0.02233	0.37189	0.40836667
RND	Karmaşık	0.99932	0.44276	0.06827	0.50345	0.83126	0.11524	0.03048	0.32566	0.83333	0.09000	0.02403	0.31579	0.38163222

Stokastik (rastgele) sezgisel yöntemler kesin bir çözümü garanti etmez, ancak kural olarak, kabul edilebilir bir sürede pratik kullanım için yeterince yakın çözümler bulmaya olanak sağlar. Bununla birlikte, pratikte bazı algoritmaların mükemmel yakınsama yetenekleri gösterebildiği görülmüştür, ancak bu durum FSS için geçerli değildir. Genel olarak, balık sürüsü arama algoritması, parçacık sürüsüne dayalı algoritmaların özel bir durumudur. Bu nedenle, hem avantajları hem de dezavantajları miras almıştır. Benzersiz algoritma özellikleri, parçacık sürüsünde gözlemlenmeyen ‘balık sürüsünün ayrı gruplara bölünmesi’ni içerir. FSS'nin çok değişkenli fonksiyonlarla iyi başa çıkacağına dair bir kesinlik olmasa da algoritma düzgün fonksiyonlarla nispeten iyi başa çıkmaktadır.

Avantajları:
1. Algoritma düzgün fonksiyonları oldukça iyi idare etmektedir.
2. Balık sürüsünün ayrı gruplara bölünebilmesi, algoritmanın diğer potansiyel olarak iyi yerel ekstremumları daha fazla keşfetmesine olanak sağlar.

Dezavantajları:
1. Bireysel testlerde sonuçların büyük ölçüde dağılması algoritmanın istikrarsızlığını gösterir.
2. Ayrık fonksiyonlar ve kesikli fonksiyonlar üzerinde çok zayıf yakınsama. Ayrık fonksiyonlar için neredeyse uygulanamaz.
3. Zayıf ölçeklenebilirlik.

MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/11841

Ekli dosyalar |

ZIP indir

7_The_world_of_AO_yFSSa.zip (64.26 KB)

Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.

Bu yazarın diğer makaleleri

Tartışmaya git

Relative Vigor Index göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?

En popüler teknik göstergelere dayalı ticaret sistemlerini nasıl geliştireceğimizi öğrendiğimiz serimizin yeni makalesindeyiz. Bu makalede Relative Vigor Index göstergesi üzerinde çalışacağız.

DeMarker göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?

En popüler teknik göstergelere dayalı ticaret sistemlerini nasıl tasarlayacağımızı öğrendiğimiz serimizin yeni makalesindeyiz. Bu makalemizde, DeMarker göstergesiyle bir ticaret sisteminin nasıl geliştirileceğini öğreneceğiz.

Awesome Oscillator göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?

Serimizin bu yeni makalesinde, ticaretimizde faydalı olabilecek yeni bir teknik araç hakkında bilgi edineceğiz. Bu, Awesome Oscillator (AO) göstergesidir. Bu göstergeyi kullanarak bir ticaret sisteminin nasıl tasarlayacağını öğreneceğiz.

Mağazadan bir Uzman Danışman seçmenin doğru yolu

Bu makalede, bir Uzman Danışman satın alırken dikkat etmeniz gereken bazı önemli noktaları ele alacağız. Ayrıca kârı artırmanın, akıllıca para harcamanın ve bu harcamalardan kazanç elde etmenin yollarını arayacağız. Ek olarak, makaleyi okuduktan sonra, basit ve ücretsiz ürünler kullanarak bile kazanç elde etmenin mümkün olduğunu göreceksiniz.