Gerenciamento de dinheiro revisitado

Epigrafo:

Introdução

A atividade de negociação pode ser dividida em duas partes relativamente independentes. A primeira parte chamada de sistema de negociação (ТS) analisa a situação atual, toma decisões para entrar no mercado, define o tipo de posição (comprar/vender) e momento de sair do mercado. A quantidade de fundos usados em cada negócio é definida pela segunda parte chamada sistema de gerenciamento de dinheiro. Nesse artigo vamos tentar analisar algumas estratégias de MM dependendo das mudanças em seus parâmetros. O método de simulação foi selecionado para análise. Entretanto, resultados de decisões analíticas são também consideradas em alguns casos. As ferramentas de análise são o terminal de negócios MT4 e o Excel. As bibliotecas fornecendo a geração de números pseudo-aleatórios (PRNG) [1], funções estatísticas [2] e o módulo para transmitir dados do MT4 para o Excel [3] são adicionalmente usadas.

Assume-se que qualquer atividade de negociação (TA) tem algum grau de incerteza. Em outras palavras, parâmetros de TA são conhecidos com algum grau de precisão e nunca podem ser definidos com precisão. A estratégia de "apostas aleatórias" pode servir como um bom exemplo, e talvez, o mais simples de tal atividade TA. Usando essa estratégia um investidor aleatoriamente (por exemplo, jogando uma moeda) aposta se a taxa de uma moeda vai aumentar ou diminuir para um determinado número de pontos relativo um ao outro. Mais provavelmente a geração das taxas de moedas não é relacionada aos resultados para jogar uma moeda. Portanto, temos um TA, no qual os resultados de negócios não são relacionados um ao outro (os de Bernoulli). Além disso, somos incapazes de definir o resultado da próxima jogada da moeda, bem como prever se ela corresponde à direção do dinheiro no futuro. Somente sabemos que a correspondência ocorrerá aproximadamente em 50 casos de 100 no caso de um grande número de tentativas. Muitos investidores acreditam que sua negociação é diferente disso. Talvez, estejam certos, mas primeiro vamos observar esse caso em particular. Então, analisamos o comportamento e desempenho do sistema, no qual mais de 50 casos dentre 100 podem ser previstos.

Estruturalmente, o artigo é disposto de modo que os parâmetros mais interessantes de MM sejam analisados primeiro usando exemplos "teóricos". Depois, vamos tentar modelar o comportamento do MM com dados similares aos das condições de negociação Forex reais. Deve ser notado que nenhum TS em particular será analisado. Assume-se que independente do TS usado, ele meramente nos fornece dados em ganhos e perdas com uma probabilidade especificada, bem como valores predefinidos de ganhos e perdas. Problemas relacionados à definição de independência (Bernoulli) dos resultados dos negócios atuais e a avaliação de TS estacionário no momento não são considerados aqui.

Como já mencionado, a simulação será usada. A essência da simulação é o fato de que o resultado da próxima aposta (ganhar ou perder) é definido com base na geração de números pseudo-aleatórios com parâmetros predefinidos. O tamanho da aposta é definido pela estratégia MM selecionada. No caso de uma perda, a aposta colocada é subtraída dos fundos atuais do investidor. No caso de sucesso, os fundos são aumentados. Um número específico de negócios é simulado e os resultados totais são calculados posteriormente. Então o processo é repetido múltiplas vezes (de algumas centenas para várias centenas de milhares), após isso sendo feita uma média dos resultados da maneira mais adequada.

Alguns termos básicos e abreviações

O conceito de Riqueza Relativa Final (TWR ) deve ser mencionado primeiro. Ele representa o lucro total das séries de transações como um multiplicador do capital inicial. Em outras palavras, se dividirmos os fundos finais pelos iniciais, obteremos o TWR. Por exemplo, se o lucro compreende 12%, TWR=1,12. Se a perda compreende 18%, TWR=0.82. É possível comparar os resultados de vários TAs independente do valor absoluto dos fundos iniciais. O termo TWR é usado por analogia com [4], [5] e [6].

A próxima coisa mais importante é o conceito de "ganhar". Qualquer resultado é considerado um ganho se seu valor exceder o inicial. Em outras palavras, ganhar é um caso onde TWR>1. Conformemente, a perda é um resultado que não satisfaz a condição mencionada, isso é, TWR<=1. Assim, o caso onde os fundos finais são iguais aos fundos iniciais, TWR=1, são também considerados perdas. Mas nesse caso será considerado separadamente se necessário. Adicionalmente, há o conceito de "perda" indicando a perda de fundos, tanto com um resultado de uma única transação ou série de negócios, seguido pela incapacidade de continuar a atividade de negociação. Por exemplo, pode ser a perda de todos os fundos (TWR<=0) ou ter fundos que sejam menores do que um determinado mínimo (depósito de segurança).

Agora, vamos considerar sinais convencionais usados no artigo. A probabilidade de ganhos são marcadas com o símbolo p. Sua dimensão normal é em frações unitárias. O mesmo se aplica a probabilidade de perda, q=1- p. Número total de negócios - N, número de negócios rentáveis - V, enquanto o número de negócios com perdas - L. O tamanho dos negócios ganhos em termos absolutos é definido como a, enquanto o tamanho dos com perdas é b, a razão de lucro/perda é k= a/b. Caso falemos sobre os tamanhos dos negócios com ganhos/perdas relativo ao tamanho dos fundos, os símbolos são a% e b% respectivamente. Razão de a%para b% é k. O tamanho da aposta relativo aos fundos é indicado com f.

A probabilidade dos eventos recebidos durante os cálculos é indicada como Prob. Outros sinais serão também implementados se necessário.

Além disso, não há distinção entre os conceitos de "aposta" e "negócio" nesse artigo. Eles se referem à mesma coisa - uma única operação de negociação (SТО). Uma série de tais STOs é chamada de um jogo ou negociação, dependendo do contexto. Embora muitos investidores não gostem, a palavra jogo caracteriza adequadamente as incertezas que ocorrem durante as atividades das negociações.

Passado histórico

As propriedades de um TS com base na jogada de uma moeda foram pesquisadas por muito e muito tempo. Em sua forma mais simples, era um jogo chamado "cara ou coroa". O jogo é jogado por dois jogadores que inicialmente tem alguns fundos. Uma moeda é jogada e o jogador que escolher o lado que cair para cima recebe alguma parte dos fundos do outro jogador. Inversamente, o jogador tem que dar uma parte dos seus fundos. É o clássico problema de "ruína de apostador" para matemáticos. É estudado muito bem e os resultados dependendo dos parâmetros iniciais são bem conhecidos.

Resultados fundamentais para resolver o problema da "ruína do apostador jogando contra um oponente muito rico" são mais importantes para os investidores. Um oponente muito rico é representado por um centro de distribuição (DC) aqui. Se você tiver certeza de que não está agindo contra o DC, você pode considerar todos os outros participantes do Forex como sendo oponentes muito ricos.

Qual é o problema nesse tipo de jogo? Não discutiremos os casos do jogo infinito. Ninguém pode jogar infinitamente e os possíveis resultados são deploráveis de qualquer forma. Vamos considerar que o jogo é finito e consiste de N negócios. Suponha que a probabilidade do seu palpite certo seja de p>0,50, enquanto os valores de ambas ganhas e perdas sejam iguais ao outro, a=b. Vamos também supor que você quer que seus ganhos por N negócios sejam os maiores possíveis.

A melhor estratégia para alcançar o lucro máximo nesse jogo é colocar a aposta máxima possível, isso é, todos os fundos que você tem. Entretanto, já foi matematicamente provado que neste caso a probabilidade de ruína pode ser calculada pela equação 1-(p^N) e que a possibilidade depende de N. [7][8] Quanto maior o valor de N, isto é, o número de apostas, maior a probabilidade de ruína. Consequentemente, a ruína é o caso menos provável de N=1 caso o jogo seja obrigatório. Se o jogo não for obrigatório, a estratégia com mais sucesso não é jogar, já que a probabilidade de ruína é zero.

Nota: há uma má interpretação muito comum. Muitos acreditam que se as probabilidades de um jogo são iguais então seus ganhos possíveis são aproximados de zero. Esse seria o caso se jogassem contra um oponente com um volume similar de fundos.

Nas negociações reais, isso significa que mesmo que você consiga ganhar em 2 casos de 3 colocando todos os seus fundos na aposta todas as vezes, a seguinte coisa irá acontecer. A probabilidade de ruína durante a primeira negociação é igual a 1/3. Esse é um bom resultado mas será igual a ~0.98 já por volta da décima aposta.

Assim, a exigência para maximizar os lucros leva a uma situação absurda onde todos os fundos devem ser colocados em risco, mas somente uma vez. Isso não é certamente uma solução desejável pra você, já que você espera que quanto mais apostas faça, maior seja o lucro final em seu jogo.

É possível aumentar a duração de tal jogo e reduzir a probabilidade de ruína eliminando a exigência de lucro máximo. Em outras palavras, somente parte dos fundos devem ser usadas ao fazer apostas. Se essa parte for bem pequena, o jogo pode durar então por muito tempo. Isso também já foi provado matematicamente. [7][8] Entretanto, nesse caso, o ganho final também será pequeno. Assim, apostas altas aumentam os lucros em potencial, enquanto também aumentam os riscos de perdas. Baixas apostas reduzem os riscos diminuindo o lucro em potencial. Assim há uma pergunta sobre qual parte dos fundos é a mais razoável para ser usada no jogo (de um determinado ponto de vista).

Essas são as linhas gerais de raciocínio e suposições. Essa questão já foi amplamente estudada. O campo chamado "Gerenciamento de dinheiro" apareceu para solucionar isso. Existem vários métodos de MM fornecendo várias oportunidades para satisfazer as exigências da probabilidade de ruína e valor dos lucros. Não examinaremos todos os métodos porque o artigo tem limitações, portanto iremos focar em dois deles: o método baseado na definição de apostas de tamanho fixo e o método de colocar uma fração fixa dos fundos em jogo.

Um pouco de teoria

Se omitirmos toda a sabedoria matemática, o momento chave em MM é uma pergunta que pode ser formulada da seguinte forma: qual é a probabilidade de que um evento (por exemplo, crescimento de fundos ou ruína) após um determinado período de tempo (por exemplo, número de negociações). De fato, é uma questão que abrange perspectivas, portanto, o tempo pode ser fixo e somente dois parâmetros podem ser considerados - a probabilidade do evento e o evento em si.

Se considerarmos o "cara ou coroa" em sua forma mais simples, então podemos calcular algumas coisas bem facilmente, sabendo o número de N apostas. Por exemplo, a expectativa matemática (МО) de receita por uma aposta (1) ou a receita esperada por uma série de apostas (2). Note que МО é definida relativa aos fundos iniciais aqui. Significa que teremos expectativas positivas no caso de МО>0 e se МО<0, espera-se que cada aposta gere uma perda na média.

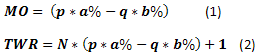
Para o caso mencionado em [9]: p=0,45, q=0,55, a%=0,08, b%=0,05, N=20, os resultados são MO=0,0085, TWR=1,170. Esse caso é interessante em que a probabilidade de ganho p<0,5, МО permanece positiva em uma aposta e consequentemente um lucro de ~17% nos fundos iniciais é esperado.

Aviso: outro método MM é examinado em [9]. Portanto, os resultados serão diferentes independente dos dados de entrada similares.

Entretanto, tais expectativas são parecidas com a média geral. Isso não diz nada sobre a probabilidade de ocorrência de alguns dos resultados dependendo do número de apostas ganhas, complicando a avaliação dos riscos. Portanto, vamos introduzir duas equações adicionais: para calcular o lucro para uma determinada quantidade de apostas (3) e calcular a probabilidade de ocorrência de uma determinada quantidade de apostas ganhadoras em uma série (4):

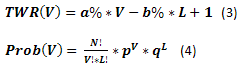
Agora somente temos que calcular os valores para todos V= 0,1,...,N, L=N-V e criar o gráfico da dependência de Prob(V) a partir de TWR(V). Para o caso descrito anteriormente, o gráfico se parece com o seguinte: Note que o gráfico mostra os eixos Prob e TWR sem o índice (V). Isso foi feito somente para tornar o gráfico menos complicado.

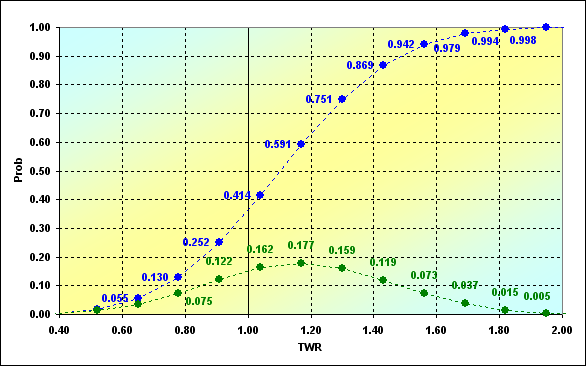
Fig. 1

Os resultados dos nossos cálculos usando equações (3) e (4) são mostrados como pontos verdes. O gráfico pode ser interpretado como a seguir. Por exemplo, a probabilidade de ocorrência dos resultados das séries de apostas, na qual TWR=1,04, é 0,162. Com mais frequência, com a probabilidade de 0,177, TWR=1,170 e assim por diante. Os pontos azuis representam os mesmos dados na forma de probabilidade cumulativa. Assim, a probabilidade de perda (isso é, algumas rodadas do jogo têm TWR<=1,00) para nossa entrada de dados compreende 0,252. Valores extremos não são exibidos no gráfico O caso da ruína (TWR=0,00) foi Prob=6,4E-06. Ganho máximo TWR=2,60, - Prob=1,2E-07. Essas são probabilidades muito pequenas. Entretanto, sua existência cria ainda outra questão importante.

Vamos tentar demonstrar isso com o seguinte exemplo. Cálculos foram realizados para as seguintes condições: p=0,45, q=0,55, a%=0,05, b%=0,05, N=50. Os resultados são exibidos no gráfico.

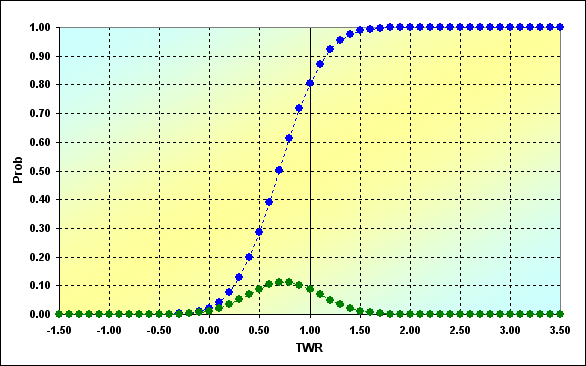
Fig. 2

Como podemos ver, TWR pega os valores de -1,50 até 3,50. TWR=-1,50 é possível somente no caso em que o jogo foi realizado com a quantidade de fundos menor do que 0,0. Assim, as equações que usamos não consideram o fato de que os fundos foram gastos em um dos negócios intermediários e o jogo não poderia ter continuado. Portanto, a nova tarefa surgiu, chamada de "questão de absorção limítrofe". Essa questão considera que há algum limite para os fundos existentes. Quando esse limite é alcançado o jogo para. Em sua forma mais simples, assume-se que o limite é =0. Entretanto, estamos mais interessados no caso em que ele pode ter valores arbitrários. Alguns aspectos da solução analítica dessa questão são revelados em [7].

Faixa de oportunidades

Vamos tentar resolver esse problema numericamente primeiro usando cálculos iterativos, e segundo, usando modelagem de situações com base em métodos estocásticos (método de Monte Carlo). Primeiro, vamos examinar a imagem e tentar resolver o problema.

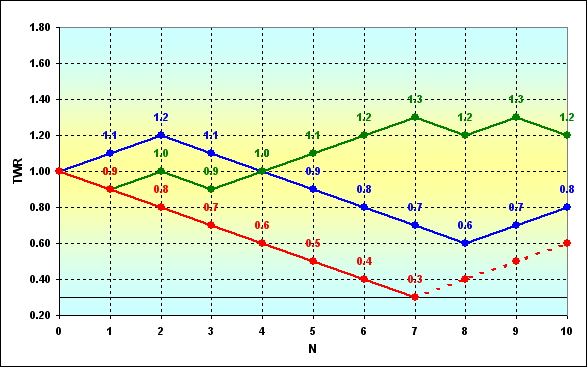
Fig. 3

A imagem esquematicamente exibe possíveis mudanças de trajetória dos fundos durante o jogo. Três casos são exibidos, embora existam muitos outros deles, naturalmente. Assume-se que os jogadores com fundos que excedam, por exemplo, 0,.3 (exigências colaterais) sejam permitidos de participar no jogo. Suponha que o jogo levou o curso vermelho e se tornou impossível continuar a jogar. A absorção limítrofe da trajetória ocorreu, significando a ruína completa. O jogador sai do jogo, diferente de jogos que tomaram os cursos verde ou azul. Assim, precisamos definir a probabilidade de ruína nos passos anteriores para poder defini-la em outro passo definitivo.

A técnica mais simples, intuitiva e mais antiga que pode ser usada para executar tal cálculo é o triângulo de Pascal. De fato, esse é um procedimento recursivo no qual o próximo valor é calculado usando os anteriores. O triângulo levemente modificado é exibido abaixo.

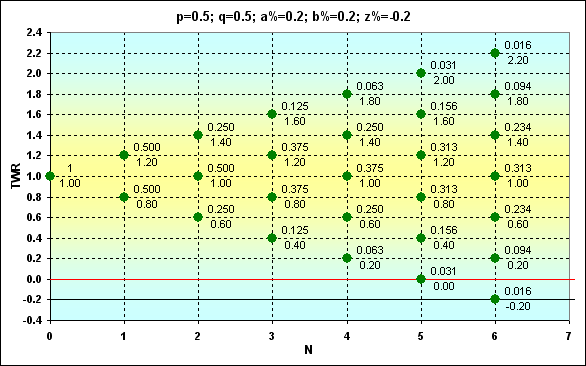
Fig. 4

Pontos verdes indicam locais possíveis no gráfico TWR em que a trajetória pode passar. Nesse caso, TWR pode ser calculado usando a equação (3). Os pontos têm valores Prob (numerador) e valores TWR (denominador). O símbolo z% aponta o valor limítrofe no qual a absorção ocorre (linha preta). A linha horizontal vermelha é desenhada através do valor z%+b%.

O que o local dos pontos relativos à linha vermelha representa? Se o ponto está localizado mais alto, a próxima rodada é possível. Quando a linha vermelha cruza o ponto, essa é a última chance para mais um passo. Caso tenha sucesso, o jogo continua, de outro modo, ocorre a absorção. Os pontos entre as linhas vermelha e preta são alcançáveis, mas o próximo passo fora deles é impossível, já que os fundos serão insuficientes para a próxima aposta. Em outras palavras, essa não é uma ruína completa mas o jogo não pode ser continuado.

Nota: Claro, isso não é possível no caso de apostas integrais, como quando usando moedas, mas se a aposta é igual a, digamos, 0,15 dos fundos, a imagem geral é exatamente como a descrita acima.

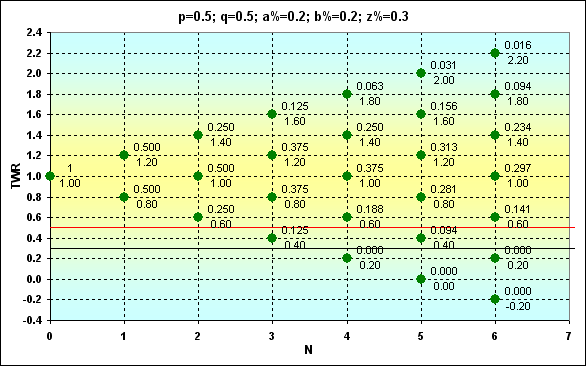
Fig. 5

Aqui está outra imagem contendo os resultados de cálculos no caso de condições limítrofes diferentes. Se compararmos ela com a anterior, devemos ser capazes de notar a diferença.

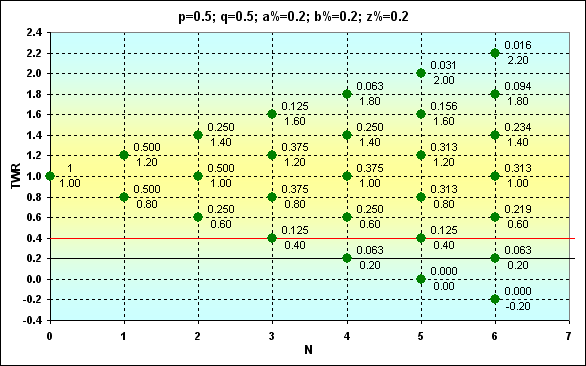
Fig. 6

Agora, com tais dados, somos capazes de saber a probabilidade de qualquer evento. Por exemplo, o que Prob é de TWR=1,4 no caso de N=6 para a fig. 6? A resposta é is 0,234. Ou o que Prob é de TWR>1 no caso deN=6? Valores Prob correspondentes devem ser somados. A resposta é is 0,344. Ou o que Prob é de TWR=1,1 no caso deN=6? A resposta é is 0. E assim por diante.

O último exemplo dessa série com valores de entrada "desfigurados": p=2/3, q=1/3, a%=0,1, b%=0,2, z%=0,2 é mostrado para demonstrar como Prob e TWR mudam neste caso. Como podemos ver, a probabilidade de ganhar excede a de perder por duas vezes. Entretanto, a quantia ganha é metade do tamanho de uma perda.

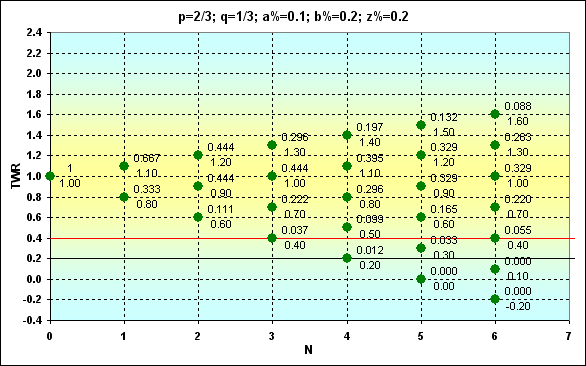
Fig. 7

Se TWR>1, Prob=0,351. Esse valor Prob está bem perto do caso mostrado na figura 6. Mas está claro que valores TWR que podem ser alcançados em um número comparável de apostas são muito menores.

Outra coisa importante que não falamos ainda é com relação ao parâmetro f indicando a ação de fundos envolvida na aposta. De fato, essa é a ação dos fundos que são usados no negócio, isso é b%. No jogo clássico de "cara ou coroa" é possível perder somente um número contável de "moedas". Portanto, tal expressão como 1/f exibe o número de perdas consecutivas que leva à ruína. O parâmetro 1/f pode ser não integral em nosso caso. Ao mesmo tempo, o número de apostas não pode ser não integral, considerando a não divisibilidade de apostas. Isso significa que alguma parte dos fundos podem ainda sobrar quando o jogo não puder ser continuado (e essa parte será menor que b%). Em outras palavras, essa parte é absolutamente livre de riscos, já que não pode ser perdida. Nesse sentido, a quantidade real de fundos participando no jogo é menor por este valor. Assim, o parâmetro z% real é maior por este valor (veja a figura 5). Nesse caso, se z%>0, então f tende a exceder b%. Considerando tudo isso, o f real pode ser calculado da seguinte forma:

onde o símbolo int significa truncagem. Para o exemplo exibido na figura 5, b%=1/5, mas na verdade f=1/3.

Duração de oportunidades

Vamos considerar nossos resultados como uma correspondência entre Prob e TWR. Muitos conjuntos diferentes de dados de entrada foram selecionados como um exemplo. Todas as séries possuem o mesmo tamanho - N=15.

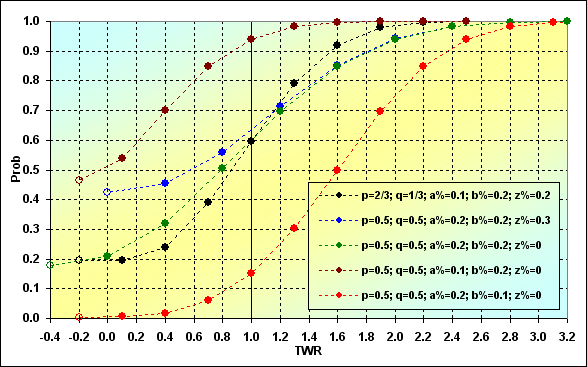
Fig. 8

Abaixo estão algumas explicações com relação a o que e como é exibida no gráfico. Cada curva começa com um ponto "vazio" (se olharmos da esquerda para a direita). Esses são pontos condicionais (em alguns casos), que podem não existir de fato. Independente, eles são aplicados indicando a probabilidade da absorção ocorrer em algumas das etapas intermediárias. Em outras palavras, isso é a probabilidade da trajetória não alcançar a próxima etapa. O próximo ponto no gráfico representa dados atuais sobre a probabilidade da absorção ocorrendo na última etapa, considerando todas as ruínas anteriores (com algumas exceções que não são importantes aqui).

A próxima imagem demonstra como a probabilidade de ruína muda dependendo do comprimento N das séries. A mesma entrada de dados para a figura 8 foi usada para o exemplo. Como veremos posteriormente, os resultados são significativamente diferentes um do outro.

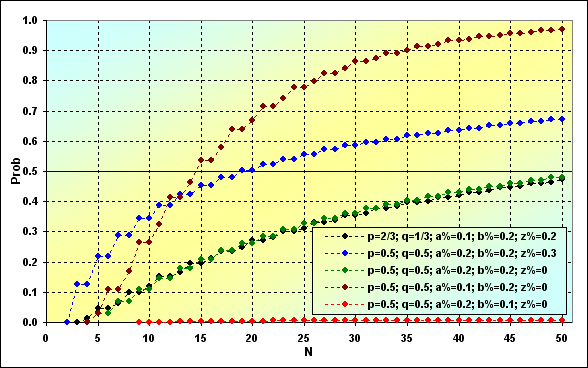
Fig. 9

A coisa mais importante é que se o comprimento das séries aumenta, o mesmo ocorre com a probabilidade de ruína. Essa questão chave não pode ser eliminada no caso de um jogo de absorção limítrofe. Entretanto, nem tudo é tão ruim quanto parece ser à primeira vista. A probabilidade de ruína pode se tornar muito pequena, dependendo dos parâmetros TS (veja a linha vermelha). Se os parâmetros TS não tiverem muito êxito, a ruína ocorre rapidamente (veja a linha marrom).

Outra coisa importante é a probabilidade de ganhos totais. Já consideramos o caso de TWR<(z%+b%), agora é hora de definir o comportamento de probabilidade TWR>1 dependendo de N.

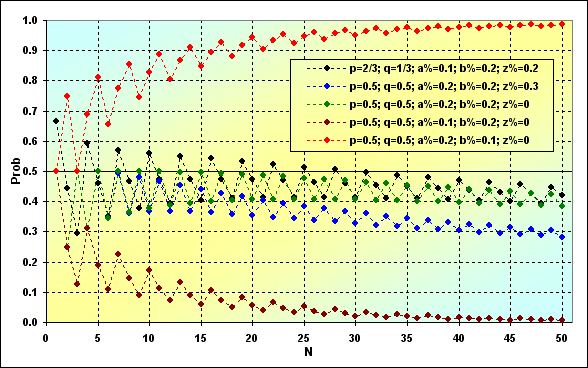
Fig. 10

No caso mostrado em cores verde e preta, lidamos com estratégias neutras, ou seja, as que tenham MO=0 e temos todas as razões para esperar que a probabilidade de ganho seja de cerca de 0.5. Entretanto, não é esse o caso. E isso tem a ver com a absorção limítrofe.

É assim que a probabilidade de um possível TWR ocorrer em determinadas observações de etapas. Neste caso, N=50, que é similar ao valor da figura 10.

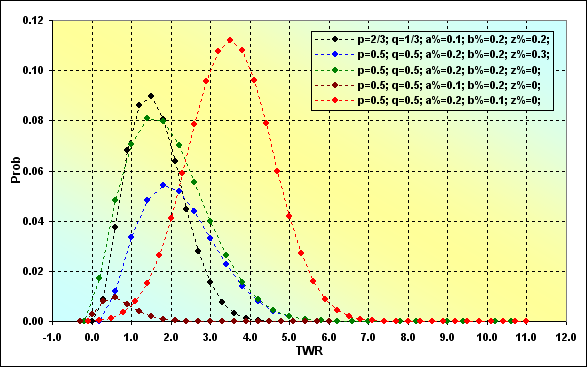
Fig. 11

Essas são curvas ordinárias de distribuição. Sua diferença das curvas de distribuição convencionais é que elas são assimétricas em relação ao seu valor máximo, bem como seu valor mínimo e máximo de TWR. Além disso, algumas curvas são notavelmente mais retorcidas e lembram curvas lognormais. Outro momento interessante é que se compararmos as figuras 10 e 11 veremos o seguinte. Enquanto a maioria das distribuições na figura 11 possuem o valor mais provável de TWR ser maior que 1, a probabilidade do valor de TWR ser maior que 1 é menor do que 0,5. Além do mais, para casos com MO=0 (linhas pretas e verdes), o TWR mais provável também não é igual a 1, como poderia ser esperado. Não há paradoxo nisso.

Agora é hora de terminar nossa breve revisão de alguns aspectos da "tarefa de absorção limítrofe". A próxima coisa que devemos fazer é realizar uma simulação estocástica e comparar os resultados com os anteriormente obtidos para avaliar a exatidão do raciocínio e precisão da simulação.

Simulação

Em geral, o seguinte algoritmo de simulação é usado. A quantidade de fundos é verificada antes de cada jogada da "moeda". Se os fundos forem insuficientes para continuar o jogo, ele para. Se o jogo puder continuar, PRNG é usado para definir se a aposta ganhou ou perdeu. Os fundos então aumentam ou diminuem conforme o resultado. O algoritmo permanece o mesmo até o fim do jogo. A grande quantidade de rodadas do jogo são realizadas e os resultados são medidos. É tudo muito simples. O único problema de métodos estocásticos está em sua precisão. Ao usar esse método, a solução da precisão da tarefa é impossível e isso foi provado matematicamente (veja o paradoxo de deMoivre). Portanto, devemos definir até onde os resultados são consistentes com outros antes de usar esse modelo em cálculos posteriores.

Vamos comparar os dois casos de solução para os seguintes parâmetros: p=0,5, q=0,5, a%=0,2, b%=0,1, z%=0,0. Abaixo estão duas figuras (12 e 13) exibindo a correspondência dos resultados.

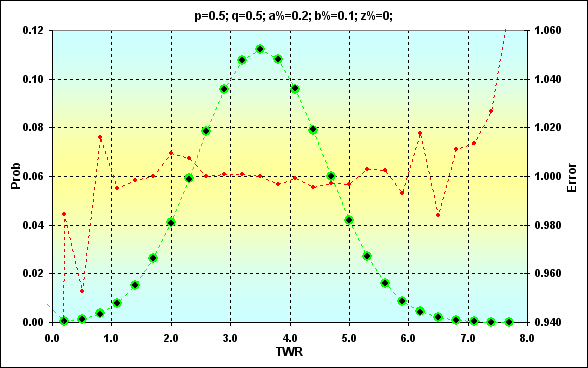
Fig. 12

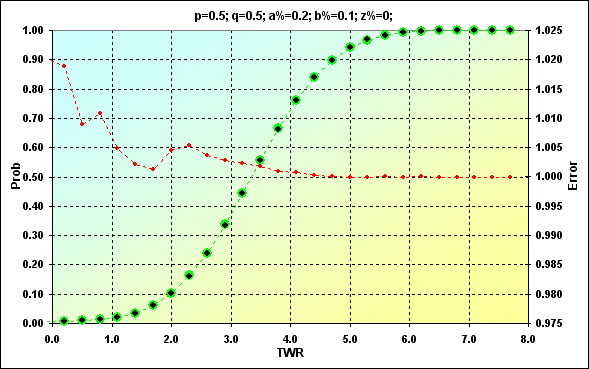
Fig. 13

Valores obtidos anteriormente são mostrados em verde. Pontos pretos mostram resultados da simulação. A cor vermelha representa o erro, a razão do valor esperado com o da simulação. A figura 12 mostra os valores enquanto a 13 é um total acumulado. A correspondência é muito boa. A taxa de erro no ponto médio dos valores é menor que 0,5%. Naturalmente, a taxa de erro é maior nas extremidades da faixa. Entretanto, não há nada com o que se preocupar. Devemos somente considerar isso no futuro. Além disso, estamos muito mais interessados na soma acumulada. A taxa de erro é muito menor ali (esse é um recurso das curvas cumulativas quando erros de valores diferentes cancelam um ao outro).

Outro recurso dos resultados da simulação é que é quase impossível receber a probabilidade de valores extremamente raros. No exemplo acima, o máximo TWR=11, enquanto Prob= 8,88E-16. Estes valores não poderiam ser obtidos na simulação.

Outro exemplo que demonstra o fato mencionado acima no caso de N=250: p=0,5, q=0,5, a%=0,1, b%=0,1, z%=0,0. Não são necessários mais comentários aqui.

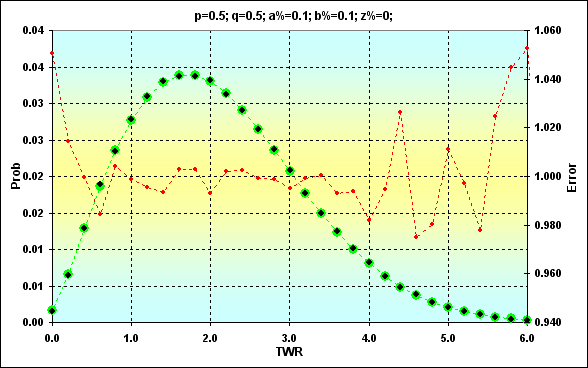
Fig. 14

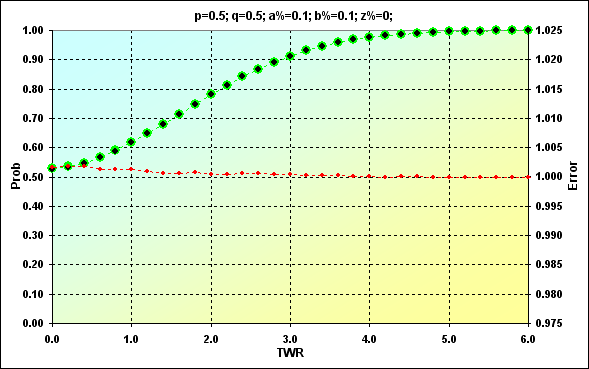
Fig. 15

Agora podemos usar esse modelo como uma base para resolver o problema mais complexo do que o que consideramos acima.

Operações de negociação

Antes de continuarmos nossa discussão, gostaria de focar nos conceitos e equações. Em um primeiro momento, as negociações reais são muito diferentes do jogo de "cara ou coroa" descrito acima - considerando que esse fato exige esforços adicionais durante a simulação. Portanto, é necessário esclarecer logo o que teremos que fazer no futuro. Naturalmente, a maioria dos leitores tem suas próprias ideias sobre isso. Abaixo estão alguns conceitos e anotações úteis.

Nota: para simplificar, somente transações com pares de "cotações diretas" como EURUSD e GBPUSD, serão examinados. Pares de "cotação indireta" e taxas cruzadas são calculadas de maneira diferente. Para os pares de cotação indireta, o preço do ponto muda de acordo com a cotação atual. Para taxas cruzadas, a cotação atual da moeda base (primeira) para USD é considerada. Além disso, os conceitos de ASK (venda) e BID (compra) não são usados aqui.

Os fundos usados nas negociações serão chamados de Deposit (Depósito). Temos direito de comprar e vender contratos com determinado LotSize usando Leverage. O contrato pode ser fracionado, então precisamos do conceito de Lots como um parâmetro indicando o tamanho do contrato aplicado. O tamanho real do lote usado na moeda base será chamado de LotPrice adequadamente. Devemos pagar Margin (Margem) para o direito de compra e venda. Se expressarmos Margin como uma parte de Deposit, recebemos o parâmetro Margin%. Também usaremos StopOut indicando a parte mínima de Margin. Alcançar ela leva ao fechamento do negócio atual e as negociações são paradas de maneira forçada. Assim, existem duas situações diferentes quando negociações posteriores são possíveis, (na taxa desejada de LotPrice), ou seja, no caso de ruína. Outro parâmetro Sigma foi adicionalmente incluso. Essa é a razão dos fundos usados em operações de negócios considerando o crédito para capital próprio. A razão dos fundos usados para o capital atual, ou seja, o análogo de um nivelamento, embora seja aplicado em todo Deposit ao invés de LotPrice.

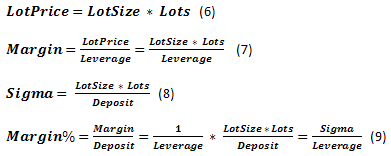
Um dos conceitos básicos que caracterizam o processo de negociação é Quote - a cotação atual da moeda. A mudança de taxa mínima é Tick. O tamanho da mudança mínima da taxa do símbolo é TickPrice considerado como parte de Deposit - Tick%.

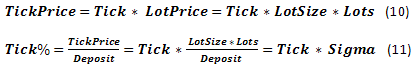
Além do mais, temos alguns outros parâmetros conectados com a mudança de taxa: o chamado TP (Obter Lucro, ou TakeProfit) e SL (Parar Perdas, ou StopLoss) - mudança de taxa, na qual o lucro ou perda é fixo. Se expressarmos esses parâmetros na moeda, eles serão chamados de TPprice e SLprice. Os expressos como parte do Deposit serão chamados de TP% e SL%. E também, existem várias comissões dos distribuidores, incluindo Spread, Swap etc. Não iremos examinar toda a diversidade destes parâmetros, focando somente em Spread, que é tradicionalmente exibido em pontos de mudança de taxa. Se necessário, dados de Swap podem ser considerados facilmente se já forem também exibidos em pontos. Se Swap for apresentado como uma taxa de juro real em fundos emprestados usados com a ajuda de um nivelamento, a situação se torna um pouco mais complicada.

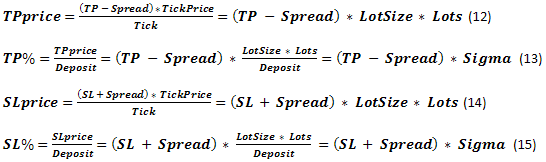
Vamos comparar os parâmetros obtidos com os usados no problema "absorção limítrofe". SL% claramente corresponde a b%, enquanto TP% = a%. Os fundos iniciais foram apresentados como TWR=1. O caso atual é similar, já que nossos cálculos são baseados nos parâmetros exibidos em frações de uma unidade. O valor limítrofe de z%+b% pode ser convencionalmente considerado como Margin%. Há alguma diferença entre estes conceitos, mas não é tão crítico caso não consideremos a existência de StopOut. Parece que as tarefas são similares em uma primeira vista. Veremos isso posteriormente.

Se examinarmos de perto as equações (9, 11, 13, 15), veremos o parâmetro Sigma em todas elas. Como já mencionado, esse é um equivalente de um nivelamento usado em todas as equações críticas. Leverage pode diretamente afetar somente Margin%.

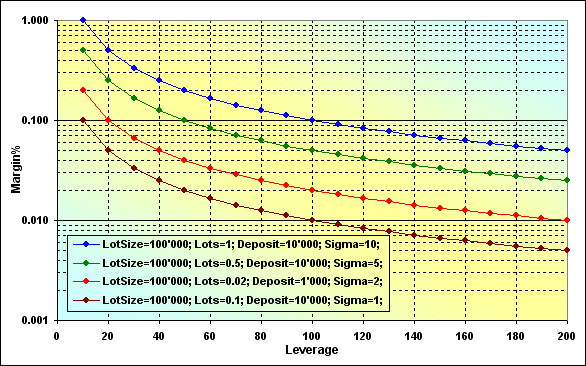
Fig. 16

A exatidão dos cálculos pode ser verificada pelo seguinte exemplo. Suponha que se Leverage=100, LotSize=100000, Lots=0,1, Deposit=10000, o tamanho da margem é 100. Se olharmos no gráfico adequado (marrom), veremos que Margin%=0,01. No caso de Deposit=10000, receberemos 100.

Duas características podem ser observadas nos gráficos: primeiro, o valor de Sigma maior, e Margin% maior, em outras palavras, menos fundos livres para serem usados nas negociações. E segundo, diminuir o valor de Leverage também aumenta Margin%. Vamos examinar a figura 9 onde casos similares são vistos (linhas azul e verde). Esses casos somente se diferem no valor z%. Pode ser visto que o aumento do valor limítrofe também leva a um aumento da probabilidade de ruína sendo as restantes condições iguais.

Já que não há relação direta entre SL% e Leverage, vamos examinar como esse parâmetro depende de Sigma e (SL+Spread).

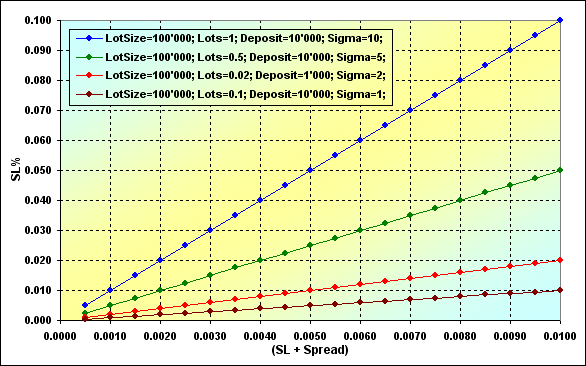
Fig. 17

O aumento do parâmetro Sigma leva a um aumento de SL%. Assim, a ruína se torna muito mais provável, novamente. Essa dependência é linear. Na verdade é que para poder diminuir SL%, precisamos ou diminuir (SL+Spread) ou Lots, já que todos os outros valores inclusos em Sigma provavelmente não podem ser alterados.

Então, terminamos com as equações. Agora vamos descrever brevemente como a simulação foi conduzida. O processo é quase indistinguível do anterior. A possibilidade de negociação foi verificada, a operação de compra foi feita nas condições de mercado atuais, a taxa foi determinada com a ajuda de PRNG, a operação de venda foi realizada e o nível de fundos atual foi calculado. Tudo isso foi repetido múltiplas vezes no ciclo. Os resultados das negociações foram eventualmente definidos. Nenhum formulário analítico específico foi usado, toda a simulação foi feita "como está". Tick e outros conceitos relacionados, bem como Swap não foram usados, já que não foram necessários.

Para poder avaliar os resultados de simulação, usamos um exemplo com os seguintes parâmetros básicos: Deposit=1000, Leverage=100, LotSize=100000, Lots=0,1, TP=0,0040, SL=0,0040, Spread=0,0002, p=0,5, N=250. O valor do comprimento das séries é aproximadamente igual ao número de dias trabalhados por ano, Assim, se assumimos que uma negociação foi realizada por dia (negócios no mesmo dia, portanto, Swap não é usado), os resultados serão anualizados. Após aplicar as equações (9, 13, 15), iremos receber os resultados a seguir: TP%=0,038=a%, SL%=0,042=b%, Margin%=0,1 (assim, z%=0,058). Vamos fazer uma simulação estocástica e cálculos similares aos exibidos na figura 4.

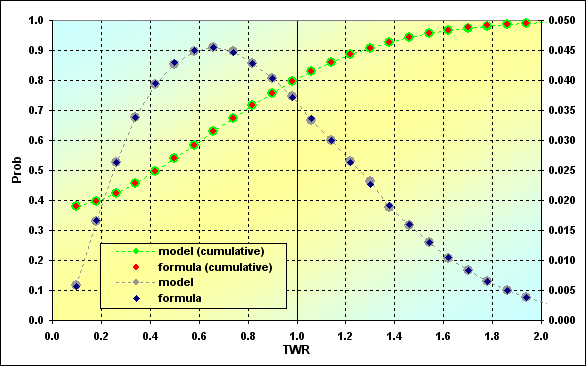
Fig. 18

Os cálculos baseados na simulação e nas equações são comparados aqui. Como podemos ver, os resultados de vários cálculos possuem uma boa correspondência. Essa é outra razão para dizer que o processo de negociação não é muito diferente do clássico jogo de "cara ou coroa" quando lidamos com o problema de "absorção limítrofe".

Abaixo estão alguns breves comentários sobre o gráfico. O gráfico mais à esquerda e o menor ponto da linha verde e vermelha exibem a probabilidade de ruína. Em nosso caso, ela é TWR<= Margin% - 0,375. A probabilidade de perda é quando TWR<=1, - 0,795, portanto, a probabilidade de ganho é de 0,205.

ММ - Tamanho fixo (FixSize)

A ideia principal desse método MM é de que uma parte fixa dos fundos iniciais são usados a cada vez apesar de qualquer circunstância. De fato, recursos convencionais de gerenciamento de tamanho de lote fornecidos aos investidores pelas agências distribuidoras diretamente corresponde a esse método. Além do mais, esse método é implementado no jogo de "cara ou coroa". Já que cobrimos os recursos básicos desse método antes, vamos continuar com a questão de parâmetros individuais afetando o sistema. Usaremos o nosso modelo para lidar com esse problema.

Como consideramos uma solução numérica mais do que uma analítica, a única maneira de avaliar o efeito das mudanças nos parâmetros de entrada é comparar os resultados dos cálculos. Consertaremos os dados, mudaremos alguns dos dados em alguma faixa e observaremos as mudanças.

Vamos voltar para o caso exibido na figura 16. Faça os cálculos com os seguintes parâmetros: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= { 0,0030, 0,0040, 0,0050, 0,0060}, Spread=0,0002, p=0,5, N=250, Leverage= { 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

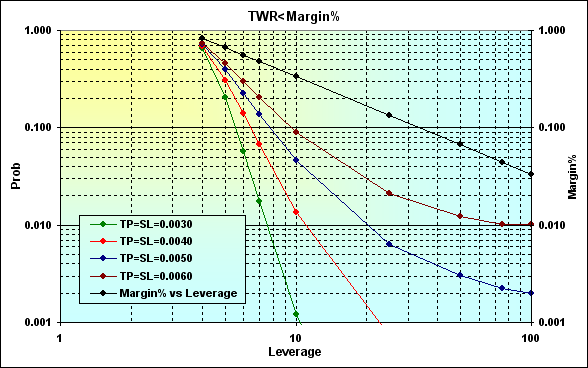
Fig. 19

Os resultados dos cálculos são mostrados em uma escala logarítmica para maior clareza. Na verdade, a diminuição de Leverage leva ao aumento de Margin% (linha preta) aumentando a probabilidade de ruína. A correlação entre a probabilidade de ruína e a de nivelamento não é linear e seu maior impacto pode ser sentido na área de pequenos valores de Leverage. O efeito negativo causado pela diminuição de Leverage pode ser reduzido diminuindo os níveis de TP e SL. Mas mesmo se o valor de Leverage for pequeno o suficiente (em nosso caso é 4) a probabilidade de ruína ainda é muito alta. Adicionalmente, há um outro recurso que é exibido na figura abaixo.

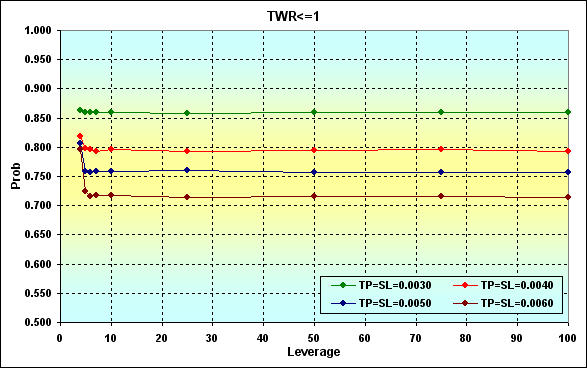
Fig. 20

A figura mostra como a probabilidade de perda muda dependendo da alteração do valor Leverage. Como podemos ver, a perda se torna mais provável quando TP e SL diminuem.

Se aumentarmos os fundos para, digamos, 10 000, a ruína se torna impossível no caso de N=250. Se compararmos as imagens 20 e 21, veremos que os resultados coincidem em uma área de Leverage>10.

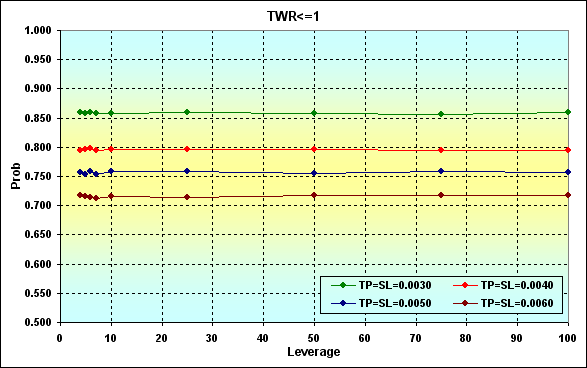
Fig. 21

Vamos considerar um exemplo no qual a probabilidade de ganho em um negócio é maior do que a probabilidade de perda, em outras palavras, p>0,50. Faça os cálculos com os seguintes parâmetros: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL={ 0,0030, 0,0040, 0,0050, 0,0060}, Spread=0,0002, p=0,52, N=250, Leverage={ 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

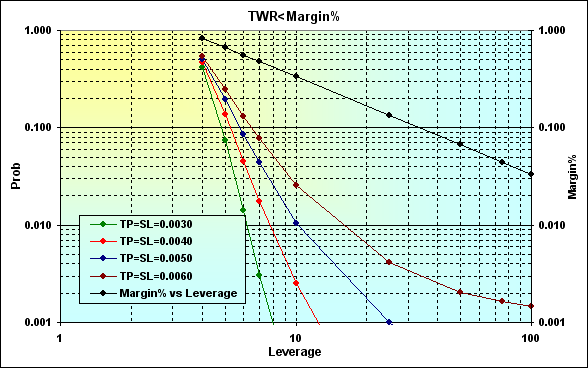
Fig. 22

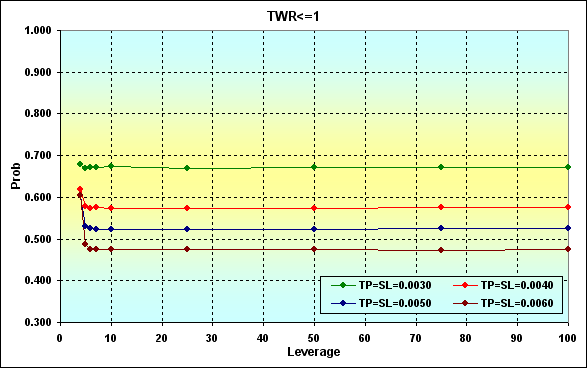
Fig. 23

Se compararmos os resultados dos cálculos exibidos na imagem 19, veremos que aumentando o ganho por um negócio diminui as probabilidades de ruína e perdas. Esse é um resultado natural e esperado.

O exemplo a seguir mostra como a probabilidade de ganho afeta a de perda em um negócio considerando o nível de TP, SL. Os parâmetros são como a seguir: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL={ 0,0020, 0,0030, 0,0040, 0,0050, 0,0060}, Spread=0,0002, p={ 0,48, 0,49, 0,50, 0,51, 0,52, 0,53, 0,54, 0,55, 0,56, 0,57}, N=250, Leverage=100.

Observação: O exemplo foi selecionado de modo que o valor da probabilidade da ruína seja irrelevante e pode ser descartado. A maior probabilidade de ruína para o pior caso compreende cerca de 0,04.

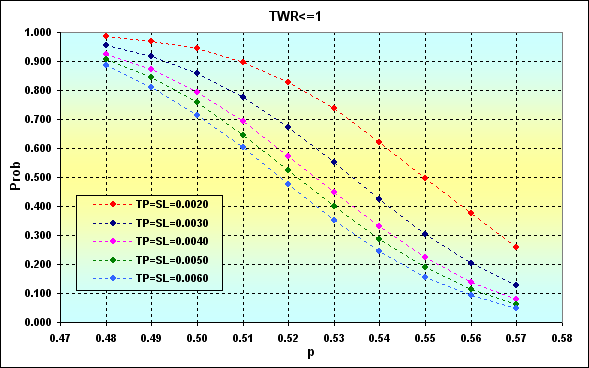
Fig. 24

A primeira coisa importante é que aumentar o p diminui a probabilidade de perda. A diminuição dos níveis de TP e SL tem o efeito oposto. Isso acontece devido ao valor fixo de Spread. Outra conclusão que pode ser feita destes resultados é de que negociar com baixos níveis em cada negociação é algo bem arriscado.

O exemplo abaixo demonstra a extensão à qual o valor de Spread afeta a probabilidade de perda. Parâmetros principais da simulação: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL={ 0,0020, 0,0030, 0,0040, 0,0050, 0,0060}, Spread={ 0,00000, 0,00005, 0,00010, 0,00015, 0,00020, 0,00025, 0,00030, 0,00035, 0,00040, 0,00045}, p=0,55, N=250, Leverage=100.

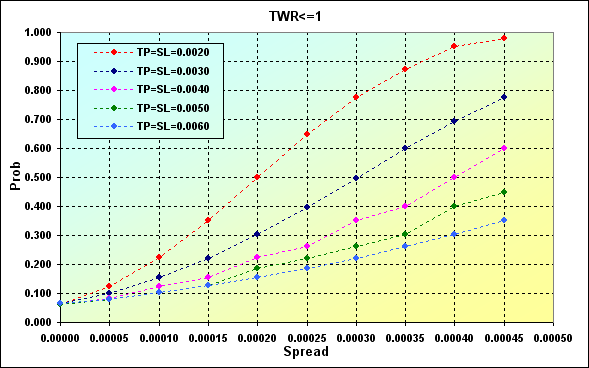
Fig. 25

A próxima imagem demonstra a correspondência entre a probabilidade de perda e MO do negócio calculado ao usar a equação (1) para os dados exibidos na figura 24. Ao invés de valores de a% e b%, os valores adequados TP% e SL% foram usados.

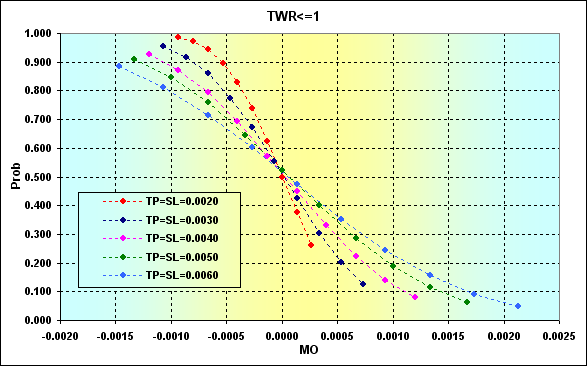
Fig. 26

Como podemos ver, o aumento em MO do negócio reduz a probabilidade de perda, embora não possa ser reduzido a zero. Significa que somente o MO positivo sozinho não garante a proteção contra perdas, bem como a ruína. Níveis maiores de TP e SL certamente reduzem a probabilidade de perda. Mas ao mesmo tempo (veja as imagens 19 e 22), que aumentam a probabilidade de ruína.

Em outras palavras, novamente retornamos a nossa declaração anterior que eu falei ao descrever o clássico jogo de "cara ou coroa". O aumento em apostas leva a um aumento de possíveis ganhos (e reduz a probabilidade de perda), enquanto torna a ruína mais provável. Infelizmente, não existe um método seguro matematicamente para selecionar um volume de negócios ao aplicar esse método MM. Podemos somente usar nossas preferências pessoais sobre qual nível de ruína ou perda é aceitável em cada caso.

Vamos considerar a questão para determinar a probabilidade de alcançar um determinado nível de TWR durante o jogo. Parâmetros principais da simulação: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL= 0,0030, Spread=0,0002, p={ 0,48, 0,49, 0,50, 0,51, 0,52}, N=250, Leverage=100.

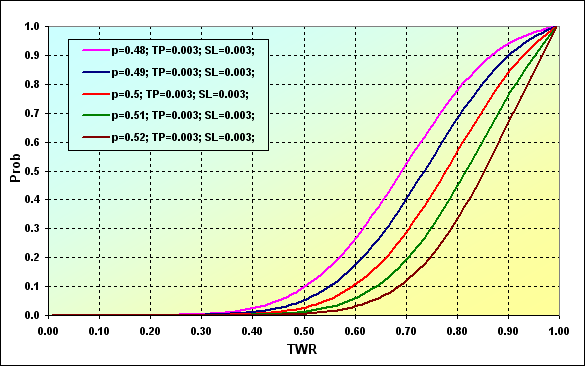
Fig. 27

Os dados gráficos podem ser interpretados da seguinte forma: A probabilidade do valor de TWR diminuir para ~0.,0 no caso de p=0,48 é ~0,93. Se f=0,52, o valor é ~0,68.

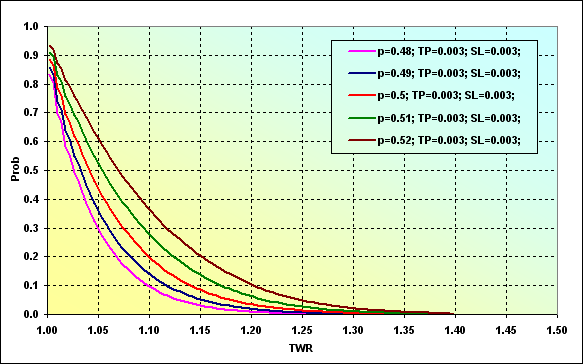
Fig. 28

Essa imagem exibe a probabilidade do nível de TWR aumentar até um determinado valor durante o jogo. Por exemplo, a probabilidade do valor de TWR alcançar ~1,10 em p=0,48 é ~0,09. No caso de p=0,52, o valor é ~0,37. É bem lógico que o aumento da probabilidade de ganho em um negócio leve ao aumento da probabilidade de alcançar um certo nível.

Agora, algumas palavras sobre Drawdown (perdas). O script [10] com poucas mudanças foi usado para avaliar esse parâmetro. Além disso, diferente do script original, o cálculo foi realizado considerando o Spread.

Parâmetros principais da simulação: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL=0,0030, Spread=0,0002, p={ 0,48, 0,49, 0,50, 0,51, 0,52}, N=250, Leverage=100.

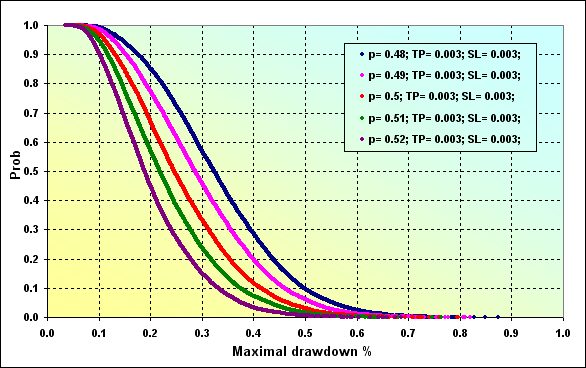
Fig. 29

No caso dos parâmetros iniciais similares à fig. 27, a probabilidade de Maximal Drawdown % ~0,20 em p=0.48 é ~0,85. No caso de p=0,52, o valor é ~0,47.

O último e final exemplo: Deposit=2000, LotSize=100000, Lots=0,1, TP=SL={ 0,0020, 0,0030, 0,0040, 0,0050, 0,0060}, Spread=0,0002, p=0,50, N=250, Leverage= 100.

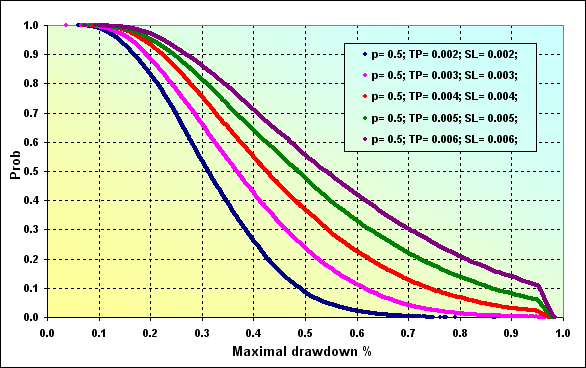
Fig. 30

Uma pequena consideração com a figura 30. O nível de Maximal Drawdown % é de 0,96 se igualando aproximadamente ao nível de Margin. É por isso que vemos uma quebra acentuada nas linhas nos gráficos. Como podemos ver a probabilidade de alcançar valores de Maximal Drawdown % maiores aumentou, quando comparado ao caso mostrado na figura 29 (linha vermelha).

Antes de terminar nossa discussão sobre alguns recursos do MM ter o tamanho fixo, vamos examinar mais duas distribuições de tais características de modelagem como Profit Factor e Expected Payoff.

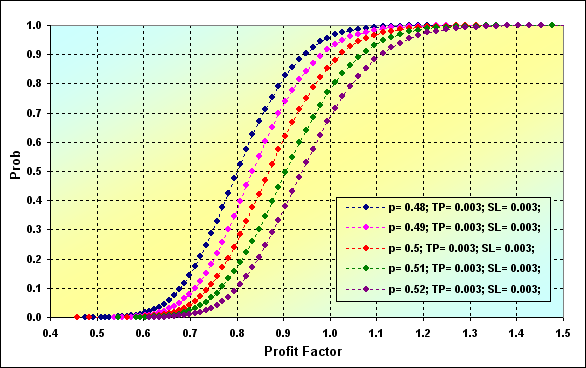
Fig. 31

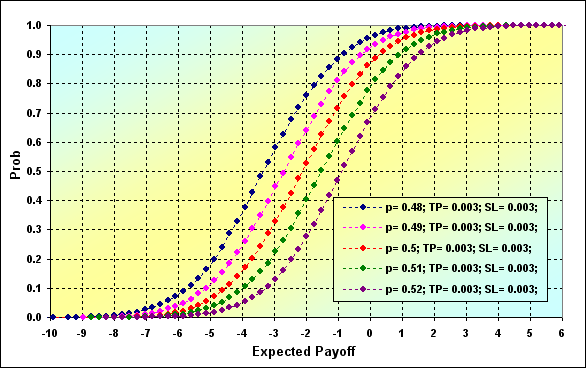
Fig. 32

Parâmetros principais da simulação para as figuras 31 e 32: Deposit=3000, LotSize=100000, Lots=0,1, TP=SL= 0,0030, Spread=0,0002, p={ 0,48, 0,49, 0,50, 0,51, 0,52}, N=250, Leverage=100.

ММ - Fração fixa (FixFrac)

Esse método compreende o MM com uma aposta como fração fixa dos fundos atuais. O tamanho da ação é determinado inicialmente, por exemplo, 10% para participação em negociações. A quantidade de fundos usados nas negociações é calculado com base na quantidade atual de fundos gerais posteriores, independente dos resultados das negociações. Assim, cada negociação com sucesso aumenta o volume da próxima e vice-versa. Algumas vezes, esse sistema é chamado de anti-martingale (embora, estritamente falando, está incorreto), Esse sistema presume o reinvestimento de possíveis lucros, oposto ao MM possuir um tamanho fixo.

Vantagens e desvantagens deste método MM já são bem conhecidas. Esse método fornece o crescimento rápido de fundos no caso de negócios com sucesso. Esse crescimento tem a forma de uma progressão geométrica ao contrário de uma aritmética no caso do método com tamanho fixo. Teoricamente, esse método evita a perda total de fundos no caso da divisibilidade infinita de apostas (embora esse não seja o caso para as negociações reais, claro),

Uma das desvantagens do método é o chamado efeito de nivelamento assimétrico. Ele significa que a próxima aposta após a que foi perdida tem menor volume. Assim, um investidor deve ter mais negócios de sucesso do que perdas para poder recuperar suas perdas. Além disso, séries escondidas nas sequências de negócios podem afetar os resultados desse método (não Bernoulli).

Durante seu uso prático, esse método MM pode apresentar um problema ao selecionar os fundos de ações que fornecem as melhores taxas de crescimento de fundos com probabilidade aceitável de ruína. Tal estratégia de jogo otimizado assintomaticamente foi oferecida por Kelly.

Mas primeiro, vamos examinar algumas teorias e equações. Se soubermos o número de apostas rentáveis e com perdas, bem como os valores de ganhos e perdas por uma aposta, podemos calcular TWR(V) e Prob(V) da mesma maneira como no caso do método de tamanho fixo. A equação (17) é similar a (4).

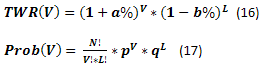
Um exemplo de cálculo usando equações (16) e (17) é exibido abaixo. A probabilidade de alcançar valores diferentes de TWR é mostrada como um valor acumulado.

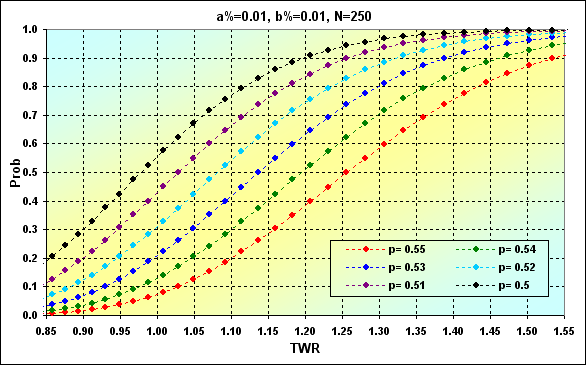
Fig. 33

A próxima imagem mostra os dois casos com condições similares mas MM diferente. O caso de tamanho fixo foi tomado da figura 8. O tamanho de MM fixo (FixSize) é mostrado em vermelho, enquanto o tamanho de fração fixa (FixFrac) em preto

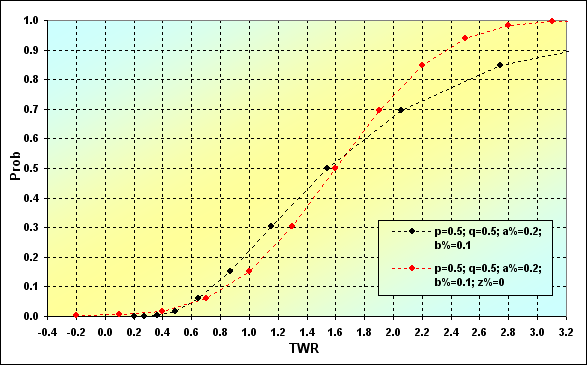
Fig. 34

A equação descrevendo a velocidade do crescimento dos fundos no caso de valores de ganhos e perdas iguais se parece da seguinte forma:

Usando transformações e raciocínio simples [8] e minimizando o crescimento geométrico médio esperado, podemos produzir a seguinte equação mostrando o tamanho otimizado da aposta f*.

Esse é chamado de critério de Kelly. Sua ideia é bem simples. Se você tem um TS com a probabilidade de ganho excedendo 0,5, e os valores de lucros e perdas são iguais, então você precisa usar as ações dos fundos calculadas usando a equação (19) ao colocar uma aposta. Por exemplo, p=0,55, neste caso, f*=0,55-0,45=0,10. Significa que você precisa usar um décimo dos fundos ao colocar uma aposta para poder fazer os fundos crescerem de modo eficiente.

Aviso: note que a equação do valor de aposta otimizado de Kelly é diferente do oferecido por Vince em [4]. Não há erros do lado de Vince aqui e explicarei isso posteriormente.

Observação: Se calcularmos o valor da ação dos fundos otimizados para p=0,50, então naturalmente teremos 0,00. Em outras palavras, é recomendado não jogar.

Caso os ganhos e perdas sejam k vezes diferentes, devemos usar outras equações ao invés de (18) e (19). [8][5].

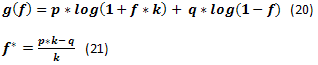
Se criarmos a mudança gráfica g(f) de f usando a equação (20), veremos algo parecido com a seguinte imagem. Essa figura é marcada por um ponto f*. Esse é o maior ponto do gráfico onde a taxa de crescimento dos fundos alcança seu máximo. Além disso, há um ponto fc representando o ponto de interseção do gráfico e uma linha zero. É o ponto onde o crescimento de fundos é zero.

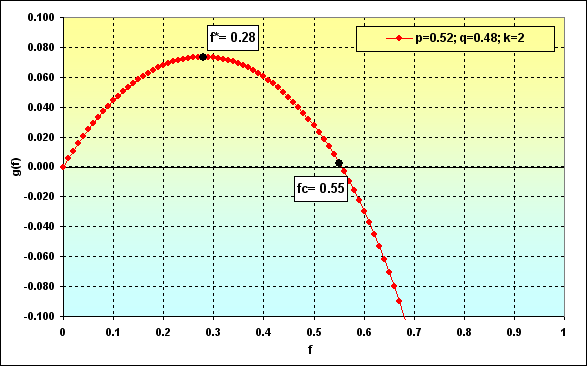
Fig. 35

Observação: k=2 foi selecionado somente como uma ironia direcionada aos gráficos adequadamente exibidos nos livros de Vince. Mesmo assim, tal valor de k fornece uma maior "clareza" e "beleza" para os métodos que ele apoia.

Em [8], é dito que se o jogo for feito de acordo com as condições especificadas, então f* fornece a taxa máxima de crescimento de fundos e probabilidade zero de ruína. Se a ação menor do que f* for usada, a probabilidade de ruína é também zero, embora a taxa de crescimento dos fundos seja mais lenta. Se a ação dos fundos usados excede fc, a ruína é iminente (neste caso, qualquer estoque de fundos significa uma ruína, não importando o quão baixo é). Se os fundos ocupam a faixa de f* até fc, a taxa de crescimento é mais lenta do que a máxima, embora não exista probabilidade de ruína.

Os resultados são impressionantes o suficiente. Entretanto, esses cálculos teóricos não levam as características do mundo real em consideração. Portanto, Vince recomenda calcular o fс otimizado com consideração para as perdas máximas. Isso leva para o fato de que o valor dele para f* se torna menor do que aquele calculado estritamente matematicamente com todas as consequências posteriores.

Vamos tentar considerar como isso pode parecer nos gráficos. Vamos ver o seguinte caso: Deposit=1000, LotSize=100000, f={ 0,01, 0,02, 0,03, 0,04, 0,05}, TP=SL=0,01, Spread=0,0000, p=0,51, N=250, Leverage= 100. Com estes dados de entrada, os lotes iniciais Lots=0,01, enquanto TP%=SL%=0,01. Ademais, f*=0,02 e fc=0,04, como mostrado na figura a seguir.

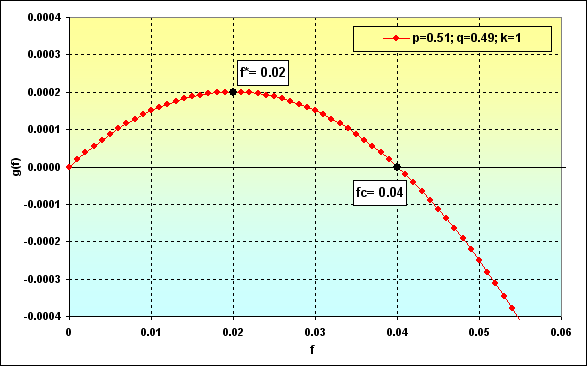
Fig. 36

Caso o f mude, teremos as seguintes correlações entre Prob e TWR. Vamos fazer alguns cálculos para demonstrar isso.

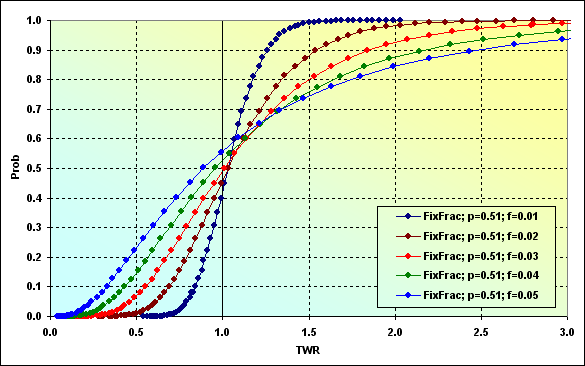
Fig. 37

Vamos considerar isso em mais detalhes. A linha correspondendo a f=0,01 demonstra o caso discutido anteriormente de f<f* quando a taxa de crescimento de fundos é menor do que a máxima possível, enquanto a probabilidade de ruína é zero. Nesse caso, a probabilidade de perda TWR<=1 é igual a ~0,40.

O próximo caso, f=0,02 é onde a ação desses fundos usados é a otimizada. A probabilidade de perda é ~0,45. Em outras palavras, espera-se que mais da metade das rodadas de um jogo sejam rentáveis.

Calculando a versão f*<f<fc, isso é, f=0,03. A probabilidade de perda é ~0,45. A ruína se torna impossível sob essas condições no jogo. Entretanto, os valores nos quais TWR pode cair são mais significativos do que nos casos anteriores. Maiores lucros também são possíveis.

Agora a probabilidade de perda é de ~0,50, ou seja, f=fc=0,04. É falado que neste caso, TWR quase certamente irá flutuar entre 0 até o +infinito.

E o último caso, f>fc. A probabilidade de perda é ~0,55. Ganhos muito consideráveis são possíveis nesse caso, mas todos os fundos serão perdidos a longo prazo (infinito) e TWR será reduzido ao nível que poderá ser classificado como ruína.

Mais algumas equações. g(f) a taxa de crescimento de fundos pode ser avaliada usando as equações (18) e (20). Já que a taxa de crescimento de g(f) e a quantidade de negociações de N são conhecidas, é possível calcular TWR usando a equação (22). Além disso, seria mais correto avaliar o lucro médio esperado da negociação para MM usando ações de fundo fixo como a média geométrica Gmean usando a equação (23) ao invés de uma aritmética.

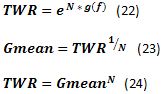
Recomendação: Seria bom incluir o cálculo da média geométrica dos negócios no relatório padrão de testes do MT. Isso permitiria aos usuários avaliar os sistemas de negociação usando MMs de fração fixa mais corretamente.

Abaixo estão dois exemplos de cálculos usando as equações (23) e (24) e dados da figura 36.

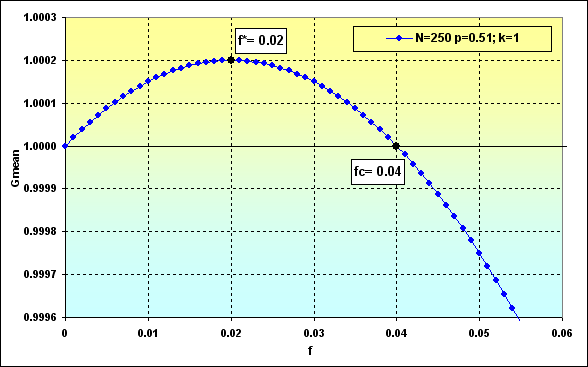
Fig. 38

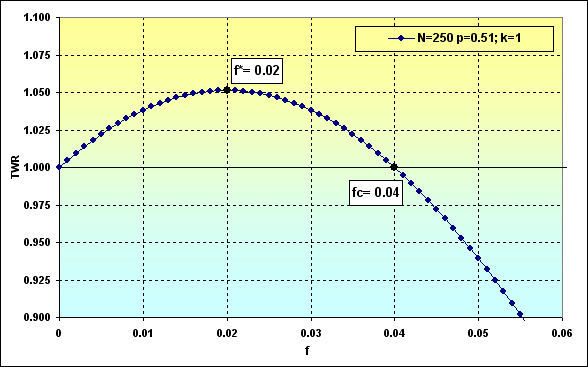
Fig. 39

Assim, com base na figura 39, os fundos gerais tendem a TWR=1,05 sob as condições dadas e com a ação otimizada nas apostas. Com podemos ver na figura 37, a probabilidade de perda é de ~0,45.

Seria interessante saber o comportamento de MMs diferentes com as mesmas condições iniciais. Se usarmos os dados da figura 36, veremos a seguinte figura.

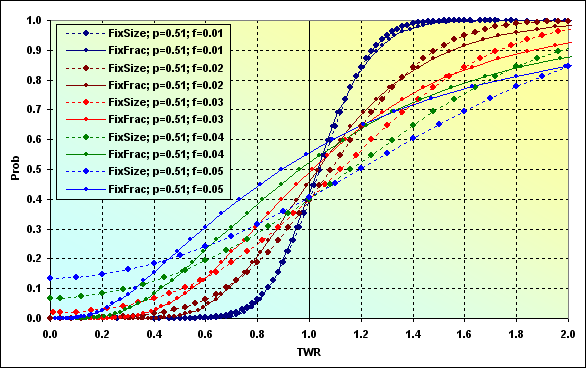
Fig. 40

No caso de f=0.01, as tabelas são muito similares, enquanto MMs são diferentes. Em outras palavras, os resultados podem ser similares sob certas circunstâncias. Todos os outros casos mostram que o MM de tamanho fixo tem menor probabilidade de perda (TWR<=1) do que a fração fixa sob as mesmas condições iniciais.

Aviso: A observação acima somente se aplica ao dado de entrada selecionado. Em nenhum outro caso ela deve ser considerada uma regra geral.

Vamos mostrar outra circunstancia interessante - uma correlação dos valores, para a qual TWR tende, com as ações de fundos usadas em uma negociação. O cálculo para esses valores pode ser feito para MMs de tamanho fixo como uma multiplicação de MO por N, enquanto a equação (22) é usada para o MM de fração fixa.

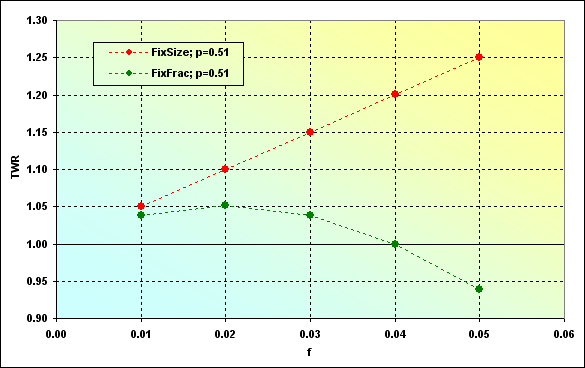
Fig. 41

Como podemos ver, o pagamento esperado ao usar o MM de tamanho fixo é maior (para os dados de entrada usados). Entretanto, isso não é sempre o caso.

É possível examinar como as correlações, para as quais TWR tende, mudam, considerando várias probabilidades de ganhos por uma negociação. Os gráficos para o comprimento da série N=250 são mostrados abaixo.

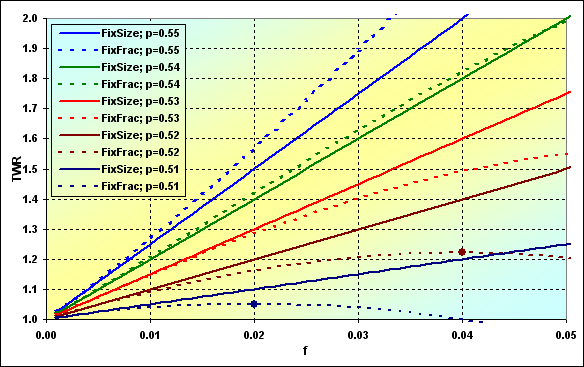
Fig. 42

Como podemos ver, sob certas circunstâncias, em termos do TWR esperado, existem muitas situações onde o MM de tamanho fixo é mais preferencial do que o de fração fixa. Entretanto, se considerarmos essa questão junta com a probabilidade de ruína, o todo não parece tão óbvio.

Ademais, o valor do TWR esperado é afetado significativamente pelo comprimento da série N. Em geral, quanto maior a série, maior o benefício do MM de fração fixa.

Agora, vamos terminar nossa examinação de alguns aspectos teóricos e avançar para a simulação. De fato, nada mudou em nosso modelo inicial, além do fato de que é necessário adicionar conceitos de lote mínimo e máximo, MinLot e MaxLot. Alem disso, precisamos do valor LotStep caracterizando o passo mínimo possível de mudança do lote. O algoritmo para o cálculo geral permanece o mesmo. O conceito de MinDeposit é inicialmente introduzido como um valor de depósito mínimo possível. Assim, as negociações podem continuar se o valor do depósito exceder Margin e MinDeposit.

Abaixo está um exemplo de simulação de vários MMs com o seguinte dado de entrada. Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.01, Spread=0.0000, p=0.54, N=250, Leverage=100. Note que Spread não é usado nesse cálculo.

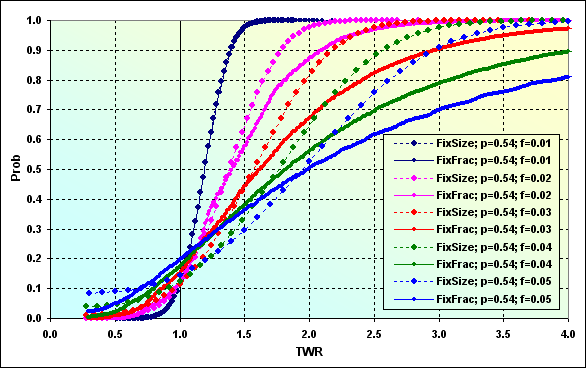
Fig. 43

A introdução de MinDeposit nos cálculos leva ao fato de que MMs de fração fixa que tinham teoricamente probabilidade de ruína zero (em f<fc) agora possui alguns diferentes de zero. Ademais, a discretização e limitações de tamanho de lote também levam para a probabilidade de ruína sob certas condições (não exibidas aqui). O impacto desses fatores negativos pode ser reduzido tomando a diferença dos valores de Deposit e MinDeposit como os fundos iniciais. De fato, é isso que Vince sugere - somente uma parte dos fundos deve ser usada para calcular a ação dos fundos otimizada. Parece ser uma decisão inteligente mas ela naturalmente nos leva a uma redução de TWR.

Agora, deixe-me fazer alguns esclarecimentos com relação à figura 43. Vamos encontrar "FixFrac; p=0,54; f=0,05" no gráfico onde ele corresponde a Prob=0,50. Essa é uma média, o valor, acima e abaixo de onde 50% de todos os valores estão localizados. Nesse caso, ele corresponde a TWR~2,00. Em outras palavras, metade de todos os jogos tem pelo menos dobrado os fundos iniciais. A probabilidade de perda compreende ~0,20, enquanto a probabilidade de ruína é ~0,03. Comparando com o gráfico "FixSize; p=0,54; f=0,05", podemos notar que a probabilidade de ruína pode aumentar a até ~0,08, enquanto a probabilidade de perda diminui para ~0,14, mas a média corresponde a aproximadamente TWR~2,00. Se tivermos sorte de chegar a um número de casos onde TWR>2,00, o resultado será mais provavelmente menor do que quando usamos o MM de fração fixa.

Comparando os gráficos nas figuras 42 e 43, devemos notar que os valores da figura 42, para o qual TWR tende, nada mais são do que a média na figura 43.

Agora, vamos considerar o caso exibido na figura 43 com Spread=0,0002. Todos os outros dados de entrada permaneceram os mesmos.

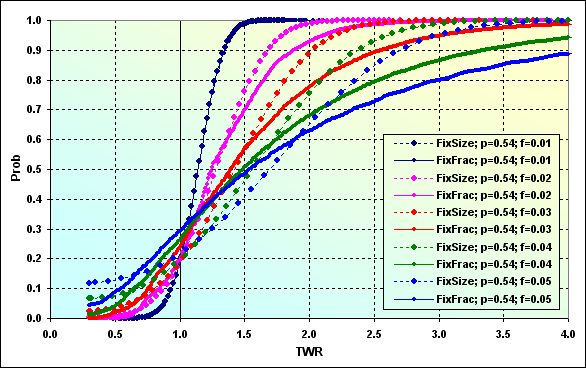
Fig. 44

Como podemos ver, Spread compreendendo de 0,4% a 2% do nível de lucro\perdas por negócio leva à mudança considerável de toda a figura. Isso pode ser melhor visto na seguinte figura onde dois casos de cálculo são comparados (das figuras 43 e 44).

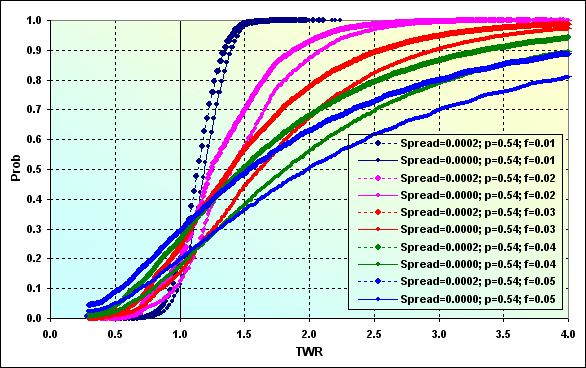
Fig. 45

Assim, a consideração do Spread diminui a média de TWR (por exemplo, linhas azuis) de 2,00 para 1,50. A probabilidade de perda aumentou de 0,20 para 0,30. A diferença não parece ser muito grande, somente 0,10, mas se tratada de modo diferente, um em cinco jogadores irão perder (embora não até a ruína) no primeiro caso enquanto será um em três jogadores no segundo caso.

Vamos tentar examinar como a probabilidade de perda muda, afetada pela probabilidade de ganho por uma negociação considerando vários f, simulando vários MMs com os seguintes dados de entrada: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0,01, LotStep=0.01, MaxLot=100, f={ 0,01, 0,02, 0,03, 0,04, 0,05}, TP=SL=0,0100, Spread=0,0002, p={ 0,48, 0,49, 0,50, 0,51, 0,52, 0,53, 0,54, 0,55, 0,56, 0,57}, N=250, Leverage=100.

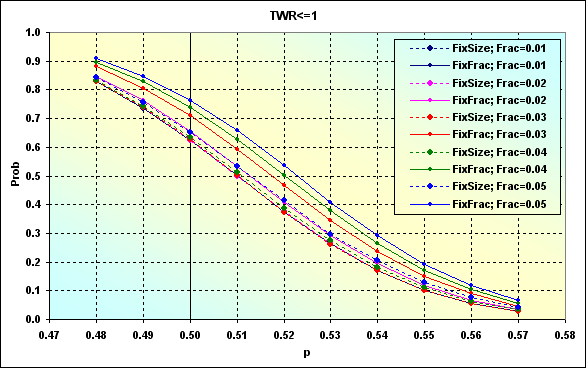
Fig. 46

Esse exemplo é diferente do exibido na figura 24 pelo fato de que os níveis de TP e SL são fixos aqui mas tamanhos de lote são alteráveis. A figura 47 mostra o caso com os dados similares à figura 46 em TP=SL=0.0050.

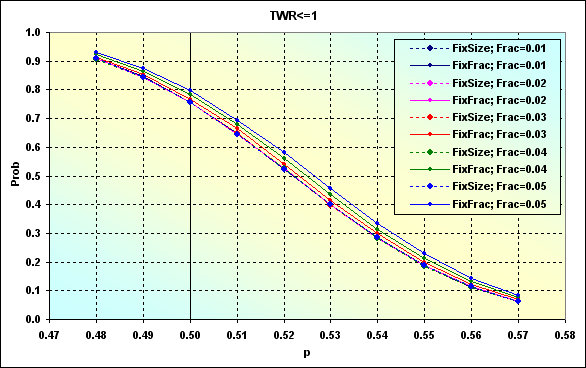
Fig. 47

Similar ao caso exibido na figura 24, diminuir os níveis de TP e SL leva ao aumento da probabilidade de perda. Além do mais, a dispersão dos valores entre vários casos foi diminuída. Os gráficos se tornaram mais "densos". Em outras palavras, o efeito do valor f diminuiu. Isso é particularmente evidente na imagem abaixo.

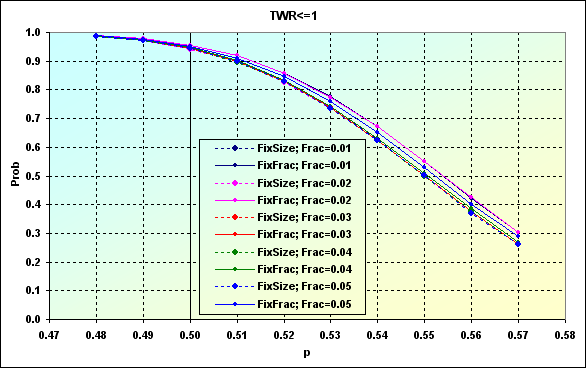
Fig. 48

Níveis TP=SL=0,0020 foram usados neste caso. Como podemos ver, para poder compensar a influência do Spread (dispersão) e reduzir a probabilidade de perda para menos do que 0,50, precisaremos de um TS capaz de fornecer p=>0,56. Mas geralmente, se um TS pode ser rentável somente em 50 casos dentre 100, os resultados permanecem os mesmos, a probabilidade de perda após 250 negócios é de ~0,95 independente do tipo de MM e de tipos f.

Vamos fazer os cálculos para poder mostrar como TWR se parecerá no caso de TP=SL=0,0020 e p=0,56. O resultado é mostrado abaixo. Isso é na verdade um caso com a probabilidade de perda de cerca de 0,40, como na figura 48, enquanto o valor esperado de TWR é 1,01...1,04. MMs diferentes mostram valores similares.

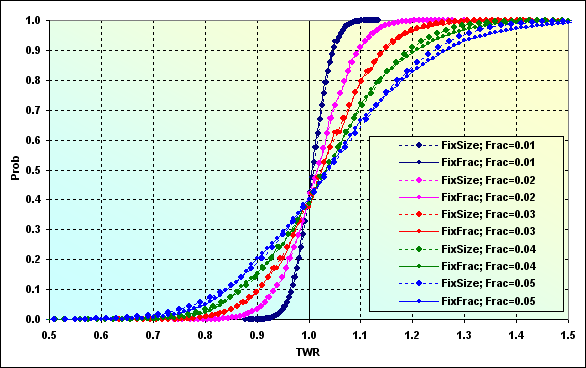
Fig. 49

Como já mencionei antes, isso é típico para casos com pequenos níveis. Se Spread fosse um valor flutuante e fosse carregado como um valor percentual do tamanho da aposta, toda a imagem seria diferente. Isso é exatamente o que acontece em outros mercados diferentes do "Forex para uma ampla gama de consumidores".

Vamos voltar para os cálculos com os seguintes dados de entrada: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0,01, LotStep=0,01, MaxLot=100, f={ 0,01, 0,02, 0,03, 0,04, 0,05}, TP=SL=0,0100, Spread=0,0002, p=0,51, N=250, Leverage=100. Vamos considerar como diminuir a probabilidade TWR se parece até certo nível.

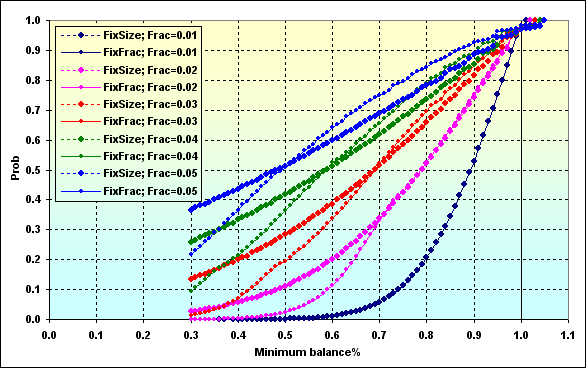
Fig. 50

Os dados do gráfico devem ser interpretados da mesma forma que na figura 27. A probabilidade do valor de TWR diminuir até ~0,70 em f=0,05 é ~0,76 caso a fração fixa MM seja usada. Se f=0,02, o valor é ~0,34.

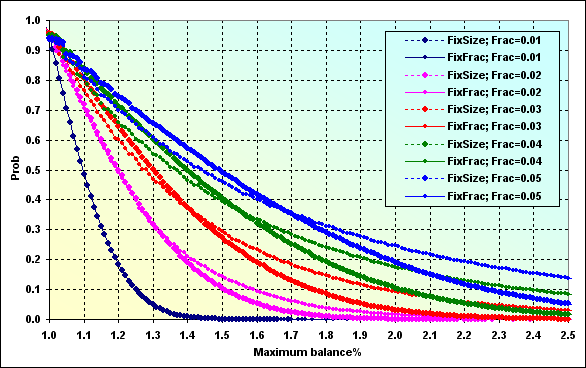
Fig. 51

E é essa a probabilidade do depósito aumentar durante o jogo até um certo valor. Esse gráfico deve ser interpretado de modo similar à figura 28.

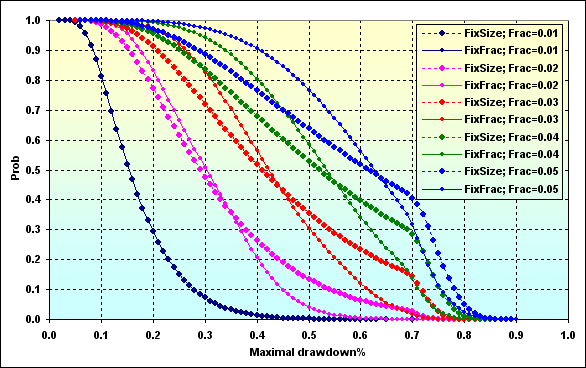
Fig. 52

O último gráfico exibe a probabilidade Maximal Drawdown % de um certo valor dependendo das ações dos fundos usados. Em geral. podemos assumir que o MM de fração fixa leva a Drawdown maior do que usar um de tamanho fixo. Isso pode ser explicado pelo efeito de nivelamento assimétrico. Entretanto, se fc>f>f* for usado, um Drawdown menor poderá ser esperado, enquanto o lucro pode ser similar ao caso f<f*.

Conclusão

Examinamos dois métodos de gerenciamento de dinheiro, revisamos seus históricos de desenvolvimento e também brevemente aprendemos sobre alguns aspectos teóricos dessa questão e algumas equações simples. Fizemos pesquisas de simulação estocástica e avaliamos os resultados obtidos comparando-os a métodos diferentes. Talvez a conclusão mais importante que pode ser feita deste estudo é que é impossível selecionar o melhor método absoluto dentre estes dois examinados. A eficácia do MM depende de uma grande quantidade de fatores. Várias combinações desses fatores fornecem resultados diferentes. Portanto, em cada caso definido devemos selecionar o MM mais adequado dependendo das propriedades TS, condições do centro de distribuição bem como as possibilidades e preferências de um investidor. Nosso artigo destacou algumas soluções possíveis e recursos cruciais. Espero que pelo menos alguns investidores tenham achado esse texto útil. Boa sorte para todos!

Meus planos futuros incluem a examinação de martingale (acho que essa parte não levará muito tempo nem espaço, já que as propriedades desse método são muito óbvias), bem como revisar o método de R. Jones (o autor afirma que ele foi desenvolvido como uma combinação de vantagens entre os dois métodos MM examinados).

Referências e links da web (na ordem de aparecimento no texto)

1. Agner Fog - Pseudo random number generators - http://www.agner.org/random
2. strator - Probability Library (parte do Cephes) - https://www.mql5.com/pt/code/10101 (em Russo)
3. Suvorov V. - MS Excel: Data Exchange and Management - https://www.mql5.com/pt/code/8175
4. Vince R. - The Mathematics of Money Management.
5. Bershadsky А.V. - Research and Development of Risk Management Scenario Methods. - Dissertação, 2002 (em Russo).
6. Smirnov А.V., Guryanova Т.V. - On Ralph Vince's "optimal f" (em Russo).
7. W. Feller - An Introduction to Probability Theory and Its Applications.
8. E. Thorp - The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market.
9. S. Bulashov - Statistics for Traders. (versão online, p. 199, em Russo)
10. Starikoff S. - Como avaliar os resultados dos testes do Expert - https://www.mql5.com/pt/articles/1403

Exemplos

Bibliotecas disponíveis publicamente usadas ao escrever esse artigo estão anexadas abaixo. Os scripts e o aplicativo não estão em anexo. Isso foi feito deliberadamente para estimular o desenvolvimento dos emuladores de servidores de negócios entre os membros da comunidade MQL. Um emulador de servidor de negócios foi usado nessa simulação.

Isenção de Responsabilidade, também conhecido como Desculpas

O autor deste artigo não assume a responsabilidade por nada. Reclamações e sugestões serão aceitas por meio escrito, na seção de discussões ou pelo e-mail. Sugestões sensíveis serão consideradas, enquanto outras levianas serão ignoradas. Todos os direitos autorais são especificados se forem conhecidos. Caso contrário, o autor é desconhecido ou o direito autoral foi perdido.

O autor admite que o texto e cálculos podem conter imprecisões ou erros. O texto é muito extenso e o assunto é bem complicado, então erros serão inevitáveis. Portanto, o autor oferece uma bonificação de $1 para cada falha detectada, de modo similar ao que D. Knuth fez. Mas a vida fez algumas mudanças. Os ventos gélidos da crise financeira global ainda estão furiosos por todo o país. Os mais vulneráveis e fracos entre nós - crianças órfãs - são geralmente as que mais sofrem nestes momentos. Para poder ajudá-los, o autor decidiu não oferecer essa bonificação pelos erros encontrados, mas sim distribuir todo valor para caridade. Selecionei vários orfanatos em províncias remotas da Rússia e enviei minha modesta poupança para eles.

Foi um sentimento indescritível quando recebi uma carta de resposta do diretor de um destes orfanatos. Foi uma carta simples, escrita à mão, em uma folha de papel pautado de um caderno. Naturalmente, ela continha palavras de gratidão, mas o mais importante ali foi a lista de itens comprados. Aquela inteligente gestora não gastou o dinheiro com um computador novo para copiar e colar cartas de gratidão, nem comprou novas cortinas para seu escritório, nem para comprar comida que já é fornecida pelo estado, embora seja bem diferente da que é servida em Moscou. Todo o dinheiro foi investido na educação daquelas crianças.

Cadernos para anotações, canetas, marcadores, jogos de aprendizado, livros de exercício, tintas. Todos os materiais de despesas que são críticas para o desenvolvimento das crianças vivendo em uma cidade bem pequena e provinciana ou uma vila em um velho prédio de madeira, possivelmente construído por nossos ancestrais que haviam acabado de chegar da Grande Guerra Patriótica. Então, se você puder, se não for seu último dinheiro, por favor, ajude-os, não seja ganancioso ou preguiçoso. isso não passará despercebido. De fato, não tenho certeza. Talvez essa carta tenha sido escrita por um vigilante noturno que estava bebendo esse presente inesperado. Não estou interessado nisso e nunca saberei a verdade. Somente fiz uma aposta, embora uma pequena, de que a probabilidade do fato de que vivo entre pessoas normais é muito maior. Ao contrário do jogo de cara ou coroa, esse jogo é mais justo para todos nós.