資金管理について

エピグラフ：

概論

取引のプロセスは、比較的独立した2つの部分に分けることができます。1つ目は、現在の状況を分析をしたり、取引開始や取引タイプ（買い/売り）、そして取引完了の瞬間の決定を下す、取引システム（TS）と呼ばれるものです。各取引に使われる資金の額は、資産管理システム（MM）と呼ばれる2つ目の部分によって決定されます。この記事では、ストラテジーのパラメータの変更による、いくつかの資産管理戦略の分析を試みます。分析の為に、イミテートシュミレーション法を選びました。しかしながら、いくつかの場合においては、分析判断の結果も検証されます。分析ツールとしては、MT4取引ターミナルとExcelを選択しました。疑似乱数（PRNG）生成ライブラリ[1]、統計関数[2]、そして、МТ4からExcelへのデータ転送モジュール[3]を追加で使用します。

初めから、いかなる取引プロセスにも、ある程度の不確実性があることが想定されます。これは、取引プロセスの性質について、ある程度の確実性は知られているが、その確実性を正確に定義することはできないということにあります。このような取引プロセスの、最も簡単な例として、『ランダム賭け』があります。その際は、トレーダーは例えばコインを投げるように、1つの通貨レートが他の通貨に対してポイントを一定数上昇させるか、もしくは下降させるかに対し、ランダムに賭けを行います。通貨レートの形成プロセスは、おそらく、トレーダーのコイントスの結果とは関係がありません。したがって、私たちは、取引結果がお互いに関連していない（ベルヌーイ試行）取引プロセスを有していることになります。加えて、私たちは、次の回にコインがどう落ちるか、またコインが将来のレートの動きを当てているのかを確実に知ることはできません。十分に多い回数の試みの際に、100回のうち約50回は当たる可能性があるということしかわかりません。多くのトレーダーは、自分たちの取引はこれとは異なるものだと信じています。そうかもしれませんが、まずは初めにこのケースについて検証していきましょう。そしてその後、100のうち50回以上の予想に成功したシステムの動作や、こういったシステムの成果に何が影響を与えるのかを検証していきます。

構成的に、記事では、最も興味深い資産運用システムの性質を『理論上の』例で検証をしていきます。その次に、実際の外国為替証拠金取引市場での取引の条件に近いデータで、資産運用システムの動作をシュミレーションしようと考えています。その際、直接的な形でいかなる取引システムも検証することはないということを申し上げておきたいと思います。どんな取引システムを使ったとしても、それは勝ちと負けの指定された確立と、勝ちと負けそのものの大きさについてのデータを我々に与えるだけであるとします。実際の取引結果の独立性（ベルヌーイ試行）、また、時間内の取引システムの性能の不変性に関してはこの記事では触れません。

前述したように、シュミレーションを使います。シミュレーションのプロセスは、事前に設定された特徴を伴う疑似乱数の生成に基づいて、勝ちか負けかの次の賭けの結果の特徴が確立するということです。賭け額は、選択した資産管理戦略によって決まります。負けてしまった場合、ベッドされた賭け金はトレーダーの現在の資産から差し引かれます。もし勝った場合、資産は増えます。特定数の取引のシュミレーションが行われた後、合計結果が計算されます。その後、そのプロセスを更に多数回（数百～数十万回）繰り返し、それから平均の結果を導き出します。

いくつかの基本的な用語と略語

まず初めに、今後考察する最終資産比率（英：Terminal Wealth Relative、以下、TWR ）について説明させていただきたいと思います。これは初期投資の乗数として、一連の取引の利益総額を算出します。つまり、最終資金を初期投資で割るとTWRになります。例えば、利益が12%である場合は、 TWR=1.12となります。または、損失が18%である場合、 TWR=0.82となります。これを使うことの利点は、初期資金の絶対値に関係なく、様々な取引プロセスの結果を比較することができることにあります。TWR という用語自体は、[4], [5], [6]から類比として用いられています。

次に言わなければならないのは、『勝ち』の概念です。どんな結果も、もしその数字が初期資金よりも大きいのであれば、勝ちとみなすことができます。つまり、TWR>1の場合、勝ちとなります。したがって、勝ちではないもの、つまりTWR<=1は全て『負け』とみなされます。このように、最終資産が初期資産と同じ（TWR=1）である場合も、負けと考えられます。しかし、こうなることが必須である場合は、個別に検証します。またその他に、1つの取引または一連の取引の結果かは重要ではなく、その後に取引を行うことが不可能である負けを意味する『破産』という概念があります。例えば、全ての資金を失ってしまったり(TWR<=0)、一定の最小額（保証金）よりも資金が少なくなってしまった場合です。

次に、これから使用する略語について触れたいと思います。勝率は、pという記号で表記されます。通常は、単位分数です。同じように、敗率は、q=1- pとして表記されます。総取引数はN、その際の勝ち取引数は、V、負け取引数はLとなります。絶対値での勝ち取引のサイズはa、負け取引のサイズはb、その際の勝ち取引の負け取引に対する比率は、k= a/bと表記されます。資金の額に対する割合としての勝ち/負け取引のサイズは、それぞれ、a%、 b%と表記されます。 b%に対するa%の比率は、kとなります。資金からの賭け額は、fと表記されることに注意してください。

計算中に取得される事象の確率は、Probとします。必要に応じて、他の記号も使用されます。

また、この記事では、『賭け』と『取引』という概念に区別がありません。そいて、単一取引操作（STO）と同じことを意味します。このようなSTOの系列は、文脈によってゲームまたは取引と呼ばれます。多くのトレーダーには好まれませんが、「ゲーム」という用語のほうが、取引の際に起こる不確実性をよく表現しています。

歴史的背景

コインを投げた結果に基づく取引システムの特性研究の歴史は、十分に長い年月に亘るものです。最も単純な形のものとしては、『コイントス』と呼ばれる運頼みのゲームがありました。2人のプレイヤーは、最初からいくらかの資産を持っています。コインを投げ、もしコインが表を向けて落ちた場合、1人のプレイヤーはもう１人のプレイヤーから彼の資産の一部を受け取ります。逆の場合には、自分の資産の一部を差し出します。数学者にとってはこれは、古典的な『賭博者の破産についての問題』です。これはかなり良く研究されていて、初期パラメータによって予想されるゲームの結果についても知られています。

『非常に裕福な相手と対戦するプレイヤーの破産についての問題』を解決する重大な結果は、トレーダーにとって最も興味のあることでしょう。非常に裕福な対戦相手は、ここでは取引センター（Dealing Center）を意味しています。もしくは、もしあなたが取引センターと対戦しているわけではないと思うのなら、外国為替証拠金取引市場の全ての参加者を非常に裕福な対戦者として考えてください。

この種のゲームの問題点とは何でしょうか？私たちは無限に続くゲームについては検証を行いません。誰も際限なく長くゲームをすることはできませんし、結果も安心を与えるものではありません。N 数の取引からなる有限のゲームの場合を考えてみましょう。あなたが予想することができる確率はp>0.50で、そして勝ち取引と負け取引のサイズが同等（a=b）とします。同様に、あなたはN の取引の勝ちが可能な限り大きいものであってほしいとしましょう。

このゲームで勝ちを最大限にするための最善の戦略は、毎回可能な限りの最大の賭け、つまり全ての資金を賭けることです。しかし、この場合の破産の確率は、式1-(p N)によって求められ、Nに依存するということが数学的にしっかりと証明されています。[7][8]N、つまり賭けの数が大きければ大きいほど、破産の可能性は高くなります。その結果、もしゲームをしなければいけない場合、N=1の時が最も破産の可能性が低いことになります。もしゲームをすることが必須ではない場合、一番の勝つための戦略は、全くゲームをしないことであり、そうすれば破産の確率はゼロパーセントになります。

注意：一般的な誤解があることにご注意ください。多くの人が、もしゲームでのチャンスが同等であるならば、彼らの利益は大体ゼロになると考えています。これは、彼らが同等の資本を持つ対戦相手とゲームをする場合になります。

実際の取引で考えると、3回中2回勝つことができるとあなたが予測できたとして、しかし毎回自身の全資産を賭けたとすると、結果は以下のようになります。最初の取引で、破産する確率は1/3になります。ちなみに、それは悪くない数字ですが、10番目の取引にはその確率は~0.98になります。

このように、最大の利益の獲得を望むと、全資金を賭けるが、たった一度だけという馬鹿げた状況をもたらします。無論、これは取引数が多い時に、ゲームの最終利益が高くなるということが明確であり、あまり魅力的ではありません。

最大利益を望むことをやめること、つまり、最大ベットでのゲームをやめ、全資金のうちの一部のみ使用することで、このようなゲームの続行回数を長くし、その上、破産の確率を下げることができます。もしこの一部がとても少額だとしたら、ゲームをとても長く続けることができます。これは数学的に証明されています。[7][8] しかし、こういった場合には、最終利益が小さくなるという状況が起こります。つまり、大きな賭け金は全体の利益の拡大につながるが、同時に損失を拡大するリスクも大きくすることになるというわけです。小さな掛けはリスクを軽減させるけれども、同様に利益も減らしてしまいます。だから自然と、資金のうちのどれ程を使うのが最適なのか（一定の観点から見て）という疑問が沸いてきます。

このような一般的な議論と前提条件の連鎖です。この問題の研究は今も続いています。一般的に『資金管理』と呼ばれる、この問題を解決に導くための分野が登場しました。求める破産の確率と利益の大きさを満たす、あらゆる可能性を与えるいくつかの資金管理方法が存在します。これらを全て検証することは、記事の制限からすることはできません。したがって、固定サイズの賭け金を定める方法と、資金の一部を固定して賭け金とする方法の2つについて論じていきたいと思います。

理論から少し

数学的なうんちくはさておき、資産管理システムの重要な瞬間は次の方法でまとめることができる問題です。一定の時間経過後（例：取引数）どのような事象（例：資産の成長が２倍、または破産）発生の確率になるかということです。要は、これは予想に関する問題なので、時間を固定し、事象の確率と事象そのものという2つのパラメータだけを検証することになります。

もし賭けの数Nを認識しつつ、『コイントス』を最も簡単な形で検証すると、いくつかのものは十分簡単に計算することができます。例えば、（1）1つの賭けに対する収益の期待値(МО)、もしくは、（2）一連の賭けに対する収益の期待値です。この場合の期待値は、初期資本に相関して定義されることに注意をしてください。これは、期待値>0の時はプラスの期待値、МО<0の時はそれぞれの賭けは平均して損失をもたらすことを意味しています。

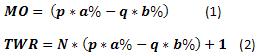
[9]の場合、 p=0.45、q=0.55、a%=0.08、b%=0.05、N=20となり、結果はMO=0.0085、TWR=1.170となります。このケースは、勝ちの確率が p<0.5の時、どちらにしても1つの賭けにプラスの期待値があり、そして結果として初期資本に対して~17%の利益が期待できる点が面白いです。

注意：[9] では別の資金管理システムを検証している為、同じソースデータにも関わらず、結果が異なります。

しかしながら、期待値は様々な患者の間で平均体温を測ることと同じようなものです。勝ちの賭けの数から、どんな結果が現れる可能性があるのか、何も知ることができません。しかしこれ無しではリスクを評価することは難しくなります。したがって、もう2つの方程式を導入します。勝ちの賭け数が明らかな時の利益の計算式（3）、そして一定数の勝ちの賭けがある組の中での事象の発生確率の計算式です。

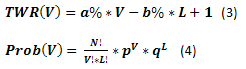
全てのための値を計算し、V= 0,1、...,N、L=N-V、そしてProb(V)の変化のグラフをTWR(V)から作図します。上に引用した事例のグラフは以下のようになります。グラフ上のProbとTWRの軸には(V)のインデックスがないことに注意をしてください。これは理解しやすくするために行いました。

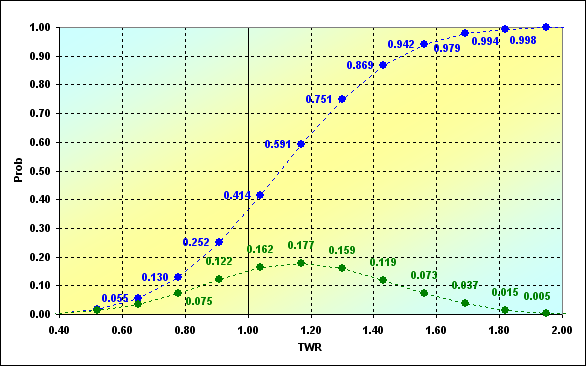
図1

方程式（3）と（4）の計算結果は、緑色の点で表されています。グラフの解説は次のように行うことができます。例えば、TWR=1.04となる一連の取引の結果での事象の発生確率は 0.162となります。ほとんどの場合、0.177の確率では、TWR=1.170となります。そのデータは累積確率として青色の点で表示されています。このように、私たちのソースデータでは、ゲームの一部がTWR<=1.00となる確率、つまり、負けが0.252となると言うことができます。グラフ上には極値は表示されていません。破産の状況、つまりTWR=0.00は、Prob=6.4E-06となります。最大利益はTWR=2.60、- Prob=1.2E-07となります。これはとても小さな確率ですが、これらの存在に関わるもう１つの重要な問題があります。

これを以下の例でデモンストレーションしてみましょう。以下の条件に基づいて計算されました：p=0.45、 q=0.55、a%=0.05、b%=0.05、 N=50。そして計算結果はグラフ上に表示されています。

図2

グラフからわかるように、TWRの数値は-1.50から3.50になります。TWR=-1.50は、0.0以下の資産になった場合のみに起こります。つまり、私たちが使った方程式は、どこか途中の取引で資金がなくなり、ゲームを続行できなくなった場合を考慮していません。これに関連して、『吸収境界条件の課題』と呼ばれる新しい課題が出てきました。この課題では、資金にはある境界（限界）があると考えられており、そこに到達するとゲームは終了します。通常、最も簡単な形式では境界は=0ですが、私たちにとってはるかに面白いバリエーションは、この境界がランダムな数値をとる可能性がある時です。この問題の解析解のいくつかの側面は、[7]で知ることができます。

好機の範囲

数字上でこの課題を解決してみましょう。まず第1に反復計算を使用し、第2に確率的方式に基づいた模倣シュミレーション（モンテカルロ法）を使います。まず初めに図を見て、問題の解決を試みてみましょう。

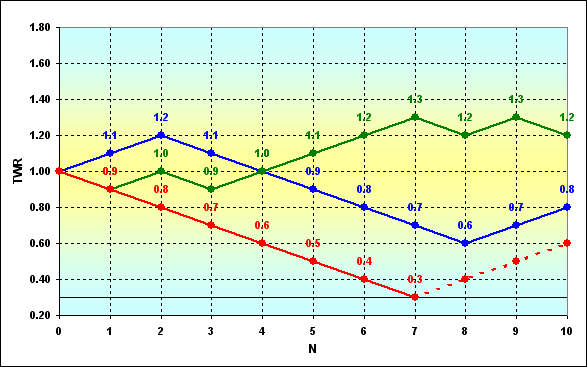
図3

図では、ゲーム中の資金の変化の軌跡がどのように起こりうるかを、概略的に表しています。条件をつけて3つのバリエーションを示しています。（勿論実際にはこれらは遥かに多いですが）ゲームには、例えば、0.3以上の資金（必要担保）を持つプレイヤーが参加することを許可されると仮定します。ゲームが赤の方向へ進み、何かの瞬間にゲームを続けることが不可能になったとします。吸収境界、つまり完全な破産が起こりました。プレイヤーは緑色や青色で表示されたゲームと違い、ゲームから除外されます。このようにして、一連の取引のなかの特定の回での破産の確率を定義するためには、過去の回の破産の可能性を全て見積もらなければなりません。

このような計算を行うことができる、もっとも簡単で、わかりやすくて、そしてとても古い手法は、パスカルの三角形です。これの要点は、過去の数値を用いて現在の数値を算出する再帰的な手順です。パスカルの三角形に少し改変を加えたバージョンが、以下のものになります。

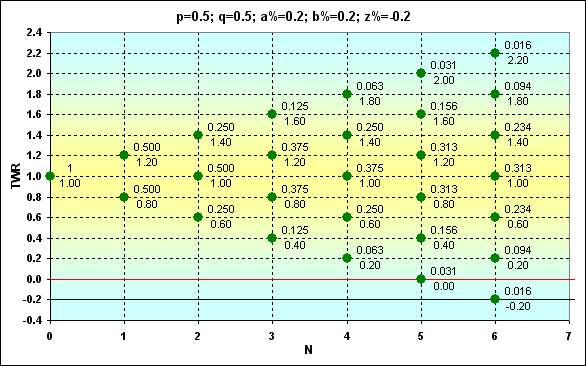
図4

この場合に方程式（3）で算出することができるTWR線の軌道を通過する点が緑色で表示されています。点はProb値（分子）とTWR値（分母）で記されています。記号z%は、吸収境界が起こる限界数値を意味しています。（黒色の線）赤い水平の線はz%+b%の値に基づいて描かれています。

点の位置は赤色の線に対して、何を意味するのでしょうか。もし緑の点が赤い線より上にある場合、賭けを問題なく続けることができるということです。赤い線が緑の点を通過する場合、これはもう一手を賭ける最後のチャンスということです。運が良ければ、賭けをまだ続けられ、運が悪ければ吸収が起こります。点が赤と黒の線の間にある場合でも取引はできますが、次の賭けへの資金が不足する為、その後の賭けはできなくなります。言い換えるならば、これは完全な資金の枯渇ではないが、ゲームを続けることは不可能ということです。

注意：勿論、コインの時のように、整数の賭け金の場合、こういったことは不可能ですが、例えば資金の0.15の賭け金の場合、状況はまさにこのようになります。

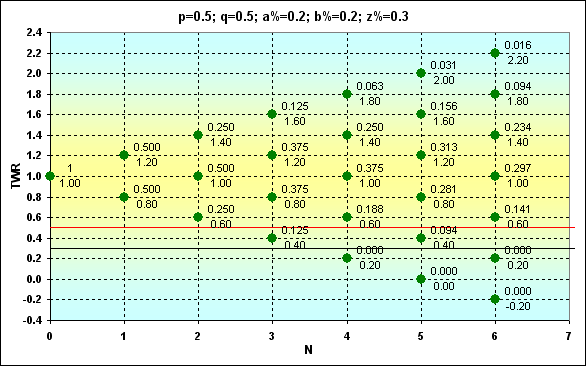
図5

そして、他の境界条件の場合の計算結果を表したもう一つのグラフです。これを前のグラフと比べると、違いに気づくことができます。

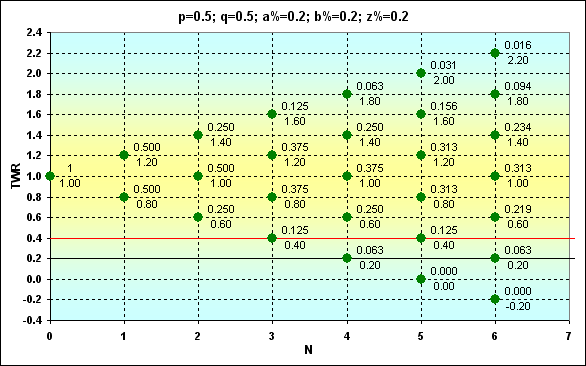
図6

このようなデータを持つことで、何かしらの事象の確率を知ることができます。例えば、図6の場合、N=6TWR=1.4の時、Probはどうなるでしょうか？答えは0.234です。もしくは、では、N=6 TWR>1である場合、Probはどうなるのでしょうか？しかるべきProbを加算する必要があり、答えはProb=0.344となります。そして、N=6 TWR=1.1 の場合、Probはどうなるか？答えは0になります。。

このシリーズの最後の例です。ProbとTWRがこの場合にどのような変化をするかを示すために、『歪んだ』入力値、p=2/3、q=1/3、 a%=0.1、b%=0.2、z%=0.2を用います。図からわかるように、勝つ確率は負けの確率の2倍ですが、勝ち取引の量は負け取引の量の半分となります。

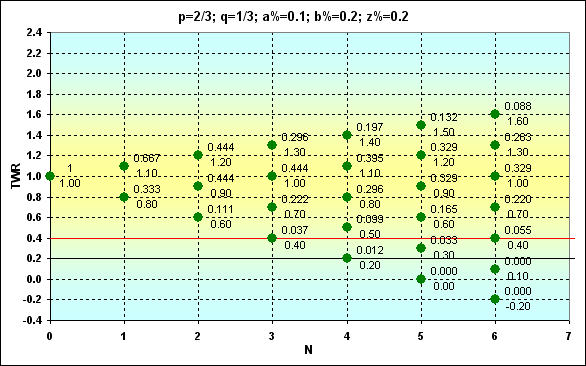
図7

TWR>1の時、Prob=0.351となります。基本的に、このProb値は図6の値に十分に近いです。しかし、賭けの数と同等になりうるTWR値は、はるかに小さいことがわかります。

私たちがまだ考察していない、もう１つの重要なことがあります。賭けに関わる資金の一部を意味するfというパラメータです。事実上、これは取引の中で賭けられる資金の一部、つまりb%です。『コイン』の可算数のみ負ける可能性のある、古典的な『コイントス』の場合、1/fは破産につながる一連の負けの数を表しています。私たちの場合、パラメータ1/fは非整数であることがあります。同時に、賭けの値が整数になると、賭けの数量の値も整数になります。これは、ゲームを続けることが不可能なのに、資金の一部（b%よりも少なくなります）が残っているという最悪の場合につながります。つまり、この一部は絶対的にリスクフリーであり、これを失うことは不可能です。これに関連して、ゲームに使用する実際の資金のサイズは、この数値によって小さくなります。同様に、この数値によって実際のz%は大きくなります。（図5参照）また、もしz%>0の場合、 fはb%を超える傾向にあります。上述のことを全て考慮しつつ、実際のf値は、次の方法で算出することができます。

ここでのintは、端数処理です。図5の例ではb%=1/5ですが、実際のｆはf=1/3です。

機会の期間

上記の結果をProbとTWRの間のつり合いとして見てみましょう。例として、様々な入力データのセットをいくつか選出しました。全てのセットの長さは同じで、N=15となります。

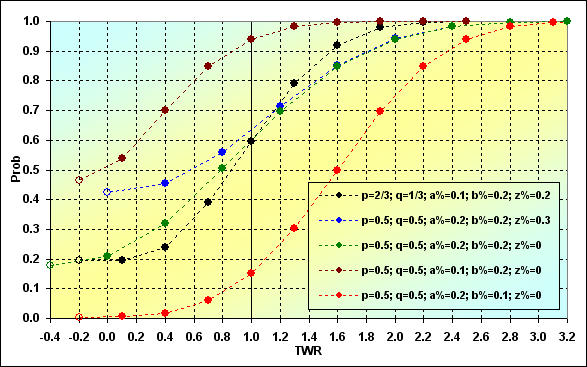
図8

図に何がどう書き入れられたのかについての理解を助ける為に、いくつか説明をしたいと思います。それぞれの曲線は『空の』点から始まります。（もし左から右に見た場合）概して言えば、これは仮定点（いくつかの場合において）であり、これらは実際にはありえないものです。しかし、それにも関わらず、これらの点はどの段階で吸収が起こるかの確率を示してくれます。つまり、軌道が最後の段階に達しない可能性を表しています。グラフ上の１つ目のすぐ後の点は、全ての過去の破産（ここでは重要ではないいくつかの例外を含む）を考慮して、最後の一手で吸収が起こる確率についての実際のデータです。

次の図では、破産の確率が一連の長さのNによってどのように変わるかを示しています。例として、図8と同じ入力データを使いました。見ると分かるように、結果は互いに大きく異なります。

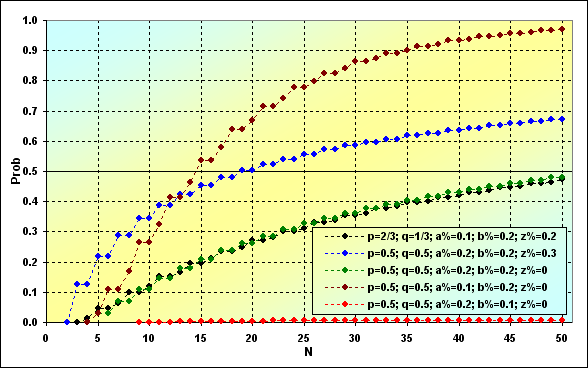
図9

次のことに注目してください。ここで一番重要なのは、取引の全数が多ければ多いほど、破産の確率も高くなるということです。吸収を伴うゲームでは、この重要な要素に何もすることはできません。しかしながら、一見思われるほど、全てがそう悪いわけではありません。取引システムのパラメーターによっては、破産の確率自体はとても小さくなることがあるということです。（赤い線を参照）同時に、もし取引システムがあまり首尾の良いものでない場合、破産が起こるのがとても早くなります。（茶色の線を参照）

もう一つの重要なポイントは、検討中の問題に関連する、トータルの勝ちの確率です。これまで、私たちはTWR<(z%+b%)という場合を検証しましたが、今度はNによってTWR>1の確率がどうなるのかを見ていきましょう。

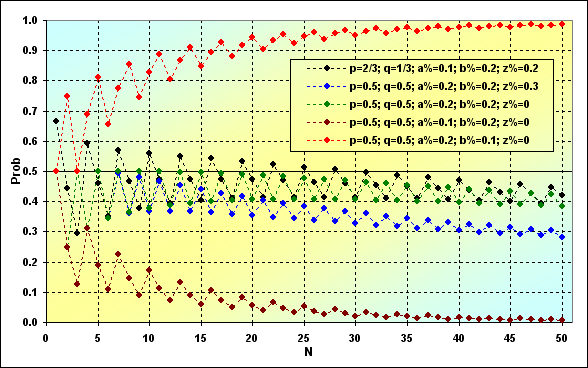
図10

黒や緑の色で示したケースでは、いわゆる期待値=0の中立的ストラテジーを持っており、約0.5という勝ちの確率に期待が持てそうなものです。しかしながら、そうはなりません。そして、これは吸収境界条件に関係しています。

一定の段階で予想されるTWR発生確率は以下のようになります。この場合、N=50で、図10と全く同様です。

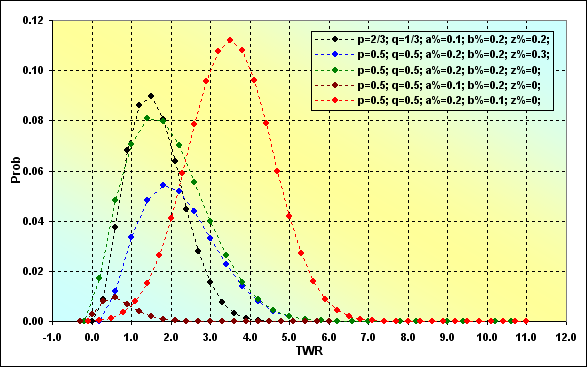
図11

これは通常の分布曲線です。これらの曲線が、従来の分布曲線と異なるのは、TWRの最大値・最小値に対し非対称になる点です。その上、いくつかの曲線が『横に傾いている』のがわかり、対数正規分布曲線と似ています。またもう１つの面白いポイントは、図10と図11を比べると、以下のことが分かる点です。図11で多くの場合、最も可能性のあるTWR値は1以上ですが、同時にTWR値が1以上になる確率は0.5です。さらに、期待値=0の場合（黒や緑の線）、最も可能性のあるTWRは、予想できるように、同様に1と同等ではありません。ここにいかなる矛盾もありません。

これで、『吸収境界条件の課題』のいくつかの側面の簡単な検証を終わります。次に、統計的シュミレーションを行い、推論の正確さとシュミレーションの精度を評価する為に、以前に取得した結果と比較します。

シュミレーション

概してシュミレーションのアルゴリズムは次のようになります。毎回『コイン』を投げる前に、資金の状態をチェックします。もし、資金がゲームを続行するのに十分でない場合、ゲームは終了します。ゲームをすることができる場合、擬似乱数生成器によって勝敗を明確にします。これに応じて、資金が増減します。このように、ゲーム終了まで続きます。多数のゲームが行われ、結果が平均化されます。これが全てで、とてもシンプルなものだといえます。確率モデルの唯一の問題点は、その正確さです。実は、この方法を使った場合、正確に問題を解決することができないということが、数学的に証明されています。（ドモアブルの定理を参照）したがって、今後の計算でモデルを使う前に、どれくらい結果が他のものと一致しているかを評価する必要があります。

以下の場合の、２つの解決法を比較してみましょう。: p=0.5、 q=0.5、a%=0.2、b%=0.1、z%=0.0。その結果を示した2つの図（図12と図13）が以下となります。

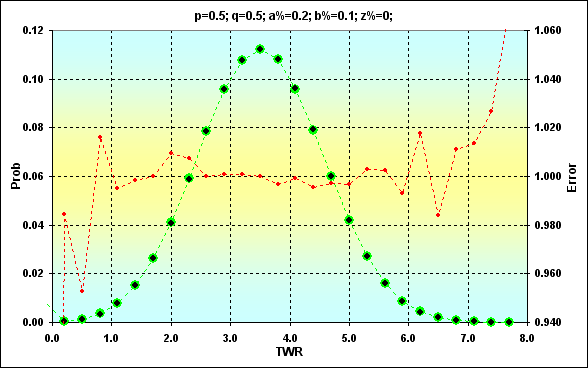
図12

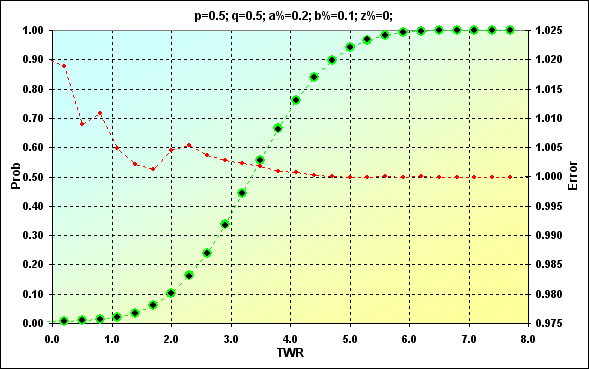
図13

緑色で示された値は、以前に取得したものです。黒い点は、シュミレーションの結果を示しています。赤い点は、シミュレーションに対する期待値の誤差率を表示しています。図12は、値そのものを示しています。図13は、蓄積額です。十分に良く符合しています。値の真ん中の部分では誤差レベルは0.5%以下となっています。領域の両端では勿論誤差レベルが高くなります。これについては特に恐ろしいこともないので、ただこれから先頭の隅に入れておきましょう。また、より私たちの興味を引くのは蓄積額で、こちらで誤差レベルがはるかに低くなっています。（これは累積曲線の特徴で、異なる値の誤差が相殺されます）

シミュレーションの結果の他の特徴は、非常に稀な値の確率を求めることができないことです。上記の例では、たとえばProb= 8.88E-16の際の最大TWRは11です。そして、シミュレーションではこのような値は出ません。

もう一つの上述したシュミレーションの例は、N=250である場合です。: p=0.5、q=0.5、a%=0.1、b%=0.1、z%=0.0特に付記するコメントはありません。

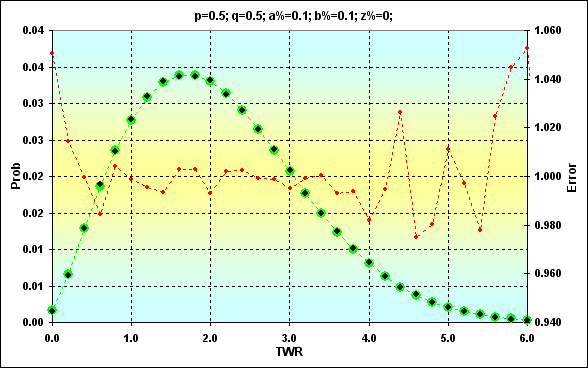
図14

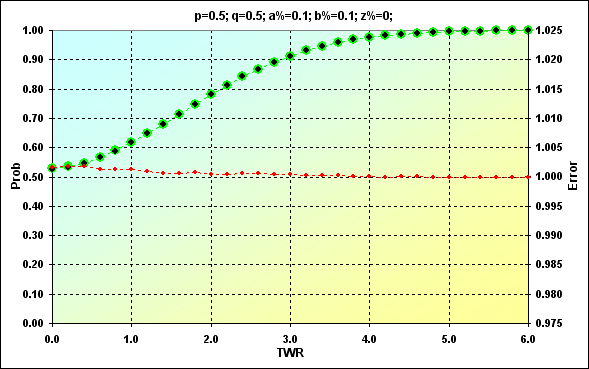
図15

これで、上部で私たちが検証したものよりも、より難解な問題を解決するためのベースとしてこのモデルを用いることができます。

取引操作

検証を進める前に、いくつかの概念と方程式について説明します。実際の取引は、一見、上で検証したゲーム『コイントス』と大きく異なり、この事情をふまえ、シミュレーションに際し、追加の努力が必要となります。したがって、今後何をすべきかをすぐに明らかにする必要があります。恐らく、ほとんどの読者の方々は、この件について独自のアイディアを持っていることでしょう。ということで、私たちに必要となる、いくつかの概念と記号です。

注：分かり易くするため、EURUSD, GBPUSDなどの『直接引用』のペアの取引操作を検証します。『間接相場』とクロスレートのペアは、若干異なると考えられています。間接相場の通貨ペアの場合、ポイントの価格が、現在の相場によって変動します。クロスレートの場合、アメリカドルに対するベースの（初めの）現在の相場が追加で考慮されます。その上、ここではASKとBIDの概念は使われません。

Depositは、取引に使用される資金を意味します。Leverageを使って、 指定されたLotSize（LotSize）で取引することができます。約定が分数である可能性があるので、どのようなサイズの約定を私たちが操作するのかを示す特徴としてLotsという概念が私たちに必要になります。したがって、基本通貨で操作する実際のロットサイズはLotPriceと呼びます。Marginとは、取引を行なうための証拠金のことです。MarginをDepositの一部とすると、パラメータはMargin%となります。またこれと共に、そこに到達した場合、現在の取引の終了や取引の強制終了をもたらすMarginの最少額を意味するStopOutの概念を使用します。 さらに、以後に取引を行うことができない、2つの異なる状況（希望のLotPriceの時）、つまり破産の状況が存在します。加えて、Sigmaと呼ばれる、もう一つのパラメータを導入しました。要はこれは、全ての所有する資金のサイズに対する、取引操作で使用されるレバレッジを含めた資金の割合です。実際の資金に対して、取引する資金の割合、つまり、レバレッジのアナログですが、ただ全Depositに対するものであり、LotPriceに対するものではありません。

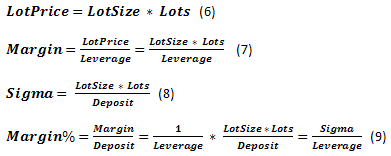
取引プロセスを特徴づける基本的な概念の１つに、Quoteがあります。これは現在の為替レートです。Tickとは、為替の時々刻々と変わる細かい値動きのことです。シンボルのレートの最小変動サイズはTickPrice、Depositの一部として検証されるものはTick%です。

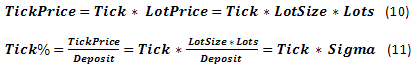
さらに、レート変動に関するいくつかのパラメータがあります。TP (TakeProfit) とSL (StopLoss)とは、損益の確定が起こる為替の変動です。 これらのパラメータを通貨で表したものを、TPpriceとSLpriceと呼ぶことにします。そして、それに応じて、Depositの一部として表されたものをTP%とSL%とします。同様に、様々な種類の業者手数料があり、これらはSpreadや Swapなどと言います。私たちはこれらの多様なパラメータの全てに言及はせず、従来的に為替変動で表現されるSpreadにのみ焦点を当てます。. もしSwapを、レバレッジで借りた資金の使用への実際の銀行の金利として表す場合、状況は少し複雑になります。

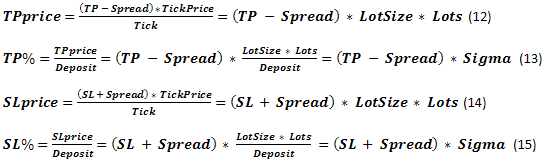
私たちが取得したデータを、私たちが『吸収境界』についての問題で使用したデータと比較してみましょう。SL%はb%と一致することが明らかです。同様にTP% = a%です。初期資金はTWR=1として提示されました。この場合、分数で表されるパラメータで私たちの計算は行われるので、同じようになります。z%+b%の境界値の使用で、Margin%を計算することができます。これらの2つの概念にはある違いがありますが、もしStopOutの存在に注視しなければ、これはそれほど重要なものではありません。最初の近似値において、これらの課題は似ているように思えます。もう少し後でこの見解を検証することにしましょう。

9・11・13・15の方程式を注意深く見ると、どこにでもSigmaというパラメータが含まれています。すでに述べたように、これはレバレッジのアナログで、全ての重要な方程式で使用されます。直接Leverageに影響を受けるのはMargin%のみです。

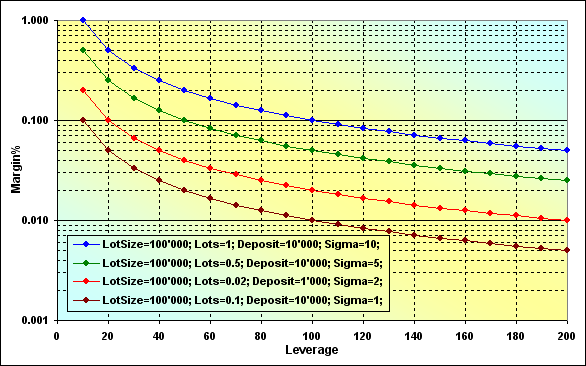
図16

計算の正確さは、次の例で確認することができます。Leverage=100、 LotSize=100000、Lots=0.1、 Deposit=10000の際、保証金のサイズは100となることは知られています。対応するグラフ（茶色）を見ると、Margin%=0.01となるのがわかり、Deposit=10000 の場合は、これは100となります。

グラフに見られる2つの特徴は、第一にSigmaが大きければ大きいほど、Margin%は高くなるということです。言い換えるならば、取引に使用できる自由な資金がより少ないということです。第二に、Leverageが少なくなればなるほど、同様にMargin%の上昇につながるという点です。似たようなケースが検証された図9を見てください。（青色と緑色の線）これらのケースは、z%のサイズが異なるだけです。境界値の増大とともに、その他の同様の条件下での破産の確率が高まることがわかります。

SL%とLeverage直接的な関係はないので、このパラメータがどのようにSigmaと(SL+Spread)から影響を受けるのかを見てみましょう。

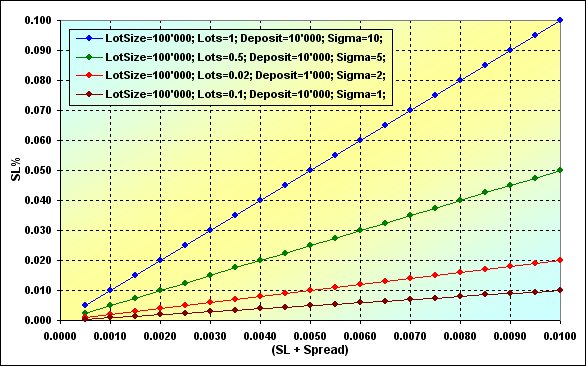
図17

パラメータSigmaの増大は、SL%の上昇をもたらし、つまり、同様に破産のリスクを高めることにつながります。この関係性はまさに直線的です。SL%を下げる為には、(SL+Spread)を下げるか、もしくはLotsを小さくする必要があります。というのは、Sigmaに含まれている他の数値は、おそらく変更することができないからです。

これで方程式の検証を終わります。どのようにシュミレーションが行われたかについて、少しお話ししたいと思います。このプロセスは、以前に適用されたものと、何ら変わりのあるものではありませんでした。取引の可能性が確認され、現在のレートで買いが行われ、疑似乱数生成器を使ってレートの変動を明確にし、売りが行われ、そして現在の資金レベルが算出されました。これはサイクルの中で何度も繰り返されました。そして、最後に取引結果を判定しました。いかなる特別な分析形式は使用せずに、『ありのまま』でシュミレーションしました。Tickとそれに関連するSwapという概念は必要にならなかったため使用しませんでした。

シュミレーション結果の正確さを評価する為に、次の主な特徴を有する例をしようしました。Deposit=1000、Leverage=100、 LotSize=100000、Lots=0.1、TP=0.0040、SL=0.0040、Spread=0.0002、p=0.5、N=250。一年の労働日数とほぼ等しい数字のため、シリーズの数字の長さはこのようなものを選択しました。このようにして、一日一取引として計算するならば（その日のうちなのでSwapは使用しません）、年間算出で結果が出ます。方程式9、13、15を適用し、取得した結果は以下の通りです。TP%=0.038=a%、SL%=0.042=b%、Margin%=0.1 (したがって、 z%=0.058)。確率論的シュミレーションを行うと、計算は図4と同様のものになります。

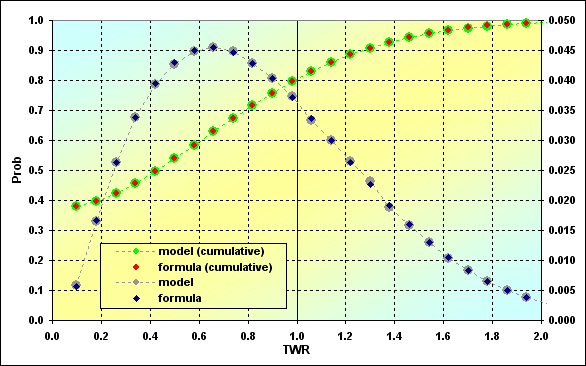
図18

ここでは、シュミレーションと方程式に基づく計算の比較が行われました。分かるように、異なる方法に基づく計算の結果は、とても良く相互に一致しました。これは、『吸収境界条件』についての問題で、取引のプロセスが古典的『コイントス』と、そこまで違わないということを証明するもう１つの理由です。

図に関して、短くコメントをしたいと思います。緑と赤色の線の一番左の最小点は、破産の確率を表しています。この場合、これはTWR<= Margin% - 0.375です。TWR<=1である場合、負けの確率は0.795、勝ちの確率は0.205になります。

資金管理ー固定サイズ (FixSize)

この資金管理法の要点は、毎回他の要因に関係なく、取引において初期資金の決められた一部を使用するという点にあります。実際に、ディーラーがトレーダーに提供しているロットサイズ管理の従来の能力は、ずばりこの方法に相当してます。さらに、この資金管理法は『コイントス』のゲームで実装されていますこの方法の特徴についてはすでに言及済みなので、どのように個々のパラメータがこのシステムの性能に影響を及ぼすのかという問題に真っ直ぐ移行したいと思います。この為に、私たちのシュミレーションを使用します。

分析的でなく数学的な問題解決を考慮に入れるので、入力パラメータの変更への反映評価の唯一の方法は、計算結果を比較することです。データを確定し、それらの内の１つを何某かの範囲で変更し、それがどのような変化をもたらすのかを観察します。

図16で示されている状況に戻ります。このようなパラメータで計算を行います。Deposit=3000、 LotSize=100000、Lots=0.1、 TP=SL= { 0.0030, 0.0040, 0.0050, 0.0060}、 Spread=0.0002、p=0.5、N=250、Leverage= { 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}。

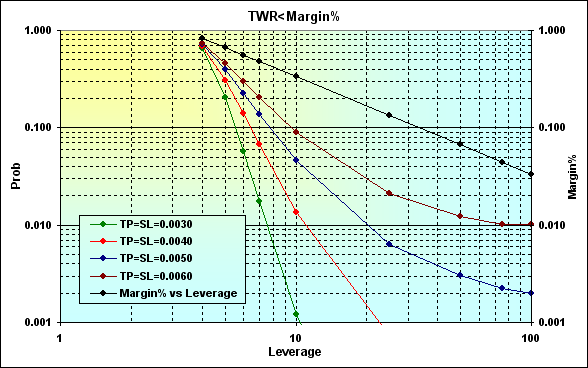
図19

計算結果を明確にするため、対数目盛りで表示します。実際に、Leverageの減少は、Margin%(黒線)の上昇をもたらします、つまり、破産の確率が高まります。破産の確率とレバレッジの間の相関関係は直線的ではなく、最も大きな影響はLeverageが小さい値の領域で感じられることに留意する必要があります。TPとSLのレベルを下げることで、Leverageの減少によるいくつかの負の効果を減らすことができます。しかし、ここで注意したいのは、非常に小さい値のLeverageの場合（私たちの場合、4）でも、破産の確率は高いままという点です。そして、もう一つ特徴的なことが以下の図からわかります。

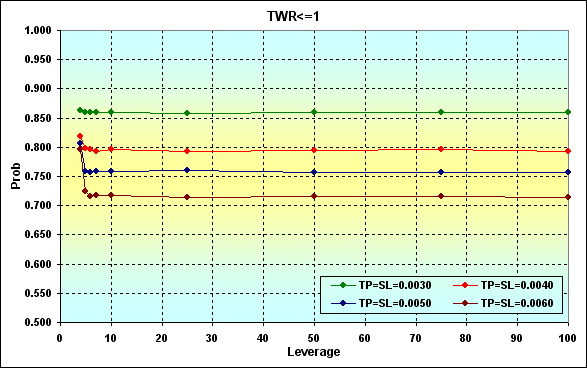
図20

ここでは、負けの確率がLeverageの変化に影響され、どのように変化するかが示されています。分かるように、TPとSLが減少すると負けの確率が上昇します。

もし資金を、例えば10000まで上げると、N=250の場合に、破産する可能性がなくなります。図20と21を比べた場合、Leverage>10の範囲では結果が一致することがわかります。

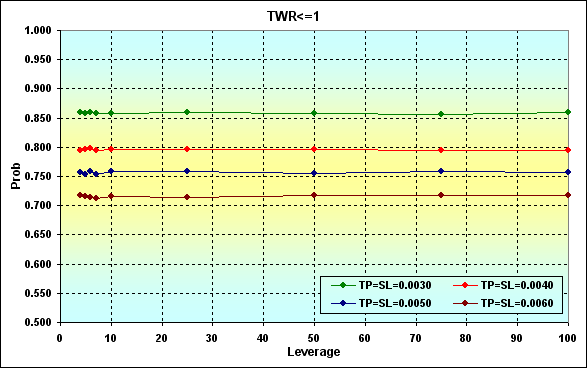
図21

１つの取引において勝ちの確率が負けの確率よりも高い例、つまりp>0.50を見てみましょう。次のパラメータで計算を行います。Deposit=3000、 LotSize=100000、Lots=0.1、 TP=SL={ 0.0030, 0.0040, 0.0050, 0.0060}、 Spread=0.0002、p=0.52、N=250、 Leverage={ 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}。

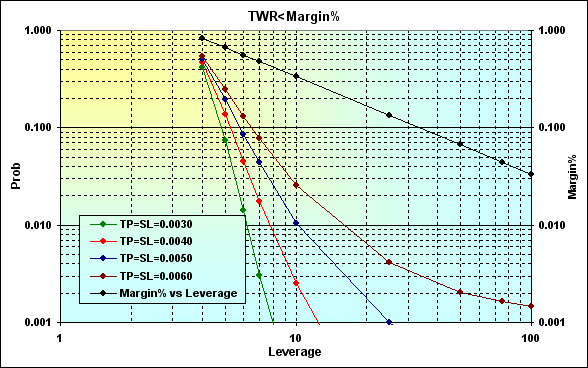
図22

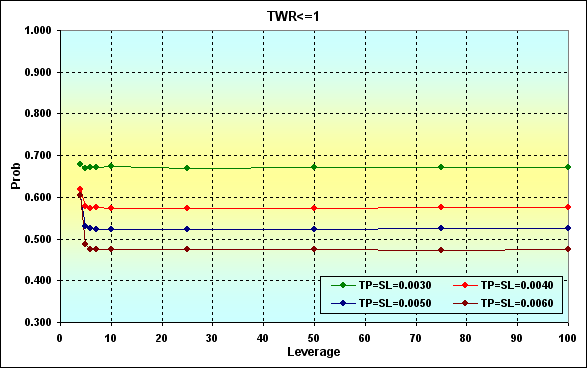
図23

図19で表示されたものと計算結果を比較すると、１取引での勝ちの増加が、破産と負けの確率の減少をもたらしていることがわかります。理に適った、そして予想できる結果です。

次の例は、TPとSLのレベルを考慮に入れた１取引において、負けの確率が勝ちの確率によってどう変わっていくのかを示しています。データは次のようになります。Deposit=3000、 LotSize=100000、Lots=0.1、 TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}、 Spread=0.0002、p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}、N=250、 Leverage=100。

注：破産の確率の値が小さく、またそれを検証する必要がないように、例を選びました。最も最悪な場合の、破産確率の最大値は、約0.04となりました。

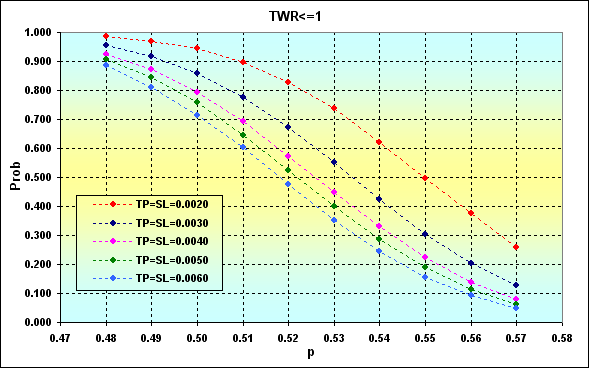
図24

何に気を付けるべきか。まず、最も明確なのは、pの上昇とともに、負けの確率が低くなることです。一方、TPとSLのレベルの減少が、負けの確率を高くさせます。その理由は、決められたSpreadの値があるからです。これらの結果から出すことができるもう１つの結論は、各取引においてレベルの低い取引は、リスクを伴うものであるということです。

以下の例では、Spreadの値が負けの確率に与える程度を表しています。シュミレーションの主なパラメータです。Deposit=3000、 LotSize=100000、Lots=0.1、 TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}、 Spread={ 0.00000, 0.00005, 0.00010, 0.00015, 0.00020、 0.00025, 0.00030, 0.00035, 0.00040, 0.00045}、p=0.55、 N=250、Leverage=100。

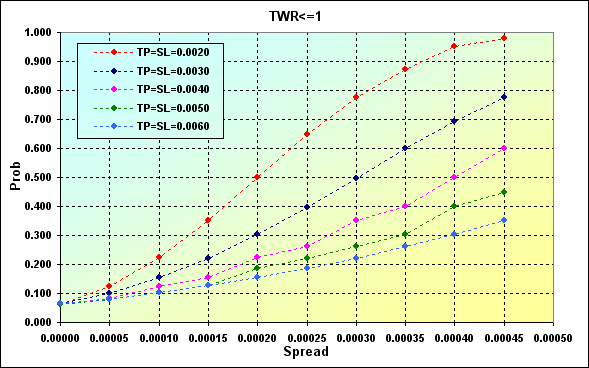
図25

次の図では、図24で引用されているデータに対する、方程式（1）で計算された、負けの確率と取引の期待値の間の一致を示しています。a%とb%の値の代わりに、TP%とSL%の適切な値が使用されました。

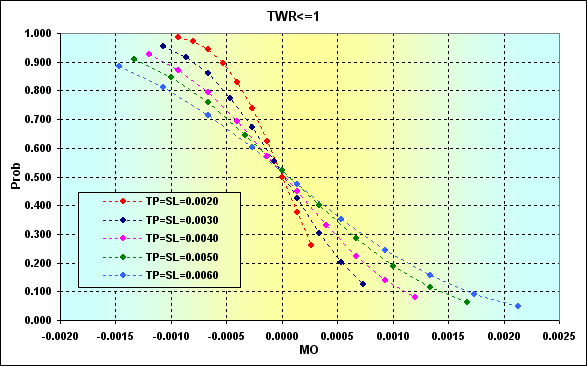
図26

図からわかるように、取引の期待値の増加は負けの確率の減少につながりますが、負けの確率はゼロにはなりません。これはつまり、プラスの期待値自体は、負けからの保護を保障するわけではないということです。破産からの保護も同様です。やはり、TPとSL の高いレベルは、負けの確率を低くしますが、それと同時に（図19と22を参照）これは破産の確率を上昇させます。

言い換えれば、私たちは古典的なコイントスのゲームについて結論したときに、証明されたことに戻ります。賭けの量を上げると勝つ確率の上昇（負けの確率の低下）につながりますが、それと同時に、破産の確率が高くなります。残念ながら、この資金管理メソッドを適用した際の、数学的に論拠された取引の量を選択する方法がありません。 それぞれの場合に、どのような破産または負けのレベルが妥当であるかという個人的な選択があるだけです。

ゲーム時に一定のTWRのレベルに達する確率の判別問題を見ていきましょう。シュミレーションの主なパラメータです。：Deposit=3000、 LotSize=100000、Lots=0.1、TP=SL= 0.0030、Spread=0.0002、p={ 0.48, 0.49, 0.50, 0.51, 0.52}、N=250、Leverage=100。

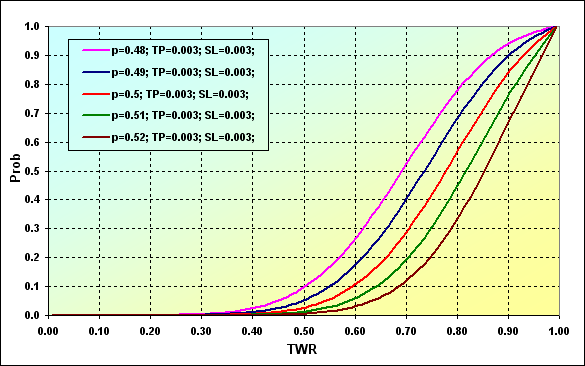
図27

グラフのデータは次のように解説することができます。p=0.48の場合に、TWR値がゲームの間に~0.90まで下がる確率は、~0.93です。p=0.52の場合は、~0.68になります。

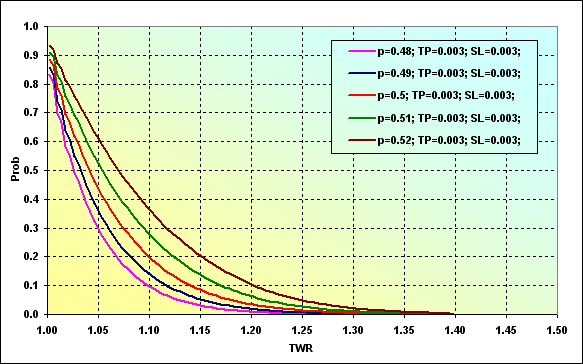
図28

この図では、ゲーム中にTWRのレベルが一定の値まで上昇する確率を表示しています。例えば、p=0.48の場合に、TWRの値がゲーム中に~1.10に到達する可能性は、~0.09となります。p=0.52の場合は、~0.37となります。１取引での勝ちの確率の上昇したときに、一定のレベルに確率が達するのは、十分論理的です。

ここでDrawdownについて少しお話しします。このパラメータの評価の為に、スクリプト[10]に若干の修正を加えたものを使用しました。さらに、オリジナルのスクリプトと違い、Spreadを含めて計算されます。

シュミレーションの主なパラメータです。：Deposit=3000、 LotSize=100000、Lots=0.1、 TP=SL=0.0030、Spread=0.0002、p={ 0.48, 0.49, 0.50, 0.51, 0.52}、N=250、Leverage=100。

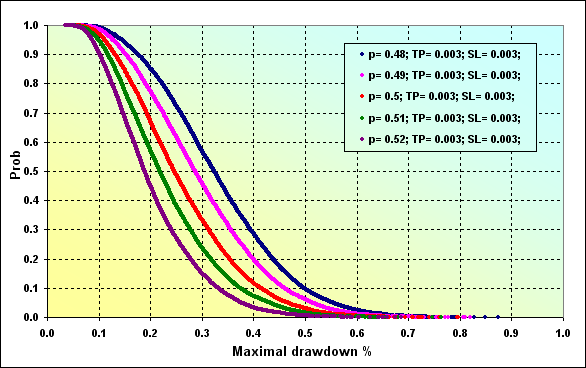
図29

図27で指定された初期パラメータを入力すると、p=0.48の場合、Maximal Drawdown % ~0.20が発生する確率は~0.85となります。p=0.52の場合は、~0.47となります。

次が最後の例です。：Deposit=2000、LotSize=100000、Lots=0.1、TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}、Spread=0.0002p=0.50、N=250、Leverage= 100。

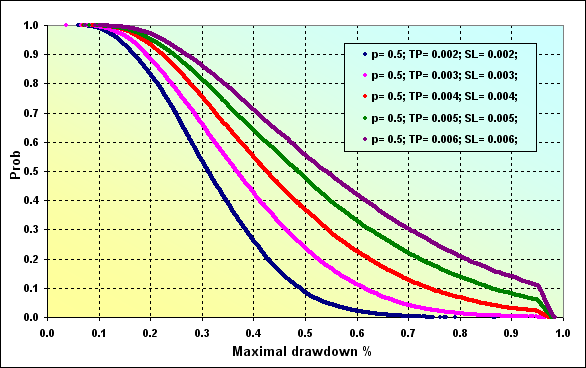
図30

図30に１つだけ小さい説明を加えたいと思います。Maximal Drawdown %=0.96のレベルは、Marginのレベルとほぼ同じなので、グラフ上では急激な線の折れ目があります。図29（赤い線）に引用された場合と比較すると、大きなMaximal Drawdown %に到達する確率が上がったことがわかります。

FixSizeの資金管理法のいくつかの特徴の考察を終える前に、このようなシュミレーションの評価のもう2つの分類、Profit FactorとExpected Payoffを引用したいと思います。

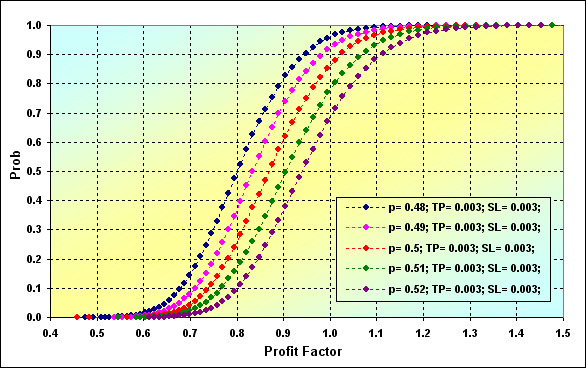
図31

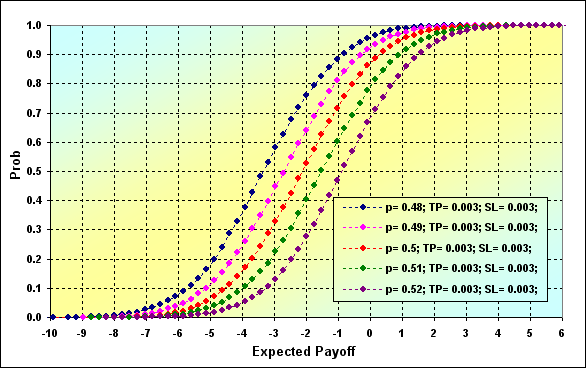
図32

図31と32のシュミレーションの主なパラメータです。： Deposit=3000、LotSize=100000、Lots=0.1、TP=SL= 0.0030、Spread=0.0002、p={ 0.48, 0.49, 0.50, 0.51, 0.52}、N=250、Leverage=100。

資金管理―固定割合(FixFrac)

現在の資金の量からの固定割合としての賭け金を持つ資金管理法の要点は、次のようになります。最初に、取引に使用する割合の量が、例えば10%と決定します。次に、取引結果にかかわらず、取引される資金の量が現在の資金の量から算出されます。このようにして、うまくいった取引の後で資金は増加し、その結果、次の取引の量も増加します。逆の場合も同じで、取引がうまくいかなかった場合、次の取引の量は減少します。時折、このような賭けのシステムはアンチマーチンゲールと呼ばれます。（が、概してこれはあまり正確ではない）このようなシステムは、決められた量の資金管理システムと違い、可能な利益を再投資することを前提としています。

説明：martingaleという用語には、いくつかの表記があることに関連して、この記事の目的は、それらのうちのどれが最も正しいかという問題を明らかにすることではないので、進歩的な方法のコイントスで決めた『マーチンゲール』という表記を使用します。　

このような資金管理法の長所と短所はよく知られています。一連の勝ち取引が行われる場合、このメソッドは資金の急速な成長を提供します。決められた量の方法において等差数列的に資金が増加するのに対し、ここでは等比数列として表されます。理論的には、賭けが無限に割り切れる場合、このメソッドでは全資産を負けることはありません（勿論、これは実際の取引の条件下ではこうはなりません）

メソッドの短所として、いわゆる「非対称レバレッジ効果」が挙げられます。この資金管理法では、負けの賭け場合に、それに続く次の勝ちの賭けは量が少なくなるということです。つまり、失敗してしまった賭けの組の『負けを取り返す』ためには、多数の成功した賭けが必要になります。その上、このメソッドの結果に、隠された一連の取引の組（非ベルヌーイ）を判別することがあります。

この資金管理法の実用の領域では、最も早い資金の成長を与え、その上、妥当な破産の確率を与える資金の一部の値を選択しなければいけないという問題があります。このような漸近的に最適なゲーム戦略を提議したのは、ケリー氏です。

しかし、初めに少し理論や数式についてお話しをしたいと思います。もし勝ちと負けの数、1取引あたりの勝ちと負けの量がわかっている場合、FixSizeの方法の時と同じように、TWR(V)とProb(V)を算出することができます。方程式（17）は方程式（4）と同一です。

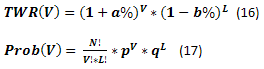
方程式16と17に基づいた計算例は以下のようになります。TWRの様々な値に達する確率は、累積値として引用されました。

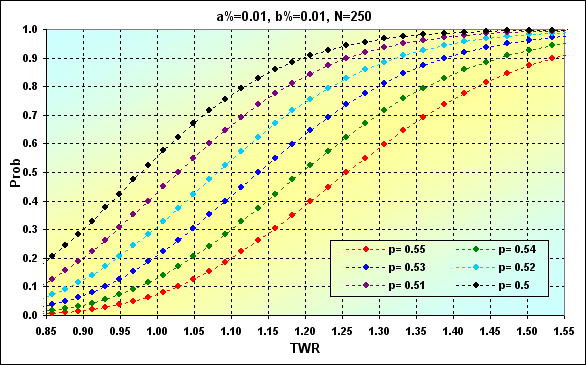
図33

次の図では、初期の条件は同じであるが、異なる資金管理法を持つ、2つのバージョンがお互いにどう関係していくかを示しています。決められた賭けのサイズを持つバージョンは、図8の例から引用しました。決められた賭けのサイズを持つ資金管理法(FixSize)のバージョンは赤色で、初期資金のうちから決められた割合を持つ資金管理法(FixFrac)は黒色で示しています。

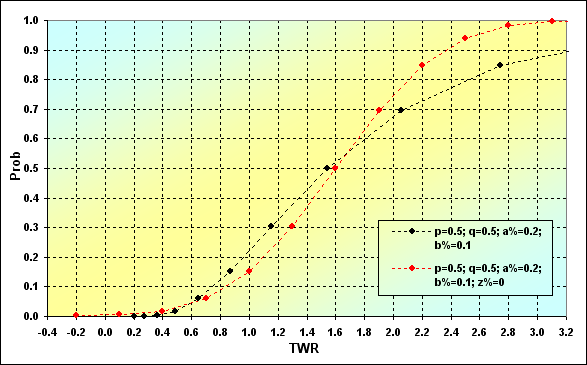
図34

利益と損失のサイズが等しい場合の、資金増加の速度を表す方程式は以下のようになります。

単純な変換と[8]の考察で、予想平均の幾何学的成長を最小化し、最適な賭けの量をf*を評定する次の式へ進むことができます。

それは、いわゆる「ケリー基準」です。その内容はとても簡単です。もしあなたに的中率が0.5以上の取引システムがあり、勝ち取引の量が負け取引の量に等しい場合、方程式19に基づき計算された資金の一部を毎回賭ける必要があります。例えば、p=0.55ならば、f*=0.55-0.45=0.10です。つまり、常に資金の10分の1を賭ける必要があり、これが資金拡大の最大限に可能なスピードを提供します。

注：ケリーの最適な賭けのサイズの式は、[4]で引用されたヴィンスの最適な賭けのサイズの式とは異なります。。いかなる間違いもヴィンスの式にはありません。また、それはなぜなのかをこれから先に明らかになります。

注：p=0.50の場合に、方程式に基づいて資金の割合の最適値を計算すると、結果は理に適って0.00になり、つまりこれ以上プレイしないことを勧めるものになることが興味深いです。

勝ち取引の量と負け取引の量がk倍違う場合、18と19の方程式の代わりに他の方程式を使用する必要があります。[8][5]。

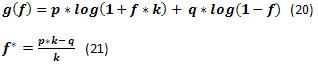
方程式20にを使用し、fからのg(f)の変化グラフを作成すると、以下のような図を見ることができます。この図ではf*の点がマークされていますが、これは資金の拡大速度が最大である場所、グラフの最高点です。また、追加の点fcが表示されていますが、これは資金の拡大速度がゼロになる場所、ゼロラインとの交差ポイントです。

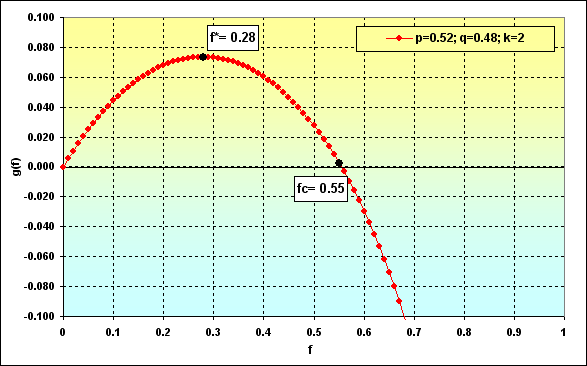
図35

説明： 図35の計算の為に選択されたパラメータk=2はヴィンスの本の中で引用されているグラフに対する皮肉として使用されています。しかしながら、このようなкは、大きな『可視性』と『審美性』を提供します。

[8]では、指定された条件でゲームが行われる場合、f*は、最大の資金拡大速度と0％の破産率を与えると証明しています。そのうえ、使用する資金の割合がf*よりも少ない場合、破産の確率は同様にゼロになりますが、資金拡大速度は遅くなります。もし使用される資金の割合がfcよりも多い場合、破産は避けられません。（この場合における破産とは、あらゆる少額の資金の値を意味します）もし資金の割合が、f*からfcまでの範囲内にある場合、拡大速度は同様に最大のものよりも遅くなりますが、破産の可能性はありません。

非常に印象的な結果ですが、これは理論的な計算であり、いくつかの現実を考慮したものではないことに留意する必要があります。それ故、ヴィンス氏[4] は、最大損失を含めたfсの最適値を計算することを勧めています。これは、全ての出た結果とともに数学的に厳しく計算されたものよりもf*の値が低くなることにつながります。

これがグラフ上で、どのように見えるのかを見てみましょう。このような場合を用います。：Deposit=1000、 LotSize=100000、f={ 0.01, 0.02, 0.03, 0.04, 0.05}、TP=SL=0.01、Spread=0.0000、p=0.51、N=250、Leverage= 100。これらの入力データの時、初期のLotsは0.01で、TP%=SL%=0.01となります。そのほか、f*=0.02とfc=0.04で、次の図で示されています。

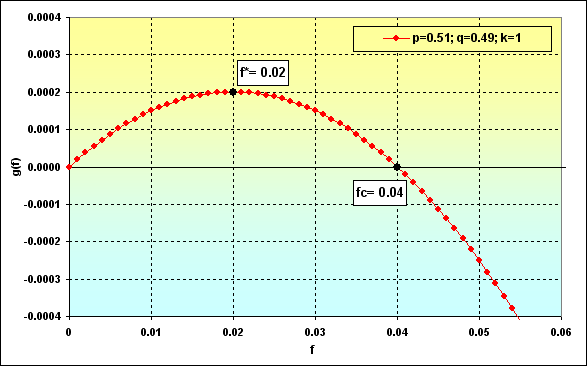
図36

fが変わった場合、次のようなTWRからのProbの変化の関係になります。これの為にいくつかの計算を行います。

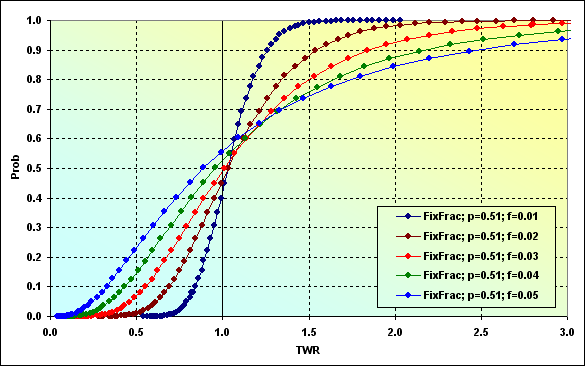
図37

詳しく見ていきましょう。f=0.01の線は、f<f*という資金成長速度が最大値よりも少なく、同時に破産率はゼロである状態を表しています。その際、負けの確率TWR<=1は~0.40ぐらいです。

次は、使用する資金の割合が最適であるf=0.02という場合です。負けの確率は~0.45となりました。いいかえれば、ゲームの大半は利益をもたらすはずです。

計算のバージョンはf*<f<fc、つまりf=0.03です。負けの確率は~0.45となりました。この条件下では破産はありえません。しかし、TWRがそこまで低くなることがある値は、以前の場合よりもより重要です。同様に、大きな利益の可能性があります。

ここで、負けの確率が~0.50になる条件、つまりf=fc=0.04です。この場合、TWRはほぼ確実に0から+無限までの間で変動します。

そして、最後のバージョンは、f>fcです。負けの確率は~0.55です。非常に大きな利益がでる可能性がありますが、最終的には（「無限」の場合に）全ては損失になり、TWRは破産に分類することができるレベルまで下がります。

もう少し方程式についてお話しをします。資金成長速度の評価g(f)は、方程式18と20で行うことができます。成長速度g(f)と取引数Nを知ることで、 TWRを方程式22で算出することができます。その他、FixFracの資金管理法の為の、取引からの平均利益の期待値を算術平均としてではなく、幾何平均Gmeanとして方程式（23）で評価した方がより正確です。

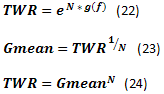
アドバイス：メタトレーダーのストラテジーテスターの標準レポートで、取引の幾何平均計算がオンになっていることが望ましいです。これによって、FixFracの資金管理法を使っている取引システムの質をより正確に評価することができます。

図36のデータを使用した、方程式（23）と（24）による計算の2つの例は、以下の通りです。

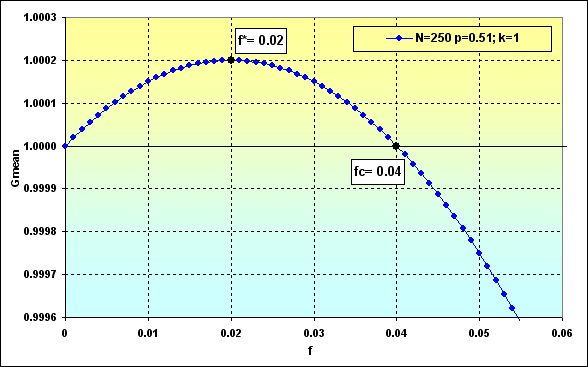
図38

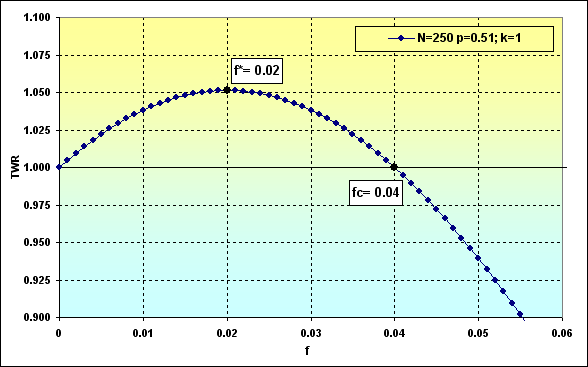
図39

このように、図39からわかるように、指定された条件で最適な賭けの割合の場合、総資産はTWR=1.05という値に向かいます。さらに、図37で指摘されているように、負けの確率は~0.45になります。

同じ初期条件下で、異なる資金管理法がどうなるのかを比較するのは面白いと思います。図36のデータを使用する場合、このような図になります。

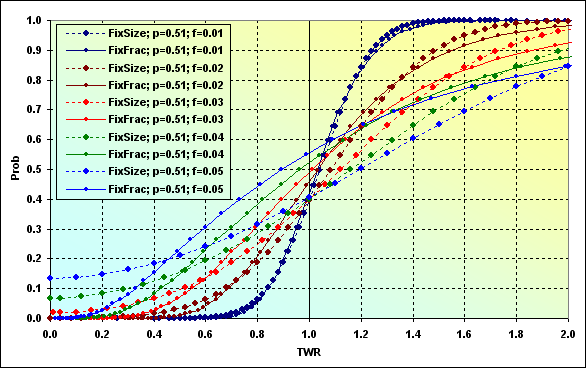
図40

f=0.01の場合に、異なる資金管理法のグラフはお互いにとても類似しています。つまり、特定の条件下では同じような結果になるということです。他の場合では、同じ初期条件下での、FixSizeの資金管理の負けの確率(TWR<=1) は、FixFracの資金管理の負けの確率より低いことがわかります。

注意：上記の結果は、選択された入力データのみに適用されるものであり、どのような場合にも原則として適用されるものではありません。

取引に使用する資金の割合によって、TWRが向かう値がどう依存するかという、もう一つの面白い事象を見てみましょう。FixSizeの資金管理法のこれらの値は、期待値にNを掛け、FixFracの資金管理の方法のこれらの値は方程式22に基づくことで算出することができます。

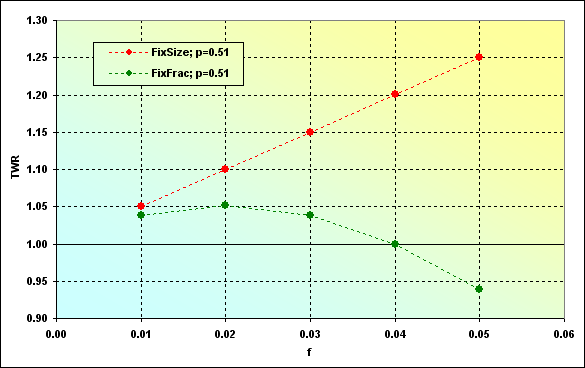
図41

見るとわかるように、FixSizeの資金管理法を使用した際の期待利益の方が多いです。（使用した入力データの場合）しかしながら、これはいつもこうなるわけではありません。

１取引における異なる勝率を含む資金の割合から、TWRが受ける影響がどのように変わるのかを見ていきましょう。N=250の組の長さのグラフを以下に引用します。

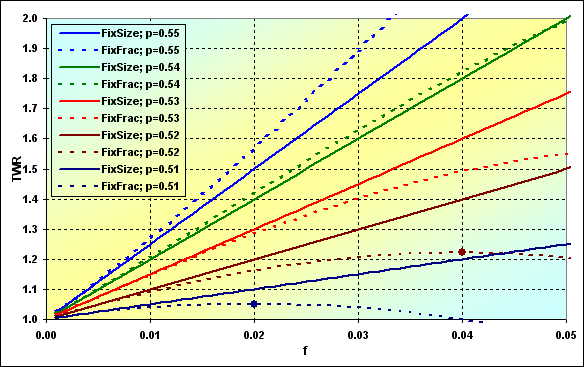
図42

このようにして、特定の条件下では、TWRの期待値という観点で見ると、FixSizeの資金管理法の方がFixFracの資金管理法よりも望ましい状況があり得ます。しかしながら、破産到来の確率と一緒に見た場合、これはそれほど明らかではありません。

その他にも、TWRの期待値に、Nの組の長さが大きく影響を与えます。組の長さが長ければ長いほど、FixFracの資金管理法の方が優勢になります。

これで、いくつかの理論的ポイントの検証を終わりにし、シュミレーションへ移りましょう。実際には、最小ロットと最大ロット（MinLotとMaxLot）という概念を追加しなければいけないこと以外、初期のシュミレーションでは何も変わりありませんでした。また、私たちにはLotStep値というロット変更の最低限の値が必要になります。計算実行のアルゴリズムは以前のものになります。その他、MinDepositという最低可能デポジット値の概念が追加されます。このようにして、デポジットの値がMarginとMinDepositの値を超える場合のみ、取引を続けることができます。

以下に、次の入力データによる異なる資金管理法のシュミレーション例が引用されています。Deposit=1000、MinDeposit=300、LotSize=100000、MinLot=0.01、LotStep=0.01、MaxLot=100、f={ 0.01, 0.02, 0.03, 0.04, 0.05}、TP=SL=0.01、Spread=0.0000、p=0.54、N=250、Leverage=100。個別に注意をしておきたいのですが、この計算ではSpreadは使用されていません。

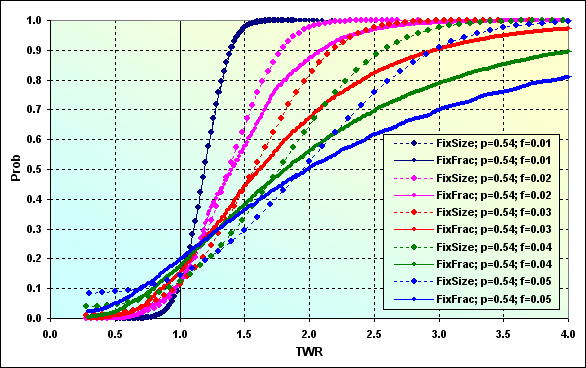
図43

計算へMinDepositを追加することで、理論的に破産が不可能なFixSizeの資金管理（f<fcの場合）にその可能性を生じさせました。そして、特定の条件下では（ここでは書かれていません）離散化やロットサイズの制限が、同様に破産の可能性の発生につながります。計算の中でDepositとMinDepositの値の差を初期資金に適用することで、マイナス要因の影響を下げることができます。実際に、それはまさにヴィンス氏が提案したように、最適な資金の割合を計算するためには、資金の一部のみを使ったほうがいいということです。とても合理的な解決策ではありますが、これは原則的にTWRの低下につながります。

ここで、もう少し図43に説明を加えたいと思います。グラフ上でProb=0.50と一致する、『FixFrac; p=0.54; f=0.05』の値を見つけてみましょう。これは中央値で、これより小さかったり大きかったりする値は、全ての値の50%です。この場合ではTWR~2.00と一致します。言い換えれば、ゲームの全ての結果の半分は、少なくとも初期資金を２倍にしました。この時、負けの確率は~0.20で、破産の確率は~0.03となりました。『FixSize; p=0.54; f=0.05』のグラフと比べることで、破産の確率は~0.08まで上昇し、負けの確率は~0.14まで低下しますが、中央値はほぼTWR~2.00に一致することに気が付くことができます。もし幸運にも、TWR>2.00である、この半分の事例に当たることがあれば、FixFracの資産管理法を使用した時よりも結果は低くなるでしょう。

図42と図43のグラフを比較すると、図42にあるTWRが向かう値が、図43の中央値ではないことに気づくことができます。

次に、図43の場合で、ただし今回はSpread=0.0002を含めた事例を見てみましょう。全ての他の入力データは以前のものです。

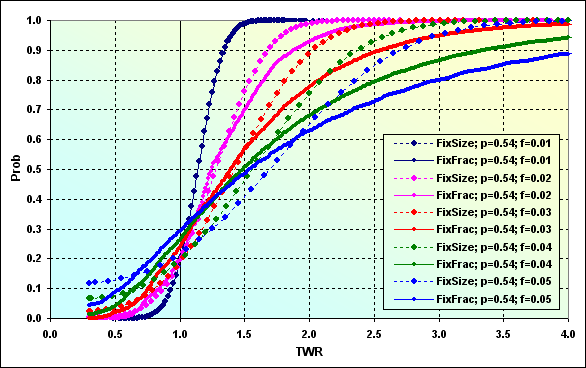
図44

見るとわかるように、１取引あたりの勝ち/負けレベルの0.4%から2%までで形成されるSpreadは、大きなグラフの変化をもたらします。これがよくわかるのが、図43と44の2つの計算の比較を示す次の図です。

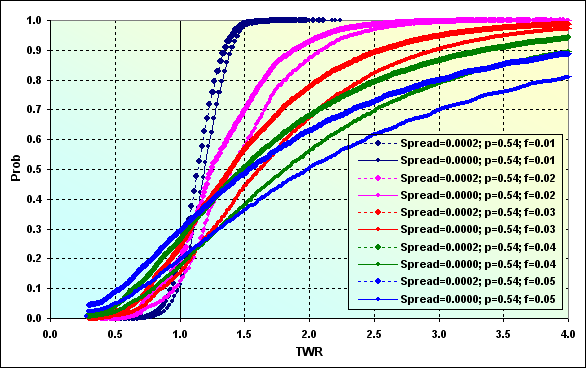
図45

このようにして、Spreadを考慮にいれることで、TWRの中央値（例えば、青色の線）が、2.00から1.50まで下がりました。負けの確率は0.20から0.30まで上がりました。この差は全部で0.10とあまり大きくないように思えますが、別の方法で見た場合、一つ目の場合では５人に１人が負け（負けではあっても破産ではない）、２つ目の場合では３人に１人が負けになると言えます。

次の入力データを使用した異なる資金管理法をシュミレーションしつつ、異なるfを含んだ１取引での勝ちの確率から負けの確率がどのように変わるかを見ていきましょう。: Deposit=1000、MinDeposit=300、LotSize=100000、MinLot=0.01、LotStep=0.01、MaxLot=100、f={ 0.01, 0.02, 0.03, 0.04, 0.05}、TP=SL=0.0100、Spread=0.0002、p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}、N=250、Leverage=100。

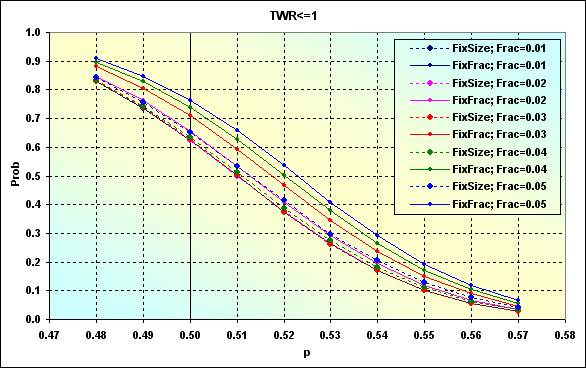
図46

図24に示された例とこの場合では、TPとSLのレベルが固定されていて、しかしロットサイズが変わるという点が異なります。図47では、図46と同じデータであるが、TP=SL=0.0050である場合を表示しています。

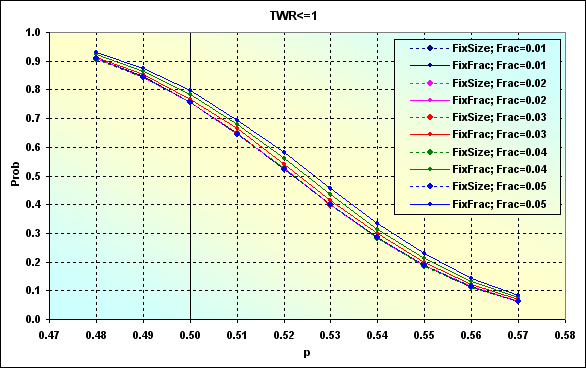
図47

図24で表される状態と同じように、TPとSLのレベルの低下は、負けの確率の上昇をもたらしました。 又は、異なる事例の間の数値でのばらつきが減ります。グラフがより『集中的』になりました。言い換えれば、f値の影響が減ったということです。次の図で、特にそれが良く分かります。

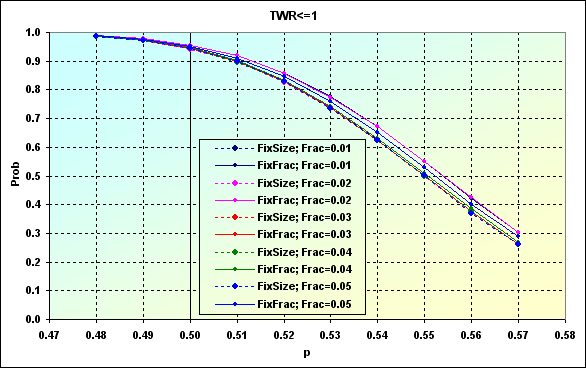
図48

この場合には、TP=SL=0.0020というレベルが使用されました。図からわかるように、Spreadの影響を相殺し、負けの確率がせめて0.50以下になるようにする為に、この場合ではp=>0.56を与えることができる取引システムが必要になります。しかし、一般的に、もし取引システムが100の事例のち50を当てることができるだけならば、この場合、どんな資金管理システムを使っても、そんなfのレベルを適用しても、結果は大体同じようなもので、250回の取引後の負けの確率は、~0.95になります。

TP=SL=0.0020でp=0.56である場合のTWRがどう見えるかを示す為に、計算を行います。結果は以下の通りです。これは、まさに図48にあるような負けの確率が約0.40のバージョンであり、その際のTWR の期待値は1.01...1.04です。そして、異なる資金管理法がお互いに近い値を示しています。

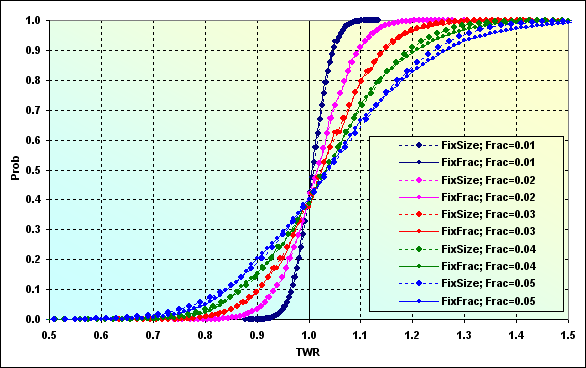
図49

もう一度注意をしておきますが、これは小さいレベルの場合のものです。もしSpreadが浮動値で、賭けの量とは関係のない固定の手数料としてではなく、賭けの量からのパーセントで徴収されたとしたら、『幅広い需要者のためのFX』ではない、他の市場で起こるような、違った状況になっていたでしょう。

入力データの計算に戻りましょう。: Deposit=1000、MinDeposit=300、LotSize=100000、MinLot=0.01、LotStep=0.01、MaxLot=100、f={ 0.01, 0.02, 0.03, 0.04, 0.05}、TP=SL=0.0100、Spread=0.0002、p=0.51、N=250、Leverage=100。一定のレベルまでのTWRの低下の確率がどう見えるかを見ていきましょう。

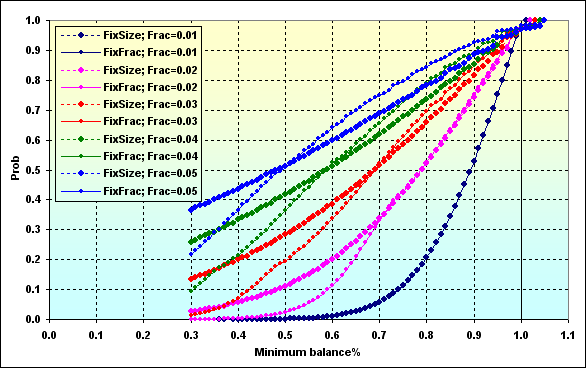
図50

グラフのデータの解釈は、図27と全く同じように行う必要があります。FixFracの資金管理法を使用した時のTWRの値がゲーム中に ~0.70まで下がる確率は、f=0.05の場合には~0.76になります。f=0.02の場合には、~0.34になります。

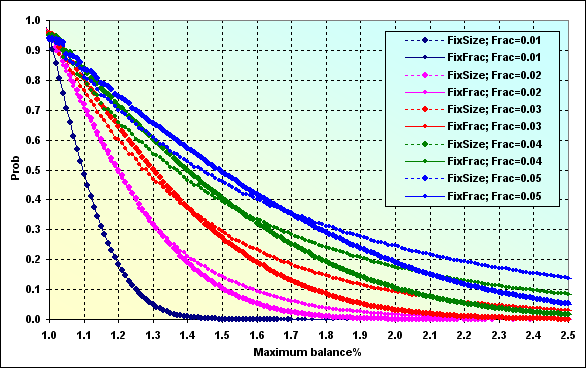
図51

ゲーム中にデポジットが一定の値に増加する確率はこのようになります。グラフのデータの解釈は図28と同じように行う必要があります。

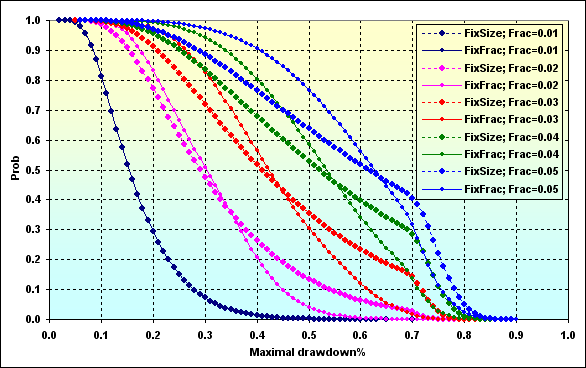
図52

最後のグラフは、使われる資金の割合に応じた特定の値のMaximal Drawdown %の確率を表示したものになります。一般に、FixFracの資金管理の方法はFixSizeの資金管理の方法に比べて、大きなDrawdownの値に達します。これは非対称レバレッジに関係しています。その他にも、もしfc>f>f*,である場合、f<f*の事例に応じた同じ収益量である時、より小さいDrawdownが予想されます。

まとめ

私たちは2つの資金管理方法を検証し、この方面の発展を促した前提条件を検証し、簡単にいくつかの理論的側面といくつかの最も簡単な方程式を調査しました。また、私たちは確率論的シュミレーションを行い、取得した結果を評価し、それらを様々な方法で比較することを試みました。そして、おそらく、この研究から出すことができる最も重要な結論―２つの研究したもののうちから一義的に優れたものを選ぶことは不可能です。資金管理法の効果は、実に多くの要因に影響をされます。これらの要因の様々な組み合わせが、異なる結果を与えます。したがって、取引システムの特性や、取引センターの条件、トレーダーの能力や希望によって、最も適している資金管理システムを選択する必要があります。この問題を解決するいくつかの方法、注意をしなければならない特性についてもこの記事に記しました。読者の皆さんの内の誰かに、この退屈な記事が多少でも役に立つことをとても願っています。皆様に幸運を。

これからの計画としては、マーチンゲールの検証（このメソッドの性質の明確さゆえ、あまり大きな記事にはならないと思います）とR.ジョーンズ氏のメソッド（著者によると、2つの研究を行った資金管理法の長所を合わせたもの）の検証を行いたいと思います。

ネット上にあるリソースへのリンクと文献（本文中の記載順）

1. Agner Fog - Pseudo random number generators - http://www.agner.org/random
2. strator - Probability Library (part of Cephes) - https://www.mql5.com/ru/code/10101
3. Suvorov V. - MS Excel: Data Exchange and Management - https://www.mql5.com/en/code/8175
4. R.ヴィンス- 資金管理の数学
5. ベルシャスキーA.V. - リスク管理の方法の研究(2002年)
6. スミルノフ А.V., グリヤノヴァ Т.V. - 『ラルフ・ヴィンスの最適 f 値』について
7. フェラー V. - 確率論とその応用
8. トルプ E. - ブラックジャックやルーレット、金融証券所でのケリー基準
9. ブラシャエフ S. - トレーダーの為の統計(電子版、199ページ)
10. スタリコフ S. - EAバックテストの結果の独自評価 -  https://www.mql5.com/ru/articles/1403

例

記事にはこれを執筆した際に使用した公共ライブラリが添付されています。スクリプトやプログラム自体は添付しません。これはMQLトレーダーコミュニティーの、取引サーバーの利用可能なエミュレーターの書き込みを活気づける為に、故意に行ったことです。まさに取引サーバーのエミュレーターがシュミレーションに使用されました。

言い訳

筆者が読者に対して一切の責任を負いません。苦情や提案は書面やメールで受け付けています。賢明な提案は拝見しますが、愚かしい苦情は無視させていただきます。分かっている著作権は全て記載しています。そうしないと、著者不明もしくは著作権が失われてしまいますから。

筆者は文面や計算で不正確さや間違いをしている可能性があることを認めます。長文で内容も難しいので、これは避けられません。その為、D.クヌトの例のように、１つの間違いを見つけるごとに1ドルの賞金を出したいと思いました。しかし、人生が自分の修正を行いました。世界金融危機の北風が国の上に吹き続けています。いつもと同じように、こういった場合には、私たちの中の最も弱く無防備な人々ー孤児になった子供達がもっとも苦しみます。彼らを助けたいと思い、筆者は自分の失敗に対してお金を出すのではなく、慈善団体に全ての可能な金額を送ろうと決めました。幾つかのロシアの国立孤児院をランダムに選んで、この孤児院の住所にお金を送りました。

孤児院の院長から寄付金に対しての手紙を受け取った時は、何とも言い難い感動でした。普通の郵便で、学校のブロックノートの紙に書かれた手書きの質素な手紙です。勿論、感謝の言葉もありましたが、一番はこのお金で何が買われたかが全て書かれているリストです。この聡明な女性は、このお金を感謝の気持ちをコピーアンドぺーストするのに楽になるパソコンに使いませんでした。自分のオフィスの新しいカーテンを買ったわけでもありません。首都のようにきらびやかではなくとも、国家が子供達に食べさせているような食べ物に使ったのでもありません。全て子供達の未来や子供達の教育に使われていました。

ノート、マーカー、ペン、教育ゲーム、教科書、絵の具。全て正常な発達の為に必要で、すぐに無くなってしまうものです。小さな地方の町や田舎に住む子供達の古い木造の家は、祖国戦争から戻ってきた私たちの祖父たちが手作業で建てたものかもしれません。もしそれがあなたの最後のお金ではないなら、けちらずに面倒臭がらずに、彼らを助けてあげてください。これはあなたの為になります。実際、この手紙を酒飲みの警備員が予期せぬ幸福に対して書いたものかどうかもわかりません。しかし、私にはそれは興味がありませんし、私は本当はどうだったのか知ることはありません。私はただ、自分がまともな人々の中で生きている確率が遥かに高いことに小さいながらも賭けているだけです。そしてこのゲームは、コインゲームとは異なり、私たち皆に平等なものです。