К вопросу об управлении капиталом

Эпиграф:

Введение

Процесс торговли условно можно разделить на две относительно независимые части. Первая часть, называемая торговой системой (ТС), выполняет роль анализа текущей ситуации, принятия решения о начале сделки, её типе (покупка\продажа) и моменте завершения сделки. Размеры средств, которые участвуют в каждой сделке, определяются второй частью, называемой системой управления капитала. В данной работе проведена попытка анализа некоторых стратегий ММ в зависимости от изменения их параметров. Для анализа выбран метод имитационного моделирования. Однако в некоторых случаях будут рассматриваться и результаты аналитических решений. Средствами проведения анализа выбраны торговый терминал МТ4 и Excel. Дополнительно используются библиотеки обеспечивающие генерацию псевдослучайных чисел (ГПСЧ) [1], статистические функции [2] и модуль передачи данных из МТ4 в Excel [3].

Изначально предполагается, что любой процесс торговли (ПТ) обладает некоторой степенью неопределенности. Выражается это в том, что характеристики ПТ известны с некоторой степенью достоверности и никогда не известны точно. Хорошим, и наверное самым простым, примером такого ПТ может служить стратегия "случайных ставок". При ней трейдер случайным образом (например, подбрасывая монетку) делает ставку на то, вырастет курс одной валюты относительно другой на определенное количество пунктов или снизится. Процесс образования курсов валют, скорее всего, никак не связан с результатами подбрасывания монетки трейдера. Следовательно, мы имеем ПТ, в котором результаты сделок ни как не связаны друг с другом (бернуллиевы). Кроме того, мы не можем точно знать, как именно выпадет монетка в следующий раз, и угадает ли она движение курсов в будущем. Известно лишь, что совпадение будет примерно в 50 случаях из 100 при достаточно большом количестве попыток. Многие трейдеры уверены, что их торговля отличается от такой. Возможно это и так, но для начала мы рассмотрим именно этот случай. В дальнейшем посмотрим, как ведет себя система, в которой удается угадывать более 50 случаев из 100, и что влияет на результативность таких систем.

Структурно статья построена таким образом, чтобы сначала были рассмотрены наиболее интересные характеристики ММ на "теоретических" примерах. Далее мы попытаемся провести моделирование поведения ММ с данными похожими на условия реальной торговли на ФОРЕКС. При этом хотелось бы отметить, никакая ТС не будет рассматриваться в непосредственном виде. Предполагается, что какая бы ТС не использовалась, она всего лишь обеспечивает нас данными о выигрышах и проигрышах с заданной вероятностью и размерами самих выигрышей и проигрышей. Вопросы, связанные с определением независимости (бернуллиевости) результатов реальных сделок, а так же оценкой стационарности свойств ТС во времени, в данной работе не рассматриваются.

Как уже говорилось, будет использовано моделирование. Процесс моделирования состоит в том, что на основе генерации псевдослучайных чисел с заранее заданными характеристиками устанавливается характер результата очередной ставки, выигрыш или проигрыш. Размер ставки определяется выбранной стратегией ММ. Если произошел проигрыш, то сделанная ставка вычитается из текущего капитала игрока. Если выигрыш, то капитал увеличивается. Моделируется определенное число сделок, по окончанию которых происходит расчет общих результатов. После этого всё повторяется большое количество раз (от нескольких сотен до нескольких сот тысяч), после чего результаты усредняются подходящим для этого образом.

Некоторые базовые понятия и сокращения

В первую очередь хотелось бы сказать об используемом в дальнейших рассуждениях понятии "относительного финального результата" - TWR (Terminal Wealth Relative). Он представляет собой общий доход от серии сделок в виде множителя к начальному капиталу. Т.е. если конечный капитал разделить на начальный, то это и будет TWR. Например, если доход составил 12%, то TWR=1.12. Или если проигрыш составил 18%, то TWR=0.82. Удобство его использования состоит в том, что появляется возможность сравнивать результаты различных ПТ вне зависимости от абсолютной величины начального капитала. Сам термин TWR взят по аналогии с [4], [5], [6].

Следующее, о чем необходимо сказать, - это понятие "выигрыша". Выигрышем будет считаться любой результат, если его значение больше начального. Т.е. выигрыш - это ситуация, когда TWR>1. Соответственно, "проигрышем" будет считаться всё, что не является выигрышем, TWR<=1. Таким образом, случай, когда конечный капитал равен начальному, TWR=1, так же будет входить в понятие проигрыша. Но там, где это будет необходимо, данный случай будет рассматриваться отдельно. Кроме этого, существует понятие "краха", обозначающее такой проигрыш средств, неважно в результате единичной сделки или в результате серии сделок, после которого невозможна дальнейшая торговля. Например, проигрыш всех средств (TWR<=0) или случай наличия средств менее некоторого определенного минимума (залога).

Теперь несколько слов о сокращениях, которые будут использоваться далее. Вероятность выигрыша будет обозначаться символом p. Обычная размерность для неё - доли единицы. То же самое касается вероятности проигрыша, символ q=1- p. Общее число сделок - N, при этом число выигрышных сделок - V, и проигрышных - L. Размер выигрышных сделок в абсолютных величинах будет обозначен символом a, проигрышных сделок - b, при этом отношение размера выигрыша к проигрышу - как k= a/b. Если речь будет идти о размерах выигрышных\проигрышных сделок в долях относительно величины капитала, то обозначения будут соответственно a%, b%. Отношение a% к b% будет k. Отмечу, что величина ставки от капитала будет обозначаться как f.

Вероятность событий, которые мы будем получать по время расчетов, будет обозначать как Prob. Другие обозначения будут вводиться по мере необходимости.

Кроме того принято, что в данной статье не различаются понятия "ставка" и "сделка". И обозначают одно и то же - единичную торговую операцию (ЕТО). Серия таких ЕТО будет называться игрой или торговлей в зависимости от контекста. Хотя многим трейдерам это и не нравится, но термин игра хорошо характеризует те неопределенности, которые возникают во время торговли.

История вопроса и предпосылки

История рассмотрения свойств ТС, основанной на результатах бросков монетки, насчитывает довольно большой промежуток времени. В самом простом виде это была азартная игра, которая называется "орлянка". Игра состоит в том, что два игрока изначально обладают каким-то капиталом. Подбрасывается монетка, и если она выпадает "орлом", то один игрок получает от другого игрока часть его капитала. В обратном случае отдает часть своего капитала. Для математиков это - классическая "задача о разорении игрока". Она довольно хорошо изучена, и известны результаты игр, которые можно ожидать в зависимости от начальных параметров.

Для трейдеров наиболее интересны принципиальные результаты решения "задачи о разорении игрока, играющего против очень богатого соперника". Под очень богатым соперником здесь подразумевается дилинговый центр (ДЦ). Или если вы уверены, что вы действуете не против ДЦ, то считайте своим очень богатым соперником всех участников ФОРЕКС.

В чем суть проблемы в такого рода игре? Мы не будем рассматривать варианты с бесконечно продолжающейся игрой. Никто не играет бесконечно долго, да и выводы там неутешительны. Рассмотрим случай, когда игра конечна и состоит из N сделок. Допустим, что вероятность, с которой вы можете угадывать, - p>0.50, а размер выигрыша и проигрыша равны, a=b. Также допустим, что вы хотите, чтобы ваш выигрыш за N сделок был наибольшим из возможных.

Наилучшая стратегия добиться максимального выигрыша в этой игре состоит в том, чтобы каждый раз ставить максимально возможную ставку, т.е. все средства. Но математически строго доказано, что в этом случае вероятность краха можно вычислить по формуле 1-(p N) и она зависит от N. [7][8] Чем больше N, т.е. количество ставок, тем выше вероятность краха. Следовательно, наименьшая вероятность краха будет при N=1, если играть обязательно. Если играть не обязательно, то самая выигрышная стратегия - вообще не играть, вероятность краха нулевая.

Примечание: обращаю внимание на одно распространенное заблуждение. Многие полагают, что если в игре шансы равны, то их выигрыш примерно нулевой. Это было бы так, если бы они играли против соперника с сопоставимым капиталом.

Применительно к реальному трейдингу это означает, что даже если вы умеете угадывать выигрыш в 2 случаях из 3, но каждый раз заходите всеми своими средствами, то произойдет следующее. Вероятность краха на первой сделке будет равна 1/3 - и это неплохо, но уже к десятой сделке вероятность того, что вы потерпите крах ~0.98.

Таким образом, требование получить максимальную прибыль приводит к абсурдной ситуации - сыграть на все деньги, но всего лишь один раз. Конечно, это не очень привлекательно, так как очевидно, что в вашей игре конечный выигрыш должен быть выше при большем количестве ставок.

Увеличить продолжительность такой игры и при этом снизить вероятность краха можно за счет отказа от требования максимального выигрыша, т.е. отказаться от игры с максимальной ставкой, использовать только часть средств от всего капитала. Если эта часть очень маленькая, то игра может продолжаться очень долго. Это тоже доказано математически. [7][8] Но при этом возникает ситуация, что и окончательный выигрыш будет небольшим. Получается, что большие ставки ведут к увеличению общего выигрыша, но и к увеличению риска проигрыша. Маленькие ставки уменьшают риск, но также уменьшают и выигрыш. Поэтому закономерно встает вопрос о том, какую часть капитала наиболее оптимально (с определенной точки зрения) использовать.

Такова обычная цепь рассуждений и предпосылки. Изучение данного вопроса не стояло на месте. Появилось целое направление, призванное решать данную проблему, которое называется в общем виде "управление капиталом". Существует несколько методов ММ, которые обеспечивают те или иные возможности по удовлетворению требований вероятности краха и размера выигрыша. Все эти методы мы рассмотреть не сможем в виду ограниченности рамок статьи, поэтому остановимся на двух из них: метод, основанный на определении ставок фиксированного размера, и метод ставок фиксированной доли от капитала.

Немного из теории

Если опустить все математические премудрости, то ключевым моментом в ММ является вопрос, который можно сформулировать следующим образом: какова вероятность наступления того или иного события (например, рост капитала вдвое или разорения) через определенное время (например, числа сделок). По существу, это - вопрос о перспективах, поэтому время можно зафиксировать и рассматривать только два параметра - вероятность события и само событие.

Если рассматривать "орлянку" в самом простом её виде, то зная количество ставок N, можно рассчитать некоторые вещи довольно легко. Например, математическое ожидание (МО) дохода за одну ставку (1) или ожидаемый доход за серию ставок (2). Обращаю внимание, что МО в данном случае определяется относительно начального капитала. Это означает, в случае МО>0 - положительное ожидание, и в случае МО<0 ожидается, что каждая ставка в среднем приносит убытки.

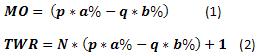
Для случая, упомянутого в [9]: p=0.45, q=0.55, a%=0.08, b%=0.05, N=20, результаты будут - MO=0.0085, TWR=1.170. Случай данный интересен тем, что при вероятности выигрыша p<0.5 всё равно получается положительное МО на одну ставку, и, как результат, ожидается выигрыш ~17% к первоначальному капиталу.

Предупреждение: в [9] рассматривается другой метод ММ, поэтому, несмотря на одни и те же исходные данные, результаты будут различаться.

Однако ожидание сродни средней температуре по больнице. Ничего не говорит нам о том, какова вероятность появления тех или иных результатов в зависимости от конкретного числа выигрышных ставок. А без этого трудно оценить риски. Поэтому введем ещё две формулы: для расчета дохода при известном количестве выигрышных ставок (3) и расчета вероятности появления в серии определенного количества выигрышных ставок (4):

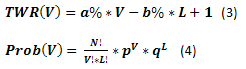
Теперь остается посчитать значения для всех V= 0,1,...,N, L=N-V и построить график изменения Prob(V) от TWR(V). Для приводимого ранее случая график будет выглядеть следующим образом. Обращаю внимание, что на графике указаны оси Prob и TWR без индекса (V). Сделано это исключительно для упрощения восприятия.

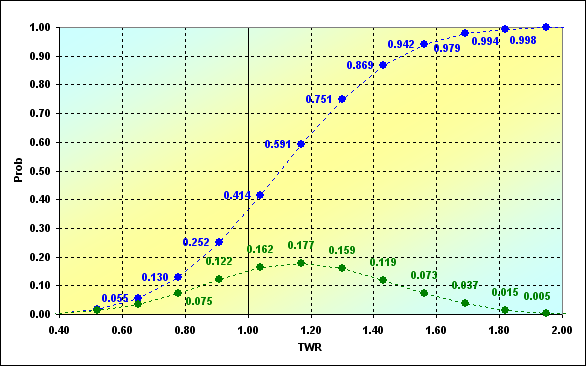
Рис.1

Результаты наших расчетов по формулам (3) и (4) представлены зелеными точками. Интерпретировать график можно следующим образом. Например, вероятность появления среди результатов серии сделок таких, у которых TWR=1.04, составляет 0.162. Чаще всего, с вероятностью 0.177, ожидается появление TWR=1.170. И так далее. Синими точками указаны те же данные, но уже в виде накопленной вероятности. Таким образом, можно сказать, что для наших исходных данных вероятность того, что часть игр будет иметь TWR<=1.00, то есть - проигрыш, составит 0.252. На графике не показаны самые крайние значения. Так ситуация краха, то есть TWR=0.00, имеет Prob=6.4E-06. Максимальный выигрыш TWR=2.60, - Prob=1.2E-07. Это очень маленькие вероятности, тем не менее, в связи с их существованием есть ещё один важный вопрос.

Попробуем продемонстрировать это на следующем примере. Расчеты проведены для условий: p=0.45, q=0.55, a%=0.05, b%=0.05, N=50, результаты представлены на графике.

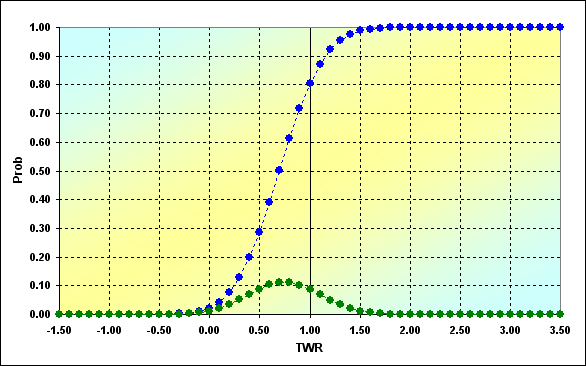
Рис.2

Как мы видим, TWR принимает значения от -1.50 до 3.50. TWR=-1.50 возможен только в том случае, если шла игра при капитале меньше 0.0. То есть формулы, которыми мы воспользовались, не учитывают того, что где-то на промежуточной сделке капитал кончился, и игра не могла продолжаться. Это действительно так, и в связи с этим возникла новая задача, так называемая "задача о поглощении на стенке". В этой задаче учитывается то, что существует некая граница для капитала, при достижении которой игра прекращается. Обычно в самом простейшем виде считается, что граница =0, однако нам гораздо интереснее вариант, когда эта граница может принимать произвольные значения. С некоторыми аспектами аналитического решения данной проблемы можно ознакомиться в [7].

Веер возможностей

Попробуем решить данную задачу численно, во-первых, с помощью итерационных вычислений, во-вторых, с помощью имитационного моделирования на основе стохастических методов (метод Монте-Карло). Для начала обратимся к рисунку и попробуем разобраться в проблеме.

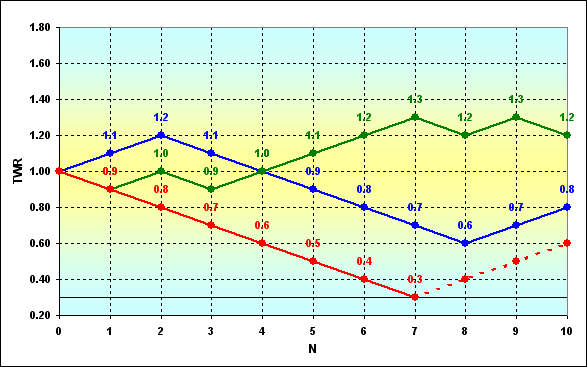
Рис.3

На рисунке схематично изображено, как могли бы проходить траектории изменения капитала в течение игры. Условно показано три варианта, хотя их конечно гораздо больше. Предполагается, что для участия в игре допускаются игроки с капиталом более чем, например, 0.3 (залоговые требования). Предположим, что игра пошла по красному сценарию, и в какой-то момент продолжение игры стало невозможно. Произошло поглощение траектории на границе (стенке) - полное разорение, крах, игрок выбывает из игры, в отличие от игр, проходивших как показано зеленым или синим цветов. Таким образом, для того чтобы определить вероятность разорения на определенном шаге серии нужно учесть все возможности краха на предыдущих шагах.

Наиболее простой, наглядный и очень старый метод, с помощью которого можно провести такие расчеты, - это треугольник Паскаля. По своей сути это - рекуррентная процедура, в которой расчет очередного значения выполняется с использованием предыдущих. В немного модифицированном виде вариант такого треугольника показан ниже.

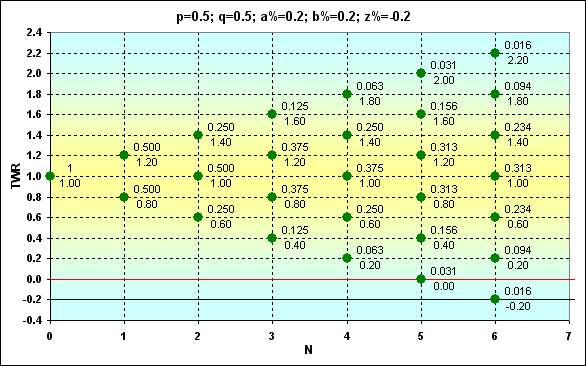
Рис.4

Зелеными точками показаны возможные места на графике, через которые может пройти траектория TWR, который в данном случае можно рассчитать по формуле (3). Точки подписаны значениями Prob (числитель) и значениями TWR(знаменатель). Символ z% обозначает граничное значение, при достижении которого происходит поглощение, черная линия. Красная горизонтальная линия проведена по значению z%+b%.

Что означает положение точек относительно красной линии. Если точка расположена выше, то следующий ход возможен. Когда красная линия проходит через точку - это последний шанс на ещё один шаг. Если повезет, то можно играть дальше, - нет, то произойдет поглощение. Точки, попавшие в область между красной и черной линиями, достижимы, но следующий шаг из них невозможен, так как капитала не хватает на очередную ставку. Другими словами, это не полное окончание капитала, но играть дальше нельзя.

Предупреждение: конечно, такое невозможно в случае целочисленных ставок, таких как монетки, но если речь идет, например, о ставке в 0.15 от капитала, то картина именно такая.

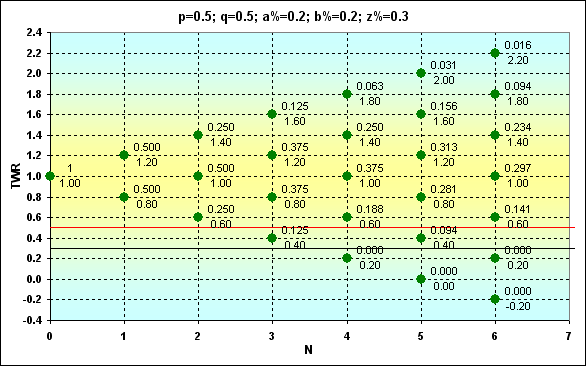
Рис.5

И ещё один рисунок с результатами расчетов при других граничных условиях. Если сравнивать его с предыдущим, то должна быть заметна разница.

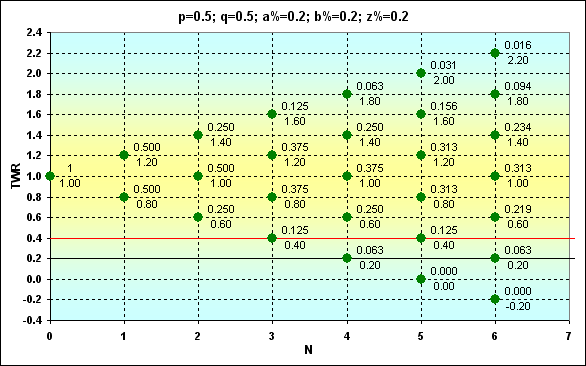
Рис.6

Теперь имея такие данные, можно знать вероятность каких либо событий. Например, для рисунка 6 - какова Prob того, что при N=6 TWR=1.4 - ответ 0.234. Или какова Prob того, что при N=6 TWR>1, нужно сложить соответствующие Prob, ответ 0.344. Или какова Prob того, что при N=6 TWR=1.1 - ответ 0. И так далее.

Последний пример из этой серии. С "перекошенными" исходными значениями: p=2/3, q=1/3, a%=0.1, b%=0.2, z%=0.2 - приводится для того, чтобы показать, как меняются Prob и TWR в этом случае. Как видим, вероятность того, что будет выигрышная ставка, в два раза выше проигрыша, но вместе с тем и размер выигрыша в два раза меньше размера проигрыша.

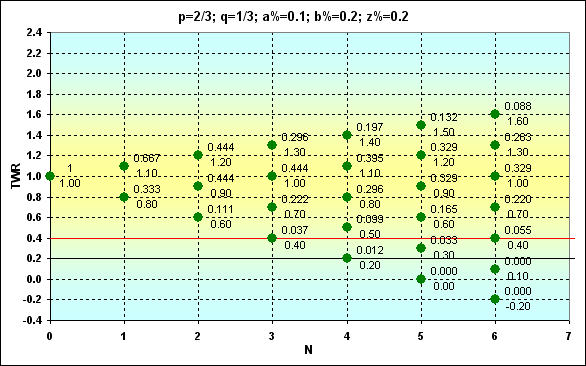
Рис. 7

При TWR>1, - Prob=0.351. В принципе, это довольно близкое значение Prob к тому случаю, который приведен на рисунке 6. Но видно, что величины TWR, которые могут быть достигнуты за сопоставимое число ставок, гораздо меньше.

Ещё один важный момент, который мы до сих пор не обсуждали. Касается это параметра f, обозначающего долю капитала, задействованного в ставке. Фактически, это та доля капитала, которой рискуют в сделке, т.е. b%. В случае классической "орлянки", когда можно проиграть только счетное количество "монеток", такое выражение как 1/f показывает количество проигрышей подряд, которое ведет к краху. В нашем случае, вообще говоря, параметр 1/f может быть нецелочисленным. В то же время, в условиях неделимости ставок количество ставок не может быть нецелым. Это приводит к тому, что в самом худшем случае, когда продолжение игры невозможно, всё равно может оставаться какая-то часть капитала (и она будет меньше b%). Т.е. эта часть абсолютно безрисковая, её невозможно проиграть. В связи с этим, фактический размер капитала, который участвует в игре, меньше на эту величину. Соответственно, на эту же величину фактический z% больше (см. рис.5). При этом, если z%>0, то f имеет тенденцию к превышению над b%. С учетом всего вышесказанного, фактический f можно вычислить следующим образом:

где символ int обозначает операцию выделения целой части числа. Для примера, приведенного на рис.5, b%=1/5, но фактический f=1/3.

Продолжительность возможностей

Попробуем рассмотреть наши результаты как соответствие между Prob и TWR. В качестве примера было выбрано несколько различных наборов исходных данных. Длина серий одинакова - N=15.

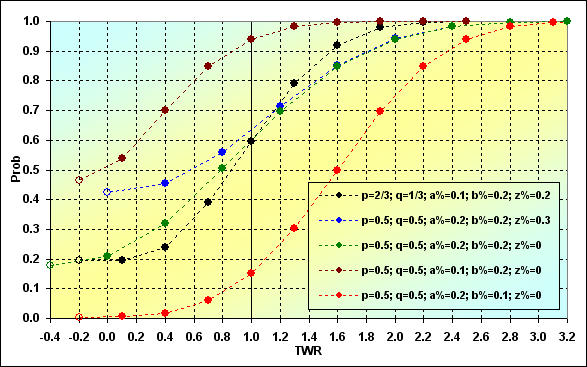
Рис. 8

Несколько пояснений, которые помогут разобраться с тем, что и как нанесено на графике. Каждая кривая начинается с "пустой" точки (если смотреть слева на право). Вообще-то говоря, это - условные точки (в некоторых случаях), их не может быть в природе. Но тем не менее они нанесены и обозначают вероятность того, что поглощение произойдет на каком-то из промежуточных шагов. Т.е. это вероятность того, что траектория не достигнет последнего шага. Следующая точка на графике вслед за первой - это уже реальные данные о том, с какой вероятностью на последнем шаге произойдет поглощение с учетом всех предыдущих крахов (с некоторыми оговорками, которые сейчас не принципиальны).

На следующем рисунке продемонстрировано, как меняется вероятность краха в зависимости от длины серии N. Для примера взяты те же самые исходные данные, что и для рисунка 8. Как мы увидим, результаты существенно различаются между собой.

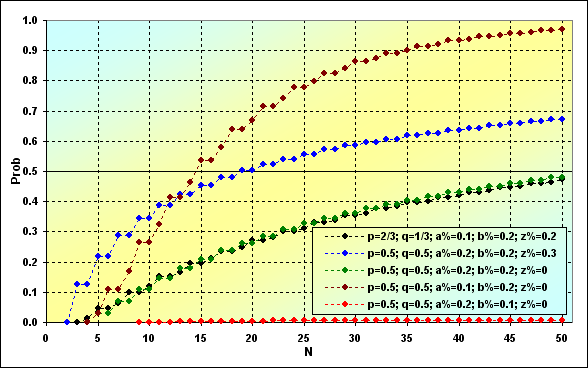
Рис.9

Что хотелось бы отметить следующее. Самое главное - с ростом длины серии вероятность краха возрастает. С этим принципиальным моментом в игре с поглощением на стенке ничего нельзя поделать. Однако не всё так плохо, как кажется на первый взгляд. Дело в том, что сама вероятность краха может быть очень небольшой, в зависимости от параметров ТС (см. красную линию). В то же время, если параметры ТС не очень удачные, то крах наступает очень быстро (см. коричневую линию).

Ещё один важный момент, связанный с обсуждаемым вопросом, - это вероятность общего выигрыша. До этого мы рассматривали случай TWR<(z%+b%), теперь настало время посмотреть, как себя ведет вероятность TWR>1 в зависимости от N.

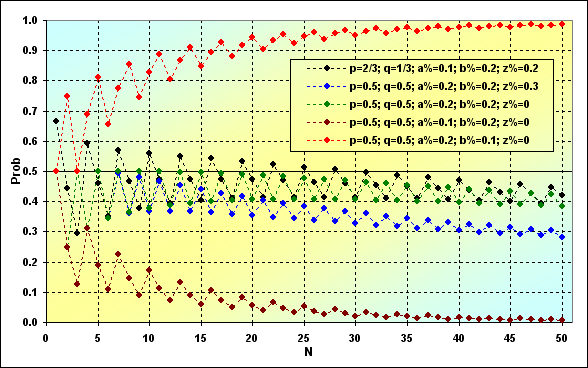
Рис.10

Интересно, что в случае, показанном зеленым и черным цветами, мы имеем дело с в общем-то нейтральными стратегиями, т.е. такими, у которых MO=0, и были бы в праве ожидать, что вероятность выигрыша должна быть около 0.5. Однако это не так. И связано это с поглощением на стенке.

Так выглядит вероятность появления возможных TWR на определенном шаге. В данном случае N=50, точно такое же, как и на рисунке 10.

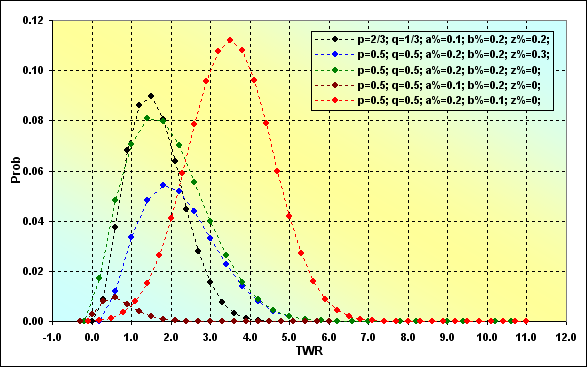
Рис.11

Это обычные кривые распределения. Чем они отличаются от традиционной нормальной кривой распределения, - тем, что они несимметричны относительно максимального своего значения и относительно минимального и максимального TWR. Кроме того, некоторые кривые заметно "скошены в бок" и напоминают скорее логнормальные кривые. Ещё один интересный момент: если сравнить рисунки 10 и 11, то видно следующее. При том, что у большинства распределений на рисунке 11 наиболее вероятное значение TWR больше 1, но в то же время вероятность того, что значение TWR будет больше 1 меньше 0.5. Более того, для случаев с MO=0, черная и зеленая линии, максимально вероятная TWR тоже не равна 1, как это могло бы ожидаться. Никакого парадокса в этом нет.

На этом можно закончить краткое рассмотрение некоторых аспектов "задачи о поглощении на стенке". Следующее, что планировалось сделать, это провести стохастическое моделирование и сравнить результаты с полученными ранее для того, чтобы оценить корректность рассуждений и точность моделирования.

Моделирование

В общих чертах алгоритм моделирования следующий. Перед каждым броском "монеты" проверяется состояние капитала. Если капитала недостаточно для продолжения игры, то она заканчивается. Если играть можно, то с помощью ГПСЧ определяется, выигрышная или проигрышная была ставка. В зависимости от этого капитал увеличивается или уменьшается. И так до конца игры. Проводится большое количество игр, результаты усредняются. Это всё, очень просто. Единственная проблема стохастических методов - это их точность. Дело в том, что при использовании этого метода точное решение задачи невозможно, и это доказано математически (см. парадокс де Муавра). Поэтому прежде чем использовать модель в дальнейших расчетах, придется оценить, насколько результаты совпадают с другими.

Сравним два варианта решений для случая: p=0.5, q=0.5, a%=0.2, b%=0.1, z%=0.0. Ниже приведены два рисунка (12 и 13) на которых показано соответствие результатов.

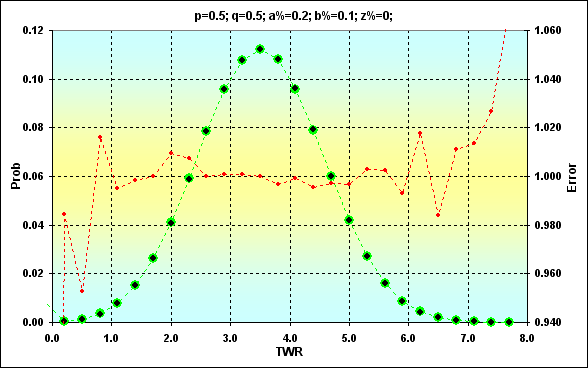
Рис.12

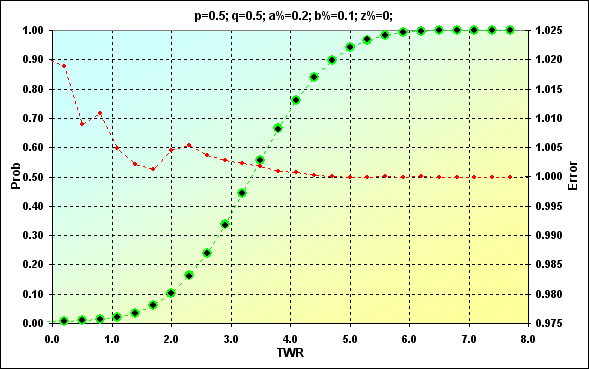
Рис.13

Зеленым цветом отмечены значения, полученные ранее. Черные точки показывают результаты моделирования. Красным цветом показана ошибка, отношение ожидаемого значения к модельному. Рисунок 12 демонстрирует непосредственно сами значения. Рисунок 13 - это накопленная сумма. Совпадение достаточно неплохое. Уровень ошибок в средней части значений составляет менее 0.5%. На краях диапазона уровень ошибок, конечно, выше. В этом нет ничего страшного, просто это нужно учитывать в дальнейшем. К тому же, нас больше будет интересовать накопленная сумма, а там уровень ошибок гораздо меньше (это свойство кумулятивных кривых, ошибки от разных значений компенсируют друг друга).

Другая особенность результатов моделирования - практически невозможно получить вероятность крайне редких значения. Так, в приведенном примере максимальное TWR=11, при Prob= 8.88E-16, и эти значения не могли быть получены при моделировании.

Еще один пример для демонстрации вышесказанного, но уже при N=250: p=0.5, q=0.5, a%=0.1, b%=0.1, z%=0.0. Никаких дополнительных комментариев не будет.

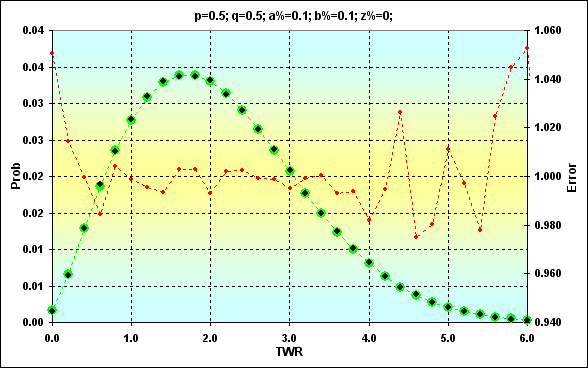
Рис.14

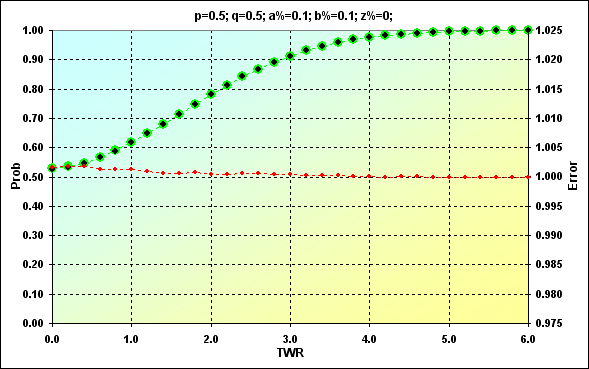
Рис.15

Теперь мы можем использовать эту модель как основу для решения более сложной задачи чем та, которую мы рассматривали выше.

Торговые операции

Прежде чем мы продолжим дальнейшее обсуждение, хотелось остановиться на понятиях и формулах. Дело в том, что реальная торговля, на первый взгляд, значительно отличается от рассмотренной выше игры в "орлянку", - учет этого обстоятельства потребует дополнительных усилий при моделировании. Поэтому необходимо сразу же прояснить, с чем же придется иметь дело в дальнейшем. Безусловно, большинство читателей имеет собственные представления об этом. Итак, некоторые понятия и обозначения, которые нам понадобятся.

Примечание: для простоты будут рассматриваться торговые операции пар с "прямой котировкой", такие как EURUSD, GBPUSD. Пары с "обратной котировкой" и кросс-курсы считаются несколько иначе. Для валютных пар с обратной котировкой стоимость пункта меняется в зависимости от текущей котировки. Для кросс-курсов дополнительно учитывается текущая котировка базовой (первой) валюты к доллару США. Кроме того, здесь не используется понятие ASK и BID.

Капитал, который участвует в торговле, назовем Deposit. Нам предоставляется право, используя кредитное плечо Leverage, покупать и продавать контракт определенного размера LotSize. Контракт может быть дробным, поэтому нам понадобится понятие Lots, как характеристика, указывающая на то, каким размером контракта мы оперируем. Соответственно, фактический размер оперируемого лота в базовой валюте будем именовать LotPrice. За право купить или продать мы должны вносить Margin. Если выразить Margin как долю от Deposit, то мы получим параметр Margin%. Совместно с эти мы будем использовать понятие StopOut, которое обозначает минимальную часть Margin, достижение которой приводит к закрытию текущей сделки и принудительному завершению торговли. Таким образом, существует две разные ситуации, когда дальнейшая торговля невозможна (при желаемом размере LotPrice), т.е ситуация краха. Дополнительно был введен ещё один параметр, который условно назван Sigma. По существу это - отношение используемых в торговой операции средств с учетом кредита к размеру всех собственных средств. Отношение оперируемых средств к фактическому капиталу, т.е. аналог кредитного плеча, только отнесенного ко всему Deposit, а не к LotPrice.

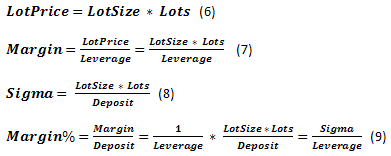
Одно из основных понятий, характеризующее процесс торговли, это Quote - текущий обменный курс. Минимальное изменение курса будем называть Tick. Размер минимального изменения курса инструмента - TickPrice, рассматриваемый как часть Deposit - Tick%.

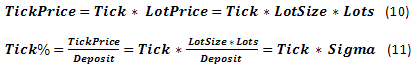
Кроме того, у нас есть ещё несколько параметров, связанных с изменением курса: так называемые TP (TakeProfit) и SL (StopLoss) - изменение курса, при которых происходит фиксация прибыли или убытка. Если выразить эти параметры в валюте, то будем называть их TPprice и SLprice. И, соответственно, выраженные как часть Deposit, назовем TP% и SL%. Также есть различного рода комиссии дилера, такие как Spread, Swap и т.д. Мы не будем рассматривать всё многообразие этих параметров, остановимся только на Spread, который традиционно выражается в пунктах изменения курса. Данные о Swap, если он выражается также в пунктах, достаточно легко учесть в случае необходимости. Если Swap представлен как реальный банковский процент на используемые за счет кредитного плеча заёмные средства, то ситуация несколько сложнее.

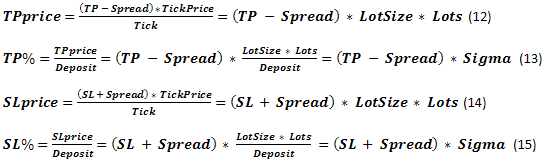
Попробуем сравнить полученные нами параметры с теми, которые мы использовали в задаче о "поглощении на стенке". Очевидно, что SL% соответствует b%. Так же как, TP% = a%. Начальный капитал у нас был представлен как TWR=1. В этом случае то же самое, так как наши расчеты строятся на параметрах, выраженных в долях единицы. Использованное граничное значение z%+b% можно условно считать Margin%. Между этими понятиями есть некоторая разница, но она не так принципиальна, если не принимать во внимание существование StopOut. В общем-то, оказалось, что задачи похожи в первом приближении. Позднее мы проверим это утверждение.

Если внимательно посмотреть на формулы (9, 11, 13, 15), то везде в них присутствует параметр Sigma. Как уже упоминалось, это аналог кредитного плеча, и он используется во всех важных формулах. Напрямую от Leverage зависит только Margin%.

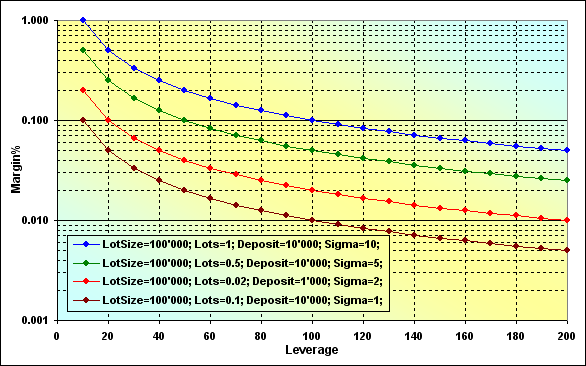
Рис.16

Корректность расчетов можно проверить на следующем примере. Известно, что при Leverage=100, LotSize=100000, Lots=0.1, Deposit=10000 размер залога составляет 100. Если мы посмотрим на соответствующий график (коричневый), то увидим, что Margin%=0.01, при Deposit=10000 это и есть 100.

Две характерные особенности, которые можно наблюдать на графиках: во-первых, чем больше Sigma, тем выше Margin%. Другими словами, меньше свободных средств которые можно использовать при торговле. Во-вторых, уменьшение Leverage также приводит к увеличению Margin%. Обратимся к рисунку 9, на котором рассмотрены схожие случаи (синяя и зеленая линии). Эти случаи различаются только размером z%. Видно, что с увеличением граничного значения увеличивается вероятность краха при прочих равных условиях.

Так как прямой зависимости между SL% и Leverage нет, то рассмотрим, как этот параметр зависит от Sigma и (SL+Spread).

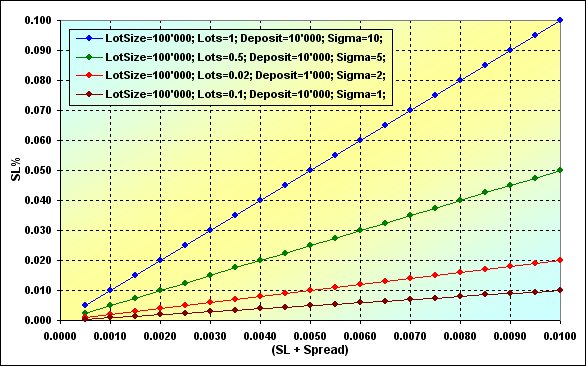
Рис. 17

Увеличение параметра Sigma приводит к увеличению SL%, то есть также приводит к усилению риска краха. Зависимость эта совершенно линейная. Получается, что для того, чтобы уменьшить SL%, необходимо либо снизить (SL+Spread), либо уменьшить Lots, так как другие значения, входящие в Sigma, скорее всего, изменить не удастся.

На этом рассмотрение формул закончим. Несколько слов о том, как проходило моделирование. Процесс этот почти ничем не отличался от того, который был применен ранее. Проводилась проверка на возможность торговли, совершалась покупка по текущему курсу, с помощью ГПСЧ определялось изменение курса, происходила продажа, и вычислялся текущий уровень капитала. Всё это повторялось в цикле много раз. В конце определялись результаты торгов. Никаких особых аналитических форм не использовалось, моделировалось "так как есть". Понятие Tick и связанные с ним, а также Swap, не использовались в виду того, что в них не было необходимости.

Для оценки корректности результатов моделирования использовался пример со следующими основными характеристиками: Deposit=1000, Leverage=100, LotSize=100000, Lots=0.1, TP=0.0040, SL=0.0040, Spread=0.0002, p=0.5, N=250. Длина серии выбрана такой, потому что это число приблизительно равно количеству рабочих дней в году. Таким образом, если считать что в день происходит одна сделка (внутри дня, поэтому Swap не используется), то результаты будут в годовом исчислении. Применим формулы (9, 13, 15) и получим следующие результаты: TP%=0.038=a%, SL%=0.042=b%, Margin%=0.1 (следовательно, z%=0.058). Проведем стохастическое моделирование и расчеты такие же, как и для рисунка 4.

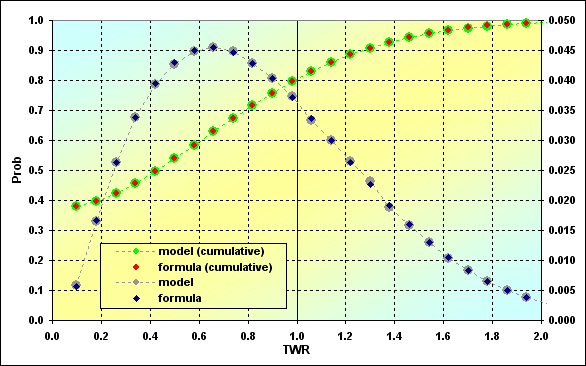
Рис.18

Здесь приведено сравнение расчетов по модели и по формулам. Как видим, результаты расчетов по разным методикам очень хорошо совпали между собой. Это ещё один повод утверждать о том, что процесс торговли мало чем отличается от классической "орлянки" в задаче о "поглощении на стенке".

Несколько кратких комментариев по графику. Самая левая, наименьшая, точка зелено-красной линии указывает на вероятность краха. В данном случае это TWR<= Margin% - 0.375. Вероятность проигрыша, т.е. случай TWR<=1, - 0.795, следовательно вероятность выигрыша - 0.205.

ММ - фиксированный размер (FixSize)

Суть этого метода ММ состоит в том, чтобы каждый раз вне зависимости от других факторов использовать в сделках фиксированную часть начального капитала. Фактически, традиционные возможности по управлению размером лота, которые дилеры предоставляют трейдерам, напрямую соответствуют этому методу. Кроме того, этот метод ММ реализуется в игре "орлянка". Так как мы уже рассмотрели основные особенности этого метода раньше, то перейдем непосредственно к вопросу о том, как именно влияют отдельные параметры на характеристики этой системы. Воспользуемся для этого нашей моделью.

В связи с тем, что мы рассматриваем не аналитическое решение, а численное, то единственный метод оценки отклика на изменение входных параметров - это сравнение результатов расчетов. Будем фиксировать данные, менять в каком-то диапазоне один из них и наблюдать, к каким изменениям это приводит.

Вернемся к ситуации, изображенной на рисунке 16. Проведем расчеты при таких параметрах: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= { 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.5, N=250, Leverage= { 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

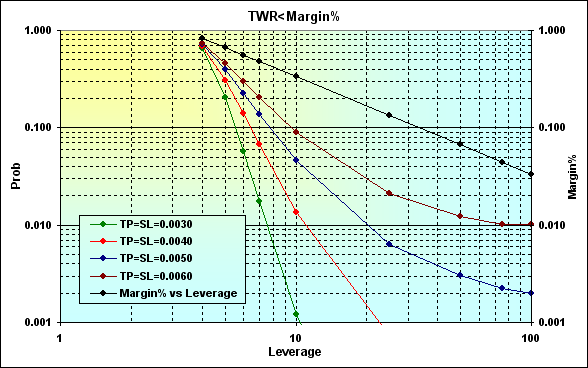
Рис.19

Для большей наглядности результаты расчетов показаны в логарифмическом масштабе. Действительно, уменьшение Leverage ведет к увеличению Margin% (черная линия), а следовательно, к увеличению вероятности краха. Нужно отметить, что взаимосвязь между вероятностью краха и кредитным плечом нелинейная, и наибольшее влияние её ощущается в области малых значений Leverage. Несколько уменьшить негативный эффект от уменьшения Leverage можно уменьшив уровни TP и SL. Однако следует заметить, что при очень небольших Leverage (в нашем случае 4) вероятности краха всё равно остаются высокими. Кроме того, есть ещё одна особенность, которая продемонстрирована на следующем рисунке.

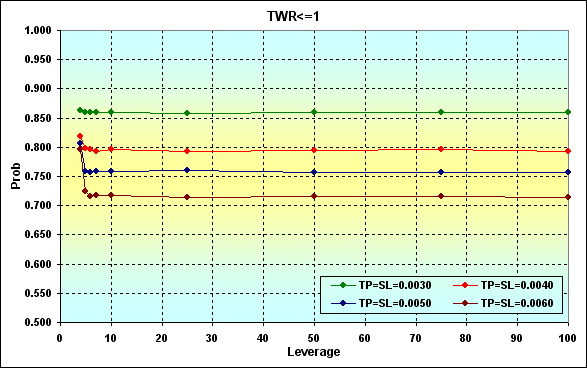
Рис.20

Здесь показано, как изменяется вероятность проигрыша в зависимости от изменения Leverage. Как видим, при уменьшении TP и SL происходит увеличение вероятности проигрыша.

Если увеличить капитал, например, до 10000, это приведет к тому, что крах станет невозможен при заданных N=250. Если сравнить рисунки 20 и 21, то видно, что в области Leverage>10 результаты совпадают.

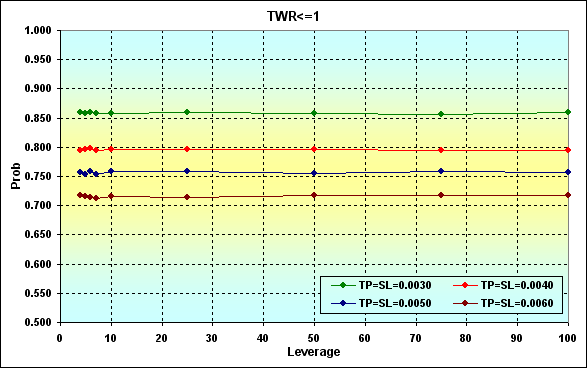
Рис.21

Рассмотрим пример, в котором вероятность выигрыша в одной сделке больше, чем вероятность проигрыша, т.е. p>0.50. Проведем расчеты при следующих параметрах: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.52, N=250, Leverage={ 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

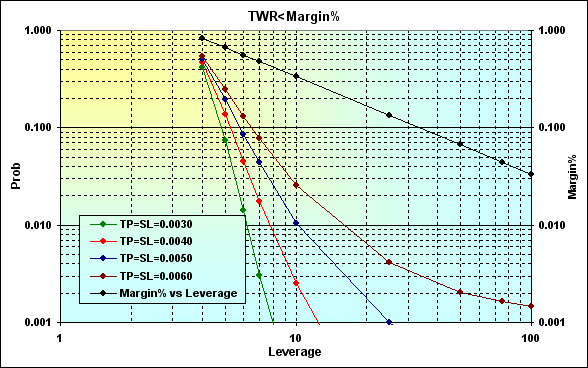
Рис.22

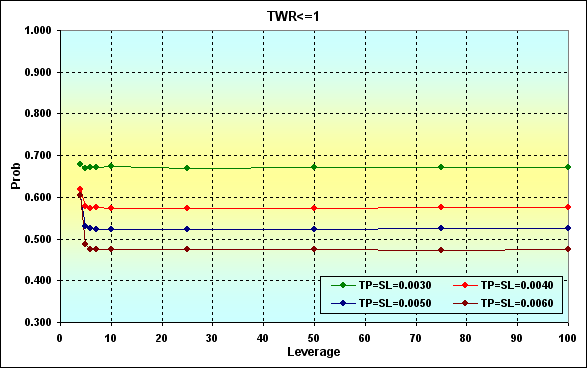
Рис.23

Если сравнить результаты расчетов с вариантом, показанным на рисунке 19, то видно, что увеличение выигрыша в одной сделке ведет к уменьшению вероятности краха и к уменьшению вероятности проигрыша. Закономерный и ожидаемый результат.

Следующий пример показывает, как меняется вероятность проигрыша от вероятности выигрыша в одной сделке с учетом уровня TP, SL. Данные следующие: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}, N=250, Leverage=100.

Примечание: Пример подобран таким образом, чтобы величина вероятности краха была мала, и её можно было бы не рассматривать. Максимальное значение вероятности краха для наиболее худшего случая составило около 0.04.

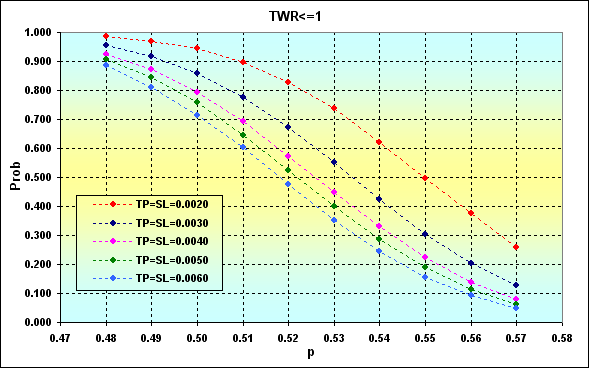
Рис.24

На что хотелось бы обратить внимание. Первое, и наиболее очевидное, - с увеличением p происходит уменьшение вероятности проигрыша. С другой стороны, к увеличению вероятности проигрыша ведет уменьшение уровней TP и SL. Происходит это из-за того, что существует Spread фиксированной величины. Другой вывод, который можно сделать из этих результатов: торговля с небольшим уровнем целей в каждой сделке в каком-то смысле - рискованное дело.

Пример ниже демонстрирует степень влияния величины Spread на вероятность проигрыша. Основные параметры модели: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread={ 0.00000, 0.00005, 0.00010, 0.00015, 0.00020, 0.00025, 0.00030, 0.00035, 0.00040, 0.00045}, p=0.55, N=250, Leverage=100.

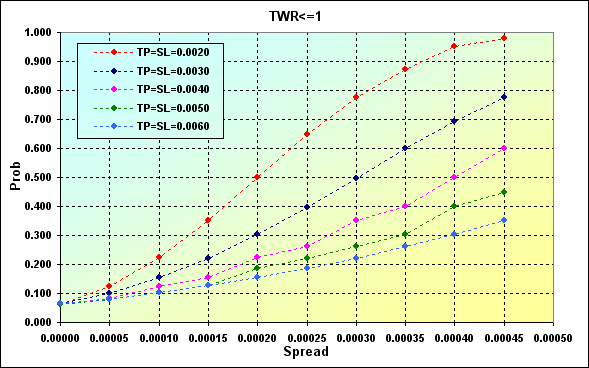
Рис.25

На следующем рисунке показано для данных, приведенных на рисунке 24, соответствие между вероятностью проигрыша и MO сделки, расcчитанное по формуле (1). Вместо значений a% и b% использовались соответствующие значения TP% и SL%.

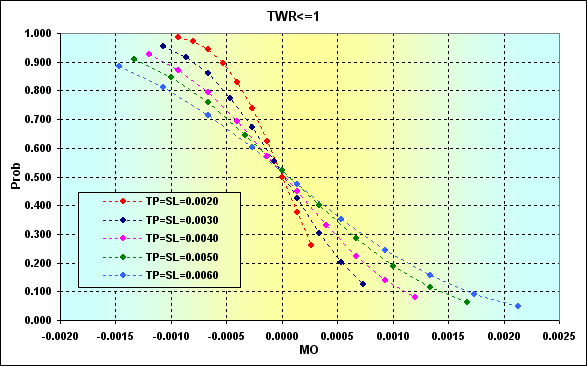
Рис.26

Как видим, увеличение MO сделки ведет к тому, что вероятность проигрыша уменьшается, но не становится нулевой. Это значит, что само по себе положительное MO не гарантирует защиту от проигрыша. Так же как и от краха. Безусловно, бОльшие уровни TP и SL ведут к уменьшению вероятности проигрыша, но в то же время (см. рисунки 19 и 22) это ведет к увеличению вероятности краха.

Другими словами, мы вернулись к тому, о чем утверждалось в начале, когда рассуждали о классической игре в орлянку. Увеличение ставок ведет к увеличению возможного выигрыша (уменьшению вероятности проигрыша) и в то же время ведет к увеличению вероятности краха. К сожалению, ни какого математически обоснованного метода выбора размера сделки, при применении данного метода ММ, не существует. Есть только личные предпочтения, какой уровень краха или проигрыша приемлем в каждом конкретном случае.

Рассмотрим вопрос определение вероятности достижения того или иного уровня TWR во время игры. Основные параметры модели: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= 0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

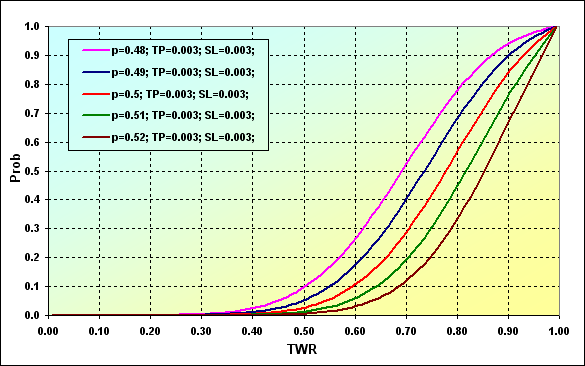
Рис.27

Интерпретировать данные графиков можно следующим образом. Вероятность того, что значение TWR может во время игры снизиться до значения ~0.90 при p=0.48 составляет ~0.93. Для случая p=0.52 составит ~0.68.

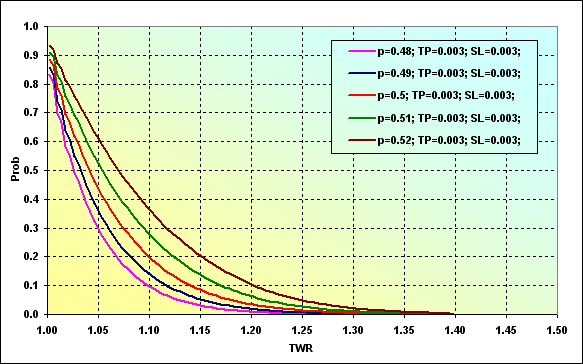
Рис.28

На этом рисунке показана вероятность того, что уровень TWR увеличится во время игры до определенной величины. Например, вероятность того, что значение TWR может за время игры достигнуть значения ~1.10 при p=0.48 составляет ~0.09. Для случая p=0.52 составит ~0.37. Это вполне логично, когда при увеличении вероятности выигрыша в одной сделке происходит увеличение вероятности достижения определенного уровня.

Теперь несколько слов о Drawdown. Для оценки данного параметра был использован скрипт [10] с небольшими изменениями. Кроме того, в отличие от оригинального скрипта расчет происходит с учетом Spread.

Основные параметры модели: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL=0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

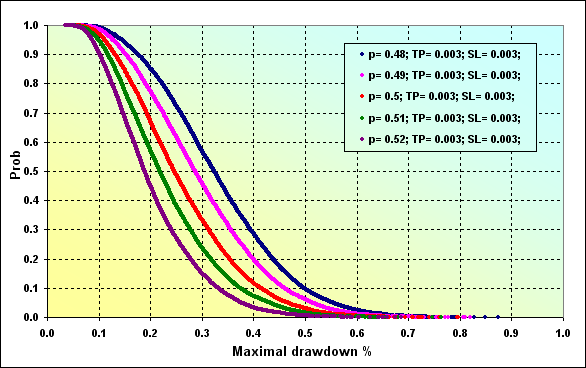
Рис.29

При заданных начальных параметрах как для рисунка 27 вероятность возникновения Maximal Drawdown % ~0.20 при p=0.48 составляет ~0.85. При p=0.52 составляет ~0.47.

Следующий и последний пример: Deposit=2000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.50, N=250, Leverage= 100.

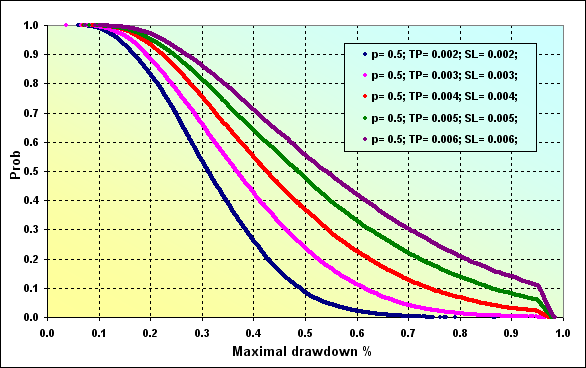
Рис.30

Одно небольшое пояснение к рисунку 30. Уровень Maximal Drawdown %=0.96 приблизительно соответствует уровню Margin, поэтому на графиках присутствует резкий перелом линий. Как видно, по сравнению со случаем приведенным на рисунке 29 (красная линия) вероятность достижения бОльших Maximal Drawdown % увеличилась.

Прежде чем закончить обсуждение некоторых особенностей ММ фиксированного размера приведем ещё два распределения таких характеристик моделей, как Profit Factor и Expected Payoff.

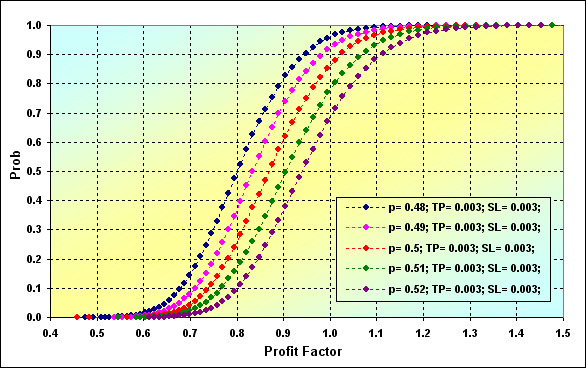
Рис.31

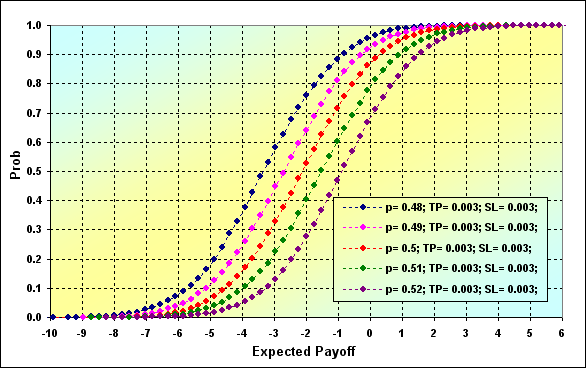
Рис.32

Основные параметры модели для рисунков 31 и 32: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= 0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

ММ - фиксированная доля (FixFrac)

Суть метода ММ со ставкой в виде фиксированной доли от размера текущего капитала заключается в следующем. Изначально определяется размер доли, например, 10% для участия в сделках. В последующем вне зависимости от результатов торгов размер средств участвующий в сделках вычисляется от размера текущего капитала. Таким образом достигается эффект, когда после удачной сделки капитал возрастает, а следовательно, и возрастает размер следующей сделки. И наоборот, в случае неудачной сделки следующая сделка проводится меньшим объемом. Иногда такую систему ставок называют анти-мартингал (что, в общем-то, не очень корректно). Подобная система подразумевает реинвестирование возможной прибыли в отличие от ММ с фиксированным размером.

Пояснение: В связи с тем, что в русскоязычной транскрипции термин martingale имеет несколько вариантов написаний, а целью данной статьи не является выяснение вопроса о том, какой из них наиболее корректный, будет использоваться начертание "мартингал", выбранное прогрессивным методом подбрасывания монетки.

Достоинства и недостатки такого метода ММ известны. Данный метод в случае удачной серии сделок обеспечивает быстрый рост капитала. Рост этот выражается как геометрическая прогрессия в отличие от арифметической прогрессии роста капитала при методе фиксированного размера. Теоретически, в условии бесконечной делимости ставок данный метод не позволяет проиграть капитал полностью (конечно же, это не так в условиях реальной торговли).

К недостаткам метода можно отнести так называемое влияние ассиметричного рычага. Дело в том, что при данном методе ММ в случае проигрыша ставки следующая за ней выигрышная ставка меньше по размеру. То есть, для того, чтобы "отыграть" серию неудачных сделок, нужно бОльшее количество удачных. Кроме того, на результаты данного метода может оказывать наличие скрытых серий в последовательности сделок (небернуллиевость).

В области практического использования данного метода ММ стоит проблема выбора значения доли капитала, которая бы обеспечивала наилучшую скорость роста капитала и при этом обеспечивала бы приемлемую вероятность краха. Такая асимптотически оптимальная стратегия игры была предложена Келли.

Но сначала немного теории и формул. Если известно количество выигрышных и проигрышных ставок, размеры выигрыша и проигрыша на одну ставку, то так же как и для метода фиксированного размера можно вычислить TWR(V) и Prob(V). Формула (17) идентична формуле (4).

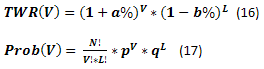
Пример расчета по формулам (16) и (17) приведен ниже. Вероятность достижения разных значений TWR приведена в виде накопленного значения.

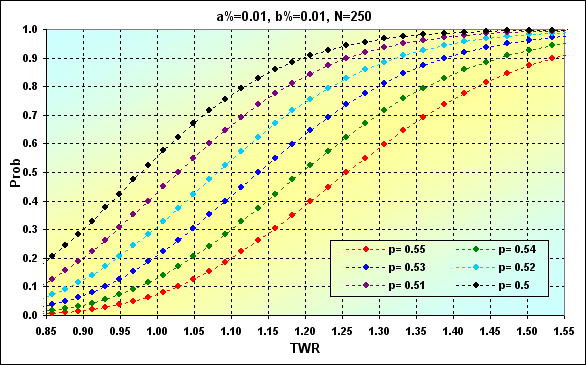
Рис.33

На следующем рисунке показано, как соотносятся друг относительно друга два варианта с одинаковыми начальными условиями, но разными ММ. Вариант с фиксированным размером ставки взят из примера на рисунке 8. Красным цветом отмечен вариант ММ с фиксированным размером ставки (FixSize), черным - с ММ фиксированной долей от начального капитала (FixFrac).

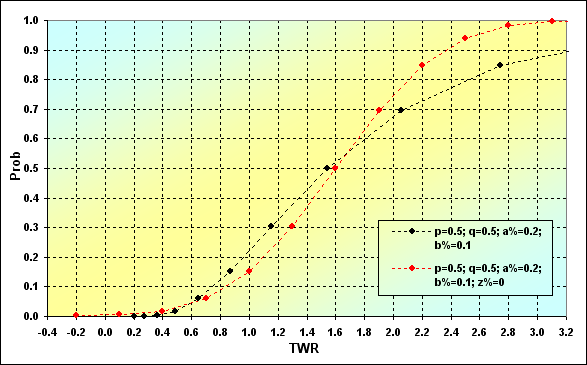
Рис.34

Формула, описывающая скорость роста капитала, для случая равных размеров выигрыша и проигрыша выглядит следующим образом.

Путем несложных преобразований и рассуждений [8], минимизируя среднеожидаемый геометрический рост, можно придти к следующей формуле, характеризующей оптимальный размер ставки f*.

Это и есть так называемый критерий Келли. Суть его очень проста. Если у вас есть ТС с вероятностью угадывания больше 0.5, а размеры выигрыша и проигрыша равны, то необходимо каждый раз ставить часть капитала, вычисленную по формуле (19). Например, p=0.55, тогда f*=0.55-0.45=0.10. То есть нужно будет всегда ставить одну десятую капитала, и это обеспечит максимально возможную скорость роста капитала.

Предупреждение: Обращаю внимание, что формула оптимального размера ставки по Келли отличается от формулы оптимального размера ставки, приведенной Винсом в [4]. Никакой ошибки у Винса нет, и далее будет показано почему.

Примечание: Интересно, что если рассчитывать по формуле оптимальное значение доли капитала для случая p=0.50, то в результате закономерно будет 0.00, то есть рекомендуется вообще не играть.

В случае, когда размеры выигрыша и проигрыша отличаются друг от друга в k раз, необходимо использовать вместо формул (18) и (19) другие формулы. [8][5].

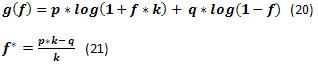
Если построить график изменения g(f) от f используя формулу (20), то можно увидеть примерно такую картину. На этом рисунке отмечена точка f*, это наивысшая точка графика, место, где скорость роста капитала наибольшая. Кроме того, показана дополнительная точка fc - точка пересечения графика с нулевой линией, место, в котором скорость роста капитала становится нулевой.

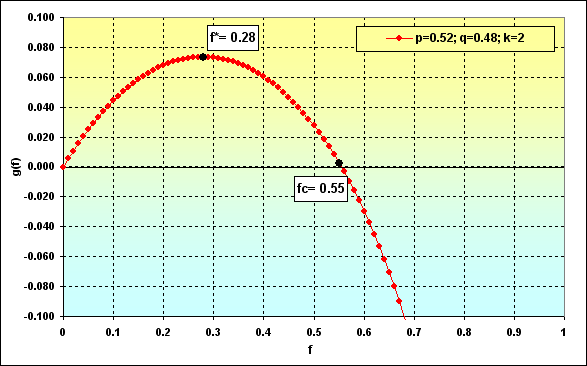
Рис.35

Пояснение: Выбранный для расчетов рисунка 35 параметр k=2 использован исключительно как ирония над соответствующими графиками, приведенными в книгах Винса. Хотя, безусловно, такой к обеспечивает большую "наглядность" и "красивость" пропагандируемых им подходам.

В [8] утверждается, что если игра ведется с заданными условиями, то f* обеспечивает максимальную скорость роста капитала и нулевую вероятность краха. При этом, если используется доля капитала меньше f*, то вероятность краха так же нулевая, но скорость роста капитала меньше. Если используется доля капитала больше fc, то крах неизбежен (в данном случае под крахом имеется в виду сколь угодно малое значение капитала). Если доля капитала находится в интервале от f* до fc, то скорость роста также медленнее, чем максимальная, хотя при этом вероятность краха отсутствует.

Очень впечатляющие результаты, однако нужно заметить, что это теоретические расчеты, не учитывающие некоторых реальностей. Поэтому Винс [4] рекомендует рассчитывать оптимальный fс с учетом наибольшей потери. Это приводит к тому, что его значение f* становится ниже рассчитанного строго математически со всеми вытекающими из этого последствиями.

Попробуем рассмотреть, как это может выглядеть на графиках. Возьмем случай: Deposit=1000, LotSize=100000, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.01, Spread=0.0000, p=0.51, N=250, Leverage= 100. При этих исходных данных начальный Lots=0.01, а TP%=SL%=0.01. Кроме того, f*=0.02 и fc=0.04, что и продемонстрировано на следующем рисунке.

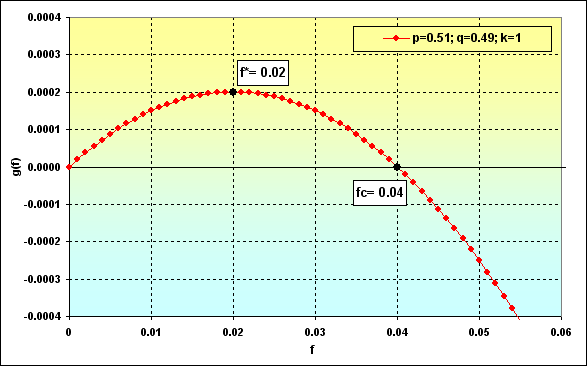
Рис.36

При изменении f получаются следующие зависимости изменений Prob от TWR. Для этого проведем несколько расчетов.

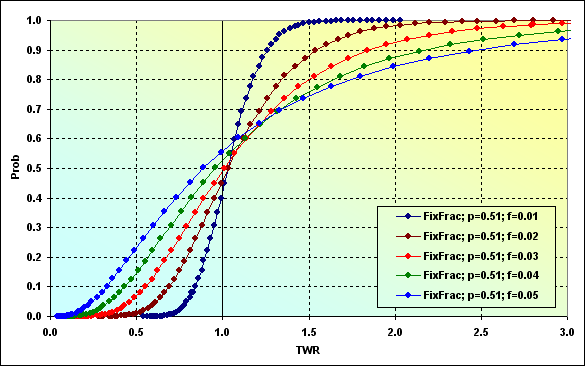
Рис.37

Рассмотрим поподробнее. Линия, соответствующая f=0.01, демонстрирует обсуждавшийся ранее случай f<f*, при котором скорость роста капитала меньше максимально возможной, и в то же время вероятность краха нулевая. При этом вероятность проигрыша TWR<=1 равна ~0.40.

Следующий случай, f=0.02 это случай, когда доля используемого капитала оптимальна. Вероятность проигрыша составила ~0.45. Другими словами, ожидается, что более половины игр закончится выигрышем.

Вариант расчета f*<f<fc, то есть f=0.03. Вероятность проигрыша составила ~0.45. Крах невозможен при заданных условиях игру. Однако значения, до которых может снижаться TWR, более существенны, чем в предыдущих случаях. Так же, как и возможны бОльшие выигрыши.

Теперь условия, которые обеспечивают вероятность проигрыша ~0.50, то есть f=fc=0.04. Утверждается, что в этом случае TWR почти достоверно будет колебаться в интервале от 0 до +бесконечность.

И последний вариант, f>fc. Вероятность проигрыша ~0.55. Возможны очень большие выигрыши, но в конечном счете (в <бесконечной> перспективе) все они будут проиграны, а TWR снизится до уровня, который можно будет классифицировать как крах.

Ещё немного формул. Оценку скорости роста капитала g(f) можно провести по формулам (18) и (20). Зная скорость роста g(f) и количество сделок N, можно вычислить TWR по формуле (22). Кроме того, ожидаемый средний доход от сделки для ММ фиксированной долей капитала правильнее оценивать не как среднее арифметическое, но как среднее геометрическое Gmean по формуле (23).

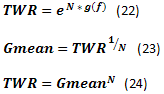
Пожелание: Хорошо бы, если в стандартный отчет тестера МТ был включен расчет среднего геометрического сделок. Это позволило бы более корректно оценивать качество торговых систем, использующих ММ фиксированной доли.

Два примера расчета по формулам (23) и (24) с использованием данных рисунка 36.

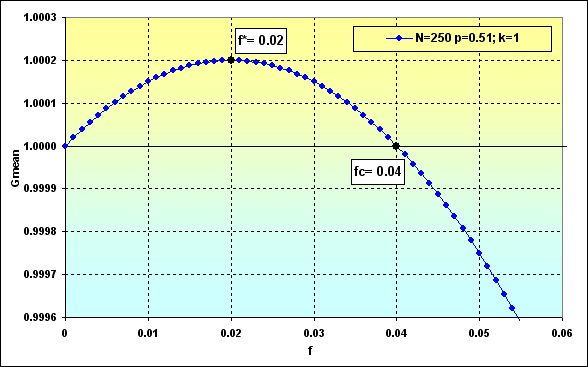
Рис.38

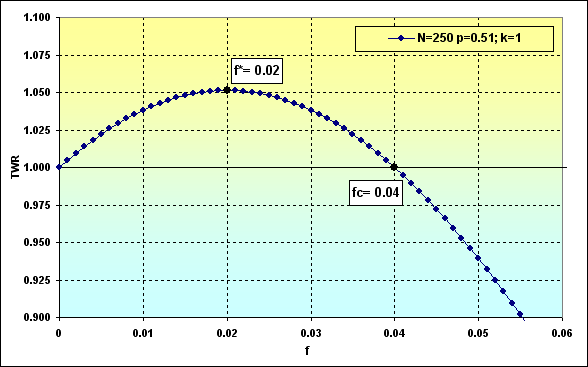
Рис.39

Таким образом, исходя из рисунка 39, при заданных условиях и с использованием оптимальной доли в ставках общий капитал будет стремиться к значению TWR=1.05. При этом, как отмечено на рисунке 37, вероятность проигрыша ~0.45.

Интересно было бы сравнить, как ведут себя разные ММ при одинаковых стартовых условиях. Если использовать данные рисунка 36, то получится вот такой рисунок.

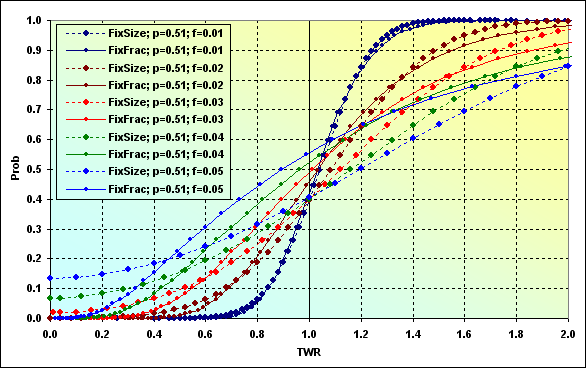
Рис.40

Случай f=0.01, графики при различных ММ очень похожи между собой. То есть при определенных условиях дают похожие результаты. Все остальные случаи демонстрируют нам, что ММ фиксированного размера имеет вероятность проигрыша (TWR<=1) меньше чем ММ фиксированной доли при одинаковых стартовых условиях.

Предупреждение: Наблюдение, сделанное выше, относится исключительно к выбранным исходным данным и ни в коем случае не распространяется как всеобщее правило.

Продемонстрируем ещё одно интересное обстоятельство, построим зависимость значений, к которым стремиться TWR, от доли капитала участвующего в сделке. Расчет этих значений можно провести для ММ фиксированного размера как произведение MO на N, для ММ фиксированной доли по формуле (22).

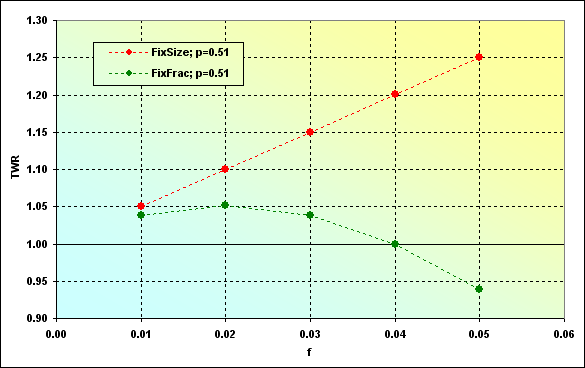
Рис.41

Как видим, ожидаемый доход при использовании ММ фиксированного размера получается выше (для использованных исходных данных). Однако так случается не всегда.

Можно рассмотреть, как меняются зависимости, к которым стремиться TWR, от доли капитала с учетом различных вероятностей выигрыша в одной сделке. Ниже приведены графики для длины серии N=250.

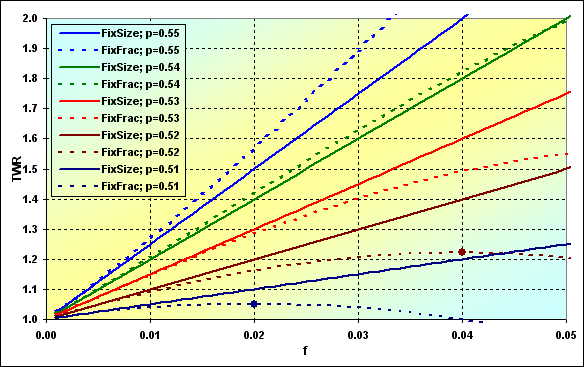
Рис.42

Таким образом, при определенных условиях с точки зрения ожидаемого TWR возможны ситуации, когда ММ фиксированного размера предпочтительнее ММ фиксированной доли. Однако если рассматривать это совместно с вероятностью наступления краха, то всё не так очевидно.

Кроме того, на величину ожидаемого TWR существенно влияет длина серии N. В общем случае чем длиннее серия, тем больше преимущество ММ фиксированной доли.

Этим закончим рассмотрение некоторых теоретических моментов и перейдем к моделированию. Собственно говоря, ничего в исходной модели не изменилось, кроме того, что необходимо будет добавить понятия минимального и максимального лота, MinLot и MaxLot. Кроме того, нам понадобится величина LotStep, характеризующая минимально возможную величину изменения лота. Общий алгоритм проведения расчетов остается прежним. Дополнительно вводится понятие MinDeposit как величины минимального возможного депозита. Таким образом, продолжение торговли возможно, если величина депозита больше Margin и больше MinDeposit.

Ниже приведен пример моделирования различных ММ со следующими исходными данными. Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.01, Spread=0.0000, p=0.54, N=250, Leverage=100. Отдельно обращаю внимание, что в этом расчете не используется Spread.

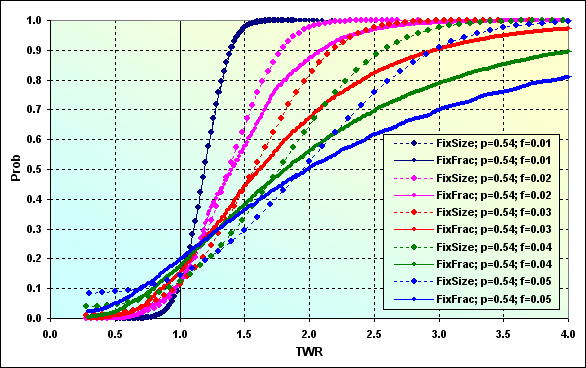
Рис.43

Введение в расчеты MinDeposit привело к тому, что у ММ фиксированной доли с теоретической невозможностью краха (при f<fc) эта возможность появилась. Кроме того, при определенных условиях (здесь не показано) дискретизация и ограничения размера лота также приводит к возникновению вероятности краха. Уменьшить влияние этих негативных факторов можно за счет того, что в расчетах принимать за начальный капитал разность значений Deposit и MinDeposit. По существу, именно это и предлагает Винс - использовать для расчета оптимальной доли капитала только часть капитала. Очень разумное решение, однако это приведет к тому, что закономерно снизится и TWR.

Теперь ещё несколько пояснений к рисунку 43. Найдем на графике "FixFrac; p=0.54; f=0.05" значение, где он соответствует Prob=0.50. Это медиана, значение, меньше и больше которого находится 50% всех значений. В данном случае оно соответствует TWR~2.00. Другими словами, половина всех результатов игр привела как минимум к удвоению начального капитала. При этом вероятность проигрыша составила ~0.20, а вероятность краха ~0.03. Сравнивая с графиком "FixSize; p=0.54; f=0.05", можно отметить, что вероятность краха может возрасти до ~0.08, вероятность проигрыша снизится до ~0.14, но медиана будет примерно соответствовать TWR~2.00. Если посчастливится попасть в ту половину случаев, где TWR>2.00, то скорее всего результат будет ниже, чем в случае использования ММ фиксированной доли.

Сравнивая графики на рисунках 42 и 43 можно отметить, что представленные на рисунке 42 значения, к которым стремится TWR, есть ни что иное как медиана с рисунка 43.

Далее рассмотрим случай, изображенный на рисунке 43, но теперь уже с учетом Spread=0.0002. Все остальные исходные данные остались прежними.

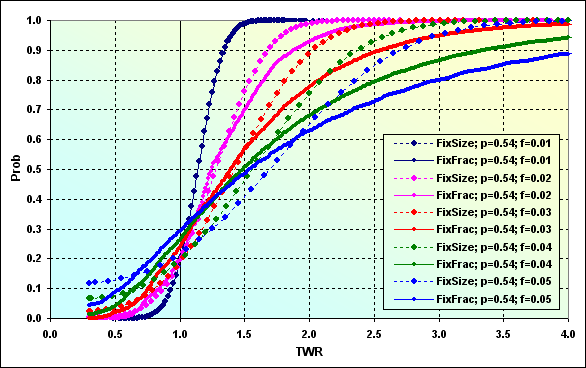
Рис.44

Как видим, Spread, составляющий всего от 0.4% до 2% от уровня выигрыша\проигрыша в одной сделке, приводит к существенному изменению картины. Лучше всего это видно на следующем рисунке, где дано сравнение двух вариантов расчета - с рисунков 43 и 44.

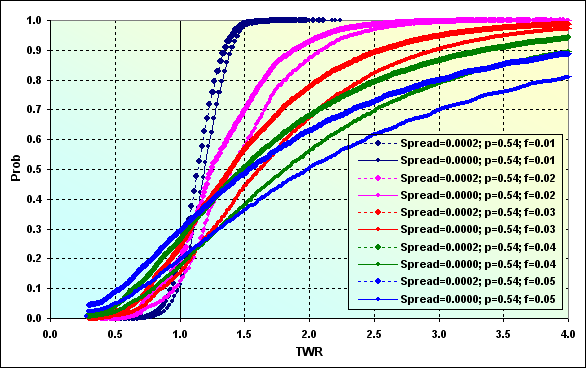
Рис.45

Таким образом, учет Spread ведет к тому, что медиана TWR (например, синие линии) снизилась с 2.00 до 1.50. Вероятность проигрыша увеличилась с 0.20 до 0.30. Казалось бы, разница очень не большая, всего 0.10, однако если рассматривать по-другому, то можно сказать, что в первом случае проигравшим (проигравшим, но не потерпевшим крах) будет каждый пятый, а во втором случае каждый третий.

Попробуем рассмотреть, как меняется вероятность проигрыша от вероятности выигрыша в одной сделке с учетом разных f, моделируя различные ММ со следующими исходными данными: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.0100, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}, N=250, Leverage=100.

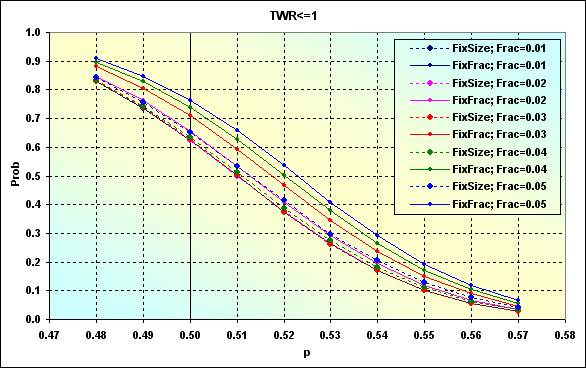
Рис.46

От примера, приведенного на рисунке 24, этот случай отличается тем, что здесь уровни TP, SL зафиксированы, но меняются размеры лота. На рисунке 47 показан случай при тех же данных, что и для рисунка 46, но TP=SL=0.0050.

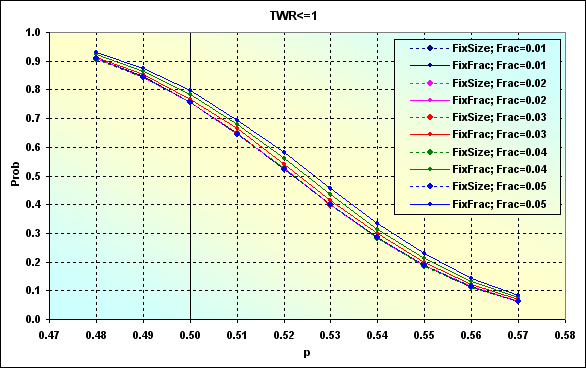
Рис.47

Так же как и для случая, показанного на рисунке 24, снижение уровней TP, SL привело к тому, что увеличилась вероятность проигрыша. Кроме того, уменьшился разброс в значениях между различными случаями. Графики стали проходить более "кучно". Другими словами, уменьшилось влияние величины f. Особенно хорошо это видно, на следующем рисунке.

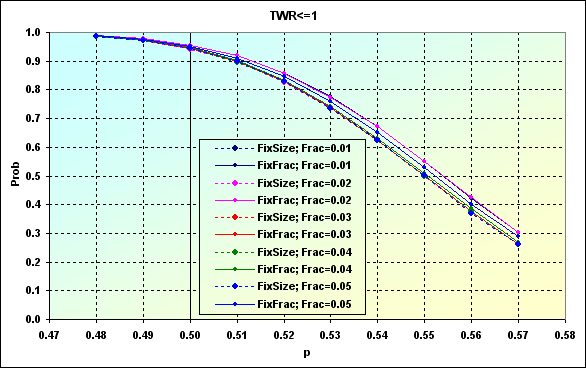
Рис.48

В данном случае использовались уровни TP=SL=0.0020. Как видно, для того чтобы компенсировать влияние Spread и добиться того, чтобы вероятность проигрыша была хотя бы менее 0.50, в этом случае понадобится ТС, способная обеспечивать p=>0.56. Но в целом, если ТС способна правильно угадывать только в 50 случаях из 100, в этом случае, какую бы ММ не использовали, какие бы уровни f не применялись, результат примерно один и тот же, вероятность проигрыша после 250 сделок ~0.95.

Чтобы показать, как будет выглядеть TWR в случае TP=SL=0.0020 и p=0.56, проведем расчет. Результат показан ниже. Это действительно вариант с вероятностью проигрыша около 0.40, как и на рисунке 48, при этом ожидаемое значение TWR 1.01...1.04. И различные ММ показывают близкие между собой значения.

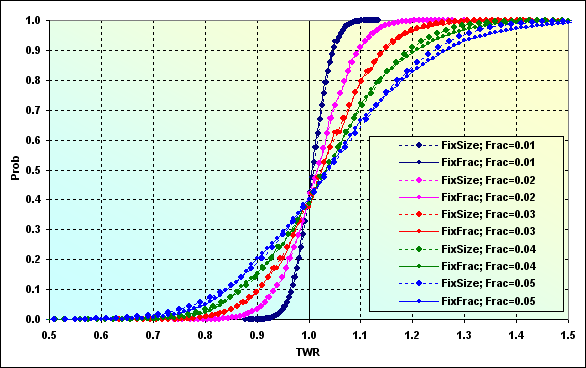
Рис.49

Ещё раз обращаю внимание, это характерно для случаев с небольшими целями. Если бы Spread был величиной плавающей и взимался как процент от размера ставки, а не как фиксированная комиссия вне зависимости от размера ставки, то картина была бы другая, что и происходит на других рынках, не на "ФОРЕКС для широкого круга потребителей".

Вернемся к расчетам с входными данными: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.0100, Spread=0.0002, p=0.51, N=250, Leverage=100. Рассмотрим, как выглядит вероятность уменьшения TWR до определенного уровня.

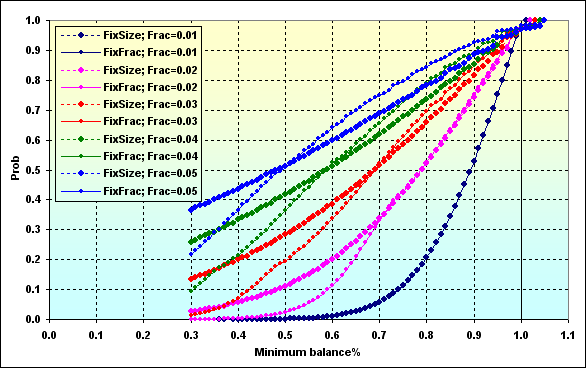
Рис.50

Интерпретировать данные графиков нужно точно так же, как и рисунок 27. Вероятность того, что значение TWR при использовании ММ фиксированной доли может во время игры снизиться до значения ~0.70, при f=0.05, составляет ~0.76. Для случая f=0.02 составит ~0.34.

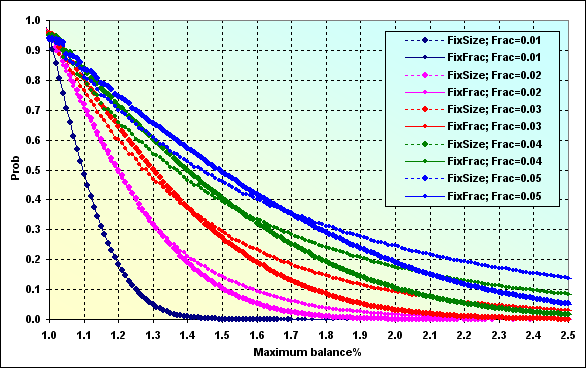
Рис.51

А так выглядит вероятность того, что депозит возрастет за время игры на определенное значение. Интерпретировать данный график нужно как рисунок 28.

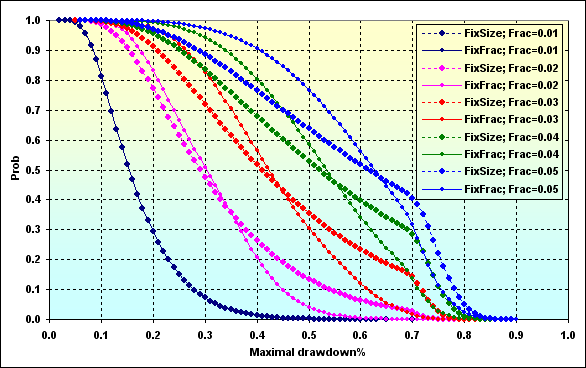
Рис.52

Ну и последний график, показывающий вероятность Maximal Drawdown % определенной величины в зависимости от использованной доли капитала. В общем виде можно считать, что ММ фиксированной доли приводит к тому, что достигается Drawdown большего значения, чем при использовании ММ фиксированного размера. Это связанно с эффектом ассиметричного плеча. Кроме того, если используется fc>f>f*, то при возможной одинаковой доходности с соответствующим случаем f<f* можно ожидать меньшего Drawdown.

Заключение

Мы рассмотрели два метода управления капиталом, рассмотрели предпосылки, побудившие развитие этого направление, кратко ознакомились с некоторыми теоретическими аспектами проблемы и с некоторыми наиболее простыми формулировками. Мы провели стохастическое моделирование и оценили полученные результаты, пытались сравнивать между собой разные методы. И, пожалуй, самый главный вывод, который можно сделать из этого исследования, - это то, что нельзя выбрать однозначно лучший метод из двух рассмотренных. Эффективность ММ зависит от очень большого количества фактором. Различные комбинации этих факторов дают различные результаты. Поэтому в каждом конкретном случае, в зависимости от свойств ТС, условий ДЦ, возможностей и пожеланий трейдера нужно выбирать наиболее подходящий для этого случая ММ. Некоторые пути решения этой проблемы, характеристики на которые следует обращать внимание и были приведены в данной статье. Очень надеюсь, что среди читателей найдутся такие, для кого это скучное действо было небесполезным. Удачи всем.

В дальнейших планах - рассмотрение мартингала (думаю, это будет не очень большая часть ввиду очевидности свойств этого метода) и рассмотрение метода Р. Джонса (по утверждению автора, разработанный им как сумма положительных свойств двух рассмотренных методов ММ).

Литература и ссылки на сетевые ресурсы (в порядке упоминания по тексту)

1. Agner Fog - Pseudo random number generators - http://www.agner.org/random
2. strator - Probability Library (part of Cephes) - https://www.mql5.com/ru/code/10101
3. Suvorov V. - MS Excel: Data Exchange and Management - https://www.mql5.com/en/code/8175
4. Винс Р. - Математика управления капиталом.
5. Бершадский А.В. - Исследование и разработка сценарных методов управления риском. (дисс. 2002г.)
6. Смирнов А.В., Гурьянова Т.В. - Об "оптимальном f" Ральфа Винса.
7. Феллер В. - Введение в теорию вероятностей и её приложения.
8. Торп Э. - Критерий Келли в блек-джеке, спортивных тотализаторах и на фондовой бирже.
9. Булашев С. - Статистика для трейдеров. (электронная версия, стр.199)
10. Starikoff S. - Самостоятельная оценка результатов тестирования эксперта -  https://www.mql5.com/ru/articles/1403

Примеры

К статье прилагаются использованные при её написании общедоступные библиотеки. Сами скрипты и программы не прилагаются. Это сделано умышленно для того чтобы стимулировать в трейдерском сообществе MQL написание доступных эмуляторов торговых серверов. Именно эмулятор торгового сервера был использован при моделировании.

Declaimers ака Отмазки

Автор статьи ни за что никакой ответственности не несет. Претензии и предложения принимаются в письменном виде, в обсуждении и/или мылом. Толковые предложения будут рассмотрены, глупые претензии проигнорированы. Все копирайты, если они известны, указаны. Иначе автор неизвестен или копирайт утерян.

Автор допускает, что в текст или расчеты могли прокрасться неточности или ошибки. Текст большой, а материал сложный, и это неизбежно. Поэтому автор хотел, по примеру Д.Кнута, назначить из гонорара награду в $1 за каждую замеченную оплошность. Однако жизнь внесла свои коррективы. Северный ветер мирового финансового кризиса продолжает бушевать над страной. Как всегда в таких случаях больше всего пострадают самые слабые и незащищенные среди нас - дети, которые остались без родителей. Желая помочь им, автор решил не платить за собственные ошибки, а направить весь возможный гонорар на благотворительные цели. Будет выбрано несколько детских домов где-нибудь в далекой российской провинции, в адрес которых и будут переведены небольшие средства.

Это было непередаваемое чувство, когда в ответ на пожертвование пришло письмо от руководителя детского дома. Обыкновенной почтой, простое письмо, написанное от руки, на бумаге из школьной тетради в клеточку. Конечно же, слова благодарности, но главное - список всего, что было закуплено на эти средства. Эта мудрая женщина потратила их не на компьютер, на котором удобно копипастить благодарности. Не на новые занавески в своём кабинете. Не на еду, которой и так кормит государство этих детей, пусть и не так гламурно как в столице, но кормит. Всё было вложено в будущее детей, в их образование.

Тетради, фломастеры, ручки, развивающие игры, учебники, краски. Всё, что нужно для нормального развития и что так быстро кончается у детей. Детей, живущих в маленьком провинциальном городке или поселке, в старом деревянном здании, возможно, срубленное руками наших дедов, вернувшихся после Отечественной домой. Пожалуйста, если вы можете, если это не последние ваши деньги, не жадничайте и не ленитесь, помогайте им. Вам это зачтется. На самом деле я не знаю точно, может быть то письмо писал ночной сторож, как раз пропивающий свалившееся на него нежданное счастье. Мне это неинтересно, и я никогда не узнаю, как было на самом деле. Я просто делаю ставку, пусть и небольшую, на то, что вероятность того, что живу среди нормальных людей, гораздо выше. И эта игра, в отличие от игр в монетки, справедлива для всех нас.