Sistema de Negociação Mecânica "Triângulo de Chuvashov's"
1 698
0
Introdução
O artigo lida com possibilidades de cálculo da localização das barras e intersecção de linhas de tendência com o tempo em perspectiva. As linhas de tendências tem o princípio de formação próxima de T, relacionadas com a construção do indicador DeMark (Tom DeMark) nos últimos intervalos.
O aplicativo oferecido pode ser integrado dentro de um sistema de negociação mais complexo, embora seja um Expert Advisor automatizado de pleno direito.
Princípios Básicos na Construção de Intersecção de Canais
A essência do padrão "Triângulo de Chuvashov" encontra-se na idéia de que temos sempre os dois últimos fractais de baixa e dois últimos de alta em qualquer ponto de todos os timeframes. Linhas de tendência são desenhadas através dos dois fractais de alta e dois de baixa.
Se estas 2 linhas se cruzam quando se delocam à direita formando um triângulo, então nós temos um padrão chamado "Triângulo de Chuvashov". O ponto de intersecção dessas duas linhas se cruzando é chamado de Ápice, totalizando 4 fractais de acordo com a sequência que ocorrem (esquerda para a direita).
Uma linha linha vertical é desenhada cruzando o segundo fractal esquerdo, também é desenhada uma linha vertical cruzando o Ápice (apex). O número de velas (candles) entre estas duas linhas verticais, incluindo as velas sobre as linhas, são divididas por 3 (arredondando), configuradas à esquerda do Ápice e uma terceira linha vertical é desenhada na vela atual.
A distância entre a vertical traçada no segundo fractal e a vertical na vela corrente ( 3ª linha vertical do meio) formam a atual área de rompimento.
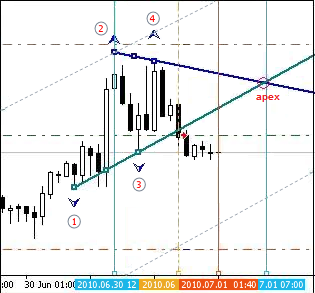
Fig. 1. Desenhando o triângulo
Vamos partir para desenhar o triângulo.
Não podem existir múltiplas posições dos últimos 4 fractais, pois é impossível desenhar o triângulo ou ele acaba por ser demasiado curto ou longo.
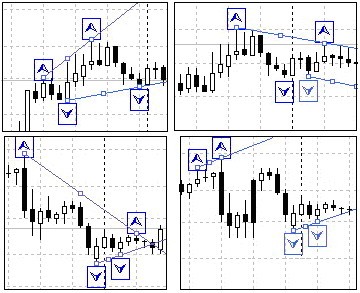
Fig. 2. Exemplos de posições desfavorável dos fractais
Portanto, é necessário introduzir uma série de condições que são suficientes para desenhar o triângulo.
Lembrando, a numeração dos pontos de referência é realizada considerando que a "indexação dos elementos da série temporal é realizada para trás, do último ao primeiro, a barra atual que está sendo plotada é o último array com índice igual a 0". Segue então alguns requisitos de convergência das linhas do triângulo:
- Os primeiros fractais das linhas superiores e inferiores devem ter distância entre eles maiores do que 20-30 pips de altura (este valor pode ser buscado com exatidão durante os testes).
- A distância entre os primeiros fractais das linhas superior e inferior deve ser menor do que a distância entre os segundos fractais destas linhas.
- Primeiro fractal da linha superior deve ser menor do que o segundo fractal da mesma linha, enquanto primeiro fractal da linha inferior deve estar acima do segundo da mesma linha.
Estas condições adicionais foram consideradas no bloco de programa do padrão das condições de formação.
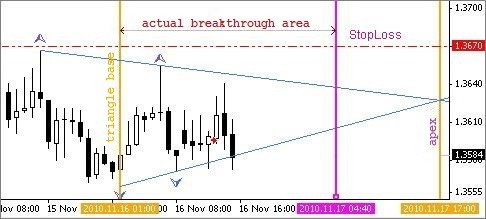
Fig. 3. Atual área de rompimento
Parece ser claro, vamos olhar para a Fig 3. Como podemos definir o número de barras, em que a intersecção das duas linhas irá ocorrer?
No momento do rompimento da linha, não se sabe ainda se este rompimento é real, embora já seja o momento de entrar no mercado! O bloco de cálculo da atual área de rompimento resolve este problema utilizando parâmetros de tempo, ou seja, define a intersecção das linhas de trabalho no intervalo de tempo.
Sabemos que cada barra aparece no gráfico depois de um certo tempo. Por exemplo, novas barras aparecerem no timeframe H1 a cada uma hora. Conhecendo a taxa de mudança de preço por unidade de tempo de cada uma das duas linhas, é possível calcular o tempo da intersecção. Sabendo qual a quantidade de tempo a partir da "base" do Triângulo até ao momento da intersecção (Ápice), é possível calcular o número de barras (unidades de tempo) antes da intersecção. A atual área de rompimento é definida no mesmo bloco.
O Expert Advisor foi projetado com uma base de bloco a bloco.
Os blocos funcionais mais frequentemente utilizados são tipicamente localizados no início do programa: abertura e fechamento de posições, as funções para desenhar os sinais e as linhas. O principal programa executável também contém blocos separados, tais como:
- Bloco para pesquisar fractais de alta e e baixa;
- Bloco para formar o padrão das condições;
- Bloco para cálculo da atual área de rompimento;
- Bloco de condições para abertura de posição
O fragmento dos blocos funcionais é mostrado abaixo.
// --------------------------------------------------------------------+ void Op_Sell_Ch() { if(!OrderSend(Symbol(),OP_SELL,Lots,Bid,2,Ask+SL_S*Point, Bid-TP_S*Point," ",Magic,0,Red)) { Print(" SELL order open error # ",GetLastError()); } return(0); } // --------------------------------------------------------------------+ void Op_Buy_Ch() { if(!OrderSend(Symbol(),OP_BUY,Lots,Ask,2,Bid-SL_B*Point, Ask+TP_B*Point," ",Magic,0,Blue)) { Print(" SELL order open error # ",GetLastError()); } return(0); } //+--------------------------------------------------------------------+ void Close_S_Ch() { if(!OrderClose(OrderTicket(),OrderLots(),Ask,2,Aqua)) {Print(" Cl.ord.# ",OrderTicket()," Error # ",GetLastError());} return(0); } //+--------------------------------------------------------------------+
Os pontos de referência superior e inferior para a construção das linhas do triângulo são encontrados na classificação das barras através de um loop, conforme as regras da criação dos fractais.
A numeração dos pontos de referência é realizada considerando que "indexação dos elementos da série temporal é realizada para trás, do último ao primeiro. A barra atual que está sendo plotada é o último array com índice igual a 0".
// ====================================================================+ // (Fractais de alta e de baixa sendo procurados no bloco) ------------+ for (i=M;i<=N;i++) // Pontos de referência (fractais) no loop de busca {//loop b // buscando por fractais de alta -----------------------------------+ if(High[i]>High[i+1] && High[i]>High[i+2] && High[i]>High[i-1] && High[i]>High[i-2]) {// frac_b Tfnb++; // contador // ---------------------------- if(Tfnb==1) { // 1º fractal: preço, índice e tempo. TF1B=High[i]; Tf1b=i; timf1b=iTime(Symbol(),Period(),i); }//-counter_1 // ---------------------------- if(Tfnb==2) {//counter_2 // preço, índice e tempo. TF2B=High[i]; Tf2b=i; timf2b=iTime(Symbol(),Period(),i); break; }//-counter_2 // ---------------------------- }//-frac_b }//-b loop // --------------------------------------------------------------------+ for (i=M;i<=N;i++) // Pontos de referência (fractais) no loop de busca {//s loop // buscando por fractais de baixa ----------------------------------+ if(Low[i]<Low[i+1] && Low[i]<Low[i+2] && Low[i]<Low[i-1] && Low[i]<Low[i-2]) {// frac_s Tfns++; if(Tfns==1) {//counter_1 // preço, índice e tempo TF1S=Low[i]; Tf1s=i; timf1s=iTime(Symbol(),Period(),i); }//-counter_1 if(Tfns==2) {//counter_2 // preço, índice e tempo. TF2S=Low[i]; Tf2s=i; timf2s=iTime(Symbol(),Period(),i); break; }//-counter_2 }//-frac_s }//- loop s // ------------(Fractais de alta e de baixa buscando bloco)------------+
Lembrando novamente, a numeração dos pontos de referência é realizada considerando que a "indexação dos elementos da série temporal é realizada para trás, do último ao primeiro, a barra atual que está sendo plotada é o último array com índice igual a 0". As condições a seguir foram incluídas no bloco de convergência das linhas para formar o triângulo:
- Os primeiros fractais devem estar espaçados numa distância maior do que 20-30 pips;
- Os primeiros fractais da linha devem ser menores do que os segundos fractais de uma e outra;
- Todos os quatro pontos de referência são diferentes de "0", ou seja, eles têm valores reais;
- Parâmetros de tempo dos pontos de referência deve ser diferente de "0";
- O primeiro ponto de referência superior está abaixo do segundo superior e o primeiro ponto inferior é maior do que o segundo ponto inferior;
- A diferença entre as linhas dos segundos fractais não devem exceder a150 pips.
// ---------------------------------------------------------------------------+ if((TF1B-TF1S)>25*Point && Tf1b<=Tf2s && Tf1s<=Tf2b && TF1B>0 && TF1S>0 && TF2B>0 && TF2S>0 && timf1b!=0 && timf2b!=0 && timf1s!=0 && timf2s!=0 && TF1B<TF2B && TF1S>TF2S && (TF2B-TF2S)/Point<150) {// condições para desenhar os triângulos //===========================================================================+
Depois de cumprir as condições preliminares, calcular as taxas das variações de preços para as linhas de trabalho superiores e inferiores:
// --------------------------------------------------------------------------+ // - (Bloco de cálculo da taxa de mudança do preço) (pips superiores e inferiores por uma barra) if(TF1B!=TF2B) {RatePriceH=MathAbs((TF2B-TF1B)/(Tf2b-Tf1b));} // para a linha superior if(TF1S!=TF2S) {RatePriceS=MathAbs((TF1S-TF2S)/(Tf2s-Tf1s));} // para a linha inferior // Imprimir(" RatePriceS= ",RatePriceS); Imprimir(" RatePriceH= ",RatePriceH); // -----------------------(Bloco de preço altera cálculo da taxa ------------+
Neste ponto, os 4 últimos fractais estão localizados de acordo com a condições de formação do triângulo, embora ainda não esteja claro o ponto do Ápice e onde a efetiva atual área de ruptura está localizada. O cálculo do Ápice (Apex) depende da localização do segundo fractal entre os últimos quatro formados (da esquerda para a direita no gráfico).
O ponto de partida da linha de trabalho deve ser definida como um ponto de intersecção de uma vertical traçada através do segundo fractal de alta, a linha inicia no 2º fractal (de alta) e define a direção no 4º fractal (de alta). A este respeito, o algoritmo do programa é ramificado em duas direções para cálculo da atual área de ruptura: 2º fractal de alta maior e 4ª fractal de alta menor.
Fragmentos da base de código relativos a uma das direções são mostrados abaixo. A segunda direção é calculada usando o mesmo algoritmo.
// жжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжж 1. A linha de trabalho superior é maior do que a inferior жжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжжж+ // - (Bloco de busca do ponto de intersecção da linha de trabalho) -----------------------------------------------------------+ // Se a linha de trabalho superior é maior do que a inferior - encontra o ponto de intersecção em 50 barras if(Tf2b>Tf2s && TF2B>TF1B && TF2S<TF1S) {// A linha de trabalho superior é nos fractais de alta // O preço de partida para o cálculo dos valores em cada barra da linha de trabalho superior Starting_Price_H=TF2B-RatePriceH*(Tf2b-Tf2s); // O preço de partida para o cálculo dos valores em cada barra da linha de trabalho superior Starting_Price_S=TF2S; // o tempo para desenhar a linha vertical na base do triângulo time_starting=timf2s; // ------------------------------------ for(int k=1;k<=50;k++) {//50b loop PricB[k]=Starting_Price_H-RatePriceH*k; // diminui taxa descendente PricS[k]=Starting_Price_S+RatePriceS*k; // soma taxa ascendente // Se os preços das projeções das linhas superiores e inferiores coincidem if(PricB[k]<=PricS[k]) // Tornou-se menor do que a inferior, então existe a intersecção com a linha de trabalho {//existe a intersecção P_Tria=PricB[k-1]; // Preço da interseção da linha de trabalho (-1) - deve ser uma barra menor cut_left=k; break; // Número de barras a partir da base até o ponto de interseção }//- existe uma intersecção }//-50b loop // -------------------------------------- (Bloco de busca do ponto de interseção da linha de trabalho)+-----------------------+
Agora, podemos começar a calcular os parâmetros de tempo da atual área de rompimento:
// ---------------------------------------------------------------------------+ // - (Bloco de calcular intervalos de tempo para a atual área de rompimento)------------------+ // Apresenta duas limitações adicionais: // 1. O Ápice (Apex) não deve estar localizado mais do que 50 barras da base do triângulo // 2. O Ápice (Apex) não deve estar localizada a menos do que 15 barras da base do triângulo. if(cut_left<50 && cut_left>12) {//triângulo com todas as limitações time_Apex=timf2s+cut_left*T_period; // Tempo de formação do Ápice // Dividir o número de barras por três, tomar 2/3 e arrendodar para o número inteiro maior // valor: MathRound(cut_left/3*2) - número de barras para atual área de rompimento time_bar_zona=time_starting+MathRound(cut_left/3*2)*T_period; //tempo de área // condições cumpridas para criação padrão, calculada a atual área de rompimento PatternTch=true; // formado o padrão "Triângulo de Chuvashov" {//-triângulo com todas as limitações // -----(Bloco de calcular intervalos de tempo para a atual área de rompimento)-----+
Agora, depois do padrão ter sido formado, o bloco de desenho do triângulo pode iniciar a sua operação:
// - (Bloco de desenho do triângulo após o padrão foi formado) -----------+ if(PatternTch==true) {//existe um padrão Del_Frb(); Del_Frs(); // Excluir fractais superiores e inferiores anteriores CreateArrow_Frb(); CreateArrow_Frs(); // Desenhar fractais superiores e inferiores Create_Tr_H(); Create_Tr_S(); // Desenhar linhas de tendência superior e inferior CreateLzona(); CreateLbasis(); CreateLApex(); // Desenhar linhas verticais CreateTriangleH(); // Desenhar o triângulo pela linha superior, ObjectDelete("TRS"); // deletar o desenho do triângulo pela linha inferior // -----(Bloco de desenho do triângulo após o padrão formado) --------+A imagem abaixo mostra a operação do bloco de desenho padrão "Triângulo de Chuvashov" :
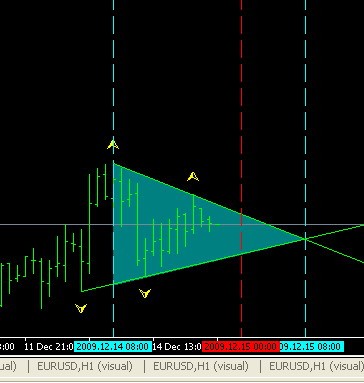
O bloco de abertura de posições, passando para a ação.
Se estiverem reunidas as condições para uma abertura de posição, o desenho do canal com a linha de trabalho superada pelo preço é calculado. O canal é criado.
StopLoss e TakeProfit serão calculados considerando-se os requisitos do sistema de gestão de dinheiro e a posição será aberta (neste caso, uma posição COMPRADA - veja a imagem abaixo).
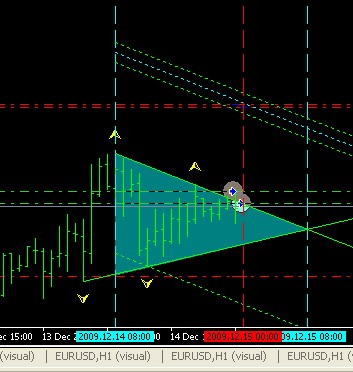
No entanto, as posições podem ser abertos em ambos os sentidos, se estiverem reunidas as condições para a abertura em ambas as direções (veja a imagem abaixo).
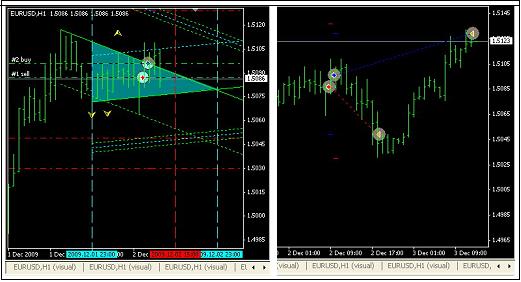
O programa então controla o tempo de vida do padrão.
Se o tempo corrente excede o tempo do atual rompimento, o programa proibe a abertura de posições. Se o tempo corrente excede o Ápice, o programa elimina todos os desenhos padrão, limpando o gráfico dos sinais e linhas já desnecessárias.
Código do bloco de vida padrão é mostrado abaixo.
// - (Bloco definindo o tempo de vida do padrão) ------------------------+ // Se o tempo corrente exceder o tempo limite da atual área de rompimento, o padrão perde o seu poder if((TimeCurrent()-time_bar_zona)>=T_period) { PatternTch=false; // o padrão está desatualizado - proibir a abertura de posições } // após o tempo corrente exceder o Ápice if((TimeCurrent()-time_Apex)>=T_period) { // deletar sinais padrão e linhas do gráfico Del_Frs(); Del_Frb(); Del_TrLin(); // deletar as linhas do canal tamanho do lucro pela linha de trabalho superior ObjectDelete("Tr_B1h"); ObjectDelete("Tr_B1hh"); ObjectDelete("Tr_B1hs");ObjectDelete("Tr_B1s"); // deletar as linhas do canal tamanho do lucro pela linha de trabalho inferior ObjectDelete("Tr_S1s"); ObjectDelete("Tr_S1sh"); ObjectDelete("Tr_S1ss");ObjectDelete("Tr_S1h"); // deletar as linhas verticais da atual área de rompimento ObjectDelete("L1");ObjectDelete("zona");ObjectDelete("Ap"); ObjectDelete("TRH"); ObjectDelete("TRS"); } // ------(Bloco de definição de tempo de vida do padrão) -+
Os resultados desta operação do bloco são apresentados no lado direito da imagem anterior.
O Expert Advisor aqui apresentado mostrara resultado positivo como um sistema de negociação mecânico durante o teste automático:
- O índice de lucro bruto e perda bruta - P/F = 38869/16480 = 2,36 (mais de 2);
- Número de negócios = 101 (não inferior a 100);
- Percentual de Rebaixamento = 25,18% (ver arquivo anexo).
A breve conclusão é a seguinte:
A técnica descrita pode ser utilizada por traders como um componente do sistema de negociação, mas filtros de abertura de posição devem ser adicionados como uma melhoria.
Os filtros propostos anteriormente aqui neste documento podem ser melhorados, tal como recomendado pelo autor da técnica Stanislav Chuvashov.
Notas para os arquivos anexados:
- Triangle_H1_v46.mq4 – offered МТС
- Strategy_Tester_Report_46.zip – resultado do teste
- table_3.zip – para os fãs de análise
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1364
LibMatrix: Biblioteca de Álgebra Matricial (Parte I)
Expert Advisor MetaTrader 4 para Intercâmbio de Informações com o Mundo Exterior
Lendo Feeds de Notícias RSS Via MQL4
Uma Sandbox Aleatória
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso