MetaTrader 5 / 機械学習
English Русский Deutsch
preview
モデル解釈をマスターする：機械学習モデルからより深い洞察を得る

モデル解釈をマスターする：機械学習モデルからより深い洞察を得る

MetaTrader 5 — 機械学習 | 19 3月 2024, 15:58
110 0
Gamuchirai Zororo Ndawana
Gamuchirai Zororo Ndawana

はじめに

機械学習の分野では、トレードオフの観点から考えることがよくあります。あるパフォーマンス指標を最適化する一方で、別のパフォーマンス指標を妥協してしまうことがよくあります。ますます大規模で複雑なモデルが進化する傾向にあり、その理解、説明、デバッグは手ごわい作業となっています。モデルの表層に潜む複雑さ、モデルが下す決断の「理由」を読み解くことが重要です。この明確さがなければ、どのようにして、このモデルを自分たちの望む目的に沿って監督できると確信できるのでしょうか。  モデルが意図しない形で機能し、努力が無駄になるリスクを冒すわけにはいきません。本稿では、こうした複雑な問題を掘り下げ、以下のトピックを明らかにすることを目的とします。

  1. 重要な特徴の特定：モデルはどの特徴が重要だと考えたか

  2. 単一特徴のインパクトの解読：各特徴がモデルのパフォーマンスに与える影響を理解する

  3. 集団的特徴の影響力の把握：特徴量がモデルの予測に与える広範な影響を探る

私たちの旅は、機械学習の複雑さの核心をナビゲートし、モデルの動作をよりよく理解し、修正する力を与えます。この知識を受け入れ、機械学習の真の可能性を活用しましょう。


重要な理由

デバッグ：

図1：デバッグの極意

過ちを犯すことは人間的であり、許すことは神的である」～アレクサンダー・ポープ

一見、デバッグは平凡に見えるかもしれませんが、その意義は領域を超えています。ランタイムエラーをこっそりと回避し、気づかれずにすり抜けるような、とらえどころのないバグを思い浮かべてください。しかし、このページに織り込まれた知識で武装すれば、モデルが織りなす複雑なパターンを読み解くことができるようになります。これらのパターンが、現実世界の理解と調和しているかどうかを見極めるのです。現実のプロジェクトの迷宮の中で、自分のバグを巧みに探し出し、克服します。

より良い特徴量エンジニアリング

特徴量エンジニアリング

図2：特徴量エンジニアリング

「継続的な改善は遅れた完璧に勝る」～マーク・トウェイン

それでは、魅惑的な特徴量エンジニアリングの領域へと足を踏み入れてみましょう。円を想像してください。直径に沿って赤い線を引きます。単純な行為ですが、意味を孕んでいます。さて、考えてみましょう。直径は、円の円周を優雅に何回カーブできるでしょうか。答えは自ずと明らかです。--約3.145、円周率として誰もが知る定数です。

この思考実験は、プレゼンテーションが私たちの学習能力に与える影響を浮き彫りにし、私たちのガイドとなります。円の曲率がフィット感に影響するように、特徴変換はデータセットの調和を高めます。新しい柱を造形することで、日常を超越し、予測精度を驚異的な高みへと引き上げます。ここでは直感が羅針盤となり、未知の海を進む舵取りをしてくれます。しかし、直感が鈍ったらどうなるでしょうか。恐れることはありません。このオデッセイは、最も惑わされやすい地形でさえもナビゲートする戦略を明らかにしてくれます。しかし、私たちはそれだけにとどまらず、導入したこれらの新機能の効果を実証的に測定していきます。


今後のデータ収集の方向性

図3：データ収集の改善


「未来を知りたければ、過去を見よ」～アルバート・アインシュタイン

データの世界を横断するとき、古くからの知恵が響きわたります。未来への鍵は過去の記録の中にあるのです。特徴量エンジニアリングはもう限界なのでしょうか。恐れることはありません。データの世界では、過去こそが道標なのです。新しいデータ型が手招きし、モデルに生命を吹き込むことを約束しています。私たちの忠実な伴侶である洞察は、データの山の中にある宝石へと私たちを導く代理人としての役割を果たします。洞察が深まるごとに、新機能への道筋が明確になり、未来は無限の可能性に満ちていくのです。

意思決定の改善

図4：意思決定の改善

「少しの学習は危険なことである」～アレクサンダー・ポープ

機械学習のシンフォニーでは、あなたがハンドルを握ります。モデルはあなたの曲に合わせて踊り、その予測に命を吹き込む決断の証となります。機械学習は単なる予測を超え、真の宝が埋もれている洞察の深みにまで踏み込みます。あなたの理解と熟練は、あなたの野心を支える岩盤を形成します。一つひとつの洞察、貴重な塊が、あなたの努力に影響を与えます。

探検家の皆さん、機械学習の謎を解き明かすとき、この言葉に導かれることにしましょう。


理論的基礎

この記事では、価格回帰分析をおこなうために、CatBoost Pythonライブラリで容易に利用できる勾配ブースティング木モデルを採用することを目的とします。しかし、冒頭で注目すべき課題が浮上し、モデルの精査と影響力のある特徴の特定が必要となりました。私たちのモデルにブラックボックス説明技術を適用する前に、私たちのブラックボックスモデルに内在する限界と、この文脈でブラックボックス説明者を採用する根拠を理解することが不可欠です。

勾配ブースティング決定木は、分類タスクにおいて称賛に値する性能を示しますが、それにもかかわらず、特定の時系列回帰問題に適用すると、明確な限界が現れます。機械学習モデルのファミリーに属するこれらの木は、目標値に基づいて入力を集団に分類します。その後、アルゴリズムは各集団内の目標値の平均を計算し、これらの集団平均を予測に利用します。特筆すべきは、訓練中に確立されたこれらの集団平均は、さらなる訓練が実施されない限り固定されることです。この固定的な性質から重大な欠点が浮かび上がります。勾配ブースティング木は通常、トレンドを効果的に外挿するのに苦労するからです。学習範囲外の入力値に直面した場合、モデルは反復的な予測をしがちで、既知の集団から得られた平均値に頼ることになりますが、これは観察された学習範囲を超えた根本的な傾向を正確に捉えていない可能性があります。

さらに、このモデルは、似たような特徴値が似たような目標値をもたらすことを前提としていますが、これは金融商品の取引における集団的経験とは矛盾する仮定です。金融市場では、価格パターンが類似性を示しながら、結論が異なる場合があります。この乖離は、生成プロセスが均質な集団に分類されるデータを生成するというモデルの仮定に挑戦するものです。その結果、これらの仮定に違反すると、モデルにバイアスが生じます。

これらの観察を実証するために、この現象を独自に観察したことのない読者のためにデモンストレーションをおこないます。私たちのコミットメントは、すべての読者に包括的な理解を保証することです。

必要な依存関係を読み込むことから始めます。

#pip install pandas if you haven't installed it allready
#We'll use pandas to store and retrieve data
import pandas as pd       

#pip install pandas-ta if you haven't installed it allready
#We'll use pandas_ta to calculate technical indicators
import pandas_ta as ta    

#pip install numpy if you haven't installed it allready
#We'll use numpy to perform optmized vector calculations 
import numpy as np

import matplotlib.pyplot as plt

#pip install numpy if you haven't installed it allready
#We'll use MetaTrader 5 connect to and control our MetaTrader 5 Terminal 
import MetaTrader5 as MT5

#Standard python library
import time
次にログイン情報を入力します。 
login = enter_your_login
password =  enter_your_password
server = enter_your_broker_server
MetaTrader 5ターミナルを初期化し、ログインします。 
if(MT5.initialize(login=login, password= password, server=server)):
    print("Logged in succesfully")
else:
    print("Failed to initialize the terminal and login")
ログイン成功です。
ボラティリティ75指数、またはお好きな銘柄のM1データを100万行リクエストしてみましょう。

data = pd.DataFrame(MT5.copy_rates_from_pos("Volatility 75 Index",MT5.TIMEFRAME_M1,0,100000))
data

マーケットデータ

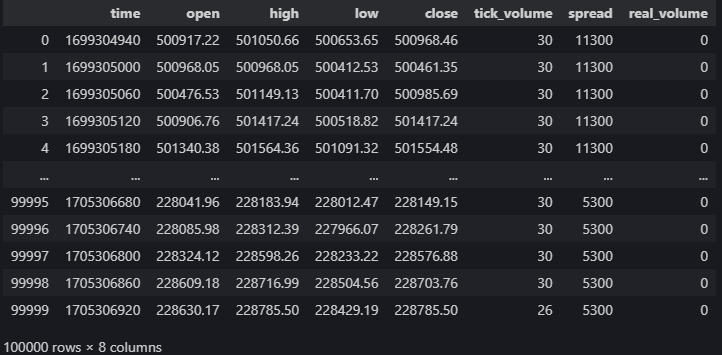
図5：MetaTrader 5ターミナルからのマーケットデータ

価格予測に役立つテクニカル指標を計算してみましょう。

#20 period exponential moving average
data["ema_20"] = data.ta.ema(length=20)
#40 period exponential moving average
data["ema_40"] = data.ta.ema(length=40)
#100 period exponential moving average
data["ema_100"] = data.ta.ema(length=100)
#20 period relative strength indicator
data.ta.rsi(length=20,append=True)
#20 period bollinger bands with 3 standard deviations
data.ta.bbands(length=20,sd=3,append=True)
#14 period average true range
data.ta.atr(length=14,append=True)
#Awesome oscilator with default settings
data.ta.ao(append=True)
#Moving average convergence divergence (MACD)
data.ta.macd(append=True)
#Chaikins commidity index
data.ta.cci(append=True)
#Know sure thing oscilator
data.ta.kst(append=True)
#True strength index
data.ta.tsi(append=True)
#Rate of change
data.ta.roc(append=True)
#Slope between 2 points
data.ta.slope(append=True)
#Directional movement
data.ta.dm(append=True)

ターゲットを設定します。

data["target"] = data["close"].shift(-30)

ブラックボックスモデルを設定します。

from catboost import CatBoostRegressor

訓練とテストを準備します。

train_start = 100
train_end   = 10000

test_start = train_end + 100
test_end = test_start + 30000

predictors = [
    "open",
    "high",
    "low",
    "close",
    "KSTs_9",
    "KST_10_15_20_30_10_10_10_15",
    "CCI_14_0.015",
    "AO_5_34",
    "ATRr_14",
    "BBM_20_2.0",
    "BBP_20_2.0",
    "BBB_20_2.0",
    "BBU_20_2.0",
    "BBL_20_2.0",
    "RSI_20",
    "ema_20",
    "ema_40",
    "ema_100",
    "SLOPE_1",
    "ROC_10",
    "TSIs_13_25_13",
    "TSI_13_25_13",
    "MACD_12_26_9",
    "MACDh_12_26_9",
    "MACDs_12_26_9",
    "DMP_14",
    "DMN_14"
]
target = "target"
決定木はスケールに敏感なので、入力値を正規化し、各特徴の最初の読み取り値をfirst_valuesという配列に格納します。
first_values = {}
#Iterating over the columns in the dataset
for col in data.columns:
    #Which of those columns are part of the model inputs?
    if col in predictors:
        #What was the first value in that column?
        first_values[col] = data[col][train_start]
        data[col] = data[col]/first_values[col]

Trainテストを実行します。

train_x = data.loc[train_start:train_end,predictors]
train_y = data.loc[train_start:train_end,target]

test_x = data.loc[test_start:test_end,predictors]
test_y = data.loc[test_start:test_end,target]
ブラックボックスモデルをフィッティングします。 

cat_full = CatBoostRegressor()
cat_full.fit(train_x,train_y)
ブラックボックスモデルから予測を取得します。 
cat_full_predictions = pd.DataFrame(index=test_x.index)
cat_full_predictions["predictions"] = cat_full.predict(test_x)
cat_full_predictions.plot(label=True)
test_y.plot()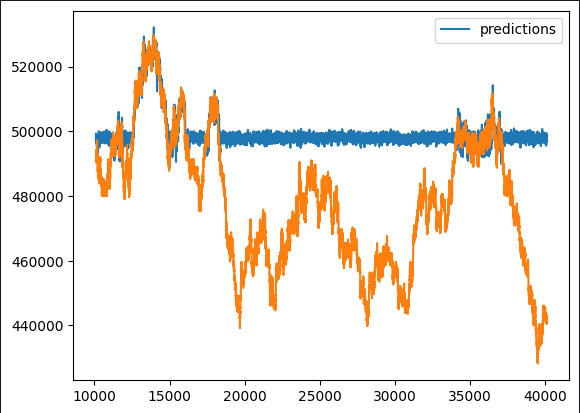

ブラックボックス予想

図6：ブラックボックス予想


最初の観察で、予測モデルが非典型的な平坦期を示すことが明らかになりました。勾配ブースティングアルゴリズムの典型的な実装の包括的な概要を考えれば、このようなパターンは予想外ではないはずです。私たちの興味は、どの特徴がモデルの性能にプラスに寄与し、どの特徴が潜在的なノイズ源となりうるかを見極めることにあります。そのためには、特徴量エンジニアリングの機会を徹底的に検討する必要があります。

このようなニュアンスを解明するために、ブラックボックス的な説明の仕方を提案します。しかし、やみくもにこれらの説明を適用する前に、ブラックボックス説明アルゴリズムの根本的なメカニズムを把握することが不可欠です。これには、その前提条件を批判的に評価し、その前提条件が守られているか、あるいは違反する可能性があるかを確認することが含まれます。

このような基礎的な理解をもってブラックボックス説明技術の応用に取り組むことで、それぞれの説明を慎重に解釈することができます。説明の技法を精査し、その妥当性を評価することで、導き出された洞察に適切なレベルの信頼性を与えることができます。この理路整然としたアプローチは、意味のある情報を抽出し、ブラックボックス説明プロセスの結果に基づいて、十分な情報に基づいた決断を下す能力を高めてくれます。


ブラックボックス説明アルゴリズム

Drop Column Importance

Drop Column Importance手法は、最初にすべての予測変数を考慮し、その後1つの列を繰り返し削除し、その結果の精度への影響を観察することで、モデルの精度を評価するために採用される手法です。このアプローチにより、モデル全体のパフォーマンスに対する各列の具体的な寄与について、貴重な洞察が得られます。

Drop Column Importanceの特徴は、その実用性と合理性にあります。この技法の根底にある仮定は、データの不整合が頻繁に発生する現実世界のシナリオと一致しています。インターネット接続の中断、停電、悪天候、その他の不測の事態が原因であろうと、この方法は、実際の運用環境での発生を反映するロバストモデルをエミュレートします。このリアリズムが、実用的で日常的な状況で遭遇する可能性のあるシナリオに対処するための技術の適用性と有効性を高めています。

長所

  • モデル性能の向上：無関係な列や冗長な列を削除することで、ノイズを減らし、S/N比を改善することで、機械学習モデルのパフォーマンスを向上させることができます。
  • モデルの簡易化：不要な列を削除することで、よりシンプルで解釈しやすいモデルになり、利害関係者への理解や説明が容易になります。

短所

  • 情報の喪失：列を削除すると貴重な情報が失われる可能性があり、データの重要なパターンを捉えられない単純化されすぎたモデルになる可能性があります。
  • 下流工程への影響：その列がその後の分析で使用されたり、特定のビジネスプロセスで必要であったりする場合、その列を削除すると、それらのワークフローが中断される可能性があります。

機会

  • 特徴量エンジニアリング：列の削除は、特徴量エンジニアリングの機会を提供し、既存のデータに基づいて新しい特徴を作成したり、モデルのパフォーマンスを向上させるために残りの特徴を変更したりすることができます。
  • リソースの最適化：不要な列を削除することで、特に大規模なデータセットでは、メモリ、ストレージ、処理時間といったリソースの節約につながります。

脅威

  • モデルの偏り：取り除かれた列が偏りのない予測に重要な情報を含んでいる場合、その列が取り除かれることでモデルにバイアスがかかり、不正確な結果や不公平な結果につながる可能性があります。
  • データの完全性に関する懸念：データを十分に理解せずに列を削除すると、データの整合性に問題が生じ、データセットの全体的な品質とその後の分析に影響を与える可能性があります。


Permutation Importance

Permutation Importanceは、特定の列の値を無作為に並べ替え、その結果生じるモデルのエラーメトリクスへの影響を評価することで、特徴の重要性を評価する代替方法を提供します。核となる考え方は、ある列がモデルに影響を与える重要な役割を担っている場合、その元の値を崩すとエラーメトリックスが増加し、全体的な精度が低下するはずだという前提に基づいています。逆に、列の影響が最小限であれば、観測可能な変化は限定的であり、場合によってはパフォーマンスが向上することさえあります。

この技法は、特徴の重要性についての微妙な視点を提供し、モデルの予測能力に対する各特徴の貢献度を動的に評価することを可能にします。並べ替えプロセスは、個々の特徴に対するモデルの感度を明らかにするのに役立つランダム性のレベルを導入し、予測フレームワークにおけるそれらの重要性をより包括的に理解することを可能にします。

長所

  • モデルを問わない：Permutation Importanceはモデルにとらわれません。つまり、基礎となるアルゴリズムについて仮定することなく、どんな教師あり学習モデルにも適用できます。そのため、汎用性が高く、幅広く応用できる技術となっています。
  • 直感的な解釈：Permutation Importanceの概念は比較的理解しやすいです。これは、特定の特徴の値を無作為に並べ替えたときのモデル性能の変化を測定するもので、特徴の重要性を明確に解釈することができます。

短所

  • 計算強度：Permutation Importanceを計算するには、各特徴の並べ替えに対してモデルの性能を再評価する必要があるため、計算量が多く、特に大規模なデータセットでは時間がかかる可能性があります。
  • サンプルサイズに対する感度：Permutation Importanceはデータセットのサイズに敏感です。小さなデータセットでは、特徴の並べ替えの影響が誇張され、重要度の推定の信頼性が低くなる可能性があります。

機会

  • 特徴選択のガイダンス：Permutation Importanceの結果は、どの特徴がモデルの性能に最も寄与するかを特定することにより、特徴の選択を導くことができます。この情報は、モデルを単純化し、次元を小さくするのに役立ちます。
  • 非線形関係の識別：線形モデルとは異なり、Permutation Importanceは特徴量と対象変数の間の非線形関係を捉えることができ、データ内の複雑なパターンに対する洞察を提供します。

脅威

  • 相関する特徴の影響：Permutation Importanceは、特徴の相関が高い状況をうまく扱えない可能性があります。2つの特徴量に相関関係がある場合、もう一方の特徴量が同様の情報を提供していれば、一方の特徴量を入れ替えてもモデルの性能に大きな影響を与えない可能性があります。
  • 過剰学習の可能性：特にモデルが複雑すぎたり、データセットが小さかったりする場合、Permutation Importanceを使用すると過剰学習の危険性があります。重要度スコアは、新しいデータにうまく一般化できないかもしれません。

PDP (Partial Dependence Plot)とICE (Individual Conditional Expectation)プロット

モデルの振る舞いをより微妙に理解するために、PDP (Partial Dependence Plot)とICE (Individual Conditional Expectation)プロットを採用します。PDP (Partial Dependence Plot)は，1つの予測変数が変化するとき，他のすべての予測変数を一定に保ちながら，予測された結果がどのように変化するかを説明します。一方、ICEプロットは、各インスタンスについて個別の曲線を表示することで、特徴の重要性について詳細な視点を提供し、各特徴の影響の包括的な分析を容易にします。

PDPプロットとICEプロットを併用することで、トレンドの集計にとどまらない強固な視覚的表現が可能になります。PDPが特定の予測因子とモデルの予測との間の関係の包括的なビューを提供する一方、ICEプロットは、それぞれが異なるインスタンスにわたるその予測因子の個別化された影響を表す一連の曲線を提示することによって、ニュアンスを掘り下げます。この複合的なアプローチは、異なる予測値に対するモデルの反応における複雑なパターンとバリエーションを識別する能力を強化し、全体的な予測フレームワークにおける特徴の重要性をより完全に理解することを促進します。

長所

  • 解釈の可能性：PDPは、特徴と予測結果の関係を直感的かつ視覚的に表現し、専門家でなくても特定の特徴がモデルの予測に与える影響を容易に解釈理解できるようにします。
  • パターンの特定：PDPは、特徴と予測結果の関係のパターンや傾向を特定するのに役立ち、特徴の変化がモデルの予測にどのように影響するかをより深く理解することができます。

短所

  • 独立の前提：PDPは、関心のある特徴が他の特徴から独立していることを前提としています。相関する特徴を持つ複雑なモデルでは、PDPの解釈は困難であり、プロットは真の関係を正確に反映していない可能性があります。
  • 限界効果に限定：PDPは、他の特徴を固定したまま、1つの特徴の限界効果を示しています。複数の特徴間の複雑な相互作用を捕捉できない可能性があり、モデルの複雑性を完全に明らかにする能力が制限されます。

機会

  • モデルの検証：PDPはモデル検証のツールとして使用できます。PDPから得られた洞察をドメインの知識や予想と比較することで、実務者はモデルが機能の予想される動作と一致しているかどうかを評価することができます。
  • 特徴重要度ランキング：PDPは、モデルの予測に最も大きな影響を与える特徴を視覚的に強調することで、特徴重要度ランキング（FIR、Feature Importance Ranking）を支援することができます。この情報は、特徴の選択やモデルの簡略化の指針となります。

脅威

  • 誤解の可能性：統計の概念を正しく理解しなければ、誤った解釈をする危険性があります。特に、潜在的な交絡変数やモデルの複雑さを認識していない場合、観察された関連に因果関係があると誤認する可能性があります。
  • 高次元データの複雑さ：PDPは、可能な特徴の組み合わせが爆発的に増えるため、高次元空間では解釈が難しくなります。複数の特徴間の相互作用を視覚化することは、ますます複雑になります。


SHAP (SHapley Additive exPlanation)


Lloyd Shapely

図7：2016年3月12日にアリゾナ州ツーソンで逝去したロイド・シャープレーを偲んで。彼のアイデアは永遠に生き続ける。

先駆者ロイド・シャープレーにちなんで名付けられたSHAP値は、予測に対する各特徴の寄与を帰属させることで、モデルの出力を説明するために使用されます。

SHAP値は、特徴の可能なすべての組み合わせについてモデルの出力を評価することによって計算することができます。もっと簡単に言えば、特定の特徴の値をシャッフルし、他は一定に保ち、モデルの予測に与える影響を観察することです。

ゲームにおける選手と同じように、ある特徴がその値をシャッフルしても一貫してモデルの出力に変化を与えない場合（例：ある選手がチームの成績に影響を与えない）、その特徴のSHAP値は低くなる傾向があります。対照的に、特徴を変更することがモデルの出力に大きく影響する場合、SHAP値は高くなり、より実質的な寄与を示します。

SHAP値は、各特徴の貢献度を定量的に示す指標となります。異なる特徴間でSHAP値を比較することで、どの特徴がモデルの予測により大きな影響を与えるかを推測することができます。

つまり、ある特徴量を繰り返し除外（値をシャッフルしたり変化させたり）しても、モデルの性能が大きく変化しない場合、モデルの予測に対するその特徴量の寄与が相対的に小さい可能性が示唆されます。

長所

  • モデルを問わない：SHAP値はモデルにとらわれません。つまり、アンサンブル法、ニューラルネットワーク、サポートベクトルマシンなどの複雑なモデルを含む、あらゆる機械学習モデルに適用できます。
  • 大域的な解釈可能性と局所的な解釈可能性：SHAP値は、大域的な解釈可能性と局所的な解釈可能性の両方を提供します。個々の特徴が特定の予測に与える影響（局所的な解釈可能性）と、データセット全体にわたる各特徴の全体的な寄与（全体的な解釈可能性）を説明することができます。

短所

  • 計算量が多い：SHAP値の計算は、特に大規模なデータセットや複雑なモデルの場合、計算量が多くなる可能性があります。これは、リアルタイムアプリケーションや、計算リソースが限られている状況では、課題となるかもしれません。
  • 高次元データの解釈可能性への挑戦：特徴数が多いモデルのSHAP値の解釈は難しいことがあります。多数の特徴の寄与を視覚化し理解することは、高次元空間ではより複雑になります。

機会

  • 特徴重要度ランキング：SHAP値は、モデル予測への影響に基づいて特徴をランク付けするために使用できます。この情報は、特徴選択とモデル内で最も影響力のある変数を特定するために貴重です。
  • 説明的な視覚化：SHAP値は、SHAPのsummary plotや個々のforce plotなど、洞察に満ちたビジュアライゼーションの作成を可能にし、関係者へのモデル予測や機能貢献の伝達に役立ちます。

脅威

  • 一貫性の前提：SHAP値は一貫性を仮定しており、予測に対する特徴の影響が異なるインスタンス間で一貫していることを意味します。場合によっては、この仮定が成り立たず、誤解を招く可能性もあります。
  • 解釈の複雑さ：SHAP値は貴重な洞察を与えてくれますが、それを正しく解釈するには、基礎となる概念をしっかりと理解する必要があります。ユーザーは特定の値の重要性を誤解したり、特徴の貢献のニュアンスを把握できなかったりする可能性があります。

相互情報

相互情報量（Mutual Information、MI）とは、ある変数の有無が別の変数について提供する情報量の尺度です。これは、2つの変数の間の依存性または関連性の程度を定量化するものです。

長所

  • モデルを問わない：相互情報量はモデルに依存しない指標であり、特定の機械学習モデルに依存しないことを意味します。線形および非線形の依存関係を含む、あらゆるタイプの変数間の関係に適用できます。
  • 非線形の関係を捉える：線形関係に適した相関関係とは異なり、相互情報量は変数間の非線形依存関係を捉えることができるため、様々なタイプのデータに汎用性があります。

短所

  • サンプルサイズに対する感度：相互情報量はデータセットのサイズに敏感な場合があります。小規模なデータセットでは、MIの推定が安定せず、データのわずかな変動が結果に大きな影響を与える可能性があります。
  • マグニチュードの解釈の難しさ：MIは関連性の強さの尺度を提供しますが、その絶対値を直接解釈するのは難しい場合があります。相互情報量が「高い」か「低い」かの解釈は、変数の文脈と規模に依存します。

機会

  • 特徴の選択：相互情報量は、ターゲット変数との関連性に基づいて特徴をランク付けすることにより、特徴選択に使用することができます。MI値が高い特徴量は、ターゲットを予測する上でより有益であると考えられます。
  • アンサンブルモデルにおける変数の重要性：アンサンブル学習では、変数の重要性を評価するために相互情報を使用することができ、より正確で解釈しやすいアンサンブルモデルの構築に役立ちます。

脅威

  • 独立の前提：相互情報量は、MIがゼロのとき変数が独立であると仮定します。実際には、複雑な依存関係や、潜在的要因や交絡変数に影響される関係を捉えられない可能性があります。
  • 高次元で計算集約的：高次元データの相互情報量を推定するのは、計算量が多くなる可能性があります。このことは、時間やリソースの必要性という点で課題となる可能性があります。


ありがたいことに、特化したPythonライブラリがこのプロセスを効率化し、コードのほとんどをゼロから構築する必要を省いてくれます。

この記事では、モデルの訓練やフィッティングの複雑さについては触れないことにご注意ください。その代わりに、訓練後の段階に焦点を当て、モデルのパフォーマンスをどのように評価し、解釈するかを探ります。提供されているコード例は、純粋に説明のために基本的なモデルを構築するもので、モデルを設計して訓練した後のステップを強調しています。 

始めましょう 

Drop Clumn Importance

sklearnライブラリのRFE（Recursive Feature Elimination、 再帰的特徴量削減）アルゴリズムをDrop Column Importanceの実装として使用します。

from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
RFEアルゴリズムは、教師あり学習モデルの適合と評価を期待します。
モデルは、その係数または推論された関数を通じて、特徴の重要性に関する情報を提供する必要があります。
そのモデルは、ここでの問題で使っているモデルと同じである必要はありません。
モデルはsklearnライブラリのものである必要はありませんが、少なくともsklearnラッパーを持つ必要があります。

線形モデルを使用し、無作為に特徴を削除しながらその精度を評価します。

lm = LinearRegression()
rfe = RFE(lm,step=1)

step引数は、各反復で落とす特徴の数を示します。

次に、RFEアルゴリズムを適用します。

rfe = rfe.fit(train_x,train_y)
RFEアルゴリズムがどの特徴を有益と判断したかを見てみましょう。 
rfe.support_
array([ True, True, True, True, False, False, False, False, False, True, False, True, True, True, False, True, True, True, False, False, False, False, False, False, True, False, True])
各特徴のランキングも入手できます。 

rfe.ranking_
array([ 1, 1, 1, 1, 2, 5, 14, 11, 13, 1, 7, 1, 1, 1, 8, 1, 1, 1, 12, 15, 3, 4, 9, 10, 1, 6, 1])

sklearnの実装では、train_xデータフレームの列に適用できるマスクが用意されており、RFEが重要だと判断した列の名前を見ることができます。

train_x.columns[rfe.support_]
Index(['open', 'high', 'low', 'close', 'BBM_20_2.0', 'BBB_20_2.0', 'BBU_20_2.0', 'BBL_20_2.0', 'ema_20', 'ema_40', 'ema_100', 'MACDs_12_26_9', 'DMN_14'], dtype='object')
つまり、私たちが適用したすべての指標から、以下の指標が価値ある情報を持っているようです。
    1)Open         2)High         3)Low         4)Close         6)KSTs_9         7)KST_10_15_20_30_10_10_10_15         7)All 3 exponential moving averages         8)4 Bollinger Band Components:'BBM_20_2.0' 'BBB_20_2.0' 'BBU_20_2.0' 'BBL_20_2.0'         9)MACD:'MACDs_12_26_9'10)方向性マイナス他の指標はノイズになっているかもしれませんが、これらはあくまで推定であり、ガイドの役割を果たすことを忘れないでください。
これが正確な真実であると結論づけることはできませんが、それでも私たちが主張するのは妥当なことです。


次に、Permutation Importanceの評価に移ります。

アルゴリズムを実装するために、ExplainLikeI'm5(ELI5)と呼ばれるPythonライブラリを使用します。

#pip install eli5 if you don't allready have it installed
import eli5
from eli5.sklearn import PermutationImportance
from sklearn.ensemble import GradientBoostingRegressor
gbr = GradientBoostingRegressor().fit(train_x,train_y)

permutation = PermutationImportance(gbr).fit(test_x,test_y)

次に、アルゴリズムが各特徴に割り当てた重みを評価します。

eli5.show_weights(permutation,feature_names = test_x.columns.to_list())


Permutation Importanceの重み

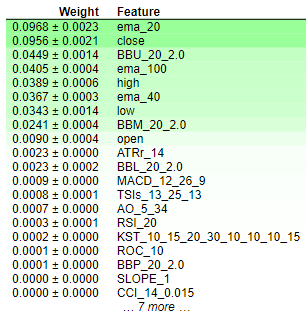
図8：Permutation Importanceの重み


Permutation Importanceの結果を解釈するのは簡単です。特徴は重要度の高い順にランク付けされ、最も重要なものは上に、重要度の低いものは下に配置されます。「0.0986+-0.0256」のような重み値は、モデルのエラーメトリクスの変化を意味します。簡潔な情報を求める読者のために、Permutation Importanceは特徴の値を無作為にシャッフルするものであることを再確認しておく価値があります。その特徴がモデルに大きな影響を与える場合、このランダム化はモデルのエラーメトリクスの増加につながるはずです。アルゴリズムの確率的性質のため、この増加分は特定の値ではなく、範囲として示されています。

逆に、重要度の低い特徴については、値を無作為にシャッフルしてもモデルのエラーメトリクスに変化はないか、場合によっては減少します。エラーメトリクスの増加または減少という結果のこの二重の性質は、各特徴の相対的な重要性を明確に示し、Permutation Importanceの結果の簡潔で理解しやすい解釈に貢献します。従って、このモデルにおける特徴量の重要性に関しては、Drop Column ImportanceとPermutation Importanceの両方が同じような感情を共有していると結論づけることができます。

PDP (Partial Dependence Plot)とICE (Individual Conditional Expectation)プロット：

#Import partial dependence display from sklearn
from sklearn.inspection import PartialDependenceDisplay

for feature_name in predictors:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature_name])
    plt.grid()
    plt.show()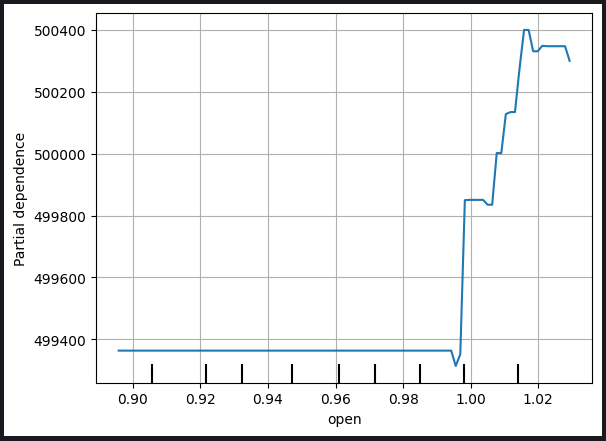

PDP始値

MACDS PDP

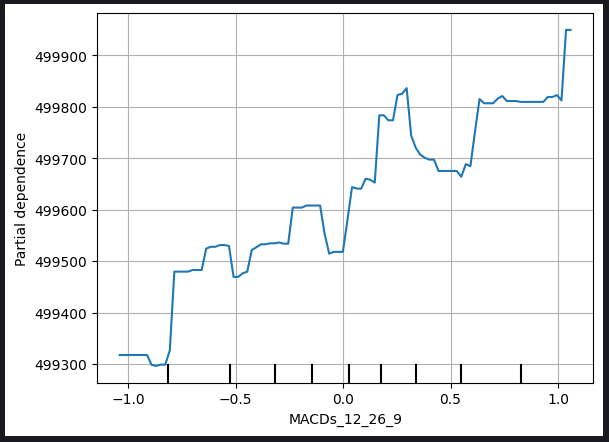
図9：始値とMACDシグナルラインのPDP (Partial Dependence Plot)



PDP (Partial Dependence Plot)は、特定の変数の変化がモデルの予測にどのような影響を与えるかを理解するための貴重なツールです。MACDシグナルラインのPDP (Partial Dependence Plot)を分析すると、一般的に、MACDシグナルラインの上昇は、モデルの予測終値の上昇と関連していることが合理的に推測できます。

しかし、以下のMACDの高さのプロットに代表されるように、PDP (Partial Dependence Plot)の解釈はより複雑になる可能性があることに注意することが重要です。

MACD高さのPDP (Partial Dependence Plot)

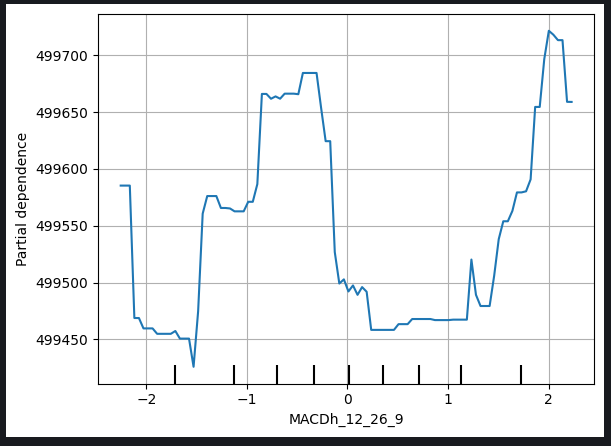
図10：MACDの高さのPDP (Partial Dependence Plot)

このようなプロットの解釈の複雑さは、非線形関係や、より微妙な分析を必要とする他の変数との相互作用から生じる可能性があります。MACDの高さのプロットの場合、MACDの高さとモデルの終値予測との間の関係の正確な性質を明らかにするために、追加の検討と調査が必要な場合があります。

この認識は、各変数のユニークな特性を考慮し、PDP (Partial Dependence Plot)を包括的に検討する必要性を強調するものであり、解釈に課題がある場合には、追加分析や専門家への相談を通じてさらなる洞察を求めるものです。

ICE (Individual Conditional Expectation)プロットは，特定の予測変数の変化に対して個々のインスタンスがどのように応答するかの詳細なビューを提供するために生成されます。ここでは、ICEプロットがどのように作られ、どのように使用されるかを順を追って説明します。

1.個々の予測のばらつき

  • 目的の予測変数と他の関連する特徴を含むデータ集合から始めます。
  • データセットから特定のインスタンスを選択します。

2.予測変数を変える

  • 選んだインスタンスについて、他の特徴を一定に保ちながら、予測変数の値を系統的に変化させます。
  • 予測変数の各変動値に対応する予測値の集合を作成します。

3.個々の曲線を作成する

  • データ集合の複数のインスタンスについて手順1～2を繰り返し、予測変数とモデルの予測値の間の関係を説明する個々の曲線のセット（各インスタンスに1つずつ）を生成します。

4.プロット

  • それぞれの曲線を同じグラフにプロットします。X軸は予測変数の値を表し、Y軸はモデルの予測値を表します。

5.解釈

  • ICEプロットを分析して，予測変数が変化するときに，各インスタンスでモデルの予測値がどのように変化するかを観察します。
  • 予測変数が個々の予測に与える影響について洞察を得るために、曲線のパターン、傾向、または変動を識別します。

6.比較分析

  • 複数のICEプロットを比較し、特に異なる事例を扱う場合は、データセット全体における変数の効果の不均一性を理解します。

使用法

  • きめ細かな洞察：ICEプロットは、予測変数が予測にどのように影響するかについての詳細でインスタンス固有のビューを提供し、よりニュアンスのある理解を可能にします。
  • モデルの理解：ユーザーが非線形の関係、相互作用、潜在的な異常を探索するのに役立ちます。
  • 機能の重要性：ICEプロットは、個々の予測に対する影響を示すことで、特定の特徴の重要性を評価することに貢献できます。
  • 意思決定支援：ICEプロットからの洞察は、特に、特定の変数の変化に応答して、特定のインスタンスについて予測がどのように変化するかを理解することが重要な場合、意思決定に役立ちます。

実際のところ、PDPプロットはICEプロットの平均値です。PDPラインは下のオレンジ色で示されています。

for feature in predictors:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature],kind='both')

ICE高値

ICE EMA

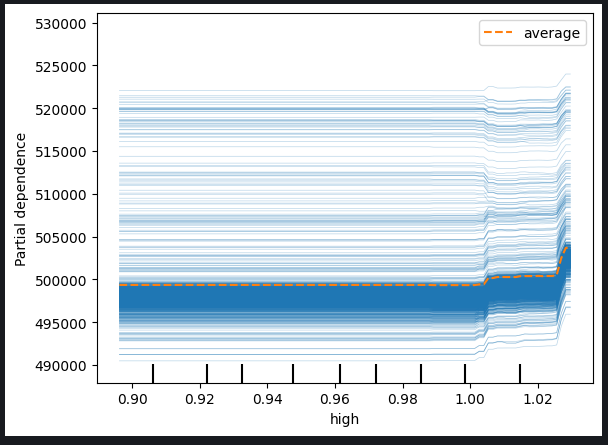
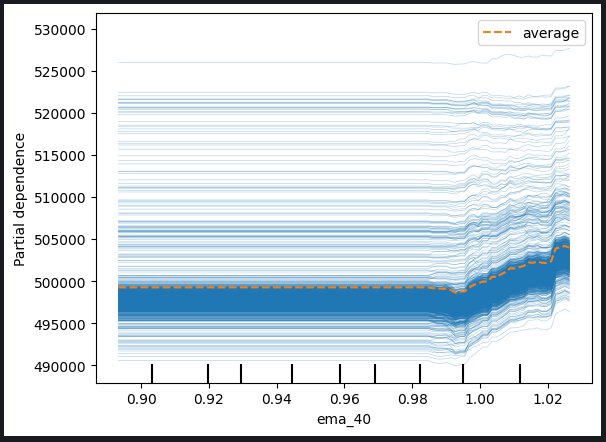
図11：高値と40期間EMAのICEプロット

観察されたプロットに基づくと、高値または指数移動平均のいずれかが上昇しても、モデルの予測に直ちに影響を与えることはないことが明らかです。それどころか、モデルの予測に顕著な変化が起こる前に、これらの変数が大幅に増加する必要があるようです。この観察結果は、モデルがこれらの特定の特徴の漸進的変化に対してあまり敏感ではないことを示唆しています。

プロットから得られた主な洞察は以下の通りです。

  1. 閾値感度：このモデルは閾値感度を示しているように見えます。つまり、予測を大幅に調整する前に、高値または指数移動平均に相当な、または閾値レベルの変化が必要なのです。

  2. 徐々の反応：前述の特徴の漸増的または中程度の変化は、モデルの予測を即座に調整するきっかけにはならないようです。この特性は、このような変動に対する反応が緩やか、あるいは控えめであることを示唆しています。

  3. 低感度：モデルがこれらの特徴の変化にあまり敏感でないという結論は、高値や指数移動平均の些細な変動がモデルの出力に顕著な影響を与える可能性は低いことを示唆しています。

異なる特徴に対するモデルの感度を理解することは、効果的なモデルの解釈と意思決定にとって極めて重要です。これらの洞察は、さらなる分析、モデルの改良の指針となり、また特定の予測因子とモデルの予測との関係の性質について関係者に知らせることができます。

2つの特徴の共同効果を見るために、2次元PDP (Partial Dependence Plot)を検査することもできます。

#Setting up the plot
fig , ax = plt.subplots(figsize=(10,5))
column_names = [('ROC_10','ATRr_14')]

#Plotting 2D PDP
disp_4 = PartialDependenceDisplay.from_estimator(cat_full, test_x[0:1000],column_names, ax=ax)
plt.show()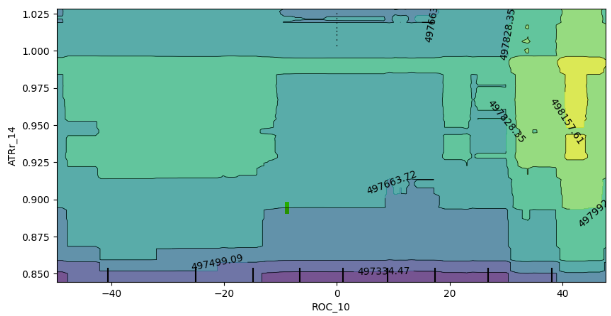

2D PDP (Partial Dependence Plot)

図12：変化率(ROC)と平均トゥルーレンジ(ATR)の2D PDP (Partial Dependence Plot)

2次元PDP (Partial Dependence Plot)の分析から、一般的に、ROC（変化率）とATR（平均トゥルーレンジ）の両指標の増加は、私たちのモデルから期待される予測値の増加に対応することが明らかになりました。この正の相関は、これらの指標の変化に対するモデルの予想される挙動と一致しています。

ただし、このプロットは、これら2つの指標の相互作用についての洞察も与えてくれます。注目すべきは、プロットの境界線が明確でないことで、関係が一貫して安定していないことを示唆しています。その代わりに、強弱が混在する領域があり、モデルの予測に対するROC指標とATR指標の影響が、プロットの異なる領域で異なる可能性があることを示しています。

強い期待の境界の中に弱い期待の無作為な飛び地が存在することは、相互作用のダイナミックな性質をさらに強調しています。観測された挙動は、サンプリング手法、特に計算効率上の理由からデータフレームのサブセットが使用された場合に影響を受ける可能性があることに注意することが重要です。

いくつかの考慮点と潜在的な影響は以下の通りです。

  1. サンプリングの限界：観察された矛盾は、計算効率を上げるために少ないサンプルを使用したことに部分的に起因している可能性があります。より広範なサンプリングアプローチによって、相互作用についてより包括的な見解が得られる可能性があります。

  2. 非直線性または相互作用：境界が明確でなく、スポットが混在していることから、ROC指標とATR指標の間に非線形性や相互作用がある可能性が示唆されます。さらに調査を進めれば、より大きなサンプルを用いれば、より微妙なパターンが明らかになる可能性があります。

  3. モデルの頑健性：相互作用のばらつきを理解することは、モデルの頑健性と、入力特徴の異なる組み合わせに対する感度を評価するのに役立ちます。

結論として、2次元PDP (Partial Dependence Plot)の解釈は、ROC指標とATR指標の変化に対するモデルの反応について貴重な洞察を与えてくれます。観察されたパターンにサンプルサイズが影響する可能性を考慮すると、さらなる調査と、もし可能であれば、より広範なサンプリング戦略が、これらの知見の精度を高める可能性があります。


Shapely Additive Explanations (SHAP) の値

#pip install shap if you don't have it installed
#Import SHAP
import shap

#Initialise the shap package
shap.initjs()

考慮すべき点がいくつかあります。

  • SHAP値は、特徴が独立/非相関であることを前提とします。

  • SHAP値を正確に計算するには計算コストがかかるが、この問題はデータセットの次元が高くなるにつれて悪化します。

  • SHAP値はモデルにとらわれません。つまり、特定のモデル特有の振る舞いを捕らえるのに役立たないかもしれませんが、これは皮肉なことに長所でもあり短所でもあります。

  • SHAPの値は入力順序に敏感です！

私たちのデータセットには強い相関項があり、これはSHAP値を計算する際の大きな問題です。特徴が独立しているという前提に違反します。幸いなことに、この問題を処理する方法は数多くあります。たとえば、次のとおりです。

  • 相関性のある機能を削除します。これは最も単純な解決策ですが、ほとんどの場合、最後に考えるべきです。

  • 主成分分析などの特徴削減技法や、お馴染みの他の特徴選択法の使用を検討します。

  • 特徴をビンに離散化することで、SHAP値の計算における相関の悪影響を軽減することができます。

  • 相関データを扱うように設計されたSHAPアルゴリズムを使用します。

  • 無相関の特徴量を使用することで、例えば私たちのケースでは、出来高とハイロースプレッドはほとんど相関がありません。

この練習では、相関データを扱うように設計された特定のSHAPアルゴリズムを使用した4番目の解決策を使用します。ツリーベースのSHAPアルゴリズムは相関をうまく扱うことができます。

#Initialise shap value calculator
tree_explainer = shap.TreeExplainer(cat_full)

#Store SHAP values
shap_values = tree_explainer.shap_values(test_x)

#Plot SHAP values
shap.summary_plot(shap_values,test_x)

SHAPの値

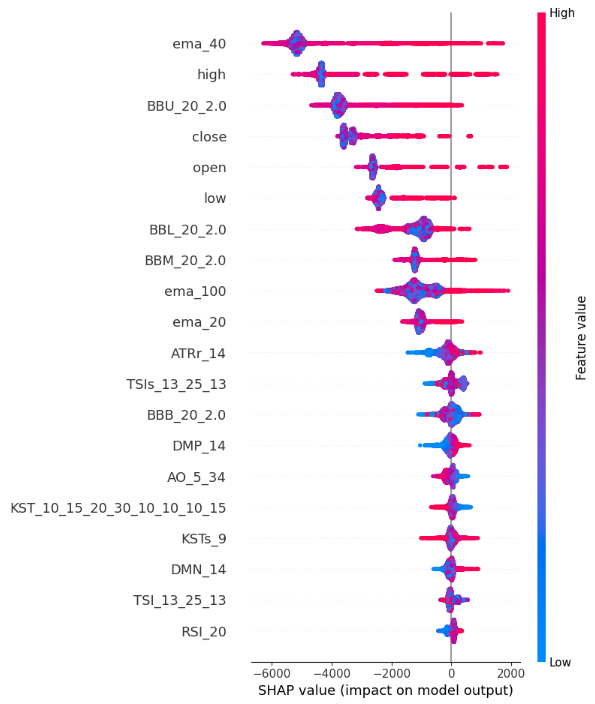
図13：SHAPバリュープロット

SHAP summary plotの解釈は次の通りです。

  1. 機能の重要性：Y軸の上部に記載された特徴は、終値の上昇に強い影響を与え、Y軸の下部に記載された特徴は、終値の下落に強い影響を与えます。 

  2. インパクトの方向：各特徴はX軸に沿って色分けされた点を持っています。青い点は低い特徴値を、赤い点は高い特徴値を象徴します。これらの点の水平方向の位置関係から、その機能の価値が終値に与える影響を知ることができます。つまり、SHAP値の計算は、High_Low_Sreadが終値をあまり示していないことを物語っています。

  3. 位置の大きさ：x軸に沿った各ポイントの水平方向の位置は、影響の大きさを表し、したがって、極端な高値と安値は、このデモの例では、Volume,、Open、High_Low_Spreadの特徴と比較して、終値に比較的強い影響を与えます。


相互情報量

from sklearn.feature_selection import mutual_info_regression
mi_scores = mutual_info_regression(train_x, train_y)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=train_x.columns)
mi_scores = mi_scores.sort_values(ascending=False)
mi_scores

ema_100                                       1.965130

ema_40                                         1.960548

ema_20                                         1.933651

BBM_20_2.0                                   1.902066

BBL_20_2.0                                   1.895867

BBU_20_2.0                                  1.881435

high                                             1.795941

low                                              1.786879

close                                            1.783567

open                                            1.777118

TSIs_13_25_13                              0.232247

ATRr_14                                        0.215980

MACDs_12_26_9                            0.214559

KST_10_15_20_30_10_10_10_15    0.208868

KSTs_9                                         0.205177

MACD_12_26_9                            0.174518

TSI_13_25_13                              0.168086

AO_5_34                                     0.128653

BBB_20_2.0                                 0.104481

RSI_20                                         0.095368

MACDh_12_26_9                          0.076360

DMP_14                                      0.060191

DMN_14                                     0.048856

ROC_10                                     0.042115

BBP_20_2.0                               0.028558

CCI_14_0.015                            0.022320

SLOPE_1                                   0.004144

def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")
plt.figure(dpi=100, figsize=(8, 5))
plt.grid()
plot_mi_scores(mi_scores)


相互情報プロット

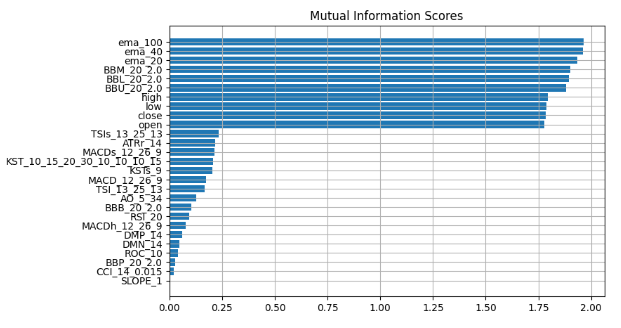
図14：相互情報スコア

すべてのブラックボックス説明技術にわたって一貫したコンセンサスが観察されており、これらの説明で一貫して強調されている特徴には、効果的に活用できる実質的な情報が含まれている可能性が高いことが示唆されています。指数移動平均、ボリンジャーバンド、始値、高値、安値、終値は一貫して上位に位置しているため、中心傾向の尺度を用いれば、論理的にこれらの特徴が非常に有益であるという結論に達することができます。 

調査結果を検証してみましょう。

単純な線形回帰と強力なブラックボックスの2つのモデルを使用します。ブラックボックス説明技術から得た洞察を用いて、特徴を厳選します。 

まず、必要な依存関係をインポートします。

from sklearn.linear_model import LinearRegression
from catboost import CatBoostRegressor
from sklearn.metrics import mean_squared_error

    次に、より単純なモデルを最初に当てはめます。

    #First we fit the simpler model
lm = LinearRegression()

lm.fit(train_x.loc[:,["open","high","low","close"]],train_y)

    そして、よりシンプルなモデルがどれだけ訓練データにフィットするかを評価します。

    lm_predictions = pd.DataFrame(lm.predict(train_x.loc[:,["open","high","low","close"]]), index = train_y.index)
lm_fit = lm.predict(train_x.loc[:,["open","high","low","close"]])
residuals = pd.DataFrame(train_y - lm_fit)

    ここで、より強力なブラックボックスモデルを導入して、より単純なモデルの残差を学習させます。

    #Now we bring in our more powerfull black-box model
cat = CatBoostRegressor()
cat.fit(
    train_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]],
    residuals)

    利用可能なすべての特徴を利用した初期のブラックボックスモデルの性能と、精緻化されたモデルの精度を評価することで、テストデータにおける誤差レベルの比較をおこないます。洗練されたモデルは、より単純な線形回帰の助けを取り入れ、慎重に選択された特徴のサブセットを戦略的に採用しています。

    lm_test_predictions = pd.DataFrame(lm.predict(test_x.loc[:,["open","high","low","close"]]),index=test_y.index)
cat_full_test_predictions = cat_full.predict(test_x[predictors])

cat_residuals_predictions = pd.DataFrame(cat.predict(test_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]]),index=test_y.index)

    最初のブラックボックスのエラーレベルを評価します。

    full_error = mean_squared_error(test_y,cat_full_test_predictions)

    そして、私たちの新しいブラックボックスハイブリッドのエラーレベルと比較します。

    hybrid_predictions = lm_test_predictions.iloc[:,0] + cat_residuals_predictions.iloc[:,0]
hybrid_error = mean_squared_error(test_y, hybrid_predictions)
    delta_error = full_error - hybrid_error
(delta_error / full_error) * 100

    94.428

    新しいブラックボックスハイブリッドのエラー指標は94%改善されました。

    hybrid_predictions.plot()

    ハイブリッドブラックボックス予想

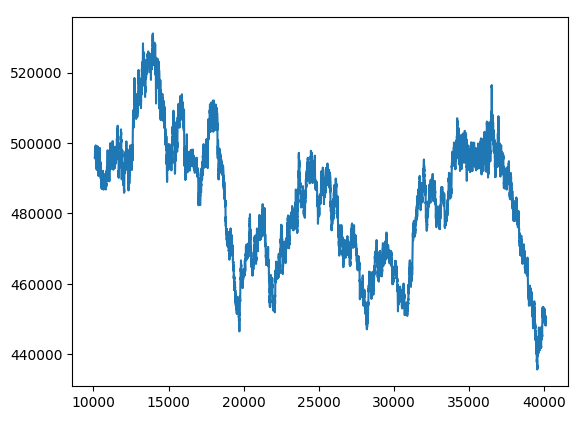
    図15：新しいブラックボックス予想

    最も重要なのは、当初観測された不自然なフラットピリオドを排除し、新しいブラックボックス予測の現実性を顕著に向上させたことです。読者にとって重要なのは、私たちが現在、合理化された一連の機能で精度を高めていることを認識することです。これは、効果的に実行されれば、より少ないことはより多いという原則を強調しています。


    まとめ

    私たちは、すべての構成要素を包括的な取引戦略に統合する態勢を整えています。

    MARKET_SYMBOL = "Volatility 75 Index"
DEVIATION = 100
VOLUME = 0
symbol_info = MT5.symbol_info(MARKET_SYMBOL)
VOLUME = symbol_info.volume_min * 1
    def preprocess(df):
    #20 period exponential moving average
    df["ema_20"] = df.ta.ema(length=20)
    #40 period exponential moving average
    df["ema_40"] = df.ta.ema(length=40)
    #100 period exponential moving average
    df["ema_100"] = df.ta.ema(length=100)
    #20 period bollinger bands with 3 standard deviations
    df.ta.bbands(length=20,sd=2,append=True)
    df = df.loc[100:,:]
    def fetch_prices():
    current_prices = pd.DataFrame()
    current_prices = pd.DataFrame(MT5.copy_rates_from_pos(MARKET_SYMBOL,MT5.TIMEFRAME_M1,0,200))
    preprocess(current_prices)
    return(current_prices)
    def normalise_prices(raw_data):
    for col in raw_data.columns:
        if col in first_values:
            raw_data[col] = raw_data[col] / first_values[col]
    model_forecast = 0
    def hybrid_forecast(model_1,model_2):
    market_data = fetch_prices()
    normalise_prices(market_data)
    forecast_1 = model_1.predict(market_data.loc[199:200,["open","high","low","close"]])
    forecast_2 = model_2.predict(market_data.loc[199:200,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]])
    out = forecast_1 + forecast_2
    return(out)
    INITIAL_BALANCE = MT5.account_info().balance
CURRENT_BALANCE = 0
    if __name__ == "__main__":
    while True:
        
        #Account standing
        info = MT5.account_info()
        CURRENT_BALANCE = info.balance
        profit = CURRENT_BALANCE - INITIAL_BALANCE
        
        model_forecast = hybrid_forecast(lm,cat)
        print("Current forecast: ",model_forecast)
        
        #We have no open positions
        if(MT5.positions_total() == 0):
            print("No open positions")
            
            #Buy
            if(model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast buy")
                MT5.Buy(MARKET_SYMBOL,VOLUME)
                last_trade = 1
                        
            #Sell    
            elif(model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast sell")
                MT5.Sell(MARKET_SYMBOL,VOLUME)
                last_trade = 0
                
        elif(MT5.positions_total() > 0):
            print("Checking model forecast")
            
            if((model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 0)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
            
            elif((model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 1)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
                
        print("Total Profit/Loss: ",profit)
        time.sleep(60)

    現在の予想：[239100.04622681]オープンポジションなしモデル予想に従った買い総損益：0.0


    結論

    より大きく、より洗練されたモデルを訓練するようになると、理解、説明、デバッグが難しくなります。機械学習モデルが中で何をしているのか、なぜそのような判断に至るのかを完全に理解できなければ、モデルが私たちの意図したとおりに機能しているかどうかを確かめることはできません。モデルを理解し、トラブルシューティングに失敗したからといって、これらの技法を採用することで複雑さが増すことを正当化することはできません。  ツールから一貫して活用できる価値は、そのツールを理解している範囲に限られます。自分のモデルにもっと自信を持ち、機械学習モデルという悪名高いブラックボックスの中で回転する歯車について、より深い洞察を引き出せるようにするために、この記事を書いたのです。

    MetaQuotes Ltdにより英語から翻訳されました。
    元の記事: https://www.mql5.com/en/articles/13706

    添付されたファイル |
    ZIPをダウンロード
    Black_Box_Interpretation_Toolkit.py (13.27 KB)
    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この著者による他の記事

    ディスカッションに移動
    MQL5を使ったシンプルな多通貨エキスパートアドバイザーの作り方（第4回）：三角移動平均 — 指標シグナル MQL5を使ったシンプルな多通貨エキスパートアドバイザーの作り方（第4回）：三角移動平均 — 指標シグナル
    この記事の多通貨エキスパートアドバイザー(EA)は、1つの銘柄チャートからのみ複数の銘柄ペアの取引（注文を出す、注文を決済する、トレーリングストップロスとトレーリングプロフィットなどで注文を管理するなど）ができるEAまたは自動売買ロボットです。今回は、多時間枠または単一時間枠の「三角移動平均」という1つの指標のみを使用します。
    MQL5入門（第１部）：アルゴリズム取引入門ガイド MQL5入門（第１部）：アルゴリズム取引入門ガイド
    この初心者向けMQL5プログラミングガイドで、魅力的なアルゴリズム取引の世界へ飛び込みましょう。MetaTrader 5を動かす言語であるMQL5のエッセンスを発見し、自動売買の世界を解明します。基本を理解することからコーディングの第一歩を踏み出すことまで、この記事はプログラミングの知識がなくてもアルゴリズム取引の可能性を解き放つ鍵となります。MQL5のエキサイティングな宇宙で、一緒に、シンプルさと洗練が出会う旅に出ましょう。
    知っておくべきMQL5ウィザードのテクニック（第08回）：パーセプトロン 知っておくべきMQL5ウィザードのテクニック（第08回）：パーセプトロン
    パー​​セプトロン（単一隠れ層ネットワーク）は、基本的な自動取引に精通していて、ニューラルネットワークを試してみようとしている人にとって、優れた入門編となります。エキスパートアドバイザー(EA)用のMQL5ウィザードクラスの一部であるシグナルクラスアセンブリでこれをどのように実現できるかを段階的に見ていきます。
    ソフトウェア開発とMQL5におけるデザインパターン（第2回）：構造パターン ソフトウェア開発とMQL5におけるデザインパターン（第2回）：構造パターン
    この記事では、MQL5だけでなく他のプログラミング言語でも拡張可能で信頼性の高いアプリケーションを開発するために、デザインパターンのトピックが開発者としてどれほど重要であるかを学んだ後、当トピックについての記事を続けます。デザインパターンのもう1つのタイプである構造デザインパターンについて学び、クラスにあるものを使ってより大きな構造を形成することによってシステムをデザインする方法を学びます。