精通模型解释：从您的机器学习模型中获取深入见解

概述

在机器学习领域，我们经常会考虑权衡取舍。在优化一个性能度量衡时，我们往往要牺牲另一个性能度量衡。随着模型越来越大、越来越复杂的发展趋势，理解、解释和调试它们业已变为一项艰巨的任务。模型表面之下的复杂性，破译我们的模型在制定决策时“为什么”这样做至关重要。缺乏这种明确性，我们如何坚定地相信我们可以监督这个模型达到我们渴望的结局？我们不能冒险让模型以意想不到的方式运行，致使我们的努力徒劳无功！本文深入探究了这些复杂性，旨在阐明以下主题：

1. 识别关键特征：您的模型认为哪些特征很重要

2. 解码单个特征影响：了解每个特征如何影响您的模型性能

3. 把握集并特征影响：探索特征对模型预测的更广泛影响

我们的旅程将以机器学习复杂性的核心为导向，令您能够更好地理解和修改模型的行为。拥抱这些知识，并把您的机器学习的真正潜力发挥到极致。

为什么它很重要？

调试：

图例 1：调试的艺术

“人皆犯错，谅解至圣” ~ 亚历山大·波普（Alexander Pope）

初看，调试也许看似很平凡，但其意义超越了界域。构想难以捉摸的错误，那种偷偷地逃避运行时的错误，不注意就会溜走。然而，依靠这些纸面中编织的知识，您就能全副武装地破译您的模型当中编织的复杂范型。您将辨别这些范型是否与您对现实世界的认知相一致。在现实生活中的迷宫项目中，您将熟练地追踪并克服自身的错误，因为它们是精通路上的垫脚石。

更佳的特征工程：

图例 2：特征工程

“持续改进总比拖延不止的完美主义好” ~ 马克·吐温（Mark Twain）

现在，我们冒险进入特征工程的迷人领地。想象一个圆。沿其直径画一条红线；一个简单的行为，却孕育着意义。现在，考虑一下：您的直径可以围绕圆的圆周优雅地弯曲多少次？答案不言而喻 — 大约 3.145，一个众所周知的常数 pi（π）。

这个思想实验作为我们的指南，强调了表述对我们学习能力的影响。正如圆的曲率会影响其拟合度一样，特征变换也会强化数据集的和谐度。通过雕刻新的柱子，我们超越了平凡，将我们的预测准确性提升到了非凡的高度。在此，直觉成为我们的指南针，引导我们穿越未涉足的水域。但是，当直觉动摇时会发生什么？不要害怕；这段艰苦旅程揭示的策略，即便是最令人困惑的地形也能导航。但我们并不会止步于此，我们将继续根据经验衡量我们引入的这些新工程特征的有效性

指导未来数据收集：

图例 3：改进的数据收集

“如果你想知晓未来，就看看过去” ~ 阿尔伯特·爱因斯坦（Albert Einstein）

当我们巡视数据地貌时，一个古老的智慧在回响 — 未来的关键在于过去的编年史。我们的特征工程已经压榨殆尽了吗？不要害怕，对于数据世界当中，过去是我们的灯塔。新的数据类型在召唤，有望为我们的模型注入活力。洞察力，是我们忠实的伙伴，作为领路人，引导我们走向数据宝库中的宝石。随着每次见解的汇集，我们通往新特征的道路变得更加清晰，将未来涂抹上无限可能的色调。

改进决策制定：

图例 4：改进决策制定

“一点点学习是一件危险的事情” ~ 亚历山大·波普

在机器学习的交响乐中，您驾驭着车轮。该模型会随着您的曲调起舞，这证明了决策为其预测注入了活力。机器学习超越了单纯的预测；它深入到见解的深层，那里埋藏着真正的宝藏。您的理解度，您的精通度，搭起了您雄心壮志的基石。每一个见解，都是宝贵的金块，会影响您的极致。

故此，探险家们，当我们揭开机器学习的奥秘时，让这些词语来指导您。

理论基础

在本文中，我们的意向是采用 CatBoost Python 库中现成的梯度助推树模型来执行价格回归分析。然而，从一开始就出现了一个值得注意的挑战，需要对模型进行更仔细的检查，并识别有影响力的特征。在深入研究黑盒解释技术应用于我们的模型之前，必须明白我们的黑盒模型固有的局限性，以及在这种境况下使用黑盒解释器的背后理由。

梯度助推树在分类任务中展现出值得称赞的性能；尽管如此，当应用于特定的时间序列回归问题时，它们还是有明显的局限性。这些树属于机器学习模型家族，基于目标值把输入归类到组中。随后，该算法计算每个组内的平均目标值，并利用这些组内平均值进行预测。值得注意的是，除非以后再次训练，否则在训练期间建立的这些组内平均值将保持不变。这种固化性质产生了一个关键的缺点，因为梯度助推树典型情况下难以有效地推断趋势。当面对超出其训练范围的输入值时，模型容易出现重复预测，依靠衍生自已知的组内平均值，这也许不能准确捕获已观察训练范围之外的潜在趋势。

甚至，该模型的前提是相似的特征值将产生相似的目标值，这一假设与我们在交易金融产品方面的集并经验不一致。在金融市场中，价格形态也许会表现出相似性，而结局大相径庭。这种偏差是对模型假设的挑战，即生成过程产生的数据陷入同质组。由此，违反这些假设会给我们的模型引入乖离。

为了证实这些观察结果，我们将为那些未能独立观察到这种现象的读者奉献一场演示。我们的承诺是确保所有读者都能全面理解。

我们首先加载必要的依赖项

#pip install pandas if you haven't installed it allready
#We'll use pandas to store and retrieve data
import pandas as pd       

#pip install pandas-ta if you haven't installed it allready
#We'll use pandas_ta to calculate technical indicators
import pandas_ta as ta    

#pip install numpy if you haven't installed it allready
#We'll use numpy to perform optmized vector calculations 
import numpy as np

import matplotlib.pyplot as plt

#pip install numpy if you haven't installed it allready
#We'll use MetaTrader 5 connect to and control our MetaTrader 5 Terminal 
import MetaTrader5 as MT5

#Standard python library
import time

然后我们输入我们的登录凭证

login = enter_your_login
password =  enter_your_password
server = enter_your_broker_server

现在我们初始化 MetaTrader 5 终端，并登录

if(MT5.initialize(login=login, password= password, server=server)):
    print("Logged in succesfully")
else:
    print("Failed to initialize the terminal and login")

成功登录

我们请求 Volatility 75 指数（或您喜欢的任意品种）的 100 万行 M1 数据。

data = pd.DataFrame(MT5.copy_rates_from_pos("Volatility 75 Index",MT5.TIMEFRAME_M1,0,100000))
data

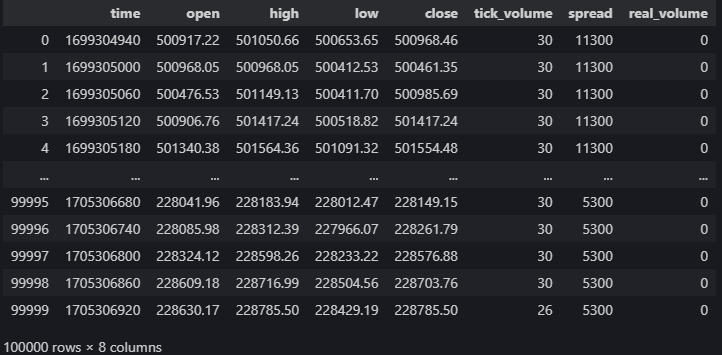
图例 5：来自 MetaTrader 5 终端的市场数据

我们计算技术指标，也许有助于我们预测价格

#20 period exponential moving average
data["ema_20"] = data.ta.ema(length=20)
#40 period exponential moving average
data["ema_40"] = data.ta.ema(length=40)
#100 period exponential moving average
data["ema_100"] = data.ta.ema(length=100)
#20 period relative strength indicator
data.ta.rsi(length=20,append=True)
#20 period bollinger bands with 3 standard deviations
data.ta.bbands(length=20,sd=3,append=True)
#14 period average true range
data.ta.atr(length=14,append=True)
#Awesome oscilator with default settings
data.ta.ao(append=True)
#Moving average convergence divergence (MACD)
data.ta.macd(append=True)
#Chaikins commidity index
data.ta.cci(append=True)
#Know sure thing oscilator
data.ta.kst(append=True)
#True strength index
data.ta.tsi(append=True)
#Rate of change
data.ta.roc(append=True)
#Slope between 2 points
data.ta.slope(append=True)
#Directional movement
data.ta.dm(append=True)

设置目标

data["target"] = data["close"].shift(-30)

我们设置黑盒模型

from catboost import CatBoostRegressor

准备我们的训练和测试起止时间

train_start = 100
train_end   = 10000

test_start = train_end + 100
test_end = test_start + 30000

predictors = [
    "open",
    "high",
    "low",
    "close",
    "KSTs_9",
    "KST_10_15_20_30_10_10_10_15",
    "CCI_14_0.015",
    "AO_5_34",
    "ATRr_14",
    "BBM_20_2.0",
    "BBP_20_2.0",
    "BBB_20_2.0",
    "BBU_20_2.0",
    "BBL_20_2.0",
    "RSI_20",
    "ema_20",
    "ema_40",
    "ema_100",
    "SLOPE_1",
    "ROC_10",
    "TSIs_13_25_13",
    "TSI_13_25_13",
    "MACD_12_26_9",
    "MACDh_12_26_9",
    "MACDs_12_26_9",
    "DMP_14",
    "DMN_14"
]
target = "target"

决策树对尺度很敏感，因此我们将对输入值进行常规化，因此我们将每个特征的第一个读数存储在称为 “first_values” 的数组之中。

first_values = {}

#Iterating over the columns in the dataset
for col in data.columns:
    #Which of those columns are part of the model inputs?
    if col in predictors:
        #What was the first value in that column?
        first_values[col] = data[col][train_start]
        data[col] = data[col]/first_values[col]

执行训练测试拆分

train_x = data.loc[train_start:train_end,predictors]
train_y = data.loc[train_start:train_end,target]

test_x = data.loc[test_start:test_end,predictors]
test_y = data.loc[test_start:test_end,target]

拟合我们的黑盒模型

cat_full = CatBoostRegressor()
cat_full.fit(train_x,train_y)

从我们的黑盒模型中获取预测

cat_full_predictions = pd.DataFrame(index=test_x.index)
cat_full_predictions["predictions"] = cat_full.predict(test_x)
cat_full_predictions.plot(label=True)
test_y.plot()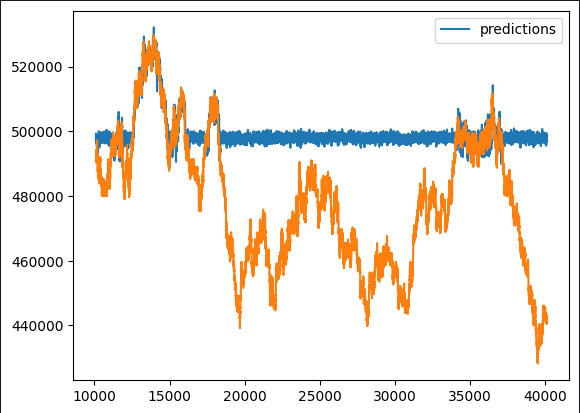

图例 6：我们的黑盒预测

在最初的观察中，很明显预测模型表现出非典型的横盘区间。鉴于我们对梯度助推算法的典型实现的全面概览，这种形态应该不出所料。我们的兴趣在于辨别哪些特征对模型的性能有积极贡献，哪些特征也许成为潜在的噪声源。这需要对特征工程时机通盘检验。

为了解开这些细微差别，我们提议利用一个黑盒解释器套件。然而，在盲目应用这些解释器之前，必须掌握黑盒解释器算法的底层机制。这涉及对其操作的假设进行关键性评估，令我们能够查清这些假设是否得到遵守、或潜在被违反。

依照这种基本理解来应用黑盒解释技术，令我们能够明智地解释每个说法。通过仔细检查解释技巧，并权衡它们的相关性，我们可以将相应的置信度定性给所得到的见解。这种有条不紊的方式强化了我们的能力，使之提取有意义的信息，并基于黑盒解释过程的结果做出明智决策。

黑盒解释算法

舍弃列重要性：

“舍弃列重要性”技术是一种评估模型准确性的方法，它最初考虑所有预测因子，随后迭代删除一个单列，观察对准确性的影响。这种方式可得到每列对整体模型性能的具体贡献的有益见解。

"舍弃列重要性"的区别在于它的实用性和合理性。假设的基础，是该技术与真实世界场景对标，其中频繁出现数据不一致。无论是由于互联网连接中断、停电、恶劣天气条件、还是其它不可预见的事件引起，该方法都模拟了一个稳健模型，能镜像实际操作环境中发生的一切。这种真实感强化了该技术在解决实际日常情况下可能遇到的场景的适用性和有效性。

优势：

• 改进的模型性能：舍弃不相关或冗余的列，可以降低噪声并提高信噪比，如此来强化机器学习模型的性能。
• 简化模型：删除不必要的列，可以令模型更简单、更易于解释，从而更易于利益相关者理解和解释。

弱点：

• 信息丢失：删除列可能会导致有价值的信息丢失，潜在地会导致模型过于简陋，无法捕获数据中的重要形态。
• 对下游流程的影响：如果该列用于后续分析、或某些业务流程需要该列，则删除该列也许会打断这些工作流。

机遇：

• 特征工程：删除列也许会为特征工程提供机遇，允许您基于现有数据创建新特征、或修改其余特征，从而获得更佳的模型性能。
• 资源优化：删除不必要的列可以在内存、存储和处理时间方面节省资源，尤其是大数据。

凶险：

• 模型乖离：如果舍弃的列包含对于无乖离预测至关重要的信息，则删除也许会将乖离引入模型，从而导致不准确、或不公正的结果。
• 数据完整性忧虑：尚未通盘理解数据就舍弃列，也许会引入数据完整性忧虑，从而影响数据集和后续分析的整体品质。

排列重要性：

“排列重要性”提供了一种评估特征重要性的替代方法，其随机排列特定列的值，并评估对模型误差度量衡的影响。其核心思路基于这样一个前提，即如果列在影响模型方面发挥重要作用，则破坏其原始值应导致误差度量衡增加、和整体准确性降低。反之，如果列的影响很小，可观察到的变化有限，在某些情况下，甚至可能改善性能。

该技术提供了对特征重要性的细致入微的视角，允许动态评估每个特征对模型预测能力的贡献。排列过程引入了一定程度的随机性，有助于揭示模型对单个特征的敏感性，从而更全面地明了它们在预测框架中的显要程度。

优势：

• 模型无关：排列重要性与模型无关，这意味着它可以应用于任何监督学习模型，而无需对底层算法进行假设。这令它成为一种通用且广泛适用的技术。
• 直观解释：排列重要性的概念相对容易理解。当具体特征的值随机排列时，它衡量模型性能的变化，从而提供特征重要性的清晰解释。

弱点：

• 计算密集：排列重要性的计算涉及针对每个特征排列重新评估模型的性能，致其计算密集、且潜在地非常耗时，尤其是对于大数据。
• 对样本规模的敏感性：排列重要性可能对数据集的规模敏感。在小型数据集中，排列特征的影响可能会被夸大，从而导致重要性估值的可靠性降低。

机遇：

• 特征选择指南：排列重要性结果可以指导特征选择，即辨别哪些特征对模型性能的贡献最大。这些信息对于简化模型和降低维数很有价值。
• 非线性关系的识别：与线性模型不同，排列重要性可以捕获特征和目标变量之间的非线性关系，从而提供了数据中的复杂形态的见解。

凶险：

• 相关特征的影响：排列重要性也许无法很好地处理特征高度相关的状况。如果两个特征是相关的，如果其它特征仍提供相似的信息，则置换一个特征也许不会明显影响模型的性能。
• 潜在的过度拟合：在某些情况下，使用排列重要性时存在过度拟合的风险，尤其是在模型过于复杂、或数据集较小的情况下。重要性得分也许无法很好地普适新数据。

部分依赖性图（PDP）和独立条件期望（ICE）图：

为了更细致地理解模型的行为，我们采用了部分依赖性图（PDP）和独立条件期望（ICE）图。部分依赖性图勾勒出预测结果如何随着单个预测变量的变化而演变，从而保持所有其它预测变量一致。同时，ICE 图针对每个实例呈现独立的曲线，提供了有关特征重要性的详细视角，有助于全面分析每个特征的影响。

PDP 和 ICE 图共同提供的强大视觉表现力，超越了总体趋势。PDP 提供了特定预测变量与模型预测之间关系的顶视图，而 ICE 图则通过呈现一组曲线来深入研究细微差别，每条曲线都代表该预测变量在不同实例中的独特性影响。这种组合方式强化了我们辨别模型响应不同预测变量值产生复杂形态和变化的能力，从而促进了对整个预测框架内特征重要性的更透彻理解。

优势：

• 可解释性：PDP 提供了特征与预测结果之间关系的直观和可视化表述，即使非专家也能更容易解释和理解特定特征对模型预测的影响。
• 形态识别：PDP 可以帮助识别特征与预测结果之间关系的形态和趋势，从而更深入地理解特征的变化如何影响模型的预测。

弱点：

• 独立性假设：PDP 假定感兴趣的特征独立于其它特征。在具有相关特征的复杂模型中，对 PDP 的解释也许会有挑战性，并且绘图也许无法准确反映真实关系。
• 受限于边际效应：PDP 展示单个特征的边际效应，同时保持其它特征固化。它们也许无法捕获多个特征之间的复杂交互，从而限制了它们揭示模型全部复杂性的能力。

机遇：

• 模型验证：PDP 可用作模型验证工具。从 PDP 中获得的见解，与界域知识或期望进行比较，从业者可以评估模型是否与特征的预期行为对接齐整。
• 特征重要性排位：PDP 可以辅助特征重要性排名，即直观地强调对模型预测影响最大的特征。该信息可以指导特征选择和模型简化。

凶险：

• 潜在的误解：如果对统计概念没有正确的理解，就存在误解的风险。用户也许会错误地将因果关系归因于观察到的关联，尤其是在他们未意识到潜在的混杂变量、或底层模型复杂性的情况下。
• 高维数据的复杂性：PDP 在高维空间中变得具有挑战性，这是由于可能的特征组合规模爆炸性膨胀。可视化多个要素之间的交互变得越来越复杂。

沙普利（Shapley）加法解释（SHAP 值）：

图例 7：敬爱的劳埃德·沙普利（Lloyd Shapley），他逝于 2016 年 3 月 12 日亚利桑那州图森市。他的思想永存。

SHAP 值以其先驱者劳埃德·沙普利的姓氏命名，它按照每个特征对于预测的贡献来解释模型的输出。

SHAP 值是依据所有可能的特征组合来评估模型输出进行计算。简单来说，它涉及对特定特征的值进行洗牌，同时保持其它特征不变，并观察对模型预测的影响。

就像游戏中的玩家一样，如果某个特征在洗牌时始终没有改变模型的输出（例如，当一个玩家未参与时，他不影响团队的表现），则该特征的 SHAP 值往往会较低。与之对比，如果改变特征显著影响到模型的输出，则 SHAP 值会较高，表示贡献更大。

SHAP 值提供了每个特征贡献的量化度量。通过比较不同特征的 SHAP 值，可以推断出哪些特征对模型的预测影响更大。

因此，如果一个特征被反复遗漏（其值被洗牌或变化），而模型的性能没有显著变化，则表明该特征对模型预测的贡献也许相对较小。

优势：

• 与模型无关：SHAP 值与模型无关，这意味着它们可应用于任何机器学习模型，包括复杂的模型，诸如融汇方法、神经网络、以及支持向量机。
• 全局和局部可解释性：SHAP 值提供全局和局部可解释性。它们可以解释独立特征对特定预测的影响（局部可解释性），以及每个特征在整个数据集中的总体贡献（全局可解释性）。

弱点：

• 计算密集：计算 SHAP 值可能是计算密集型，尤其是对于大型数据集、或复杂模型。这也许会给实时应用程序、或计算资源有限的情况带来挑战。
• 高维数据的可解释性挑战：对于拥有大量特征的模型，解释其 SHAP 值颇具挑战性。在高维空间中，可视化和理解众多特征的贡献变得更加复杂。

机遇：

• 特征重要性排位：SHAP 值可基于特征对模型预测的影响为特征进行排位。该信息对于特征选择和识别模型中最具影响力的变量很有价值。
• 解释性可视化：SHAP 值支持创建富有见解的可视化，例如 SHAP 汇总图、或独立推力图，有助于将模型预测和特征贡献传达给利益相关者。

凶险：

• 一致性假设：SHAP 值假定一致性，这意味着特征对预测的影响在不同实例中是一致的。在某些情况下，这种假设也许不成立，从而导致潜在的误解。
• 解释的复杂性：虽然 SHAP 值提供了有价值的见解，但正确解释它们需要对底层概念有扎实的理解。用户可能会误解某些值的重要性，或者无法掌握特征贡献的细微差别。

互关信息：

互关信息（MI）是一个变量提供有关另一个变量的信息量多寡的度量。它量化了两个变量之间的依赖性、或关联程度。

优势：

• 与模型无关：互关信息是一个与模型无关的度量，这意味着它不依赖于特定的机器学习模型。它可以应用于变量之间的任何类型的关系，包括线性和非线性依赖关系。
• 捕获非线性关系：与更适合线性关系的相关性不同，互关信息可以捕获变量之间的非线性依赖关系，故其适用于各种类型的数据。

弱点：

• 对样本规模的敏感性：互关信息也许对数据集的规模敏感。在小型数据集中，MI 的估算可能稳定性较低，数据的微小变化也许会对结果产生更明显的影响。
• 解释量级的困难：虽然 MI 提供了关联强度的度量，但直接解释其绝对值也许是个挑战。对“高”或“低”互关信息的解释取决于上下文和变量的尺度。

机遇：

• 特征选择：互关信息可用于特征选择，即基于特征与目标变量的相关性对特征进行排位。具有较高 MI 值的特征被认为对预测目标更具信息性。
• 融汇模型中的变量重要性：在融汇学习中，可以利用互关信息来评估变量的重要性，有助于构建更准确和可解释的融汇模型。

凶险：

• 独立性假设：互关信息假设变量在 MI 为零时是独立的。在实践中，它可能无法捕获受潜在因素、或混杂变量影响的复杂依赖性或关系。
• 高维计算密集型：估算高维数据的互关信息可能是计算密集型的。这也许会在时间和资源需求方面带来挑战。

庆幸地是，专门的 Python 库将该过程流线化，以致我们无需从头开始构建大部分代码。

重点要注意的是，本文不会深入探讨训练和拟合模型的复杂性。代之，它将专注于训练后阶段，探索如何评估和解释模型的性能。提供的代码示例所构建的基本模型，纯粹出于概括目的，强调在设计和训练您的模型之后采取的步骤。 

我们开始吧 

舍弃列重要性

我们将利用 sklearn 库中的递归特征消除算法来实现舍弃列重要性

from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR

递归特征消除算法期望我们验证可以拟合和评估的监督学习模型。
该模型应通过其系数或指定函数提供有关特征重要性的信息。
该模型不必与我们在问题中所用的模型相同。
模型不必来自 sklearn 库，但至少应该有一个 sklearn 包装器

我们将使用一个线性模型，并在随机舍弃特征时评估其准确性。

lm = LinearRegression()

rfe = RFE(lm,step=1)

step 参数表示每次迭代要舍弃的特征数量。

然后我们拟合递归特征消除算法

rfe = rfe.fit(train_x,train_y)

我们检查一下我们的 RFE 算法在哪些特征发现了信息

rfe.support_

array([ True, True, True, True, False, False, False, False, False, True, False, True, True, True, False, True, True, True, False, False, False, False, False, False, True, False, True])

我们还可以获得每个特征的排位

rfe.ranking_

array([ 1, 1, 1, 1, 2, 5, 14, 11, 13, 1, 7, 1, 1, 1, 8, 1, 1, 1, 12, 15, 3, 4, 9, 10, 1, 6, 1])

sklearn 实现为我们提供了一个掩码，我们可以将其应用于 train_x 数据帧中的列，以便查看 RFE 发现重要性的列名。

train_x.columns[rfe.support_]

Index(['open', 'high', 'low', 'close', 'BBM_20_2.0', 'BBB_20_2.0', 'BBU_20_2.0', 'BBL_20_2.0', 'ema_20', 'ema_40', 'ema_100', 'MACDs_12_26_9', 'DMN_14'], dtype='object')

如此，据我们所应用的所有指标，看出以下指标似乎携带有价值的信息：
    1)Open         2)High         3)Low         4)Close         6)KSTs_9         7)KST_10_15_20_30_10_10_10_15         7)所有 3 条指数移动平均线         8)4 布林带分量: 'BBM_20_2.0' 'BBB_20_2.0' 'BBU_20_2.0' 'BBL_20_2.0'         9)MACD: 'MACDs_12_26_9'         10)方向走势负数    其它指标可能也产生了噪音，但请记住，这些只是估值，仅供参考！
我们不能得出结论这就是事情的真相，不过这对我们来说仍然是一个合理的断言。

接下来，我们转到评估排列重要性

我们将使用一个名为 “Explain Like I'm 5（ELI5）” 的 Python 库来实现该算法

#pip install eli5 if you don't allready have it installed
import eli5
from eli5.sklearn import PermutationImportance
from sklearn.ensemble import GradientBoostingRegressor

gbr = GradientBoostingRegressor().fit(train_x,train_y)

permutation = PermutationImportance(gbr).fit(test_x,test_y)

现在，我们将评估算法分配给每个特征的权重

eli5.show_weights(permutation,feature_names = test_x.columns.to_list())

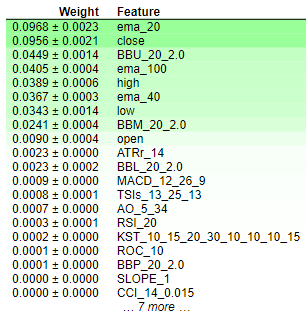
图例 8：排列重要性权重

解释排列重要性的结果很简单。这些特征按重要性降序排列，最关键的要素位于顶部，不太重要的要素位于底部。权重值，譬如 “0.0986 +- 0.0256”，表示模型误差指标的变化。对于寻求简明信息的读者来说，值得重申的是，排列重要性涉及特征值的随机洗牌。如果该特征对模型有显著影响，则该随机化会导致模型误差度量的增加。由于算法的随机性质，这种增长会以范围的形式呈现，而非特定值。

相反，对于缺乏重要性的特征，当数值随机洗牌时，模型的误差度量要么没有变化，要么在某些情况下会减少。结果的这种双重性质 — 误差度量的增加或减少 — 清楚地表明了每个特征的相对重要性，有助于对排列重要性结果进行简洁易懂的解释。因此，我们可以得出结论，在我们的模型中，舍弃列重要性与排列重要性两者具有相似的特征重要性。

部分依赖图和独立条件期望（ICE）图：

#Import partial dependence display from sklearn
from sklearn.inspection import PartialDependenceDisplay

for feature_name in predictors:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature_name])
    plt.grid()
    plt.show()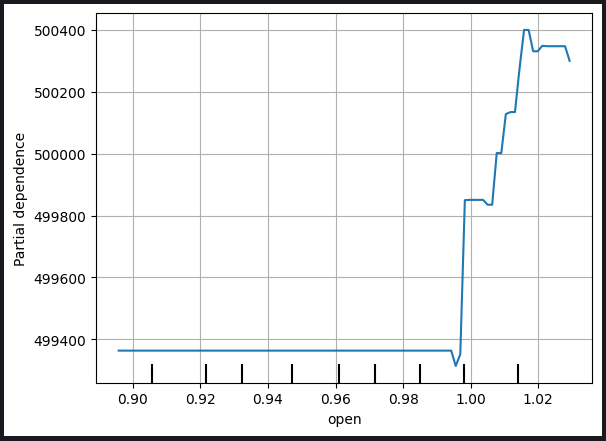

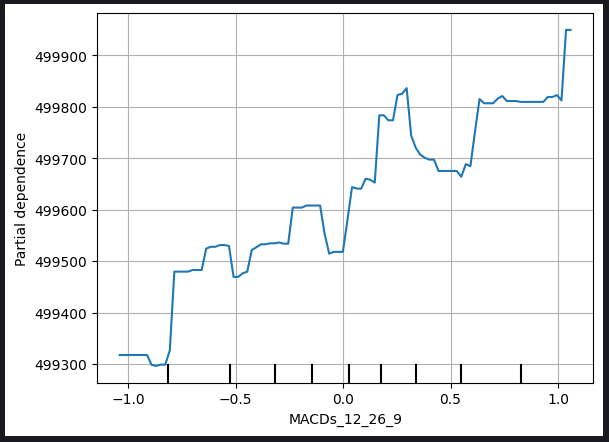
图例 9：开盘价和 MACD 信号线的部分依赖图

部分依赖图是了解特定变量的变化如何影响模型预测的宝贵工具。通过分析 MACD 信号线的部分依赖关系图，我们可以合理地推断，一般来说，MACD 信号线的增加与模型预测收盘价的上升有关。

不过，重点要注意的是，部分依赖图解释起来可能更错综复杂，如下面的 MACD 高度图所示。

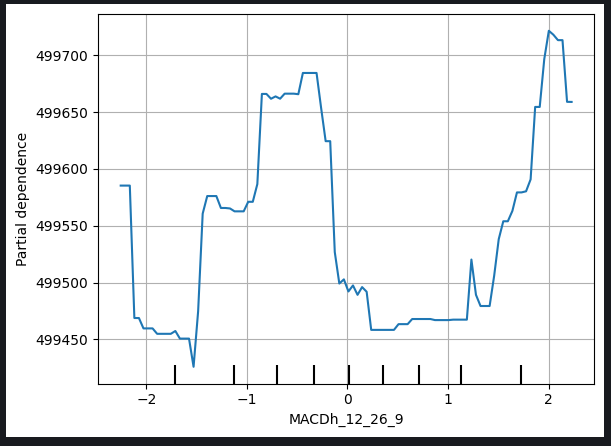
图例 10：MACD 高度的部分依赖图

解释此类绘图的复杂性也许源于非线性关系、或与其它变量的交叉作用，需要更细致的分析。在 MACD 高度图的情况下，可能需要额外的考量和探索，才能揭示 MACD 高度与模型预测收盘价之间关系的确切性质。

这种认知强调了需要对部分依赖图进行全面检验，考虑每个变量的独特特征，并在面临解释方面的挑战时，通过额外的分析或专业咨询，来寻求进一步的见解。

生成独立条件期望（ICE）图，提供独立实例如何响应特定预测变量变化的精细视图。以下是有关如何制作和使用 ICE 图的分步说明：

1. 独立预测变化：

• 从包含相关预测变量和其它相关特征的数据集开始。
• 从数据集中选择一个特定实例。

2. 改变预测变量：

• 对于所选实例，系统地改变预测变量的值，同时保持其它特征不变。
• 创建一组预测，对应于预测变量的每个变量值。

3. 创建独立曲线：

• 对数据集中的多个实例重复 1-2 步骤，生成一组独立曲线（每个实例一条），从而勾勒出预测变量与模型预测之间的关系。

4. 绘图：

• 在同一张图形上绘制每条独立的曲线。x 轴表示预测变量的值，y 轴表示模型的预测。

5. 解释：

• 分析 ICE 图，观察模型的预测如何随着预测变量的变化而改变。
• 识别曲线中的形态、趋势、或变化，从而洞悉预测变量对独立预测的影响。

6. 比较分析：

• 比较多个 ICE 图，尤其是在处理不同实例时，从而理解整个数据集中变量效应的异质性。

用法：

• 细粒度洞察：ICE 图提供了预测变量如何影响预测的细节、具体实例的视图，从而可以更细致地理解。
• 模型理解：它们有助于用户探索在聚合视图中可能不明显的非线性关系、交汇、和潜在异常。
• 特征重要性：ICE 图可以通过说明具体特征对独立预测的影响来帮助评估其重要性。
• 决策支持：来自 ICE 图的见解可为制定决策提供信息，尤其是在理解具体实例的预测如何响应特定变量的变化时至关重要。

事实上，PDP 图只是所绘制的 ICE 图的平均值。PDP 线在下面以橙色显示。

对于预测的特征:
    PartialDependenceDisplay.from_estimator(cat_full,test_x,[feature],kind='both')

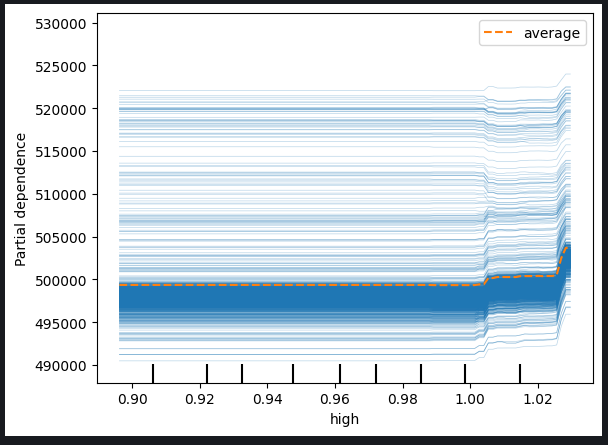
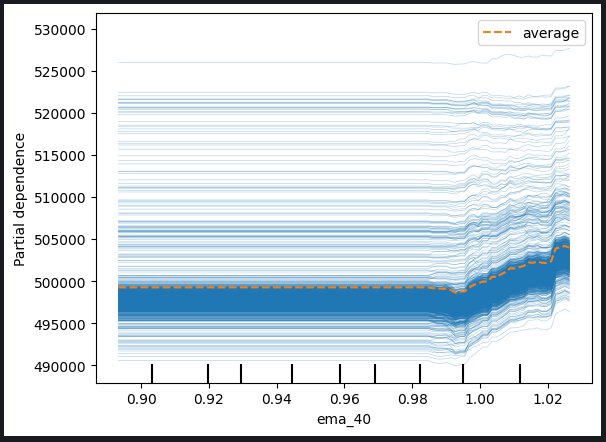
图例 11：最高价和 40 周期 EMA 的 ICE 图

基于观察到的绘图，很明显，最高价或指数移动平均线的增加不会对我们模型的预测产生直接影响。取而代之，有迹象表明，预期模型的预测发生任何可观变化之前，这些变量需要经历明显增长。这一观察给出建议，该模型对这些具体特征的增量变化不是很敏感。

从这些图中获得的关键见解包括：

1. 阈值灵敏度：该模型似乎表现出阈值敏感性，这意味着在大幅调整其预测之前，它需要最高价或指数移动平均线有一个较大幅度的阈值级别变化。

2. 渐进式响应：上述特征的增量或适度变化看似不会立即触发模型预测的调整。这一特征表明对这种变化的反应是渐进式的、或温和的。

3. 低灵敏度：模型对这些特征的变化不是很敏感的结论，意味着最高价或指数移动平均线的微小波动不太可能对模型的输出产生明显影响。

明白模型对不同特征的敏感性，对于有效的模型解释和制定决策至关重要。这些见解可以指导进一步的分析、模型改进，或告知利益相关者特定预测变量与模型预测之间关系的性质。

我们还可以检查二维部分依赖图，以便查看 2 个特征的联合效应

#Setting up the plot
fig , ax = plt.subplots(figsize=(10,5))
column_names = [('ROC_10','ATRr_14')]

#Plotting 2D PDP
disp_4 = PartialDependenceDisplay.from_estimator(cat_full, test_x[0:1000],column_names, ax=ax)
plt.show()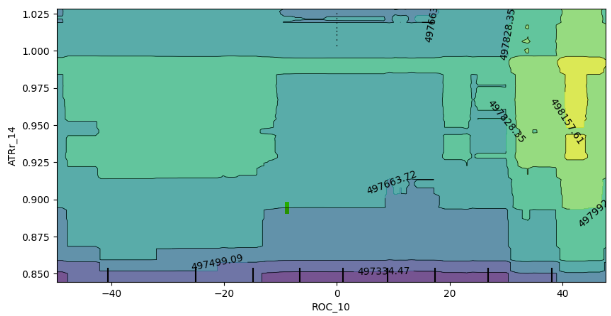

图例 12：变化率（ROC）和平均真实范围（ATR）指标的 2D 部分依赖图。

二维部分依赖图的关系分析表明，一般来说，ROC（变化率）和 ATR（平均真实范围）指标的增加对应于我们模型的预期预测的增加。这种正相关关系与模型响应这些指标变化的预期行为一致。

不过，该图也提供了对这两个指标之间相互作用的见解。值得注意的是，图中缺乏明确的边界表明这种关系并非持久稳定。代之，存在强弱混杂的区域，表明 ROC 和 ATR 指标对模型预测的影响可能因图的不同区域而异。

在强期望的边界之内，存在弱期望的随机飞地，进一步强调了交汇作用的动态性质。重点要注意的是，观察到的行为也许会受到采样方式的影响，特别是如果出于计算效率原因使用了数据帧的子集。

一些注意事项和潜在影响包括：

1. 采样限制：观察到的不一致部分归因于使用较小的样本来提高计算效率。更广泛的抽样方式也许会提供更全面的交汇视图。

2. 非线性或交汇：缺乏明确定义的边界，以及混杂斑点的存在，表明 ROC 和 ATR 指标之间存在潜在的非线性或交汇作用。进一步的探索，可能依据更大的样本，可以揭示更微妙的形态。

3. 模型稳健性：明白交汇作用的可变性有助于评估模型的稳健性、及其对不同输入特征组合的敏感性。

总结，二维的部分依赖图的解释，为模型响应 ROC 和 ATR 指标的变化，提供了有价值的见解。认识到样本规模对于所观察形态的潜在影响，进一步调查，如果可行，采取更广泛的抽样策略，也许会提高这些发现的精确度。

沙普利（Shapley）加法解释（SHAP）值

#pip install shap if you don't have it installed
#Import SHAP
import shap

#Initialise the shap package
shap.initjs()

需要考虑的几件事：

• SHAP 值假定特征是独立/不相关的

• 准确计算 SHAP 值成本很高，数据集维数的增加更加剧了这个问题。

• SHAP 值与模型无关，这意味着它们也许无法帮助我们捕获某些模型的特殊行为，讽刺的是，这既是一个优势、也是一个劣势。

• SHAP 值对输入顺序很敏感！

我们的数据集具有很强的相关项，这是计算 SHAP 值时的一个主要问题，它违反了特征是独立的假设，幸运的是有很多方法可以解决这个问题，例如：

• 舍弃相关特征，这是最简单的解决方案，但在大多数情况下应考虑作为最后手段。

• 考虑使用特征缩减技术（如主成分分析），或您熟悉的其它特征选择方法

• 将特征离散化有助于减轻 SHAP 值计算中相关性的不利影响

• 使用 SHAP 算法旨在处理相关性数据

• 使用不相关的特征，例如在我们的例子中，交易量与最高价/最低价之间点差的相关性非常小。

在本练习中，我们将使用第 4 个方案，即采用旨在处理相关性数据的特定 SHAP 算法。基于树的 SHAP 算法可以很好地处理相关性。

#Initialise shap value calculator
tree_explainer = shap.TreeExplainer(cat_full)

#Store SHAP values
shap_values = tree_explainer.shap_values(test_x)

#Plot SHAP values
shap.summary_plot(shap_values,test_x)

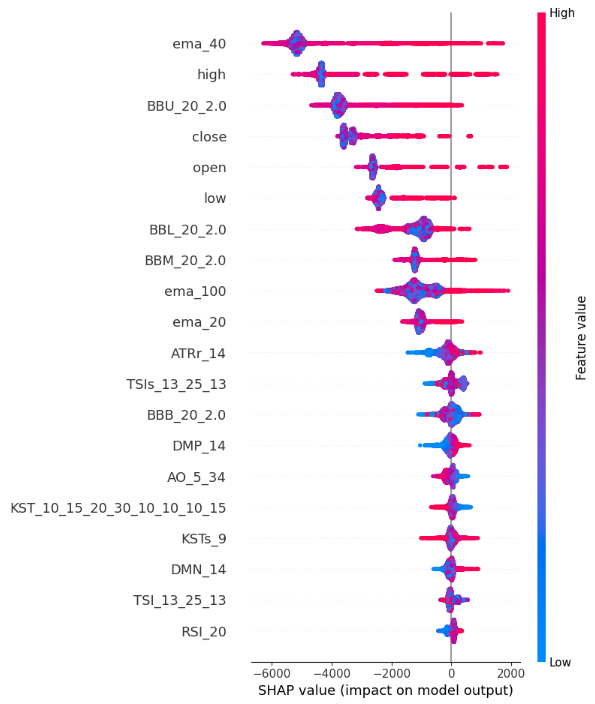
图例 13：SHAP 数值图

以下是我们对 SHAP 汇总图的解释：

1. 特征重要性：y-轴顶部列出的特征对提高收盘价的影响更大，而 y-轴底部的特征对拉低收盘价的影响更大。 

2. 冲突方向：沿 x-轴，每个特征都有颜色编码的点。蓝点表示较低的特征值，红点表示较高的特征值。这些点的水平定位告诉我们特征值对收盘价的影响。故此，我们的 SHAP 值计算表明，High_Low_Sread 并不能很好地指示收盘价。

3. 位置大小：沿 x-轴的每个点的水平位置表示影响的大小，因此与该演示示例中的成交量、开盘价和 High_Low_Spread 量值特征相比，极端最高价和最低价对收盘价的影响相对较强。

互关信息

from sklearn.feature_selection import mutual_info_regression

mi_scores = mutual_info_regression(train_x, train_y)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=train_x.columns)
mi_scores = mi_scores.sort_values(ascending=False)
mi_scores

ema_100                                       1.965130

ema_40                                         1.960548

ema_20                                         1.933651

BBM_20_2.0                                   1.902066

BBL_20_2.0                                   1.895867

BBU_20_2.0                                  1.881435

high                                             1.795941

low                                              1.786879

close                                            1.783567

open                                            1.777118

TSIs_13_25_13                              0.232247

ATRr_14                                        0.215980

MACDs_12_26_9                            0.214559

KST_10_15_20_30_10_10_10_15    0.208868

KSTs_9                                         0.205177

MACD_12_26_9                            0.174518

TSI_13_25_13                              0.168086

AO_5_34                                     0.128653

BBB_20_2.0                                 0.104481

RSI_20                                         0.095368

MACDh_12_26_9                          0.076360

DMP_14                                      0.060191

DMN_14                                     0.048856

ROC_10                                     0.042115

BBP_20_2.0                               0.028558

CCI_14_0.015                            0.022320

SLOPE_1                                   0.004144

def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")

plt.figure(dpi=100, figsize=(8, 5))
plt.grid()
plot_mi_scores(mi_scores)

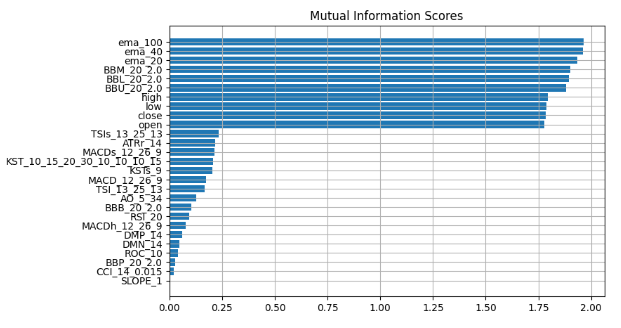
图例 14：互关信息得分

我们观察到所有黑盒解释技术都达成了一致的共识，这表明这些解释中始终强调的特征可能包含我们可以有效利用的重大信息。指数移动平均线、布林带、和开盘价/最高价/最低价/收盘价始终排名靠前，因此，通过衡量中心趋势，我们可以合乎逻辑地得出结论，这些特征也许非常丰富，故我们可以舍弃其它一切。 

我们来验证我们的发现。

我们将使用 2 个模型，一个简单的线性回归，和我们强大的黑盒。我们将用我们从黑盒解释技术中获得的洞察力来精心挑选特征。 

首先，我们将导入所需的依赖项。

from sklearn.linear_model import LinearRegression
from catboost import CatBoostRegressor
from sklearn.metrics import mean_squared_error

然后我们将首先拟合较简单的模型

#First we fit the simpler model
lm = LinearRegression()

lm.fit(train_x.loc[:,["open","high","low","close"]],train_y)

然后，我们将评估较简单模型与训练数据的拟合程度。

lm_predictions = pd.DataFrame(lm.predict(train_x.loc[:,["open","high","low","close"]]), index = train_y.index)
lm_fit = lm.predict(train_x.loc[:,["open","high","low","close"]])
residuals = pd.DataFrame(train_y - lm_fit)

我们现在将引入更强大的黑盒模型来学习较简单模型的残差，我们将为我们的黑盒模型提供我们认为最有用的特征

#Now we bring in our more powerfull black-box model
cat = CatBoostRegressor()
cat.fit(
    train_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]],
    residuals)

我们将依据测试数据进行误差级别比较，通过评估初始黑盒模型的性能，其利用所有可用特征，阻碍改进模型的准确性。改进的模型结合了较简单线性回归的协助，并策略性地采用精心挑选的特征子集。

lm_test_predictions = pd.DataFrame(lm.predict(test_x.loc[:,["open","high","low","close"]]),index=test_y.index)
cat_full_test_predictions = cat_full.predict(test_x[predictors])

cat_residuals_predictions = pd.DataFrame(cat.predict(test_x.loc[:,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]]),index=test_y.index)

我们将评估初始黑盒的误差级别

full_error = mean_squared_error(test_y,cat_full_test_predictions)

并将其与我们的新黑盒混合体的误差级别进行比较。

hybrid_predictions = lm_test_predictions.iloc[:,0] + cat_residuals_predictions.iloc[:,0]
hybrid_error = mean_squared_error(test_y, hybrid_predictions)

delta_error = full_error - hybrid_error
(delta_error / full_error) * 100

94.428

我们的新黑盒混合体的误差指标提高了 94%。

hybrid_predictions.plot()

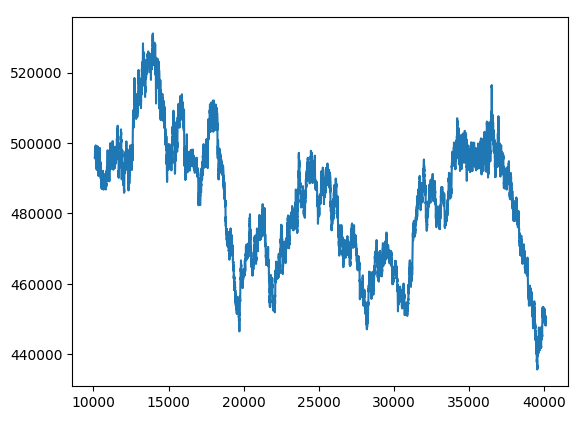
图例 15：新的黑盒预测

最重要的是，我们的新黑盒预测的真实性有了显著提高，没有了最初观察到的不自然的钝化区域。对于读者来说，至关重要的是要认识到我们现在正在通过流线化的特征来达成更高的准确性。这条划重点的原则，即如果执行得当，少即是多。

将一切糅合到一起

我们准备将所有部件整合到一个综合的交易策略之中。

MARKET_SYMBOL = "Volatility 75 Index"
DEVIATION = 100
VOLUME = 0
symbol_info = MT5.symbol_info(MARKET_SYMBOL)
VOLUME = symbol_info.volume_min * 1

def preprocess(df):
    #20 period exponential moving average
    df["ema_20"] = df.ta.ema(length=20)
    #40 period exponential moving average
    df["ema_40"] = df.ta.ema(length=40)
    #100 period exponential moving average
    df["ema_100"] = df.ta.ema(length=100)
    #20 period bollinger bands with 3 standard deviations
    df.ta.bbands(length=20,sd=2,append=True)
    df = df.loc[100:,:]

def fetch_prices():
    current_prices = pd.DataFrame()
    current_prices = pd.DataFrame(MT5.copy_rates_from_pos(MARKET_SYMBOL,MT5.TIMEFRAME_M1,0,200))
    preprocess(current_prices)
    return(current_prices)

def normalise_prices(raw_data):
    for col in raw_data.columns:
        if col in first_values:
            raw_data[col] = raw_data[col] / first_values[col]

model_forecast = 0

def hybrid_forecast(model_1,model_2):
    market_data = fetch_prices()
    normalise_prices(market_data)
    forecast_1 = model_1.predict(market_data.loc[199:200,["open","high","low","close"]])
    forecast_2 = model_2.predict(market_data.loc[199:200,["BBM_20_2.0","BBL_20_2.0","BBU_20_2.0","ema_40","ema_20","ema_100"]])
    out = forecast_1 + forecast_2
    return(out)

INITIAL_BALANCE = MT5.account_info().balance
CURRENT_BALANCE = 0

if __name__ == "__main__":
    while True:
        
        #Account standing
        info = MT5.account_info()
        CURRENT_BALANCE = info.balance
        profit = CURRENT_BALANCE - INITIAL_BALANCE
        
        model_forecast = hybrid_forecast(lm,cat)
        print("Current forecast: ",model_forecast)
        
        #We have no open positions
        if(MT5.positions_total() == 0):
            print("No open positions")
            
            #Buy
            if(model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast buy")
                MT5.Buy(MARKET_SYMBOL,VOLUME)
                last_trade = 1
                        
            #Sell    
            elif(model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask):
                print("Following model forecast sell")
                MT5.Sell(MARKET_SYMBOL,VOLUME)
                last_trade = 0
                
        elif(MT5.positions_total() > 0):
            print("Checking model forecast")
            
            if((model_forecast > MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 0)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
            
            elif((model_forecast < MT5.symbol_info(MARKET_SYMBOL).ask) & (last_trade == 1)):
                print("Model is forecasting a move that hurts our exposure. Closing positions")
                MT5.Close()
                
        print("Total Profit/Loss: ",profit)
        time.sleep(60)

当前预测： [239100.04622681] 无持仓，模型预测 “买入” 总盈亏：0.0

结束语

随着我们继续训练更大、更复杂的模型，它们变得难以理解、解释和调试。如果不能完全理解我们的机器学习模型到底在做什么，以及为什么它们会做出正在制定的决策，我们就无法判定模型是否真如我们预期的方式运行。如果无法理解模型，并对其进行故障排除，则不能保证采用这些技术会带来额外的复杂性。我们能够持续从工具中攫取的价值，仅限于我们对该工具的理解。故而，正是朝着该结局，我们撰写了这篇文章，令您对自己的模型更有信心，并深入洞察机器学习模型中不为人知的黑盒之内的转动齿轮。