AIS Adaptive Nonlinear Smoothing MT5

Muy a menudo, en el estudio de series financieras se aplica su suavizado. Mediante el suavizado, puede eliminar componentes de alta frecuencia; se cree que están causados ​​por factores aleatorios y, por lo tanto, no son significativos. El suavizado siempre incluye alguna forma de promediar los datos, en la que los cambios aleatorios en las series de tiempo se absorben mutuamente. Muy a menudo, para este propósito, se utilizan métodos de media móvil simple o ponderada, así como el suavizado exponencial.

Cada uno de estos métodos tiene sus ventajas y desventajas. Por lo tanto, un promedio móvil simple es simple e intuitivo, pero su aplicación requiere la estabilidad relativa de los componentes periódicos y de tendencias de la serie temporal. Además, un retraso en la señal es característico de una media móvil. El método de suavizado exponencial está libre del efecto de retraso. Pero incluso aquí hay fallas: el suavizado exponencial es efectivo solo cuando se alinea la serie con valores atípicos aleatorios.

Un compromiso razonable entre promedios simples y exponenciales es el uso de un promedio móvil ponderado. Sin embargo, existe el problema de elegir valores de peso específicos. Vamos a tratar de solucionar esto juntos.

Entonces, primero defina lo que nos gustaría lograr a partir del procedimiento de suavizado:

• primero, debemos eliminar los cambios aleatorios y el ruido de las series de precios;

• en segundo lugar, nos gustaría identificar las emisiones anormales y el comportamiento inusual de los precios, que también se puede utilizar en el comercio;

• y finalmente, el procedimiento de promediación debe identificar tendencias sostenibles si están presentes en el mercado.

Y, por supuesto, nos gustaría que el procedimiento de suavizado se adaptara a la situación actual del mercado.

Para obtener el resultado deseado, calcularemos los pesos según la distancia a la que se encuentre este nivel de precios respecto a los precios máximos y mínimos del período de estudio. A través de este enfoque, obtenemos un filtro que implementa el procedimiento de suavizado en función de la distribución de precios para el período de interés.

La principal ventaja de este algoritmo de suavizado es su estabilidad con respecto a varios tipos de emisiones: las desviaciones de los precios pueden ser muy grandes, pero el filtro seguirá las tendencias más significativas. Además, con diferentes datos iniciales, podemos obtener diferentes efectos en su esencia. Por lo tanto, si los precios se distribuyen más o menos uniformemente, obtendremos un filtro de mediana móvil. Si los precios se acumulan en torno a un valor y una diferencia suficientemente grande entre el máximo y el mínimo, se obtiene un suavizado modal. Si todos los precios se encuentran dentro de un intervalo muy estrecho, entonces obtenemos un promedio móvil simple.

La principal desventaja de este método es que el suavizado se realiza sin tener en cuenta los cambios de precios a lo largo del tiempo. De hecho, podemos cambiar arbitrariamente el orden de los precios dentro del período analizado, esto no afecta el resultado de los cálculos. Por lo tanto, podemos decir que este algoritmo considera el cambio de precio como un proceso aleatorio.

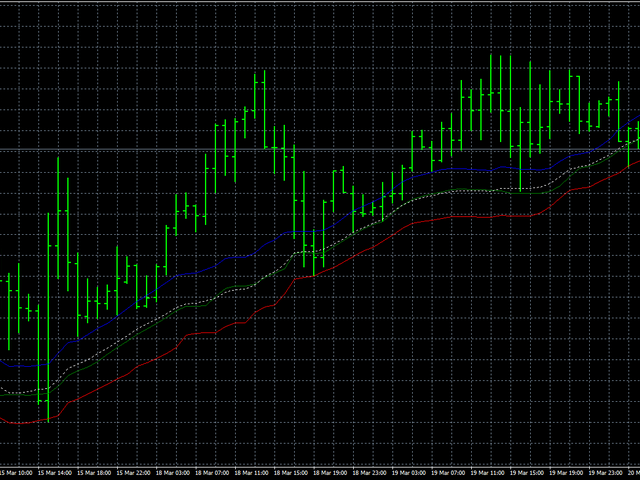
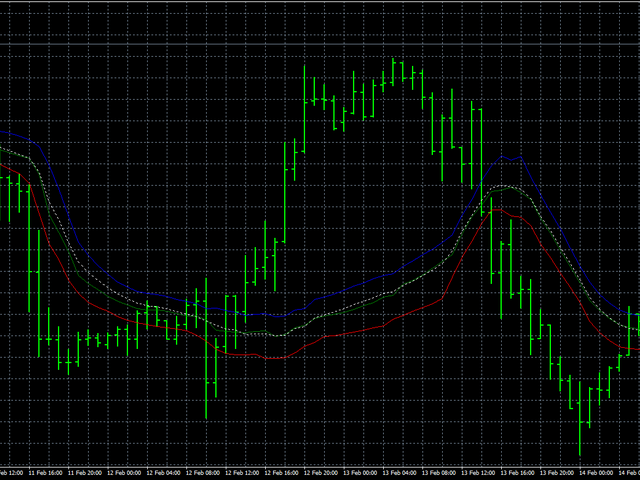
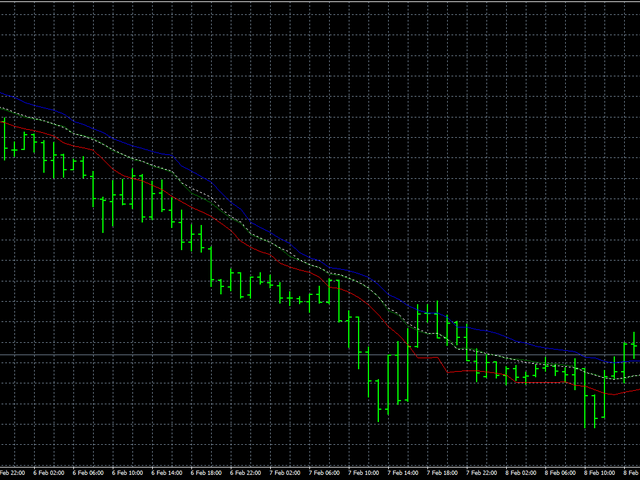
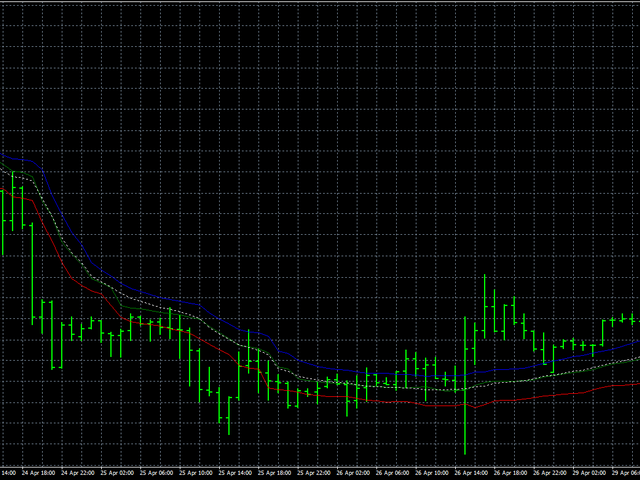
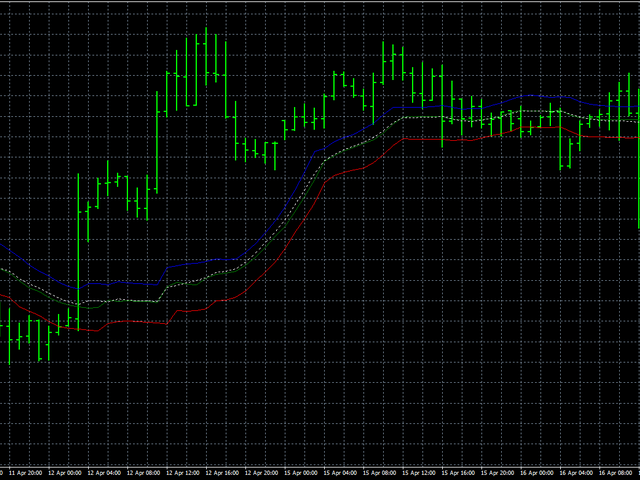
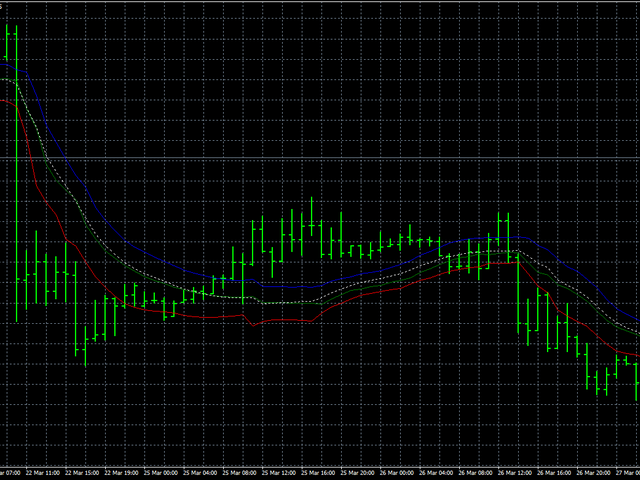
A pesar de este inconveniente, veamos cómo funciona este algoritmo en datos reales. En este caso, procedemos de la siguiente manera: primero, suavizaremos los precios de Abierto, Alto y Bajo por separado, y luego todos los precios juntos. Suavizar todos los precios al mismo tiempo nos permitirá juzgar qué tan estable es el comportamiento de los precios en general. La línea azul mostrará el suavizado de los precios Altos, la línea roja - Baja y la línea verde indicará el suavizado de los precios de apertura. La línea de puntos blanca muestra el suavizado de todos los precios al mismo tiempo.

• LH es un parámetro que establece el número de barras utilizadas para el análisis. Su valor permitido está en el rango de 0 a 255, mientras que el número real de barras es uno más.