MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
Indicadores personalizados e infografía en CCanvas

Indicadores personalizados e infografía en CCanvas

MetaTrader 5 — Ejemplos | 21 agosto 2017, 12:56
1 190 1
Alexander Fedosov
Alexander Fedosov

Contenido

Introducción

En el artículo anterior analizamos los principios de construcción de indicadores gráficos usando métodos de creación de primitivas gráficas de la clase CCanvas. Pero las posibilidades de uso de la biblioteca de gráficos personalizados no se limita a esto, por ello, proponemos al lector nuevos tipos de indicadores con una estructura de implementación más compleja. Además, intentaremos construir tipos de indicadores de pseudo-3D y una infografía de cambio de dinámico.


Clase del indicador lineal redondeado CLineRounded

Para implementar los objetos gráficos en este artículo no hemos vuelto a crear de nuevo la estructura general de las clases básicas: en su lugar, usaremos la biblioteca CustomGUI ya preparada, que fue descrita en el anterior artículo. Concretamente, nuestra clase básica será CCanvasBase; las clases desarrolladas a continuación completarán la lista en el archivo CustomGUI.mqh.

A la hora de crear un indicador lineal simple, primero hay que definir su estructura y elementos básicos. En la fig.1 se muestran los elementos que se pueden gestionar al usar este tipo de indicador. Debemos notar que no se trata de elementos simples. 


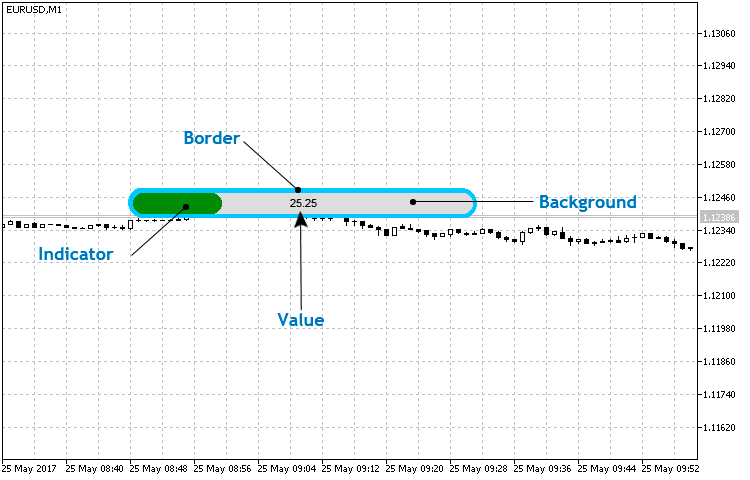
Fig. 1. Estructura básica del indicador lineal simple.

En este caso, un elemento simple (básico) es aquel que se implementa con los métodos de la clase CCanvas. Por ejemplo, en un indicador lineal, solo será sencillo el Valor, puesto que se implementa con la ayuda del método CCanvas::TextOut(). Los otros tres son idénticos en cuanto a su forma y constan de tres figuras básicas: dos círculos coloreados (implementación CCanvas::FillCircle()) y un rectángulo (CCanvas::FillRectangle()).

Creamos en la carpeta CustomGUI/Indicators el archivo LineRounded.mqh, y en dicho archivo, creamos la clase СLineRounded, haciendo básica para ella la clase CCanvasBase creada con anterioridad.

//+------------------------------------------------------------------+
//|                                                  LineRounded.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#include "..\CanvasBase.mqh"
//+------------------------------------------------------------------+
//| Indicador lineal redondeado                                  |
//+------------------------------------------------------------------+
class CLineRounded : public CCanvasBase

Asimismo, lo añadimos a la lista en el archivo CustomGUI.mqh, que posibilita el acceso rápido a todas las clases de la biblioteca. Teniendo en cuenta las clases desarrolladas con anterioridad, su código tendrá el aspecto siguiente:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
//+------------------------------------------------------------------+

La lista completa de propiedades y métodos de la clase СLineRounded se puede estudiar en el archivo CustomGUI/Indicators/LineRounded.mqh. Nos detendremos con detalle en los métodos de creación del indicador, la instalación y la actualización. Como se ha dicho más arriba, el indicador constará de elementos compuestos. En la lista de abajo se ha comentado por bloques aparte la implementación de estos elementos.

//+------------------------------------------------------------------+
//| Crea el indicador                                                |
//+------------------------------------------------------------------+
void CLineRounded::Create(string name,int x,int y)
  {
//--- Corrige la posición del indicador con respecto a los ejes de coordenadas
   x=(x<m_x_size/2)?m_x_size/2:x;
   y=(y<m_y_size/2)?m_y_size/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(m_x_size);
   YSize(m_y_size);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Marco
   m_canvas.FillRectangle(YSize()/2,0,XSize()-YSize()/2,YSize(),ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2-1,YSize()/2,ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2-1,YSize()/2,YSize()/2,ColorToARGB(m_border_color,m_transparency));
//--- Fondo posterior
   m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.Update();
  }

Como podemos ver, el Marco y el Fondo posterior se han implementado usando dos métodos. No olvide que estos objetos constituyen capas y se dibujan superponiéndose unas sobre otras. Por eso, primero se dibuja el marco, después sobre él se dibujan el fondo posterior (de un tamaño menor), la escala del indicador y el valor numérico.

Vamos a analizar el método CLineRounded::NewValue(). 

//+------------------------------------------------------------------+
//| Establece y actualiza el valor del indicador                    |
//+------------------------------------------------------------------+
void CLineRounded::NewValue(double value,double maxvalue,int digits=0)
  {
   int v;
   v=int((XSize()-YSize()/2)/maxvalue*value);

//--- Fondo posterior
   m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
//--- Escala
   if(v>=YSize()/2 && v<=(XSize()-YSize()/2))
     {
      m_canvas.FillRectangle(YSize()/2,m_border,v,YSize()-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(v,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
     }
   else if(v>(XSize()-YSize()/2))
     {
      m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
     }
   else if(v>0 && v<YSize()/2)
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));

//--- Valor numérico
   m_canvas.FontSizeSet(m_font_size);
   m_canvas.TextOut(XSize()/2,YSize()/2,DoubleToString(value,digits),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.Update();
  }
//+------------------------------------------------------------------+
Como podemos ver, al inicio del método está de nuevo presente el bloque de implmentación del fondo posterior. ¿Para qué se necesita? Recordemos el dibujado por capas de los elementos, con la ayuda de la aplicación por turnos de los métodos correspondientes. Es decir, en este caso, primero dibujamos el fondo de la escala, y sobre ella el propio indicador, cuya longitud viene determinada por el valor máximo del parámetro. Cuando llega un nuevo valor del indicador, se redibuja una vez más, primero la capa con el fondo trasero, y ya sobre él, la escala con la nueva longitud.

La creación y la transmisión del valor se implementan de forma muy sencilla. En la lista de abajo vemos dos indicadores con pequeños ajustes y que solo se diferencian en que uno de ellos tiene el valor máximo dos veces superior. 

//+------------------------------------------------------------------+
//|                                                          001.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CLineRounded ind1,ind2;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   ind1.XSizeInd(350);
   ind1.YSizeInd(30);
   ind1.Create("line1",300,100);
//---
   ind2.XSizeInd(350);
   ind2.YSizeInd(30);
   ind2.ScaleColor(clrFireBrick);
   ind2.Create("line2",300,150);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ind1.NewValue(50,100,2);
   ind2.NewValue(50,200,2);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
  }
//+------------------------------------------------------------------+

En la fig.2 se ve perfectamente que, incluso teniendo los mismos valores y diferentes dimensiones, la longitud de la escala del indicador tiene su propia magnitud. El valor 50 y los máximos (100 para el primero y 200 para el segundo) se han elegido de tal forma que se pueda evaluar el resultado de la representación incluso de forma visual.

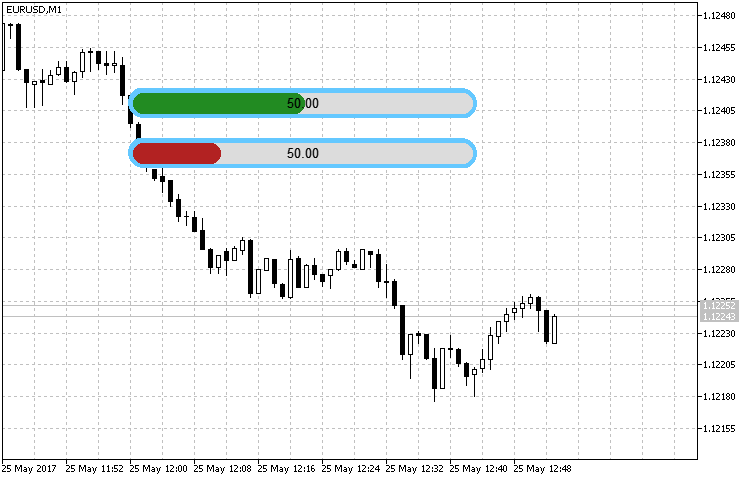
Fig.2. Ejemplo de funcionamiento del indicador lineal redondeado.


Clase del indicador hexagonal CHexagon

Para construir un indicador con la forma de un hexágono regular con la ayuda de las primitivas establecidas por la clase CCanvas, podemos elegir varios métodos. Puede tratarse tanto de la construcción de polilíneas y el posterior coloreado de la zona, como del "montaje" de seis triángulos equiláteros, como sucede con una pizza. Pero nuesto objetivo es alcanzar la máxima sencillez, para que sea fácil de comprender. Por eso, reuniremos un hexágono regular de tres primitivas-rectángulos y dos triángulos isósceles.


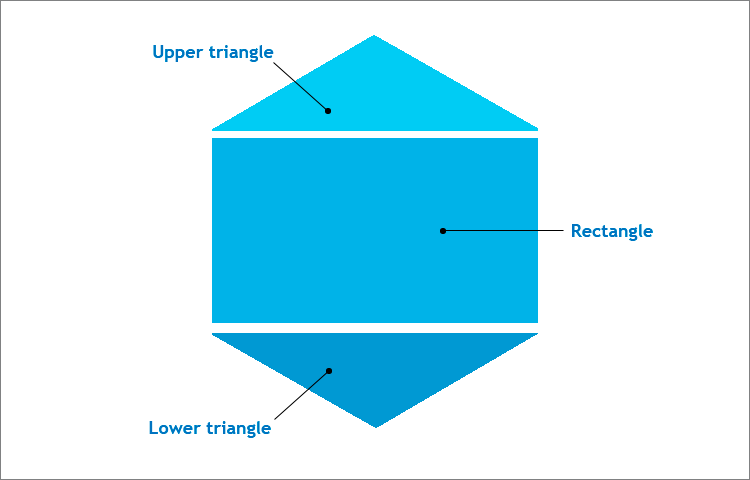
Fig.3. Estructura del hexágono regular.

El hexágono regular se inscribirá en un lienzo cuadrado. En este caso, además, hay que recordar las propiedades de esta figura, que son precisamente:

  • El lado del hexágono regular es igual al radio del círculo cincunscrito a su alrededor o, en nuestro caso, a la mitad de un lado del lienzo. Necesitaremos esto al construir el rectángulo.
  • El ángulo del hexágono es igual a 120 grados, por eso, los ángulos en la base de los triángulos isósceles tendrán 30 grados cada uno. Esta información es necesaria para determinar la altura del triángulo y, por consiguiente, para encontrar las coordenadas de los puntos de la base de los triángulos al usar el método CCanvas::FillTriangle().

La estructura básica del propio indicador es bastante sencilla y, aparte del hexágono, incluye 2 objetos de texto: un valor de número entero y la descripción (fig.4).



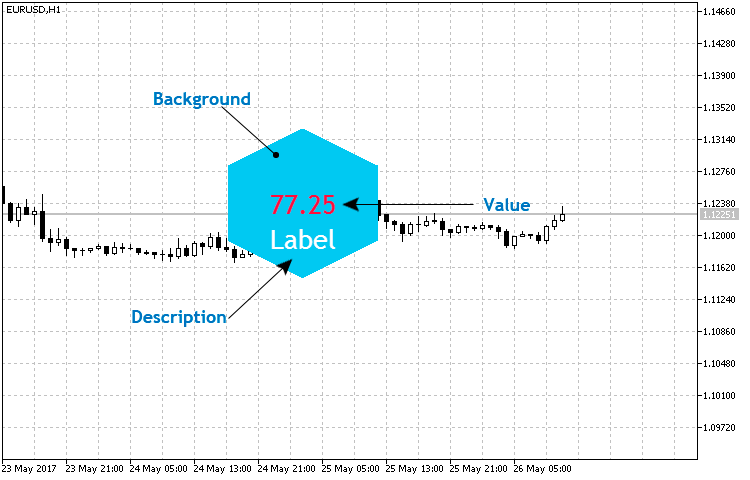
Fig.4. Estructura básica del indicador hexagonal.

Creamos en la carpeta CustomGUI/Indicators el archivo Hexagon.mqh, y en dicho archivo, creamos la clase СHexagon, haciendo básica para ella la clase CCanvasBase creada con anterioridad. La incluimos en la lista general:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
//+------------------------------------------------------------------+

Podemos familiarizarmos con la lista general de propiedades y métodos en el archivo creado más arriba. Vamos a detenernos un momento en los métodos responsables de la visualización del indicador. 

//+------------------------------------------------------------------+
//| Crea el indicador                                                |
//+------------------------------------------------------------------+
void CHexagon::Create(string name,int x,int y)
  {
   int a,r;
   r=m_size;
//--- Corrige la posición del indicador con respecto a los ejes de coordenadas 
   x=(x<r/2)?r/2:x;
   y=(y<r/2)?r/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(r);
   YSize(r);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Calcula la altura de los triángulos
   a=int(YSize()/2*MathSin(30*M_PI/180));
//--- Forma hexagonal
   m_canvas.FillTriangle(XSize()/2,0,0,a,XSize(),a,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillRectangle(0,a,XSize(),a+YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillTriangle(0,a+YSize()/2,XSize(),a+YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
//--- Descripción y valores numéricos
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r/2,r/2,"-",ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r/2,r/2+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
//---
   m_canvas.Update();
  }

En el método Create() a la variable a se le asigna el valor de la altura de los triángulos isósceles, es decir, en esencia, de esta forma encontramos las coordenadas de los puntos del triángulo por el eje de coordenadas(Y). El método de transmisión y actualización del valor numérico se diferencia solo por el hecho de que al objeto de texto responsable del dibujado del valor numérico, se le transmite el valor del argumento value:

//+------------------------------------------------------------------+
//| Establece y actualiza el valor del indicador                    |
//+------------------------------------------------------------------+
void CHexagon::NewValue(double value,int digits=2)
  {
   int a,r;
   r=m_size;
//--- Calcula la altura de los triángulos
   a=int(YSize()/2*MathSin(30*M_PI/180));
//--- Forma hexagonal
   m_canvas.FillTriangle(XSize()/2,0,0,a,XSize(),a,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillRectangle(0,a,XSize(),a+YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillTriangle(0,a+YSize()/2,XSize(),a+YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
//--- Texto
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r/2,r/2,DoubleToString(value,digits),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r/2,r/2+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
//---
   m_canvas.Update();
  }
//+------------------------------------------------------------------+

Como ejemplo, implementaremos un pequeño conjunto de indicadores del tipo hexagonal:

//+------------------------------------------------------------------+
//|                                                          002.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CHexagon ind1,ind2,ind3,ind4,ind5,ind6,ind7,ind8,ind9,ind10,ind11,ind12,ind13,ind14;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---   
   ind1.BgColor(clrWhite);
   ind1.Size(110);
   ind1.Create("hex1",300,200);
   ind2.BgColor(C'60,170,220');
   ind2.Create("hex2",300,200);
//---
   ind3.BgColor(clrWhite);
   ind3.Size(110);
   ind3.Create("hex3",300,80);
   ind4.BgColor(C'230,80,25');
   ind4.Create("hex4",300,80);
//---
   ind5.BgColor(clrWhite);
   ind5.Size(110);
   ind5.Create("hex5",300,320);
   ind6.BgColor(C'150,190,15');
   ind6.Create("hex6",300,320);
//---
   ind7.BgColor(clrWhite);
   ind7.Size(110);
   ind7.Create("hex7",180,140);
   ind8.BgColor(C'10,115,185');
   ind8.Create("hex8",180,140);
//---
   ind9.BgColor(clrWhite);
   ind9.Size(110);
   ind9.Create("hex9",420,140);
   ind10.BgColor(C'20,150,150');
   ind10.Create("hex10",420,140);
//---
   ind11.BgColor(clrWhite);
   ind11.Size(110);
   ind11.Create("hex11",420,280);
   ind12.BgColor(C'225,0,80');
   ind12.Create("hex12",420,280);
//---
   ind13.BgColor(clrWhite);
   ind13.Size(110);
   ind13.Create("hex13",180,280);
   ind14.BgColor(C'240,145,5');
   ind14.Create("hex14",180,280);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ind3.Delete();
   ind4.Delete();
   ind5.Delete();
   ind6.Delete();
   ind7.Delete();
   ind8.Delete();
   ind9.Delete();
   ind10.Delete();
   ind11.Delete();
   ind12.Delete();
   ind13.Delete();
   ind14.Delete();
  }
//+------------------------------------------------------------------+

El resultado del funcionamiento se muestra en la fig.5. Esta plantilla básica es muy fácil de configurar y modificar. 

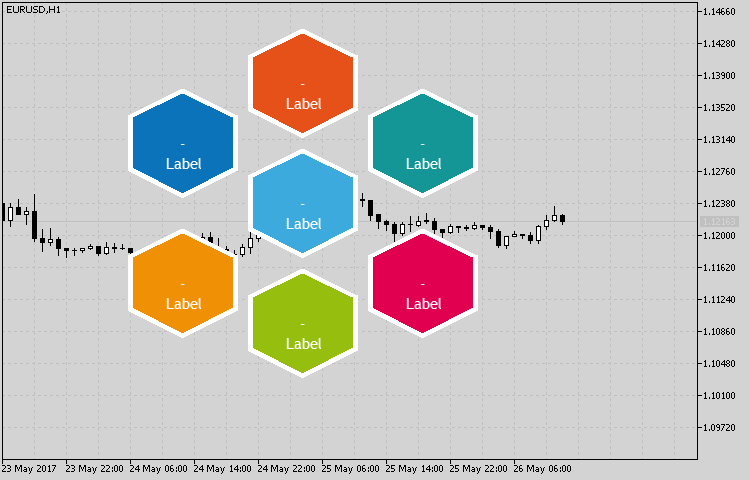
Fig.5. Ejemplo de implementación de un conjunto de indicadores usando la clase CHexagon.


Clase del indicador de pétalo CPetal

En la implementación del indicador en forma de pétalo se necesitan 2-3 primitivas del conjunto de métodos de la clase CCanvas. Se trata del elemento círculo coloreado (método FillCircle()) y, dependiendo de la forma, de 1-2 triángulos coloreados (FillTriangle()). La estructura y el conjunto de elementos se muestran en la figura.6.


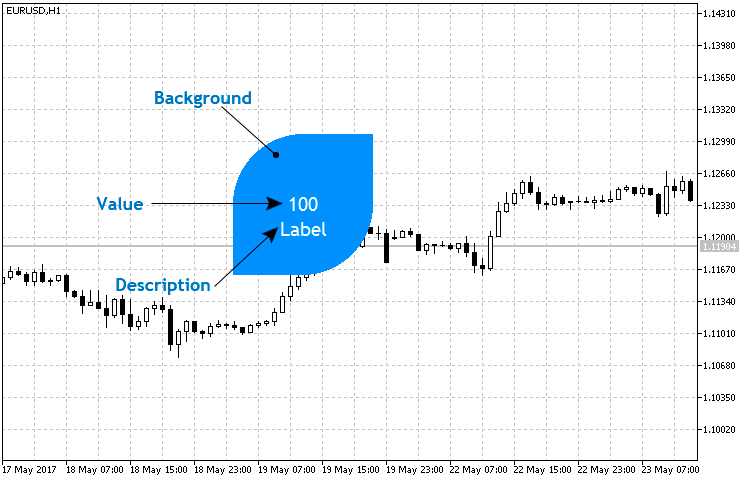
Fig.6. Estructura básica del indicador de pétalo.

Como podemos ver, aquí se usan 2 triángulos, pero nosotros incluiremos en la clase varios tipos de formas con la ayuda de la lista enum. Vamos a ver estos tipos con más detalle:

enum ENUM_POSITION
  {
   TOPRIGHT=1,
   TOPLEFT=2,
   BOTTOMRIGHT=3,
   BOTTOMLEFT=4,
   BOTHRIGHT=5,
   BOTHLEFT=6
  };
  • TOPRIGHT — consta de un círculo y un triángulo, cuyo pico visible está dirigido hacia el ángulo superior derecho.
  • TOPLEFT — consta de un círculo y un triángulo, cuyo pico visible está dirigido hacia el ángulo superior izquierdo.
  • BOTTOMRIGHT — consta de un círculo y un triángulo, cuyo pico visible está dirigido hacia el ángulo inferior derecho.
  • BOTTOMLEFT — consta de un círculo y un triángulo, cuyo pico visible está dirigido hacia el ángulo inferior izquierdo.
  • BOTHRIGHT — consta de un círculo y dos triángulos, en este caso, el triángulo superior se encuentra en la esquina superior derecha.
  • BOTHLEFT— consta de un círculo y dos triángulos, en este caso, el triángulo superior se encuentra en la esquina superior izquierda.


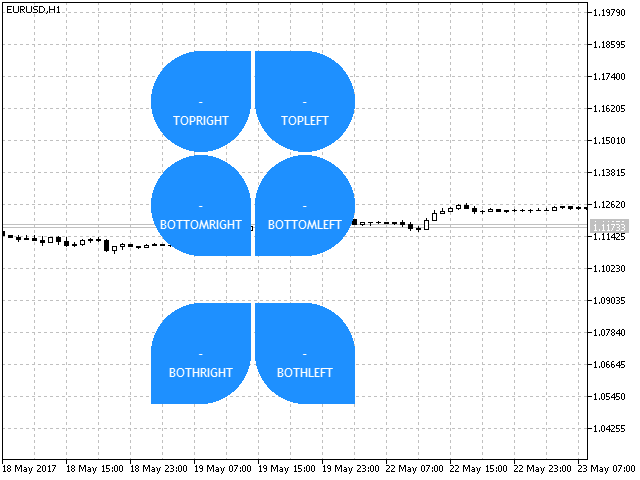
Fig.7. Tipos de forma del indicador de pétalo.

Vamos a pasar a la implementación. Creamos en la carpeta CustomGUI/Indicators el archivo Petal.mqh, y en dicho archivo, creamos la clase СPetal, haciendo básica para ella la clase CCanvasBase creada con anterioridad. Asimismo la incluimos en la lista general, que ahora tendrá el aspecto siguiente:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
#include "Indicators\Petal.mqh"
//+------------------------------------------------------------------+

No vamos a detenernos en las propiedades estándar. Analizaremos los métodos de creación del indicador y las actualizaciones de sus valores. En el método Create() después de construir el círculo coloreado, dependiendo de la propiedad "tipo de forma" vista anteriormente, con la enumeración ENUM_POSITION se dibujan triángulos coloreados en las posiciones indicadas:

//+------------------------------------------------------------------+
//| Crea el indicador                                                |
//+------------------------------------------------------------------+
void CPetal::Create(string name,int x,int y)
  {
   int r=m_radius;
//--- Corrección de la posición del indicadtor con respecto al radio
   x=(x<r)?r:x;
   y=(y<r)?r:y;
   Name(name);
   X(x);
   Y(y);
   XSize(2*r+1);
   YSize(2*r+1);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//---
   m_canvas.FillCircle(r,r,r,ColorToARGB(m_bg_color,m_transparency));
   if(m_orientation==TOPRIGHT)
      m_canvas.FillTriangle(XSize()/2,0,XSize(),0,XSize(),YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==TOPLEFT)
      m_canvas.FillTriangle(0,0,XSize()/2,0,0,YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTTOMRIGHT)
      m_canvas.FillTriangle(XSize(),YSize(),XSize(),YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTTOMLEFT)
      m_canvas.FillTriangle(0,YSize(),0,YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTHRIGHT)
     {
      m_canvas.FillTriangle(XSize()/2,0,XSize(),0,XSize(),YSize()/2,ColorToARGB(m_bg_color,m_transparency));
      m_canvas.FillTriangle(0,YSize(),0,YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
     }
   else if(m_orientation==BOTHLEFT)
     {
      m_canvas.FillTriangle(0,0,XSize()/2,0,0,YSize()/2,ColorToARGB(m_bg_color,m_transparency));
      m_canvas.FillTriangle(XSize(),YSize(),XSize(),YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
     }
//--- Descripción y valores numéricos
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r,r,"-",ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r,r+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.Update();
  }

Como ejemplo, mostraremos la plantilla para crear un indicador en forma de mariposa.

//+------------------------------------------------------------------+
//|                                                          003.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CPetal ind1,ind2,ind3,ind4;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   int b=2;
//---   
   ind1.BgColor(C'230,80,80');
   ind1.Orientation(BOTHLEFT);
   ind1.Create("petal1",200-b,100-b);

   ind2.BgColor(C'35,170,190');
   ind2.Orientation(BOTHRIGHT);
   ind2.Create("petal2",300+b,100-b);

   ind3.BgColor(C'245,155,70');
   ind3.Orientation(BOTHRIGHT);
   ind3.Create("petal3",200-b,200+b);

   ind4.BgColor(C'90,200,130');
   ind4.Orientation(BOTHLEFT);
   ind4.Create("petal4",300+b,200+b);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ind3.Delete();
   ind4.Delete();
  }
//+------------------------------------------------------------------+


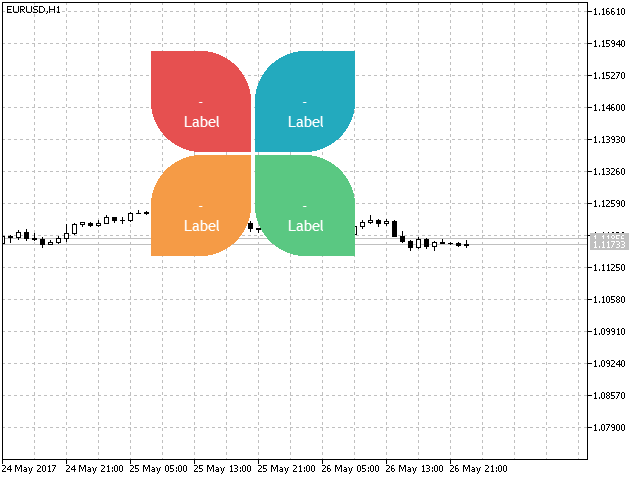
Fig.8. Ejemplo de uso del indicador de pétalo.

Clase del indicador de histograma CHistogram

Al construir la clase del histograma, se ha tomado como base la clase CLIneGraph, para ser más exactos, la estructura general de construcción de los ejes de coordenadas, de las divisiones y de sus valores. Por eso, describir esta etapa resulta excesivo. Nos detendremos con más detalle en los tipos de histograma y en la propia realización con la ayuda de las primitivas de la clase CCanvas. Antes de analizar la implementación del indicador de tipo histograma, vamos a definir los tipos de forma.

enum ENUM_TYPE_HISTOGRAM
  {
   SIMPLE=1,
   TRIANGLE=2,
   RECTANGLE=3
  };
  • SIMPLE — se ha decidido tomar como base de la forma sencilla un histograma en forma de triángulo (fig.10), cuya altura será un valor numérico en el gráfico.
  • TRIANGLE — histograma en forma de triángulo de tipo pseudo-volumen (fig.11).
  • RECTANGLE — aspecto clásico del histograma en forma de columnas (fig.12).


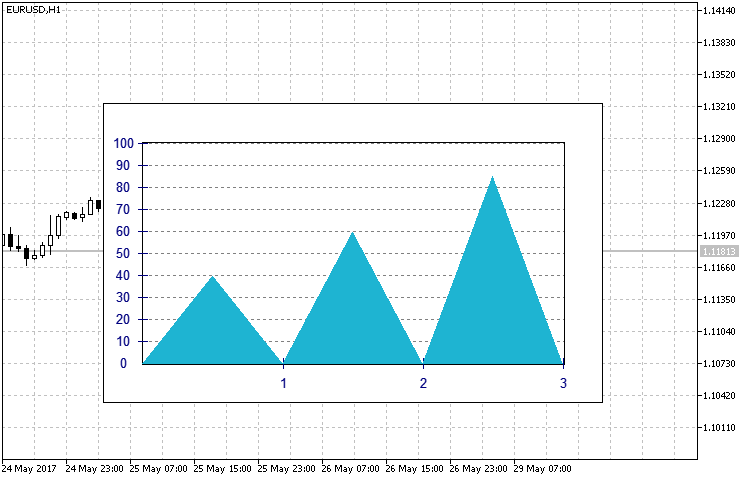
Fig.10. Aspecto simple del histograma del tipo SIMPLE.


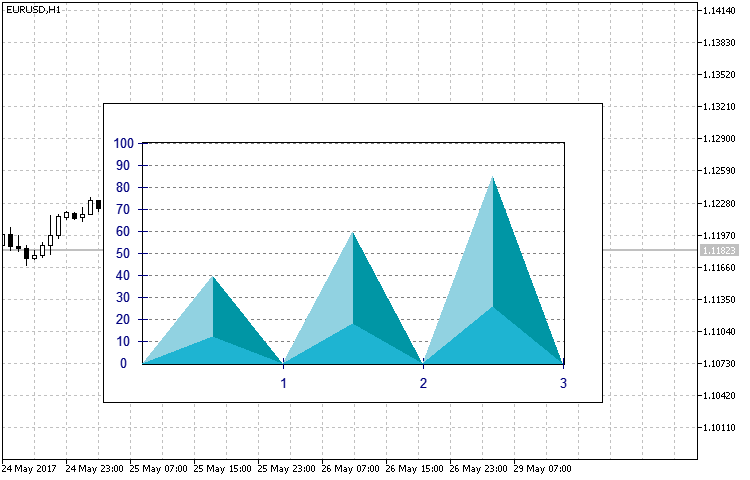
Fig.11. Aspecto del histograma del tipo TRIANGLE.

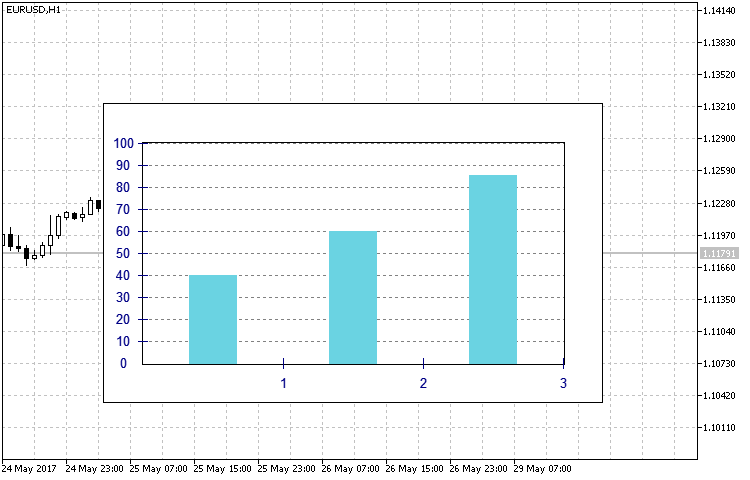
Fig.12. Aspecto del histograma del tipo RECTANGLE.

Creamos en la carpeta CustomGUI/Indicators el archivo Histogram.mqh, y en dicho archivo, creamos la clase СHistogram, haciendo básica para ella la clase CCanvasBase creada con anterioridad. Asimismo, la incluimos en la lista común en el archivo CustomGUI.mqh. La mayoría de los métodos y propiedades de la clase son idénticos a la clase CLineGraph, incluido el método Create(). Por eso, solo analizaremos las diferencias principales, concretamente, el método SetArrayValue().

//+------------------------------------------------------------------+
//| Establece la matriz de datos de entrada                              |
//+------------------------------------------------------------------+
void CHistogram::SetArrayValue(double &data[])
  {
   int x,y,y1,y2;
//--- Crea los marcos del gráfico y el fondo posterior
   m_canvas.FillRectangle(0,0,XSize(),YSize(),ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillRectangle(1,1,XSize()-2,YSize()-2,ColorToARGB(m_bg_color,m_transparency));
//--- Crea los ejes y el fondo del gráfico
   m_canvas.FillRectangle(m_gap-1,m_gap-1,XSize()-m_gap+1,YSize()-m_gap+1,ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillRectangle(m_gap,m_gap,XSize()-m_gap,YSize()-m_gap,ColorToARGB(m_bg_graph_color,m_transparency));
//--- Si el valor máximo en la matriz de datos supera el límite superior del eje Y, escalamos el eje.
   if(data[ArrayMaximum(data)]>m_y_max)
      m_y_max=data[ArrayMaximum(data)];
//--- Crea las divisiones del eje y sus valores
   VerticalScale(m_y_min,m_y_max,m_num_grid);
   HorizontalScale(ArraySize(data));
   ArrayResize(m_label_value,ArraySize(data));
//--- Construye el histograma según la matriz de datos
   for(int i=0;i<ArraySize(data);i++)
     {
      if(data[i]>0)
        {
         x=int(m_x[i]+(m_x[i+1]-m_x[i])/2);
         y=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]);
         y1=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]*0.3);
         y2=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]*0.1);
         y=(y<m_gap)?m_gap:y;
         if(m_type==SIMPLE)
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,m_x[i+1],YSize()-m_gap,x,y,ColorToARGB(m_graph_color1,m_transparency));
         else if(m_type==TRIANGLE)
           {
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,x,y,x,y1,ColorToARGB(m_graph_color1,m_transparency));
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,m_x[i+1],YSize()-m_gap,x,y1,ColorToARGB(m_graph_color2,m_transparency));
            m_canvas.FillTriangle(x,y,x,y1,m_x[i+1],YSize()-m_gap,ColorToARGB(m_graph_color3,m_transparency));
           }
         else if(m_type==RECTANGLE)
           {
            int x1,x2;
            x1=int(m_x[i]+(m_x[i+1]-m_x[i])/3);
            x2=int(m_x[i]+2*(m_x[i+1]-m_x[i])/3);
            m_canvas.FillRectangle(x1,y,x2,YSize()-m_gap,ColorToARGB(m_graph_color1,m_transparency));
           }
         //--- Descripción y valores numéricos
         m_canvas.FontNameSet("Trebuchet MS");
         m_canvas.FontSizeSet(m_value_font_size);
         m_canvas.TextOut(x,y2,DoubleToString(data[i],2),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
         m_canvas.TextOut(x,y-5,m_label_value[i],ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
        }
     }
   m_canvas.Update();
  }

Una diferencia sustancial reside en que en el bloque de construcción del histograma según la matriz de datos indicada, se considera el tipo de histograma ENUM_TYPE_HISTOGRAM, analizado un poco más arriba. Como ejemplo de uso se ha implementado el método de representación visual de tres indicadores RSI con diferentes periodos.

//+------------------------------------------------------------------+
//|                                                          004.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Alexander Fedosov"
#property link      "https://www.mql5.com/ru/users/alex2356"
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//+------------------------------------------------------------------+
//|  Parámetros de entrada del indicador                                    |
//+------------------------------------------------------------------+

input int                  RSIPeriod1=10;        //Period of the indicator1
input int                  RSIPeriod2=14;        //Period of the indicator2
input int                  RSIPeriod3=18;        //Period of the indicator3
input ENUM_TYPE_HISTOGRAM  Type=RECTANGLE;       //Type Histogram
//---
CHistogram ind;
int InpInd_Handle1,InpInd_Handle2,InpInd_Handle3;
double rsi1[],rsi2[],rsi3[],ex[3];
string descr[3];
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---- obteniendo el manejador del indicador
   InpInd_Handle1=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod1,PRICE_CLOSE);
   InpInd_Handle2=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod2,PRICE_CLOSE);
   InpInd_Handle3=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod3,PRICE_CLOSE);
   if(InpInd_Handle1==INVALID_HANDLE ||
      InpInd_Handle2==INVALID_HANDLE ||
      InpInd_Handle3==INVALID_HANDLE
      )
     {
      Print("Failed to get indicator handle");
      return(INIT_FAILED);
     }
//---
   descr[0]="RSI("+IntegerToString(RSIPeriod1)+")";
   descr[1]="RSI("+IntegerToString(RSIPeriod2)+")";
   descr[2]="RSI("+IntegerToString(RSIPeriod3)+")";
   ind.NumGrid(10);
   ind.YMax(100);
   ind.Type(Type);
   ind.Create("rsi",350,250);
   ind.SetArrayLabel(descr);
//---
   ArraySetAsSeries(rsi1,true);
   ArraySetAsSeries(rsi2,true);
   ArraySetAsSeries(rsi3,true);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(CopyBuffer(InpInd_Handle1,0,0,1,rsi1)<=0   ||
      CopyBuffer(InpInd_Handle2,0,0,1,rsi2)<=0   ||
      CopyBuffer(InpInd_Handle3,0,0,1,rsi3)<=0
      )
      return(0);
   ex[0]=rsi1[0];
   ex[1]=rsi2[0];
   ex[2]=rsi3[0];
   ind.SetArrayValue(ex);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind.Delete();
   ChartRedraw();
  }
//+------------------------------------------------------------------+


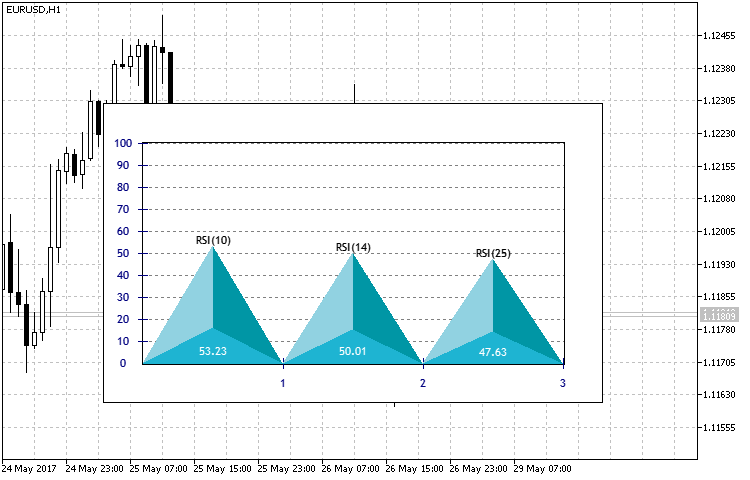
Fig.13. Resultado del funcionamiento del indicador en forma de histograma para tres periodos del indicador RSI.


Clase del indicador de pirámide CPyramid

Ya hemos analizado las clases y los principios de construcción de figuras complejas con la ayuda de primitivas. En la clase de la construcción de indicadores de tipo histograma se ha tocado parcialmente el tema de la construcción de un espacio bidimensional de objetos que parecen estar en 3D (fig.13) gracias a la elección del color. Sin embargo, la pirámide no es una figura plana, por eso, al construirla en el sistema bidimensional indicado, usaremos su proyección isométrica. La estructura básica no se distingue por su gran número de elementos (fig.14), sin embargo, el método de construcción de la proyección de la pirámide y su visualización son la parte principal de la implementación de esta clase.


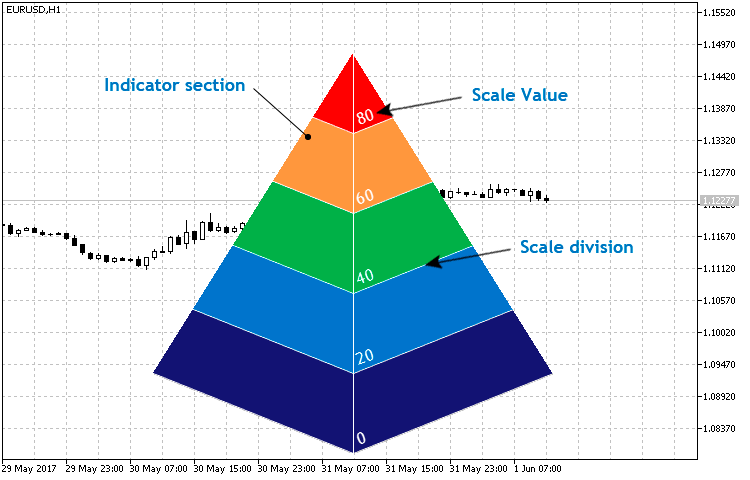
Fig.14. Estructura básica de la clase CPyramid.

Creamos en la carpeta CustomGUI/Indicators el archivo Pyramid.mqh, y en dicho archivo, creamos la clase СPyramid, haciendo básica para ella la clase CCanvasBase creada con anterioridad. Asimismo, la incluimos en la lista común en el archivo CustomGUI.mqh. Ahora la lista común de clases incluidas será de la forma siguiente:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
#include "Indicators\Petal.mqh"
#include "Indicators\Histogram.mqh"
#include "Indicators\Pyramid.mqh"
//+------------------------------------------------------------------+

Podemos familiarizarnos con la lista completa de todas las propiedades en la propia clase, nos detendremos en las más importantes. Antes de analizar los métodos principales Create() y NewValue() nos detendremos en aquellos métodos privados que ya se usan. 

//+------------------------------------------------------------------+
//| Registra en la matriz los coeficientes de la ecuación de la recta de dos puntos |
//+------------------------------------------------------------------+
void CPyramid::Equation(double x1,double y1,double x2,double y2,double &arr[])
  {
   ArrayResize(arr,2);
   arr[0]=(y1-y2)/(x1-x2);
   arr[1]=y2-arr[0]*x2;
  }

El método Equation() sirve para encontrar la ecuación de la recta de dos puntos, en concreto, define los coeficientes k y b para la ecución general y = kx + b de la ecuación canónica de la recta de dos puntos:

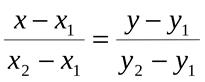
Este método es necesario para definir las ecuaciones de las rectas según los puntos establecidos y, en lo sucesivo, para encontrar los puntos de cruce de las aristas AB y AC de la pirámide y las rectas paralelas a los lados de la base de la pirámide. Las coordenadas de los puntos mostrados en la fig.15 son necesarias para construir triángulos similares a los límites laterales de la pirámide. A su vez, son también secciones de nuestro indicador.

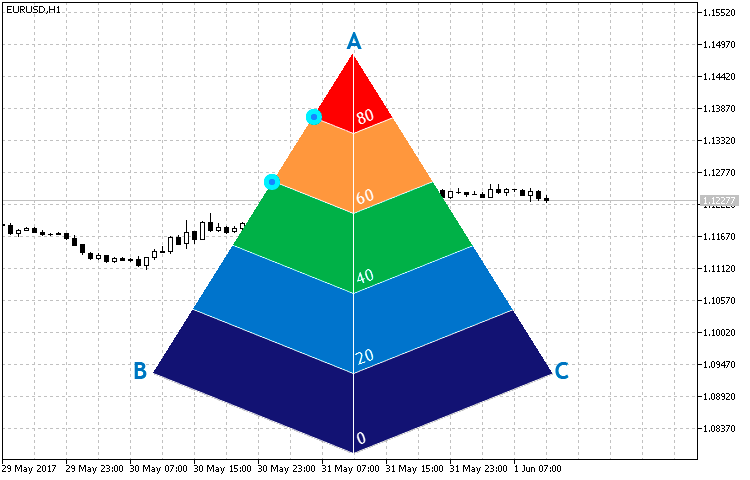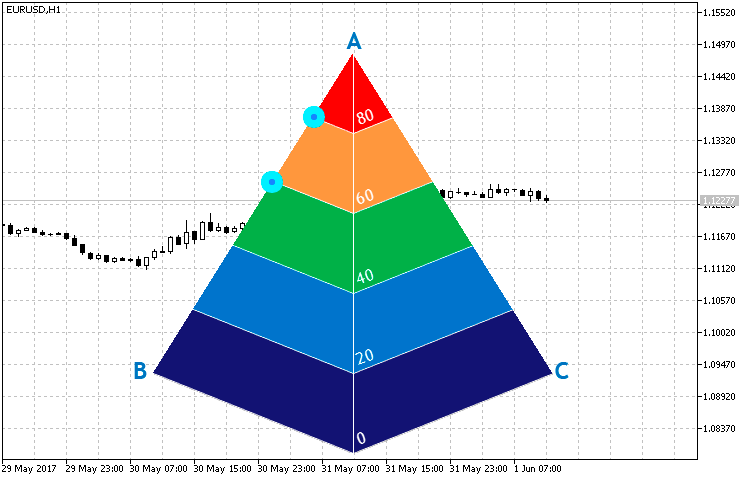
Fig.15. Puntos de cruce de las aristas de la pirámide y las rectas paralelas a los lados de la base de la pirámide.

Conociendo los coeficientes de dos rectas, vamos a calcular las coordenadas del punto de cruce con la ayuda de un sistema de ecuaciones. El método Cross() se encargará de ello:

//+---------------------------------------------------------------------------------+
//| Registra en una matriz las coordenadas del punto de cruce de dos rectas según sus coeficientes |
//+---------------------------------------------------------------------------------+
void CPyramid::Cross(double k1,double b1,double k2,double b2,double &arr[])
  {
   double x,y;
   ArrayResize(arr,2);
   y=(b1*k2-b2*k1)/(k2-k1);
   x=(y-b2)/k2;
   arr[0]=x;
   arr[1]=y;
  }
//+------------------------------------------------------------------+

Ahora que tenemos una idea de las funciones usadas al crear la pirámide, podemos analizar con detalle el método Create().

//+------------------------------------------------------------------+
//| Crea el indicador                                                |
//+------------------------------------------------------------------+
void CPyramid::Create(string name,int x,int y)
  {
   int size=m_size;
//--- Corrección de la posición del indicador con respecto a su tamaño
   x=(x<size/2)?size/2:x;
   y=(y<size/2)?size/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(size);
   YSize(size);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Descripción y valores numéricos
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_font_size);
   m_canvas.FontAngleSet(200);
//--- Encuentra la ecuación de la recta AB
   double x1,x2,y1,y2;
   x1=XSize()/2;y1=0;
   x2=0;y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Construye las secciones izquierdas del indicador
   for(int i=5;i>0;i--)
     {
      //--- Define las ordenadas de dos puntos 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Define las coordenadas del punto de cruce de la arista AB y la recta paralela al lado de la base de la pirámide
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      //--- Construye las divisiones de la escala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
     }
//--- Encuentra la ecuación de la recta AC
   x1=XSize()/2;y1=0;
   x2=XSize();y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Construye las secciones derechas del indicador
   for(int i=5;i>0;i--)
     {
      //--- Define las ordenadas de dos puntos 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Define las coordenadas del punto de cruce de la arista AC y la recta paralela al lado de la base de la pirámide
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1]));
      //--- Construye las divisiones de la escala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
      //--- Construye los valores de la escala
      m_canvas.TextOut(int(x1+2),int(y2+YSize()/6)," - ",ColorToARGB(m_label_color,m_transparency),TA_LEFT|TA_VCENTER);
     }
   m_canvas.LineVertical(XSize()/2,0,YSize(),ColorToARGB(m_scale_color,m_transparency));
   m_canvas.Update();
  }

El algoritmo de construcción de la pirámide es el siguiente:

  • Construimos el lado izquierdo de la pirámide. Se definen las coordenadas de los puntos A y B, se encuentra con ellas la ecuación de la recta.
  • A continuación, en el ciclo encontramos consecutivamente las ecuaciones de las rectas paralelas a los lados de la base de la pirámide y encontramos su punto cruce con la arista AB.
  • Según los puntos encontrados, construimos las secciones y las divisiones de la escala.
  • Construimos el lado derecho de la pirámide de forma análoga.
  • Además de las secciones y divisiones de la escala, en la parte derecha añadimos los valores de la escala.
  • Separación vertical de las dos secciones.

El método de establecimiento y actualización de datos tiene dos argumentos: el valor actual transmitido y el valor máximo. La esencia del método consiste en que, partiendo del valor máximo establecido, se definen los valores umbral. Cuando estos son superados, cada sección cambia de color. Si se supera el valor umbral, la sección se pone del color indicado. De forma análoga, cuando el valor umbral es cruzado hacia abajo, la sección se pone del color establecido a tal efecto. 

//+------------------------------------------------------------------+
//| Establece y actualiza el valor del indicador                    |
//+------------------------------------------------------------------+
void CPyramid::NewValue(double value,double maxvalue)
  {
//---
   double s;
   color col;
//--- Encuentra la ecuación de la recta AB
   double x1,x2,y1,y2;
   x1=XSize()/2;y1=0;
   x2=0;y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Construye las secciones izquierdas del indicador
   for(int i=5;i>0;i--)
     {
      //--- Encuentra los valores de la división de la escala
      s=maxvalue-(i-1)*maxvalue/5;
      //--- Define el color de las secciones
      col=(value>=s)?m_section_color[i-1]:m_bg_color;
      //--- Define las ordenadas de dos puntos 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Define las coordenadas del punto de cruce de la arista AB y la recta paralela al lado de la base de la pirámide
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(col,m_transparency));
      //--- Construye las divisiones de la escala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(clrWhite));
     }
//--- Encuentra la ecuación de la recta AC
   x1=XSize()/2;y1=0;
   x2=XSize();y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Construye las secciones derechas del indicador
   for(int i=5;i>0;i--)
     {
      //--- Encuentra los valores de la división de la escala
      s=maxvalue-(i-1)*maxvalue/5;
      //--- Define el color de las secciones
      col=(value>=s)?m_section_color[i-1]:m_bg_color;
      //--- Define las ordenadas de dos puntos 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Define las coordenadas del punto de cruce de la arista AC y la recta paralela al lado de la base de la pirámide
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(col,m_transparency));
      //--- Construye las divisiones de la escala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
      //--- Construye los valores de la escala
      m_canvas.TextOut(int(x1+2),int(y2+YSize()/6),DoubleToString(s,0),ColorToARGB(m_label_color,m_transparency),TA_LEFT|TA_VCENTER);
     }
   m_canvas.LineVertical(XSize()/2,0,YSize(),ColorToARGB(m_scale_color,m_transparency));
   m_canvas.Update();
  }

A pesar de que la implementación del dibujado del indicador sea más compleja, crear, ajustar y usar el indicador no resulta más complicado que en los casos anteriores. Como pequeño ejemplo, lo usaremos para representar los valores del ADX estándar. En este caso, dependiendo de su ubicación, añadiremos el indicador circular arriba a la izquierda para comparar la representación y hacerla más visual.

//+------------------------------------------------------------------+
//|                                                          005.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Alexander Fedosov"
#property link      "https://www.mql5.com/ru/users/alex2356"
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//+------------------------------------------------------------------+
//|  Parámetros de entrada del indicador                                    |
//+------------------------------------------------------------------+
input int               period=10;                                //ADX Period
input double            maxval=50;                                //Max value
//---
CPyramid ind1;
CCircleSimple ind2;
int InpInd_Handle;
double adx[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---- obtiene el manejador del indicador
   InpInd_Handle=iADX(Symbol(),PERIOD_CURRENT,period);
   if(InpInd_Handle==INVALID_HANDLE)
     {
      Print("Failed to get indicator handle");
      return(INIT_FAILED);
     }
   ArraySetAsSeries(adx,true);
//---
   ind1.Size(250);
   ind1.Create("pyramid",200,0);
//---
   ind2.FontSize(ind1.FontSize());
   ind2.LabelSize(ind1.FontSize());
   ind2.Label("ADX");
   ind2.Radius(30);
   ind2.Create("label",ind1.X()-ind1.Size()/3,ind1.Y()-ind1.Size()/4);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(CopyBuffer(InpInd_Handle,0,0,2,adx)<=0)
      return(0);
   ind1.NewValue(adx[0],maxval);
   ind2.NewValue(adx[0]);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ChartRedraw();
  }
//+------------------------------------------------------------------+

Como se ve en la fig. 16, el indicador circular representa el valor por encima del tercer valor umbral 30, por eso se han coloreado tres secciones. Todo ello teniendo en cuenta el valor máximo actual, que en este caso se ha establecido en 50.

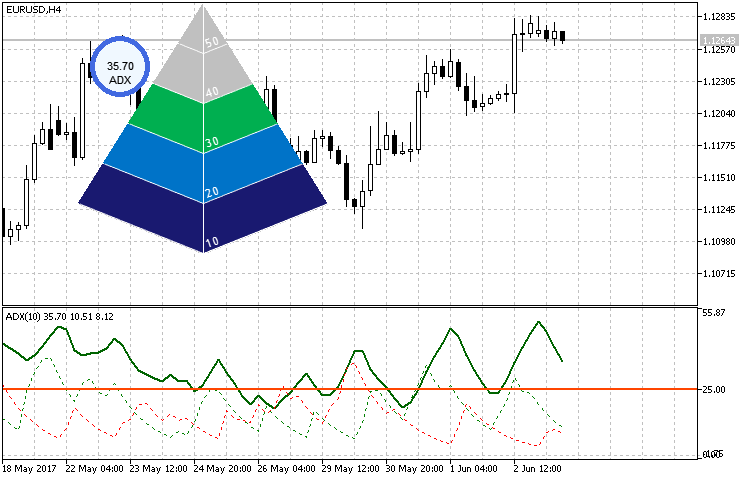
Fig.16. Ejemplo de uso del indicador en forma de pirámide.

Conclusión

Como podemos ver por las implementaciones de la clase CCanvas analizadas en este artículo, las posibilidades de la biblioteca en el plano gráfico son muy amplias. Los tipos y métodos de representación de este tipo de indicadores solo están limitados por nuestra propia imaginación. Además, la creación y organización de estos indicadores en forma de biblioteca de clases a incluir no necesita de esfuerzos o conocimientos especiales.

Al final del artículo se adjunta un directorio con todos los archivos usados en el artículo, clasificados por carpetas. Por eso, para que funcione correctamente, basta con colocar la carpeta MQL5 del directorio en la carpeta raíz del terminal. 

Programas incluidos en el directorio, y utilizados en el artículo:

#
  Nombre
 Tipo
 Descripción
1
 CanvasBase.mqh Biblioteca  Clase básica de gráficos personalizados
2
 CustomGUI.mqh Biblioteca  Archivo con la lista de inclusión de todas las clases de la biblioteca 
3 CircleArc.mqh Biblioteca  Contiene la clase del indicador circular con indicación en arco CCircleArc
4 CircleSection.mqh Biblioteca  Contiene la clase del indicador circular con indicación de secciones en arco CCircleSection
5 CircleSimple.mqh Biblioteca  Contiene la clase del indicador circular simple CCircleSimle
6  LineGraph.mqh Biblioteca  Contiene la clase del gráfico lineal CLineGraph
7 LineRounded.mqh  Biblioteca   Contiene la clase del indicador lineal redondeado CLineRounded
 8 Hexagon.mqh  Biblioteca   Contiene la clase del indicador hexagonal CHexagon
 9 Petal.mqh  Biblioteca   Contiene la clase del indicador de pétalo CPetal
 10 Histogram.mqh  Biblioteca   Contiene la clase del indicador de histograma CHistogram
 11 Pyramid.mqh  Biblioteca   Contiene la clase del indicador de pirámide CPyramid
12 CLineRounded.mq5 Indicador  Ejemplo de implementación de la clase CLineRounded
13 CHexagon.mq5 Indicador  Ejemplo de implementación de la clase CHexagon
14 CPetal.mq5 Indicador  Ejemplo de implementación de la clase CPetal
 15 CHistogram.mq5 Indicador  Ejemplo de implementación de la clase CHistogram
 16 CPyramid.mq5  Indicador   Ejemplo de implementación de la clase CPyramid

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/3298

Archivos adjuntos |
Descargar ZIP
MQL5.zip (29.49 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Últimos comentarios | Pasar a la discusión en el foro de los operadores (1)
manumanos
manumanos | 22 ago. 2017 en 10:54

Se lo ve interesante, me lo guardo para leerlo más tarde, un saludo 

Optimización Walk-Forward en MetaTrader 5 con sus propias manos Optimización Walk-Forward en MetaTrader 5 con sus propias manos
En este artículo se consideran las técnicas que permiten emular con precisión la optimización walk-forward a través del Probador incorporado y librerías auxiliares implementadas en MQL.
Interfaces gráficas XI: Controles dibujados (build 14.2) Interfaces gráficas XI: Controles dibujados (build 14.2)
En la nueva versión de la librería, todos los controles van a dibujarse en los objetos gráficos separados tipo OBJ_BITMAP_LABEL. Además, seguiremos describiendo la optimización del código: es decir, analizaremos los cambios en las clases que representan el núcleo de la librería.
Patrones disponibles al comerciar con cestas de divisas. Parte III Patrones disponibles al comerciar con cestas de divisas. Parte III
Este es el artículo final dedicado a los patrones que aparecen al comerciar con cestas de parejas de divisas. Se han analizado varios indicadores combinados de tendencia, así como la aplicación de las construcciones gráficas habituales.
Métodos de ordenamiento y su visualización a través de MQL5 Métodos de ordenamiento y su visualización a través de MQL5
Para trabajar con la gráfica, en MQL5 ha sido creada una librería especial— Graphic.mqh. El ejemplo de su aplicación práctica se describe en este artículo y se explica la esencia de los ordenamientos. Existe por lo menos un artículo separado para cada tipo de ordenamiento, y para algunos de ellos ya has sido publicadas las investigaciones completas, por eso aquí se describe sólo la idea general.