MetaTrader 5 / Beispiele
English Русский 中文 Español 日本語 Português
Die benutzerdefinierten Indikatoren und die Informationsgrafik in CCanvas

Die benutzerdefinierten Indikatoren und die Informationsgrafik in CCanvas

MetaTrader 5 — Beispiele | 21 Juni 2017, 09:08
622 0
Alexander Fedosov
Alexander Fedosov

Inhalt

Einführung

Im vorhergehenden Artikel betrachteten wir die Prinzipien des Aufbaues der graphischen Indikatoren unter Verwendung der Erstellungsmethoden der einfachen Ringpuffer der Klasse CCanvas. Aber damit werden die Möglichkeiten der Bibliothek-Verwendung des Benutzer-Charts nicht beschränkt, deshalb biete ich an, die neuen Arten der Indikatoren zu betrachten, die eine kompliziertere strukturelle Realisierung haben. Zu alledem werden wir versuchen, die pseudoräumlichen Typen der Indikatoren und eine dynamisch ändernden Informationsgrafik zu erstellen.

Die Klasse des abgerundeten linearen Indikators CLineRounded

Für die Realisierung der graphischen Objekte in diesem Artikel habe ich nicht angefangen, eine allgemeine Struktur der grundlegenden Klassen zu erstellen — wir verwenden die fertige Bibliothek CustomGUI, die in dem vorhergehenden Artikel beschrieben wurde. Insbesondere wird als die grundlegende Klasse, die Klasse CCanvasBase sein, und die weiter entwickelten Klassen werden die Liste in der Datei CustomGUI.mqh ergänzen.

Für die Erstellung des einfachen linearen Indikators werden wir seine Struktur und die grundlegenden Elementen klarstellen. Auf der Abb.1 wurden die Elemente dargestellt, die man unter Anwendung dieser Indikatorart steuern kann. Wir bemerken jedoch, dass sie keine einfachen Elemente sind. 


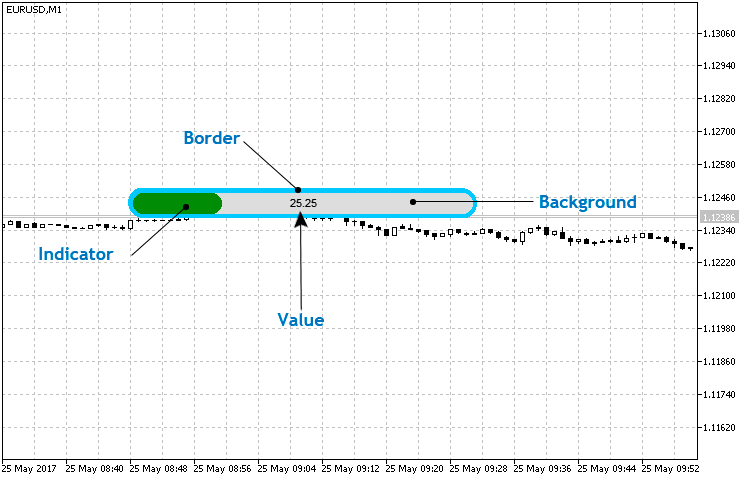
in Abb.1. Die Grundlegende Struktur des einfachen linearen Indikators.

Das einfache (grundlegende) Element ist in diesem Fall dieses Element, welches von den Methoden der Klasse CCanvas realisiert wird. Zum Beispiel, im linearen Indikator ist das einfache Element nur der Wert, da er mit Hilfe der Methode CCanvas::TextOut() realisiert wurde. Drei Andere nach ihrer Form sind identisch und bestehen aus drei grundlegenden Figuren — zwei gefärbten Kreise (die Realisierung CCanvas:: FillCircle()) und das Rechteck (CCanvas:: FillRectangle()).

Wir erstellen im Ordner CustomGUI/Indicators die Datei LineRounded.mqh, und darin — die Klasse СLineRounded und stellen es für die vorher erstellten Klasse CCanvasBase als die grundlegende Klasse win.

//+------------------------------------------------------------------+
//|                                                  LineRounded.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#include "..\CanvasBase.mqh"
//+------------------------------------------------------------------+
//| der abgerundete lineare Indikator                                |
//+------------------------------------------------------------------+
class CLineRounded : public CCanvasBase

Auch ihn fügen wir zur Listein der Date CustomGUI.mqh, der einen schnellen Zugang auf alle Klassen der Bibliothek gewährleistet. Mit der Berücksichtigung auf den früher entwickelten Klassen wird sein Code so aussehen:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
//+------------------------------------------------------------------+

Die volle Liste der Eigenschaften und der Methoden der Klasse СLineRounded kann man in der Datei CustomGUI/Indicators/LineRounded.mqh erfahren. Wir werden uns auf die Methoden der Indikatorserstellung konzentrieren, auf seine Setzung und Erneuerung seiner Werte. Wie es höher gesagt wurde, wird der Indikator aus den Komponenten bestehen. Im Listing unten wurden die Realisierungen dieser Elemente in den separaten Blöcken kommentiert.

//+------------------------------------------------------------------+
//| Er erstellt den Indikator                                        |
//+------------------------------------------------------------------+
void CLineRounded::Create(string name,int x,int y)
  {
//--- Die Korrektion des Standortes des Indikators von den Koordinatenachsen
   x=(x<m_x_size/2)?m_x_size/2:x;
   y=(y<m_y_size/2)?m_y_size/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(m_x_size);
   YSize(m_y_size);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Der Rahmen
   m_canvas.FillRectangle(YSize()/2,0,XSize()-YSize()/2,YSize(),ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2-1,YSize()/2,ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2-1,YSize()/2,YSize()/2,ColorToARGB(m_border_color,m_transparency));
//--- Der Hintergrund
   m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.Update();
  }

Wie man es sehen kann, wurden der Rahmen und der Hintergrund unter Verwendung zwei Methoden realisiert. Vergessen Sie nicht, dass diese Objekte die Schichten sind und werden durch das Auflegen aufeinander gezeichnet. Deshalb zeichnen wir erstmal den Rahmen und dann auf ihn - den Hintergrund einer kleineren Größe, das Skala des Indikators und den Zahlenwert.

Wir betrachten die Methode CLineRounded::NewValue(). 

//+------------------------------------------------------------------+
//| Er setzt und erneut den Wert des Indikators                      |
//+------------------------------------------------------------------+
void CLineRounded::NewValue(double value,double maxvalue,int digits=0)
  {
   int v;
   v=int((XSize()-YSize()/2)/maxvalue*value);

//--- Der Hintergrund
   m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_bg_color,m_transparency));
//--- Skala
   if(v>=YSize()/2 && v<=(XSize()-YSize()/2))
     {
      m_canvas.FillRectangle(YSize()/2,m_border,v,YSize()-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(v,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
     }
   else if(v>(XSize()-YSize()/2))
     {
      m_canvas.FillRectangle(YSize()/2,m_border,XSize()-YSize()/2,YSize()-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
      m_canvas.FillCircle(XSize()-YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));
     }
   else if(v>0 && v<YSize()/2)
      m_canvas.FillCircle(YSize()/2,YSize()/2,YSize()/2-m_border,ColorToARGB(m_scale_color,m_transparency));

//--- Der Zahlenwert
   m_canvas.FontSizeSet(m_font_size);
   m_canvas.TextOut(XSize()/2,YSize()/2,DoubleToString(value,digits),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.Update();
  }
//+------------------------------------------------------------------+
Wie man es sehen kann, am Anfang der Methode wieder einen Realisierungsblock des Hintergrunds gibt. Wozu braucht man das? Erinnern uns an die schichtweise Zeichnung der Elemente, mit Hilfe der konsequenten Anwendung der entsprechenden Methoden. Das heißt, in diesem Fall zeichnen wir zuerst den Hintergrund der Skala, und auf ihr — den Indikator, dessen Länge vom maximalen Wert des Parameters bestimmt wird. Wenn ein neuer Wert des Indikators kommt, wird zuerst die Schicht mit dem Hintergrund umgezeichnet, und dann, schon darauf — die Skala mit der neuen Länge.

Die Erstellung und die Sendung des Wertes in den Indikator werden sehr einfach realisiert. Im Listing unten sehen Sie zwei Indikatoren mit den kleinen Einstellungen und welche sich nur davon unterscheiden, dass bei einem von ihnen der maximale Wert zweimal mehr ist. 

//+------------------------------------------------------------------+
//|                                                          001.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CLineRounded ind1,ind2;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   ind1.XSizeInd(350);
   ind1.YSizeInd(30);
   ind1.Create("line1",300,100);
//---
   ind2.XSizeInd(350);
   ind2.YSizeInd(30);
   ind2.ScaleColor(clrFireBrick);
   ind2.Create("line2",300,150);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ind1.NewValue(50,100,2);
   ind2.NewValue(50,200,2);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
  }
//+------------------------------------------------------------------+

Auf der Abb. 2 ist es sehr gut sichtbar, dass bei den identischen Werten und verschiedenen Maßstäben das Maß der Skala des Indikators einen entsprechenden Wert hat Der Wert 50 und die maximalen (100 für Ersten und 200 für Zweiten) wurden so gewählt, dass man das Ergebnis der Abbildung sogar visuell bewerten kann.

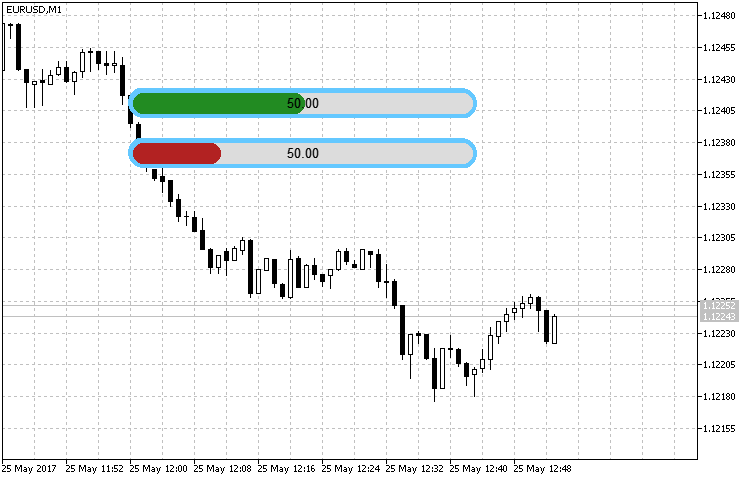
in Abb.2. Das Beispiel der Arbeit des abgerundeten linearen Indikators.


Die Klasse des sechseckigen Indikators CHexagon

Für den Aufbau des Indikators in Form vom richtigen Sechseck mit Hilfe der von der Klasse CCanvas gegebenen Ringpuffer können die folgenden Arten ausgewählt werden. Es können sowohl die Aufbaus der Halbe-Linie, als auch das nachfolgende Färben des Gebietes, und "die Montage" von sechs gleichseitigen Dreiecken, in der Art der Pizza-Stückchen. Aber unser Ziel — die maximale Einfachheit für das Verständnis. Deshalb werden wir das richtige Sechseck aus drei Ringpuffern sammeln — aus einem Rechteck und zwei gleichschenkligen Dreiecken.


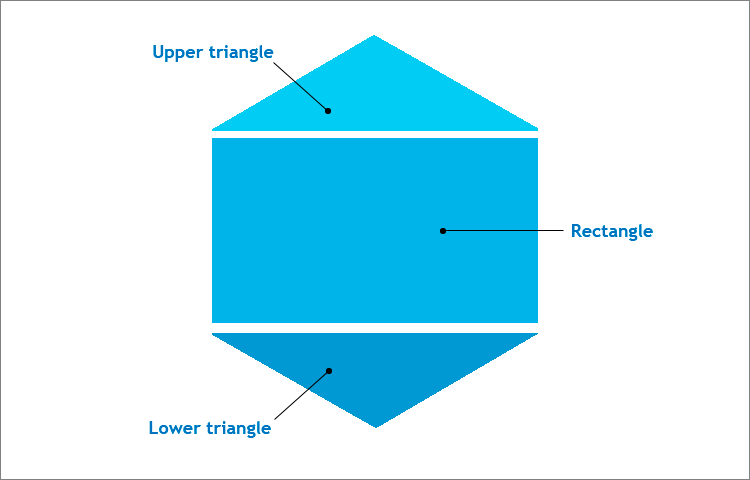
in Abb.3. Die Struktur des richtigen Sechseckes.

Das richtige Sechseck wird in die quadratische Leinwand geschrieben. Dabei muss man sich an die Eigenschaft dieser Figur erinnern, und zwar:

  • Die Seite des richtigen Sechseckes ist dem Radius des neben ihm beschriebenen Kreises gleich, oder in unserem Fall — der Hälfte der Seite der Leinwand. Es wird bei dem Aufbau des Rechteckes gefordert.
  • Der Winkel des Sechseckes ist 120 Grad gleich, deshalb werden die Winkel bei der Basis der gleichschenkligen Dreiecke 30 Grad. Diese Informationen sind für die Bestimmung der Höhe des Dreieckes nötig und entsprechend, und um die Koordinaten der Basispunkte der Dreiecke unter Anwendung der Methode CCanvas:: FillTriangle() zu finden.

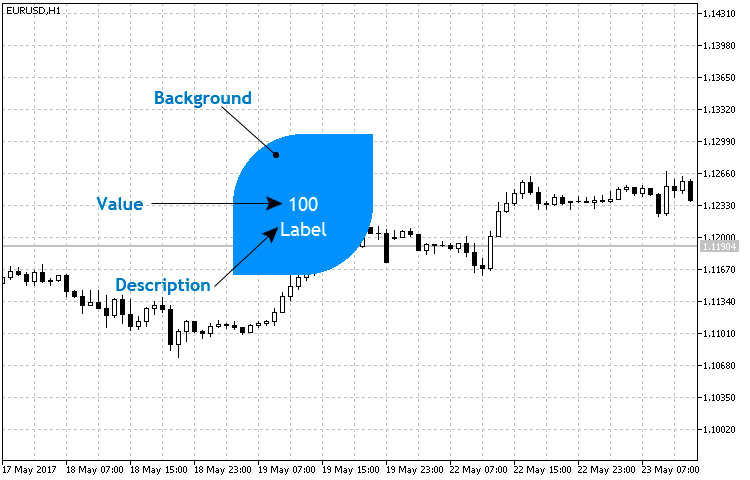
Die grundlegende Struktur des Indikators ist ziemlich einfach, außer dem Sechseck gehört dazu 2 Textobjekte — der numerische Wert und die Beschreibung (die Abb.4).


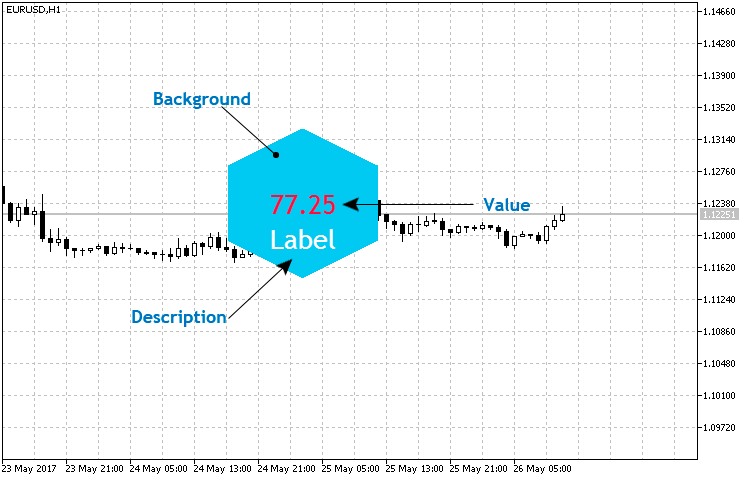
in Abb.4. Die Grundlegende Struktur des sechseckigen Indikators.

Wir erstellen im Ordner CustomGUI/Indicators die Datei Hexagon.mqh, und darin — die Klasse СHexagon und stellen es für sie die vorher erstellten Klasse CCanvasBase als Grundlegende. Wir fügen ihn zur allgemeinen Liste hinzu:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
//+------------------------------------------------------------------+

Die allgemeine Liste der Eigenschaften und Methoden kann man in der Datei erfahren, die höher erstellt wurde. Wir betrachten nur die Methoden, die für die Visualisierung des Indikators verantwortlich sind. 

//+------------------------------------------------------------------+
//| Er erstellt den Indikator                                        |
//+------------------------------------------------------------------+
void CHexagon::Create(string name,int x,int y)
  {
   int a,r;
   r=m_size;
//--- Die Korrektion des Standortes des Indikators von den Koordinatenachsen 
   x=(x<r/2)?r/2:x;
   y=(y<r/2)?r/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(r);
   YSize(r);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Die Berechnung der Höhe des Dreiecks
   a=int(YSize()/2*MathSin(30*M_PI/180));
//--- Die sechseckige Form
   m_canvas.FillTriangle(XSize()/2,0,0,a,XSize(),a,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillRectangle(0,a,XSize(),a+YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillTriangle(0,a+YSize()/2,XSize(),a+YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
//--- Die Beschreibung und der Zahlenwert
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r/2,r/2,"-",ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r/2,r/2+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
//---
   m_canvas.Update();
  }

In der Methode Create() der Variabel a wird der Wert der Höhe der gleichschenkligen Dreiecken verliehen, d.h. eigentlich, auf diese Weise finden wir die Koordinaten der Punkte des Dreieckes nach der Ordinatenachse (Y). Der Unterschied zwischen der Methode der Sendung und der Erneuerung des Zahlenwertes liegt nur daran, dass ins Textobjekt, welches für das Abzeichen des Zahlenwertes verantwortlich ist, der Wert des Argumentes gegeben wird value:

//+------------------------------------------------------------------+
//| Er setzt und erneut den Wert des Indikators                      |
//+------------------------------------------------------------------+
void CHexagon::NewValue(double value,int digits=2)
  {
   int a,r;
   r=m_size;
//--- Die Berechnung der Höhe des Dreiecks
   a=int(YSize()/2*MathSin(30*M_PI/180));
//--- Die sechseckige Form
   m_canvas.FillTriangle(XSize()/2,0,0,a,XSize(),a,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillRectangle(0,a,XSize(),a+YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   m_canvas.FillTriangle(0,a+YSize()/2,XSize(),a+YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
//--- Text
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r/2,r/2,DoubleToString(value,digits),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r/2,r/2+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
//---
   m_canvas.Update();
  }
//+------------------------------------------------------------------+

Als Beispiel realisieren wir den kleinen Satz aus den Indikatoren des sechseckigen Typs:

//+------------------------------------------------------------------+
//|                                                          002.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CHexagon ind1,ind2,ind3,ind4,ind5,ind6,ind7,ind8,ind9,ind10,ind11,ind12,ind13,ind14;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---   
   ind1.BgColor(clrWhite);
   ind1.Size(110);
   ind1.Create("hex1",300,200);
   ind2.BgColor(C'60,170,220');
   ind2.Create("hex2",300,200);
//---
   ind3.BgColor(clrWhite);
   ind3.Size(110);
   ind3.Create("hex3",300,80);
   ind4.BgColor(C'230,80,25');
   ind4.Create("hex4",300,80);
//---
   ind5.BgColor(clrWhite);
   ind5.Size(110);
   ind5.Create("hex5",300,320);
   ind6.BgColor(C'150,190,15');
   ind6.Create("hex6",300,320);
//---
   ind7.BgColor(clrWhite);
   ind7.Size(110);
   ind7.Create("hex7",180,140);
   ind8.BgColor(C'10,115,185');
   ind8.Create("hex8",180,140);
//---
   ind9.BgColor(clrWhite);
   ind9.Size(110);
   ind9.Create("hex9",420,140);
   ind10.BgColor(C'20,150,150');
   ind10.Create("hex10",420,140);
//---
   ind11.BgColor(clrWhite);
   ind11.Size(110);
   ind11.Create("hex11",420,280);
   ind12.BgColor(C'225,0,80');
   ind12.Create("hex12",420,280);
//---
   ind13.BgColor(clrWhite);
   ind13.Size(110);
   ind13.Create("hex13",180,280);
   ind14.BgColor(C'240,145,5');
   ind14.Create("hex14",180,280);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ind3.Delete();
   ind4.Delete();
   ind5.Delete();
   ind6.Delete();
   ind7.Delete();
   ind8.Delete();
   ind9.Delete();
   ind10.Delete();
   ind11.Delete();
   ind12.Delete();
   ind13.Delete();
   ind14.Delete();
  }
//+------------------------------------------------------------------+

Das Ergebnis der Arbeit ist auf der Abb.5. dargestellt Dieses grundlegende Muster ist es sehr einfach, um zu ändern und einzustellen. 

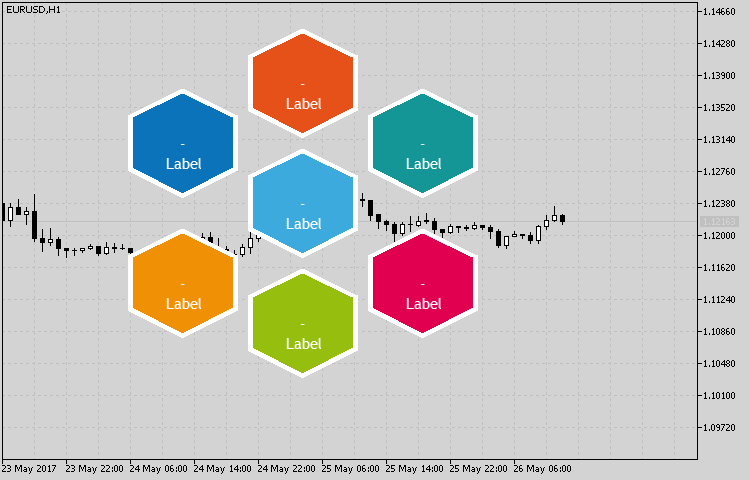
in Abb.5. Das Beispiel der Realisierung des Satzes der Indikatoren unter Verwendung der Klasse CHexagon.


Die Klasse des blätternden Indikators CPetal

In der Realisierung des Indikators in Form vom Blatt werden 2-3 Ringpuffer aus dem Satz der Methoden der Klasse CCanvas gefordert. Es ist das Element, welches in Form eines gefärbten Kreises (der Methode FillCircle () )aussieht und, je nach der Form, 1-2 gefärbter Dreiecke ( FillTriangle () ). Die Struktur und der Satz der Elemente wurden auf der Abb.6 dargestellt.


in Abb.6. Die Grundlegende Struktur des blätternden Indikators.

Wie man es sehen kann, werden hier 2 Dreiecke verwendet, aber wir werden zur Klasse einige Arten der Formen mit Hilfe der Aufzählung enum hinzufügen. Lassen Sie uns den Code gründlicher betrachten:

enum ENUM_POSITION
  {
   TOPRIGHT=1,
   TOPLEFT=2,
   BOTTOMRIGHT=3,
   BOTTOMLEFT=4,
   BOTHRIGHT=5,
   BOTHLEFT=6
  };
  • TOPRIGHT — Es besteht aus dem Kreis und dem Dreieck, dessen sichtbarer Spitze an den ober rechten Winkel gerichtet ist.
  • TOPLEFT — Es besteht aus dem Kreis und dem Dreieck, dessen sichtbarer Spitze an den ober linken Winkel gerichtet ist.
  • BOTTOMRIGHT — Es besteht aus dem Kreis und dem Dreieck, dessen sichtbarer Spitze an den untere rechten Winkel gerichtet ist.
  • BOTTOMLEFT — Es besteht aus dem Kreis und dem Dreieck, dessen sichtbarer Spitze an den untere linken Winkel gerichtet ist.
  • BOTHRIGHT — Es besteht aus dem Kreis und zwei Dreiecken, das obere Dreieck befindet sich im rechten oberen Winkel.
  • BOTHLEFT— Es besteht aus dem Kreis und zwei Dreiecken, das obere Dreieck befindet sich im linken oberen Winkel.


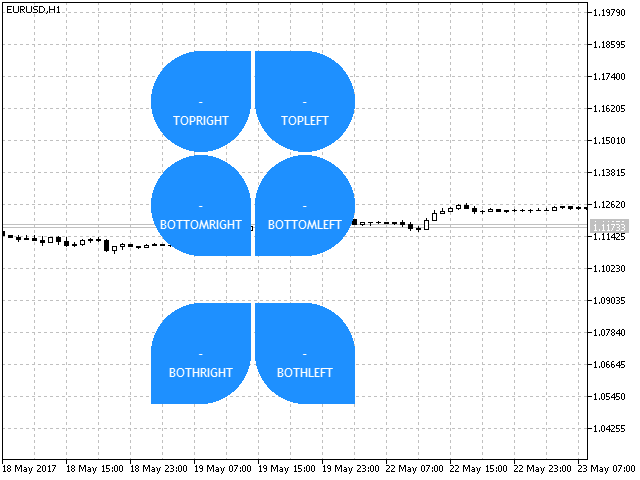
in Abb.7. Die Aussicht der Formen des blätternden Indikators.

Also, fangen wir an, zu realisieren. Wir erstellen im Ordner CustomGUI/Indicators die Datei Petal.mqh, und darin — die Klasse СPetal und stellen es für sie die vorher erstellten Klasse CCanvasBase als Grundlegende. Auch werden wir es zur allgemeinen Liste hinzufügen, die jetzt so aussehen wird:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
#include "Indicators\Petal.mqh"
//+------------------------------------------------------------------+

Wir halten uns nicht bei den Standardeigenschaften auf. Betrachten wir die Methoden der Erstellung des Indikators und der Erneuerung seiner Werte. In der Methode Create() nach dem Aufbau des gefärbten Kreises, je nach früher betrachten Eigenschaft "die Aussicht der Form", mit der Aufzählung ENUM_POSITION wird die gefärbten Dreiecke in den gegebenen Positionen gezeichnet:

//+------------------------------------------------------------------+
//| Er erstellt den Indikator                                        |
//+------------------------------------------------------------------+
void CPetal::Create(string name,int x,int y)
  {
   int r=m_radius;
//--- Die Korrektion des Standortes des Indikators vom Radius
   x=(x<r)?r:x;
   y=(y<r)?r:y;
   Name(name);
   X(x);
   Y(y);
   XSize(2*r+1);
   YSize(2*r+1);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//---
   m_canvas.FillCircle(r,r,r,ColorToARGB(m_bg_color,m_transparency));
   if(m_orientation==TOPRIGHT)
      m_canvas.FillTriangle(XSize()/2,0,XSize(),0,XSize(),YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==TOPLEFT)
      m_canvas.FillTriangle(0,0,XSize()/2,0,0,YSize()/2,ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTTOMRIGHT)
      m_canvas.FillTriangle(XSize(),YSize(),XSize(),YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTTOMLEFT)
      m_canvas.FillTriangle(0,YSize(),0,YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
   else if(m_orientation==BOTHRIGHT)
     {
      m_canvas.FillTriangle(XSize()/2,0,XSize(),0,XSize(),YSize()/2,ColorToARGB(m_bg_color,m_transparency));
      m_canvas.FillTriangle(0,YSize(),0,YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
     }
   else if(m_orientation==BOTHLEFT)
     {
      m_canvas.FillTriangle(0,0,XSize()/2,0,0,YSize()/2,ColorToARGB(m_bg_color,m_transparency));
      m_canvas.FillTriangle(XSize(),YSize(),XSize(),YSize()/2,XSize()/2,YSize(),ColorToARGB(m_bg_color,m_transparency));
     }
//--- Die Beschreibung und der Zahlenwert
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_value_font_size);
   m_canvas.TextOut(r,r,"-",ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.FontSizeSet(m_label_font_size);
   m_canvas.TextOut(r,r+m_value_font_size,m_label_value,ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
   m_canvas.Update();
  }

Als Beispiel werden wir die Muster für die Erstellung des Indikators in Form vom Schmetterling aufführen.

//+------------------------------------------------------------------+
//|                                                          003.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//---
CPetal ind1,ind2,ind3,ind4;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   int b=2;
//---   
   ind1.BgColor(C'230,80,80');
   ind1.Orientation(BOTHLEFT);
   ind1.Create("petal1",200-b,100-b);

   ind2.BgColor(C'35,170,190');
   ind2.Orientation(BOTHRIGHT);
   ind2.Create("petal2",300+b,100-b);

   ind3.BgColor(C'245,155,70');
   ind3.Orientation(BOTHRIGHT);
   ind3.Create("petal3",200-b,200+b);

   ind4.BgColor(C'90,200,130');
   ind4.Orientation(BOTHLEFT);
   ind4.Create("petal4",300+b,200+b);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ind3.Delete();
   ind4.Delete();
  }
//+------------------------------------------------------------------+


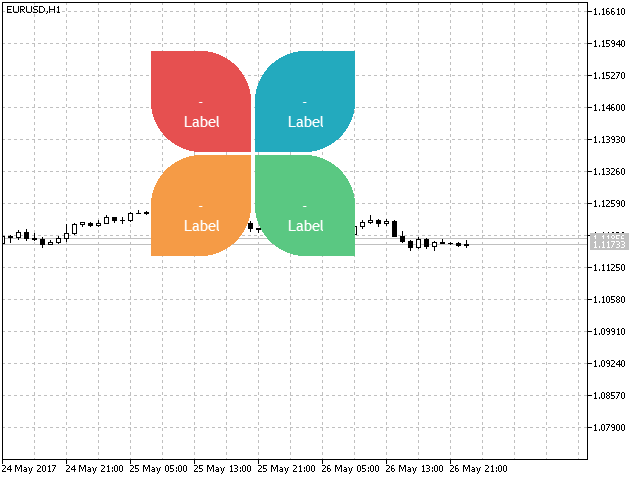
in Abb.8. Das Beispiel der Verwendung des blätternden Indikators.

Die Klasse des Indikators, das Histogramm CHistogram

Bei dem Aufbau der Klasse der Histogramme als die Grundlage wurde die Klasse CLIneGraph genommen, und genauer gesagt — die allgemeine Struktur des Aufbaus der Koordinatenachsen, der Teilungen der Achse und ihrer Werte. Deshalb ist es noch früh, diese Stufe zu beschreiben. Wir betrachten mehr die Arten der Histogramme und der Realisierung mit Hilfe der Ringpuffer der Klasse CCanvas. Bevor wir die Realisierung des Indikators eines Histogramm-Typs betrachten, werden wir die Arten der Formen feststellen.

enum ENUM_TYPE_HISTOGRAM
  {
   SIMPLE=1,
   TRIANGLE=2,
   RECTANGLE=3
  };
  • SIMPLE — als die Grundlage der einfachen Form wurde es entschieden, das Histogramm in Form vom Dreieck (die Abb.10) zu nehmen, dessen Höhe ein Zahlenwert auf dem Chart sein wird.
  • TRIANGLE — das Histogramm in Form vom Dreieck des pseudoräumlichen Typs (die Abb.11).
  • RECTANGLE — die klassische Aussicht des Histogramms in Form von Spalten (die Abb.12).


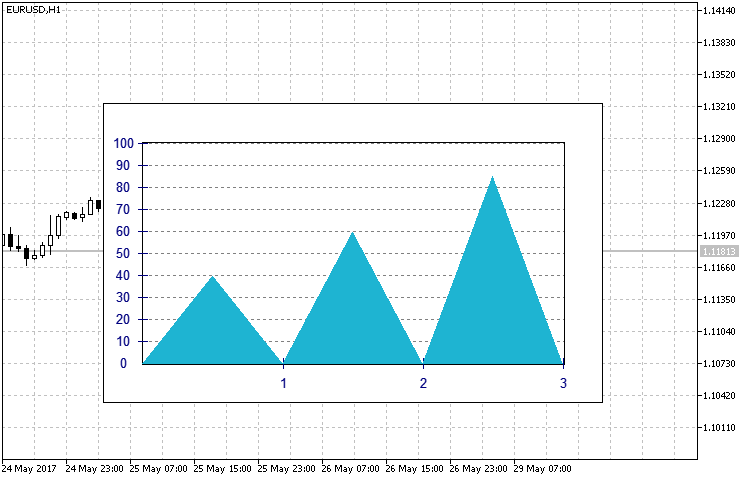
in Abb.10. Die Aussicht des Histogramms des Typs SIMPLE.


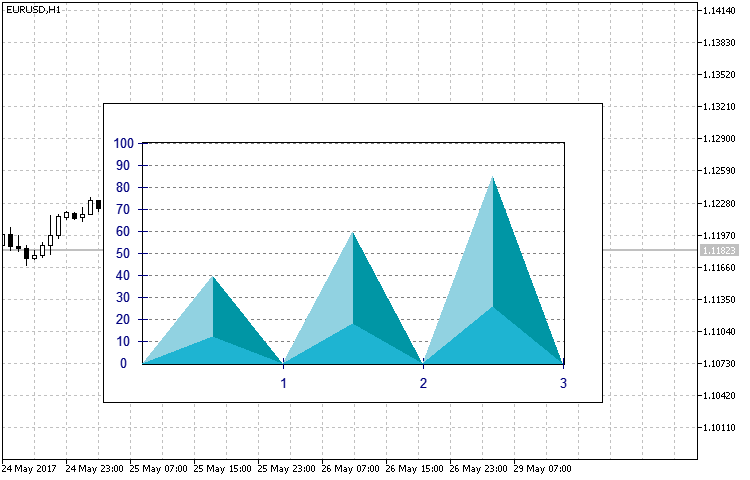
in Abb.11. Die Aussicht des Histogramms des Typs TRIANGLE.

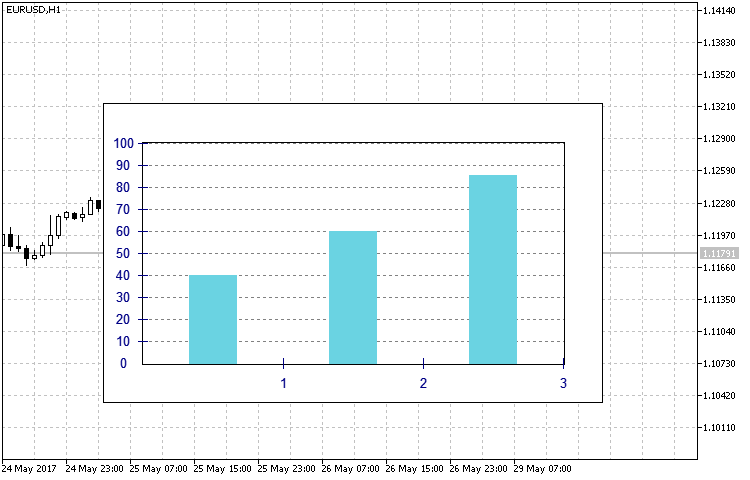
in Abb.12. Die Aussicht des Histogramms des Typs RECTANGLE.

Wir erstellen im Ordner CustomGUI/Indicators die Datei Histogram.mqh, und darin — die Klasse СHistogram und stellen es für sie die vorher erstellten Klasse CCanvasBase als Grundlegende. Auch werden wir ihn zur allgemeinen Liste zur Datei CustomGUI.mqh hinzufügen. Die Mehrheit der Methoden und Eigenschaften der gegebenen Klasse sind der Klasse CLineGraph identisch, einschließlich auch die Methode Create(). Deshalb betrachten wir nur die prinzipiellen Unterschiede, und zwar — die Methode SetArrayValue().

//+------------------------------------------------------------------+
//| setzt das Array der Eingangsdaten                                |
//+------------------------------------------------------------------+
void CHistogram::SetArrayValue(double &data[])
  {
   int x,y,y1,y2;
//--- Die Erstellung des Rahmens des Charts und des Hintergrunds

   m_canvas.FillRectangle(0,0,XSize(),YSize(),ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillRectangle(1,1,XSize()-2,YSize()-2,ColorToARGB(m_bg_color,m_transparency));
//--- Die Erstellung der Achsen und des Hintergrunds des Charts
   m_canvas.FillRectangle(m_gap-1,m_gap-1,XSize()-m_gap+1,YSize()-m_gap+1,ColorToARGB(m_border_color,m_transparency));
   m_canvas.FillRectangle(m_gap,m_gap,XSize()-m_gap,YSize()-m_gap,ColorToARGB(m_bg_graph_color,m_transparency));
//--- Wenn der maximale Wert im Array der Daten die obere Grenze der Achse Y übertritt, so messen wir die Achse aus.
   if(data[ArrayMaximum(data)]>m_y_max)
      m_y_max=data[ArrayMaximum(data)];
//--- Die Erstellung der Teilungen der Achse und ihrer Werte
   VerticalScale(m_y_min,m_y_max,m_num_grid);
   HorizontalScale(ArraySize(data));
   ArrayResize(m_label_value,ArraySize(data));
//--- Der Aufbau des Histogramms nach dem Datenarray
   for(int i=0;i<ArraySize(data);i++)
     {
      if(data[i]>0)
        {
         x=int(m_x[i]+(m_x[i+1]-m_x[i])/2);
         y=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]);
         y1=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]*0.3);
         y2=int((YSize()-m_gap)-(YSize()-2*m_gap)/m_y_max*data[i]*0.1);
         y=(y<m_gap)?m_gap:y;
         if(m_type==SIMPLE)
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,m_x[i+1],YSize()-m_gap,x,y,ColorToARGB(m_graph_color1,m_transparency));
         else if(m_type==TRIANGLE)
           {
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,x,y,x,y1,ColorToARGB(m_graph_color1,m_transparency));
            m_canvas.FillTriangle(m_x[i],YSize()-m_gap,m_x[i+1],YSize()-m_gap,x,y1,ColorToARGB(m_graph_color2,m_transparency));
            m_canvas.FillTriangle(x,y,x,y1,m_x[i+1],YSize()-m_gap,ColorToARGB(m_graph_color3,m_transparency));
           }
         else if(m_type==RECTANGLE)
           {
            int x1,x2;
            x1=int(m_x[i]+(m_x[i+1]-m_x[i])/3);
            x2=int(m_x[i]+2*(m_x[i+1]-m_x[i])/3);
            m_canvas.FillRectangle(x1,y,x2,YSize()-m_gap,ColorToARGB(m_graph_color1,m_transparency));
           }
         //--- Die Beschreibung und der Zahlenwert
         m_canvas.FontNameSet("Trebuchet MS");
         m_canvas.FontSizeSet(m_value_font_size);
         m_canvas.TextOut(x,y2,DoubleToString(data[i],2),ColorToARGB(m_value_color,m_transparency),TA_CENTER|TA_VCENTER);
         m_canvas.TextOut(x,y-5,m_label_value[i],ColorToARGB(m_label_color,m_transparency),TA_CENTER|TA_VCENTER);
        }
     }
   m_canvas.Update();
  }

Der wesentliche Unterschied besteht darin, dass der Typ des Histogramms ENUM_TYPE_HISTOGRAM im Block des Aufbaues der Histogramme nach dem gegebenen Datenarray berücksichtigt wird, welches höher betrachtet wurde. Als Beispiel der Verwendung wurde die visuelle Darstellungsart drei Indikatoren RSI mit verschiedenen Perioden realisiert.

//+------------------------------------------------------------------+
//|                                                          004.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Alexander Fedosov"
#property link      "https://www.mql5.com/de/users/alex2356"
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//+------------------------------------------------------------------+
//|  Eingangsparameter des Indikators                                |
//+------------------------------------------------------------------+

input int                  RSIPeriod1=10;        //Period of the indicator1
input int                  RSIPeriod2=14;        //Period of the indicator2
input int                  RSIPeriod3=18;        //Period of the indicator3
input ENUM_TYPE_HISTOGRAM  Type=RECTANGLE;       //Type Histogram
//---
CHistogram ind;
int InpInd_Handle1,InpInd_Handle2,InpInd_Handle3;
double rsi1[],rsi2[],rsi3[],ex[3];
string descr[3];
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---- Die Erhaltung des Handles des Indikators
   InpInd_Handle1=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod1,PRICE_CLOSE);
   InpInd_Handle2=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod2,PRICE_CLOSE);
   InpInd_Handle3=iRSI(Symbol(),PERIOD_CURRENT,RSIPeriod3,PRICE_CLOSE);
   if(InpInd_Handle1==INVALID_HANDLE ||
      InpInd_Handle2==INVALID_HANDLE ||
      InpInd_Handle3==INVALID_HANDLE
      )
     {
      Print("Failed to get indicator handle");
      return(INIT_FAILED);
     }
//---
   descr[0]="RSI("+IntegerToString(RSIPeriod1)+")";
   descr[1]="RSI("+IntegerToString(RSIPeriod2)+")";
   descr[2]="RSI("+IntegerToString(RSIPeriod3)+")";
   ind.NumGrid(10);
   ind.YMax(100);
   ind.Type(Type);
   ind.Create("rsi",350,250);
   ind.SetArrayLabel(descr);
//---
   ArraySetAsSeries(rsi1,true);
   ArraySetAsSeries(rsi2,true);
   ArraySetAsSeries(rsi3,true);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(CopyBuffer(InpInd_Handle1,0,0,1,rsi1)<=0   ||
      CopyBuffer(InpInd_Handle2,0,0,1,rsi2)<=0   ||
      CopyBuffer(InpInd_Handle3,0,0,1,rsi3)<=0
      )
      return(0);
   ex[0]=rsi1[0];
   ex[1]=rsi2[0];
   ex[2]=rsi3[0];
   ind.SetArrayValue(ex);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind.Delete();
   ChartRedraw();
  }
//+------------------------------------------------------------------+


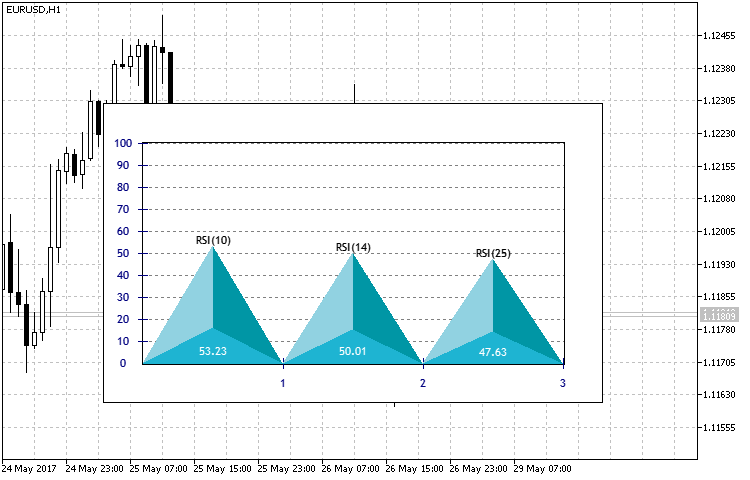
in Abb.13. Das Arbeitsergebnis des Indikators in Form vom Histogramm für drei Perioden des Indikators RSI.


Die Klasse des Indikators, die Pyramide CPyramid

Wir betrachteten schon die Klassen und Prinzipien des Aufbaues der komplizierten Figuren mit Hilfe der Ringpuffer. Und in der Klasse des Indikatoren-Aufbaues des Histogramm-Typs wurde teilweise das Thema des Aufbaues im zweidimensionalen Raum der Objekte betrachtet, die (die Abb.13) wegen der Farbenauswahl räumlich scheinen. Jedoch die Pyramide — keine flache Figur, deshalb bei ihrem Aufbau im gegebenen zweidimensionalen Koordinatensystem verwenden wir ihre isometrische Projektion. Die grundlegende Struktur unterscheidet sich nicht durch die große Anzahl der Elemente (die Abb. 14), aber nichtsdestoweniger, die Art des Aufbaues der Pyramide-Projektion und ihre Visualisierung — ist der Hauptteil der Realisierung dieser Klasse.


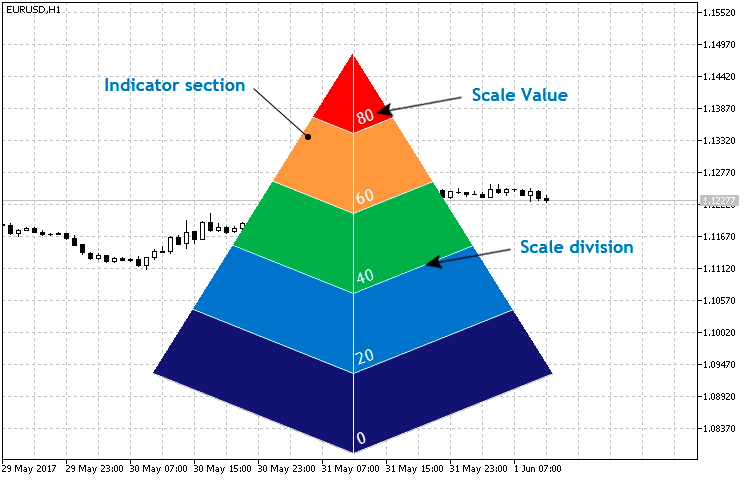
in Abb.14. Die grundlegende Struktur der Klasse CPyramid.

Wir erstellen im Ordner CustomGUI/Indicators die Datei Pyramid.mqh, und darin — die Klasse СPyramid und stellen es für sie die vorher erstellten Klasse CCanvasBase als Grundlegende. Auch werden wir ihn zur allgemeinen Liste zur Datei CustomGUI.mqh hinzufügen. Jetzt wird die allgemeine Liste der hinzugefügten Klassen so aussehen:

//+------------------------------------------------------------------+
//|                                                    CustomGUI.mqh |
//+------------------------------------------------------------------+
#include "Indicators\CircleSimple.mqh"
#include "Indicators\CircleArc.mqh"
#include "Indicators\CircleSection.mqh"
#include "Indicators\LineGraph.mqh"
#include "Indicators\LineRounded.mqh"
#include "Indicators\Hexagon.mqh"
#include "Indicators\Petal.mqh"
#include "Indicators\Histogram.mqh"
#include "Indicators\Pyramid.mqh"
//+------------------------------------------------------------------+

Die volle Liste aller Eigenschaften und die Methoden kann man in der Klasse erfahren, wir betrachten mehr die Wichtigsten. Bevor wir die Hauptmethoden Create() und NewValue() betrachten, geben wir Acht auf die Privat-Methoden, welche an Ihnen verwendet werden. 

//+----------------------------------------------------------------------------------------------+
//| Es zeichnet ins Array die Koeffizienten der Angleichung einer gerade Linie nach zwei Punkten |
//+----------------------------------------------------------------------------------------------+
void CPyramid::Equation(double x1,double y1,double x2,double y2,double &arr[])
  {
   ArrayResize(arr,2);
   arr[0]=(y1-y2)/(x1-x2);
   arr[1]=y2-arr[0]*x2;
  }

Die Methode Equation() ist für die Suche nach der Angleichung der gerade Linie nach zwei Punkten vorgesehen, unter anderem — findet sie die Koeffizienten k und b für die allgemeine Angleichung y = kx + b aus der kanonischen Angleichung der gerade Linie nach zwei Punkten:

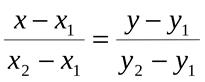
Diese Methode ist nötig, um die Angleichungen der der gerade Linien nach den gegebenen Punkten zu rechnen und im Folgenden — für die Suche nach den Schnittpunkten der Rippen AB und AC der Pyramide und der gerade Linien, die zu den Seiten der Grundfläche der Pyramide parallel sind. Die Koordinaten der Punkte, die auf der Abb. 15 dargestellt sind, sind für den Aufbau der Dreiecke nötig, welche Ähnlichkeitssätze zu den Winkeln der Pyramide haben. Seinerseits sind sie die Sektionen unseres Indikators.

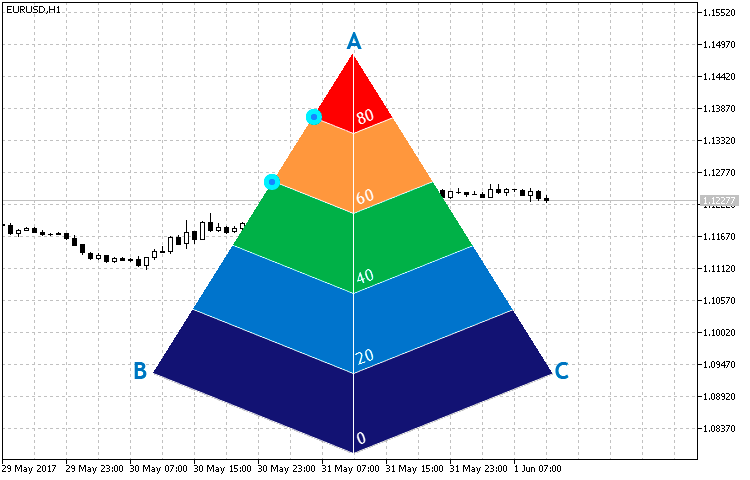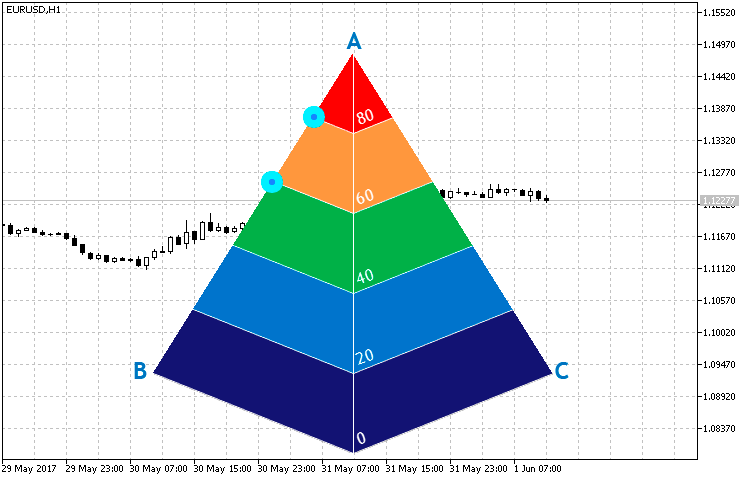
in Abb.15. Die Schnittpunkte der Rippen der Pyramide und der gerade Linien, die parallel zu den Seiten der Grundfläche der Pyramide sind.

Denn wir wissen die Koeffizienten zwei gerade Linien, mit Hilfe des Systems der Angleichungen rechnen wir die Koordinaten des Schnittpunktes aus. Dafür ist die Methode Cross() verantwortlich:

//+------------------------------------------------------------------------------------------------------+
//| Es zeichnet ins Array die Koordinaten des Schnittpunktes zwei gerade Linien nach ihren Koeffizienten |
//+------------------------------------------------------------------------------------------------------+
void CPyramid::Cross(double k1,double b1,double k2,double b2,double &arr[])
  {
   double x,y;
   ArrayResize(arr,2);
   y=(b1*k2-b2*k1)/(k2-k1);
   x=(y-b2)/k2;
   arr[0]=x;
   arr[1]=y;
  }
//+------------------------------------------------------------------+

Jetzt, wir haben den Einblick auf die Funktionen, die bei der Erstellung der Pyramide verwendet werden, können wir gründlich die Methode Create() betrachten. 

//+------------------------------------------------------------------+
//| Er erstellt den Indikator                                        |
//+------------------------------------------------------------------+
void CPyramid::Create(string name,int x,int y)
  {
   int size=m_size;
//--- Die Korrektion des Standortes des Indikators von seiner Größe
   x=(x<size/2)?size/2:x;
   y=(y<size/2)?size/2:y;
   Name(name);
   X(x);
   Y(y);
   XSize(size);
   YSize(size);
   if(!CreateCanvas())
      Print("Error. Can not create Canvas.");
//--- Die Beschreibung und der Zahlenwert
   m_canvas.FontNameSet("Trebuchet MS");
   m_canvas.FontSizeSet(m_font_size);
   m_canvas.FontAngleSet(200);
//--- Die Suche nach der Gleichung der gerade Linie AB
   double x1,x2,y1,y2;
   x1=XSize()/2;y1=0;
   x2=0;y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Der Aufbau der linken Sektionen des Indikators
   for(int i=5;i>0;i--)
     {
      //--- Die Berechnung der Ordinaten zwei Punkte 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Die Berechnung der Koordinaten des Schnittpunktes der Rippe AB und der gerade Linie, die parallel zur Seite der Grundfläche der Pyramide ist
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      //--- Der Aufbau der Teilungen der Skala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
     }
//--- Die Suche nach der Gleichung der gerade Linie AC
   x1=XSize()/2;y1=0;
   x2=XSize();y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Der Aufbau der rechten Sektionen des Indikators
   for(int i=5;i>0;i--)
     {
      //--- Die Berechnung der Ordinaten zwei Punkte 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Die Berechnung der Koordinaten des Schnittpunktes der Rippe AC und der gerade Linie, die parallel zur Seite der Grundfläche der Pyramide ist
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1]));
      //--- Der Aufbau der Teilungen der Skala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
      //--- Der Aufbau der Werte der Skala
      m_canvas.TextOut(int(x1+2),int(y2+YSize()/6)," - ",ColorToARGB(m_label_color,m_transparency),TA_LEFT|TA_VCENTER);
     }
   m_canvas.LineVertical(XSize()/2,0,YSize(),ColorToARGB(m_scale_color,m_transparency));
   m_canvas.Update();
  }

Der Algorithmus des Aufbaues der Pyramide sieht folgendermaßen aus:

  • Wir bauen die linke Seite der Pyramide. Es werden die Koordinaten der Punkte A und B gefunden, und nach ihnen wird die Angleichung der gerade Linie gefunden.
  • Weiterhin finden wir im Loop nacheinander die Angleichungen der gerade Linie, die zu der Grundfläche der Pyramide parallel sind, und wir finden den Punkt ihrer Kreuzung mit der Rippe AB .
  • Nach den bekommenden Punkten bauen wir die Sektionen und die Teilungen der Skala auf.
  • Wir bauen ähnlich die rechte Seite der Pyramide auf.
  • Außer den Sektionen und den Teilungen der Skalen, fügen wir auf der rechten Seite die Werte der Skala hinzu.
  • Die senkrechte Teilung zwei Sektionen.

In der Methode der Installierung und der Erneuerung der Daten gibt es zwei Argumente: das ist ein laufender übergebener Wert und der maximale Wert. Der Kern der Methode besteht darin, dass ausgehend von dem maximal bestimmten Wert, wird die Schwellenwerte gefunden, bei deren Durchgang jede Sektion ihre Farbe ändert . Bei der Überschreitung der Schwellenwerte wird die Sektion für sie bestimmte Farbe übernehmen, bei der Senkung — wird sie in die Farbe gefärbt, die inaktiv bestimmt ist. 

//+------------------------------------------------------------------+
//| Er setzt und erneut den Wert des Indikators                      |
//+------------------------------------------------------------------+
void CPyramid::NewValue(double value,double maxvalue)
  {
//---
   double s;
   color col;
//--- Die Suche nach der Gleichung der gerade Linie AB
   double x1,x2,y1,y2;
   x1=XSize()/2;y1=0;
   x2=0;y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Der Aufbau der linken Sektionen des Indikators
   for(int i=5;i>0;i--)
     {
      //--- Die Suche nach den Werten der Teilungen der Skala
      s=maxvalue-(i-1)*maxvalue/5;
      //--- Die Definition der Sektionsfarbe
      col=(value>=s)?m_section_color[i-1]:m_bg_color;
      //--- Die Berechnung der Ordinaten zwei Punkte 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Die Berechnung der Koordinaten des Schnittpunktes der Rippe AB und der gerade Linie, die parallel zur Seite der Grundfläche der Pyramide ist
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(col,m_transparency));
      //--- Der Aufbau der Teilungen der Skala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(clrWhite));
     }
//--- Die Suche nach der Gleichung der gerade Linie AC
   x1=XSize()/2;y1=0;
   x2=XSize();y2=4*YSize()/5;
   Equation(x1,y1,x2,y2,m_line1);
//--- Der Aufbau der rechten Sektionen des Indikators
   for(int i=5;i>0;i--)
     {
      //--- Die Suche nach den Werten der Teilungen der Skala
      s=maxvalue-(i-1)*maxvalue/5;
      //--- Die Definition der Sektionsfarbe
      col=(value>=s)?m_section_color[i-1]:m_bg_color;
      //--- Die Berechnung der Ordinaten zwei Punkte 
      y1=i*YSize()/5;
      y2=(i-1)*YSize()/5;
      Equation(x1,y1,x2,y2,m_line2);
      //--- Die Berechnung der Koordinaten des Schnittpunktes der Rippe AC und der gerade Linie, die parallel zur Seite der Grundfläche der Pyramide ist
      Cross(m_line1[0],m_line1[1],m_line2[0],m_line2[1],m_cross);
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_section_color[i-1],m_transparency));
      m_canvas.FillTriangle(int(x1),0,int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(col,m_transparency));
      //--- Der Aufbau der Teilungen der Skala
      m_canvas.LineAA(int(x1),int(y1),int(m_cross[0]),int(m_cross[1]),ColorToARGB(m_scale_color,m_transparency));
      //--- Der Aufbau der Werte der Skala
      m_canvas.TextOut(int(x1+2),int(y2+YSize()/6),DoubleToString(s,0),ColorToARGB(m_label_color,m_transparency),TA_LEFT|TA_VCENTER);
     }
   m_canvas.LineVertical(XSize()/2,0,YSize(),ColorToARGB(m_scale_color,m_transparency));
   m_canvas.Update();
  }

Trotz der komplizierteren Realisierung des Abzeichens des Indikators, seine Erstellung, Einstellung und Verwendung sind nicht komplizierter als bei den Vorherigen. Als kleines Beispiel verwenden wir es für die Abbildung der Werte des standardmäßigen ADXs. Dabei, je nach seinem Standort, werden wir den kreisförmigen Indikator links oben für den Vergleich und die Anschaulichkeit der Abbildung hinzufügen.

//+------------------------------------------------------------------+
//|                                                          005.mq5 |
//|                                Copyright 2017, Alexander Fedosov |
//|                           https://www.mql5.com/de/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Alexander Fedosov"
#property link      "https://www.mql5.com/de/users/alex2356"
#property version   "1.00"
#property indicator_plots 0
#property indicator_chart_window

#include <CustomGUI\CustomGUI.mqh>
//+------------------------------------------------------------------+
//|  Eingangsparameter des Indikators                                |
//+------------------------------------------------------------------+
input int               period=10;                                //ADX Period
input double            maxval=50;                                //Max value
//---
CPyramid ind1;
CCircleSimple ind2;
int InpInd_Handle;
double adx[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//---- Die Erhaltung des Handles des Indikators
   InpInd_Handle=iADX(Symbol(),PERIOD_CURRENT,period);
   if(InpInd_Handle==INVALID_HANDLE)
     {
      Print("Failed to get indicator handle");
      return(INIT_FAILED);
     }
   ArraySetAsSeries(adx,true);
//---
   ind1.Size(250);
   ind1.Create("pyramid",200,0);
//---
   ind2.FontSize(ind1.FontSize());
   ind2.LabelSize(ind1.FontSize());
   ind2.Label("ADX");
   ind2.Radius(30);
   ind2.Create("label",ind1.X()-ind1.Size()/3,ind1.Y()-ind1.Size()/4);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(CopyBuffer(InpInd_Handle,0,0,2,adx)<=0)
      return(0);
   ind1.NewValue(adx[0],maxval);
   ind2.NewValue(adx[0]);
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ind1.Delete();
   ind2.Delete();
   ChartRedraw();
  }
//+------------------------------------------------------------------+

Wie man es auf der. Abb.16 sehen kann, der kreisförmige Indikator stellt die Werte höher als der dritte Schwellenwert 30 dar, deshalb wurden drei Sektionen gefärbt. Selbstverständlich bei dem laufenden maximalen Wert, der in diesem Fall in 50 eingestellt ist.

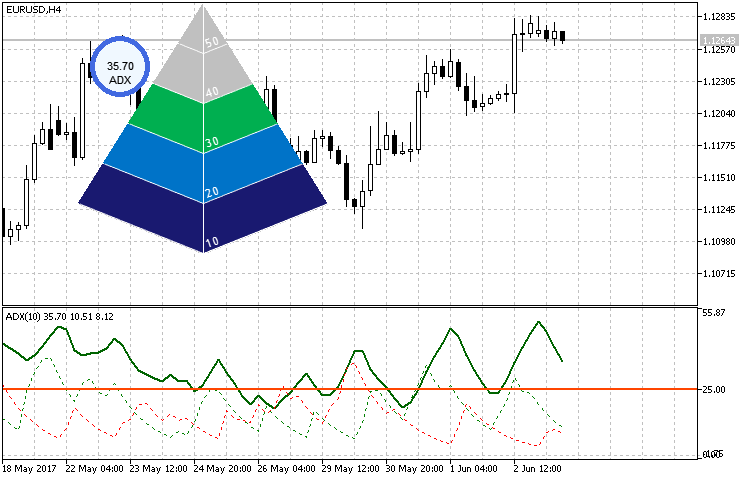
in Abb.16. Das Beispiel der Verwendung des Indikators in Form einer Pyramide.

Fazit

Wie man aus den betrachteten Realisierungen der Klassen aufgrund CCanvas im vorliegenden Artikel sehen kann, sind die Charts-Möglichkeiten der Bibliothek sehr umfangreich. Die Arten und die Weisen der Abbildung eines solchen Typs der Indikatoren sind vielleicht nur in der Phantasie beschränkt. Dabei fordert die Erstellung und die Organisation solcher Indikatoren in Form einer Bibliothek aus hinzugefügten Klassen keine besondere Erkenntnis oder Bemühungen.

Am Ende des Artikels findet man im Anhang das Archiv mit allen Dateien, die im Artikel verwendet wurden und die nach den Ordnern geordnet sind. Deshalb ist es für die korrekte Arbeit ausreichend, den Ordner MQL5 aus dem Archiv im Verzeichnis des Terminalen zu ordnen. 

Die Programme, die im Archiv sind und die  im Artikel verwendet wurde:

#
  Der Name
 Typ
 Beschreibung
1
 CanvasBase.mqh Bibliothek  Die grundlegende Klasse des Benutzer-Charts
2
 CustomGUI.mqh Bibliothek  Die Datei der Liste des Hinzufügens aller Klassen der Bibliothek 
3 CircleArc.mqh Bibliothek  Es enthält die Klasse des kreisförmigen Indikators mit der Bogen-Indikation CCircleArc
4 CircleSection.mqh Bibliothek  Es enthält die Klasse des kreisförmigen Indikators mit der Bogen-Sektionsindikation CCircleSection
5 CircleSimple.mqh Bibliothek  Es enthält die Klasse des einfachen runden Indikators CCircleSimle
6  LineGraph.mqh Bibliothek  Es enthält die Klasse des linearen Charts CLineGraph
7 LineRounded.mqh  Bibliothek   Es enthält die Klasse des abgerundeten linearen Indikators CLineRounded
 8 Hexagon.mqh  Bibliothek   Es enthält die Klasse des sechseckigen Indikators CHexagon
 9 Petal.mqh  Bibliothek   Es enthält die Klasse des blätternden Indikators CPetal
 10 Histogram.mqh  Bibliothek   Es enthält die Klasse des Indikators, das Histogramm CHistogram
 11 Pyramid.mqh  Bibliothek   Es enthält die Klasse des Indikators, die Pyramide CPyramid
12 CLineRounded.mq5 Indikator  Das Beispiel der Realisierung der Klasse CLineRounded
13 CHexagon.mq5 Indikator  Das Beispiel der Realisierung der Klasse CHexagon
14 CPetal.mq5 Indikator  Das Beispiel der Realisierung der Klasse CPetal
 15 CHistogram.mq5 Indikator  Das Beispiel der Realisierung der Klasse CHistogram
 16 CPyramid.mq5  Indikator   Das Beispiel der Realisierung der Klasse CPyramid

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3298

Beigefügte Dateien |
ZIP herunterladen
MQL5.zip (29.88 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Wie soll man eine qualitative Analyse der Handelssignale durchführen und die Beste von ihnen wählen? Wie soll man eine qualitative Analyse der Handelssignale durchführen und die Beste von ihnen wählen?
Im Artikel werden die Bewertungsfragen der statistischen Kennziffer der Verwalter im Service "Signale" betrachtet. Zum Urteil des Lesers werden einige zusätzliche Kennwerte angeboten, die helfen werden, die Ergebnisse des Handels nach dem Signal ein wenig von anderer Seite zu beleuchten als im traditionellen Herangehen. Es werden solche Begriffe betrachtet, wie die richtige Steuerung und das ideale Trade. Auch werden die Fragen der optimalen Auswahl aus den bekommenden Ergebnissen und der Kompilation der Aktentasche aus einigen Signale-Quellen.
Erstellung der Dokumentation basierend auf Quellcodes von MQL5 Erstellung der Dokumentation basierend auf Quellcodes von MQL5
Der Artikel beschäftigt sich mit der Erstellung der Dokumentation zu einem Code in MQL5 und beginnt mit der Automatisierung der Platzierung von Tags. Weiter wird die Arbeit mit dem Programm Doxygen beschrieben, ihre Konfiguration und das Erhalten von Ergebnissen in verschiedenen Formaten: in HTML, HtmlHelp und in PDF.
Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil III Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil III
Das ist der abschließende Artikel zum Thema "Muster, die beim Handeln mit Körben von Währungspaaren auftreten". Der Artikel beschäftigt sich mit vereinigten Trendindikatoren und der Anwendung gewöhnlicher grafischer Konstruktionen.
Analyse der Grafiken Kontostand/Equity nach Symbolen und nach ORDER_MAGIC von Expert Advisors Analyse der Grafiken Kontostand/Equity nach Symbolen und nach ORDER_MAGIC von Expert Advisors
Die Einführung der Hedging-Option in MetaTrader 5 ermöglichte es, gleichzeitig mehrere Expert Advisors auf einem Handelskonto handeln zu lassen. Dabei ist die Situation möglich, dass eine Strategie profitabel ist, während die andere Verluste bringt. Als Ergebnis schwankt die Grafik um Null. Für diesen Fall ist es praktisch, Kontostand- und Equity-Grafiken für jede Handelsstrategie separat zu zeichnen.