
在 MetaTrader 4 中的投资组合交易
周而复始的大周期
Publius Vergilius Maro, Eclogues
概论
投资组合的理论很久以前就很著名了。通过在若干方向上的多样化布局, 投资者创建了自己的投资组合来降低整体亏损风险, 并让收益平稳增长。当 Harry Markowitz 于 1950 年提出了第一个投资组合数学模型之后, 投资组合理论得以强劲推动。在 20 世纪 80 年代, 来自摩根斯坦利的一个研究小组开发出第一种价差交易策略, 为市场群的中性策略铺平了道路。当今的投资组合理论是如此的多样化和复杂化, 使得几乎无法在一篇文章中描述所有的投资组合策略。所以, 在此只研究 MetaTrader 4 平台上的小范围投机策略以其可能实现。
本文中所用的一些定义如下:
- 投资组合 (篮子, 合成工具) — 具有优化交易量的多种交易工具集合。有时会保留仓位, 持续跟踪并根据共同的账面结果平仓。
- 投资组合 (篮子, 合成工具) 调整 — 为让亏损最小化或修整过渡结果, 改变投资组合内的工具, 和/或它们的交易量。
- 合成交易量 — 合成仓位的数量 (买入或卖出投资组合的倍数)。
- 虚拟盈利/亏损 — 获取一定时间段内的持仓账面结果。
经典的投资组合通常应用于股票市场。然而, 这种方法不太适合外汇, 因为这里的大多数投资组合是投机性的。它们的创建和交易略有不同。对于外汇而言, 投资组合交易实际上是一个多币种交易, 但并非所有的多币种策略都属投资组合之一。如果交易品种独立, 且并未跟踪彼此间的动态结果, 则其为多币种交易策略。若有多个独立的系统在单个交易账户内进行交易, 这是一种策略组合。在此我们将要研究狭义的交易投资组合 — 由若干品种形成合成的仓位, 并进行后期管理。
原理
开发投资组合由两个阶段组成: 选择品种, 以及计算手数和它们的方向。在此, 我们只讨论少量含算法例程的开发简单投资组合的方法。特别是, 我们提议最小二乘法 (OLS) 和主成分分析 (PCA), 作为基础。更多信息可以在这里找到:
当开发一个投资组合时, 通常需要定义期望投资组合的图示行为。投资组合图示呈现一定时间段内投资组合所包含的所有仓位的总利润变化。投资组合优化是寻找最适合的手数和方向的组合。例如, 根据我们的任务, 投资组合也许有必要具有周期性均值, 或是清晰的趋势标记属性, 或者其图表应与某函数的图表相吻合。
三种投资组合类型 (趋势, 横盘, 函数):
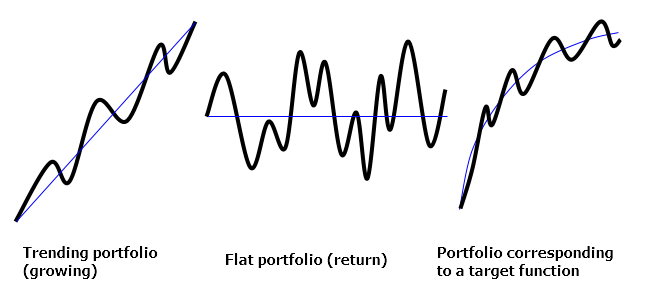
投资组合可由以下方程表示:
A*k1 + B*k2 + C*k3 + ... = F,
此处
A, B, C ... 投资组合品种的相应时间序列
k1, k2, k3 ... 品种的手数 (正数 — 买入, 负数 — 卖出)
F — 目标函数 (数值按照时间序列的点数设置)
这是一个零常数项的多元线性回归方程。它的根可以很容易地使用 OLS 找到。首先, 时间序列应制定可比较的均价, 以便价格点能变换到存款货币。在此情况下, 每条时间序列中的每个元素在特定时间可表示为相应品种的单手虚拟利润值。在统计应用任务中, 通常建议使用初步价格对数或价格差值。然而, 在我们的情况里, 这并无必要, 甚至是有害的, 因为整体品种的动态数据临界值将会被这种方法破坏。
目标函数定义投资组合图形的类型。目标函数值应在每个相应点预先计算。例如, 当开发一个简单增长投资组合 (趋势组合) 时, 目标函数的值会是 0, 1*S, 2*S, 3*S, 等等, 此处 S 是一个增量 — 资金值, 其为预判时间段内投资组合在每根柱线上的应增利润。OLS 算法加上 A, B, C, ... 时间序列, 以便用它们的总和来寻找重复的目标函数图表。为达成这个目标, OLS 算法将序列合计与目标函数之间的差价平方和最小化。这是一个标准统计任务。无需了解算法操作的细节, 因为您可以使用现成的库。
也可能发生目标函数仅包含一个零值 (横盘投资组合)。在此情况下, 应添加一个额外的合计限制比值 (例如: k1 + k2 + k3 + ... = 1) 来绕过解一个零根方程。另一替代方法是将方程的一项移到右侧, 令目标函数接受 -1 比值, 而其余的项如常优化。在此情况下, 我们把工具篮子与所选工具划等号, 从而创建一个价差投资组合。最后, 更先进的 PCA 算法可用来开发这种投资组合。它利用工具的协方差矩阵来计算对应于点数云与投资组合的最小剩余方差横截面的系数向量。同样, 您也不需要了解此处算法的细节, 因为您可以使用现成的库。
算法
现在, 是时候来使用 MQL 语言实现上述的所有想法。我们将使用众所周知的 ALGLIB 数学库 MT4 版。有时, 问题会在安装期间出现, 所以我将在此多停留一会儿。如果在一台 PC 上安装若干终端, 找到正确的数据文件夹十分重要, 因为如果库文件位于其它终端的数据文件夹, 编译器将无法找到它。
安装 ALGLIB 库:
- 下载库文件 (https://www.mql5.com/zh/code/11077), 解压 zip 文件;
- 打开 'include' 文件夹并找到其内的 Math 目录;
- 启动 МetaТrader 4 平台, 库文件应该已加入;
- 选择菜单命令:文件 — 打开数据文件夹;
- 打开 MQL4 和 Include 子文件夹;
- 拷贝 Math 文件夹至终端的 Include 文件夹;
- 检查结果: *.mhq 文件应在 MQL4\Include\Math\Alglib 之内。
计算合约价格的简单函数如下所示:
double ContractValue(string symbol,datetime time,int period) { double value=MarketInfo(symbol,MODE_LOTSIZE); // 接收手术大小 string quote=SymbolInfoString(symbol,SYMBOL_CURRENCY_PROFIT); // 接收计算的货币 if(quote!="USD") // 如果计算货币不是 USD, 执行转换 { string direct=FX_prefix+quote+"USD"+FX_postfix; // 从直盘报价计算币值 if(MarketInfo(direct,MODE_POINT)!=0) // 检查它是否存在 { int shift=iBarShift(direct,period,time); // 按照时间查找柱线 double price=iClose(direct,period,shift); // 接收柱线的报价 if(price>0) value*=price; // 计算价格 } else { string indirect=FX_prefix+"USD"+quote+FX_postfix; // 从反比报价计算币值 int shift=iBarShift(indirect,period,time); // 按照时间查找柱线 double price=iClose(indirect,period,shift); // 接收柱线的报价 if(price>0) value/=price; // 计算价格 } } if(Chart_Currency!="USD") // 如果目标货币不是 USD, 执行转换 { string direct=FX_prefix+Chart_Currency+"USD"+FX_postfix; // 从直盘报价计算币值 if(MarketInfo(direct,MODE_POINT)!=0) // 检查它是否存在 { int shift=iBarShift(direct,period,time); // 按照时间查找柱线 double price=iClose(direct,period,shift); // 接收柱线的报价 if(price>0) value/=price; // 计算价格 } else { string indirect=FX_prefix+"USD"+Chart_Currency+FX_postfix; // 从反比报价计算币值 int shift=iBarShift(indirect,period,time); // 按照时间查找柱线 double price=iClose(indirect,period,shift); // 接收柱线的报价 if(price>0) value*=price; // 计算价格 } } return(value); }
此函数将会在今后一直使用。它可工作于货币对, 指数, 期货以及差价合约。此外, 它还考虑了某些经纪商为品种添加的前缀和后缀 (FX_prefix, FX_postfix)。结果被转换成目标货币 (Chart_Currency)。如果我们将返回的函数值乘以当前品种价格, 我们获得品种的每一手价格。投资组合中考虑到手数的所有合约价格汇总之后, 我们得到了整个投资组合的价格。如果我们及时将函数值乘以差价, 我们得到价格变化期间产生的盈亏。
下一步是为所有手数合约计算虚拟利润。计算以二维数组实现, 第一维是计算间隔内的价格点索引, 而第二维是品种索引 (第二维的大小由投资组合中已知的品种数量限制, 显而易见不可超过):
double EQUITY[][100]; // 第一维用于柱线, 而第二维用于品种
首先, 我们应保存所有品种的初始价格 (计算间隔的左边界)。之后, 计算间隔内每一点的初始和最终价格的差价并乘以合约价格。每次, 我们在循环中向右平移一个时间段:
for(int i=0; i<variables+constants; i++) // 投资组合品种循环 (变量和模型常量) { int shift=iBarShift(SYMBOLS[i],Timeframe,zero_time); // 接收柱线的时间索引用于零点 opening[i]=iClose(SYMBOLS[i],Timeframe,shift); // 接收柱线的价格并将它保存在数组里 } points=0; // 计算变量中的点 datetime current_time=zero_time; // 从零点开始循环 while(current_time<=limit_time) // 在优化间隔内传递时间标签 { bool skip_bar=false; for(int i=0; i<variables+constants; i++) // 投资组合品种循环 (变量和模型常量) if(iBarShift(SYMBOLS[i],Timeframe,current_time,true)==-1) // 检查品种是否存在 skip_bar=true; // 如果柱线不存在, 忽略它继续下一个品种 if(!skip_bar) // 如果所有品种间的柱线已同步, 继续操作 { points++; // 逐一增加点数 TIMES[points-1]=current_time; // 在内存里保存时间标签 for(int i=0; i<variables+constants; i++) // 计算所有品种主要利润点数的循环 { int shift=iBarShift(SYMBOLS[i],Timeframe,current_time); // 接收柱线的时间索引 closing[i]=iClose(SYMBOLS[i],Timeframe,shift); // 接收柱线的价格 double CV=ContractValue(SYMBOLS[i],current_time,Timeframe); // 计算合约价格 profit[i]=(closing[i]-opening[i])*CV; // 通过差价计算利润和成本 EQUITY[points-1,i]=profit[i]; // 保存利润值 } } current_time+=Timeframe*60; // 平移到下一个时间段 }
在以上的代码片段里, zero_time — 计算时间段时间左边界, limit_time — 计算时间段右边界, Timeframe — 操作时间帧的每根柱线分钟数, points — 计算时间段内检测到的总点数。以上例程中, 使用了严格的时间标签守则。即使只在一个品种里缺失一根确定时间标签的柱线, 此位置被忽略并平移下一根。对于初步数据的准备, 时间标签的管理十分重要, 因为不同品种的数据错位也许会导致投资组合的严重扭曲。
三个品种的投资组合数据样本和一个独立函数 (平方根抛物线):
DATE/TIME AUDJPY GBPUSD EURCAD MODEL 03.08.16 14:00 0 0 0 0 03.08.16 15:00 -61,34 -155 -230,06 10,21 03.08.16 16:00 -82,04 -433 -219,12 14,43 03.08.16 17:00 -39,5 -335 -356,68 17,68 03.08.16 18:00 147,05 -230 -516,15 20,41 03.08.16 19:00 169,73 -278 -567,1 22,82 03.08.16 20:00 -14,81 -400 -703,02 25 03.08.16 21:00 -109,76 -405 -753,15 27 03.08.16 22:00 -21,74 -409 -796,49 28,87 03.08.16 23:00 51,37 -323 -812,04 30,62 04.08.16 00:00 45,43 -367 -753,36 32,27 04.08.16 01:00 86,88 -274 -807,34 33,85 04.08.16 02:00 130,26 -288 -761,16 35,36 04.08.16 03:00 321,92 -194 -1018,51 36,8 04.08.16 04:00 148,58 -205 -927,15 38,19 04.08.16 05:00 187 -133 -824,26 39,53 04.08.16 06:00 243,08 -249 -918,82 40,82 04.08.16 07:00 325,85 -270 -910,46 42,08 04.08.16 08:00 460,02 -476 -907,67 43,3 04.08.16 09:00 341,7 -671 -840,46 44,49
现在, 我们已经准备好数据, 是时候将它们发送到优化模型。使用来自 ALGLIB 库中的 LRBuildZ, LSFitLinearC 和 PCABuildBasis 函数进行优化。这些函数的简要描述包含在库本身之内, 还有官方网站: http://www.alglib.net/dataanalysis/linearregression.php 和这里: http://www.alglib.net/dataanalysis/principalcomponentsanalysis.php。
首先, 确保包含库文件:
#include <Math\Alglib\alglib.mqh>
其次, 涉及模型功能的代码片段应为每个优化模型进行设置。我们先来查看样品趋势模型:
if(Model_Type==trend) { int info,i,j; // 定义工作变量 CLinearModelShell LM; // 定义指定对象模型 CLRReportShell AR; // 定义指定对象报告 CLSFitReportShell report; // 定义其它对象 CMatrixDouble MATRIX(points,variables+1); // 定义保存所有数据的矩阵 if(Model_Growth==0) { Alert("零模型成长!"); error=true; return; } // 验证模型参数 for(j=0; j<points; j++) // 计算优化间隔点的目标函数 { double x=(double)j/(points-1)-Model_Phase; // 计算 X 坐标 if(Model_Absolute) x=MathAbs(x); // 如有必要则让模型对称 MODEL[j]=Model_Growth*x; // 计算 Y 坐标 } double zero_shift=-MODEL[0]; if(zero_shift!=0) for(j=0; j<points; j++) MODEL[j]+=zero_shift; // 模型垂线平移到零点 for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // 下载品种数据至矩阵 for(j=0; j<points; j++) MATRIX[j].Set(variables,MODEL[j]); // 下载模型数据至矩阵 CAlglib::LRBuildZ(MATRIX,points,variables,info,LM,AR); // 启动回归计算 if(info<0) { Alert("回归模型出错l!"); error=true; return; } // 检查结果 CAlglib::LRUnpack(LM,ROOTS,variables); // 接收方程的根 }
起初, 这好似很复杂, 但基本上所有东西都很简单。开始之时, 计算线性趋势函数且其数值被放进 MODEL 数组。参数 Model_Growth 设置整个计算间隔的成长值 (此数值应为按照存款货币为单位的投资组合增长)。Model_Absolute 和 Model_Phase 参数是选项, 在目前阶段并不重要。矩阵是为计算 (MATRIX) 而创建。来自 EQUITY 数组的所有合约的虚拟利润数据, 以及来自 MODEL 数组的目标函数值, 均被下载到矩阵的最后一行。独立回归方程的变量数量被存储在 'variables' 里。然后调用 LRBuildZ 函数执行计算。此后, 使用 LRUnpack 函数将回归方程的根写入 ROOTS 数组。所有复杂的数学均封装在库中, 而您可以使用现成的函数。主要困难在于此处的技术性质, 相关的所有调用设置正确, 和准备期间的数据维护。
相同的代码片段可用于任何函数。简单地用您的目标函数替换 MODEL 数组内容。样本平方根抛物线函数的计算如下所示:
for(j=0; j<points; j++) // 计算优化间隔点的目标函数 { double x=(double)j/(points-1)-Model_Phase; // 计算 X 轴数值 int sign=(int)MathSign(x); // 定义数值符号 if(Model_Absolute) sign=1; // 如有必要则让模型对称 MODEL[j]=sign*Model_Growth*MathSqrt(MathAbs(x)); // 计算 Y 轴数值 }
下面是一个风复杂的函数例程, 它表示线性趋势和谐波振荡之合:
for(j=0; j<points; j++) // 计算优化间隔点的目标函数 { double x=(double)j/(points-1)*Model_Cycles-Model_Phase; // 计算 X 轴数值 if(Model_Absolute) x=MathAbs(x); // 如有必要则让模型对称 MODEL[j]=Model_Amplitude*MathSin(2*M_PI*x); // 计算 Y 轴数值 }
在以上例程中, 它可能管理一个趋势大小 (使用 Model_Growth 参数) 和振荡振幅 (使用 Model_Amplitude 参数)。振荡周期数由 Model_Cycles 设置, 即使用 Model_Phase 进行振荡相位平移。
此外, 应执行垂直移位令函数在零点等于零, 以确保计算是正确的:
double zero_shift=-MODEL[0]; // 在零点读取模型值 if(zero_shift!=0) // 确认它非零 for(j=0; j<points; j++) // 沿所有间隔点传递 MODEL[j]+=zero_shift; // 平移所有模型点
这些例程可轻松开发自定义函数。您可以根据您的任务和交易设置创建任何函数类型。函数类型越复杂, 越难以选择最佳方案, 因为市场不会强制遵循函数。在此, 函数只是近似。
您不需要目标函数来创建差价并返回横盘投资组合。例如, 如果您打算在两个品种的篮子之间创建一个差价, 优化的篮子下载到矩阵的主要部分, 参考篮子用作目标函数并下载到矩阵的最后一列作为总数量:
for(i=0; i<variables; i++) // 优化篮子中的品种循环 for(j=0; j<points; j++) // 计算间隔点循环 MATRIX[j].Set(i,EQUITY[j,i]); // 加载优化篮子的品种值到矩阵列 for(i=variables; i<variables+constants; i++) // 参考篮子品种循环 for(j=0; j<points; j++) // 计算间隔点循环 MODEL[j]+=EQUITY[j,i]*LOTS[i]; // 加载参考篮子品种的值到矩阵最后列
以下是计算横盘投资组合的示例, 函数 LSFitLinearC 在计算间隔内尽可能地令投资组合围绕零点对称:
if(Model_Type==fitting) { int info,i,j; // 定义工作变量 CLSFitReportShell report; // 定义特殊对象模型 CMatrixDouble CONSTRAIN(1,variables+1); // 定义线性限制的矩阵 CMatrixDouble MATRIX(points,variables); // 定义保存所有数据的矩阵 ArrayInitialize(MODEL,0); // 模型清零 CONSTRAIN[0].Set(variables,1); // 设置唯一的限制 for(i=0; i<variables; i++) CONSTRAIN[0].Set(i,1); // 根之合应等于一 for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // 下载品种数据到矩阵 CAlglib::LSFitLinearC(MODEL,MATRIX,CONSTRAIN,points,variables,1,info,ROOTS,report); // 使用 OLS 计算优化模型 if(info<0) { Alert("线性过滤模型错误!"); error=true; return; } // 检查结果 }
以下是另一个使用 PCA 方法利用最小方差计算横盘投资组合的示例。在此, PCABuildBasis 函数计算比率, 以便投资组合图形保持尽可能地在计算间隔内压缩:
if(Model_Type==principal) { int info,i,j; // 定义工作变量 double VAR[]; // 定义最小方差数组 ArrayResize(VAR,variables); // 转换数组到必要维度 CMatrixDouble VECTOR(variables,variables); // 定义系数向量矩阵 CMatrixDouble MATRIX(points,variables); // 定义保存所有数据的矩阵 for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // 加载品种数据到矩阵 CAlglib::PCABuildBasis(MATRIX,points,variables,info,VAR,VECTOR); // 使用 PCA 计算正交基 if(info<0) { Alert("主成分模型错误!"); error=true; return; } // 检查结果 for(i=0; i<variables; i++) ROOTS[i]=VECTOR[i][variables-1]; // 加载优化比率 }
如果所有这些数学概念令您不知所措, 不要担心。正如我所说的, 您并不需要了解所有的数学细节来开发和利用投资组合。通常, 阶段的顺序如下所示:
| 1 | 计算投资组合品种的单手虚拟利润 |
| 2 | 计算目标函数值 |
| 3 | 手数优化算法 |
| 4 | 投资组合交易量规范化 |
| 5 | 利用投资组合计算图形并交易 |
现在我们已经历一些过程获取优化比率的 ROOTS 数组, 是将比率调整手数的时候了。为此, 我们需要规范化: 缩放和舍入。设置所需的缩放率使得手数方便交易。舍入是必要的, 以便手数容量符合经纪商的要求。有时候, 建议依照投资组合的总保证金执行规范化, 但是这种方法有严重的缺点 (因为各独立品种的保证金是变化且可改变的)。因此, 依照投资组合价格或其波动执行规范化更合理。
以下是依照投资组合价格规范化算法的一个简单示例:
double total_value=0; // 定义投资组合价格变量 for(int i=0; i<variables+constants; i++) // 顺序传递所有投资组合品种 total_value+=closing[i]*ContractValue(SYMBOLS[i],limit_time,Timeframe)*MathAbs(LOTS[i]); // 计算并汇总价格元件 if(total_value==0) { Alert("Zero portfolio value!"); error=true; return; } // 确认结果非零 scale_volume=Portfolio_Value/total_value; // 查找缩放率 for(int i=0; i<variables+constants; i++) // 再次顺序传递所有投资组合品种 LOTS[i]=NormalizeDouble(LOTS[i]*scale_volume,Lots_Digits); // 转换手数到所需总价格
在此, 组合的价格等同于按比例所需的一个。Portfolio_Value — 所需的组合价格, total_value — 带有省缺比率的组合总价格, scale_volume — 缩放比率, Lots_Digits — 手数容量, LOTS — 适合交易的手数值数组。
来自最终投资组合结构的手数值。正手数对应于多头仓位, 而负手数 — 对应于空头。了解了组合结构, 我们就可以绘制投资组合的图表, 并进行交易操作。以下是投资组合结构经规范化之后的示例:
| 品种 | AUDJPY | GBPUSD | EURCAD |
| 手数 | -0,07 | -0,11 | -0,11 |
投资组合图形只使用收盘价作图, 并显示在一个单独的指标子窗口。为了构建投资组合图形, 我们需要如同之前计算每个单独品种的虚拟利润一样计算每根图表柱线。不过, 现在它们综合考虑分配的手数:
for(int j=draw_begin; j>=draw_end; j--) // 在图表柱线绘图间隔内循环 { double profit=0; // 开始数值 for(int i=0; i<variables; i++) // 顺序传递所有品种 { if(Fast_Period>0 && Slow_Period>0 && number!=N_TOTAL) // 执行辅助检查 { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // 获取柱线的时间索引 double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // 计算合约价格 double fast=iMA(SYMBOLS[i],Period(),Fast_Period,0,MODE_SMA,PRICE_CLOSE,shift); // 计算慢速均值 double slow=iMA(SYMBOLS[i],Period(),Slow_Period,0,MODE_SMA,PRICE_CLOSE,shift); // 计算快速均值 profit+=(fast-slow)*CV*LOTS[i]; // 计算振荡模型 } else { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // 接收柱线的时间索引 double closing=iClose(SYMBOLS[i],Period(),shift); // 接收品种价格的点数 double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // 计算合约价格 profit+=(closing-OPENINGS[i])*CV*LOTS[i]; // 通过差价计算利润和成本 } } BUFFERS[number].buffer[j]=NormalizeDouble(profit,2); // 在指标数组里保存盈利值 }
在此代码片段里, 我们看到图表在初始和最终柱线之间绘制: draw_begin 和 draw_end。投资组合的价值等于所有已计算品种的利润/亏损 (差价乘以合约价格以及之前计算的手数) 之合。我已经跳过了有关指标缓存区, 格式等等的技术面。现成的投资组合指标示例在下面的章节描述。
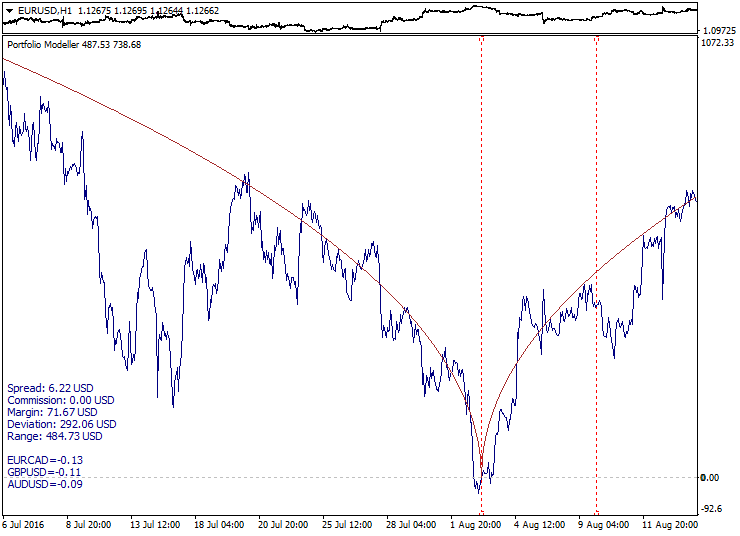
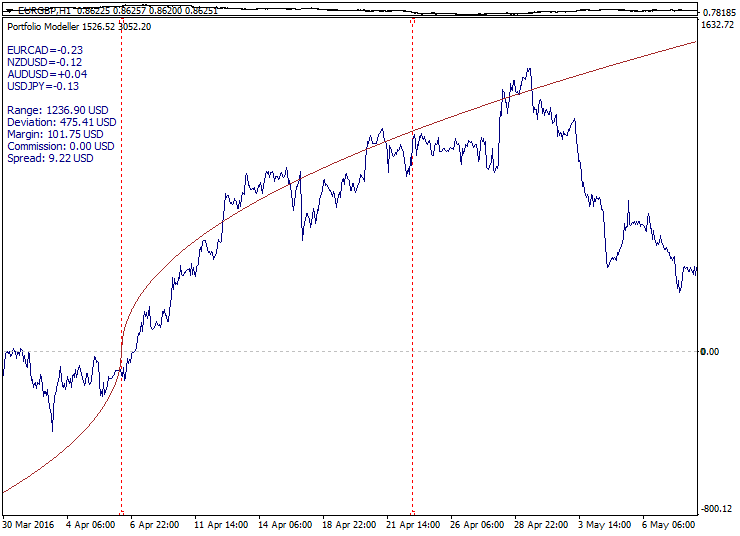
在此, 您可以检查附加了目标函数图形的投资组合图形结构 (指标底下的子窗口) 示例。
此处, 平方根抛物线相对于参考点对称 (Model_Absolute=true) 并用作目标函数。计算的间隔边界以红色虚线显示, 而投资组合图形趋向于沿计算间隔的目标函数的进、出曲线移动。
您可以如同普通品种的价格图表那样对投资组合图形进行技术分析, 包括应用移动均线, 趋势线和级别。这种扩展分析和交易能力允许您选择投资组合结构, 在投资组合图形上形成确定的交易设置, 例如, 在趋势脉冲之后的盘整, 趋势衰竭, 横盘退出, 超买超卖, 收敛发散, 突破, 价位整理和其它设置。交易设置的品质所受影响包括投资组合构成、优化方法、目标函数和所选的历史片段等等。
有必要了解投资组合的波动性来选择适当的交易量。由于投资组合图表基于存款货币进行初始化, 您可以使用 "十字线" 光标和 "平拖" 模式, 直接以该货币评估投资组合的波动范围和潜在的回撤深度。
一个交易系统应基于投资组合行为属性和设置的统计数据。截至目前, 我们还未提及的事实就是投资组合的行为也许在优化间隔之外显著变化。横盘也许会转化为趋势, 而趋势也会反向翻转。一个交易系统还应考虑到投资组合属性很容易随时间而变化。这个问题将在下面讨论。
运用投资组合交易操作时, 按照已计算的交易量一次性买入/卖出组合包含的所有品种。为了更加便利, 由一款特殊的 EA 来执行所有的日常工作是合理的, 包括获取投资组合结构数据, 准备仓位合成, 跟踪入场价位, 锁定盈利并限定亏损。我们为关注的 EA 应用以下条款: 多头合成组合仓位和空头合成组合仓位 (多头仓位将由空头仓位替换, 反之亦然)。该 EA 应能够累积仓位, 跟踪合成交易量, 以及进行投资组合的净持和转换。示例 EA 会在下一章节研究, 尽管由于文章篇幅的限制其结构并未解释。
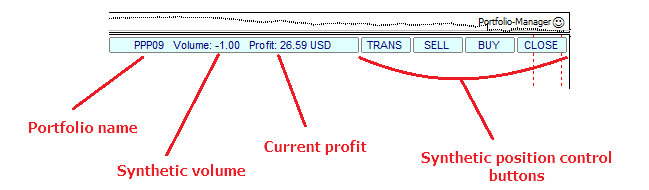
以下是一个投资组合 EA 的简约界面示例:
有时候, 有必要建立不只一个而是若干个投资组合。在最简单的情况下, 需要比较两个组合。有些任务需要整个投资组合系列建立在一个单独的段历史片段上, 而这是含有确定形态的一组投资组合得到的结果。为了实现这一任务, 需要根据确定的模板算法产生投资组合。这种指标的实现例程可在下一章节中找到。在此, 我们仅继续描述其最关键的操作功能。
我们需要分配一个结构数组来存储多个投资组合的数据, 例如:
struct MASSIVE // 定义结构包括多种数据类型 { string symbol[MAX_SYMBOLS]; // 用于投资组合的文本数组 double lot[MAX_SYMBOLS]; // 数字数组用于手数 string formula; // 投资组合方程字符串 double direction; // 投资组合方向属性 double filter; // 滤波器属性 }; MASSIVE PORTFOLIOS[DIM_SIZE]; // 为投资组合群创建结构数组
在此代码片段中, DIM_SIZE 设置存储投资组合的最大尺寸。结构按照以下方式组织: 品种 — 投资组合品种数组, 手数 — 投资组合品种的手数数组, 公式 — 投资组合方程的字符串文本, 方向 — 投资组合方向 (多头或空头), 滤波器 — 滤波器属性 (包括/排除)。运用结构数组比使用单独的数组更方便, 更合理。
创建的结构数组也可用于存储投资组合图形缓存区数组:
struct STREAM{double buffer[];}; // 定义包含数字数组的结构 STREAM BUFFERS[DIM_SIZE]; // 创建结构数组
集合内的投资组合因其品种组合而变化。这些组合可预先定义或根据一定的规则产生。依据任务, 一套投资组合的运作也许包括若干阶段。我们来研究以下阶段顺序:
| 1 | 计算单独投资组合的图表 |
| 2 | 在零点组合一套投资组合 |
| 3 | 相对于零轴翻转投资组合 |
| 4 | 为一套投资组合应用滤波器 |
| 5 | 汇总 — 形成一个超级组合 |
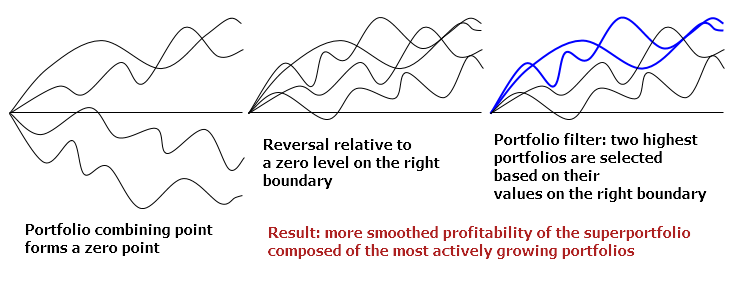
下图说明了这些步骤:
垂直移位是用于合并投资组合。投资组合乘以 -1 则翻转。最后, 用滤波器进行排序和数值采样。在此没有提供这些算法的详细描述, 以避免例行代码的体量庞大。
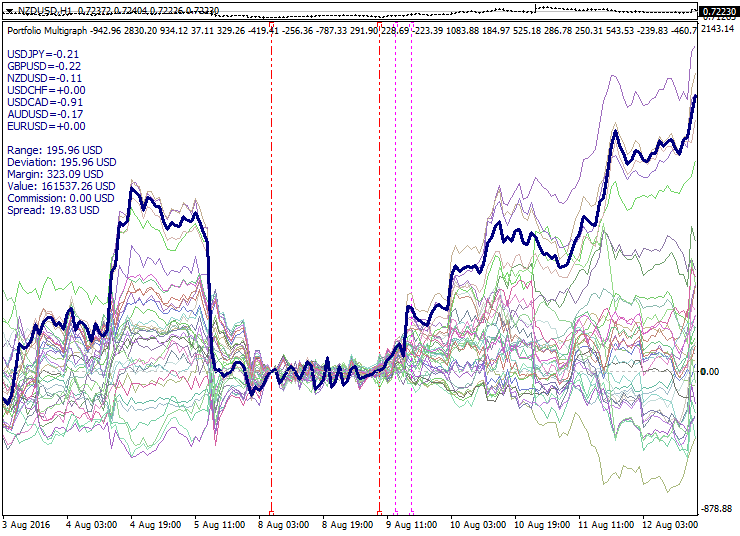
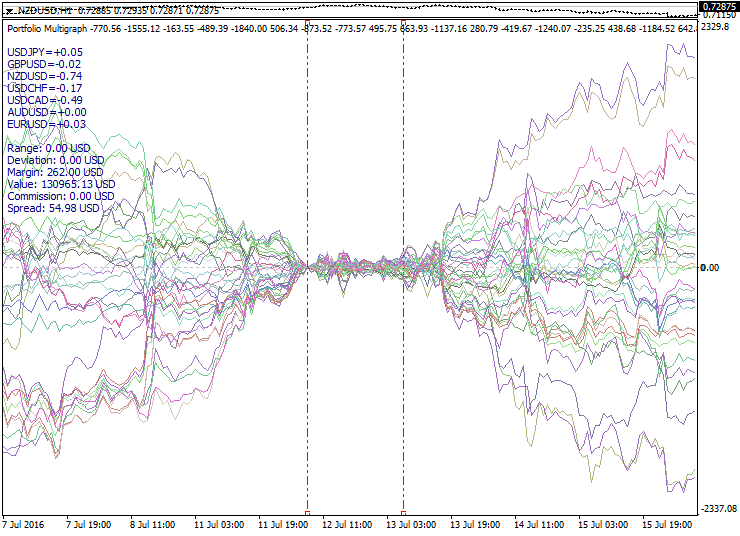
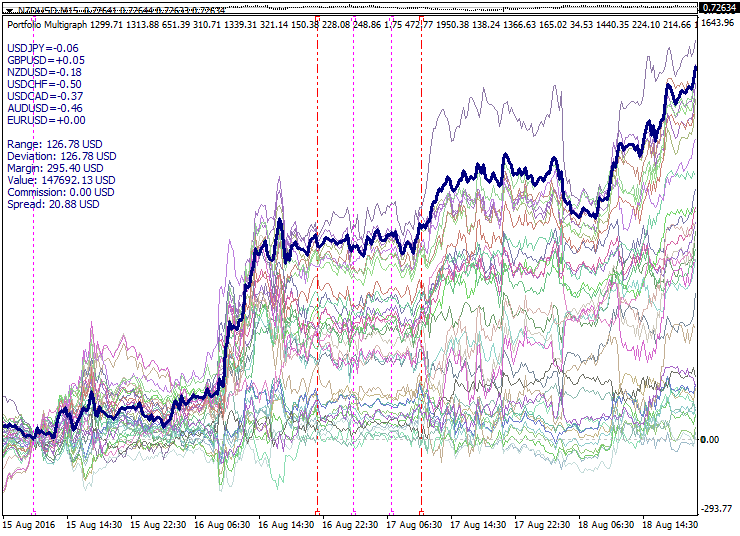
以下是依据提及的原理构造的投资组合集合示例:
图形展示经 PCA 模型计算而来的一组短期投资组合。计算间隔的边界显示为红色虚线。在此我们可以看到在优化间隔两侧投资组合集合的扩张。在优化间隔左侧边界选择的零点, 相对于零的翻转走势和过滤应用由紫色虚线标记。粗线勾勒出由最活跃投资组合构成的超级组合, 且自零点运行得相当不错。
合并投资组合为分析和开发交易策略提供了额外的可能性, 例如投资组合之间的多样化, 投资组合之间的差价, 投资组合集合的收敛-发散, 等待投资组合集合的扭转, 从一个投资组合转移到另一个以及其它方法。
实现示例
当前文章中所描述的方法已经实现, 可作为投资组合指标和半自动化 EA。在这里您可以找到指导, 下载源代码, 并根据您的需求进行修改:
-
投资组合建模 — 投资组合开发器和优化器。它具有若干含配置参数的优化模型类型。此外, 您可以添加自己的模型和目标函数。还有用于投资组合技术分析的基本工具, 以及多种图表格式选项。
-
投资组合多重图 — 含相同模型、参数和选项的投资组合集生成器, 用于投资组合转换及过滤, 还可创建超级投资组合。
-
投资组合管理器 — 用于操作投资组合及超级投资组合的 EA。它与投资组合指标联用, 可以开仓并管理合成仓位, 并有投资组合调整功能, 且自动交易模式基于虚拟订单的图形线。
下载链接: https://www.mql5.com/zh/code/11859 (俄语)
交易策略
有很多交易策略基于合成工具的应用。我们来研究一些创建投资组合交易策略时很有用的想法。在同一时间, 我们不要忘记风险和限制。
生成投资组合的最经典方法是识别那些被低估但具有增长潜力的资产, 将具有上涨预期的纳入投资组合。投资组合的波动总是低于所包含工具的波动总和。这种方法对于股票市场和优秀, 但在外汇市场有使用限制, 因为货币不像股票, 通常它不会表现出持续的增长。
以下是沃特·巴菲特的长期投资组合:
当运作标准投资组合时, 有必要在价格向下运动时仔细评估货币资产状态再买入。
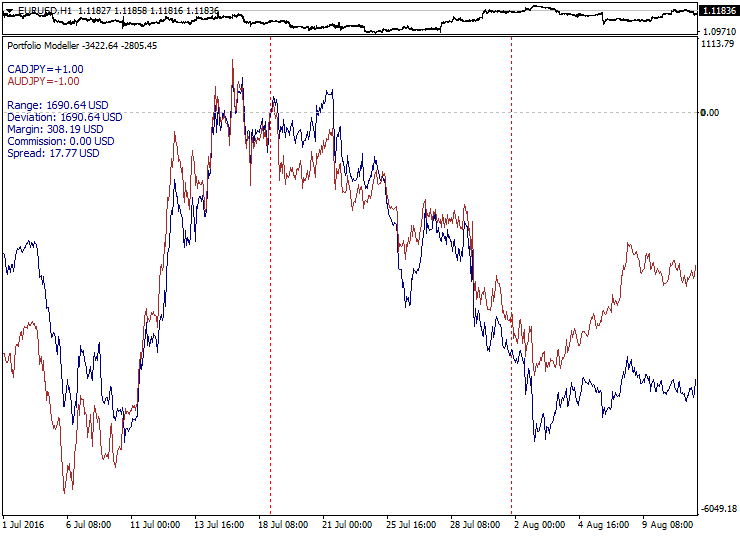
对于投机性投资组合交易, 最先且最容易的选项是配对交易 — 创建两个相关品种的差价。对于外汇, 这种方法明显受限, 因为即使高相关性货币对没有共振, 以致随着时间的推移显著发散。在此情况下, 我们要处理 "差价破位"。此外, 这样的配对交易会变为合成交叉汇率交易, 因为由一般货币进行配对时通常包括点差。这种配对交易是一个非常糟糕的主意。通过差价开相对仓位后, 直到曲线再次收敛之前, 我们有时需要等待很长一段时间。
以下是高度相关性货币对的渐进与不可避免的发散示例:
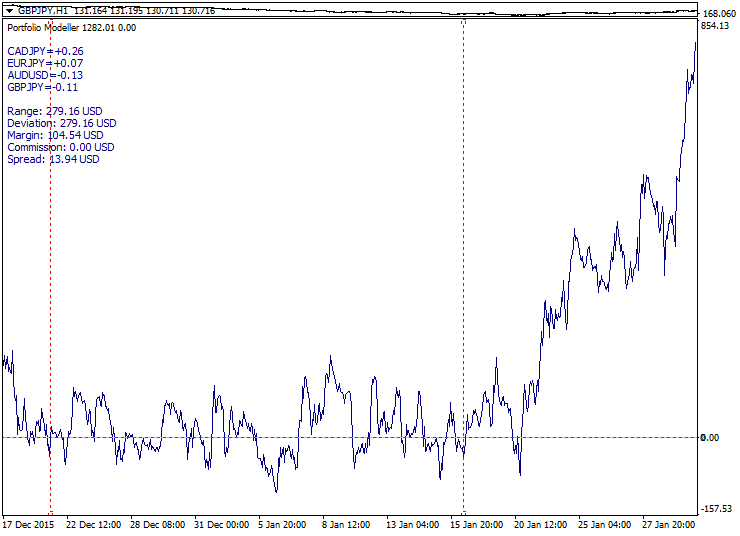
这种方法的扩展是将三个或更多货币对纳入差价时的多边价差交易。这比配对交易更好, 因为它更容易创建一个大量组合选项数目的更均匀差价。然而, 相同风险依然存在: 一个差价可能发散, 而不会再次收敛。在平静的市场上很容易实现良好的差价回报, 但在一段时间后, 强劲的基本面消息会引发快速和不可逆转的发散。有趣的是, 如果我们在差价中增加工具数量, 发散可能增长良好, 因为更多的货币参与, 在新闻发布时有些事情发生的概率会更大。等待差价再次收敛将是一个极为不利的策略, 因为这仅在平静的横盘市场才能发挥作用。
以下是一个新闻发布期间多边差价行为的示例:
差价交易在股票或证券市场上有更多的机会, 在那种背景下, 资产之间有些基本面相联系。但是, 在除息日或期货合约到期日, 仍然不能保证对抗差价缺口。差价也可以由市场指数和期货构成, 但这需要考虑证券交易功能。
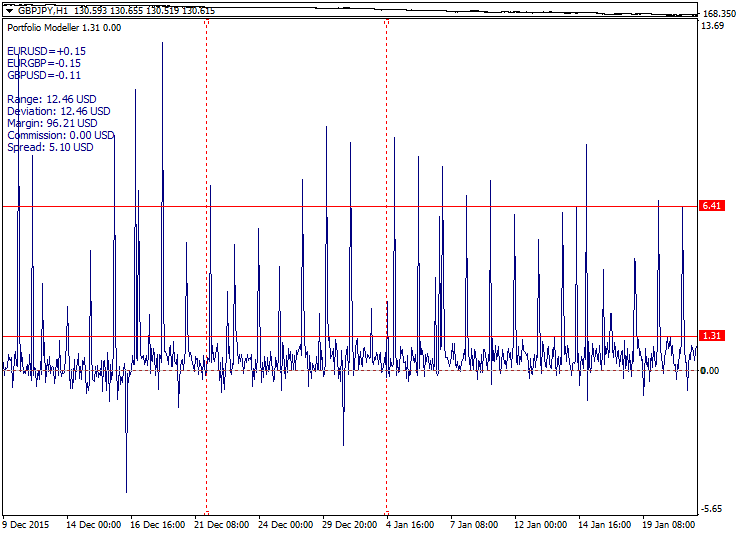
差价交易的一个死胡同表现为多锁, 当选择周期性相关货币对 (例如, EURUSD-GBPUSD-EURGBP) 并用其形成一个平衡的差价。在此情况下, 我们有一个不可交易的完美差价, 因为总差价和佣金过高。如果我们尝试一下非平衡手数, 图形变得更加像趋势, 这与差价交易相矛盾, 而成本居高不下令这种方法毫无意义。
以下是一个平衡多锁的示例。总差价如两条红线所示:
价差交易的缺陷令我们切换到趋势模型。乍一看, 所有的一切似乎在此都很和谐: 识别趋势, 在调整时入场并在更高位置获利了结。
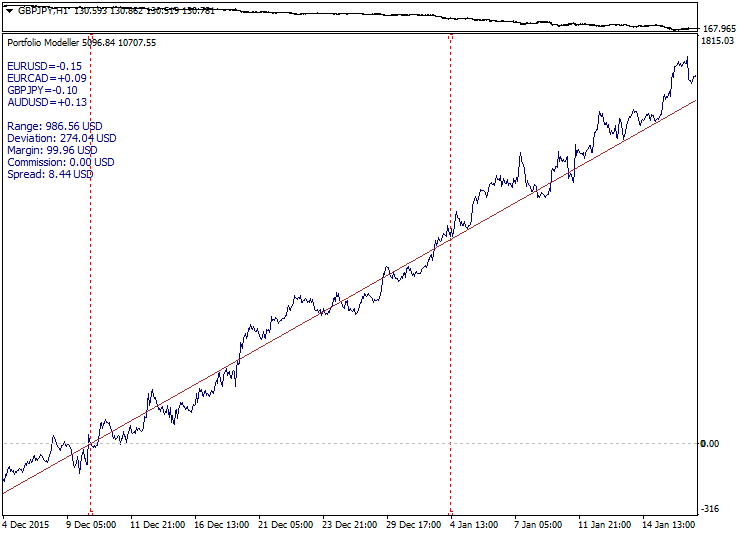
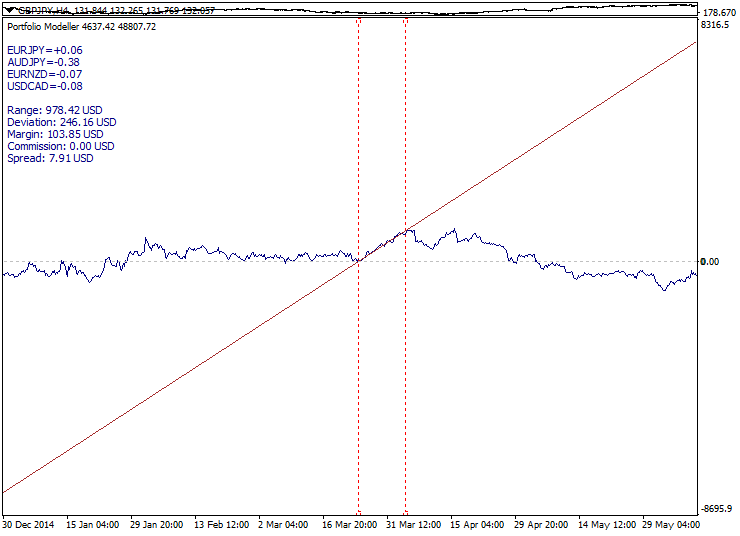
以下是一个良好的趋势模型示例:
然而, 趋势模型可能有时会变得并非如此简单和方便。有时候, 一个投资组合拒绝进一步增长, 且有时它反身急剧下降。在此情况下, 我们要处理 "趋势破位"。这会经常发生在短线和中线的模型。交易效率在很大程度上取决于此时的市场局面。当市场处于趋势时, 系统将运行良好。如果市场横盘或特别动荡, 可能会出现巨额亏损。
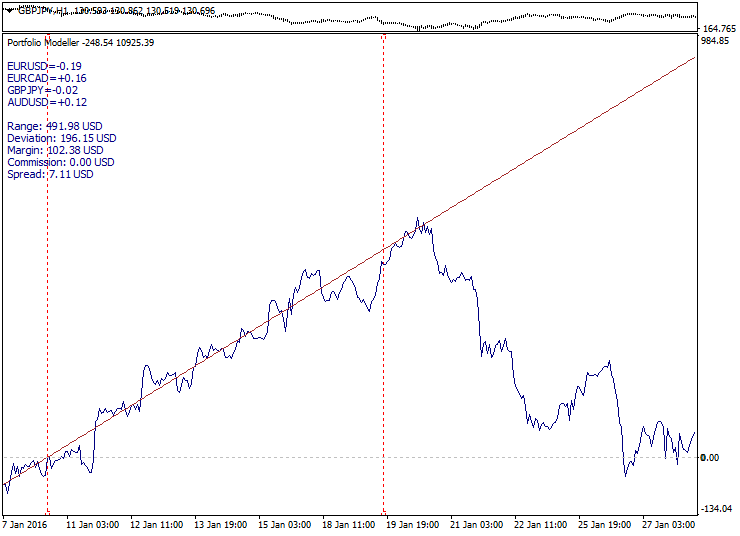
以下您可看到一个凌厉的趋势完毕:
这些缺点让我们重新考虑传统的方法。现在, 我们来看看差价突破和趋势反转的交易方法。一般的假设是, 既然我们无法避免投资组合的不稳定, 我们应该学会如何利用它。
为了开发差价突破的设置, 我们需要创建一个非常紧凑的, 在强劲走势的预期里波动最小的短线差价。我们越是压缩投资组合的波动, 其 "爆发" 越厉害。为了加速差价突破, 有可能在交易时段和新闻开始之前选择一个平静的市场间隔形成设置。PCA 优化方法最适合于波动压缩。在此设置中, 我们预先不知道会在哪个方向发生突破, 因此, 当在差价边界移动时, 入场已定义。
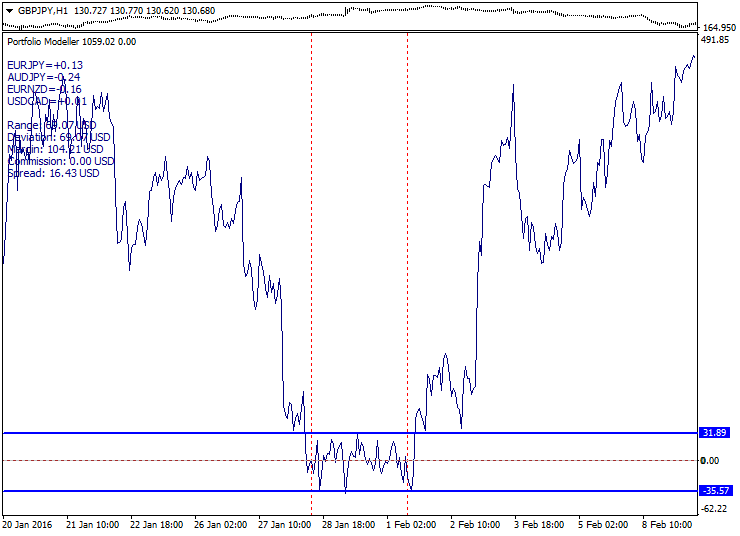
以下是从短线差价通道中退出的示例, 差价通道边界以高亮标示:
此方法的优点: 在图表上, 短线差价频繁, 且在爆发后波动往往超过差价走廊的宽度。而缺点: 差价在新闻发布时扩张, 且在价格上下移动几次时可能形成 "锯齿"。在走廊边界可能的调整期间, 建议在退出差价走廊之后可保守入场。
为了创建一个趋势反转设置, 先创建一个趋势模型, 并转变走势及跟踪投资组合的价位。走势方向已清晰定义, 但我们预先不知道何时趋势反转。跟踪内部趋势线交叉, 反向调整和回滚, 以便保守入场行动。跟踪外部趋势线的触发和回滚, 以便激进入场行动。
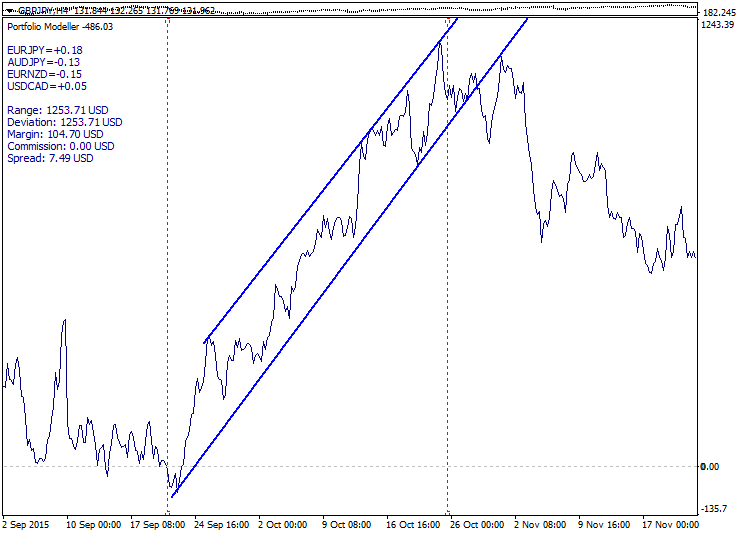
以下是一个显示内外趋势线的趋势投资组合示例:
此方法的优点: 不错的入场价格, 方便性, 有利于在价格极端不稳定的场合进行设置工作。缺点: 投资组合的价格可能由于基本面的原因沿趋势向上。为了改进这种情况, 我们可以在多个价位分批入场。
类似的设置可以用平方根抛物线函数模型来实现。设置基于众所周知的属性: 当价格达到行情分布范围的理论极限时, 其进一步的移动会受到阻碍。就像在其它情况时, 目标优化函数被调整为当前的行情分布。如果行情呈现正常的高斯分布, 基于时间的平方根律会始终完美地工作, 但由于行情分布呈分形和非稳定的性质, 则需要态势调整。
您可以在埃德加·彼得斯所著的以下书籍里找到更多的有关行情分布内容:
- 在资本市场中的混沌与秩序
- 分形行情分析
以下是一个投资组合从抛物线函数移开的示例:
这种设置完美的适应中线波动。然而, 就像趋势设置的情况下, 投资组合价格也许由于基本面因素向上移动。市场没有义务遵循任何目标函数的行为, 但它虽无义务, 不过从中偏离为好。在任何时候都保持一点自由度和二元性。所有交易设置并非绝对意义上的市场中立, 而是基于某种形式的技术分析上。
趋势和横盘的双重性质如下所示。一个趋势模型在一个更大的尺度看上去就类似一个不平坦的横盘:
当开发投资组合时, 除了品种组合和模型类型, 估计间隔的边界位置也是非常重要的。当配置投资组合时, 它对于移动边界并比较结果也许是有用的。良好的边界选择可以发现更适合交易设置条件的投资组合。如果一个投资组合仓位进入回撤, 可以调整投资组合, 而无需将现有持仓平仓。平移边界改变投资组合的曲线, 令其适应不断变化的情况。再重新分配投资组合之后, 仓位也要相应地进行调整。这并不意味着回撤将在某一时刻降低, 但调整组合可能会变得更为有效。
接下来, 我们来研究投资组合集的一些性质及其在交易系统中的可能应用。
投资组合集合最先吸引眼球的属性是集合扩张, 或投资组合自零点的发散距离。这很自然, 并应当合理地在交易中使用这个属性: 买入上涨的并卖出下跌的投资组合。
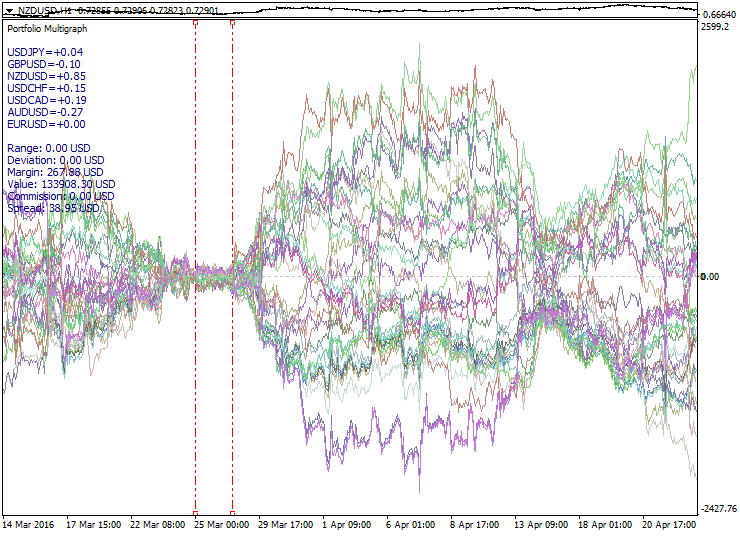
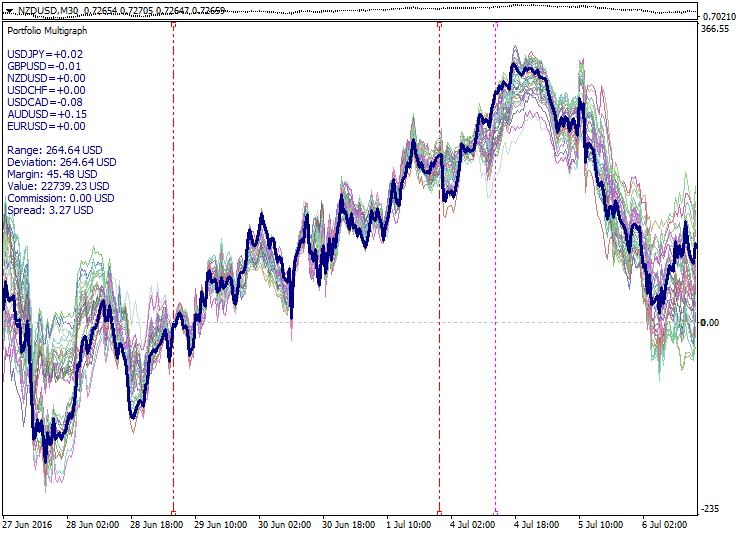
以下是投资组合集合的扩张示例:
第二个属性 — 投资组合集合压缩 (收敛) — 与之前的相对。它发生在扩张之后。这种行为的扩张和压缩周期, 可建议用来在抵达所谓的最高扩展度之后, 并预期返回集合中心时进行合成开仓。不过, 最高扩张度总在变化, 并且不可能预测集合曲线扩张的最后边界。
以下是投资组合集合的压缩示例:
各种目标函数, 过滤参数, 反转和组合的运用, 为试验并搜集高效的交易设置提供了良好机会。一般来说, 所有设置可以分为两类: 突破交易和回滚交易。
以下是第一类反转和投资组合平移的交易设置示例:
基于多趋势模型回滚交易设置的示例提供如下:
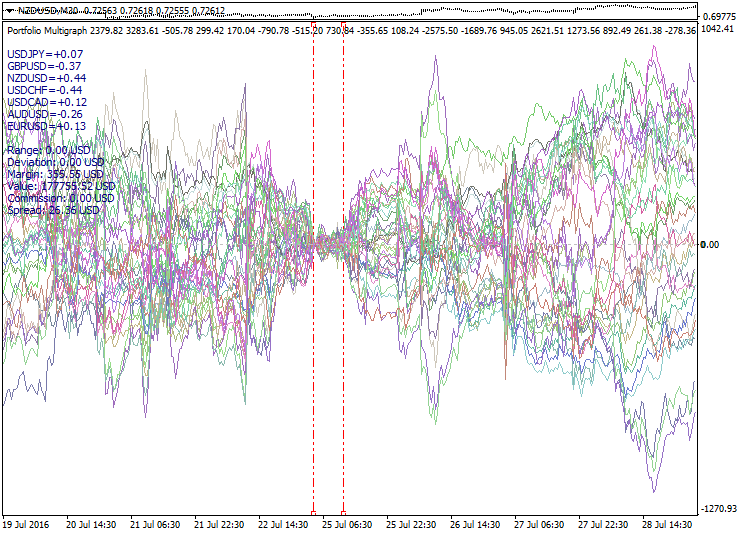
另一种回逆投资组合属性是集合扭曲 (自交叉)。典型情况下, 这对应于行情趋势的变化。如果我们预期投资组合扩张时交易, 扭曲则是负面影响, 需要重新分配集合。对于其它的策略, 一些投资组合曲线的交叉可用于识别有前途的和发挥出色的投资组合。此外, 有必要考虑行进距离, 级别, 集合的仓位以及相对于目标函数的位置。
以下是一个集合多次扭曲的示例:
到现在为止, 我们并未将注意力集中到交易量管理的问题上, 尽管这是任何交易系统的重要组成部分。通常, 我们可以描述以下方法:
- 交易单一的合成仓位 (最简单的情况)
- 切分交易量 (按照价位延伸入场)
- 在上涨投资组合里加仓 (趋势金字塔)
- 在回撤投资组合里加仓 (仓位摊平)
- 在投资组合调整后加仓 (正在完成的方法)
- 在投资组合逆转后加仓 (扩张策略)
- 增加新的投资组合 (合并投资组合)
- 组合方法 (若干方法的组合)
特殊的交易量管理方法应考虑所选交易系统的特点。当规划盈利和回撤时, 您的计算应基于投资组合的波动性。在最简单的情况里, 投资组合的波动性可根据其图形在确定时段内的走势范围进行评价。这比仅在以前的历史数据优化间隔内进行波动性评估要更好。了解投资组合的波动性, 就可以在一系列位置计算最大总回撤的理论值。依传统, 我们提请大家不要过于频繁的逆势激进加仓。在账户上为投资组合分配的总资金额度, 应考虑到所有持仓能够承受不利走势。
多重投资组合交易意味着系统化的投资组合选择与合并。如果已买入一个投资组合, 并添加另一个, 如果这个投资组合有明显的不同, 也许会有正面的多样化效果。但若投资组合是关联的, 也许会带来负面影响, 因为它们可能发现自己在不利走势的情况下都有回撤。正常时, 您应该避免添加关联的投资组合。乍一看, 在两个相关联的投资组合之间交易差价似乎是非常有前途的, 但仔细观察表明, 这种差价与平时的差价毫无二致, 因为它们不是固定的。
各种离场策略可以在多重资产组合的交易中运用, 包括:
- 根据全部投资组合的总结果平仓
- 根据群的总结果将投资组合群平仓
- 根据确定的投资组合目标和限制平仓。
对于一些策略, 入场点是至关重要的。例如, 如果一个策略在趋势逆转或调整之前运用极值价格, 则入场周期适合较短的。其它策略更加依赖加仓系统的优化计算和投资组合的选择原则。在此情况下, 个别投资组合也许会进入回撤, 但已合并的一序列内的其它 (更有效的) 投资组合可调节整体结果。
结论
投资组合交易的优势: 优化可以让您依据自己的喜好创建一个投资组合曲线, 以及形成期待的交易设置, 并如同在交易品种的价格图表上一样进行交易。不过, 如投资组合交易不同, 常规资产的购入和出售令交易员处于被动的地位 (因为他们只能接受当前价格图表或避免使用它)。此外, 随着形势的发展, 交易员可以调整自己的投资组合以适应新的市场条件。
投资组合交易的缺点: 标准挂单不可用了, 要求更严格的最低交易量, 在 30 分钟及更低周期的图表上点差更大, 日内剥头皮受限, 没有 OHLC 数据, 并不是所有的指标可以应用到投资组合。
一般来说, 这是一个交易中的特别的做法。在此, 我们只是简要介绍了投资组合的属性和工作方法。如果您打算对投资组合交易系统进行更深入的研究, 为此我建议使用 MetaTrader 5 平台, 尽管行情分布特性应该在专门的统计软件包里进行研究。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/2646
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 图形界面 VIII: 树形视图控件 (第二章)
图形界面 VIII: 树形视图控件 (第二章)
 跨平台智能交易程序: 订单
跨平台智能交易程序: 订单
新文章 在 MetaTrader 4 中的投资组合交易已发布:
作者:transcendreamer
太复杂了