MetaTrader 4 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
Cómo mejorar el simulador de estrategias para optimizar indicadores usando ejemplos de los mercados de tendencia y flat

Cómo mejorar el simulador de estrategias para optimizar indicadores usando ejemplos de los mercados de tendencia y flat

MetaTrader 4 — Ejemplos | 23 junio 2016, 14:50
2 479 0
Carl Schreiber
Carl Schreiber

Problemática

Uno de los problemas más extendidos a la hora de optimizar los robots comerciales es la enorme cantidad de parámetros utilizados.

Por ejemplo, optimizamos el experto con varios indicadores. Cada uno de ellos tiene varios parámetros. Dado que deberemos testar todas las combinaciones posibles, invertiríamos mucho tiempo en la optimización en condiciones normales. ¿Qué pasaría si pudiéramos reducir las combinaciones antes de proceder a la optimización del experto? Por ejemplo, antes de escribir el código del experto, escribiremos un pseudo-experto que le hará al mercado solo algunas preguntas concretas. De esta forma, dividimos el problema en partes más pequeñas, pudiendo así concentrarnos en cada una de ellas por separado. El pseudo-experto propuesto no realiza ninguna operación comercial. Como ejemplo elegiremos ADX y comprobaremos si es capaz de distinguir entre flat y tendencia, y también intentaremos obtener información adicional.

Imagínese la idea del comercio a corto plazo para un experto, y que este comercio dependa de la presencia del flat para el comercio con swings (comercio hacia una media móvil) o de la tendencia según una estrategia existente (comercio partiendo de una media móvil). Para definir el estado del mercado, el experto debe guiarse por el comportamiento de ADX en el marco temporal mayor: en este caso, nos referimos a las barras de horas. Aparte de ADX, el experto puede incluir 5 indicadores más, que se usan para el comercio a corto plazo. Cada uno de ellos, a su vez, puede tener 4 parámetros, y teniendo en cuenta que el salto es pequeño, cada parámetro puede adoptar 2000 valores diferentes. En total, tendríamos 2000*5*4 = 40 000. Ahora añadimos ADX, y nos encontramos con una tarea muy engorrosa: para cada combinación de los parámetros de ADX en teoría es necesario realizar 40 000 cálculos.

En este parámetro establecemos el periodo ADX' (PER), su precio (PRC) y el límite (LIM), para que podamos determinar el inicio de la tendencia, si el indicador ADX (MODE_MAIN) se eleva por encima de LIM, o del flat, si descendiende por debajo de LIM. Para el periodo PER se puede elegir 2,..,90 (Step1=> 89 valores diferentes), para el precio: 0,..,6 (=Close,..,Weighted, Step 1=> 7), y para LIM: 4,..,90 (Step1 => 87). En total, tenemos 89*7*87 = 54 201 combinaciones para la simulación. Más abajo podrá encontrar los ajustes para el simulador de estrategias:

Fig. 01 Parámetros de configuración del simulador

Fig. 02 Configuración del simulador: funciones del experto

Fig. 03 Funciones de configuración del simulador

Fig. 04 Optimización de la configuración del simulador

Al repetir esta optimización, no se olvide de limpiar el caché \tester\cache\. De otra forma, verá los resultados en "Resultados de la optimización" y "Gráfico de optimización" del simulador de estrategias comerciales, y no en un archivo csv, puesto que OnTester() en este caso no se ejecuta.

Claro que para optimizar estos diapasones normalmente se usa el simulador de estrategias, pero, en primer lugar, es necesario encontrar resultados inútiles para asegurarse de que podremos determinarlos y excluirlos, y en segundo lugar, existen motivos relacionados con el apredizaje para ampliar los diapasones. Debido a esto, nuestro pseudo-experto no comercia (no hay necesidad de usar todos los ticks), y disponemos solo de un indicador con 54 201 combinaciones que debemos testar. Podemos desactivar el modo genético y permitir al simulador que calcule todas las combinacieones por sí mismo.

Si no pudiéramos realizar una optimización preliminar de ADX o disminuir el número de combinaciones, entonces necesitaríamos multiplicar las 40 000 combinaciones de las otras variables del experto por las 54 201 combinaciones de ADX. Estará de acuerdo con que 2 168 040 000 combinaciones para la optimización es un trabajo gigantesco. Precisamente por este motivo vamos a utilizar la optimización genética.

Además, podremos hacer más que solo reducir significativamente el diapasón de los parámetros de ADX. Ahora vemos que el indicador ADX realmente es capaz de diferenciar el flat de la tendencia, incluso teniendo en cuenta que la determinación del flat se retrasa en comparación con la tendencia (no olvidemos que siempre queda la posibilidad de retocarlo). Ahora podemos aplicar y usar las nuevas ideas para determinar los stop loss y los objetivos del experto, dependiendo de los diapasones encontrados de flat y tendencia. Los periodos de ADX se testan desde PER: 11..20 (Step 1=> 10), PRC: 0,6 (Step 6=>2) y LIM: 17,..,23 (Step 1=> 7): solo son 140 combinaciones. Esto significa que en lugar de 2 168 040 000, solo nos quedan 4 680 000 combinaciones para la simulación, lo cual es 460 veces más rápido que en el modo no genético, o 460 veces mejor que en el modo genético. El simulador en el modo genético solo realiza unas 10.000 pasadas, pero en este caso, la simulación está sujeta a una cantidad sustancialmente mayor de otros parámetros del experto.

Observación al utilizar un algoritmo genético: los resultados varían mucho dependiendo de la relación de todas las combinaciones disponibles y de las pasadas ejecutadas. Cuanto peores sean los resultados durante la optimización, menos resultados buenos habrá, de los cuales se seleccionan los próximos ajustes.


Idea

Bien, creamos un pseudo-experto, entre cuyas tareas no se cuentan las operaciones comerciales. Sólo ejecuta tres funciones importantes. OnTick() se usa para comprobar los indicadores y determinar el estado del mercado, OnTester() anota el resultado final en nuestro archivo csv, y en calcOptVal() se calcula el valor OptVal, retornado con la ayuda de OnTester() al simulador de estrategias comerciales, para enviar órdenes y el algoritmo genético. La función OnTester(), que se llama al final de la pasada, retorna un valor determinado y añade una nueva línea al archivo csv para el posterior análisis al terminar por completo el proceso de optimización. 


Proyecto del pseudo-experto


Es necesario definir los criterios del cálculo del valor retornado: OptVal. Elegimos el diapasón del flat y la tendencia que se presenta como la diferencia entre el High máximo y el Low mínimo del mercado, y dividimos "TrndRange" entre "FlatRange", para que el optimizador pueda aumentar al máximo lo siguiente:
double   TrndRangHL,       // suma del High máximo - el Low mínimo de los mercados de tendencia
         TrndNum,          // número de mercados de tendencia
         FlatRangHL,       // suma del High máximo - el Low mínimo de los mercados con flat
         FlatNum,          // número de mercados con flat
         RangesRaw,        // Diapasón de mercados de tendencia, dividido entre el diapasón de mercados con flat (cuanto mayor sea, mejor)
         // ...            mire más abajo

double calcOptVal() // ¡¡primera aproximación!!
   {
      FlatRange    = FlatRangHL / FlatNum;
      TrndRange    = TrndRangHL / TrndNum;
      RangesRaw    = FlatRange>0 ? TrndRange/FlatRange : 0.0; 
      return(RangesRaw);
   }
...
double OnTester() 
   {
      OptVal = calcOptVal();
      return( OptVal );
   }




Si realizamos la optimización usando los ajustes enumerados más arriba, y OptVal = RangesRaw, entonces el resultado en el "Gráfico de optimización" tendrá el aspecto siguiente:

Fig. 05 Gráfico de optimización para Raw

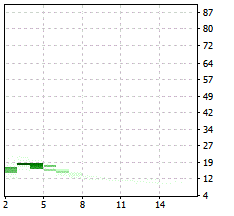
Después de familiarizarse con los mejores valores en los "Resultados de la optimización", ordenamos los "Resultados de OnTester" de arriba hacia abajo, y vemos lo siguiente:

Fig. 06 Mejores valores de optimización para Raw

Las proporciones son muy altas. Si miramos el archivo csv, veremos que la longitud media de los mercados con flat es de 1 barra (cantidad de mercados con flat + cantidad de mercados de tendencia), demasiado insignificante para usarlo con efectividad. (No debemos preocuparnos por las cifras que aparecen, como PRC=1994719249 en lugar de 0,..,6 dado que la cifra correcta del precio del indicador Adx está guardada en un archiv csv).

Este resultado insatisfactorio hace imprescindible añadir criterios adicionales para evitar la repetición de situaciones semejantes.


Retocando el pseudo-experto: cómo igualar los criterios

Al principio establecemos la longitud o el número mínimo de barras del flat o la tendencia: 

      FlatBarsAvg  = FlatBars/FlatNum; // sumar todas las 'barras de flat'  / número de barras de flat
      TrndBarsAvg  = TrndBars/TrndNum; // sumar todas las 'barras de tendencia'  / número de barras de tendencia
      BrRaw        = fmin(FlatBarsAvg,TrndBarsAvg);

Después indicamos la cantidad mínima de cambio entre flat y tendencia:

      SwitchesRaw  = TrndNum+FlatNum; // número de mercados de tendencia y de flat

Ahora nos encontramos con otro problema. RangesRaw oscilará teóricamente entre 0 y 100 000.0, BrRaw, entre 0 y 0.5, y SwitchesRaw, entre 0 y ~8000 (=Bars()) en caso de cambio en cada nueva barra.

Tenemos que igualar nuestros tres criterios. Para ellos necesitaremos una función: Arc tangens, o atan(..) en mq4. Lo hemos elegido porque al usarla, por ejemplo, desaparece el problema del cero o del valor negativo. Asimismo, atan() nunca supera el límite. De esta forma, por ejemplo en el caso de RangesRaw, la diferencia entre atan(100 000) y atan(20) está próxima a cero, y son ponderados de forma prácticamente idéntica. Esto dota de mayor influencia a los resultados de otros factores. Además, atan() proporciona un aumento constante del límite. Como contrapeso a esta función, un límite estricto del tipo if(x>limit) pondera equitativamente todos los valores que superen el límite, y de nuevo encuentra los mejores valores que estén más cerca del límite. Por qué este límite estricto no concuerda nuestros objetivos es algo de lo que hablaremos más tarde. 

Veamos cómo funciona atan(). Para construir el gráfico, he usado este instrumento:

Fig. 07 Función Atan

La versión marcada en azul pasa por el origen de las coordenadas y se limita entre -1 y +1 en el eje de las ordenadas.
La línea roja (con sus funciones) demuestra el desplazamiento conforme al eje de las abcisas x=0 a x=4.
La línea verde demuestra el cambio de la inclinación. Podemos controlar la velocidad a la que atan() se acerca a los límites y el grado paulatino al que disminuye la diferencia.

Si sustituimos 1*atan(..) por 2*atan(..), entonces el límite se desplazará a +2 y -2. Sin embargo, no será necesario que cambiemos el límite al que se aproximan nuestras versiones de atan(). 

La activación de los límites superiores e inferiores mediante el cambio de 1*atan() a -1*atan() no será necesaria. Si hacemos esto, entonces la función tenderá a -1 conforme aumente la х.

Ahora tenemos todo lo necesario para finalizar nuestro pseudo-experto.


Versión definitiva del pseudo-experto

Recordemos que el programa que estamos desarrollando no puede comerciar. Su función consiste en llamar a iADX(..) al abrir una nueva barra. Esto significa que no necesitaremos "todos los ticks" o los "puntos de control".  Por eso, al calcular el estado del mercado, podemo usar el modelo más rápido, "Solo precios de apertura" de las 2 barras anteriores del indicador ADX:

extern int                 PER   = 22;             // periodo de Adx
extern ENUM_APPLIED_PRICE  PRC   = PRICE_TYPICAL;  // precio de Adx
extern double              LIM   = 14.0;           // límite para la línea principal de Adx'
extern string            fName   = "";             // nombre del archivo en \tester\files, "" => ¡no hay archivo csv!


//+------------------------------------------------------------------+ 
//| Definiendo la variable global                                |
//+------------------------------------------------------------------+ 
double   OptVal,           // este valor se retorna con la ayuda de OnTester(), y su valor puede encontrarse en la pestaña OnTester()
         TrndHi,           // High máximo de los mercados de tendencia
         TrndLo,           // Low mínimo de los mercados de tendencia
         TrndBeg,          // precio al comienzo de los mercados de tendencia
         TrndRangHL,       // suma del High máximo - el Low mínimo de los mercados de tendencia
         TrndRangCl,       // último precio de cierre - primer precio de cierre de los mercados de tendencia (ha permanecido, pero sin uso)
         TrndNum,          // número de mercados de tendencia
         TrndBars=0.0,     // número de barras en los mercados de tendencia
         TrndBarsAvg=0.0,  // número medio de barras en los mercados de tendencia
         FlatBarsAvg=0.0,  // número medio de barras en los mercados con flat
         FlatHi,           // High máximo de los mercados con flat
         FlatLo,           // Low mínimo en los mercados con flat
         FlatBeg,          // precio al inicio de los mercados con flat
         FlatRangHL,       // suma del High máximo - el Low mínimo de los mercados con flat
         FlatRangCl,       // último precio de cierre - primer precio de cierre de los mercados con flat (ha permanecido, pero sin uso)
         FlatNum,          // número de mercados con flat
         FlatBars=0.0,     // número de barras de los mercados con flat
         FlatRange,        // tmp FlatRangHL / FlatNum
         TrndRange,        // tmp TrndRangHL / TrndNum
         SwitchesRaw,      // número de cambios
         SwitchesAtan,     // número de cambios de Atan
         BrRaw,            // Mínimo de horas del mercado con flat o de tendencia (cuantas más, mejor)
         BrAtan,           // Atan perteneciente a BrRaw
         RangesRaw,        // Diapasón de los mercados de tendencia dividido por el diapasón de los mercados con flat (cuanto mayor sea, mejor)
         RangesAtan;       // Atan pertenenciente a (TrndRange/FlatRange)

enum __Mkt // 3 estados del mercado 
 {
   UNDEF,  
   FLAT,
   TREND
 };
__Mkt MARKET = UNDEF;      // estado inicial del mercado
string iName;              // nombre del mercado
double main1,main2;        // valor de la línea principal Adx main


//+------------------------------------------------------------------+ 
//| OnTick calcula Indi, determina el estado del mercado             |
//+------------------------------------------------------------------+ 
void OnTick() 
 {
 //---
   static datetime tNewBar=0;
   if ( tNewBar < Time[0] ) 
    {
      tNewBar = Time[0];
      main1 = iADX(_Symbol,_Period,PER,PRC,  MODE_MAIN, 1); // ADX
      main2 = iADX(_Symbol,_Period,PER,PRC,  MODE_MAIN, 2); // ADX)
      iName = "ADX";

      // establecer la variable para determinar el estado adecuado del mercado
      if ( MARKET == UNDEF ) 
       { 
         if      ( main1 < LIM ) main2 = LIM+10.0*_Point; // en el MERCADO hay FLAT
         else if( main1 > LIM ) main2 = LIM-10.0*_Point; // en el MERCADO hay TENDENCIA
         FlatHi  = High[0];
         FlatLo  = Low[0];
         FlatBeg = Close[2];//
         TrndHi  = High[0];
         TrndLo  = Low[0];
         TrndBeg = Close[2];//
       }
      
      // ¿podemos comenzar a comerciar si en el mercado hay flat?
      if ( MARKET != FLAT && main2>LIM && main1<LIM)  // ADX
       {
         //finalizar una tendencia en el mercado
         TrndRangCl += fabs(Close[2] - TrndBeg)/_Point;
         TrndRangHL += fabs(TrndHi - TrndLo)/_Point;
                  
         // actualizar los valores correspondientes
         OptVal = calcOptVal();

         //establecer un nuevo flat
         MARKET  = FLAT;
         FlatHi  = High[0];
         FlatLo  = Low[0];
         FlatBeg = Close[1];//
         ++FlatNum;
         if ( IsVisualMode() )
          {
            if (!drawArrow("Flat "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 243, clrDarkBlue) ) // 39:el mercado de velas duerme
               Print("Error drawError ",__LINE__," ",_LastError);
          }
       } 
      else if ( MARKET == TREND )   // actualizar la tendencia actual
       {
         TrndHi = fmax(TrndHi,High[0]); 
         TrndLo = fmin(TrndLo,Low[0]); 
         TrndBars++;
       }
      
      // ¿podemos comenzar a comerciar si en el mercado hay tendencia?
      if ( MARKET != TREND && main2<LIM && main1>LIM) 
       { 
         // finalizar el flat en el mercado
         FlatRangCl += fabs(Close[2] - FlatBeg)/_Point;
         FlatRangHL += fabs(FlatHi - FlatLo)/_Point;
         
         // actualizar los valores correspondientes
         OptVal = calcOptVal();

         // establecer una nueva tendencia en el mercado
         MARKET  = TREND;
         TrndHi  = High[0];
         TrndLo  = Low[0];
         TrndBeg = Close[1];//
         ++TrndNum;
         TrndBars++;
         if ( IsVisualMode() )
          {
            if(!drawArrow("Trend "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 244, clrRed)) // 119:kl Diamond
               Print("Error drawError ",__LINE__," ",_LastError);
          }
       } 
      else if ( MARKET == FLAT  ) // actualizar el flat actual
       {
         FlatHi = fmax(FlatHi,High[0]);
         FlatLo = fmin(FlatLo,Low[0]); 
         FlatBars++; 
       }
      
    }
   if ( IsVisualMode() )  // representación de la situación real en el modo visual
    {
      string lne = StringFormat("%s  PER: %i    PRC: %s    LIM: %.2f\nMarket  #   BarsAvg  RangeAvg"+
                                "\nFlat:    %03.f    %06.2f         %.1f\nTrend: %03.f    %06.2f         %.1f   =>  %.2f",
                                 iName,PER,EnumToString(PRC),LIM,FlatNum,FlatBarsAvg,FlatRange,
                                 TrndNum,TrndBarsAvg,TrndRange,(FlatRange>Point?TrndRange/FlatRange:0.0)
      );
      Comment(TimeToString(tNewBar),"  ",EnumToString(MARKET),"  Adx: ",DoubleToString(main1,3),
              "  Adx-Lim:",DoubleToString(main1-LIM,3),"\n",lne);
    }
 }
Si ADX cruza LIM , significa que el anterior estado del mercado está finalizando, y que nos estamos preparando para uno nuevo. El pseudo-experto calcula todas las diferencias de las cotizaciones en puntos.

Vamos a establecer qué queremos conseguir, y a determinar qué necesitaremos para ello. Para el retorno de OnTester() es imprescindible un valor. El optimizador del simulador lo calcula según el principio "cuanto mayor, mejor". El valor retornado con la ayuda de OnTester() (OptVal) debe aumentar si la diferencia entre el flat y la tendencia se hace mejor para nuestros objetivos.

Ya hemos definido tres variables para calcular OptVal. Para dos de ellas podemos sencillamente establecer un mínimo aceptable:

  1. RangesRaw = TrndRage/FlatRange deberá ser superior a 1. El mercado de tendencia tiene un diapasón mayor comparado con el de flat. TrndRage y FlatRange se definen como los High máximos — los Low mínimos del mercado. Establecemos la intercepción del eje x con x=1.
  2. BrRaw deberá ser superior a 3 barras (= 3 horas). BrRaw = fmin(FlatBarsAvg,TrndBarsAvg).  FlatBarsAvg y TrndBarsAvg — cantidad media de barras para cada tipo de mercado. Esto es imprescindible para prevenir la aparición de valores a.m. en los límites. Vamos a establecer el eje x de esta intercepción con x=3.
  3. SwitchesRaw. Finalizamos la optimización en más de 8000 barras. El resultado, de cerca de 20 conexiones, (10 de mercado con flat y 10 de tendencia) no tiene sentido. Esto constituiría 400 horas o 16 días para cada mercado.

El problema es encontrar un límite permisible para SwitchesRaw, puesto que depende intensamente del marco temporal y de la cantidad total de barras. Aparte de 1) y 2), donde podríamos establecer una limitación de la certidumbre de nuestras consideraciones, es necesario echar un vistazo a los primeros resultados (pestaña Opti ADX TODOS en el archivo cvs adjunto) para obtener el límite:

Fig. 08 Opti ADX gráfico sin conexiones

En lugar de procesar ~2500 conexiones diferentes, usamos solo sqrt(2500) = 50 clases, con las que es mucho más cómodo trabajar. Para cada clase calculamos y construimos una media móvil. Vemos la presencia de un mínimo local con el valor 172. Vamos a usar 100, para ver cómo nuestro pseudo-experto se las apaña con este límite. Establecemos un coeficiente pequeño, 0.01, para proporcionar un aumento lento desde el límite elegido. Normalmente usaríamos un límite más alto, por ejemplo 200, pero debido a motivos relacionados con el aprendizaje, nos vemos obligados a actuar de otra forma.

Para obtener otros coeficientes, construimos el gráfico de la función. Los distribuimos de tal forma que la curva no sea demasiado suave en aquellos lugares donde esperamos resultados interesantes. La línea azul es la función para SwitchesRaw:

Fig. 09 Atan para el cambio (azul)

Vamos a echar un vistazo a nuestras dos funciones de evaluación.
La línea roja  es la función para BrRaw: el mínimo aceptable de la longitud del mercado es de 3 barras, y el coeficiente de 0.5 garantiza que incluso 8 barras (horas) pueden cambiar la situación.
La línea verde es la función para RangesRaw: el mínimo aceptable es de 1, y puesto que no esperamos un milagro, obtener más de 8 barras será muy complicado.

Fig. 10 Barras Atan (rojo) Diapasón (verde) y Cambio (azul)

Ahora podemos crear una función para calcular OptVal, que se retornará con la ayuda de OnTester().

  1. Dado que esto se aplica a las tres variables, ¡podemos multiplicarlas!
  2.  atan (..) puede tomar un valor negativo para nuestras tres funciones, por lo que es necesario evaluar: fmax (0.0, atan (..)). De lo contrario, por ejemplo, los dos resultados negativos de nuestra función atan () darán lugar a un valor positivo incorrecto para optval.
//+------------------------------------------------------------------+ 
//| calcOptVal calcula OptVal para retornarlo al simulador           |
//| y sus coeficientes para la evaluación                                    |
//+------------------------------------------------------------------+ 
// coeficientes  para SwitchesAtan, número de cambios:
double SwHigh = 1.0, SwCoeff=0.01, SwMin = 100;
// coeficientes  para BrAtan, número de barras:
double BrHigh = 1.0, BrCoeff=0.5,  BrMin = 3.0;
// coeficientes  para RangesAtan, TrendRange/FlatRange:
double RgHigh = 1.0, RgCoeff=0.7,  RgMin = 1.0;

double calcOptVal() {
   if ( FlatNum*TrndNum>0 ) {
      SwitchesRaw  = TrndNum+FlatNum;
      SwitchesAtan = SwHigh*atan( SwCoeff*(SwitchesRaw-SwMin))/M_PI_2;

      FlatBarsAvg  = FlatBars/FlatNum;
      TrndBarsAvg  = TrndBars/TrndNum;
      BrRaw        = fmin(FlatBarsAvg,TrndBarsAvg);
      BrAtan       = BrHigh*atan( BrCoeff*(BrRaw-BrMin))/M_PI_2;

      FlatRange    = FlatRangHL / FlatNum;
      TrndRange    = TrndRangHL / TrndNum;
      RangesRaw    = FlatRange>0 ? TrndRange/FlatRange : 0.0; 
      RangesAtan   = FlatRange>0 ? RgHigh*atan( RgCoeff*(RangesRaw-RgMin))/M_PI_2 : 0.0;
      return(fmax(0.0,SwitchesAtan) * fmax(0.0,BrAtan) * fmax(0.0,RangesAtan));  
   }
   return(0.0);
}

La otra parte del pseudo-experto es OnInit(). Esta se usa para anotar los encabezamientos de la columnas del archivo csv:

//+------------------------------------------------------------------+ 
//| función de inicialización del asesor                                  |
//+------------------------------------------------------------------+ 
int OnInit() 
  {
//---
   // anotar la línea del encabezamiento de la hoja de cálculos
   if ( StringLen(fName)>0 ) {
      if ( StringFind(fName,".csv", StringLen(fName)-5) < 0 ) fName = fName+".csv";    //  comprobar el nombre del archivo
      if ( !FileIsExist(fName) ) {                                                     // anotar los encabezamientos de la columna del nuevo archivo
         int fH = FileOpen(fName,FILE_WRITE);
         if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError); 
         string hdr = StringFormat("Name;OptVal;RangesRaw;PER;PRC;LIM;FlatNum;FlatBars;FlatBarsAvg;FlatRgHL;FlatRgCls;FlatRange;"+
                      "TrendNum;TrendBars;TrendBarsAvg;TrendRgHL;TrendRgCl;TrendRange;"+
                      "SwitchesRaw;SwitchesAtan;BrRaw;BrAtan;RangesRaw;RangesAtan;FlatHoursAvg;TrendHoursAvg;Bars;"+
                      "Switches: %.1f %.1f %.f, Hours: %.1f %.1f %.1f, Range: %.1f %.1f %.1f\n",
                      SwHigh,SwCoeff,SwMin,BrHigh,BrCoeff,BrMin,RgHigh,RgCoeff,RgMin);
         FileWriteString(fH, hdr, StringLen(hdr));
         FileClose(fH);
      }   
   }
//---
   return(INIT_SUCCEEDED);
  }

La función OnTester() finaliza el estado de mercado abierto y anota el resultado de optimización al final del archivo csv:

double OnTester() 
 {
   // comprobar el límite de omisión: por lo menos un cambio
   if ( FlatNum*TrndNum<=1 ) return(0.0);  // uno de ellos es igual a 0 => omitir resultados inútiles
   
   // ahora finalizamos el último mercado: flat
   if ( MARKET == FLAT ) 
    {
      TrndRangCl += fabs(Close[2] - TrndBeg)/_Point;
      TrndRangHL += fabs(TrndHi - TrndLo)/_Point;

      // actualizar los valores correspondientes
      OptVal = calcOptVal();

    } 
   else if ( MARKET == TREND ) // .. y tendencia
    {
      FlatRangCl += fabs(Close[2] - FlatBeg)/_Point;
      FlatRangHL += fabs(FlatHi - FlatLo)/_Point;

      // actualizar OptVal
      OptVal = calcOptVal();
    }
   
   // anotar los resultados en un archivo csv
   if ( StringLen(fName)>0 ) 
    {
      string row = StringFormat("%s;%.5f;%.3f;%i;%i;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.5f;%.6f;%.5f;%.6f;%.5f;%.2f;%.2f;%.0f\n",
                  iName,OptVal,RangesRaw,PER,PRC,LIM,
                  FlatNum,FlatBars,FlatBarsAvg,FlatRangHL,FlatRangCl,FlatRange,
                  TrndNum,TrndBars,TrndBarsAvg,TrndRangHL,TrndRangCl,TrndRange,
                  SwitchesRaw,SwitchesAtan,BrRaw,BrAtan,RangesRaw,RangesAtan,
                  FlatBarsAvg*_Period/60.0,TrndBarsAvg*_Period/60.0,
                  (FlatBars+TrndBars)
             );
             
      int fH = FileOpen(fName,FILE_READ|FILE_WRITE);
      if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError);
      FileSeek(fH,0,SEEK_END); 
      FileWriteString(fH, row, StringLen(row) );
      FileClose(fH);
    }
   // retornar 0.0 en lugar de los valores negativos. En nuestro caso, provocarán que el gráfico de optimización esté desordenado.
   return( fmax(0.0,OptVal) );
 }


Nuestro pseudo-experto está listo. Ahora preparamos el simulador para la optimización.

  1. Desactivamos el "algorítmo genético" para comrpobar cada combinación.
  2. Cambiamos los "Parámetros optimizados" a Custom. Esto nos da unas imágenes más interesantes en el "Gráfico de optimización".
  3. Es necesario asegurarse de que el caché en ..\tester\caches ha sido eliminado
  4. Para los archivos csv se requerirá que fName no esté vacío, y que el archivo csv existente sea eliminado de \tester\files
  5. Si dejamos el nombre del archivo para el archivo csv, el optimizador añadirá una línea tras otra hasta que comience a haber problemas con su tamaño.
  6. Elegimos el símbolo EURUSD.
  7. El periodo ha sido establecido en H1 (aquí de 2015. 08. 13 a 2015.11.20).
  8. El modelo se ha establecido como "solo precios de apertura".
  9. No se olvide de activar la "Optimización".

En mi portátil, el simulador ha realizado la optimización de los datos del año 2007 durante solo 25 minutos. El archivo csv definitivo se encuentra en ..\tester\files\.

En el gráfico de optimización podemos ver, por ejemplo, (bottom =LIM, right=PER):

Fig. 11 TesterGraph SwLim 100

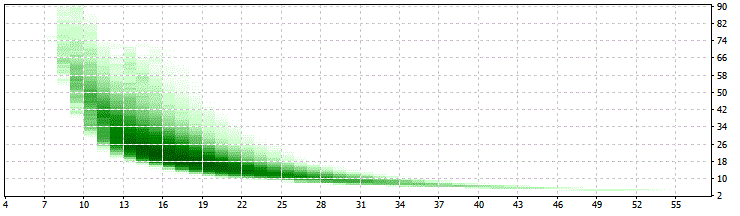
Tiene mucho mejor aspecto que nuestra optimización inicial. Vemos una zona vacía más compacta 34>PER>10 y 25>LIM>13, esto es mucho mejor que 2,..,90 y 4,..,90.

Comprobemos si los resultados para otro mínimo de cambios serán igual de estables:

SwMin = 50:

Fig. 11 TesterGraph SwLim 050

SwMin = 150

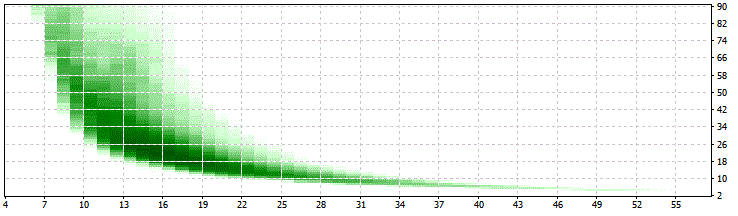
Fig. 13 TesterGraph SwLim 150

SwMin = 200:

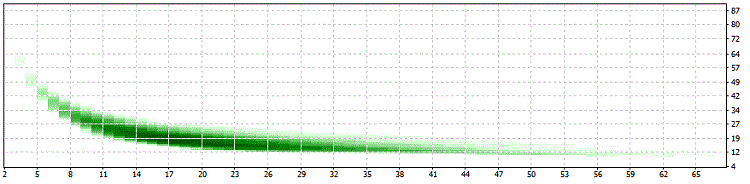
Fig. 14 TesterGraph SwLim 200

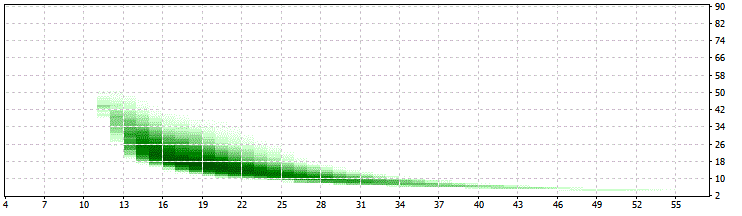
Las siguientes limitaciones son aplicables para toda la optimización: 34>PER>10 y 25>LIM>13, lo que es una buena señal de la estabilidad de este enfoque.

Brevemente:
  • Es imprescindible usar atan(..), para hacer OptVal igual de receptivo a nuestras variables.
  • Al usar atan(..) es necesario elegir correctamente los coeficientes. He invertido mucho tiempo hasta hallar resultados satisfactorios. Puede que usted tenga más suerte.
  • Podría pensarse que he introducido cambios hasta obtener el resultado necesario: como sucede al adaptar excesivamente el experto.
  • Este pseudo-experto no ha sido pensado para buscar una única mejor solución. El propósito de su uso es encontrar los límites aceptables para la reducción de la cantidad de datos necesarios para cada parámetro.


Análisis de los resultados en EXCEL, prueba de certidumbre

Cada pasada durante la optimización añade una nueva línea al archivo csv con información más detallada en comparación con la información propuesta por el simulador de estrategias comerciales, omitiendo además las categorías que no necesitamos, como por ejemplo el beneficio (Profit), las operaciones (trades), el factor de beneficio (profit factor)... Este archivo lo cargamos en Excel (o, en mi caso, en LibreOffice).

En primer lugar, necesitamos ordenarlo todo de acuerdo con OptVal y RangesRaw. Después de ello, obtenemos el siguiente resultado (pestaña: "Optimizing ADX SwLim 100 raw"):

Fig. 15 Optimizing ADX SwLim 100 raw

Vamos a ver más de cerca los 'mejores' 50 de acuerdo con OptVal. Los parámetros PER, PRC y LIM están marcados con diferentes colores para que sean más fáciles de reconocer.

  1. RangesRaw oscila entre 2.9 y 4.5. Esto significa que el diapasón del mercado de tendencia es 3-4.5 mayor que el diapasón del mercado con flat.
  2. El mercado con flat se mantiene durante 6 — 9 barras (horas).
  3. El diapasón del mercado con flat está limitado entre los 357 — 220 puntos, y esto es suficiente para comerciar en el diapasón.
  4. La tendencia se prolonga de 30 a 53 horas.
  5. El mercado de tendencia oscila entre los 1 250 y los 882 puntos.
  6. Si miramos los 200 mejores, y no los 50, entonces los diapasones RangesRaw casi son iguales: de 2.5 a 5.4. El flat se limita al diapasón de 221 — 372 puntos, la tendencia a 1,276 — 783 puntos.
  7. PER de los 200 mejores: de 14 a 20; LIM: de 14 a 20.  Sin embargo, estos parámetros debemos mirarlos con mayor detenimiento.
  8. Si estudiamos la parte en la que OptVal se convierte en 0.0, veremos valores muy altos de RangesRaw, al tiempo que los otros valores constatan que no son lo suficientemente buenos para el comercio (pestaña: "skipped OptVal=0"):

Fig. 16 skipped OptVal 0

Los valores RangesRaw son increíblemente grandes, en FlatBarsAvg son demasiado cortos para comerciar y/o los valores TrndBarsAvg son demasiados altos, con más de 1000 horas.

Ahora vamos a comprobar RangeRaw en la parte donde OptVal>0, y lo acortaremos de acuerdo con RangesRaw (pestaña: "OptVal>0 sort RangesRaw"):

Fig. 17 OptVal gt 0 sort RangesRaw

Los 50 mayores valores de RangesRaw se colocan de 20 a 11. Preste atención a TrendBarsAvg: el valor medio es de 100, eso son más de 4 días.

En general, podemos decir que OptVal ha excluido bastante bien a todos los valores de ADX que habrían dificultado el comercio. Por otra parte, el valor más alto de RangesRaw entre los mejores 200 (5.4) o los mejores 500 (7.1) tiene un aspecto prometedor.



Comprobación de los parámetros

Después de la comprobación necesaria sobre la certidumbre, analizamos los parámetros PER y PRC del indicador ADX con el límite LIM.

Hay muchos datos: 29 106 líneas, pero solo nos interesan las líneas donde el valor OptVal supera a 0. En el recuadro de valores no procesados son las primeras 4085 líneas (si están dibujadas de acuerdo con OptVal!). Lo guardamos en una nueva pestaña. Junto a PER añadimos otras tres columnas, de acuerdo con los dibujos. Todas las fórmulas están disponibles a través del archivo adjunto.

De las 5 líneas de las columnas D,E,F introducimos: AVERAGE(D$2:D5), STDEV(D$2:D5), SKEW(D$2:D5). Las celdas en esta fila solo muestran los valores de la última fila, que son el resultado estadístico de la columna RangesRaw al completo. ¿Por qué? Puesto que el recuadro está ordenado del mejor al peor, en la línea n se muestra el valor medio, la desviación estándar y la asimetría del mejor n. La comparación de los mejores valores n con todos los resultados nos podrá dar información para encontrar lo que estamos buscando (pestaña: "OptVal>0 Check PER, PRC, LIM"):

Fig. 18 OptVal gt 0 Check PER, PRC, LIM

¿Qué conclusión podemos extraer de aquí? En la segunda fila (debajo de last) podemos ver que el valor medio (Avg) de todos los valores PER es de 33.55, la desviación estándar (StdDev) es 21.60. En caso de distribuir PER de acuerdo con la distribución de Gauss, el 68% de todos los valores PER se encontrarán en los límites del valor medio +/- StdDev, y el 95%, en los límites de +/-2*StdDev. Aquí se encuentra entre 33.55 - 21.60 = 11.95 y 33.55 + 21.60 = 55,15. Ahora prestemos atención a las filas de los mejores valores. El valor medio comienza en la quinta fila desde 19 y aumenta lentamente hasta 20. Los cambios de StdDev tienen lugar desde 2.0 a 2.6. Y el 68% de todos los valores abarca el diapasón de 18 a 23. Y al fin, la asimetría. Es de 0.61 en la 2 fila para todos los parámetros PER. Esto significa que el lado izquierdo (menor) tiene más valores que el derecho, incluso si hasta este momento se subordinara a la distribución de Gauss. Si la asimetría supera +/- 1.96, no podremos presuponer que esa distrubución es gaussiana, y por eso deberemos tener mucho cuidado al usar el valor medio y la desviación estándar. Nos estorba que un lado esté demasiado 'relleno', y el otro más o menos 'vacío'. Una asimetría mayor a 0 significa que el lado derecho (>valor medio) tiene menos valores que el derecho. Por eso para PER se usa la distribución de Gauss, y se aplica el valor medio junto con StdDev. Si comparamos el desarrollo de los mejores resultados (de acuerdo con OptVal), veremos que el valor medio aumenta de 19 a 20 (fila 487!). StdDev, entretanto, aumenta de ~2.0 a 5.36 (fila 487). La asimetría nunca supera 0.4, en caso de omitir los 10 primeros resultados, y básicamente es positiva. Esto significa que debemos añadir uno (o dos) valores al lado 'izquierdo' del valor medio.

Los resultados de PRC necesitan de otra interpretación. Además de PER y LIM, los valores PRC determninan la escala nominal, cualquier cálculo entre ellos resulta inútil. Por eso, sencillamente calcularemos cuántas veces han aparecido, y también estableceremos el valor medio RangesRaw para cada PRC 0,..,6. Como podemos recordar, en nuestros planes entraba incluso comprobar conjuntos ridículos. Normalmente no usamos PRC=Open (1), PRC=High (2) o PRC=Low (3). En este caso, resulta imprescindible asegurarse de que Open es el resultado encontrado con más frecuencia entre los cincuenta mejores. Lo más seguro es que esto se deba a que usamos solo el precio de la barra, y ADX usa el High y Low de las barras, por lo que los parámetros high, low, close 'known to the open' tienen una ventaja paradójica gracias al indicador ADX, que los usa. El éxito de High y Low no es fácil de explicar. El propio hecho de que el precio de EURUSD caiga de 1.33 en agosto de 2014 a 1.08 en diciembre de 2015, explica el éxito de Low, pero no de High. Es posible que sea el resultado de una dinámica de mercado más fuerte. En cualquier caso, vamos a debilitarlos. Al comparar PER = Close, Typical, Median y Weighted, notamos que entre ellos no hay especial diferencia, si miramos a las columnas Q, R, y S. En el top 100 PRC=Typical(4) sería la mejor variante, que superaría incluso a PRC=High(2). Pero entre los mejores 500, vence PRC=Close.

Para LIM usaremos las mismas fórmulas que para PER. Es interesante observar que la 'última' asimetría (de todas) es muy superior +1.96, pero no para las mejores 100 (=0.38) o 500 (=0.46). Por eso vamos a usar solo las 500 mejores. El valor medio de las mejores 500 es 16.65, y StdDev es 3.03.  Por supuesto, LIM depende básicamente de PER: cuanto menor sea PER , mayor será LIM , y al revés. Precisamente por eso el diapasón LIM corresponde al diapasón PER.

Debido a ello, tomamos los 500 mejores resultados para los diapasones de nuestras tres variables: PER, PRC, y LIM :

  • PER Avg=20.18 +/- StdDev=5.51 Skew=0.35 (-2) => (20.18-5.41-2=) 14,..,(20.18+5.52=) 26 (Step 1 => 13).
  • PRC de acuerdo con la fila 500 solo podemos elegir para close (Step 0 => 1).
  • LIM Avg=16.64 +/- StdDev=3.03 Skew=0.46 (-2) => (16.64-3.03-2=) 12,..,(16.64+3.03=) 20 (Step 1 => 9)

En general, tenemos ahora solo 13*1*9 = 117 combinaciones para optimizar el experto.

Veamos los resultados con mayor detalle (pestaña: "OPT Top 500 Best PER's Average"):

Fig. 19 OPT Top 500 Best PER's Average

Vemos que el valor PER=18 se encuentra con frecuencia entre los mejores 500, y con PER=22 se dispone del mayor valor medio. Ambos, incluidos sus LIM, son abarcados por nuestro conjunto.


Modo visual

Vamos a comprobar al fin PER con el mejor resultado del top 500: PER=22. Cancelando la elección de PRC=Open,Low,High, encontramos estos ajustes con una relación de diapasón de 4.48 en la fila 38, con fondo amarillo en la anterior imagen de la pestaña.

Iniciamos el pseudo-experto en el modo visual con estos parámetros y utilizamos ADX con los mismos parámetros.

En el modo visual nuestro pseudo-experto ubica una flecha azul a la derecha/izquierda en la barra sieguiente donde se haya detectado el flat, y una flecha roja a la derecha/izquierda en el caso de las barras de tendencia (desde: el miér. 2015.07.30 05:00 al mar. 2015.08.04 12:00):

Fig. 20 VisualMode Per 22

Resultan obvios dos problemas de ADX, que pueden empujarnos a mejorar esta idea.

  1. ΑDX se retrasa, en especial al detectar el flat, si el valor del indicador ADX ha dado un salto. Para que se 'tranquilice' se necesitará bastante tiempo. Sería mejor que el flat fuera detectado el 2015.08.03 a las 00:00, y no el 2015.08.3 a las 09:00.
  2. Si ADX se encuentra cerca de LIM , podremos pensar que estamos recibiendo señales falsas. Por ejemplo, sería mejor si existiera la posibilidad de no detectar la tendencia del 2015.08.03 a las 14:00.
  3. Si el diapasón de barras high-low se hace menor, incluso una pareja de barras 'pequeñas' en la misma dirección se identificará como nueva tendencia. En lugar del 2015.08.03 a las 20.00, sería mejor que la nueva tendencia fuera detectada más tarde, aproximadamente el 2015.08.04 a las 07:00.
  4. El pseudo-experto presentado no percibe diferencia alguna entre tendencias ascendentes o descendentes. Dependerá de usted si va utilizar, por ejemplo, DI+ y DI del indicador ADX, u otros indicadores.
  5. Es posible que la longitud media de los mercados de tendencia (46.76, y esto son tres días) pueda resultar demasiado larga. En este caso, si SwMin es mayor (en lugar de 100) o SwCoeff es menor (en lugar de 0.01), o en ambos casos, usted obtendrá los resultados que más correspondan a sus deseos.
Estos cinco puntos le servirán como puntos de partida para encontrar o escribir el código para su propio indicador y determinar mejor el mercado con flat o el mercado de tendencia. El pseudo-experto adjunto se puede corregir fácilmente si usted tiene su propia idea sobre el diagnóstico del flat o la tendencia en el mercado.



Conclusión

Un experto que use ADX debe testar 54,201 combinaciones solo para optimizar este único indicador, con la esperanza de que ADX cumplirá con todo lo que necesitamos. Si el experto no es tan exitoso como esperábamos, entonces será difícil resolver el problema de la mejora del mismo. Después de esta optimización, que solo ocupa un par de minutos para todas las combinaciones (54,201) del indicador ADX, hemos observado lo siguiente:

  1. ADX es capaz de distinguir si el mercado con flat o el mercado de tendencia se han desarrollado hasta el momento actual. 
  2. Hemos logrado reducir la cantidad de combinaciones significativas desde las 54,201 iniciales hasta solo 117 (= 13 (PER) * 1 (PRC) * 9 (LIM)).
  3. El diapasón del flat fluctúa entre 372 y 220 puntos (top-100).
  4. El diapasón de la tendencia se encuentra entre 1,277 y 782 puntos.

Por consiguiente, podemos reducir las combinaciones iniciales del experto de 2,168,040,000 a (117*40,000=) 4,680,000. Esto constituye solo el 0.21%, un 99.7% más rápido o mucho mejor en el caso de la optimización genética, porque se comprobará un número mayor de variantes de otros parámetros que no están relacionados con ADX. Reducción de los ajustes de nuestro pseudo-experto:

Fig. 21 StratTester-Setup EA Options reduced

Fig. 22 StratTester-Setup Optimizations reduced

Además, obtenemos información valiosa sobre los criterios para comenzar a comerciar, para finalizar el comercio y para colocar/desplazar stops y objetivos.

Podrá encontrar el pseudo-experto en el archivo Excel adjunto. Hemos anotado cada paso, explicado todas nuestras acciones, y también hemos analizado las posibles trampas en las que se puede caer. Todo esto debería permitirle a usted proceder a la búsqueda de indicadores optimizados antes de usarlos en el experto. Si usted está planeando inventar un método propio para determinar el flat y la tendencia, puede comparar este con los resultados de ADX, y así encontrar la combinación de indicadores que más le convenga.

Si usted quiere utilizarlo para buscar el mejor indicador o varios indicadores para mercados con flat y de tendencia, entonces lo más probable es que tenga que cambiar los coeficientes calcOptVal(). Por ejemplo, si usted quiere usar un periodo de tiempo más largo, tendrá que, como mínimo, aumentar SwMin. Tenga en cuenta que un buen valor de OptVal permitiría al modo genético encontrar para usted los mejores ajustes de entre las numerosas combinaciones. Asimismo, usted podrá usar esta idea para optimizar los indicadores de forma completamente distinta. En este caso, usted estará obligado a reescribir por completo la función calcOptVal().

Si desea trabajar con este experto, por favor, no se olvide de hacer lo siguiente.

  1. Comprobar que el archivo cache ha sido eliminado de ..\tester\caches.
  2. Si necesita tener el archivo csv en ..\tester\files\, entonces introduzca el nombre del archivo fName y elimine el archivo csv ya existente con este nombre.
  3. Si no necesita el archivo csv, entonces deje fName en los parámetros del pseudo-experto.
  4. Si deja el nombre de archivo para el archivo csv, el optimizador añadirá una línea tras otra, hasta que comience a tener problemas con su tamaño.
  5. Sustituya los "Parámetros optimizados" por "Custom"" en la pestaña "Simulador".
  6. El modo más sencillo de influir en OptVal y los resultados del algoritmo consiste en cambiar un mínimo de tres coeficientes: SwMin, BrMin, RgMin.
  7. Establezca "Modelo" en "Solo precios de apertura", así será más rápido.
  8. Si usted usa fechas diferentes ("Use Date" : From..To), será necesario ajustar los coeficientes directamente sobre la función calcOptVal() dentro del propio experto.
  9. Después de finalizar la optimización, elija los ajustes de la pestaña "Resultado de la optimización" y comience de nuevo en el "Modo visual" , para asegurarse de que la optimización ha implementado sus ideas.
  10. La flecha azul a la derecha/izquierda designa el flat, la flecha roja a la derecha/izquierda, designa la tendencia.
  11. Si quiere crear una mejor alternativa al indicador ADX, puede que no necesite un archivo csv: solo tiene que realizar la optimización, hacer un seguimiento de los mejores resultados en el "modo visual", introducir los cambios, optimizar de nuevo y así sucesivamente, hasta que logre el resultado necesario.
  12. En lo que respecta a las preguntas de mercado no relacionadas con el flat y la tendencia, es necesario usar archivos csv y, posiblemente, otros métodos para el cálculo de OptVal.

Aun considerando todo lo anterior, por favor tenga en cuenta que no puedo darle garantías de éxito.

Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/2118

Archivos adjuntos |
Descargar ZIP
Optimizing_ADX_SpreadSheet.zip (13991.75 KB)
otimIndi_Publ.mq4 (13.4 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Interfaces gráficas V: Control "Lista combinada" (Capítulo 3) Interfaces gráficas V: Control "Lista combinada" (Capítulo 3)
En dos primeros capítulos de la quinta parte sobre las interfaces gráficas hemos desarrollado las clases para crear la barra de desplazamiento y la lista. En este capítulo vamos a hablar de la clase para la creación del control llamado “Lista combinada”. Éste también es un control compuesto que incluye los controles analizados en dos primeros capítulos de la quinta parte.
Interfaces gráficas V: Control "Lista" (Capítulo 2) Interfaces gráficas V: Control "Lista" (Capítulo 2)
En el primer capítulo de la quinta parte de la serie hemos desarrollado las clases para la creación de los controles como la barra de desplazamiento vertical y horizontal. En este artículo vamos a aplicarlas en la práctica. Esta vez diseñaremos la clase para la creación del control “Lista”, y la barra de desplazamiento vertical será su parte integrante.
Interfaces gráficas VI: Controles "Casilla de verificación", "Campo de edición" y sus tipos combinados (Capítulo 1) Interfaces gráficas VI: Controles "Casilla de verificación", "Campo de edición" y sus tipos combinados (Capítulo 1)
Este artículo empieza la sexta parte de la serie sobre el desarrollo de la librería para la creación de las interfaces gráficas en los terminales MetaTrader. En el primer capítulo hablaremos sobre los siguientes controles: “casilla de verificación”, “campo de edición” y los tipos combinados de estos controles.
Por dónde comenzar a crear un robot comercial para la Bolsa de Moscú MOEX Por dónde comenzar a crear un robot comercial para la Bolsa de Moscú MOEX
Muchos tráders de la Bolsa de Moscú querrían automatizar sus algoritmos comerciales, pero no saben por dónde empezar. El lenguaje MQL5 propone no solo un conjunto enorme de funciones comerciales, sino también clases preparadas, que facilitan al máximo los primeros pasos en el trading automático.