Enhancing the StrategyTester to Optimize Indicators Solely on the Example of Flat and Trend Markets

Problem

There are too many parameters to optimize.

A trading EA with many indicators that have multiple parameters will need a lot of time for its optimization as there will be way too many combinations to test. What if we were able to reduce this amount of combinations before we start the optimization of the trading EA? In other words, before coding the trading EA we code a pseudo-EA that asks only specific questions to the market. We split a big problem into smaller ones and solve them separately. This pseudo-EA doesn't trade! As an example we choose the ADX and check whether this indicator is capable of distinguishing between flat and trend markets, and maybe we could gain some additional information.

Imagine a short term trading idea for the trading EA that depends on knowing whether the market is flat to 'swing-trade' (trading back to the moving average) or it has a trend for a trend following strategy (trading away from the moving average). For this distinction our trading EA should use (only) the ADX on a higher timeframe - here 1h-bars. Beside the ADX the trading-EA might have 5 indicators (for its short term trade management). Each might have 4 parameters to set and and each of them has 2000 different values due to their small steps. That makes in total 2000*5*4 = 40,000. Let's now add the ADX. For each combination of the ADX' parameters, in theory, we have to pass additionally 40.000 calculations.

Here in this example we will set the ADX' Period (PER), its Price (PRC) and a Limit (LIM) so that we define a beginning trend by ADX (MODE_MAIN) rising above LIM and a flat market by falling below LIM. For the Period PER we might try 2,..,90 (Step1=> 89 different values), for  the price we can choose 0,..,6 (=Close,..,Weighted, Step 1=> 7) and for LIM we try 4,..,90 (Step1 => 87). In total we have 89*7*87 = 54,201 combinations to test. Here is the setup of the Strategy Tester:

If you repeat such optimization don't forget to delete the cache file in \tester\cache\. Otherwise you'll find the results in the Optimization Results and Optimizations Graph of the Strategy Tester but NOT in the csv-file, as OnTester() isn't executed in such a case.

Of course, normally one would use such ranges for the optimization by the Strategy Tester, but firstly we should find meaningless results to see whether we are able to detect and exclude them, and secondly there are educational reasons to expand the ranges. Due to the fact that our pseudo-EA does not trade (no need to use every tick!) and we only have one indicator with 54,201 combinations to test, we can switch off the genetic mode and let the Tester calculate all combinations.

If we would not do this pre-Adx-optimization or we were not able to reduce the number of the Adx combinations, we would have to multiply 40,000 combinations of other variables of the trading-EA with the ADX' 54,201 combinations and we would get 2,168,040,000 combinations for the optimization - quite a lot to do, so we have to use the genetic optimization.

At the end we will not only be able to reduce the Adx' parameter range drastically - that's OK, it is expected! We will get a better understanding of the ADX as we will be able to see that the ADX is indeed capable to distinguish between flat and trend markets - even if the detection of the flat market detection is a bit more lagging than the trend market (room for improvement?)! And furthermore we might get some ideas to determine the stop losses and the targets of the trading EA due to the found ranges of the flat and trend markets. The periods of the ADX are tested from PER: 11..20 (Step 1=> 10), PRC: 0,6 (Step 6=>2) and LIM: 17,..,23 (Step 1=> 7) - in total there are only 140 combinations. That means that instead of 2,168,040,000 we only have 4,680,000 combinations for the trading EA to test which is ~460 times faster in the non-genetic mode or ~460 times better in the genetic mode. In the genetic mode the tester runs only ~10.000 passes, but now a lot more values of other parameters of the trading EA are tested!

Remark if you use the Genetic Algorithm: Its results vary heavily according to the relation of the totally available combination and the actually performed passes. The worse results you have during the optimization, the smaller is the amount of good results from which next setups are selected.

The Idea

We build a pseudo-EA that does not trade. It has only three important functions. OnTick(), where we check the indicator and determine the market state, OnTester() where we write the final result to our csv-file, and calcOptVal() where we calculate the value OptVal which is returned by OnTester() to the Strategy Tester for the ordering and the Genetic Algorithm. Its OnTester() function which is called at the end of an optimization pass returns a specific value and it adds a new line to a csv-file for an analysis after the whole optimization is finished.

The Pseudo-EA, First Approach

Now we need to determine the criteria for calculating the returned value: OptVal. We choose the range of the flat and trend markets, which is the difference between the highest High and the lowest Low of the actual market, and divide "TrndRange" by "FlatRange" so that the optimizer can maximize this:

double   TrndRangHL,       // sum of the highest High - lowest Low of the trend markets
         TrndNum,          // number of the trend market
         FlatRangHL,       // sum of the highest High - lowest Low of the flat markets
         FlatNum,          // number of the flat market
         RangesRaw,        // Range of the trend market divided by range of flat markets (the bigger the better)
         // ...            see below

double calcOptVal() // first approach!!
   {
      FlatRange    = FlatRangHL / FlatNum;
      TrndRange    = TrndRangHL / TrndNum;
      RangesRaw    = FlatRange>0 ? TrndRange/FlatRange : 0.0; 
      return(RangesRaw);
   }
...
double OnTester() 
   {
      OptVal = calcOptVal();
      return( OptVal );
   }

If we run an optimization with the above mentioned settings and OptVal = RangesRaw, the result in the Optimization Graph looks as follows:

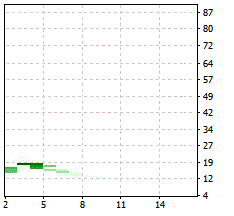
And if we look at the best values in the Optimizations Results ordered by "OnTester Result" top down, we see:

Ridiculous high relations! If we look at the csv-file, we see that the average length of the flat markets is 1 bar and the amount of switches (number of flat markets + number of trend markets) is also too small for a meaningful usage. (The strange numbers for PRC=1994719249 instead of 0,..,6 should not bother us, as the correct number for the Price of the Adx is written in the csv-file!).

This unsatisfying result means that we have to add some more criteria to exclude those ridiculous situations.

Pseudo-EA, Improving

At first we simply add a minimum length or a minimum of bars of the markets' flat or trend:

      FlatBarsAvg  = FlatBars/FlatNum; // sum all 'flat-bars'  / number of  flat markets
      TrndBarsAvg  = TrndBars/TrndNum; // sum all 'trend-bars' / number of trend markets
      BrRaw        = fmin(FlatBarsAvg,TrndBarsAvg);

Secondly, we specify a minimum of switches between the flat and trend:

      SwitchesRaw  = TrndNum+FlatNum; // number of trend and flat markets

Now we face the next problem! RangesRaw ranges from 0 to 100,000.0, BrRaw from 0 to 0.5 and SwitchesRaw from 0 to ~8000 (=Bars()) - theoretically if we have a switch on every new bar.

We need to equalize our three criteria! For all of them we use the same needed function: Arc tangens - or in mq4 - atan(..)! Other than e.g. sqrt() or log() we don't have any problem with 0 or negative values. atan() never exceeds a limit so that, for example, with RangesRaw, the difference between atan(100,000) and atan(20) becomes almost 0 and they are weighted almost equally so that the results of the other factors get more influence. Furthermore atan() provides a smooth increase to the limit, while a hard limit like if(x>limit) weights all values greater limit equally and again will find best values close to our limit but it will not be what we are looking for. You will see that later!

Lets see how atan() works (for the atan()-graphics I use this):

The blue version is (only) limited between +1 and -1 (by the division of pi/2).
The red line (and its function) shows how we can move the intercept of the x-axis away from x=0 to x=4.
The green line shows how we change the steepness. We control how fast atan() approaches the limits, how fast the differences gradually become smaller.

What we don't need here is to change the limit our atan() versions approach. But for your information, if you e.g. change the first 1*atan(..) to 2*atan(..), the limit moves to +2 and -2.

What we don't need is to switch the upper and the lower limit by setting 1*atan() to -1*atan(). Now our function is approaching -1 for greater x.

Now we have everything for our pseudo-EA. Let's start putting things together.

The Pseudo-EA, Final Version

Our pseudo-EA does not trade! It only calls iADX(..) if a new bar is opened. It means that we do not need "Every Tick" or the "Control Points"! We can use the fastest model "Open Price only" as we calculate the market state by the previous 2 bars of the ADX:

extern int                 PER   = 22;             // Adx Period
extern ENUM_APPLIED_PRICE  PRC   = PRICE_TYPICAL;  // Adx Price
extern double              LIM   = 14.0;           // Limit for Adx' mail line
extern string            fName   = "";             // file name in \tester\files, "" => no csv-file!


//+------------------------------------------------------------------+
//| Global variable definition                                       |
//+------------------------------------------------------------------+
double   OptVal,           // this value is returned by OnTester() and its value can be found in the OnTerster()-Tab of the StrategyTester
         TrndHi,           // highest High of the actual trend market
         TrndLo,           // lowest Low of the actual trend market
         TrndBeg,          // price at the beginning of a trend market
         TrndRangHL,       // sum of highest High - lowest Low of the trend markets
         TrndRangCl,       // last close - first closing of trend market (left but not used)
         TrndNum,          // number of trend market
         TrndBars=0.0,     // number of bars of the trend market
         TrndBarsAvg=0.0,  // avg bars in trend market
         FlatBarsAvg=0.0,  // avg bars in flat market
         FlatHi,           // highest High of the actual flat market
         FlatLo,           // lowest Low of the actual flat market
         FlatBeg,          // price at the beginning of a flat market
         FlatRangHL,       // sum of highest High - lowest Low of the flat markets
         FlatRangCl,       // last close - first close of a flat market (left but not used)
         FlatNum,          // number of flat market
         FlatBars=0.0,     // number of bars of the flat market
         FlatRange,        // tmp FlatRangHL / FlatNum
         TrndRange,        // tmp TrndRangHL / TrndNum
         SwitchesRaw,      // num of switches
         SwitchesAtan,     // Atan of num of switches
         BrRaw,            // Min of hours of either flat or trend market (more is better)
         BrAtan,           // Atan of BrRaw
         RangesRaw,        // Range of trend market divided by range of flat markets (the bigger the better)
         RangesAtan;       // Atan of (TrndRange/FlatRange)

enum __Mkt // 3 state of the markets 
 {
   UNDEF,  
   FLAT,
   TREND
 };
__Mkt MARKET = UNDEF;      // start state of the market.
string iName;              // indicator name
double main1,main2;        // values of the Adx main line


//+------------------------------------------------------------------+
//| OnTick calc the Indi, determin the market state                  |
//+------------------------------------------------------------------+
void OnTick() 
 {
 //---
   static datetime tNewBar=0;
   if ( tNewBar < Time[0] ) 
    {
      tNewBar = Time[0];
      main1 = iADX(_Symbol,_Period,PER,PRC,  MODE_MAIN, 1); // ADX
      main2 = iADX(_Symbol,_Period,PER,PRC,  MODE_MAIN, 2); // ADX)
      iName = "ADX";

      // set the var. that the appropriate market state is defined
      if ( MARKET == UNDEF ) 
       { 
         if      ( main1 < LIM ) main2 = LIM+10.0*_Point; // MARKET becomes FLAT
         else if ( main1 > LIM ) main2 = LIM-10.0*_Point; // MARKET becomes TREND
         FlatHi  = High[0];
         FlatLo  = Low[0];
         FlatBeg = Close[2];//
         TrndHi  = High[0];
         TrndLo  = Low[0];
         TrndBeg = Close[2];//
       }
      
      // do we enter a flat market?
      if ( MARKET != FLAT && main2>LIM && main1<LIM)  // ADX
       {
         //finalize trend market
         TrndRangCl += fabs(Close[2] - TrndBeg)/_Point;
         TrndRangHL += fabs(TrndHi - TrndLo)/_Point;
                  
         // update relevant values
         OptVal = calcOptVal();

         //set the new flat market
         MARKET  = FLAT;
         FlatHi  = High[0];
         FlatLo  = Low[0];
         FlatBeg = Close[1];//
         ++FlatNum;
         if ( IsVisualMode() )
          {
            if (!drawArrow("Flat "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 243, clrDarkBlue) ) // 39:candle market sleeps
               Print("Error drawError ",__LINE__," ",_LastError);
          }
       } 
      else if ( MARKET == TREND )   // update the current trend market
       {
         TrndHi = fmax(TrndHi,High[0]); 
         TrndLo = fmin(TrndLo,Low[0]); 
         TrndBars++;
       }
      
      // do we enter a trend market?
      if ( MARKET != TREND && main2<LIM && main1>LIM) 
       { 
         // finalize flat market
         FlatRangCl += fabs(Close[2] - FlatBeg)/_Point;
         FlatRangHL += fabs(FlatHi - FlatLo)/_Point;
         
         // update relevant values
         OptVal = calcOptVal();

         // set the new trend market
         MARKET  = TREND;
         TrndHi  = High[0];
         TrndLo  = Low[0];
         TrndBeg = Close[1];//
         ++TrndNum;
         TrndBars++;
         if ( IsVisualMode() )
          {
            if(!drawArrow("Trend "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 244, clrRed)) // 119:kl Diamond
               Print("Error drawError ",__LINE__," ",_LastError);
          }
       } 
      else if ( MARKET == FLAT  ) // update the current flat market
       {
         FlatHi = fmax(FlatHi,High[0]);
         FlatLo = fmin(FlatLo,Low[0]); 
         FlatBars++; 
       }
      
    }
   if ( IsVisualMode() )  // in VisualMode show the actual situation
    {
      string lne = StringFormat("%s  PER: %i    PRC: %s    LIM: %.2f\nMarket  #   BarsAvg  RangeAvg"+
                                "\nFlat:    %03.f    %06.2f         %.1f\nTrend: %03.f    %06.2f         %.1f   =>  %.2f",
                                 iName,PER,EnumToString(PRC),LIM,FlatNum,FlatBarsAvg,FlatRange,
                                 TrndNum,TrndBarsAvg,TrndRange,(FlatRange>Point?TrndRange/FlatRange:0.0)
      );
      Comment(TimeToString(tNewBar),"  ",EnumToString(MARKET),"  Adx: ",DoubleToString(main1,3),
              "  Adx-Lim:",DoubleToString(main1-LIM,3),"\n",lne);
    }
 }

If the ADX crosses LIM we finalize the previous market state and prepare a new one. The pseudo-EA calculates all it's quote differences in Points!

Let's look now at that what we want to achieve and determine what is needed for that. We need a number for OnTester() to return. The optimizer of the Strategy Tester calculates the greater the better. The value returned by OnTester() (OptVal) should therefore increase if the distinction between flat and trend market gets better for our needs!

We have determined three variables to calculate OptVal. For two of them we easily can set a reasonable minimum:

1. RangesRaw = TrndRage/FlatRange should be greater than 1! The trend market should have a higher range than the flat market. TrndRage and FlatRange are defined as highest High - lowest Low of the actual market. Let's set x-axis intercept at x=1.
2. BrRaw should be greater than 3 bars (= 3 hours). BrRaw = fmin(FlatBarsAvg,TrndBarsAvg).  FlatBarsAvg and TrndBarsAvg are the average number of bars of each market. We need this to prevent the a.m. values at the boundaries. Let's set the x-axis of this intercept at x=3.
3. SwitchesRaw. We are going to optimize on more than 8000 bars. A result of e.g. only 20 switches (10 flat and 10 trend markets) wouldn't make any sense.  It would mean on average 400 hours or 16 days per market?
   

The problem is to find a good limit for SwitchesRaw as it depends very much on the timeframe and on the total number of bars. Other than for 1) and 2) where we were able to set the limits due to plausibility considerations, we have to take a look into the first results (the tab:Opti ADX ALL of the attached csv-file) to derive the limit:

Instead of dealing with ~2500 different switches we use only sqrt(2500) = 50 classes which is a lot better to deal with. For each class we calculate its average and plot that. We see that there is a local minimum at 172. Let us use 100 to see how our pseudo-EA deals with this boundary. We use a small coefficient of 0.01 to guarantee slow increases from this limit, from 100. Again normally we would use a higher limit, may be 200 - but due to educational reasons ...

In order to derive other coefficients we look at the function plotter. We adapt them so that the curve is not too flat where we assume interesting results. Blue is the function for SwitchesRaw):

Let's look now at our other two evaluation functions.
Red is the function for BrRaw: Accepted minimum of any market duration is 3 bars and a coefficient of 0.5 guarantees that even 8 bars (hours) will make a difference.
Green for RangesRaw: Accepted minimum here is 1 and, as we couldn't expect a miracle, more than 8 would probably not be a serious result.

Now we can build the function that calculates OptVal which OnTester() will return.

1. As it applies for all three variables the bigger the better we can multiply them!
2. We have three variables and for all of them atan(..) can become negative so we have to evaluate: fmax(0.0,atan(..)). Otherwise e.g. two negative results of our atan() functions will result in a wrong positive value for OptVal .

//+------------------------------------------------------------------+
//| calcOptVal calc OptVal to be returned to the Strategy Tester       |
//| and its coefficients for the evaluation                          |
//+------------------------------------------------------------------+
// Coeff. for SwitchesAtan, number of switches:
double SwHigh = 1.0, SwCoeff=0.01, SwMin = 100;
// Coeff. for BrAtan, num. of bars:
double BrHigh = 1.0, BrCoeff=0.5,  BrMin = 3.0;
// Coeff. for RangesAtan, TrendRange/FlatRange:
double RgHigh = 1.0, RgCoeff=0.7,  RgMin = 1.0;

double calcOptVal() {
   if ( FlatNum*TrndNum>0 ) {
      SwitchesRaw  = TrndNum+FlatNum;
      SwitchesAtan = SwHigh*atan( SwCoeff*(SwitchesRaw-SwMin))/M_PI_2;

      FlatBarsAvg  = FlatBars/FlatNum;
      TrndBarsAvg  = TrndBars/TrndNum;
      BrRaw        = fmin(FlatBarsAvg,TrndBarsAvg);
      BrAtan       = BrHigh*atan( BrCoeff*(BrRaw-BrMin))/M_PI_2;

      FlatRange    = FlatRangHL / FlatNum;
      TrndRange    = TrndRangHL / TrndNum;
      RangesRaw    = FlatRange>0 ? TrndRange/FlatRange : 0.0; 
      RangesAtan   = FlatRange>0 ? RgHigh*atan( RgCoeff*(RangesRaw-RgMin))/M_PI_2 : 0.0;
      return(fmax(0.0,SwitchesAtan) * fmax(0.0,BrAtan) * fmax(0.0,RangesAtan));  
   }
   return(0.0);
}

The other parts of the pseudo-EA are OnInit() to write the column headers of the csv-file:

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit() 
  {
//---
   // write the header-line of the Calc.-Sheet
   if ( StringLen(fName)>0 ) {
      if ( StringFind(fName,".csv", StringLen(fName)-5) < 0 ) fName = fName+".csv";    //  check the file name
      if ( !FileIsExist(fName) ) {                                                     // write the column headers of a new file
         int fH = FileOpen(fName,FILE_WRITE);
         if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError); 
         string hdr = StringFormat("Name;OptVal;RangesRaw;PER;PRC;LIM;FlatNum;FlatBars;FlatBarsAvg;FlatRgHL;FlatRgCls;FlatRange;"+
                      "TrendNum;TrendBars;TrendBarsAvg;TrendRgHL;TrendRgCl;TrendRange;"+
                      "SwitchesRaw;SwitchesAtan;BrRaw;BrAtan;RangesRaw;RangesAtan;FlatHoursAvg;TrendHoursAvg;Bars;"+
                      "Switches: %.1f %.1f %.f, Hours: %.1f %.1f %.1f, Range: %.1f %.1f %.1f\n",
                      SwHigh,SwCoeff,SwMin,BrHigh,BrCoeff,BrMin,RgHigh,RgCoeff,RgMin);
         FileWriteString(fH, hdr, StringLen(hdr));
         FileClose(fH);
      }   
   }
//---
   return(INIT_SUCCEEDED);
  }

The OnTester() finalize the open market state and to write the result of the optimization at the end of the csv-file:

double OnTester() 
 {
   // check the knock out limit: at least one switches
   if ( FlatNum*TrndNum<=1 ) return(0.0);  // either one is 0 => skip senseless results
   
   // now finalize the last market: flat
   if ( MARKET == FLAT ) 
    {
      TrndRangCl += fabs(Close[2] - TrndBeg)/_Point;
      TrndRangHL += fabs(TrndHi - TrndLo)/_Point;

      // update relevant values
      OptVal = calcOptVal();

    } 
   else if ( MARKET == TREND ) // .. and trend
    {
      FlatRangCl += fabs(Close[2] - FlatBeg)/_Point;
      FlatRangHL += fabs(FlatHi - FlatLo)/_Point;

      // update OptVal
      OptVal = calcOptVal();
    }
   
   // write the values to the csv-file
   if ( StringLen(fName)>0 ) 
    {
      string row = StringFormat("%s;%.5f;%.3f;%i;%i;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.5f;%.6f;%.5f;%.6f;%.5f;%.2f;%.2f;%.0f\n",
                  iName,OptVal,RangesRaw,PER,PRC,LIM,
                  FlatNum,FlatBars,FlatBarsAvg,FlatRangHL,FlatRangCl,FlatRange,
                  TrndNum,TrndBars,TrndBarsAvg,TrndRangHL,TrndRangCl,TrndRange,
                  SwitchesRaw,SwitchesAtan,BrRaw,BrAtan,RangesRaw,RangesAtan,
                  FlatBarsAvg*_Period/60.0,TrndBarsAvg*_Period/60.0,
                  (FlatBars+TrndBars)
             );
             
      int fH = FileOpen(fName,FILE_READ|FILE_WRITE);
      if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError);
      FileSeek(fH,0,SEEK_END); 
      FileWriteString(fH, row, StringLen(row) );
      FileClose(fH);
    }
   // return 0.0 instead of neg. values! They mess up the Optimization Graph in our case.
   return( fmax(0.0,OptVal) );
 }

Now our pseudo-EA is ready and we prepare the Strategy Tester for the Optimization:

1. We disable "Genetic Algorithm" to test every combination.
2. Set the "Optimized parameter" to Custom. This shows us more interesting pictures in the Optimization Graph.
3. Make sure that the cache-file in ..\tester\caches was deleted
4. For a csv-file make sure that fName is not empty and an existing csv-file in \tester\files was deleted
5. If you leave a file name for the csv-file the optimizer will add a line by line making it bigger until you'll in troulbe by its size!
   
6. We choose symbol EURUSD.
7. Period is set to H1 (here from 2015. 08. 13 to 2015.11.20).
8. Model is set to "Open Price only".
9. Don't forget to enable "Optimization".
   

After 25 minutes on my laptop from 2007 the Strategy Tester has completed the optimization and we find the resulting csv-file in ..\tester\files\.

In the Optimizations Graph we can see for example (bottom =LIM, right=PER):

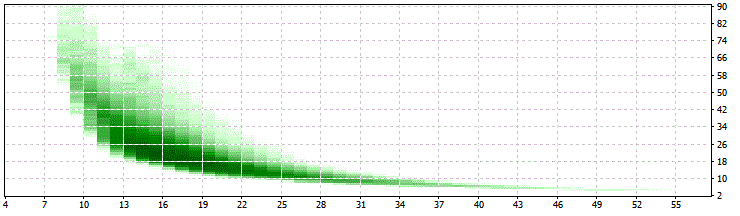
This looks a lot better than our initial optimization. We see a clear field with a higher density of 34>PER>10 and 25>LIM>13, which is a lot better than 2,..,90 and 4,..,90!

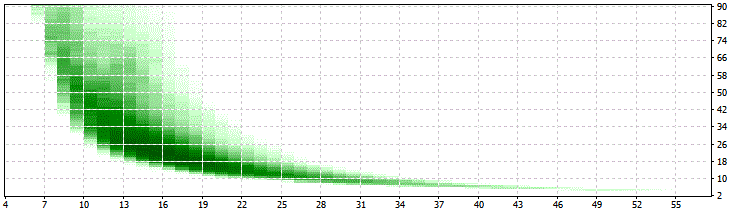
Let's just check whether the results for different minima of switches looks similar (=stable results) or not:

SwMin = 50:

SwMin = 150

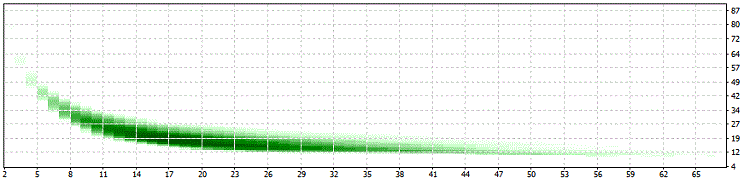
SwMin = 200:

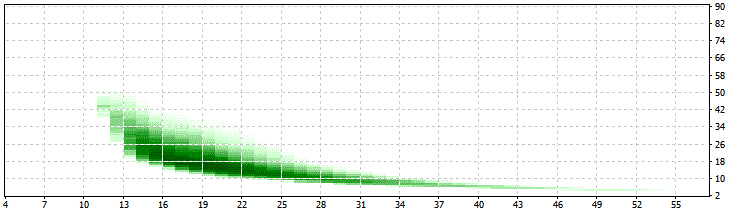
For all of the optimization are applicable these limits: 34>PER>10 and 25>LIM>13 which is a good sign for the robustness of this approach!

Remember:

• We had to use atan(..)-functions to make OptVal equally sensitive to our three variables.
• The usage of the atan-function with their different coefficients is more or less arbitrary! I tried until I had some satisfying results. There could be a better solution, try yourself!
• You might think I have modified until I get what I want to see - like over adapting an EA. Correct, that's why we have to check carefully the results!
  
• This pseudo-EA is not meant to find the best single solution but only to find reasonable smaller limits for each parameter! At the end the success is only determined by the trading-EA!
  

Analysing the results in EXCEL, Plausibility Check

Each pass during the optimization adds a new line to the csv-file with a lot more information than the Strategy Tester offers, skipping the categories we do not need like Profit, Trades, Profit Factor, ... This file we load in Excel (in my case LibreOffice).

We have to sort everything, firstly, according to our OptVal, secondly, according to RangesRaw, and then we get this (tab: "Optimizing ADX SwLim 100 raw"):

We look at the 'best' 50 according to OptVal. The varied parameters PER, PRC and LIM are coloured for an easy detection.

1. RangesRaw varies from 2.9 to 4.5. This means that the trend market has a 3 to 4.5 times greater range than the flat market.
2. The flat market lasts for 6 to 9 bars (hours).
3. The flat market's ranges vary from 357 to 220 Points - enough room for a range trading.
4. The trend lasts between 30 and 53 hours.
5. The trend market ranges from 1,250 to 882 Points.
6. If you look not only at the top 50 but at the top 200, the ranges are almost the same RangesRaw: 2.5 to 5.4, flat ranges 221 to 372, trend ranges: 1,276 to 783.
7. PER of the top 200: 14 to 20 and LIM: 14 to 20, but we have to look at this in detail!
8. If we look at the part when OptVal has become 0.0, we see very high values for RangesRaw, but other values tell us they are not good to trade (tab: "skipped OptVal=0"):
   

RangesRaw is ridiculously high but FlatBarsAvg is practically too short to trade and/or TrndBarsAvg is too high with more that 1000 hours.

Now we check the RangeRaw of the part with OptVal>0 and sort that according to RangesRaw (tab: "OptVal>0 sort RangesRaw"):

The 50 highest values of RangesRaw range from 20 to 11. But just look at the TrendBarsAvg: On average around 100, that is more than 4 days.

In total we can say OptVal has quite nicely devalued all the ADX results that would be hard to trade. On the other hand, the highest RangesRaw of the top 200 (5.4) or top 500 (7.1) look very promising.

Parameter Check

So after this necessary plausibility check we look at our parameters of the ADX PER and PRC and its LIM limit.

Due to many rows (=29,106) we need only the lines with OptVal greater than 0. In the raw table these are the first 4085 lines (if sorted acc. to OptVal!). We copy them in a new tab. There we add three columns beside PER and add this according to the pictures. All formulas you can see in the attached file.

As of line 5 of the the Columns D,E,F enter: AVERAGE(D$2:D5), STDEV(D$2:D5), SKEW(D$2:D5). The cells in row 2 only show the values of the last row which are the statistical results of the whole RangesRaw column. Why? As the table is ordered from the best to the worst, we will see in n line the average, the standard deviation and the skewness of the best n. The comparison of the best n values with all results can tell us where we can probably find what we are looking for (tab: "OptVal>0 Check PER, PRC, LIM"):

What can we learn from this? At the second row (below last) we see that the average (Avg) of all PER is 33.55 the standard deviation (StdDev) 21.60. If PER is distributed according to a Gaussian distribution we find 68% of all values of PER within the average +/- StdDev and 95% within +/-2*StdDev. Here it is between 33.55 - 21.60 = 11.95 and 33.55 + 21.60 = 55,15. Now we look at the rows of the best. The average starts at 19 in the row 5 and slowly increases to 20. The StdDev changes from 2.0 to 2.6. Now the 68% covers 18 to 23. Finally, we look at the  skewnes. It is 0.61 in row 2 for all PER. That means the left side (smaller) has more values than the right side even though it is still a Gaussian distribution. If the skewness exceeds +/- 1.96 we cannot assume a Gaussian distribution and we have to be very careful to use the average and the std.dev. as one side is heavily 'overweighted' while the other side is more or less 'empty'. A skewness greater 0 means that the right side (>average) has less values than the right side. So PER is Gaussian distributed and we can use the average and the StdDev. If we compare the development of the top results (according to OptVal) we see that the average raises slowly from 19 to 20 (row 487!). The StdDev, meanwhile, increases from ~2.0 to 5.36 (row 487). The skewness never exceeds 0.4 if we skip the first 10 results and it is mainly positive, which means that we should add one (or two) values 'on the left' side of the average.

The results of PRC have to be treated differentially! Other than PER and LIM the values of PRC define a nominal scale, any calculation between them is senseless. So we just count how many times they appear and we calculate the average of RangesRaw for each PRC 0,..,6. Remember we wanted to check even ridiculous sets. Normally we wouldn't use PRC=Open (1), PRC=High (2) or PRC=Low (3). But we have to realize that Open is the most frequent value among the top 50. This is most probably caused by the fact that we use only whole bars, the ADX uses High and Low of the bar, and therefore the high and low and close are 'known to the open' - a kind of immoral advantage as the ADX uses them. The success of High and Low? Hard to explain! The fact that the EURUSD price drops from 1.33 in Aug. 2014 to 1.08 in Dec. 2015 might explain the success of the Low, but not the High. Maybe it is a result of stronger market dynamics. Anyway, we fade them out. If we compare PER = Close, Typical, Median and Weighted we realize there is no big difference between them when looking at the columns Q, R, and S. Among the top 100 PRC=Typical(4) would be the best choice, even better than PRC=High(2). But among the top 500 PRC=Close has become the best.

For LIM we use the same formulas as for PER. Interesting to see that the 'last' skewness (of all) is way above +1.96 but not for the top 100 (=0.38) or for the top 500 (=0.46). So let's just use the best 500. The average of the top 500 is 16.65 and the StdDev 3.03.  Of course, this LIM greatly depends on PER: the smaller PER the higher LIM and vice versa. That is why the range of LIM corresponds with the range of PER.

So we choose for the ranges of our three variables PER, PRC, and LIM the results of the best 500:

• PER Avg=20.18 +/- StdDev=5.51 Skew=0.35 (-2) => (20.18-5.41-2=) 14,..,(20.18+5.52=) 26 (Step 1 => 13).
• PRC according to row 500 we can decide for only close (Step 0 => 1).
• LIM Avg=16.64 +/- StdDev=3.03 Skew=0.46 (-2) => (16.64-3.03-2=) 12,..,(16.64+3.03=) 20 (Step 1 => 9)
  

In total we have now only 13*1*9 = 117 combinations for the trading EA for its optimization.

We can take a closer look at the results (It is the sheet tab named: "OPT Top 500 Best PER's Average"):

We see that PER=18 is most frequently under the top 500 and PER=22 has the highest average. Both are covered by our selection and their LIM as well.

Visual Mode

Let's finally check PER with the best average of the top 500: PER=22. Deselecting PRC=Open,Low,High we find this set up with a range relation of 4.48 in the row 38, the yellow background in the previous picture of the tab.

We run the pseudo-EA in the Visual Mode with this set up and apply the ADX with the same setup.

(Only) In Visual Mode our pseudo-EA places a blue right-left arrow at the next bar where the flat market was detected and a red up-down arrow in case of a trend bar (here from : We. 2015.07.30 05:00 to Tu. 2015.08.04 12:00):

We can clearly see two problems of the ADX which may encourage you to improve this idea!

1. The ADX is lagging especially at the detection of the flat market if some bigger moves has just thrown up the ADX. It needs quite along time to 'calm down' again. It would have been nice if the flat market would have been detected around 2015.08.03 00:00 and not 2015.08.3 09:00.
2. If the ADX is close to LIM we realize a kind of whipsaw. For example, it would have been better if we were able not to detect the trend market at 2015.08.03 14:00.
3. If the high-low-range of the bars is becoming smaller, even a couple of 'small' bars in the same direction is recognized as a new trend. Instead of the new trend at 2015.08.03 20.00 it would have been better if the trend was detected later, maybe around 2015.08.04 07:00.
   
4. The pseudo-EA does not distinguish between uptrend or downtrend. It is up to you to either use e.g. DI+ and DI- of the ADX or to use other indicators.
   
5. May be the average length of the trend markets (46.76) which is almost 4 days(!) could be too long. In this case either a higher SwMin (instead of 100) or a smaller SwCoeff (instead of 0.01) or both will give you results that better meet your ideas.
   

These are five clear starting points for you to find or to code your own indicator or set of indicators for a better detection. You can use the ADX as a reference. The attached pseudo-EA can be easily amended if you know your definition of a flat and a trend market!

Conclusion

A trading-EA that uses the ADX would have to test 54,201 combinations just to optimize this single indicator - hoping that the ADX does what we want it to do! If the trading-EA is not as successful as we have hoped, it would be difficult to address the problem to start improving. After this optimizations that needs only a couple of minutes for all of its 54,201 combinations of the ADX we found out that:

1. The ADX is capable to distinguish between flat and trend markets and
2. We were able to reduce 54,201 to 117 (= 13 (PER) * 1 (PRC) * 9 (LIM)).
3. The flat market's range is between 372 and 220 points (top 100).
4. The trend market's range is between 1,277 and 782 points.
   

Therefore we can reduce the initial 2,168,040,000 combinations of the trading-EA to (117*40,000=) 4,680,000. That is only 0.21%, and it is either 99.7% faster or a lot better in case of the genetic optimization because more variations of other non-ADX parameters of the trading-EA will be checked. These were the reduced settings for our pseudo-EA:

Furthermore, we get (it depends on the trading ideas, of course), some valuable information for criteria to enter a trade, to exit a trade, and to set or move stops and targets.

Please find the pseudo-EA and the Excel file attached. We have explained avery step being taken, why we did it and the pitfalls that might appear. All that should enable you to start trying to find your own optimized indicators before using them in your trading EA. If you about to develop your own way to detect flat and trend markets you can use this to compare your results with the ADX, to see whether your combinations of indicators are better!

If you want to use this to find a better indicator or an indicator set for flat and trend markets, you have to most probably adjust the coefficients of the calcOptVal(). E.g. if you want to use a longer time period, you have to increase at least SwMin. Bear in mind that a good OptVal will enable the Genetic Mode to find the best setup for you out of multiple combinations!! But you can use this idea as well for a totally different optimizations of indicators only. In this case you might be forced to completely rewrite the calcOptVal()-function.

If you want to work with this EA don't forget:

1. Make sure that the cache-file in ..\tester\caches was deleted.
   
2. If you need the csv-file in ..\tester\files\ enter a file name for fName and delete an existing csv-file with this name.
3. If you don't want a csv-file, leave the fName of the pseudo-EAs setup emtpy.
4. If you leave a file name for the csv-file, the optimizer will add a line by line making it bigger, until you'll in troulbe by its size!
   
5. Set the "Optimized parameter"  to "Custom" of the "Tester"  tab.
6. The easiest way to influence OptVal and the results of the genetic algorithm is to vary the minima of the three coefficients: SwMin, BrMin, RgMin.
   
7. Set the "Model" to "Open Price only" , it's faster.
8. If you are using different dates ("Use Date" : From..To) you have to adjust the coefficients right above the calcOptVal()-function within the pseudo-EA.
9. After the optimization is complete choose a setup from the "Optimization Result"  tab and start again in "Visual mode"  to see whether the optimization fulfilled you ideas.
10. The blue right-left arrow the start of a flat market the red up-down arrow a trend market.
11. If you want to develop a better alternative to the ADX you might not need the csv-File: Just optimize, watch the best result in "Visual mode", change something, optimize,...
12. For a different question to the market than flat or trend you probaly need to use the csv-files and maybe a different way to calculate the OptVal.
    

But keep in mind there is no guaranty for a quick success or any success at all.