
Redes neuronales: así de sencillo (Parte 69): Restricción de la política de comportamiento basada en la densidad de datos offline (SPOT)
Introducción
El aprendizaje por refuerzo offline nos permite entrenar modelos basados en los datos recogidos de las interacciones con el entorno, lo cual nos permite acortar considerablemente el proceso de interacción con ella. Además, con la complejidad de la modelización del entorno, podemos recoger datos en tiempo real de múltiples agentes-exploraciones, y más tarde entrenar un modelo con ellos.
No obstante, al mismo tiempo, utilizar una muestra de entrenamiento estática reduce enormemente la información del entorno disponible. Las limitación en los recursos no nos permite conservar toda la versatilidad del entorno en la muestra de entrenamiento.
Sin embargo, durante el entrenamiento de la política óptima del Agente, existe una alta probabilidad de que sus acciones queden fuera de la distribución de la muestra de entrenamiento. Obviamente, debido a la falta de retroalimentación del entorno, no podemos obtener una evaluación real de tales acciones, y debido a la falta de datos en la muestra de entrenamiento, nuestro Crítico tampoco puede evaluarlos adecuadamente. En tal caso, podemos tener tanto expectativas infladas como rebajadas.
Debemos decir que las expectativas infladas son mucho más peligrosas que las expectativas rebajadas. Con expectativas rebajadas, el modelo puede negarse a realizar estas acciones, lo cual provocará el entrenamiento de una política de Agente subóptima. Sin embargo, en caso de sobreestimación, el modelo tenderá a repetir esas acciones, lo cual puede provocar pérdidas significativas durante la explotación. Por ello, mantener la política del Agente dentro de la muestra de entrenamiento se convierte en un aspecto importante para garantizar la solidez del aprendizaje offline.
Varios métodos de aprendizaje por refuerzo offline para resolver este problema usan la parametrización o regularización, que restringe la política del Agente para realizar acciones dentro del conjunto de soporte de la muestra de entrenamiento. Los diseños detallados suelen interferir con los modelos de Agente, que pueden generar costes operativos adicionales y no aprovechan al cien por cien los métodos establecidos de aprendizaje por refuerzo online. Los métodos de regularización reducen la discrepancia entre la política entrenada y la muestra de entrenamiento, que puede no cumplir la definición de soporte basada en la densidad y, por tanto, evitar de forma ineficiente actuar fuera de la distribución.
En este contexto, destaca positivamente el método Supported Policy OpTimisation (SPOT), presentado en el artículo "Supported Policy Optimization for Offline Reinforcement Learning". Sus planteamientos se derivan directamente de una formalización teórica de la restricción política basada en la distribución de la densidad de la muestra de entrenamiento. SPOT utiliza un estimador de densidad basado en un autocodificador variacional(VAE). Se trata de un elemento de regularización sencillo pero eficaz, que puede integrarse en algoritmos de aprendizaje por refuerzo ya existentes. SPOT consigue el mejor rendimiento de su categoría en las pruebas de referencia estándar para RL offline, y gracias a su diseño flexible, los modelos preentrenados offline con SPOT también pueden afinarse online.
1. Algoritmo SPOT (Supported Policy OpTimisation)
Las restricciones de soporte son un método típico de mitigación de errores en el aprendizaje por refuerzo offline. A su vez, la restricción de soporte puede formalizarse según la densidad de la estrategia de comportamiento. Los autores del método Supported Policy OpTimisation proponen un algoritmo de regularización con la perspectiva de una estimación explícita de la densidad. SPOT incluye un término de regularización, que se deriva directamente de la formalización teórica de la restricción de soporte por la densidad de la distribución. Como elemento de regularización, se usa un autocodificador variacional mejorado (CVAE) para aprender la densidad de la muestra de entrenamiento.
Del mismo modo que la estrategia óptima puede extraerse de la función Q óptima, la estrategia óptima soportada también puede recuperarse usando la elección codiciosa:
![]()
En el caso de la aproximación de funciones, esto se corresponde con el problema de optimización de estrategias con restricciones.
A diferencia de la parametrización específica de la política del Agente o de las penalizaciones por divergencia usadas en otros métodos para restringir el soporte, los autores de SPOT proponen utilizar directamente la densidad de la muestra de entrenamiento como restricción:
![]()
donde ϵ'=log ϵ para comodidad de notación.
La restricción que usa la densidad de comportamiento es simple y directa en el contexto de una restricción de soporte. Los autores del método sugieren usar la función de verosimilitud logarítmica en lugar de la función de probabilidad por su comodidad matemática.
A su vez, esto impone la restricción adicional, pues la densidad de la estrategia de comportamiento está acotada desde abajo en cada punto del espacio de estados, y resulta casi imposible resolver un problema así debido al gran número, incluso infinito, de restricciones. En su lugar, los autores de SPOT usan una aproximación heurística que tiene en cuenta la densidad media del comportamiento:
![]()
Vamos a convertir el problema de optimización con restricciones en un problema sin restricciones. Para ello, consideraremos el término restricción como una penalización. Así obtendremos la función objetivo del aprendizaje de estrategias:
![]()
donde λ será el multiplicador de Lagrange.
El término de regularización directa en la función de pérdida presentada anteriormente requiere acceso a la política de comportamiento usada en la recogida de la muestra de entrenamiento. Pero solo tenemos datos offline generados por esta política. Y podemos estimar explícitamente la densidad en un punto arbitrario usando varios métodos de estimación de la densidad. El autocodificador variacional (VAE) es uno de los mejores modelos de estimación de la densidad usando redes neuronales, y los autores del método deciden utilizar el autocodificador variacional ampliado como estimador de densidad. Tras entrenar el VAE, podemos utilizarlo simplemente como límite inferior.
La estructura general presentada anteriormente puede construirse sobre diversos algoritmos de aprendizaje por refuerzo tras algunas modificaciones mínimas. En su artículo, los autores del método usan TD3 como algoritmo base.
2. Implementación usando MQL5
Tras considerar los aspectos teóricos del método SPOT, comenzaremos su aplicación práctica usando MQL5. Para ello, implementaremos nuestro modelo usando como base los asesores del artículo sobre el método Real-ORL. Recordemos que el modelo de básico usado se basa en el método Soft Actor-Critic próximo al TD3 utilizado por los autores de SPOT. Para ello, nuestro modelo se complementará con una serie de enfoques que ya hemos tratado en artículos anteriores.
En primer lugar, debemos señalar que el método SPOT añade una regularización de la política del Agente basada en la densidad de datos de la muestra de entrenamiento. Dicha regularización se aplica en la fase de aprendizaje offline de la política del Agente, y no afecta en absoluto al proceso de interacción con el entorno. En consecuencia, la recogida de muestras de entrenamiento y los asesores de prueba se han trasladado sin cambios: podrá comprobarlos usted mismo en el archivo adjunto.
Así, resulta obvio que pasaremos directamente al asesor de entrenamiento de modelos. Sin embargo, hay que tener en cuenta que necesitamos entrenar el autocodificador con la función de densidad de la muestra de entrenamiento antes de poder empezar a entrenar la política. Por lo tanto, dividiremos el proceso de aprendizaje en 2 fases, y pondremos el autocodificador de entrenamiento en un asesor aparte "...\SPOT\StudyCVAE.mq5".
2.1 Entrenamiento del modelo de densidad
Antes de empezar a construir el asesor de entrenamiento del modelo de densidad, primero hablaremos de qué vamos a enseñarle y cómo. Los autores del método SPOT propusieron usar un autocodificador ampliado para estudiar la densidad de la muestra de entrenamiento. ¿Qué significa esto en la práctica?
Ya hemos hablado de las propiedades de la compresión con autocodificador y de la recuperación de datos. También hemos dicho que las redes neuronales solo pueden funcionar de manera estable en un entorno similar a la muestra de entrenamiento. En consecuencia, al suministrar al modelo datos de entrada alejados de la distribución de la muestra de entrenamiento, los resultados de su funcionamiento se aproximarán a valores aleatorios, y el error de descodificación de datos aumentará considerablemente. La combinación de estas propiedades del modelo autocodificador es lo que vamos a explotar.
Entrenaremos el autocodificador en la distribución de acciones del Agente de la muestra de entrenamiento. Durante el entrenamiento del Agente, suministraremos la entrada del autocodificador las acciones sugeridas por la política actualizada del Agente, y el error de descodificación de los datos nos dirá indirectamente la distancia de las acciones predictivas respecto a la distribución de la muestra de entrenamiento.
La funcionalidad es comprensible y encaja en la arquitectura del autocodificador, pero, ¿resultará suficiente para comprender la presencia de la acción del Agente en la muestra de entrenamiento? Al fin y al cabo, sabemos muy bien que una misma acción en diferentes estados del entorno puede provocar resultados completamente opuestos. Por ello, tendremos que entrenar el autocodificador para extraer distribuciones de acciones en diferentes estados del entorno, y llegaremos al punto en el que tendremos que suministrar un par Estado-Acción a la entrada del autocodificador. En la salida del autocodificador, esperamos obtener la Acción del Agente que se ha introducido en la entrada.
Aquí debemos señalar que al suministrar un par Estado-Acción a la entrada del autocodificador, esperamos que la información de Estado y Acción se comprima en su estado latente. No obstante, al entrenar al autocodificador para que decodifique solo la acción, es muy probable que lo entrenemos para que ignore la información sobre el estado del entorno, y el tamaño completo del estado latente se utilizará para transmitir la Acción deseada, lo que, en última instancia, nos devuelve a la situación de codificación y descodificación de Acciones sin tener en cuenta el estado, y eso resulta altamente indeseable. Por eso, es importante que hagamos hincapié en que el Autocodificador se centra en los dos componentes de los datos de entrada Estado-Acción. Para lograr este resultado, los autores del método usan un autocodificador ampliado cuya arquitectura prevé la alimentación de algunas claves para descodificar los datos. Esta clave, junto con la representación latente, se introducirá en la entrada del descodificador. En nuestro caso, usaremos el estado del entorno como Clave.
Por lo tanto, tenemos que construir un modelo de autocodificador que debe obtener 3 tensores en la entrada de la pasada directa:
- La condición del entorno (a la entrada del Codificador)
- La acción del agente (a la entrada del Codificador)
- La condición del entorno (Clave a la entrada del decodificador)
Antes, construíamos modelos solo con las entradas de 2 tensores, mientras que ahora nos enfrentamos a la cuestión de implementar los datos brutos a partir de 3 tensores. Obviamente, esta tarea puede realizarse de varias maneras.
En primer lugar, podemos combinar el par Estado-Acción en un único tensor. Entonces la Clave será el segundo tensor de datos de origen y esto encajará en el modelo que utilizamos anteriormente con 2 tensores de datos de origen. Sin embargo, la combinación de datos dispares sobre el estado del entorno y las acciones de los Agentes puede repercutir negativamente en la calidad del rendimiento del modelo y limitar nuestra capacidad de preprocesar los datos brutos sobre el estado del entorno.
La segunda opción consiste en añadir un método para ejecutar el modelo con los 3 tensores de los datos originales. Se trata de un proceso largo que puede llevar a la creación interminable de métodos para cada tarea específica, lo que hará que nuestra biblioteca resulte engorrosa y difícil de entender y mantener.
Para este artículo, hemos elegido la tercera, en mi opinión, la opción más fácil para crear modelos separados de Codificador y Decodificador, cada uno de los cuales trabaja con 2 tensores de los datos originales. Su implementación se ajusta plenamente a los métodos que hemos desarrollado anteriormente.
En teoría, ya nos hemos decidido. Vamos a describir ahora la arquitectura de nuestros modelos de Autocodificador. Este trabajo se realizará en el método CreateCVAEDescriptions. A la entrada del método suministraremos los punteros a los 2 arrays dinámicos en los que montaremos la arquitectura de los 2 modelos: el Codificador y el Decodificador. En el cuerpo del método comprobaremos los punteros obtenidos y, si es necesario, crearemos nuevos ejemplares de objetos de arrays dinámicos.
bool CreateCVAEDescriptions(CArrayObj *encoder, CArrayObj *decoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!decoder) { decoder = new CArrayObj(); if(!decoder) return false; }
En primer lugar, describiremos la arquitectura del Codificador. Luego introduciremos los datos históricos de los movimientos de precio y las lecturas de los indicadores analizados en la entrada del modelo. Los datos que se introducen en el modelo son brutos y sin procesar. Por lo tanto, realizaremos el procesamiento primario en la capa de normalización de datos por lotes.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A continuación, comprimiremos los datos y, simultáneamente, resaltaremos los patrones establecidos usando el bloque de capas de convolución.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; int prev_wout = descr.window_out = BarDescr / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
El estado del entorno así obtenido se combinará con el vector de acción del Agente.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!encoder.Add(descr)) { delete descr; return false; }
A continuación, usando 2 capas totalmente conectadas, comprimiremos los datos.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * EmbeddingSize; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Y a la salida del Codificador crearemos una representación latente estocástica utilizando la capa interna del autocodificador variacional.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = EmbeddingSize; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A continuación describiremos la arquitectura del Decodificador. La representación latente generada por Codificador se introducirá en la entrada del modelo.
//--- Decoder decoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Inmediatamente concatenaremos el tensor resultante con el vector de estado del entorno.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = EmbeddingSize; descr.window = prev_count; descr.step = (HistoryBars * BarDescr); descr.optimization = ADAM; descr.activation = LReLU; if(!decoder.Add(descr)) { delete descr; return false; }
Obsérvese que proporcionaremos los datos de descripción del entorno sin procesar a la entrada del Codificador y realizaremos su procesamiento inicial en la capa de normalización por lotes. En el Decodificador, en cambio, no tenemos forma de realizar esa normalización. Hemos decidido no realizar la normalización de datos 2 veces. Y justo en el proceso de entrenamiento y operación tomaremos los datos del Codificador después de la normalización. Esto nos permitirá simplificar un poco el Decodificador y reducir el tiempo de procesamiento.
A continuación, utilizaremos las capas totalmente conectadas para reconstruir el vector de acción a partir de los datos brutos resultantes.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NActions; descr.optimization = ADAM; descr.activation = SIGMOID; if(!decoder.Add(descr)) { delete descr; return false; } //--- return true; }
Tras describir la arquitectura de nuestro Autocodificador, pasaremos a la construcción de su asesor de entrenamiento. Como ya hemos mencionado, entrenaremos 2 modelos: El Codificador y el Decodificador.
CNet Encoder; CNet Decoder;
En el método OnInit de inicialización del programa, primero cargaremos la muestra de entrenamiento, sin olvidarnos de comprobar el resultado de la operación. Después de todo, si hay un error de carga, simplemente no tendremos nada con lo que entrenar los modelos.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
A continuación, intentaremos cargar modelos preentrenados y, si es necesario, generaremos nuevos modelos inicializados con parámetros aleatorios.
//--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new CVAE"); CArrayObj *encoder = new CArrayObj(); CArrayObj *decoder = new CArrayObj(); if(!CreateCVAEDescriptions(encoder,decoder)) { delete encoder; delete decoder; return INIT_FAILED; } if(!Encoder.Create(encoder) || !Decoder.Create(decoder)) { delete encoder; delete decoder; return INIT_FAILED; } delete encoder; delete decoder; }
Luego trasladaremos ambos modelos a un único contexto OpenCL, lo cual nos permite intercambiar datos entre los modelos sin descargarlos en la memoria principal del programa.
OpenCL = Encoder.GetOpenCL(); Decoder.SetOpenCL(OpenCL);
Aquí también realizaremos el control de arquitectura mínimo necesario de los modelos cargados (o creados), controlando obligatoriamente el resultado de las operaciones,
Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Encoder.getResults(Result); int latent_state = Result.Total(); Decoder.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Decoder doesn't match result of Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
e inicializaremos la creación del evento desencadenante del entrenamiento del modelo. Después finalizaremos el método de inicialización del programa con el resultado INIT_SUCCEED.
if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
En el método OnDeinit de desinicialización del programa, guardaremos los modelos entrenados y vaciaremos la memoria de los objetos creados en el programa.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Encoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); Decoder.Save(FileName + "Dec.nnw", Decoder.getRecentAverageError(), 0, 0, TimeCurrent(), true); delete Result; delete OpenCL; }
Tenga en cuenta que almacenaremos todos los modelos en un catálogo común de terminales. De este modo, estarán disponibles cuando se utilicen los programas en el terminal, y también en el simulador de estrategias.
El entrenamiento directo de los modelos se realiza tradicionalmente con el método Train. En el cuerpo del método, primero crearemos las variables locales necesarias.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); int bar = (HistoryBars - 1) * BarDescr;
Después organizaremos un ciclo de entrenamiento.
for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = int((MathRand() * MathRand() / MathPow(32767, 2)) * (total_tr)); int i = int((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) continue;
Tenga en cuenta que, a diferencia de nuestro trabajo reciente, aquí no utilizaremos la priorización de trayectorias. Se trata de un movimiento consciente y deliberado. La cuestión es que en esta fase pretendemos aprender la verdadera densidad de los datos de la muestra de entrenamiento, y el uso de la priorización de trayectorias puede desplazar la información en favor de las trayectorias más prioritarias. Por lo tanto, utilizaremos un muestreo uniforme de las trayectorias y los estados en ellas.
Tras muestrear la trayectoria y el estado, rellenaremos los búferes de descripción del Estado del entorno y Acciones del agente a partir de la muestra de entrenamiento.
State.AssignArray(Buffer[tr].States[i].state); Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite();
Recuerdo que en los conceptos de "descripción del entorno" solemos incluir un vector de descripción del estado de la cuenta y de las posiciones abiertas. Aquí no hemos hecho hincapié en el estado de la cuenta, ya que el sentido de abrir o mantener una posición viene determinado por el estado del mercado. La cuenta se analiza para la gestión del riesgo y el dimensionamiento de las posiciones. En esta fase, hemos decidido limitarnos a estudiar la densidad de las acciones en situaciones de mercado individuales y no hemos hecho hincapié en el modelo de gestión de riesgos.
Tras preparar los búferes de datos de origen, realizaremos una pasada directa del autocodificador. Como se ha comentado anteriormente, suministraremos el puntero del Codificador a la entrada del Decodificador dos veces. En este caso, utilizaremos la salida del modelo como principal flujo de datos de entrada, mientras que para el flujo adicional de datos brutos, tomaremos los resultados de la capa de normalización por lotes del Codificador. Asegúrese de supervisar el proceso de las operaciones.
if(!Encoder.feedForward(GetPointer(State), 1,false, GetPointer(Actions)) || !Decoder.feedForward(GetPointer(Encoder), -1, GetPointer(Encoder),1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
En el proceso de entrenamiento del Autocodificador, no necesitaremos analizar ni procesar los resultados del mismo. Solo necesitaremos especificar los valores objetivo; para ello, utilizaremos el vector de acción del Agente. Este es el mismo vector que introdujimos anteriormente en la entrada del Codificador. Es decir, tenemos el búfer de resultados ya preparado, y llamaremos a los métodos de pasada inversa de ambos modelos de autocodificador.
if(!Decoder.backProp(GetPointer(Actions), GetPointer(Encoder), 1) || !Encoder.backPropGradient(GetPointer(Actions), GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Tenga en cuenta que el Codificador actualiza sus parámetros en función del gradiente de error recibido del Decodificador. Y no necesitamos generar un búfer de valores objetivo separado para el Codificador.
En este punto, las operaciones de una iteración de entrenamiento del autocodificador pueden considerarse completas. Bastará con informar al usuario del progreso de las operaciones y pasar a la siguiente iteración del ciclo de entrenamiento del modelo.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Decoder", iter * 100.0 / (double)(Iterations), Decoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Aquí solo mostraremos la información de error para el Decodificador, ya que no se calcula ningún error para el Codificador.
Una vez completadas con éxito todas las iteraciones del ciclo de entrenamiento del autocodificador, eliminaremos el campo de comentarios del gráfico e iniciaremos el proceso de finalización del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError()); ExpertRemove(); //--- }
El código completo del asesor de entrenamiento del modelo de densidad se encuentra en el archivo adjunto. Allí también verá todos los programas utilizados en el artículo.
2.2 Entrenamiento en política del Agente
Tras entrenar el modelo de densidad, vamos a pasar al asesor de entrenamiento de la política del Agente "...\SPOT\Study.mq5". De entrada, debemos decir que el proceso de entrenamiento del Agente se mantendrá prácticamente sin cambios: solo hemos complementado ligeramente la regularización de su política de comportamiento. La arquitectura de todos los modelos entrenados también se ha copiado sin cambios. Ahora, vamos a analizar punto por punto los métodos del asesor "...\SPOT\Study.mq5". Y como siempre, podrá leer su código completo en el archivo adjunto.
Sin embargo, por pequeños que sean los cambios en el algoritmo de entrenamiento de la política del Agente, los modelos de autocodificador entrenados anteriormente estarán implicados, y deberemos añadirlos al programa.
STrajectory Buffer[]; CNet Actor; CNet Critic1; CNet Critic2; CNet TargetCritic1; CNet TargetCritic2; CNet Convolution; CNet Encoder; CNet Decoder;
En el método OnInit de inicialización del programa, cargaremos la muestra de entrenamiento como antes, controlando obligatoriamente las operaciones.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Entonces, incluso antes de cargar los modelos entrenados, cargaremos el Autocodificador. Si no podemos cargar los modelos, informaremos al usuario y finalizaremos el método de inicialización con el resultado INIT_FAILED.
//--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true)) { Print("Cann't load CVAE"); return INIT_FAILED; }
Debemos señalar aquí que, en ausencia de modelos preentrenados, no crearemos otros nuevos con parámetros aleatorios, puesto que los modelos no entrenados solo distorsionarán el proceso de entrenamiento, y los resultados de ese entrenamiento serán imprevisibles.
Por otro lado, podríamos añadir una bandera y, en ausencia de modelos de Autocodificador entrenados, implementar el entrenamiento de la política del Agente sin regularizar sus acciones, como hemos hecho anteriormente. Al trabajar en una tarea del mundo real, probablemente lo haría, pero en este caso es el rendimiento de la regularización lo que queremos evaluar. La interrupción del programa sirve, por tanto, como punto adicional de control del "factor humano".
A continuación, cargaremos los modelos entrenados y, de ser necesario, crearemos otros nuevos inicializados con parámetros aleatorios.
if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *convolution = new CArrayObj(); if(!CreateDescriptions(actor, critic, convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!Actor.Create(actor) || !Critic1.Create(critic) || !Critic2.Create(critic) || !Convolution.Create(convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!TargetCritic1.Create(critic) || !TargetCritic2.Create(critic)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } delete actor; delete critic; delete convolution; //--- TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1.0f); TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1.0f); StartTargetIter = StartTargetIteration; } else StartTargetIter = 0;
if(!Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new Encoder model"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *convolution = new CArrayObj(); if(!CreateDescriptions(actor, critic, convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!Convolution.Create(convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } delete actor; delete critic; delete convolution; }
Una vez que los nuevos modelos se hayan cargado y/o inicializado correctamente, los trasladamos a un único contexto OpenCL. En este caso, desactivaremos el modo de actualización de parámetros en los modelos de entrenamiento. Es decir, en esta fase, no adaptaremos el Autocodificador de ninguna manera.
OpenCL = Actor.GetOpenCL(); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); TargetCritic1.SetOpenCL(OpenCL); TargetCritic2.SetOpenCL(OpenCL); Convolution.SetOpenCL(OpenCL); Encoder.SetOpenCL(OpenCL); Decoder.SetOpenCL(OpenCL); Encoder.TrainMode(false); Decoder.TrainMode(false);
Tenga en cuenta que, aunque el codificador aleatorio tampoco está entrenado, no hemos cambiado su bandera de modo de entrenamiento. No es necesario. El método de cambio de modo de entrenamiento no eliminará los búferes que no estén en uso: en consecuencia, tampoco borrará la memoria, solo cambiará la bandera que rige el algoritmo de pasada inversa. No llamaremos al método de pasada inversa del codificador en el programa. Así que el efecto de cambiar la bandera de entrenamiento del codificador aleatorio será cercano a "0". En el caso del autocodificador, sin embargo, la situación es un poco distinta, y en eso nos centraremos en el método de entrenamiento del modelo Train. Ahora volvamos al método de inicialización del asesor.
Tras crear los modelos y transferirlos a un único contexto OpenCL, controlaremos de forma mínima que su arquitectura esté conforme con las constantes utilizadas en el programa.
Primero comprobaremos que el tamaño de la capa de resultados del Actor coincida con el tamaño del vector de acciones del Agente.
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
El tamaño de los datos de entrada del Actor deberá coincidir con el tamaño del vector de descripción del estado del entorno.
Actor.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
Y no olvidaremos comprobar que el tamaño de la capa latente del Actor y el búfer de datos de origen del Crítico coincidan.
Actor.GetLayerOutput(LatentLayer, Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Haremos comprobaciones similares para los modelos del Codificador y Decodificador del Autocodificador.
Decoder.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the Decoder does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
Encoder.getResults(Result); latent_state = Result.Total(); Decoder.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Decoder doesn't match result of Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Con esto concluirá nuestro trabajo de preparación de los modelos. Ahora inicializaremos el búfer auxiliar y generaremos un evento de inicio del entrenamiento.
Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Después finalizaremos el método de inicialización del asesor con un resultado positivo.
Como no cambiaremos los parámetros de los modelos de autocodificador durante el proceso de entrenamiento, no necesitaremos guardarlos una vez finalizado el programa. Por lo tanto, el método de desinicialización OnDeinit permanecerá inalterado. Podrá familiarizarse por sí mismo con el código en el archivo adjunto. Ahora pasaremos al proceso de entrenamiento del modelo y consideraremos el método Train.
El algoritmo del método de entrenamiento de la política del Actor es más exhaustivo y complejo en comparación con el método de entrenamiento del modelo de densidad comentado anteriormente. Por eso nos detendremos en él con más detalle.
Al principio del método, prepararemos algunas variables locales y matrices que utilizaremos más adelante durante el entrenamiento del modelo.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- int total_states = Buffer[0].Total; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total; vector<float> temp, next; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states, temp.Size()); matrix<float> rewards = matrix<float>::Zeros(total_states, NRewards); matrix<float> actions = matrix<float>::Zeros(total_states, NActions);
A continuación, organizaremos un sistema de ciclos de generación de incorporaciones de todos los estados a partir del búfer de reproducción de experiencias. El ciclo exterior de nuestro sistema recorrerá las trayectorias de la muestra de entrenamiento, así como que un ciclo anidado de estados del entorno que el Agente ha visitado al recorrer la trayectoria.
int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total; st++) { State.AssignArray(Buffer[tr].States[st].state);
En el cuerpo del sistema de ciclos, cargaremos un vector de descripciones de un único estado del entorno a partir de la muestra de entrenamiento. Lo completaremos con una descripción del estado de la cuenta y las posiciones abiertas.
float PrevBalance = Buffer[tr].States[MathMax(st - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st - 1, 0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
Aquí es también donde pondremos los armónicos de la marca temporal en el búfer.
double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); State.AddArray(vector<float>::Zeros(NActions));
Para evaluar los estados independientemente de las acciones realizadas por el Agente, rellenaremos el resto del búfer con valores nulos.
Tras rellenar con éxito el búfer de datos de origen, llamaremos al método de pasada directa del codificador aleatorio.
if(!Convolution.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; }
Almacenaremos sus resultados en una matriz de incorporaciones.
Convolution.getResults(temp); if(!state_embedding.Row(temp, state)) continue;
Paralelamente, guardaremos las acciones realizadas y las recompensas obtenidas como consecuencia de las transiciones posteriores.
if(!temp.Assign(Buffer[tr].States[st].action) || !actions.Row(temp, state)) continue; if(!temp.Assign(Buffer[tr].States[st].rewards) || !next.Assign(Buffer[tr].States[st + 1].rewards) || !rewards.Row(temp - next * DiscFactor, state)) continue;
Tras añadir con éxito todas las entidades a las matrices locales, incrementaremos el contador de estados procesados. Luego informaremos al usuario sobre el progreso del proceso de incorporación de estados y pasaremos a la siguiente iteración del sistema de ciclos.
state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } }
Tras completar con éxito todas las iteraciones del sistema de ciclos, ajustaremos el tamaño de las matrices locales al tamaño real de los datos utilizados, de ser necesario.
if(state != total_states)
{
rewards.Resize(state, NRewards);
actions.Resize(state, NActions);
state_embedding.Reshape(state, state_embedding.Cols());
total_states = state;
}
Y pasaremos a la siguiente fase del trabajo preparatorio, en la que entrenaremos una serie de variables locales más y daremos prioridad al muestreo de trayectorias de la muestra de entrenamiento durante el entrenamiento del modelo.
vector<float> rewards1, rewards2, target_reward; STarget target; int bar = (HistoryBars - 1) * BarDescr; //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Con esto concluiremos el trabajo preparatorio y pasaremos directamente al entrenamiento de modelos. Para ello, organizaremos un ciclo de entrenamiento con el número de iteraciones especificado en los parámetros externos del asesor.
En el cuerpo del ciclo, muestreamos una trayectoria priorizada y seleccionaremos aleatoriamente un estado en ella.
for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
A continuación, según el método SAC, tendremos que calcular la recompensa esperada hasta el final del episodio. Para ello, utilizaremos los modelos objetivo del Crítico. Sin embargo, solo realizaremos estas operaciones usando modelos preentrenados. Por lo tanto, verificaremos que se haya superado el número mínimo necesario de iteraciones de preentrenamiento antes de iniciar las operaciones.
target_reward = vector<float>::Zeros(NRewards); //--- Target if(iter >= StartTargetIter) { State.AssignArray(Buffer[tr].States[i + 1].state);
Tras controlar que todo vaya satisfactoriamente, llenaremos el búfer de datos inicial con una descripción del estado del entorno posterior.
Aparte, rellenaremos el búfer de descripción del estado de la cuenta y las posiciones abiertas.
float PrevBalance = Buffer[tr].States[i].account[0]; float PrevEquity = Buffer[tr].States[i].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i + 1].account[2]); Account.Add(Buffer[tr].States[i + 1].account[3]); Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
También le añadiremos los armónicos de la marca temporal.
double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- if(Account.GetIndex() >= 0) Account.BufferWrite();
Los datos recogidos serán suficientes para realizar la pasada directa del Actor.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Nótese que llamamos al método de pasada directa para el modelo del Actor entrenado seguido del estado del entorno. Esto nos generará la acción del Actor según la política actualizada. Así, los Críticos objetivo estimarán la recompensa esperada de la política actualizada hasta el final del episodio.
if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Utilizaremos la puntuación mínima obtenida de los 2 Críticos objetivo como valor esperado en las operaciones posteriores.
TargetCritic1.getResults(rewards1); TargetCritic2.getResults(rewards2); target_reward.Assign(Buffer[tr].States[i + 1].rewards); if(rewards1.Sum() <= rewards2.Sum()) target_reward = rewards1 - target_reward; else target_reward = rewards2 - target_reward; target_reward *= DiscFactor; target_reward[NRewards - 1] = EntropyLatentState(Actor); }
A continuación pasaremos al entrenamiento de nuestros críticos. Para que sus estimaciones sean correctas, el entrenamiento se basará en la comparación de las acciones reales y las recompensas de la muestra de entrenamiento. Pero aquí conviene recordar que en nuestro modelo utilizamos el Actor para preprocesar el estado del entorno. Por lo tanto, como antes, llenaremos los búferes de datos de origen con una descripción del estado del entorno muestreado.
//--- Q-function study
State.AssignArray(Buffer[tr].States[i].state);
Y rellenaremos el búfer describiendo el estado de la cuenta y las posiciones abiertas.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Asimismo, introduciremos los armónicos de la marca temporal,
double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
y luego realizaremos una pasada directa del Actor.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Tenga en cuenta que en este punto tendremos un conjunto completo de datos para implementar una pasada directa del Autocodificador. No vamos a aplazar lo que podamos hacer ahora. Luego llamaremos a los métodos de pasada directa del Codificador y Decodificador.
if(!Encoder.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CNet *)GetPointer(Actor)) || !Decoder.feedForward(GetPointer(Encoder), -1, GetPointer(Encoder), 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Como hemos mencionado anteriormente, el entrenamiento del Crítico se realizará sobre las acciones reales del Actor de la muestra de entrenamiento. Así que los cargaremos en el búfer de datos y llamaremos a los métodos de pasada directa de ambos Críticos.
Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
A continuación, aumentaremos el búfer de descripción del estado actual con los datos necesarios e incorporaremos el estado analizado utilizando un codificador aleatorio.
if(!State.AddArray(GetPointer(Account)) || !State.AddArray(vector<float>::Zeros(NActions)) || !Convolution.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Basándonos en los resultados de la incorporación, generaremos los valores objetivo del Actor y el Crítico.
Convolution.getResults(temp); target = GetTargets(Quant, temp, state_embedding, rewards, actions);
Después actualizaremos los parámetros de nuestros Críticos. Recordemos que el método CAGrad se utiliza para ajustar el vector gradiente con el fin de mejorar la convergencia del modelo.
Critic1.getResults(rewards1); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Critic2.getResults(rewards2); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Una vez actualizados con éxito los modelos de Crítico, pasaremos a optimizar la política de Actor. Este proceso puede dividirse a grandes rasgos en 3 bloques. En el primer bloque, ajustaremos la política del agente para que repita alguna acción recopilada a partir de acciones de la muestra de entrenamiento realizadas en estados similares y ponderadas por la recompensa recibida.
//--- Policy study Actor.getResults(rewards1); Result.AssignArray(CAGrad(target.actions - rewards1) + rewards1); if(!Actor.backProp(Result, GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
En el segundo paso, utilizaremos los resultados del Autocodificador y comprobaremos la desviación de las acciones generadas del Agente con respecto a la muestra de entrenamiento. Al superar el umbral de error de descodificación de la Acción, intentaremos devolver la política del Actor a la distribución de la muestra de entrenamiento. Para ello, realizaremos una pasada inversa del Autocodificador, y el error de codificación se pasará al Actor directamente en forma de gradiente de error. Similar a la transferencia de gradiente de error del Crítico. Para la realizar esta operación de forma segura, desactivaremos el modo de aprendizaje en el Codificador y el Decodificador en la fase de inicialización del programa.
Decoder.getResults(rewards2); if(rewards2.Loss(rewards1, LOSS_MSE) > MeanCVAEError) { Actions.AssignArray(rewards1); if(!Decoder.backProp(GetPointer(Actions), GetPointer(Encoder), 1) || !Encoder.backPropGradient((CNet*)GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
En la siguiente fase del entrenamiento de la política del Actor, comprobaremos la validez de las predicciones de nuestros Críticos. Y con suficiente confianza en sus predicciones, ajustaremos la política del Actor hacia la recompensa máxima más probable. En esta fase, también desactivaremos el modo de actualización de los parámetros del Crítico para evitar el efecto de adaptación mutua de los modelos.
CNet *critic = NULL; if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError()) critic = GetPointer(Critic1); else critic = GetPointer(Critic2); if(MathAbs(critic.getRecentAverageError()) <= MaxErrorActorStudy) { if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } critic.getResults(rewards1); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1); critic.TrainMode(false); if(!critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); critic.TrainMode(true); break; } critic.TrainMode(true); }
A continuación, nos quedará solo actualizar los modelos objetivo del Crítico.
//--- Update Target Nets if(iter >= StartTargetIter) { TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau); } else { TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1); TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1); }
E informar al usuario sobre el progreso del proceso de aprendizaje.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); str += StringFormat("%-14s %5.2f%% -> Error %15.8f\n", "Actor", iter * 100.0 / (double)(Iterations), Actor.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Una vez completadas todas las iteraciones del ciclo de entrenamiento del modelo, borraremos el campo de comentarios del gráfico. Luego enviaremos la información sobre los resultados del entrenamiento del modelo al registro e inicializaremos el proceso de finalización del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); ExpertRemove(); //--- }
Esto completará la implementación del método Supported Policy Optimization usando MQL5. El código completo de todos los programas usados en el artículo se encuentra en el archivo adjunto. Vamos a pasar a la siguiente parte de nuestro artículo. En ella comprobaremos nuestros resultados en un caso práctico.
3. Simulación
Ya hemos realizado el trabajo sobre la implementación del método SPOT usando MQL5, así que ha llegado el momento de comprobar los resultados de nuestro trabajo en la práctica. Como siempre, quiero insistir en que este artículo presenta una visión propia de los planteamientos propuestos por los autores del método. Además, estos se superponen a desarrollos creados previamente con otros métodos. Como resultado, construiremos un modelo a partir de un conglomerado de ideas diferentes ensambladas según una visión propia del proceso. Por consiguiente, todas las posibles deficiencias observadas no podrán proyectarse plenamente sobre ninguno de los métodos utilizados.
Como siempre, el entrenamiento y las pruebas de los modelos se realizarán con datos históricos del marco temporal EURUSD H1. Todos los parámetros de los indicadores se usarán por defecto. El modelo se entrenará con los datos de los 7 primeros meses de 2023. Las pruebas de los modelos entrenados se realizarán con los datos de agosto de 2023.
Como ya hemos dicho, los modelos de interacción del entorno se han mantenido sin cambios. Por consiguiente, para la primera etapa de entrenamiento, podemos utilizar la muestra de entrenamiento recogida en el marco del trabajo de Real-ORL, que sirvió de donante de los modelos. Acabo de hacer una copia de la muestra de entrenamiento llamada "SPOT.bd".
En el primer paso, realizaremos el entrenamiento del Autocodificador. La muestra de entrenamiento cuenta 500 trayectorias con 3591 condiciones del entornos en cada trayectoria. Eso suma un total de al menos 1,8 millones de conjuntos Estado-Acción-Recompensa. En esta fase, hemos implementado 5 ciclos de entrenamiento del Autocodificador de 0,5 millones de iteraciones cada uno, lo cual supone un 40% más que el tamaño de la muestra de entrenamiento.
Tras el entrenamiento inicial del Autocodificador, iniciaremos el proceso de entrenamiento de modelos en el asesor "...\SPOT\Study.mq5". Permítanme adelantar que la duración del proceso de entrenamiento del modelo será mucho mayor que la del Autocodificador.
También debemos señalar que mantener la política del Agente dentro de la muestra de entrenamiento no nos deja ninguna esperanza de obtener resultados superiores a las pasadas de la muestra de entrenamiento. Por ello, para obtener mejores políticas, necesitaremos actualizar iterativamente el búfer de reproducción de experiencias y actualizar los modelos, incluido el autocodificador.
Por lo tanto, en paralelo con el proceso de entrenamiento del modelo, ejecutaremos la optimización del asesor "ResearchExORL.mq5" en el simulador de estrategias para investigar estrategias fuera de la muestra de entrenamiento.
Tras completar el ciclo de entrenamiento del modelo, ejecutaremos la optimización del asesor "Research.mq5" en el simulador de estrategias durante 200 ejecuciones, explorando el entorno en algún entorno de la política de Actor aprendida.
Basándonos en la muestra de entrenamiento actualizada, repetiremos el entrenamiento del Autocodificador durante 0,5 millones de iteraciones. Y haremos un entrenamiento previo de la política del Actor.
Como resultado de varios ciclos de entrenamiento, podremos formar una política del Actor capaz de generar beneficios a lo largo del periodo histórico de entrenamiento y de prueba. A continuación presentamos los resultados del modelo para agosto de 2023.
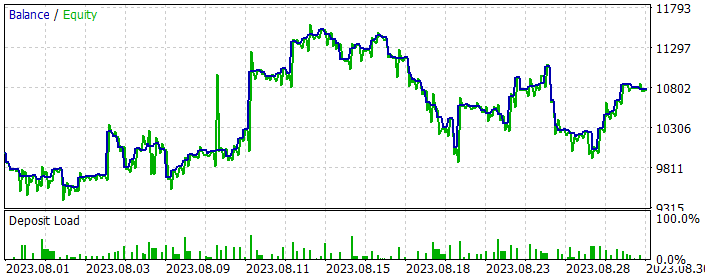
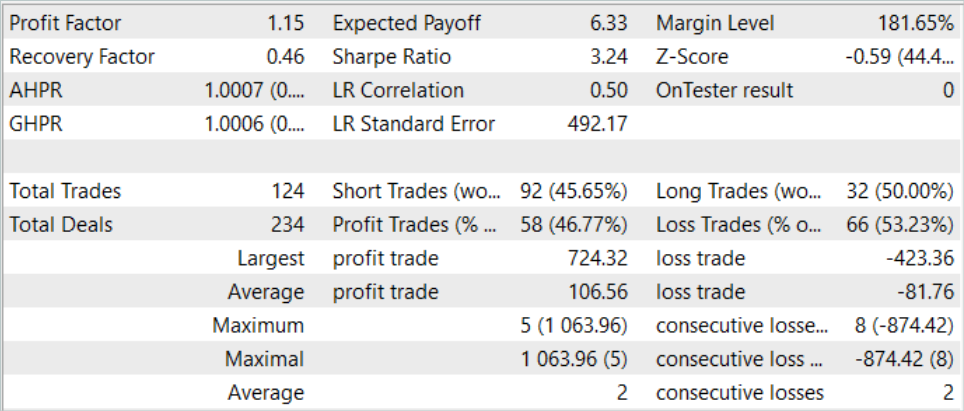
Como podemos ver en los datos presentados, el modelo ha realizado 124 operaciones (92 cortas y 32 largas) durante un mes de prueba de la estrategia. De ellas, casi el 47% se han cerrado con beneficios. Cabe destacar que la proporción de posiciones largas y cortas rentables ha sido cercana (50% y 46% respectivamente). Al mismo tiempo, la media de operaciones rentables ha sido un 25% superior a la media de pérdidas. Y la operación rentable máxima ha sido casi 2 veces la pérdida máxima. En conjunto, el factor de beneficio ha sido de 1,15 en los resultados de la operación.
Conclusión
En este artículo, hemos introducido el método Supported Policy OpTimisation (SPOT), que es una solución exitosa al problema del aprendizaje offline con una muestra de entrenamiento limitada. Su capacidad para regular la política, dada la densidad estimada de la estrategia de comportamiento, muestra un excelente rendimiento en escenarios de prueba estándar. SPOT puede integrarse fácilmente en los algoritmos de RL offline existentes, lo cual aporta flexibilidad de aplicación en diferentes contextos. Su estructura modular permite usarlo en combinación con diversos enfoques pedagógicos.
Una característica única de SPOT es el uso de una regularización basada en la estimación explícita de la densidad de los datos de la muestra de entrenamiento. Esto garantiza que las acciones políticas permitidas se gestionen con precisión, además de evitar eficazmente la extrapolación más allá de la muestra de entrenamiento.
En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Los resultados de las pruebas realizadas permiten concluir que este método es eficaz. Durante el entrenamiento, podemos destacar la estabilidad del paso por el proceso. Y, basándonos en los resultados de la entrenamiento, aún hemos conseguido encontrar una estrategia rentable para el comportamiento del Actor.
Sin embargo, cabe señalar que el mantenimiento de la política del Actor dentro de la muestra de entrenamiento limita la estimulación de la investigación fuera de ella. Por un lado, hace que el proceso de aprendizaje sea más estable. Pero por otro lado, limita la capacidad de explorar subespacios inexplorados del entorno. Podemos concluir que este método resulta más eficaz cuando hay pasadas subóptimas en la muestra de entrenamiento.
Al mismo tiempo, para estimular la exploración del entorno, podemos intentar "darle la vuelta" al método y fomentar la exploración de acciones fuera de la muestra de entrenamiento. Pero este es un tema para futuras investigaciones.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | ResearchExORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método ExORL |
| 4 | Study.mq5 | Asesor | Asesor de entrenamiento del agente |
| 5 | StudyCVAE.mq5 | Asesor | Asesor de entrenamiento de autocodificadores |
| 6 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 7 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 8 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 9 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13954
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Desarrollo de un sistema de repetición (Parte 42): Proyecto Chart Trade (I)
Desarrollo de un sistema de repetición (Parte 42): Proyecto Chart Trade (I)
 Patrones de diseño en MQL5 (Parte 4): Patrones conductuales 2
Patrones de diseño en MQL5 (Parte 4): Patrones conductuales 2
 GIT: ¿Pero qué es esto?
GIT: ¿Pero qué es esto?
 Algoritmos de optimización de la población: Algoritmos de estrategias evolutivas (Evolution Strategies, (μ,λ)-ES y (μ+λ)-ES)
Algoritmos de optimización de la población: Algoritmos de estrategias evolutivas (Evolution Strategies, (μ,λ)-ES y (μ+λ)-ES)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
¿Es intencionado que no haya archivos adjuntos en este artículo?
¿Es intencionado que no haya archivos adjuntos en este artículo?
Se trata de un desafortunado error y ya se ha publicado una versión funcional del artículo. Corregido.