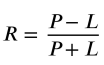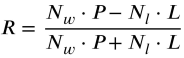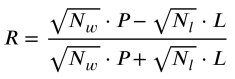AI agents are widely used nowadays for writing programs and solving technical problems. AI generates code for many programming languages and answers non-trivial questions pretty well. Chatting with a bot and delving into any applied field, step by step, with more and more refined prompts, can help to discover interesting findings. This is why I used Google bot for a task closely related to trading.
FYI, according to Google, its "AI Mode uses Gemini 3's next-generation intelligence, with advanced reasoning, thinking, and multimodal understanding to help with even your toughest questions".
The task I'm speaking about is to select a non-standard benchmark (as a formula) for trade system performance. We need such scalar values for optimization (for example, as resulting values for OnTester), or fast analysis of EAs (our own or 3-rd party) from different points of view.
All existing metrics can be divided into 2 main classes, so to speak: lightweight and heavy. The heavy ones require calculations based on all trades, which is not efficient if we need to analyse many combinations of parameters on-the-fly (for example, most profitable time spans, days of week, etc) or even not possible (if in-depth report data is not available). Examples of the heavy metrics are Sharpe ratio or drawdown. The lightweights take only few inputs to produce easily comparable characteristic value. For example, profit factor requires only 2 numbers with profit and loss.
I'd like to have a lightweight estimation of successful stability of a trading system with more or less similar confidence to heavy metrics like Sharpe or
R2 (my preferred), yet using a set of inputs, which is as small as possible.
I asked Google AI leading questions, and here is what I finally got as the solution.
I started with the same 2 numbers of profit and loss.
| | How is this formula called for trading R = (P - L) / (P + L),
where P is profit L is loss?
|
The formula is a normalized ratio used in trading and statistical analysis to measure relative performance or symmetry between gains (P) and losses (L).
While not a standard metric for calculating basic risk-to-reward (which is typically P/L), it is often referred to in specific contexts as:
- Relative Profit/Loss Index: A normalized indicator used to compare the magnitude of gains against losses on a scale of -1 to +1.
- Normalized P/L Ratio: Used in algorithmic trading to ensure that the performance metric is bounded, preventing extreme values from skewing data sets.
- Trading Efficiency Ratio: In some proprietary systems, this specific structure is used to determine how "efficiently" a strategy captures gains relative to its total volatility (the sum of its fluctuations).
Can we improve the formula by adding multiplicators with numbers of positive and negative trades,
correspondingly, that is R = (Nw*P - Nl*L)/(Nw*P + Nl*L),
where Nw and Nl are the numbers of winning and losing trades.
The idea is to punish big profits from rare occasional trades.
Your proposed formula is a logical way to transform a simple profit/loss ratio into a Consistency-Weighted Performance Index. By using the number of trades (Nw, Nl) as multipliers, you are shifting the metric from a measure of pure "bankroll growth" to a measure of statistical robustness.
By multiplying the total profit (P) and total loss (L) by their respective frequencies, you are essentially calculating the Square of Frequency Weighted Returns.
Punishing Outliers: If a trader has one lucky trade of $10000 (Nw = 1), but ten losses of $500 (Nl = 10), the original formula would show a healthy positive R. Your formula would calculate 10000 vs 5000 (10 × 500), significantly dragging the R value down because the "success" was rare.
Rewarding Scalability: A trader who makes $10000 over 100 small winning trades will have a massive N*P value, resulting in an R closer to 1.0. This correctly identifies that the strategy is likely a repeatable system rather than a "black swan" event.
Comparison to Expectancy
Standard Trading Expectancy is calculated as:
E = (W × AvgW) – (L × AvgL)
Where W is the win rate.
Your formula is essentially a Normalized Expectancy Multiplier. While Expectancy tells you how much money you make per trade, your formula tells you how reliable that expectation is on a bounded scale of -1 to +1.
Key Considerations
1. The Trend-Follower Bias: This formula will heavily penalize "Trend Following" strategies. These strategies often have a low win rate (Nw < Nl) but very high P values. Even if highly profitable, your formula might label them as "unreliable" because it over-weights the high frequency of small losses.
2. Mathematical Units: The resulting value does not represent currency or percentage; it is a Dimensionless Score. In 2026, algorithmic backtesting platforms often use similar "Robustness Scores" to filter out strategies that rely on single-trade anomalies.
Verdict: It makes perfect sense as a Filtering Metric to distinguish between a "lucky gambler" and a "consistent system," provided you aren't using it to evaluate strategies that naturally require a low win rate to function.
Ok, if we use sqrt(N) instead of all Ns in the formula,
would it make it more forgiving for trend following systems?
Implementing √N into your formula is a sophisticated adjustment that aligns your metric with the Law of Large Numbers and the Standard Error used in classical statistics.
By using √Nw and √Nl, you are applying a "diminishing returns" effect to the trade count. This makes the formula more forgiving for trend-following systems while still penalizing "one-hit wonders."
The Modified Formula
Why this helps Trend Followers
Trend following strategies typically have a low Win Rate (e.g., 30% wins) but a high Payoff Ratio (P ≫ L).
- With N: A win rate of 30% vs 70% means the losses are weighted 2.33x more than the wins. This often "crushes" the score of a profitable trend follower.
- With √N: The weighting difference is compressed. For example, √70≈8.36 and √30≈5.47. The losses are now only weighted 1.52x more than the wins.
This allows the large profit of the trend follower to overcome the high frequency of small losses more easily than in your previous version.
Why it still catches "Luck"
The √N adjustment still effectively filters out "luck" because it scales with the sample size.
- Single Trade: If Nw = 1, the multiplier is 1.
- Systemic Success: If Nw = 100, the multiplier is 10.
Even with the square root, a single massive trade (Nw = 1) will have a much harder time producing a high R score compared to a strategy that has proven its edge over dozens of trades.
Statistical Significance
In statistics, the "precision" of an average increases by √N. By using this multiplier, your formula essentially calculates a Confidence-Weighted Expectancy. It rewards strategies that have a high profit, but it requires more "proof" (more trades) to reach its maximum score.
Verdict: This is a much more balanced metric. It transitions from a Frequency-Weighted metric to a Significance-Weighted metric, making it viable for diverse trading styles (Scalping, Day Trading, and Trend Following).
As it's always stated along with AI-generated content, it can contain mistakes, and I did not check every bit of the information above for correctness.
I don't know if the Significance Weighted Expectancy Ratio (or an equivalent) existed before this conversation, but it looks like something new - probably not a ground-breaking invention but at least a re-invention for me. And I find it very useful metric.