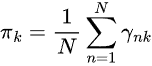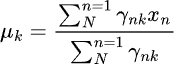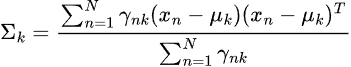
Data Science and ML (Part 43): Hidden Patterns Detection in Indicators Data Using Latent Gaussian Mixture Models (LGMM)
462
0
Contents
- Introduction
- What is a Latent Gaussian Mixture Model
- Mathematics behind LGMM
- Training LGMM on indicators data
- An MQL5 indicator based on LGMM
- Finding the best number of components for LGMM
- Latent Gaussian Mixture Model alongside a classifier model
- LGMM based trading robot
- Conclusion
Introduction
Almost all trading strategies available that we use as traders are based on some pattern identification and detection. We examine indicators for patterns and confirmations, and sometimes we even draw objects and lines, such as support and resistance lines, to identify the market's state.
While pattern detection is an easy task for us humans in financial markets, it is challenging to program and automate this process because of the nature of the markets (noisy and chaotic).
Some traders have adopted to the use of Artificial Intelligence (AI) and machine learning for this particular task using various computer vision-based techniques which process images data similar to what humans do, as we discussed in one of the previous articles.
In this article, we will discuss a probabilistic model named Latent Gaussian Mixture Model (LGMM), which is capable of detecting patterns. Given the indicators data, we will explore this model's effectiveness in detecting hidden patterns and making accurate predictions in the financial markets.
What is a Latent Gaussian Mixture Model (LGMM)?
Latent Gaussian Mixture Model is a probabilistic model that assumes data is generated from a mixture of multiple Gaussian distributions, each associated with a latent (hidden) variable.
It is an extension of the Gaussian Mixture Model (GMM) that incorporates latent variables that explain cluster assignment for each observation.
Latent Gaussian models are used to analyze data where the underlying processes generating the data are not directly observable and are assumed to have a Gaussian (normal) distribution.
The 'latent' part refers to these unobserved variables, much like the unseen electrical signals in a circuit, which influence the system's behavior but are not directly measured.
In financial markets, these latent variables can represent underlying trading patterns in the data that we often misinterpret or miss out.
Simply put, the backbone of LGMM involves:
- Latent Variables
These are unobserved variables assumed to be Gaussian, representing underlying factors that affect the observed data. - Observations
The actual data collected, which is typically non-Gaussian and may follow any distribution linked to the latent variables through a known function. - Parameters
These govern the relationship between latent variables and observations, including the means and variances of the distributions.
Mathematics behind LGMM
LGMM is a probabilistic generative model with a clustering technique at its core. It has:
Latent variables
- These are not directly observed
- They represent the component (cluster) from which a data point is drawn.
- They are often modeled as a categorical (discrete) distribution, e.g.,
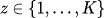
The Mixture model
The probability distribution of the data is a weighted sum of several Gaussian distributions.
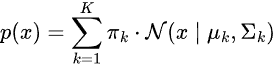
Where:
-
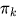is the mixing coefficient (prior probability of a component 
, 
-
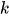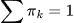
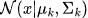= Gaussian distribution with mean 
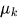and covariance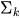 
Latent Variable Representation
Instead of modelling p(x) directly, we consider:
Where:
The Goal of this model is to estimate latent variables and the parameters 
.
The most common method used to determine these variables is the Expectation-Maximization (EM) algorithm.
Expectation-Maximization (EM) for LGMM
This involves two steps, Expectation and Minimization.
Step 01, Expectations.
This involves estimating the posterior probability that each data point belongs to each Gaussian.
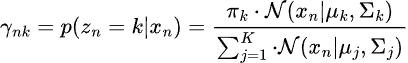
Step 02, Minimization
This step involves updating the parameters using the 
.
In training, both step 01 and step 02 are repeated until the model converges.
LGMM has been used in several applications in the real world, such as clustering the data with uncertainty (soft clustering), in detecting anomalies, in density estimation, and in voice recognition-related tasks.
Training LGMM on Indicators Data
We know that inside the indicators data, there are patterns that, as traders, we use in making informed trading decisions. Our goal is to use LGMM to detect those patterns first.
We start by collecting indicators data from MetaTrader 5 first using MQL5 language.
- Symbol = XAUUSD.
- Timeframe = DAILY.
Filename: Get XAUUSD Data.mq5
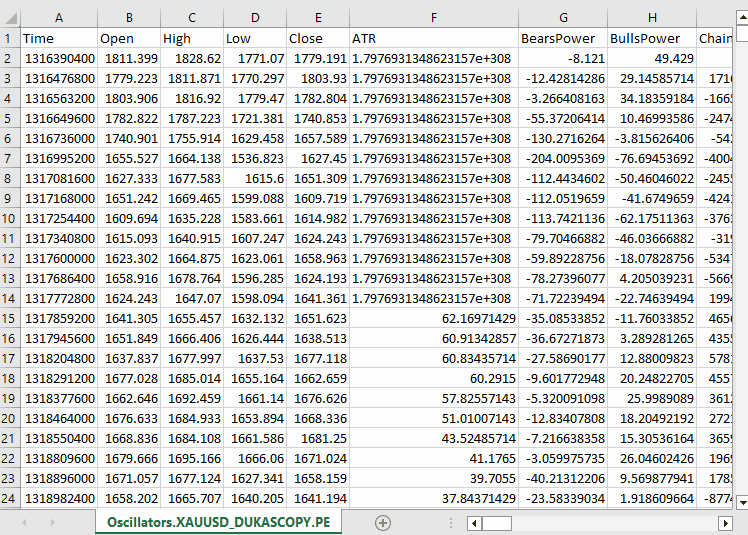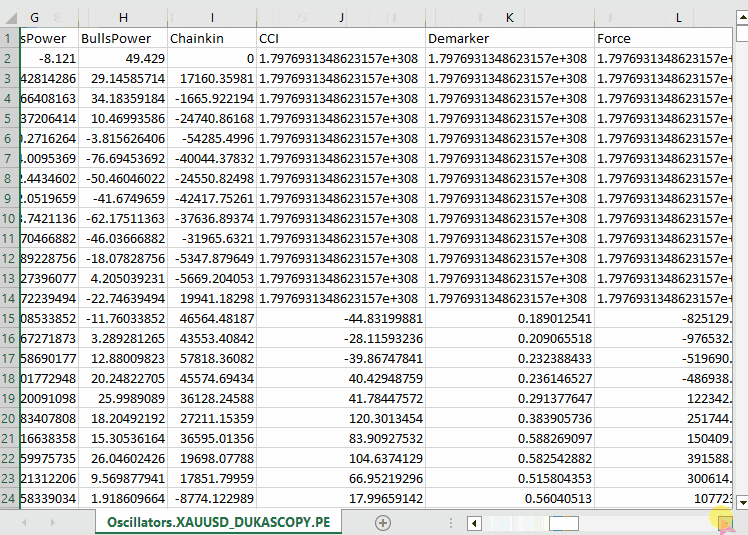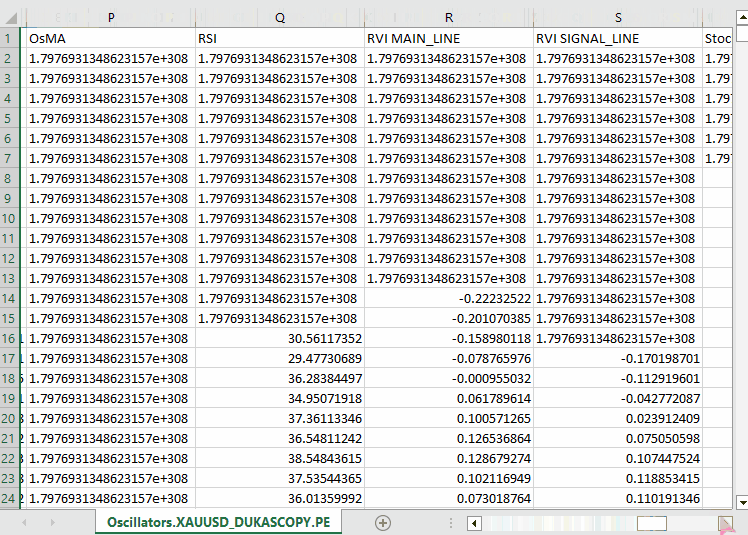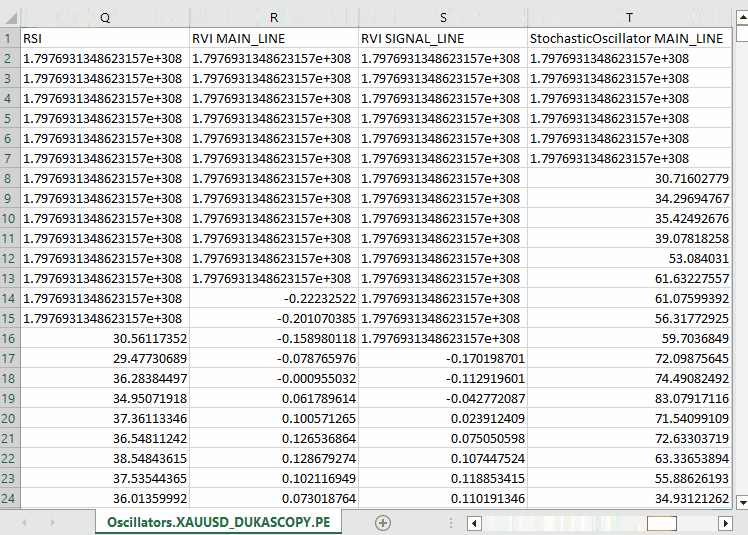
#include <Arrays\ArrayString.mqh> #include <Arrays\ArrayObj.mqh> #include <pandas.mqh> //https://www.mql5.com/en/articles/17030 input datetime start_date = D'2005.01.01'; input datetime end_date = D'2023.01.01'; input string symbol = "XAUUSD"; input ENUM_TIMEFRAMES timeframe = PERIOD_D1; struct indicator_struct { long handle; CArrayString buffer_names; //buffer_names array }; indicator_struct indicators[15]; //Structure for keeping indicator handle alongside its buffer names //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- vector time, open, high, low, close; if (!SymbolSelect(symbol, true)) { printf("%s failed to select symbol %s, Error = %d",__FUNCTION__,symbol,GetLastError()); return; } //--- time.CopyRates(symbol, timeframe, COPY_RATES_TIME, start_date, end_date); open.CopyRates(symbol, timeframe, COPY_RATES_OPEN, start_date, end_date); high.CopyRates(symbol, timeframe, COPY_RATES_HIGH, start_date, end_date); low.CopyRates(symbol, timeframe, COPY_RATES_LOW, start_date, end_date); close.CopyRates(symbol, timeframe, COPY_RATES_CLOSE, start_date, end_date); CDataFrame df; df.insert("Time", time); df.insert("Open", open); df.insert("High", high); df.insert("Low", low); df.insert("Close", close); //--- Oscillators indicators[0].handle = iATR(symbol, timeframe, 14); indicators[0].buffer_names.Add("ATR"); indicators[1].handle = iBearsPower(symbol, timeframe, 13); indicators[1].buffer_names.Add("BearsPower"); indicators[2].handle = iBullsPower(symbol, timeframe, 13); indicators[2].buffer_names.Add("BullsPower"); indicators[3].handle = iChaikin(symbol, timeframe, 3, 10, MODE_EMA, VOLUME_TICK); indicators[3].buffer_names.Add("Chainkin"); indicators[4].handle = iCCI(symbol, timeframe, 14, PRICE_OPEN); indicators[4].buffer_names.Add("CCI"); indicators[5].handle = iDeMarker(symbol, timeframe, 14); indicators[5].buffer_names.Add("Demarker"); indicators[6].handle = iForce(symbol, timeframe, 13, MODE_SMA, VOLUME_TICK); indicators[6].buffer_names.Add("Force"); indicators[7].handle = iMACD(symbol, timeframe, 12, 26, 9, PRICE_OPEN); indicators[7].buffer_names.Add("MACD MAIN_LINE"); indicators[7].buffer_names.Add("MACD SIGNAL_LINE"); indicators[8].handle = iMomentum(symbol, timeframe, 14, PRICE_OPEN); indicators[8].buffer_names.Add("Momentum"); indicators[9].handle = iOsMA(symbol, timeframe, 12, 26, 9, PRICE_OPEN); indicators[9].buffer_names.Add("OsMA"); indicators[10].handle = iRSI(symbol, timeframe, 14, PRICE_OPEN); indicators[10].buffer_names.Add("RSI"); indicators[11].handle = iRVI(symbol, timeframe, 10); indicators[11].buffer_names.Add("RVI MAIN_LINE"); indicators[11].buffer_names.Add("RVI SIGNAL_LINE"); indicators[12].handle = iStochastic(symbol, timeframe, 5, 3,3,MODE_SMA,STO_LOWHIGH); indicators[12].buffer_names.Add("StochasticOscillator MAIN_LINE"); indicators[12].buffer_names.Add("StochasticOscillator SIGNAL_LINE"); indicators[13].handle = iTriX(symbol, timeframe, 14, PRICE_OPEN); indicators[13].buffer_names.Add("TEMA"); indicators[14].handle = iWPR(symbol, timeframe, 14); indicators[14].buffer_names.Add("WPR"); //--- Get buffers for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { for (uint buffer_no=0; buffer_no<(uint)indicators[ind].buffer_names.Total(); buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start_date, end_date)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } df.to_csv(StringFormat("Oscillators.%s.%s.csv",symbol,EnumToString(timeframe)), true); //Save all the data to a CSV file }
Outputs.
Notice that, we collected roughly all oscillator indicators which are built-in in MQL5, most of which happen to produce stationary data as they usually have minimum and maximum values. For example; The RSI indicator produces values between 0 and 100.
Despite the LGMM being capable of working with data of different statistical properties, such as non-stationary data. Stationary data makes it easier for LGMM to find meaningful structures and patterns because statistical properties of stationary data remains constant through time.
You are welcome to use any kind of data you'd prefer.
We collected Open, High, Low, Close, and Time (OHLCT) variables alongside indicators data for machine learning usage. This information can be used in visualization and in making the target variable for predictive machine learning models apart from LGMM.
Inside a Python script (Jupyter Notebook), the first thing we do is load this data shortly after importing the dependencies and initializing the MetaTrader 5 desktop app.
Filename: main.ipynb
import pandas as pd import numpy as np import MetaTrader5 as mt5 import os from Trade.TerminalInfo import CTerminalInfo import matplotlib.pyplot as plt import seaborn import warnings warnings.filterwarnings("ignore") seaborn.set_style("darkgrid") if not mt5.initialize(): print("Failed to Initialize MetaTrade5, Error = ",mt5.last_error()) mt5.shutdown() terminal = CTerminalInfo() # similarly to CTerminalInfo from MQL5. For getting information about the MetaTrader5 app
We Import the data from the common path (folder), which is where we saved it using MQL5.
common_path = os.path.join(terminal.common_data_path(), "Files") symbol = "XAUUSD" timeframe = "PERIOD_D1" df = pd.read_csv(os.path.join(common_path, f"Oscillators.{symbol}.{timeframe}.csv")) # the same naming pattern as the one used in the MQL5 script # Identify max float value max_float = np.finfo(float).max # Replace all max float (double) values with NaN produced by preliminary indicator calculations df = df.replace(max_float, np.nan) df.dropna(inplace=True) df["Time"] = pd.to_datetime(df["Time"], unit="s") df.head()
Outputs.
Time Open High Low Close ATR BearsPower BullsPower Chainkin CCI ... MACD SIGNAL_LINE Momentum OsMA RSI RVI MAIN_LINE RVI SIGNAL_LINE StochasticOscillator MAIN_LINE StochasticOscillator SIGNAL_LINE TEMA WPR 0 2005-01-03 438.45 438.71 426.72 429.55 5.481429 -12.314215 -0.324215 -1079.046551 -51.013015 ... 0.175727 99.870165 -0.582169 46.666555 -0.082596 0.018515 26.976532 32.920132 -0.000089 -85.144357 1 2005-01-04 429.52 430.18 423.71 427.51 5.450000 -13.677899 -7.207899 -1129.324384 -235.622347 ... -0.000779 98.615544 -1.252741 37.393138 -0.158362 -0.048541 22.158658 27.150101 -0.000190 -82.774252 2 2005-01-05 427.50 428.77 425.10 426.58 5.162143 -10.743913 -7.073913 -1496.644248 -196.837418 ... -0.247283 97.044402 -1.816758 35.666584 -0.227422 -0.119850 17.070979 22.068723 -0.000325 -86.990027 3 2005-01-06 426.31 427.85 420.17 421.37 5.234286 -13.606211 -5.926211 -3349.884147 -164.038728 ... -0.576309 97.480164 -2.194161 34.651526 -0.269634 -0.187300 14.096364 17.775334 -0.000482 -95.312500 4 2005-01-07 421.39 425.48 416.57 419.02 5.605000 -15.098181 -6.188181 -4970.426959 -168.301515 ... -1.015433 95.440750 -2.669414 30.754440 -0.305796 -0.243045 11.442611 14.203318 -0.000670 -91.609589
Let's prepare the target variable for a classification problem for later usage in classifier machine learning models. We drop non-indicator features along the way.
lookahead = 1 df["future_close"] = df["Close"].shift(-lookahead) new_df = df.dropna() new_df["Direction"] = np.where(new_df["future_close"]>new_df["Close"], 1, -1) # if a the close value in the next bar(s)=lookahead is above the current close price, thats a long signal otherwise that's a short signal
from sklearn.model_selection import train_test_split X = new_df.drop(columns=[ "Time", "Open", "High", "Low", "Close", "future_close", "Direction" ]) y = new_df["Direction"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=42)
We have to check to ensure that we have the "indicators data" we need.
X_train.head()
Outputs.
ATR BearsPower BullsPower Chainkin CCI Demarker MACD MAIN_LINE MACD SIGNAL_LINE Momentum OsMA RSI RVI MAIN_LINE RVI SIGNAL_LINE StochasticOscillator MAIN_LINE StochasticOscillator SIGNAL_LINE TEMA WPR 1057 30.139286 34.958195 62.858195 16280.794393 268.371098 251356.076923 -1.759289 -15.645899 107.768519 13.886610 62.077386 0.229591 0.108028 92.301971 83.886543 -0.002663 -8.048595 3806 3.096429 0.724299 3.314299 -1279.189840 69.806094 696.923077 -0.121217 -0.952863 100.299538 0.831645 52.157089 0.096237 0.080054 67.031250 71.466497 -0.000077 -21.325052 38884 5.927143 -8.488258 -3.858258 -2005.866698 -213.672289 -3333.080000 -0.049837 0.496440 99.774916 -0.546277 39.550361 -0.022395 0.035070 28.046540 49.606252 0.000012 -73.130342 10351 2.060714 -0.491108 1.158892 723.246254 40.384615 2508.735385 1.293179 0.953618 100.533084 0.339561 58.791715 0.217352 0.294053 57.239819 69.770534 0.000123 -19.070322 38170 5.632143 -5.682364 -3.262364 -1321.008995 -109.039933 -1673.607692 -0.609996 0.785433 99.712893 -1.395429 41.917705 -0.062258 -0.053202 13.322009 9.490964 0.000035 -77.826942
Let's finally train LGMM .
from sklearn.mixture import GaussianMixture from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType components = 3 gmm = GaussianMixture(n_components=components, covariance_type="full", random_state=42) gmm.fit(X_train) latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
I'm using 3 components for the Gaussian Mixture model, hoping it can cluster the patterns observed in the indicators between 3 clusters. Supposedly, one cluster for bullish trend (signal), the other cluster for bearish signal, and the other for consolidation or a ranging signal. Again, this is just a guess.
Similarly to other unsupervised machine learning and clustering techniques, it is difficult to interpret the resulting components (outcomes) produced by the model. For now, we can only assume that each one of the component belongs to the three classes I just described.
You might be wondering why I am calling the model a Latent Gaussian Mixture Model (LGMM), but I end up deploying a model named GaussianMixture from Scikit-Learn?
The imported GaussianMixture model has a functionality equivalent to the LGMM as described in the mathematics section of this post. These two are theoretically the same.
Let's print the latent_features_train array.
latent_features_train
Outputs.
array([[9.48947877e-13, 1.08107288e-62, 1.00000000e+00], [9.71935407e-01, 2.80542130e-02, 1.03801388e-05], [5.35722226e-03, 9.94642667e-01, 1.10916653e-07], ..., [7.72441751e-08, 8.80712550e-41, 9.99999923e-01], [9.99975623e-01, 1.07924534e-33, 2.43771745e-05], [1.91968188e-01, 8.08030586e-01, 1.22621110e-06]], shape=(3760, 3))
LGMM has produced an array of 3 elements on every row of predictions, each column representing the probability of the received data input belonging to one of the 3 clusters. The sum of probability for all 3 columns is equal to 1 on every row.
Since this is challenging to interpret as it stands, let's convert this model into ONNX format, visualize the clusters in MQL5, and see what conclusions we can draw upon the outputs produced by this probabilistic model.
An MQL5 Indicator Based on the Latent Gaussian Mixture Model (LGMM)
We start by saving LGMM to ONNX format.
# Define input type (shape should match your training data) initial_type = [("float_input", FloatTensorType([None, X_train.shape[1]]))] # Convert the pipeline to ONNX format onnx_model = convert_sklearn(gmm, initial_types=initial_type) # Save the model to a file with open(os.path.join(common_path, f"LGMM.{symbol}.{timeframe}.onnx"), "wb") as f: f.write(onnx_model.SerializeToString())
Below is the model's architecture when opened in Netron.
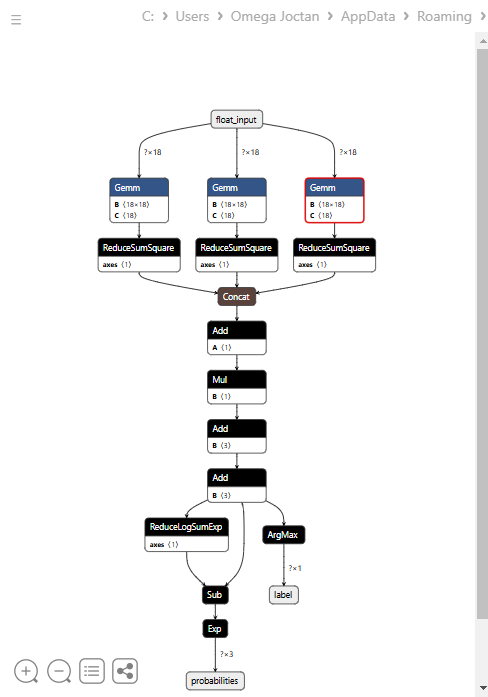
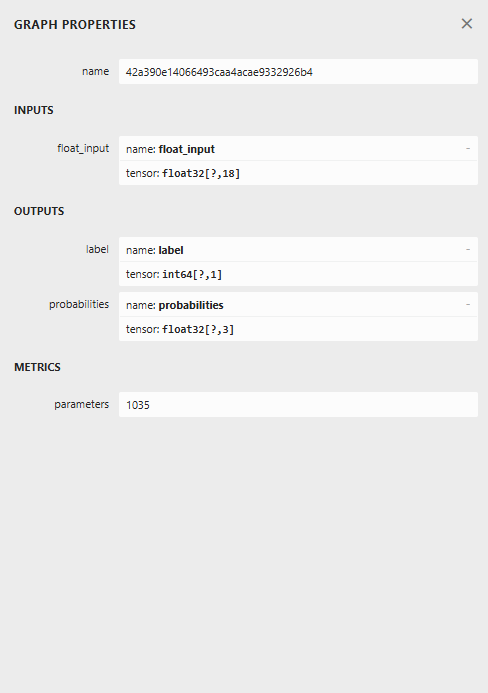
This model has a strange architecture with two outputs in the final node, one for the predicted label and the other for probabilities. We need to have this in mind when implementing the code for loading for this model in MQL5.
Loading LGMM in MQL5
Filename: Gaussian Mixture.mqh
We need the output structure that takes multiple arrays of values to accommodate two output nodes, each with an array of outputs.
class CGaussianMixture { protected: bool initialized; long onnx_handle; void PrintTypeInfo(const long num,const string layer,const OnnxTypeInfo& type_info); ulong inputs[]; //Inputs of a model in dimensions [nxn] struct outputs_struct { ulong outputs[]; } model_output_structure[]; //Outputs of the model structure array
Then.
bool CGaussianMixture::OnnxLoad(long &handle) { //--- since not all sizes defined in the input tensor we must set them explicitly //--- first index - batch size, second index - series size, third index - number of series (only Close) OnnxTypeInfo type_info; //Getting onnx information for Reference In case you forgot what the loaded ONNX is all about long input_count=OnnxGetInputCount(handle); if (MQLInfoInteger(MQL_DEBUG)) Print("model has ",input_count," input(s)"); for(long i=0; i<input_count; i++) { string input_name=OnnxGetInputName(handle,i); if (MQLInfoInteger(MQL_DEBUG)) Print(i," input name is ",input_name); if(OnnxGetInputTypeInfo(handle,i,type_info)) { if (MQLInfoInteger(MQL_DEBUG)) PrintTypeInfo(i,"input",type_info); ArrayCopy(inputs, type_info.tensor.dimensions); } } long output_count=OnnxGetOutputCount(handle); if (MQLInfoInteger(MQL_DEBUG)) Print("model has ",output_count," output(s)"); ArrayResize(model_output_structure, (int)output_count); for(long i=0; i<output_count; i++) { string output_name=OnnxGetOutputName(handle,i); if (MQLInfoInteger(MQL_DEBUG)) Print(i," output name is ",output_name); if(OnnxGetOutputTypeInfo(handle,i,type_info)) { if (MQLInfoInteger(MQL_DEBUG)) PrintTypeInfo(i,"output",type_info); ArrayCopy(model_output_structure[i].outputs, type_info.tensor.dimensions); } //--- Set the output shape replace(model_output_structure); if(!OnnxSetOutputShape(handle, i, model_output_structure[i].outputs)) { if (MQLInfoInteger(MQL_DEBUG)) { printf("Failed to set the Output[%d] shape Err=%d",i,GetLastError()); DebugBreak(); } return false; } } //--- replace(inputs); //--- Setting the input size for (long i=0; i<input_count; i++) if (!OnnxSetInputShape(handle, i, inputs)) //Giving the Onnx handle the input shape { if (MQLInfoInteger(MQL_DEBUG)) printf("Failed to set the input shape Err=%d",GetLastError()); DebugBreak(); return false; } initialized = true; if (MQLInfoInteger(MQL_DEBUG)) Print("ONNX model Initialized"); return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CGaussianMixture::Init(string onnx_filename, uint flags=ONNX_DEFAULT) { onnx_handle = OnnxCreate(onnx_filename, flags); if (onnx_handle == INVALID_HANDLE) return false; return OnnxLoad(onnx_handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CGaussianMixture::Init(const uchar &onnx_buff[], ulong flags=ONNX_DEFAULT) { onnx_handle = OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer if (onnx_handle == INVALID_HANDLE) return false; return OnnxLoad(onnx_handle); }
We made the predict method from this class to return two variables, the predicted label and a probability vector in a structure.
struct pred_struct { vector proba; long label; };
pred_struct CGaussianMixture::predict(const vector &x) { pred_struct res; if (!this.initialized) { if (MQLInfoInteger(MQL_DEBUG)) printf("%s The model is not initialized yet to make predictions | call Init function first",__FUNCTION__); return res; } //--- vectorf x_float; //Convert inputs from a vector of double values to those float values x_float.Assign(x); vector label = vector::Zeros(model_output_structure[0].outputs[1]); //outputs[1] we get the second shape (columns) from an array vector proba = vector::Zeros(model_output_structure[1].outputs[1]); //outputs[1] we get the second shape (columns) from an array if (!OnnxRun(onnx_handle, ONNX_DATA_TYPE_FLOAT, x_float, label, proba)) //Run the model and get the predicted label and probability { if (MQLInfoInteger(MQL_DEBUG)) printf("Failed to get predictions from Onnx err %d",GetLastError()); DebugBreak(); return res; } //--- res.label = (long)label[label.Size()-1]; //Get the last item available at the label's array res.proba = proba; return res; }
Let's call the predict function inside the main function of an indicator to provide us with latent features.
Filename: LGMM Indicator.mq5
int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { //--- Main calculation loop int lookback = 20; for (int i = prev_calculated; i < rates_total && !IsStopped(); i++) { if (i+1<lookback) //prevent data not found errors during copy buffer continue; int reverse_index = rates_total - 1 - i; //--- Get the indicators data vector x = getX(reverse_index, lookback); if (x.Size()==0) continue; pred_struct res = lgmm.predict(x); vector proba = res.proba; long label = res.label; ProbabilityBuffer[i] = proba.Max(); // Determine color based on histogram value if (label == 0) ColorBuffer[i] = 0; else if (label == 1) ColorBuffer[i] = 1; else ColorBuffer[i] = 2; Comment("bars [",i+1,"/",rates_total,"]"," Proba: ",proba," label: ",label); } //--- return(rates_total); }
Inside the getX() function, we have to collect all indicator buffers in the same way as we did in the script when collecting the data for training.
vector getX(uint start=0, uint count=10) { //--- Get buffers CDataFrame df; for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { uint buffers_total = indicators[ind].buffer_names.Total(); for (uint buffer_no=0; buffer_no<buffers_total; buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start, count)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } return df.iloc(-1); //Return the latest information from the dataframe which is the most recent buffer }
Note: All indicators were initialized inside the Init function right after the model was initialized from the common folder, which is where we saved it using Python.
#include <Gaussian Mixture.mqh> #include <Arrays\ArrayString.mqh> #include <MALE5\Pandas\pandas.mqh> CGaussianMixture lgmm; input string symbol = "XAUUSD"; input ENUM_TIMEFRAMES timeframe = PERIOD_D1; struct indicator_struct { long handle; CArrayString buffer_names; }; indicator_struct indicators[15]; //--- Indicator buffers double ProbabilityBuffer[]; double ColorBuffer[]; double MaBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping Comment(""); // Setting indicator properties SetIndexBuffer(0, ProbabilityBuffer, INDICATOR_DATA); SetIndexBuffer(1, ColorBuffer, INDICATOR_COLOR_INDEX); // Setting histogram drawing style PlotIndexSetInteger(0, PLOT_DRAW_TYPE, DRAW_COLOR_HISTOGRAM); // Set indicator labels IndicatorSetString(INDICATOR_SHORTNAME, "3-Color Histogram"); IndicatorSetInteger(INDICATOR_DIGITS, _Digits); //--- string filename = StringFormat("LGMM.%s.%s.onnx",symbol, EnumToString(timeframe)); if (!lgmm.Init(filename, ONNX_COMMON_FOLDER)) { printf("%s Failed to initialize the GaussianMixture model (LGMM) in ONNX format file={%s}, Error = %d",__FUNCTION__,filename,GetLastError()); } //--- Oscillators indicators[0].handle = iATR(symbol, timeframe, 14); indicators[0].buffer_names.Add("ATR"); //... //... //... indicators[14].handle = iWPR(symbol, timeframe, 14); indicators[14].buffer_names.Add("WPR"); for (uint i=0; i<indicators.Size(); i++) if (indicators[i].handle==INVALID_HANDLE) { printf("%s Invalid %s handle, Error = %d",__FUNCTION__,indicators[i].buffer_names[0],GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
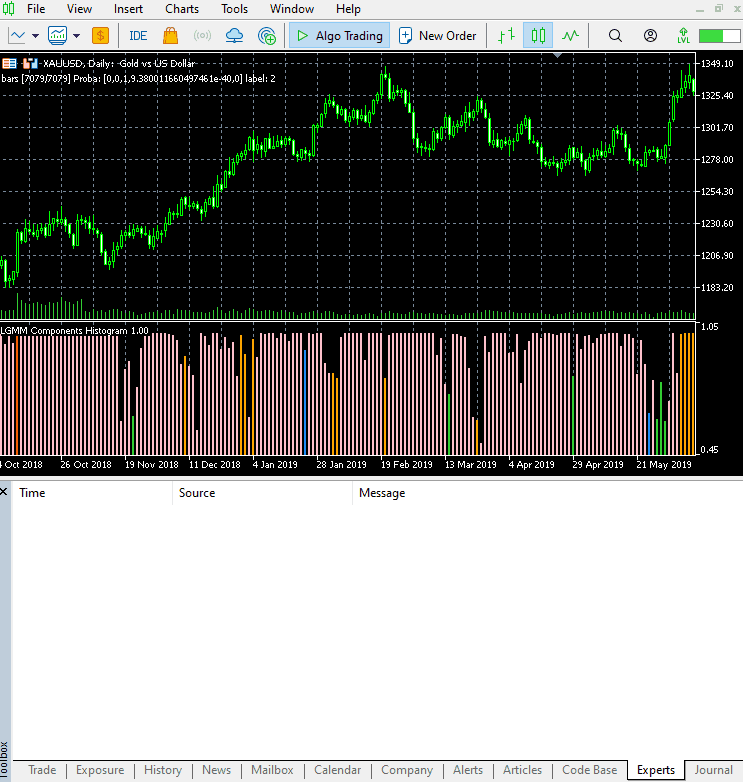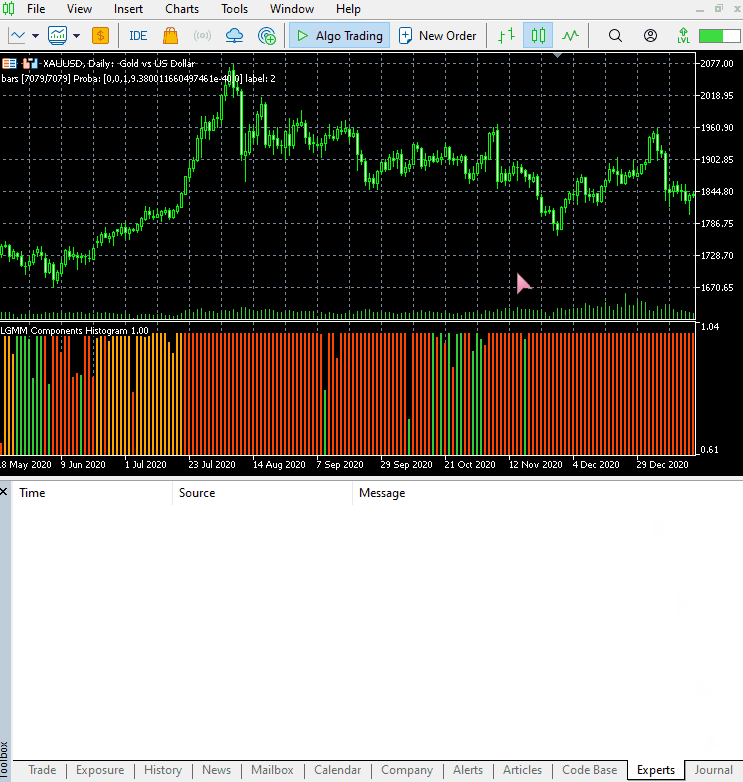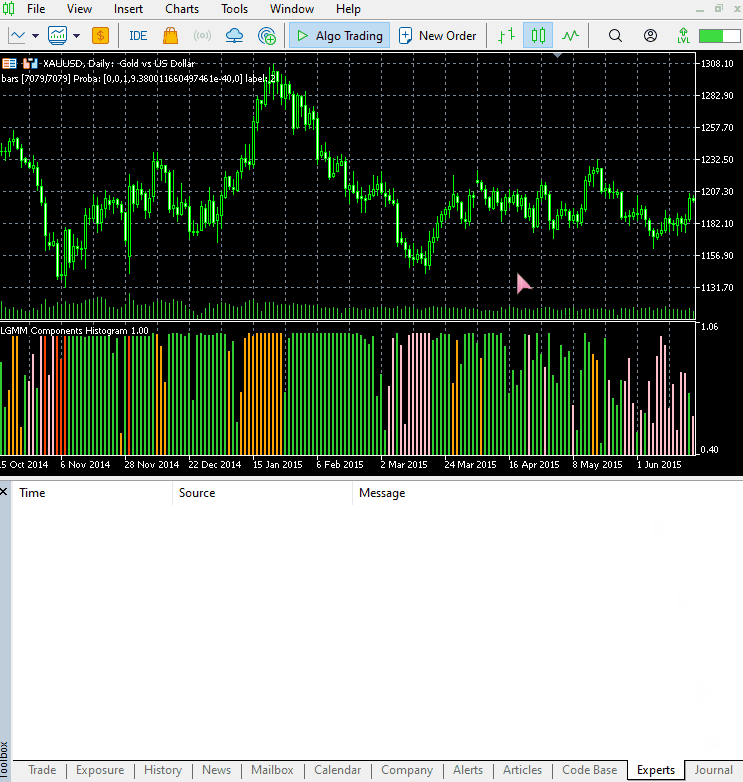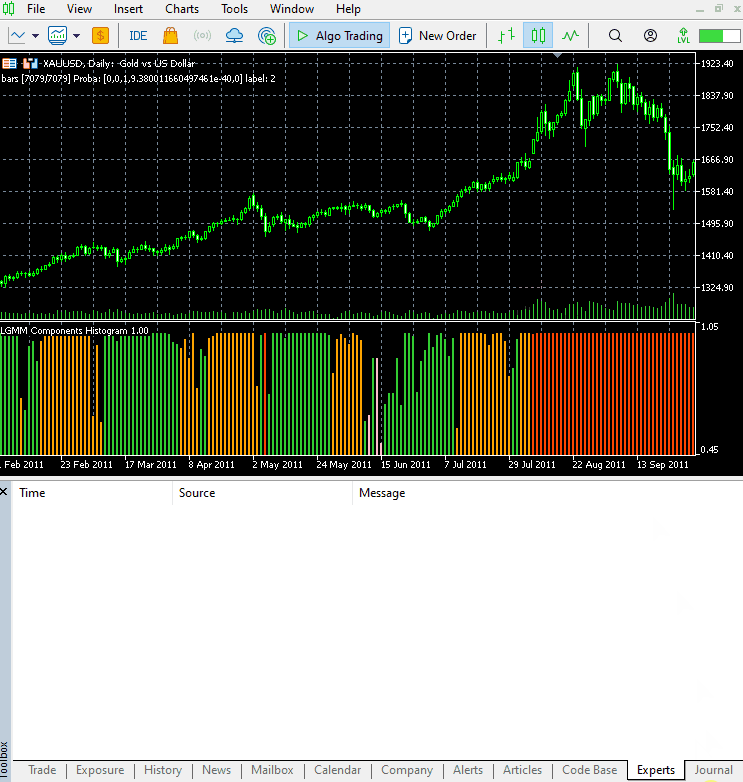
Finally, we run this indicator on the XAUUSD chart and the same timeframe that the model was trained on.
This indicator is still hard to interpret, but one pattern seems dominant, and that is the component presented in red color. It seems this pattern appears when the market is volatile (volatility is high) on either an uptrend or a downtrend. The remaining components are still not yet clear, this could be because we are not certain of the number of components we used for this model so, let us find the best number of components for this model.
Finding the Best Number of Components for LGMM
Since the Mixture Model offered by Scikit-Learn produces information criterion values, Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). Let's plot these values against their component range in one plot and spot the elbow point(s).
The elbow point in a graph is a point where adding more components to the model results in only marginal improvement in performance, i.e,. the curve flattens.
Filename: main.ipynb
lowest_bic = np.inf bic = [] aic = [] n_components_range = range(1, 10) for n_components in n_components_range: gmm = GaussianMixture(n_components=n_components, random_state=42) gmm.fit(X) bic.append(gmm.bic(X_train)) aic.append(gmm.aic(X_train)) if bic[-1] < lowest_bic: best_gmm = gmm lowest_bic = bic[-1] # Plot the BIC and AIC scores plt.figure(figsize=(8, 5)) plt.plot(n_components_range, bic, label='BIC', marker='o') plt.plot(n_components_range, aic, label='AIC', marker='o') plt.xlabel('Number of components') plt.ylabel('Score') plt.title('LGMM selection: AIC vs BIC') plt.legend() plt.grid(True) plt.show()
Outputs.
Both AIC and BIC curves drop sharply from 1 to 2 components and continue decreasing, but the rate of improvement slows down noticeably after 5 components for both. This means the best number of components that we should use for this model is 5.
Let's go back, retrain the model, and update the indicator.
Filename: main.ipynb
components = 5 # according to the elbow point gmm = GaussianMixture(n_components=components, covariance_type="full", random_state=42) gmm.fit(X_train) latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
Now that we have 5 components inside of 3, meaning the model produces 5 probabilities that we can plot, we have to increase the number of colors in the indicator to 5 for the colored histogram and handle 5 different cases for the predicted labels.
Filename: LGMM Indicator.mq5
#property indicator_color1 clrDodgerBlue, clrLimeGreen, clrCrimson, clrOrange, clrYellow
Inside OnCalculate function.
int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { //--- Main calculation loop int lookback = 20; for (int i = prev_calculated; i < rates_total && !IsStopped(); i++) { if (i+1<lookback) //prevent data not found errors during copy buffer continue; //... //... //... // Determine color based on predicted label if (label == 0) ColorBuffer[i] = 0; else if (label == 1) ColorBuffer[i] = 1; else if (label == 2) ColorBuffer[i] = 2; else if (label == 3) ColorBuffer[i] = 3; else ColorBuffer[i] = 4; Comment("bars [",i+1,"/",rates_total,"]"," Proba: ",proba," label: ",label); }
The new indicator appearance.
It looks great, but still difficult to read as we are often used to dealing with simple oscillators that often show oversold and overbought regions. Don't hesitate to explore this indicator and let us know your thoughts in the discussion section.
Now, let's use the LGMM alongside a machine learning model.
Latent Gaussian Mixture Model alongside a Classifier Model
We've now seen how we can use LGMM to produce latent features that represent the probability of a label belonging to a certain cluster, since it is difficult to understand these features. Let' use them in a Random forest classifier model alongside the indicator features hoping that this machine learning model can figure out how latent features affect the trading signals.
Filename: main.ipynb
We already created the target variable before when splitting the training and testing data, here it is again for reference.
from sklearn.model_selection import train_test_split X = new_df.drop(columns=[ "Time", "Open", "High", "Low", "Close", "future_close", "Direction" ]) y = new_df["Direction"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=42)
After training the LGMM, we used it to make predictions on the training and testing data.
latent_features_train = gmm.predict_proba(X_train) latent_features_test = gmm.predict_proba(X_test)
Since this data is difficult to read, let's add some feature names to it, making the features identifiable.
latent_features_train_df = pd.DataFrame(latent_features_train, columns=[f"LATENT_FEATURE_{i}" for i in range(latent_features_train.shape[1])]) latent_features_test_df = pd.DataFrame(latent_features_test, columns=[f"LATENT_FEATURE_{i}" for i in range(latent_features_test.shape[1])])
latent_features_train_df
Outputs.
| LATENT_FEATURE_0 | LATENT_FEATURE_1 | LATENT_FEATURE_2 | LATENT_FEATURE_3 | LATENT_FEATURE_4 | |
|---|---|---|---|---|---|
| 0 | 0.000000e+00 | 5.368039e-08 | 9.999999e-01 | 1.566000e-57 | 8.541983e-37 |
| 1 | 3.316692e-124 | 8.262106e-01 | 2.931424e-06 | 1.725415e-01 | 1.244990e-03 |
| 2 | 6.572730e-49 | 7.441120e-08 | 3.481699e-08 | 9.461818e-01 | 5.381811e-02 |
| 3 | 0.000000e+00 | 1.165057e-126 | 1.413762e-05 | 4.101964e-16 | 9.999859e-01 |
| 4 | 0.000000e+00 | 4.446778e-289 | 1.000000e+00 | 1.717945e-36 | 4.234123e-21 |
Let us stack these features alongside primary indicators data.
all_columns = X_train.columns.tolist() + latent_features_train_df.columns.tolist() X_latent_train_arr = np.hstack([X_train, latent_features_train_df]) X_latent_test_arr = np.hstack([X_test, latent_features_test_df]) X_Train_latent = pd.DataFrame(X_latent_train_arr, columns=all_columns) X_Test_latent = pd.DataFrame(X_latent_test_arr, columns=all_columns) X_Train_latent.columns
Outputs.
Index(['ATR', 'BearsPower', 'BullsPower', 'Chainkin', 'CCI', 'Demarker', 'Force', 'MACD MAIN_LINE', 'MACD SIGNAL_LINE', 'Momentum', 'OsMA', 'RSI', 'RVI MAIN_LINE', 'RVI SIGNAL_LINE', 'StochasticOscillator MAIN_LINE', 'StochasticOscillator SIGNAL_LINE', 'TEMA', 'WPR', 'LATENT_FEATURE_0', 'LATENT_FEATURE_1', 'LATENT_FEATURE_2', 'LATENT_FEATURE_3', 'LATENT_FEATURE_4'], dtype='object')
Let's pass this combined data to a random forest classifier.
from sklearn.ensemble import RandomForestClassifier from sklearn.utils.class_weight import compute_class_weight classes = np.unique(y_train) weights = compute_class_weight(class_weight='balanced', classes=classes, y=y_train) class_weights_dict = dict(zip(classes, weights)) params = { "n_estimators": 100, "min_samples_split": 2, "max_depth": 10, "max_leaf_nodes": 10, "criterion": "gini", "random_state": 42 } model = RandomForestClassifier(**params, class_weight=class_weights_dict) model.fit(X_Train_latent, y_train)
Model's evaluation.
y_train_pred = model.predict(X_Train_latent) print("Train classification report\n", classification_report(y_train, y_train_pred)) y_test_pred = model.predict(X_Test_latent) print("Test classification report\n", classification_report(y_test, y_test_pred))
Outputs.
Train classification report precision recall f1-score support -1 0.60 0.67 0.63 1766 1 0.68 0.61 0.64 1994 accuracy 0.64 3760 macro avg 0.64 0.64 0.64 3760 weighted avg 0.64 0.64 0.64 3760 Test classification report precision recall f1-score support -1 0.45 0.47 0.45 445 1 0.50 0.48 0.49 495 accuracy 0.47 940 macro avg 0.47 0.47 0.47 940 weighted avg 0.47 0.47 0.47 940
The resulting model has a bad performance on the validation sample, there is a lot we can do to improve it, but for now, let's observe the feature importance plot produced by the model.
importances = model.feature_importances_ feature_names = X_Train_latent.columns if hasattr(X_Train_latent, 'columns') else [f'feature_{i}' for i in range(X_Train_latent.shape[1])] # Create DataFrame and sort importance_df = pd.DataFrame({'feature': all_columns, 'importance': importances}) importance_df = importance_df.sort_values('importance', ascending=False) # Plot plt.figure(figsize=(8, 6)) plt.barh(importance_df['feature'], importance_df['importance'], color='red') plt.title('RFC Feature Importance (Gini Importance)') plt.xlabel('Importance Score') plt.gca().invert_yaxis() # Most important on top plt.show()
Outputs.
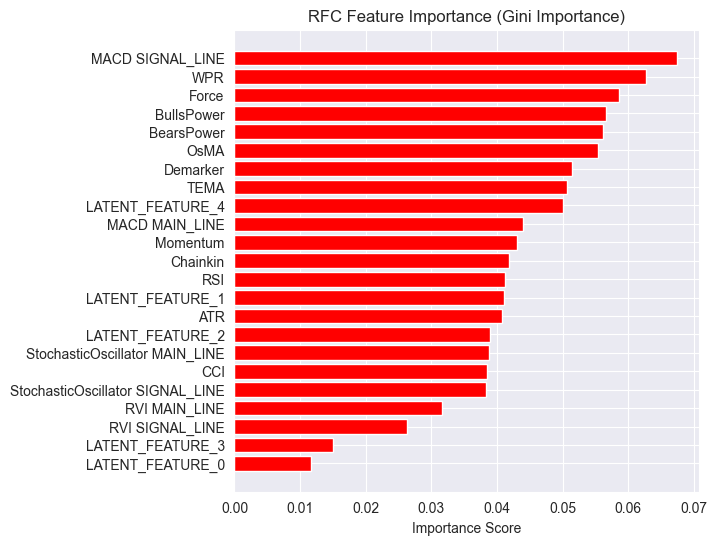
Latent features are proving to be important to the model, meaning they carry some patterns and information that contribute to the model's predictions.
The reason for this underperforming model might be due to the nature of the target variable deployed. The lookahead value of 1 might be wrong.
When using these indicators for making informed trading decisions, we don't usually use them to predict the next bar. For example, If the RSI value is below the threshold value of 30 (oversold) we can say that the market might undergo bulish for a couple of bars ahead. Not on the next bar only like the way we are currently training our model.
So let's re-create the target variable using the lookahead value of 5.
lookahead = 5 df["future_close"] = df["Close"].shift(-lookahead) new_df = df.dropna() new_df["Direction"] = np.where(new_df["future_close"]>new_df["Close"], 1, -1) # if a the close value in the next bar(s)=lookahead is above the current close price, thats a long signal otherwise that's a short signal
Now, evaluating the model on both training and validation data produces a different outcome.
Train classification report precision recall f1-score support -1 0.56 0.70 0.62 1706 1 0.69 0.54 0.61 2050 accuracy 0.61 3756 macro avg 0.62 0.62 0.61 3756 weighted avg 0.63 0.61 0.61 3756 Test classification report precision recall f1-score support -1 0.46 0.61 0.52 392 1 0.63 0.48 0.55 548 accuracy 0.54 940 macro avg 0.55 0.55 0.53 940 weighted avg 0.56 0.54 0.54 940
And a different feature importance plot.
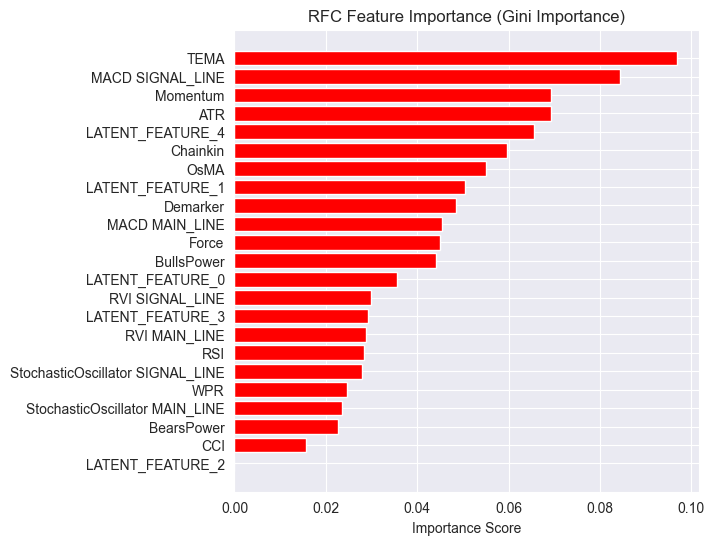
The model had an overall 54% accuracy, not a good one, but decent enough to make us believe what we are seeing on the feature importance plot.
Some of the latent features produced by the LGMM made it to the top of the most predictive features of the model.
The LATENT_FEATURE_4 being the 5th important feature to the Random forest classifier, the remaining latent features such as LATENT_FEATURE_0, and LATENT_FEATURE_1 did fairly well and surpased some raw indicators.
Overall, most features produced by LGMM have patterns beneficial to the classifier model.
Given this information, you now have a starting point for understanding the indicator.
The arrangement of the colors resembles the latent features.
LGMM-Based Trading Robot
Inside the Expert Advisor (EA), we start by importing necessary libraries.
Filename: LGMM BASED EA.mq5
#include <Random Forest.mqh> #include <Arrays\ArrayString.mqh> #include <pandas.mqh> //https://www.mql5.com/en/articles/17030 #include <Trade\Trade.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\SymbolInfo.mqh> #include <errordescription.mqh> CSymbolInfo m_symbol; CTrade m_trade; CPositionInfo m_position; CRandomForestClassifier rfc;
Again, we have to ensure that we are using the same symbol and timeframe as the one used in the training data.
#define MAGICNUMBER 11062025 input string SYMBOL = "XAUUSD"; input ENUM_TIMEFRAMES TIMEFRAME = PERIOD_D1; input uint LOOKAHEAD = 5; input uint SLIPPAGE = 100;
We initialize both models, the LGMM and the Random forest classifier model, inside the OnInit function.
int OnInit() { if (!MQLInfoInteger(MQL_DEBUG) && !MQLInfoInteger(MQL_TESTER)) { ChartSetSymbolPeriod(0, SYMBOL, TIMEFRAME); if (!SymbolSelect(SYMBOL, true)) { printf("%s failed to select SYMBOL %s, Error = %s",__FUNCTION__,SYMBOL,ErrorDescription(GetLastError())); return INIT_FAILED; } } //--- Loading the Gaussian Mixture model string filename = StringFormat("LGMM.%s.%s.onnx",SYMBOL, EnumToString(TIMEFRAME)); if (!lgmm.Init(filename, ONNX_COMMON_FOLDER)) { printf("%s Failed to initialize the GaussianMixture model (LGMM) in ONNX format file={%s}, Error = %s",__FUNCTION__,filename,ErrorDescription(GetLastError())); } //--- Loading the RFC model filename = StringFormat("rfc.%s.%s.onnx",SYMBOL,EnumToString(TIMEFRAME)); Print(filename); if (!rfc.Init(filename, ONNX_COMMON_FOLDER)) { printf("func=%s line=%d, Failed to Load the RFC in ONNX file={%s}, Error = %s",__FUNCTION__,__LINE__,filename,ErrorDescription(GetLastError())); return INIT_FAILED; } //... //... other lines of code //... }
Inside the getX function, we call LGMM to prepare latent features that can be used alongside the indicators data for final inputs of the Random forest classifier model.
vector getX(uint start=0, uint count=10) { //--- Get buffers CDataFrame df; for (uint ind=0; ind<indicators.Size(); ind++) //Loop through all the indicators { uint buffers_total = indicators[ind].buffer_names.Total(); for (uint buffer_no=0; buffer_no<buffers_total; buffer_no++) //Their buffer names resemble their buffer numbers { string name = indicators[ind].buffer_names.At(buffer_no); //Get the name of the buffer, it is helpful for the DataFrame and CSV file vector buffer = {}; if (!buffer.CopyIndicatorBuffer(indicators[ind].handle, buffer_no, start, count)) //Copy indicator buffer { printf("func=%s line=%d | Failed to copy %s indicator buffer, Error = %d",__FUNCTION__,__LINE__,name,GetLastError()); continue; } df.insert(name, buffer); //Insert a buffer vector and its name to a dataframe object } } if ((uint)df.shape()[0]==0) return vector::Zeros(0); //--- predict the latent features vector indicators_data = df.iloc(-1); //index=-1 returns the last row from the dataframe which is the most recent buffer from all indicators //--- Given the indicators let's predict the latent features vector latent_features = lgmm.predict(indicators_data).proba; if (latent_features.Size()==0) return vector::Zeros(0); return hstack(indicators_data, latent_features); //Return indicators data stacked alongside latent features }
Finally, we make a simple trading strategy that relies on trading signals produced by the random forest classifier model.
void OnTick() { //--- Close trades after AI predictive horizon is over CloseTradeAfterTime(MAGICNUMBER, PeriodSeconds(TIMEFRAME)*LOOKAHEAD); //--- Refresh tick information if (!m_symbol.RefreshRates()) { printf("func=%s line=%s. Failed to copy rates, Error = %s",__FUNCTION__,ErrorDescription(GetLastError())); return; } //--- vector x = getX(); //Get all the input for the model if (x.Size()==0) return; long signal = rfc.predict(x).cls; //the class predicted by the random forest classifier double proba = rfc.predict(x).proba; //probability of the predictions double volume = m_symbol.LotsMin(); if (!PosExists(POSITION_TYPE_SELL, MAGICNUMBER) && !PosExists(POSITION_TYPE_BUY, MAGICNUMBER)) //no position is open { if (signal == 1) //If a model predicts a bullish signal m_trade.Buy(volume, SYMBOL, m_symbol.Ask()); //Open a buy trade else if (signal == -1) // if a model predicts a bearish signal m_trade.Sell(volume, SYMBOL, m_symbol.Bid()); //open a sell trade } }
We close trades after a LOOKAHEAD number of bars have passed on the timeframe the model was trained on. LOOKAHEAD value needs to match the one used in making the target variable inside the training script.
Tester configurations.
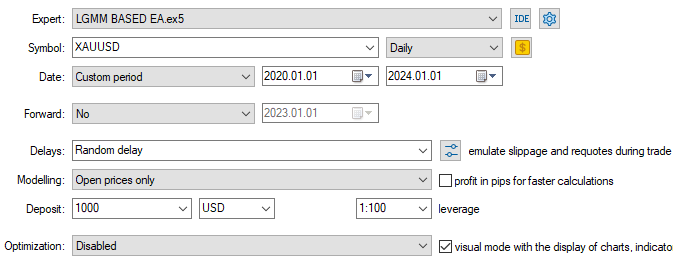
Inputs.
Tester Outcomes
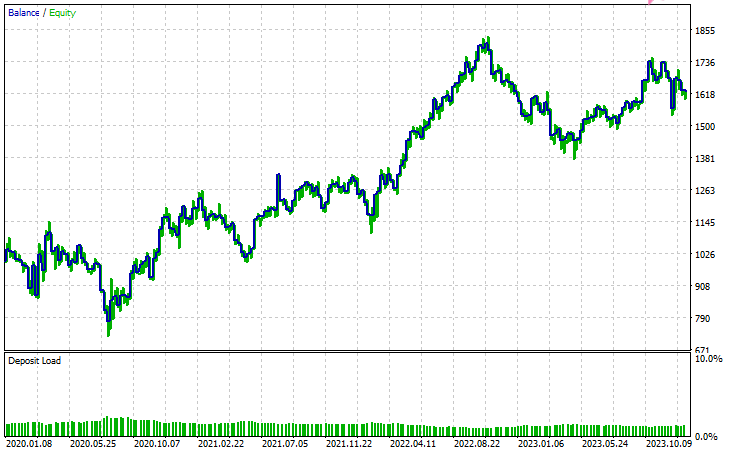
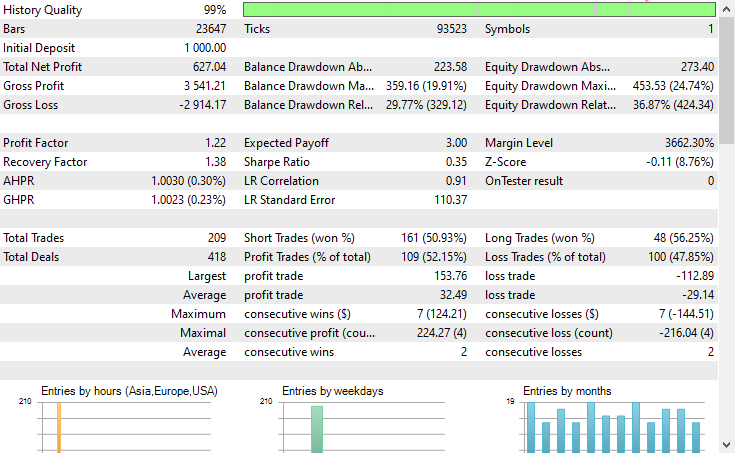
Conclusion
Latent Gaussian Mixture Model (LGMM) is a decent technique that gives us meaningful features that comprise non-observable patterns that are often useful to machine learning models. However, just like any other machine learning models and predictive techniques, it has some drawback.
Latent Gaussian Mixture Model (LGMM): Overview
| Aspect | Description |
|---|---|
| What is LGMM | A method for extracting latent (hidden) features that represent non-observable patterns in data. These features can be useful for machine learning models. |
| Main Advantage | Captures meaningful hidden structures in data that can improve model performance. |
Limitations of LGMM
| Limitation | Explanation |
|---|---|
| Assumes Gaussian distribution | LGMM assumes each data point follows a multivariate normal distribution, which is rarely the case in financial data that tends to be chaotic and non-linear. |
| Sensitive to initialization | The model requires careful selection of the number of components. Poor initialization or wrong parameter choices can significantly reduce its effectiveness. |
| Hard to interpret results | The latent features it generates are difficult to understand or explain. As an unsupervised method, it doesn't label the patterns it detects, only clusters them. |
| Sensitive to outliers | Gaussian distributions are not robust to outliers. A few extreme values can skew the mean and inflate the variance, distorting the model's results. |
This model is the most useful when it comes to dimension reduction (reducing the number of features into a few meaningful ones) and for introducing new features to enrich the model with more useful information. I believe it is best to use it this way.
Best regards.
Stay tuned and contribute to machine learning algorithms development for the MQL5 language in this GitHub repository.
Attachments Table
| Filename | Description & Usage |
|---|---|
| Include\errordescription.mqh | Contains the description of all error codes produced by MetaTrader 5 in MQL5 language. |
| Include\Gaussian Mixture.mqh | A library which contains the class for initializing and deploying the Gaussian Mixture model stored in ONNX format. |
| Include\pandas.mqh | Contains a class for data storage and manipulation similar to Pandas offered in the Python programming language. |
| Include\Random Forest.mqh | A library which contains the class for initializing and deploying the random forest classifier stored in ONNX format. |
| Indicators\LGMM Indicator.mq5 | An indicator for displaying latent features produced by the Latent Gaussian Mixture Model (LGMM). |
| Scripts\Get XAUUSD Data.mq5 | A script for collecting oscillator indicators alongside OHLCT values from MetaTrader 5 and storing them to a CSV file. |
| Experts\LGMM BASED EA.mq5 | An Expert Advisor (EA) that opens and closes trades based on the predictions offered by the random forest classifier using the data, which is the combination of latent features produced by LGMM and oscillator indicators. |
| Python Code\main.ipynb | A Jupyter notebook (Python script) for data analysis, machine learning model training, etc. |
| Python Code\Trade\TerminalInfo.py | It has a class similar to CTerminalInfo provided in MQL5 for getting information about the selected MetaTrader 5 desktop app. |
| Python\requirements.txt | Has all the Python dependencies and their version numbers used in this project. |
| Common\Files\* | Has a sample CSV which contains training data and a couple of ONNX model files used in this article, only for reference. |
Training a multilayer perceptron using the Levenberg-Marquardt algorithm
Analyzing weather impact on currencies of agricultural countries using Python
Features of Experts Advisors
Neural Networks in Trading: Directional Diffusion Models (DDM)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use