Population optimization algorithms: Artificial Multi-Social Search Objects (MSO)
1 419
7
Contents
1. Introduction
2. Algorithm
3. Test results
1. Introduction
In the previous article, we considered the evolution of social groups where they moved freely in the search space. However, here I propose that we change this concept and assume that groups move between sectors, jumping from one to another. All groups have their own centers, which are updated at each iteration of the algorithm. In addition, we introduce the concept of memory both for the group as a whole and for each individual particle in it. Using these changes, our algorithm now allows groups to move from sector to sector based on information about the best solutions.
This new modification opens up new possibilities for studying the evolution of social groups. Moving to sectors allows groups to share information and experiences within each sector, which can lead to more effective search and adaptation. The introduction of memory allows groups to retain information about previous movements and use it to make decisions about future movements.
In this article, we will conduct a series of experiments to explore how these new concepts affect the search performance of an algorithm. We will analyze the interaction between groups, their ability to cooperate and coordinate, and their ability to learn and adapt. Our findings may shed light on the evolution of social systems and help better understand how groups form, evolve and adapt to changing environments.
Finally, we discuss the possibilities for further improvement of the modified algorithm and its application in various fields. The modifications introduced in this work allow us to more efficiently explore the solution space and find optimal values. This may be useful for researchers and practitioners working in the field of optimization and solution search.
2. Algorithm
The ultimate goal of the algorithm that integrates the principles of social groups is to create an effective system of coordination and cooperation between group members. Here are the general principles that can be integrated inside such an algorithm:
- Moving algorithm allows the party to move between different sectors or areas. This will allow the group to explore a variety of resources and experiences, and exchange not just information about individual coordinates, but metadata in the form of sectors with other groups.
- Role separation and specialization allows group members to choose and specialize in certain areas. This will enable the group to effectively use its resources and skills to achieve common goals. This can be especially useful when solving problems with multidimensional spaces, where there are simultaneously surfaces of functions with different properties (both smooth and discrete).
- Cooperation and interaction allow group members to collaborate and interact with each other. This may involve sharing information, discussing ideas, and interpolating and extrapolating into unknown areas.
- Conflict and conflict resolution - mechanisms for resolving conflicts within the group. This may include establishing rules and procedures, mediation and dialog to resolve disagreements and disputes. For example, to prevent particles from competing for the same areas and allow them to save precious iterations of the algorithm.
- Leadership and organization - the possibility of having leaders in the group who provide organization, coordination and decision making. Leaders should be able to motivate and lead the group to achieve goals.
- Exchange of knowledge and experience allow the group to actively exchange knowledge and experience between participants. This will help the group learn from others, adapt to new situations and make more informed decisions. The ability to build complex logical connections between coordinates, and not just use stochastic space exploration.
- Group memory accounting allows the group to retain information about previous movements, roles, specializations, cooperation and conflict resolution. This will allow the group to use its experience to make more informed decisions about future movements and interactions.
Integrating these general principles into the algorithm will create a more efficient social system, capable of cooperation, coordination, information exchange and adaptation to a changing environment.
Let's explain the meaning of the sector for a better understanding in the context of the algorithm. A sector is part of the domain of definition of the optimized parameter (coordinate axes of multidimensional space). The division of axes into sectors is the same for all groups. Two groups G0 and G1 can be located on sectors of the corresponding coordinates, for example, like this:
G0 (X) |---V---|-------|-------|-------|-------|
G0 (Y) |-------|---V---|-------|-------|-------|
G0 (Z) |-------|-------|-------|-------|---V---|
-----------------------------------------------------
G1 (X) |-------|-------|---V---|-------|-------|
G1 (Y) |---V---|-------|-------|-------|-------|
G1 (Z) |-------|-------|-------|---V---|-------|
One of the main ideas of the algorithm is to enable groups to exchange knowledge about successful sectors, while maintaining a certain amount of stochasticity in the freedom to choose sectors.
Now let's move on to describing the first concept of our algorithm. First, let's consider an algorithm with random movement of groups across sectors, without taking into account the memory of the best solutions.
The pseudocode of the algorithm is as follows:
1. Randomly select sectors for groups
2. Create points evenly across sectors
3. Calculate fitness function
4. Update global solution (best population particle)
5. Get the value of the best particle in the group at the current iteration
6. Update the memory of the best solutions on sectors for each group
7. Update the memory of the best solutions on sectors for each particle
8. Update the best solution by group
9. For a group, ask another group whether its solution is better for each coordinate:
9. a) if yes: then take its sector
9. b) if not: choose another sector with some probability
10. Create particles by probabilities:
10. a) if yes: evenly across the sector
10. b) if not: clarify the group’s decision
11. Repeat from p.4
The group internal architecture and the marking of coordinates by sector can be presented as follows:
Group [groups]|
|-----------------------------------------
|fB
|-----------------------------------------
|fBLast
|-----------------------------------------
|cB [coords]
|-----------------------------------------
|cLast [coords]
|-----------------------------------------
|centre [coords]
|-----------------------------------------
|secInd [coords]
|-----------------------------------------
|secIndLast [coords]
|-----------------------------------------
|p [groupSize]|
| |-------------------
| |c [coords]
| |f
m [coords]|
|--------------
|min [sectNumb]
|max [sectNumb]
Let's move on to the code description.
To mark the search space into sectors, we will need to specify the boundaries of the sectors. To achieve this, we will write the S_Min_Max structure. Let's break it down piece by piece:
The S_Min_Max structure has two data fields: "min" and "max", which represent the sector boundary on the left, and "max" - the sector boundary on the right. The size of both arrays is equal to the number of sectors, which is specified by the "sectNumb" parameter.
The structure also defines the Init function, which initializes the "min" and "max" arrays. It accepts one parameter "sectNumb", which specifies the number of sectors. Inside the Init function, the size of the "min" and "max" arrays is changed in accordance with the passed "sectNumb" parameter. Thus, this structure provides a way to store sector boundaries and initialize them using the Init function.
//—————————————————————————————————————————————————————————————————————————————— struct S_Min_Max { void Init (int sectNumb) { ArrayResize (min, sectNumb); ArrayResize (max, sectNumb); } double min []; //sector border on the left, size - number of sectors double max []; //sector border on the right, size - number of sectors }; //——————————————————————————————————————————————————————————————————————————————
To describe a particle, which is a member of the group, we will write the S_Particle structure, which contains two fields: "c" and "f".
- "c" - array for storing particle coordinates. The size of the array is determined by the "coords" parameter passed to the Init function.
- "f" is the value of the particle fitness function initialized with the "-DBL_MAX" value in the Init function.
Thus, this structure provides a container for storing the coordinates of a particle and the associated function value.
//—————————————————————————————————————————————————————————————————————————————— struct S_Particle { void Init (int coords, int sectNumb) { ArrayResize (c, coords); f = -DBL_MAX; } double c []; double f; }; //——————————————————————————————————————————————————————————————————————————————
Combine a group of particles into the S_Group data structure. The S_Group structure contains several data fields:
- "p" represents the array of S_Particle structures used to store group particles. The size of the "p" array is determined by the "groupSize" parameter passed to the Init function. Inside the "for" loop, each particle is initialized using the Init function from the S_Particle structure.
- "secInd" and "secIndLast" - the arrays store sector indices at each coordinate. The size of the "secInd" and "secIndLast" arrays is determined by the "coords" parameter.
- "cB" and "cBLast" - the arrays store the best coordinates in the group and the previous best coordinates, respectively. The size of the "cB" and "cBLast" arrays is also determined by the "coords" parameter.
- "fB" and "fBLast" - the variables store the best result and the previous best result in the group, respectively.
- "centre" - the array stores the center. The size of the "centre" array is also determined by the "coords" parameter and is used to determine the best sector coordinates for the entire group.
The Init function initializes all arrays and variables in the S_Group structure. It takes three parameters: "coords" - the number of coordinates, "groupSize" - the size of the group, "sectNumb" - the number of sectors.
Thus, this structure provides a container for storing information about a group of particles. Particles obey group rules and do not interact with particles of other groups. Interaction occurs through indirect transmission of information through sectors at the group level.
//—————————————————————————————————————————————————————————————————————————————— struct S_Group { void Init (int coords, int groupSize, int sectNumb) { ArrayResize (p, groupSize); ArrayResize (secInd, coords); ArrayResize (cB, coords); ArrayResize (cBLast, coords); ArrayResize (secIndLast, coords); ArrayResize (centre, coords); for (int i = 0; i < groupSize; i++) p [i].Init (coords, sectNumb); fB = -DBL_MAX; fBLast = -DBL_MAX; } S_Particle p []; int secInd []; //sector index on the coordinate, size is the number of coordinates int secIndLast []; //previous index of the sector on the coordinate, the size is the number of coordinates double cB []; //the best coord's in the group double cBLast []; //the previous best coord's in the group double fB; //the best result in the group double fBLast; //the previous best result in the group double centre []; }; //——————————————————————————————————————————————————————————————————————————————
Let's describe the optimization agent with the S_Agent structure, through which information will be transferred from group particles to the fitness function calculation. The S_Agent structure contains two fields:
- "c" - the array stores the agent coordinates.
- "f" - stores the agent fitness function.
The Init function initializes the "c" array and the "f" variable in the S_Agent structure. It takes one parameter "coords", which specifies the size of the "c" array.
//—————————————————————————————————————————————————————————————————————————————— struct S_Agent { void Init (const int coords) { ArrayResize (c, coords); f = -DBL_MAX; } double c []; //coordinates double f; //fitness }; //——————————————————————————————————————————————————————————————————————————————
Let's describe the multi social algorithm using the C_AO_MSO class. The class contains several data fields and methods:
- "cB" - the array stores the best coordinates.
- "fB" - the variable stores the fitness of the best coordinates.
- "a" - the array of S_Agent structures that stores agents.
- "rangeMax", "rangeMin" and "rangeStep" - the arrays store the maximum and minimum search ranges and step, respectively.
The class also contains several methods:
- Init initializes all data members of the class. It accepts the following parameters: coordinatesNumberP - number of coordinates, populationSizeP - population size, groupsP - number of coordinates, sectorsNumberP - number of sectors per coordinate, probRNSectorP - random sector probability, probUniformSectorP - uniform distribution probability for a particle, probClgroupP - probability of refining the group result and powerP - power for the power law distribution function.
- Moving and Revision - the methods for performing basic operations with groups and group particles.
In general, the C_AO_MSO class is an implementation of an optimization algorithm using multiple search with an optimal distribution of agents. It contains data and methods for managing agents, groups, sectors and performing search operations and refining the result.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_MSO { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Agent a []; //agents public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int groupsP, //number of groups const int sectorsNumberP, //sectors number const double probRNSsectorP, //probability random sector const double probUniformSectorP, //probability uniform distribution const double probClgroupP, //probability of clarifying the group's result const double powerP); //power public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coords; //coordinates number private: int popSize; //population size private: int sectNumb; //sectors number private: double sectorSpace []; //sector space private: S_Group gr []; //groups private: S_Min_Max min_max_Sector []; //sector boundary by coordinates private: int groups; //number of groups private: int sectorsNumber; //sectors number private: double probRNSsector; //probability random sector private: double probUniformSector; //probability uniform distribution private: double probClgroup; //probability of clarifying the group's result private: double power; //power private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power); }; //——————————————————————————————————————————————————————————————————————————————
The Init method initializes an object of the C_AO_MSO class with the given parameters. Let's break this code down piece by piece:
At the beginning of the function, the variables and data members of the class are initialized. The random number generator is reset using the current time in microseconds. Then the "fB" variable is set to the minimum possible double value "-DBL_MAX" and the "revision" variable is set to "false".
The parameters passed to the function are then assigned to the corresponding fields of the class.
To distribute population particles into groups, the "partInSwarms" array is created. It will store the number of particles in each group. The array size is set equal to the number of groups. The "particles" variable then calculates the number of particles in each group by dividing the "popSize" total population size by the number of "groups".
If there is a "lost" excess, then it is distributed by groups. The loop runs until the excess is 0.
Next, the array sizes are changed and objects are initialized.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MSO::Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int groupsP, //number of groups const int sectorsNumberP, //sectors number const double probRNSsectorP, //probability random sector const double probUniformSectorP, //probability uniform distribution const double probClgroupP, //probability of clarifying the group's result const double powerP) //power { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coords = coordinatesNumberP; popSize = populationSizeP; groups = groupsP; sectNumb = sectorsNumberP; probRNSsector = probRNSsectorP; probUniformSector = probUniformSectorP; probUniformSector = probClgroupP; power = powerP; //---------------------------------------------------------------------------- int partInSwarms []; ArrayResize (partInSwarms, groups); int particles = popSize / groups; ArrayInitialize (partInSwarms, particles); int lost = popSize - particles * groups; if (lost > 0) { int pos = 0; while (true) { partInSwarms [pos]++; lost--; pos++; if (pos >= groups) pos = 0; if (lost == 0) break; } } //---------------------------------------------------------------------------- ArrayResize (rangeMax, coords); ArrayResize (rangeMin, coords); ArrayResize (rangeStep, coords); ArrayResize (cB, coords); ArrayResize (gr, groups); for (int s = 0; s < groups; s++) gr [s].Init (coords, partInSwarms [s], sectNumb); ArrayResize (sectorSpace, coords); ArrayResize (a, popSize); for (int i = 0; i < popSize; i++) a [i].Init (coords); } //——————————————————————————————————————————————————————————————————————————————
The Moving method is responsible for moving particles at the first iteration and performs the function of initializing groups and their particles with their initial position.
At the beginning of the function, the value of the "revision" variable is checked to ensure it is executed only once, and if it is "false".
The first part of the code is responsible for dividing the space into sectors and initializing the "min_max_Sector" array. For each "c" coordinate, the "sectorSpace[c]" sector size is calculated as the difference between "rangeMax[c]" and "rangeMin[c]", divided by the number of sectors "sectNumb". The "min" and "max" values are then initialized in the "min_max_Sector" array for each coordinate and sector.
Next, the particles are arranged in the search space. For each "s" group, random sectors are selected for each coordinate. Sector index values are stored in the "secInd" array for each group. Then the particles of the group are randomly distributed within the selected sectors. For each "p" particle and "c" coordinate, a random value "cd" is selected within the minimum and maximum value of the sector, and this value is stored in the particle coordinates.
The last block of code is responsible for sending particles to agents. The "cnt" counter is created, which will be used to enumerate agents. Then, for each "s" group and each "p" particle, the particle coordinate values are copied into the "a[cnt].c" array, where "cnt" is incremented after each copy.
So, the method is responsible for the random initial placement of particles in the optimization algorithm, divides the space into sectors, randomly selects sectors for each group and distributes particles within the selected sectors. The particles are then sent to agents for further processing.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MSO::Moving () { if (!revision) { //marking up sectors-------------------------------------------------------- ArrayResize (min_max_Sector, coords); for (int c = 0; c < coords; c++) { sectorSpace [c] = (rangeMax [c] - rangeMin [c]) / sectNumb; min_max_Sector [c].Init (sectNumb); for (int sec = 0; sec < sectNumb; sec++) { min_max_Sector [c].min [sec] = rangeMin [c] + sectorSpace [c] * sec; min_max_Sector [c].max [sec] = min_max_Sector [c].min [sec] + sectorSpace [c]; } } //-------------------------------------------------------------------------- int sect = 0; //sector double sectMin = 0.0; //sector's min double sectMax = 0.0; //sector's max int ind = 0; //index double cd = 0.0; //coordinate for (int s = 0; s < groups; s++) { //select random sectors for the group------------------------------------- for (int c = 0; c < coords; c++) { ind = (int)(RNDfromCI (0, sectNumb)); if (ind >= sectNumb) ind = sectNumb - 1; gr [s].secInd [c] = ind; gr [s].secIndLast [c] = ind; } //random distribute the particles of the group within the sectors--------- for (int p = 0; p < ArraySize (gr [s].p); p++) { for (int c = 0; c < coords; c++) { sect = gr [s].secInd [c]; cd = RNDfromCI (min_max_Sector [c].min [sect], min_max_Sector [c].max [sect]); gr [s].p [p].c [c] = SeInDiSp (cd, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //-------------------------------------------------------------------------- //send particles to agents int cnt = 0; for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { ArrayCopy (a [cnt].c, gr [s].p [p].c, 0, 0, WHOLE_ARRAY); cnt++; } } revision = true; } } //——————————————————————————————————————————————————————————————————————————————
The main operations for moving groups and their particles through the search space are performed by the Revision method:
- Updating the global best solution by comparing the fitness function values for each particle with the current best value. If the target function value for the current particle is greater than the current best value, it becomes the new best value and its coordinates are copied to the "cB" variable.
- Moving results from agents to particles and determining the best particle in each group. The value of the fitness function of each particle is set equal to the value of the goal function of the agent corresponding to this particle. If a particle fitness function value is greater than the current best value in the group, it becomes the new best value and its coordinates are copied to the group "cB" variable.
- Updating the best solution for each group. If the new best value in the group is greater than the previous one, it becomes the current best value and its coordinates are copied into the group's "cBLast" and "secIndLast" variables.
- For each coordinate of each group, it is checked whether there is another group with a better solution. If such a group exists, the sector and center of the current group are updated with the values of the sector and center of the group with the best solution. Otherwise, the sector and center remain unchanged.
- Creating new particles based on probabilities. For each group and each particle in the group, new coordinate values are generated based on probabilities. The probability of choosing a uniform distribution or a distribution using the PowerDistribution function is determined by the "probUniformSector" and "power" parameters.
- Moving created particles to agents for further use in the next iteration of the optimization algorithm.
The method updates the solutions at each iteration, using information about the best solutions in the groups and probabilities to create new particles.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MSO::Revision () { //---------------------------------------------------------------------------- //Update the best global solution for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- //Transfer the results from the agents to the particles //and get the value of the best particle in the group at the current iteration int cnt = 0; for (int s = 0; s < groups; s++) { gr [s].fB = -DBL_MAX; for (int p = 0; p < ArraySize (gr [s].p); p++) { gr [s].p [p].f = a [cnt].f; if (a [cnt].f > gr [s].fB) { gr [s].fB = a [cnt].f; ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY); } cnt++; } } int sector = 0; //---------------------------------------------------------------------------- //Update the best solution for the group for (int s = 0; s < groups; s++) { if (gr [s].fB > gr [s].fBLast) { gr [s].fBLast = gr [s].fB; ArrayCopy (gr [s].cBLast, gr [s].cB, 0, 0, WHOLE_ARRAY); ArrayCopy (gr [s].secIndLast, gr [s].secInd, 0, 0, WHOLE_ARRAY); } ArrayCopy (gr [s].centre, gr [s].cBLast); } //---------------------------------------------------------------------------- int sect = 0; //sector double sectMin = 0.0; //sector's min double sectMax = 0.0; //sector's max int ind = 0; //index double cd = 0.0; //coordinate for (int s = 0; s < groups; s++) { for (int c = 0; c < coords; c++) { if (RNDfromCI (0.0, 1.0) < 0.6) { ind = (int)(RNDfromCI (0, groups)); if (ind >= groups) ind = groups - 1; if (ind == s) ind++; if (ind > groups - 1) ind = 0; if (gr [ind].fBLast > gr [s].fBLast) { gr [s].secInd [c] = gr [ind].secIndLast [c]; gr [s].centre [c] = gr [ind].cBLast [c]; } } else { if (RNDfromCI (0.0, 1.0) < probRNSsector) { ind = (int)(RNDfromCI (0, sectNumb)); if (ind >= sectNumb) ind = sectNumb - 1; gr [s].secInd [c] = ind; sect = gr [s].secInd [c]; cd = RNDfromCI (min_max_Sector [c].min [sect], min_max_Sector [c].max [sect]); gr [s].centre [c] = SeInDiSp (cd, rangeMin [c], rangeMax [c], rangeStep [c]); } else gr [s].secInd [c] = gr [s].secIndLast [c]; } } } //---------------------------------------------------------------------------- for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { for (int c = 0; c < coords; c++) { sect = gr [s].secInd [c]; if (RNDfromCI (0.0, 1.0) < probUniformSector) { cd = RNDfromCI (min_max_Sector [c].min [sect], min_max_Sector [c].max [sect]); } else { cd = PowerDistribution (gr [s].centre [c], min_max_Sector [c].min [sect], min_max_Sector [c].max [sect], power); } gr [s].p [p].c [c] = SeInDiSp (cd, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- cnt = 0; for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { ArrayCopy (a [cnt].c, gr [s].p [p].c, 0, 0, WHOLE_ARRAY); cnt++; } } } //——————————————————————————————————————————————————————————————————————————————
Next, we will consider the same algorithm, but with the addition of memory for the group and its particles and some other changes in the logic of the search strategy.
We will change the pseudocode of the algorithm, taking into account the availability of memory for groups and particles:
- 1. Randomly select sectors for groups
- 2. Create points evenly across sectors
- 4. Calculate FF
- 5. Update global solution (best population particle)
- 6. Get the value of the best particle in the group at the current iteration
- 7. Update the memory of the best solutions on sectors for each group
- 8. Update the memory of the best solutions on sectors for each particle
- 9. Update the best solution by group
- 10. For a group, ask another group whether its solution is better for each coordinate:
- 10. a) if yes: then take its sector
- 10. b) if not: choose another sector with some probability
- 11. Create particles by probabilities:
- 11. a) if yes: evenly across the sector
- 11. b) if not: (probability ? (clarify the group’s decision) : (clarify your decision))
- 12. Repeat from p.4
Adding memory would theoretically allow the group to retain information about previous movements and use it to make decisions about future ones. This can help groups better adapt to a changing environment and explore the solution space more effectively.
Let's make changes to the internal architecture of the group as follows:
|-----------------------------------------
|fB
|-----------------------------------------
|fBLast
|-----------------------------------------
|cB [coords]
|-----------------------------------------
|cBLast [coords]
|-----------------------------------------
|secInd [coords]
|-----------------------------------------
|secIndLast [coords]
|-----------------------------------------
|sMemory [coords]|
| |---------------
| |cB [sectNumb]
| |fB [sectNumb]
|-----------------------------------------
|p [groupSize] |
| |-------------------
| |c [coords]
| |f
| |pMemory [coords]|
| |--------
| |cB [sectNumb]
| |fB [sectNumb]
Add the S_Memory structure that describes the memory. For groups and particles, the memory will look the same and contain two "cB" and "fB" arrays to store information about the best coordinates and a fitness function for these coordinates.
//—————————————————————————————————————————————————————————————————————————————— struct S_Memory { void Init (int sectNumb) { ArrayResize (cB, sectNumb); ArrayResize (fB, sectNumb); ArrayInitialize (fB, -DBL_MAX); } double cB []; //the best sector coordinate, size is the number of sectors double fB []; //FF is the best coordinate on a sector, size is the number of sectors }; //——————————————————————————————————————————————————————————————————————————————
Accordingly, add memory declarations to the structures of particles and groups:
//—————————————————————————————————————————————————————————————————————————————— struct S_Particle { <..............code is hidden.................> S_Memory pMemory []; //particle memory, size - the number of coordinates }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— struct S_Group { <..............code is hidden.................> S_Memory sMemory []; //group memory, size - number of coordinates }; //——————————————————————————————————————————————————————————————————————————————
The changes also affected the Revision method:
- Updating the best sector coordinates in the swarm memory. All sectors are enumerated for each group and each coordinate. If the "fB" value of a group on a sector is greater than the "fB" value in the sector memory, then "fB" and "cB" are updated in memory.
- Updating the best positions in particle memory. If the particle fitness function value is greater than the value in the particle memory, then "fB" and "cB" are updated in memory.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MSO::Revision () { //---------------------------------------------------------------------------- //Update the best global solution for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- //Transfer the results from the agents to the particles //and get the value of the best particle in the group at the current iteration int cnt = 0; for (int s = 0; s < groups; s++) { gr [s].fB = -DBL_MAX; for (int p = 0; p < ArraySize (gr [s].p); p++) { gr [s].p [p].f = a [cnt].f; if (a [cnt].f > gr [s].fB) { gr [s].fB = a [cnt].f; ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY); } cnt++; } } //---------------------------------------------------------------------------- //Update the best sector coordinates in the swarm's memory int sector = 0; for (int s = 0; s < groups; s++) { for (int c = 0; c < coords; c++) { sector = gr [s].secInd [c]; if (gr [s].fB > gr [s].sMemory [c].fB [sector]) { gr [s].sMemory [c].fB [sector] = gr [s].fB; gr [s].sMemory [c].cB [sector] = gr [s].cB [c]; } } } //---------------------------------------------------------------------------- //Update in the memory of the particles their best positions by sector sector = 0; for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { for (int c = 0; c < coords; c++) { sector = gr [s].secInd [c]; if (gr [s].p [p].f > gr [s].p [p].pMemory [c].fB [sector]) { gr [s].p [p].pMemory [c].fB [sector] = gr [s].p [p].f; gr [s].p [p].pMemory [c].cB [sector] = gr [s].p [p].c [c]; } } } } //---------------------------------------------------------------------------- //Update the best solution for the group for (int s = 0; s < groups; s++) { if (gr [s].fB > gr [s].fBLast) { gr [s].fBLast = gr [s].fB; ArrayCopy (gr [s].cBLast, gr [s].cB, 0, 0, WHOLE_ARRAY); ArrayCopy (gr [s].secIndLast, gr [s].secInd, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- int sect = 0; //sector double sectMin = 0.0; //sector's min double sectMax = 0.0; //sector's max int ind = 0; //index double cd = 0.0; //coordinate for (int s = 0; s < groups; s++) { for (int c = 0; c < coords; c++) { ind = (int)(RNDfromCI (0, groups)); if (ind >= groups) ind = groups - 1; if (ind == s) ind++; if (ind > groups - 1) ind = 0; if (RNDfromCI (0.0, 1.0) < 0.6) { if (gr [ind].fBLast > gr [s].fBLast) { gr [s].secInd [c] = gr [ind].secIndLast [c]; } } else { if (RNDfromCI (0.0, 1.0) < probRNSsector) { ind = (int)(RNDfromCI (0, sectNumb)); if (ind >= sectNumb) ind = sectNumb - 1; gr [s].secInd [c] = ind; sect = gr [s].secInd [c]; if (gr [s].sMemory [c].fB [sect] == -DBL_MAX) { cd = RNDfromCI (min_max_Sector [c].min [sect], min_max_Sector [c].max [sect]); gr [s].sMemory [c].cB [sect] = SeInDiSp (cd, rangeMin [c], rangeMax [c], rangeStep [c]); } } else gr [s].secInd [c] = gr [s].secIndLast [c]; } } } //---------------------------------------------------------------------------- for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { for (int c = 0; c < coords; c++) { sect = gr [s].secInd [c]; if (RNDfromCI (0.0, 1.0) < probUniformSector) { cd = RNDfromCI (min_max_Sector [c].min [sect], min_max_Sector [c].max [sect]); } else { if (RNDfromCI (0.0, 1.0) < probClgroup) { cd = PowerDistribution (gr [s].sMemory [c].cB [sect], min_max_Sector [c].min [sect], min_max_Sector [c].max [sect], power); } else { cd = PowerDistribution (gr [s].p [p].pMemory [c].cB [sect], min_max_Sector [c].min [sect], min_max_Sector [c].max [sect], power); } } gr [s].p [p].c [c] = SeInDiSp (cd, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- //send the particles to the agents cnt = 0; for (int s = 0; s < groups; s++) { for (int p = 0; p < ArraySize (gr [s].p); p++) { ArrayCopy (a [cnt].c, gr [s].p [p].c, 0, 0, WHOLE_ARRAY); cnt++; } } } //——————————————————————————————————————————————————————————————————————————————
3. Test results
The algorithm tests with no consideration to particle memory yield quite good results. The algorithm ranks among the top ten in the rating table. It is important to note that this algorithm is just an example of logic, and if it had demonstrated outstanding results, I would have included it in the table. There are also many opportunities for further implementation and modification of this algorithm.
Although the results are not outstanding, the algorithm has shown good search capabilities in exploring various areas of the search space.
C_AO_MSO|60|30|9|0.05|0.05|10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9313358190790157
25 Hilly's; Func runs: 10000; result: 0.6649184286250989
500 Hilly's; Func runs: 10000; result: 0.3282041522365852
=============================
5 Forest's; Func runs: 10000; result: 0.9522099605531393
25 Forest's; Func runs: 10000; result: 0.5542256622730999
500 Forest's; Func runs: 10000; result: 0.08984352753493675
=============================
5 Megacity's; Func runs: 10000; result: 0.7899999999999998
25 Megacity's; Func runs: 10000; result: 0.33533333333333326
500 Megacity's; Func runs: 10000; result: 0.042983333333333325
=============================
All score: 4.68905 (52.1%)
These results are for the social groups with memory. We can see a small deterioration in the overall algorithm results. Nevertheless, this algorithm takes its rightful place at the top of the rating table. This indicates the potential of the algorithm and its ability to achieve satisfactory results. The idea of considering the concept of sharing memory not only between groups, but also between their particles, is a logical step to improve the algorithm. Introducing this additional interaction can lead to new ideas and strategies. As mentioned earlier in the article, various scenarios of interaction between social groups are described, and I have included only a part of them. This means that there is ample scope for modifying and improving the algorithm.
C_AO_MSOm|60|30|9|0.1|0.9|0.1|10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9468984351872132
25 Hilly's; Func runs: 10000; result: 0.5865441453580522
500 Hilly's; Func runs: 10000; result: 0.3186653673403949
=============================
5 Forest's; Func runs: 10000; result: 0.9064162754293653
25 Forest's; Func runs: 10000; result: 0.43175851113448455
500 Forest's; Func runs: 10000; result: 0.06865408175918558
=============================
5 Megacity's; Func runs: 10000; result: 0.6783333333333333
25 Megacity's; Func runs: 10000; result: 0.213
500 Megacity's; Func runs: 10000; result: 0.03310000000000002
=============================
All score: 4.18337 (46.4%)
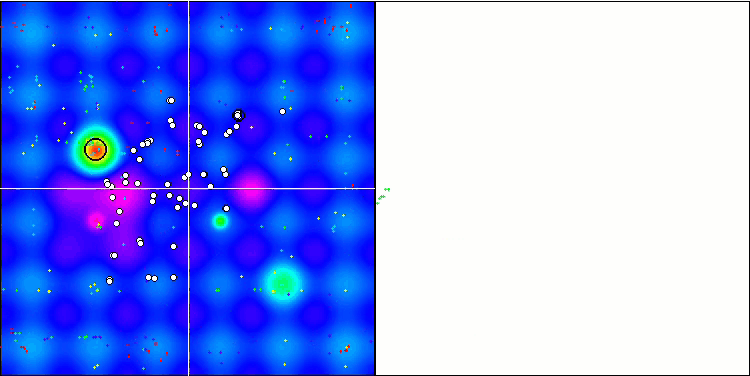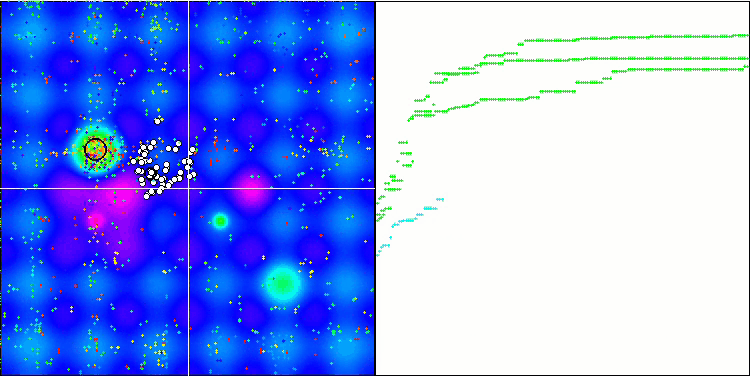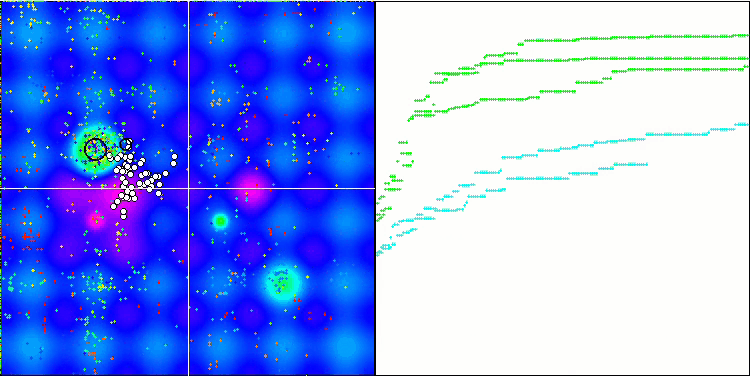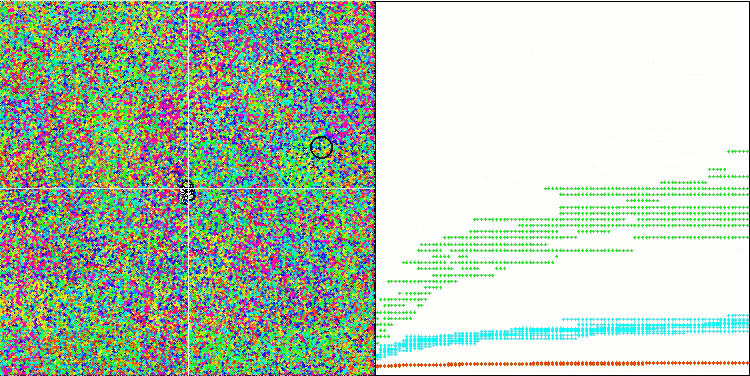
MSO on the Hilly test function
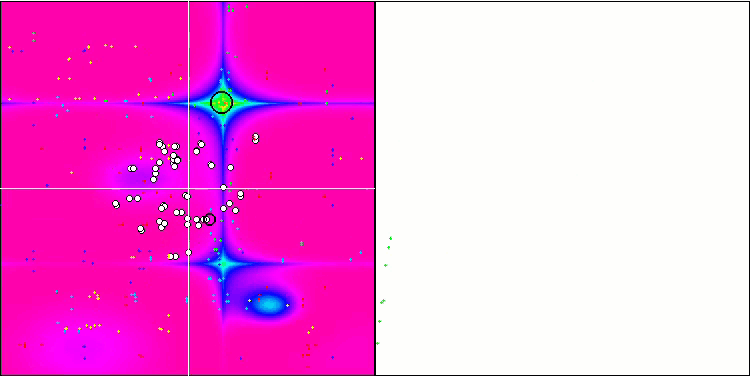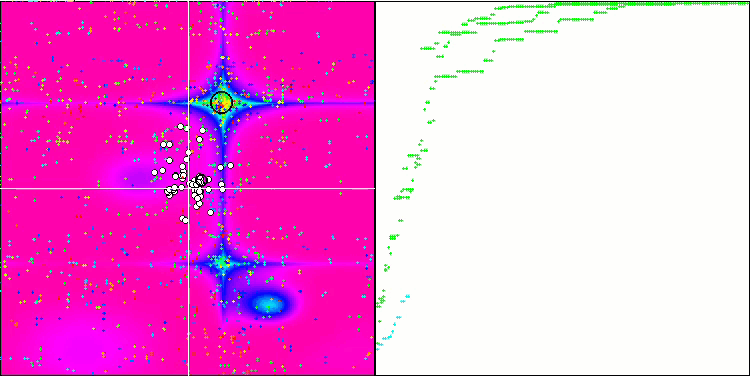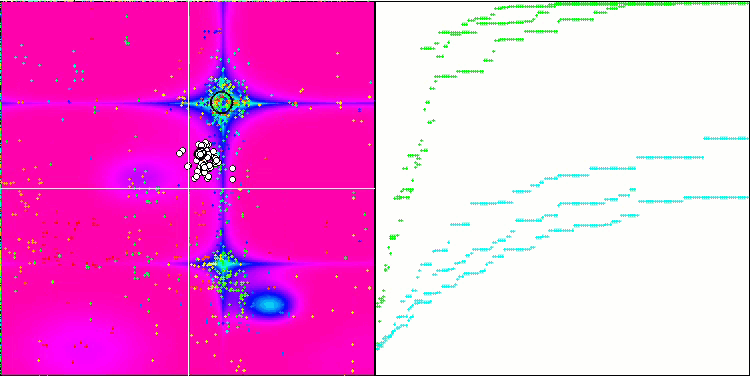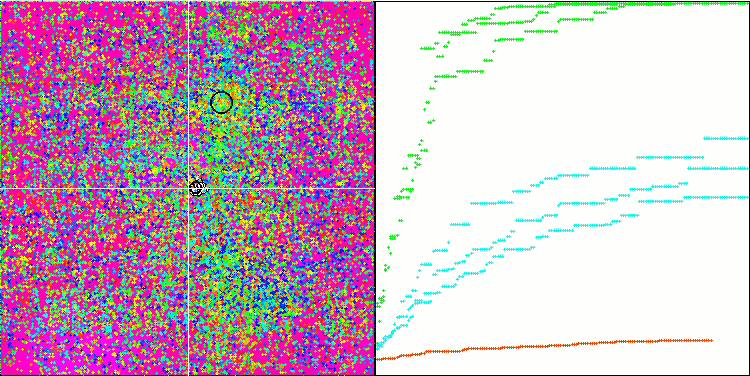
MSO on the Forest test function
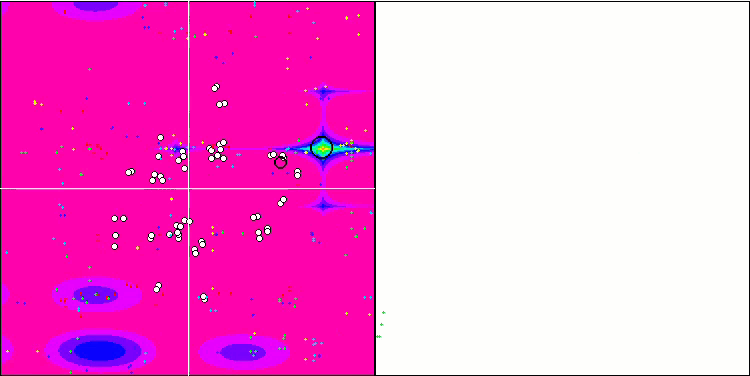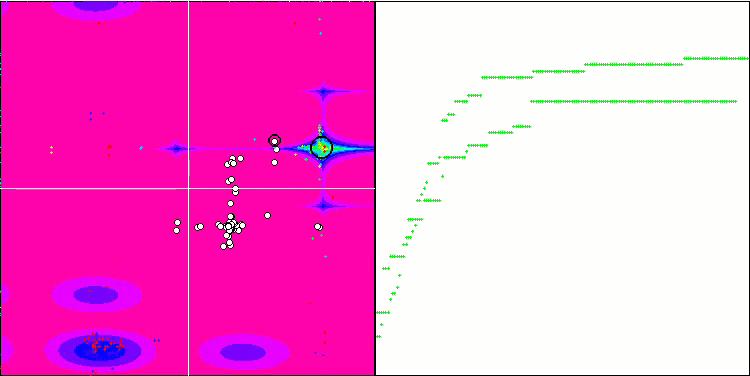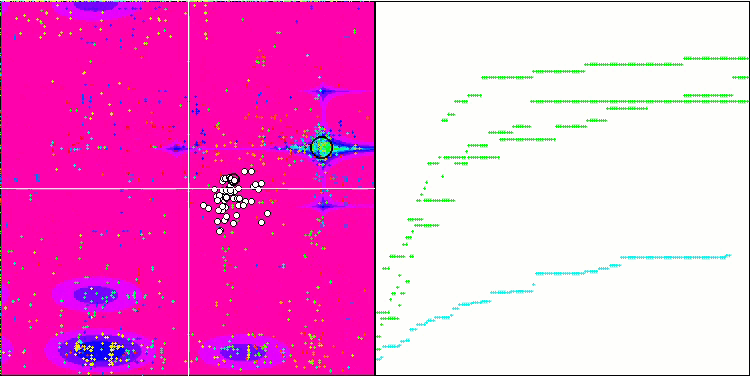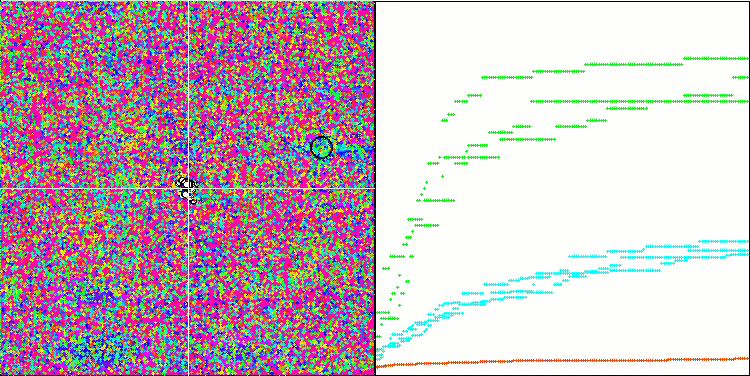
MSO on the Megacity test function
Summary
Taking into account the previous reasoning and results, I can add the following:During the experiments, it was found that the algorithm with memory showed slightly poorer results compared to the algorithm without memory. However, this does not mean that the memory-based algorithm is less promising. Most likely, it is necessary to modify the concept of memory exchange between groups and particles in order to improve its results.
In addition, it is worth noting that incorporating other principles of interaction between social groups can significantly improve the efficiency of the memory algorithm. The introduction of mechanisms for cooperation, coordination and learning between groups can lead to significant improvements in performance and let the algorithm take one of the leading positions in our rating table.
In conclusion, the study proposes a new concept for the evolution of social groups based on movement between sectors and the use of memory. These concepts open up new possibilities for studying social systems and their ability to cooperate, coordinate and adapt. I hope that the results will help to better understand how social groups function and evolve in complex social environments and will provide an opportunity for further research in this area.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/14162
Data Science and Machine Learning (Part 23): Why LightGBM and XGBoost outperform a lot of AI models?
Population optimization algorithms: Evolution of Social Groups (ESG)
Master MQL5 from beginner to pro (Part II): Basic data types and use of variable
Neural networks made easy (Part 71): Goal-Conditioned Predictive Coding (GCPC)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
On the subject of the complexity of FF as a TC.
The staff GA has finished optimising in the green box.
Re-starting the GA by first fumbling came to a much better result (red frame).
For the standard GA, multiple launches are the recommended technique (I don't know whether it is good or bad - there are arguments both for and against).
Theoretical question (can be tested in practice).
If we add a fake (not involved in FF calculations) parameter with a range of, for example, five values to the set, will the results of the algorithm improve/deteriorate?
Deterioration, unambiguously. FF runs will be wasted on futile attempts to find "good" fake parameters.
The larger the percentage of possible variants of fake parameters from the total number of possible parameter variants, the stronger the impact will be - in the limit aiming for random results.
For a standard GA, multiple starts are the recommended technique (I don't know if this is good or bad - there are arguments both for and against).
Thanks, that's built in.
Deteriorate, unequivocally. Ff runs will be wasted on futile attempts to find "good" fake parameters.
The greater the percentage of possible variants of fake parameters from the total number of possible variants of parameters, the stronger the impact will be - in the limit aiming at random results.
I'll have to check it out.
I'll have to check it out.
I'd say more correctly, fake parameters make it harder to find. But all things being equal, the results will be worse. Say, if you do 1mio runs of ff, the result will be the same, but if you do 1k runs, the difference will be noticeable.