Estimamos la rentabilidad futura usando intervalos de confianza

Introducción

Crear sistemas comerciales automatizados rentables no es tarea fácil. Incluso si alguien consigue crear un asesor rentable, queda la cuestión de si el riesgo está justificado. Podemos darnos por contentos si nuestra estrategia no destruye todo el capital asignado a ella, pero eso no es razón para entrar inmediatamente en el mercado real. En última instancia, la métrica principal es la rentabilidad, y si al cabo de un tiempo descubrimos que nuestra estrategia no es lo bastante rentable para justificar el riesgo, o produce rentabilidades bajas en comparación con otras oportunidades de inversión, sin duda lamentaremos seriamente el tiempo invertido y perdido.

Por ello, en este artículo, analizaremos varios métodos tomados del campo de la estadística que pueden ayudarnos a estimar la rentabilidad futura de un sistema comercial automatizado utilizando los datos recogidos en pruebas fuera de muestra.

¿Es lo suficientemente bueno un asesor determinado?

Cuando probamos un sistema comercial, obtenemos un conjunto de métricas de la rentabilidad diferentes. Estos datos nos ofrecerán intuitivamente una idea del beneficio potencial del sistema, pero dicha intuición puede no ser suficiente. Una estrategia que ha obtenido grandes beneficios en las pruebas podría no mostrar su mejor cara en la negociación real. ¿Existe alguna forma de saber si la rentabilidad observada durante las pruebas se mantendrá al mismo nivel? Y si no, ¿al menos cuánto empeorará?

Aquí es donde los métodos estadísticos estándar pueden resultar de ayuda. Los métodos que expondremos no pretenden ser estimaciones precisas, Más bien identificarán estrategias con una alta probabilidad de generar rentabilidades significativas o aceptables.

Conozco a tráders que utilizan los valores brutos del Ratio de Sharpe para hacer suposiciones probabilísticas sobre los resultados futuros. Y eso es peligroso. Recuerde que los resultados pasados no suponen un indicador de los beneficios futuros. No se puede jugar con los mercados financieros. Los gráficos de precios con frecuencia se mueven hacia arriba o hacia abajo por razones desconocidas. Queremos realizar predicciones de rentabilidad correctas basadas en probabilidades que podamos aplicar a nuestros procesos de toma de decisiones.

Intervalos de confianza

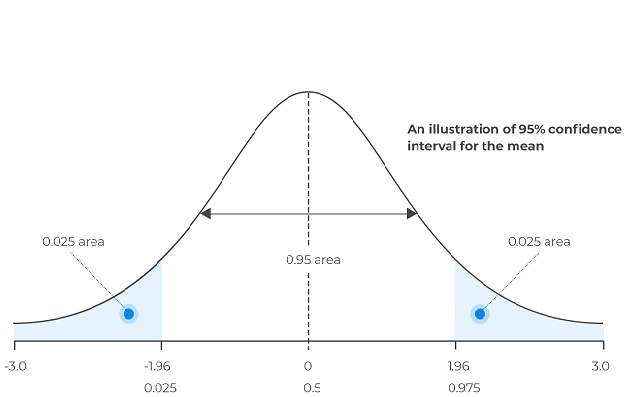
Un intervalo de confianza se refiere a la probabilidad de que una estadística concreta de un conjunto de datos o una población se sitúe dentro de un intervalo determinado a lo largo de un periodo de tiempo. Dichos intervalos miden la confianza calculando la probabilidad de que los niveles calculados contengan la verdadera estadística estimada. Los estadísticos suelen usar niveles de confianza de entre el 90% y el 99%. Estos intervalos pueden calcularse utilizando diversos métodos. En este artículo, nos centraremos en algunas técnicas habituales de bootstraping.

Bootstrapping

El bootstrapping en estadística es un procedimiento en el que se utiliza un conjunto de datos para crear muchos otros conjuntos de datos nuevos seleccionando o eligiendo aleatoriamente del original. Los nuevos conjuntos de datos tendrán los mismos elementos que los originales, pero algunos elementos de los nuevos conjuntos de datos estarán duplicados.

Original	Bootstrap1	Bootstrap2	Bootstrap3	Bootstrap4
A	A	A	A	B
B	A	B	B	B
C	B	B	B	C
D	C	D	C	D
E	D	E	C	E

La columna Original contiene el conjunto de datos original, mientras que las demás columnas representan los conjuntos de datos creados a partir de Original. Como podemos ver, las columnas bootstrap tienen uno o más duplicados. Haciendo esto muchas veces, podremos generar muchos datos para representar patrones que actualmente no podemos observar o que serían desconocidos. Ya hemos visto ejemplos de bootstrapping en trading en el artículo "Aplicando el método de Monte Carlo para optimizar estrategias comerciales".

Un aspecto central de la teoría del bootstrapping es que el conjunto de datos original deberá ser representativo de un conjunto de datos mayor, una población general (población) que no se puede observar y que se intenta modelizar. Así que cuando creamos estos bootstraps, estos se convierten en sustitutos de la colección no observada. Las propiedades estadísticas de estos bootstraps, junto con la muestra original, pueden usarse para hacer inferencias sobre una población desconocida y/o no observada.

Bootstrapping de los intervalos de confianza

Mostraremos tres métodos para el bootstrapping de intervalos de confianza: el método del pivote, el método de percentil y, por último, el método con corrección de desplazamiento y aceleración (BCD).

El método de pivotes implica la creación de numerosos bootstraps que se utilizarán para calcular las estadísticas de las pruebas. Una estadística de prueba se refiere a cualquier característica de una población que intentamos valorar, puede ser su media o su mediana. Los límites estimados se encuentran entonces ajustando el valor de la estadística de prueba del conjunto original de fechas en relación con lo que necesitamos para aumentar el valor de muestreo bootstrap esperado hasta la línea original.

El método de percentil considera la distribución de la estadística de prueba calculada a partir de muestras bootstrap. Se supone que esta distribución resultará similar a la distribución de la población desconocida. Los límites se convierten en los intervalos entre los percentiles de la distribución de la estadística de prueba calculada a partir de las muestras bootstrap.  

El método con corrección de desplazamiento y aceleración es un poco más complicado. Tras crear nuestros bootstraps y calcular las estadísticas de prueba para cada uno de ellos, calcularemos un factor de corrección del desplazamiento, que será la fracción de puntuaciones bootstrap más pequeñas que el conjunto de datos original. A continuación se calculará el factor de aceleración usando el método jackknife. Se trata de otra técnica de remuestreo usada para evaluar en qué medida la varianza de una estadística de prueba transformada depende de su valor.

A continuación, se utilizará el método de percentil para calcular los límites inferior y superior, que se modificarán según los factores de corrección de desplazamiento y aceleración. Los intervalos de confianza finales se obtendrán a partir de los valores modificados tras la clasificación.

Veamos cómo se implementan estos métodos en código.

Clase CBoostrap

CBoostrap es una clase que encapsula el cálculo de intervalos de confianza usando los tres métodos de bootstrapping que acabamos de describir. Con ella, los usuarios podrán calcular los intervalos de confianza para varias probabilidades personalizables, así como especificar el número de bootstraps que deben generarse.

#include<Math\Alglib\specialfunctions.mqh>
#include<Math\Stat\Math.mqh>
#include<UniformRandom.mqh>

La definición de la clase comenzará incluyendo algunas utilidades matemáticas importantes de la biblioteca estándar.

//+------------------------------------------------------------------+
//|Function pointer                                                  |
//+------------------------------------------------------------------+
typedef double(*BootStrapFunction)(double &in[],int stop=-1);

El puntero BootStrapFunction define la signatura de la función para calcular las estadísticas de prueba o el parámetro de población.

//+------------------------------------------------------------------+
//|Boot strap types                                                  |
//+------------------------------------------------------------------+
enum ENUM_BOOSTRAP_TYPE
  {
   ENUM_BOOTSTRAP_PIVOT=0,
   ENUM_BOOTSTRAP_PERCENTILE,
   ENUM_BOOTSTRAP_BCA
  };

La enumeración ENUM_BOOSTRAP_TYPE facilita la selección de un método específico de cálculo del bootstrap: pivotes, percentiles o BCA.

//+------------------------------------------------------------------+
//|Constructor                                                       |
//+------------------------------------------------------------------+
CBootstrap::CBootstrap(const ENUM_BOOSTRAP_TYPE boot_type,const uint nboot,const BootStrapFunction function,double &in_samples[])
  {
//--- set the function pointer
   m_function=function;
//--- optimistic initilization of flag
   m_initialized=true;
//--- set method of boostrap to be applied
   m_boot_type=boot_type;
//--- set number of boostrap iterations
   m_replications=nboot;
//---make sure there are at least 5 boostraps
   if(m_replications<5)
      m_initialized=false;
//--- initilize random number generator
   m_unifrand=new CUniFrand();
   if(m_unifrand!=NULL)
      m_unifrand.SetSeed(MathRand());
   else
      m_initialized=false;
//--- copy samples to internal buffer
   if(ArrayCopy(m_data,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- initialize shuffled buffer
   if(ArrayCopy(m_shuffled,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- set memory for bootstrap calculations container
   if(ArrayResize(m_rep_cal,(int)m_replications)!=(int)m_replications)
     {
      Print("Memory allocation error ", GetLastError());
      m_initialized=false;
     }
//--- check function pointer
   if(m_function==NULL)
     {
      Print("Invalid function pointer");
      m_initialized=false;
     }
  }

CBoostrap se define usando un constructor paramétrico cuyos parámetros de entrada definirán la naturaleza de la operación bootstrap:

• boot_type - método de cálculo bootstrap

• nboot - número de muestras bootstrap deseadas. Recomendamos tener al menos 100, aunque lo ideal sería generar miles para obtener resultados fiables.

• function - apuntar a la definición de la función ofrecida por el usuario para calcular el parámetro de población estimado. Los parámetros de esta función representan el array de muestras de datos utilizado para calcular las estadísticas de prueba. El parámetro entero del puntero de la función indica por defecto el número de miembros del array que se utilizarán en el cálculo.

• El array in_samples es el contenedor de datos a partir del cual se generarán bootstraps. El mismo conjunto de datos y sus variantes bootstrap se pasarán al puntero de la función para calcular las estadísticas de prueba.

//+------------------------------------------------------------------+
//| public method for calculating confidence intervals               |
//+------------------------------------------------------------------+
bool CBootstrap::CalculateConfidenceIntervals(double &in_out_conf[])
  {
//--- safety check
   if(!m_initialized)
     {
      ZeroMemory(in_out_conf);
      return m_initialized;
     }
//--- check input parameter values
   if(ArraySize(in_out_conf)<=0 ||
      in_out_conf[ArrayMaximum(in_out_conf)]>=1 ||
      in_out_conf[ArrayMinimum(in_out_conf)]<=0)
     {
      Print("Invalid input values for function ",__FUNCTION__,"\n All values should be probabilities between 0 and 1");
      return false;
     }
//--- do bootstrap based on chosen method
   switch(m_boot_type)
     {
      case ENUM_BOOTSTRAP_PIVOT:
         return pivot_boot(in_out_conf);
      case ENUM_BOOTSTRAP_PERCENTILE:
         return percentile_boot(in_out_conf);
      case ENUM_BOOTSTRAP_BCA:
         return bca_boot(in_out_conf);
      default:
         return false;
     }
//---
  }

Uno de los dos métodos disponibles públicamente de la clase CalculateConfidenceIntervals() tomará como entrada un array de valores de probabilidad en la cantidad requerida por el usuario. Estos valores determinarán la probabilidad de que el valor real del parámetro se encuentre dentro del intervalo de cálculo.

Por ejemplo, para calcular intervalos de confianza que tengan una probabilidad del 90%, el usuario deberá proporcionar un array con un valor de 0,9 y, a continuación, el método retornará un par de valores. Estos valores devueltos se escribirán en el mismo array proporcionado como datos de entrada. Para cada miembro individual del array de entrada, el método sustituirá un par de valores, siendo el primero de cada par el límite inferior del intervalo y el segundo el límite superior del intervalo.

Como ya hemos mencionado, podremos solicitar más de un intervalo de confianza con diferentes probabilidades. En la salida, los límites estarán clasificados de menor a mayor probabilidad, indicada como datos de entrada.

Antes de demostrar el uso de la clase, deberemos determinar qué datos utilizaremos para medir la eficacia de la estrategia comercial. Es una práctica habitual clasificar los resultados de la estrategia en función de la rentabilidad. Para calcular este valor, deberemos examinar la curva de capital, así como las series de rentabilidades.

Usando las series de rentabilidades de la estrategia, podremos calcular varias medidas de rentabilidad. Para simplificar, usaremos las rentabilidades medias anuales como estadística de prueba cuyo valor futuro queremos estimar con una confianza determinada.

Usando estas estadísticas de prueba, podremos estimar la rentabilidad media más baja que podemos esperar de la estrategia. Además, el nivel de confianza superior nos dará una idea aproximada de lo buenos que serán los resultados si todo va bien.

Clase CReturns

Usaremos la clase CReturns para recopilar las series de rentabilidades necesarias para aproximar la rentabilidad media futura. La clase está adaptada del código presentado en el artículo "Matemáticas en el trading: Ratios de Sharpe y Sortino". Una característica de esta versión será la posibilidad de seleccionar el tipo de serie de rentabilidades que utilizaremos en los cálculos de rentabilidad.

//+------------------------------------------------------------------+
//| Class for calculating Sharpe Ratio in the tester                 |
//+------------------------------------------------------------------+
class CReturns
  {
private:
   CArrayDouble*     m_all_bars_equity;
   CArrayDouble*     m_open_position_bars_equity;
   CArrayDouble*     m_trade_equity;

   CArrayDouble*     m_all_bars_returns;
   CArrayDouble*     m_open_position_bars_returns;
   CArrayDouble*     m_trade_returns;

   int               ProcessHistory(void);
   void              CalculateReturns(CArrayDouble &r,CArrayDouble &e);

public:
                     CReturns(void);
                    ~CReturns(void);

   void              OnNewTick(void);

   bool              GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[]);
   bool              GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[]);
  };

return.mqh establecerá la enumeración que definirá el tipo de serie de rentabilidades. ENUM_RETURNS_ALL_BARS define una serie de rentabilidades barra por barra para todas las barras del periodo de prueba. ENUM_RETURNS_POSITION_OPEN_BARS representa una serie de rentabilidades por barra para aquellas barras en las que se ha abierto una posición. ENUM_RETURNS_TRADES define solo las series de rentabilidades de las operaciones completadas. Con esta opción no se recogerá información de las barras.

//+------------------------------------------------------------------+
//| Enumeration specifying granularity of return                     |
//+------------------------------------------------------------------+
enum ENUM_RETURNS_TYPE
  {
   ENUM_RETURNS_ALL_BARS=0,//bar-by-bar returns for all bars
   ENUM_RETURNS_POSITION_OPEN_BARS,//bar-by-bar returns for bars with open trades
   ENUM_RETURNS_TRADES//trade returns
  };

Utilizando la clase CReturns, podremos obtener un rango de valores de equidad que definirán una curva de equidad usando el método GetEquityCurve().

//+------------------------------------------------------------------+
//| get equity curve                                                 |
//+------------------------------------------------------------------+
bool CReturns::GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[])
  {
   int m_counter=0;
   CArrayDouble *equity;
   ZeroMemory(out_equity);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         m_counter=m_all_bars_equity.Total();
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         m_counter=m_open_position_bars_equity.Total();
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         m_counter=(m_trade_equity.Total()>1)?m_trade_equity.Total():ProcessHistory();
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(m_counter < 2)
      return false;
//---
   if(ArraySize(out_equity)!=m_counter)
      if(ArrayResize(out_equity,equity.Total()) < m_counter)
         return false;
//---
   for(int i=0; i<equity.Total(); i++)
      out_equity[i]=equity[i];
//---
   return(true);
//---
  }

De forma similar, GetReturns() puede mostrar una serie de rentabilidades. Ambos métodos tomarán como entrada una serie específica de resultados deseados, así como un array en el que se recuperarán los valores.

//+------------------------------------------------------------------+
//|Gets the returns into array                                       |
//+------------------------------------------------------------------+
bool CReturns::GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[])
  {
//---
   CArrayDouble *returns,*equity;
   ZeroMemory(out_returns);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         returns=m_all_bars_returns;
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         returns=m_open_position_bars_returns;
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         if(m_trade_equity.Total()<2)
            ProcessHistory();
         returns=m_trade_returns;
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(equity.Total() < 2)
      return false;
//--- calculate average returns
   CalculateReturns(returns,equity);
//--- return the mean return
   if(returns.Total()<=0)
      return false;
//---
   if(ArraySize(out_returns)!=returns.Total())
      if(ArrayResize(out_returns,returns.Total()) < returns.Total())
         return false;
//---
   for(int i=0; i<returns.Total(); i++)
      out_returns[i]=returns[i];
//---
   return(true);
//---
  }

Ejemplo

El siguiente código de asesor mostrará cómo utilizar CReturns para recopilar una serie de rentabilidades. En nuestro ejemplo, la serie de rentabilidades se guardará en un archivo binario. Aunque el cálculo del intervalo de confianza puede realizarse usando CBootstrap en OnTester, en nuestro ejemplo analizaremos esta serie desde un programa independiente.

//+------------------------------------------------------------------+
//|                                           MovingAverage_Demo.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <Bootstrap.mqh>
#include <Files\FileBin.mqh>
#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
input ENUM_RETURNS_TYPE rtypes  = ENUM_RETURNS_ALL_BARS; // return types to record
input uint BootStrapIterations  = 10000;
input double BootStrapConfidenceLevel = 0.975;
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input bool   SaveReturnsToFile = true;
input string ReturnsFileName = "MovingAverage_Demo";

//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;
CReturns ma_returns;
#define MA_MAGIC 1234501
//+------------------------------------------------------------------+
//| Calculate optimal lot size                                       |
//+------------------------------------------------------------------+
double TradeSizeOptimized(void)
  {
   double price=0.0;
   double margin=0.0;
//--- select lot size
   if(!SymbolInfoDouble(_Symbol,SYMBOL_ASK,price))
      return(0.0);
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,price,margin))
      return(0.0);
   if(margin<=0.0)
      return(0.0);

   double lot=NormalizeDouble(AccountInfoDouble(ACCOUNT_MARGIN_FREE)*MaximumRisk/margin,2);
//--- calculate number of losses orders without a break
   if(DecreaseFactor>0)
     {
      //--- select history for access
      HistorySelect(0,TimeCurrent());
      //---
      int    orders=HistoryDealsTotal();  // total history deals
      int    losses=0;                    // number of losses orders without a break

      for(int i=orders-1; i>=0; i--)
        {
         ulong ticket=HistoryDealGetTicket(i);
         if(ticket==0)
           {
            Print("HistoryDealGetTicket failed, no trade history");
            break;
           }
         //--- check symbol
         if(HistoryDealGetString(ticket,DEAL_SYMBOL)!=_Symbol)
            continue;
         //--- check Expert Magic number
         if(HistoryDealGetInteger(ticket,DEAL_MAGIC)!=MA_MAGIC)
            continue;
         //--- check profit
         double profit=HistoryDealGetDouble(ticket,DEAL_PROFIT);
         if(profit>0.0)
            break;
         if(profit<0.0)
            losses++;
        }
      //---
      if(losses>1)
         lot=NormalizeDouble(lot-lot*losses/DecreaseFactor,1);
     }
//--- normalize and check limits
   double stepvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   lot=stepvol*NormalizeDouble(lot/stepvol,0);

   double minvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   if(lot<minvol)
      lot=minvol;

   double maxvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX);
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);
  }
//+------------------------------------------------------------------+
//| Check for open position conditions                               |
//+------------------------------------------------------------------+
void CheckForOpen(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- check signals
   ENUM_ORDER_TYPE signal=WRONG_VALUE;

   if(rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=ORDER_TYPE_SELL;    // sell conditions
   else
     {
      if(rt[0].open<ma[0] && rt[0].close>ma[0])
         signal=ORDER_TYPE_BUY;  // buy conditions
     }
//--- additional checking
   if(signal!=WRONG_VALUE)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),
                               SymbolInfoDouble(_Symbol,signal==ORDER_TYPE_SELL ? SYMBOL_BID:SYMBOL_ASK),
                               0,0);
     }
//---
  }
//+------------------------------------------------------------------+
//| Check for close position conditions                              |
//+------------------------------------------------------------------+
void CheckForClose(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- positions already selected before
   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])
      signal=true;
//--- additional checking
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);
     }
//---
  }
//+------------------------------------------------------------------+
//| Position select depending on netting or hedging                  |
//+------------------------------------------------------------------+
bool SelectPosition()
  {
   bool res=false;
//--- check position in Hedging mode
   if(ExtHedging)
     {
      uint total=PositionsTotal();
      for(uint i=0; i<total; i++)
        {
         string position_symbol=PositionGetSymbol(i);
         if(_Symbol==position_symbol && MA_MAGIC==PositionGetInteger(POSITION_MAGIC))
           {
            res=true;
            break;
           }
        }
     }
//--- check position in Netting mode
   else
     {
      if(!PositionSelect(_Symbol))
         return(false);
      else
         return(PositionGetInteger(POSITION_MAGIC)==MA_MAGIC); //---check Magic number
     }
//--- result for Hedging mode
   return(res);
  }
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit(void)
  {
//--- prepare trade class to control positions if hedging mode is active
   ExtHedging=((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE)==ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
   ExtTrade.SetExpertMagicNumber(MA_MAGIC);
   ExtTrade.SetMarginMode();
   ExtTrade.SetTypeFillingBySymbol(Symbol());
//--- Moving Average indicator
   ExtHandle=iMA(_Symbol,_Period,MovingPeriod,MovingShift,MODE_SMA,PRICE_CLOSE);
   if(ExtHandle==INVALID_HANDLE)
     {
      printf("Error creating MA indicator");
      return(INIT_FAILED);
     }
//--- ok
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   ma_returns.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
   double returns[],confidence[],params[];
   ArrayResize(confidence,1);
   confidence[0]=BootStrapConfidenceLevel;
//---
   double ret=0.0;
//---
   if(ma_returns.GetReturns(rtypes,returns))
     {
      CBootstrap minreturn(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,returns);

      if(minreturn.CalculateConfidenceIntervals(confidence))
        {
         ret=confidence[0];
         string fname=ReturnsFileName+"_"+_Symbol+".returns";
         CFileBin file;
         if(SaveReturnsToFile && file.Open(fname,FILE_WRITE|FILE_COMMON)!=INVALID_HANDLE)
            file.WriteDoubleArray(returns);

        }

     }
//---
   return(ret);
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }

El script leerá los datos almacenados y los transmitirá al ejemplar CBootstrap. La estadística de prueba se calculará con la ayuda de la función MeanReturns(), cuya signatura coincidirá con la signatura del puntero a la función BootStrapFunction. Luego llamaremos a CalculateConfidenceIntervals() con un array con valores 0,9, 0,95, 0,975, que se corresponderán con los intervalos de confianza del 90%, 95% y 97,5%.

//+------------------------------------------------------------------+
//|                                       ApproximateMeanReturns.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Math.mqh>
#include<Files\FileBin.mqh>
#include<Bootstrap.mqh>
//--- input parameters
input string   FileName="MovingAverage_Demo_EURUSD.returns";//returns file name
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input uint BootStrapIterations=10000;
input string BootStrapProbability="0.975,0.95,0.90";
//---
CBootstrap *meanreturns;
double logreturns[],bounds[],bootstraps[];
string sbounds[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int done=StringSplit(BootStrapProbability,StringGetCharacter(",",0),sbounds);
//---
   if(done)
     {
      ArrayResize(bounds,done);
      for(int i=0; i<done; i++)
         bounds[i]=StringToDouble(sbounds[i]);
      if(ArraySort(bounds))
         for(int i=0; i<done; i++)
            sbounds[i]=DoubleToString(bounds[i]);
     }
//---
   if(!done)
     {
      Print("error parsing inputs ", GetLastError());
      return;
     }
//---
   if(!LoadReturns(FileName,logreturns))
      return;
//---
   meanreturns=new CBootstrap(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,logreturns);
//---
   if(meanreturns.CalculateConfidenceIntervals(bounds))
     {
      for(int i=0; i<done; i++)
         Print(EnumToString(AppliedBoostrapMethod)," ",sbounds[i],": ","(",bounds[i*2]," ",bounds[(i*2)+1],")");
     }
//---
   delete meanreturns;
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Load returns from file                                           |
//+------------------------------------------------------------------+
bool LoadReturns(const string fname,double &out_returns[])
  {
   CFileBin file;
//---
   if(file.Open(fname,FILE_READ|FILE_COMMON)==INVALID_HANDLE)
      return false;
//---
   if(!file.ReadDoubleArray(out_returns))
     {
      Print("File read error ",GetLastError());
      return false;
     }
//---
   return true;
  }
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }
//+------------------------------------------------------------------+

Antes de mirar el resultado final de los intervalos calculados, siempre será una buena idea mirar un gráfico con la distribución de las estadísticas de la prueba bootstrap. Esto se podrá hacer trazando un gráfico con los datos disponibles a través de GetBootStrapStatistics().

Examinando los resultados del asesor de media móvil, podemos ver que OnTester retorna un número negativo, lo cual indica que el rentabilidad puede deteriorarse en el futuro, a pesar de los resultados positivos mostrados en la prueba. -0,12 es la peor rentabilidad media que podemos esperar.  

A continuación le mostramos los resultados para distintos intervalos de confianza.

ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.90000000: (-0.07040966776550685 0.1134376873958945)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.95000000: (-0.09739322056041048 0.1397669758772337)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.97500000: (-0.12438450770122121 0.1619709975134838)

Este ejemplo muestra el cálculo del rentabilidad media prevista basada en la probabilidad para el asesor Moving Average. El mismo principio puede aplicarse a otras medidas de rentabilidad. Pero hay que tener en cuenta que las métricas de rentabilidad basadas en ratios pueden ser problemáticas debido al denominador en el cálculo de la métrica. Si es demasiado pequeño, obtendremos cifras muy grandes.

La mejor forma de determinar la idoneidad de estos métodos para estimar la rentabilidad futura de una métrica concreta es examinar la distribución de las estadísticas de muestreo bootstrap. Buscamos las "colas pesadas" de las distribuciones. Los resultados obtenidos a partir de las distribuciones con "colas pesadas" deberán utilizarse con precaución.

Veamos un ejemplo de estimación del peor ratio de Sharpe para el mismo asesor. Esto se conseguirá reescribiendo la función pasada al parámetro de puntero de función del constructor CBootstrap

Los resultados de la prueba indican de nuevo una rentabilidad mucho peor en comparación con el resultado de la prueba simple.

Conclusión

Conocer la gama de rentabilidades puede ayudarnos a tomar decisiones de inversión más informadas en cuanto a la elección de estrategias. Aunque el método demostrado se basa en las estadísticas de los libros de texto, los usuarios deberán ser conscientes de sus limitaciones inherentes.

Los intervalos de confianza calculados serán tan buenos como los datos en los que se basan. Si las muestras usadas en los cálculos son erróneas, entraremos en la clásica situación de "basura entra, basura sale". Siempre resulta importante utilizar muestras adecuadas que sean representativas de las condiciones que puedan surgir en el futuro.

Nombre del archivo	Descripción
Mql5files\include\Bootstrap.mqh	Contiene la definición de la clase CBootstrap
Mql5files\include\Returns.mqh	Contiene la definición de la clase CReturns
Mql5files\include\UniformRandom.mqh	Clase para generar números uniformemente distribuidos de 0 a 1
Mql5files\scripts\ApproximateMeanReturns.mq5	Secuencia de comandos que lee el archivo guardado del simulador de estrategias y calcula los intervalos de confianza de la rentabilidad media del proyecto.
Mql5files\experts\ MovingAverage_Demo.mq5	Asesor utilizado para demostrar el uso de CBootstrap y CReturns