MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
用置信区间估计未来效能

用置信区间估计未来效能

MetaTrader 5 — 测试者 |
704 0
Francis Dube
Francis Dube

概述

创建可以获利的自动化交易系统绝非易事。即使一个人碰巧开发出了一个可以获利的 EA 交易，也存在着是否值得风险的问题。我们可能会对我们的策略不会耗尽分配给它的所有资本感到满意，但这不是立即启用实盘交易的理由。最终，利润是动机，如果我们后来发现我们的策略确实能够获利，但利润不足以证明风险的合理性，或者相对于其他投资机会产生的回报很低，我们无疑会感到非常遗憾。

因此，在本文中，我们将探索从统计学领域借来的技术，这些技术可以帮助我们使用从样本外测试中收集的数据来估计自动化交易系统的未来效能。


它足够好吗

当我们测试一个候选交易系统时，我们自然会得到各种效能指标的集合。这些数据会直观地告诉我们系统的利润潜力，但这种直觉可能还不够。一种在测试中产生大量利润的策略，在现场交易时获得的回报可能不太高。有没有办法更好地了解测试期间观察到的效能是否会继续保持在同一水平？如果没有，效能会有多差

这就是标准统计方法可以提供帮助的地方。需要注意的是，我们将要讨论的技术并不意味着它们的估计是准确的，它们永远不会是准确的。它们所做的是提供方法来识别产生很高或可接受利润的高概率策略

我见过许多人使用粗略的夏普比率数据来对未来性能进行基于概率的假设。记住，这是危险的，过去的业绩并不能预示未来的利润。金融市场不容轻视。价格图表以这样或那样的方式翻转，通常是出于未知的原因。我们想要做的是计算适当的基于概率的效能预测，我们可以将其应用于决策过程中。


置信区间

置信区间


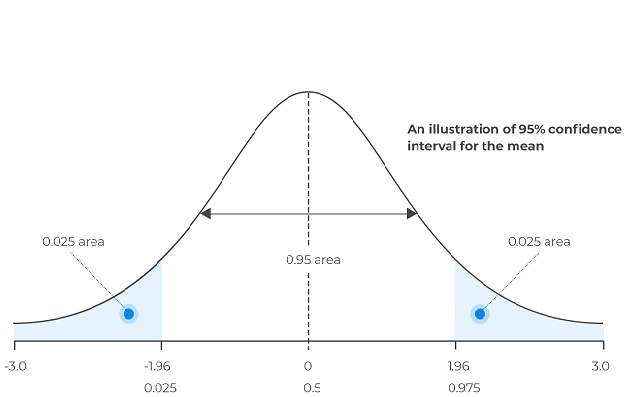
置信区间是指数据集或总体的某个统计数据在一定时间内位于某个范围内的概率。他们通过计算所计算的水平包含所估计的真实统计数据的概率来衡量确定程度。统计学家通常使用90%的置信水平，最高可达99%。可以使用各种方法来计算这些间隔。在这篇文章中，我们将集中讨论一些常见的自举法（bootstrap）技术。


自举法

统计中的自举是一种过程，通过从原始数据中随机挑选数据，使用数据集来创建许多其他新数据集。新数据集将具有与原始数据集相同的成员，但新数据集中的某些成员将是重复的。

原始
自举1
自举2
自举3
 自举4
A
 A
 A
 A
 B
B
 A
 B
 B
 B
C
 B
 B
 B
 C
D
 C
 D
 C
 D
E
 D
 E
 C
 E


上表更好地说明了这一点。原始列具有原始数据集，其他列表示由原始数据集构建的数据集。可以看出，自举的列有一个或多个重复项。通过多次这样做，我们能够生成大量数据，这些数据可以代表我们目前无法观察到或未知的样本。我们已经在“应用蒙特卡罗方法优化交易策略”一文中看到了应用于交易的自举程序示例。

自举理论的核心是，原始数据集应该代表更大的数据集合，即无法观察并试图建模的群体。因此，当我们创建这些自举时，它们会成为不可观测集合的代理。这些自举和原始样本的统计特性可用于得出未知和/或不可观测群体的结论。


自举置信区间

将演示自举置信区间的三种方法。即枢轴法、百分位法和最后的偏差修正加速法（bca）

枢轴法（pivot method）涉及生成大量的自举，这些自举将用于计算测试统计数据。测试统计指的是我们试图估计的数据集的任何特征，这可能是其平均值或中位数。然后，通过相对于将引导样本的期望值增加到原始数据集所需的值来调整原始数据集的测试统计值，来找到估计的边界

百分位数方法（percentile method）考虑引导样本的计算测试统计数据的分布。这种分布被认为与未知数据的分布相似。界限变为从引导样本获得的计算测试统计数据的分布的百分位数之间的间隔。 

偏差修正加速法（bias corrected and accelerated method，bca）稍微复杂一些。在生成我们的自举并计算每个自举的测试统计数据之后。我们计算偏差校正因子，即自举估计的比例小于原始数据集的比例。然后，通过使用一种称为 jackknife 的方法来计算加速度系数。这是另一种重采样方法，用于估计变换后的测试统计量的方差取决于其值的程度。

然后使用百分位法计算下限和上限，根据偏差校正和加速度因子对下限和上限进行修改。最后的置信区间是从排序后的修改值中获得的。

让我们看看如何在代码中实现这些技术。


CBoostrap 类

CBoostrap是一个类，它封装了使用刚才描述的三种引导方法计算置信区间。有了它，用户将能够计算多个可配置概率的置信区间，还能够指定要生成的自举次数。 

#include<Math\Alglib\specialfunctions.mqh>
#include<Math\Stat\Math.mqh>
#include<UniformRandom.mqh>


类的定义从包含标准库中的一些基本数学工具开始。 

//+------------------------------------------------------------------+
//|Function pointer                                                  |
//+------------------------------------------------------------------+
typedef double(*BootStrapFunction)(double &in[],int stop=-1);


BootStrapFunction 函数指针定义了用于计算测试统计或总体参数的函数签名。 

//+------------------------------------------------------------------+
//|Boot strap types                                                  |
//+------------------------------------------------------------------+
enum ENUM_BOOSTRAP_TYPE
  {
   ENUM_BOOTSTRAP_PIVOT=0,
   ENUM_BOOTSTRAP_PERCENTILE,
   ENUM_BOOTSTRAP_BCA
  };


ENUM_BOOSTRAP_TYPE 枚举便于选择特定的自举计算方法：即Pivot、Percentile或BCA。

//+------------------------------------------------------------------+
//|Constructor                                                       |
//+------------------------------------------------------------------+
CBootstrap::CBootstrap(const ENUM_BOOSTRAP_TYPE boot_type,const uint nboot,const BootStrapFunction function,double &in_samples[])
  {
//--- set the function pointer
   m_function=function;
//--- optimistic initilization of flag
   m_initialized=true;
//--- set method of boostrap to be applied
   m_boot_type=boot_type;
//--- set number of boostrap iterations
   m_replications=nboot;
//---make sure there are at least 5 boostraps
   if(m_replications<5)
      m_initialized=false;
//--- initilize random number generator
   m_unifrand=new CUniFrand();
   if(m_unifrand!=NULL)
      m_unifrand.SetSeed(MathRand());
   else
      m_initialized=false;
//--- copy samples to internal buffer
   if(ArrayCopy(m_data,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- initialize shuffled buffer
   if(ArrayCopy(m_shuffled,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- set memory for bootstrap calculations container
   if(ArrayResize(m_rep_cal,(int)m_replications)!=(int)m_replications)
     {
      Print("Memory allocation error ", GetLastError());
      m_initialized=false;
     }
//--- check function pointer
   if(m_function==NULL)
     {
      Print("Invalid function pointer");
      m_initialized=false;
     }
  }

CBoostrap 有一个带参数的构造函数，它的输入参数决定了自举操作的方式：

  • boot_type  - 设置自举计算的方法
  • nboot  - 表示将生成的所需自举样本的数量，建议至少有100个，但更理想的情况是生成数千个，以获得稳健的结果。
  • function -  将指向用户提供的用于计算正在估计的总体参数的函数定义。该函数的参数是用于计算测试统计的数据样本的数组。函数指针的默认整数参数定义了将在计算中使用的数组成员数。
  • 最后，in_samples数组是将从中生成自举的数据容器。这个相同的数据集和它的自举变体将被传递给函数指针，以计算测试统计数据。 
//+------------------------------------------------------------------+
//| public method for calculating confidence intervals               |
//+------------------------------------------------------------------+
bool CBootstrap::CalculateConfidenceIntervals(double &in_out_conf[])
  {
//--- safety check
   if(!m_initialized)
     {
      ZeroMemory(in_out_conf);
      return m_initialized;
     }
//--- check input parameter values
   if(ArraySize(in_out_conf)<=0 ||
      in_out_conf[ArrayMaximum(in_out_conf)]>=1 ||
      in_out_conf[ArrayMinimum(in_out_conf)]<=0)
     {
      Print("Invalid input values for function ",__FUNCTION__,"\n All values should be probabilities between 0 and 1");
      return false;
     }
//--- do bootstrap based on chosen method
   switch(m_boot_type)
     {
      case ENUM_BOOTSTRAP_PIVOT:
         return pivot_boot(in_out_conf);
      case ENUM_BOOTSTRAP_PERCENTILE:
         return percentile_boot(in_out_conf);
      case ENUM_BOOTSTRAP_BCA:
         return bca_boot(in_out_conf);
      default:
         return false;
     }
//---
  }


类中有两个公开方法，其中之一是CalculateConfidenceIntervals（），它将概率值数组作为输入参数，用户想要多少就多少。这些值定义了真实参数值位于计算区间内的概率。

例如，为了计算概率为90%的置信区间，用户将提供一个值为0.9的数组，然后该方法将返回一对值。这些返回的值将被写入作为输入参数提供的相同数组中。对于每个单个输入数组成员，该方法将替换为一对值，每对值中的第一个值是区间的下界，第二个值是上界。

如前所述，可以请求具有不同概率的多个置信区间。输出将按照指定为输入的最低概率到最高概率的顺序排列边界。

在演示类的使用之前，我们需要定义将使用哪些数据来衡量交易策略的效能。根据回报对策略效能进行分类通常是标准做法。为了计算这个值，必须检查权益曲线以及收益序列。

使用策略的收益序列，我们可以计算各种性能指标。为了简单起见，我们将使用平均年化回报率作为测试统计数据，我们希望以特定的置信度来估计其未来价值。

使用这个测试统计数据，我们可以衡量一种策略的最低平均回报率。此外，如果一切顺利，置信度上限可以大致了解表现会有多好。


CReturns 类

为了收集近似未来平均收益所需的一系列收益，我们将使用CReturns类。该类改编自“交易中的数学：夏普和索蒂诺比率”一文中的代码。此版本的一个特殊功能是能够选择要在性能计算中使用的返回序列的类型。

//+------------------------------------------------------------------+
//| Class for calculating Sharpe Ratio in the tester                 |
//+------------------------------------------------------------------+
class CReturns
  {
private:
   CArrayDouble*     m_all_bars_equity;
   CArrayDouble*     m_open_position_bars_equity;
   CArrayDouble*     m_trade_equity;

   CArrayDouble*     m_all_bars_returns;
   CArrayDouble*     m_open_position_bars_returns;
   CArrayDouble*     m_trade_returns;

   int               ProcessHistory(void);
   void              CalculateReturns(CArrayDouble &r,CArrayDouble &e);

public:
                     CReturns(void);
                    ~CReturns(void);

   void              OnNewTick(void);

   bool              GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[]);
   bool              GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[]);
  };



returns.mqh定义了一个枚举，用于确定返回序列的类型。ENUM_RETRNS_ALL_BARS为测试周期的所有柱定义一系列逐柱收益。ENUM_RETRNS_POSITION_OPEN_BARS是一系列返回值，构成一个仓位开启时柱形图的逐柱收益，ENUM_RETRURNS_TRADES仅定义已完成交易的回报系列，使用此选项不会收集逐柱信息。

//+------------------------------------------------------------------+
//| Enumeration specifying granularity of return                     |
//+------------------------------------------------------------------+
enum ENUM_RETURNS_TYPE
  {
   ENUM_RETURNS_ALL_BARS=0,//bar-by-bar returns for all bars
   ENUM_RETURNS_POSITION_OPEN_BARS,//bar-by-bar returns for bars with open trades
   ENUM_RETURNS_TRADES//trade returns
  };

使用CReturns类，可以通过GetEquityCurve（）方法检索定义权益曲线的一系列权益值。 

//+------------------------------------------------------------------+
//| get equity curve                                                 |
//+------------------------------------------------------------------+
bool CReturns::GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[])
  {
   int m_counter=0;
   CArrayDouble *equity;
   ZeroMemory(out_equity);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         m_counter=m_all_bars_equity.Total();
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         m_counter=m_open_position_bars_equity.Total();
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         m_counter=(m_trade_equity.Total()>1)?m_trade_equity.Total():ProcessHistory();
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(m_counter < 2)
      return false;
//---
   if(ArraySize(out_equity)!=m_counter)
      if(ArrayResize(out_equity,equity.Total()) < m_counter)
         return false;
//---
   for(int i=0; i<equity.Total(); i++)
      out_equity[i]=equity[i];
//---
   return(true);
//---
  }

类似地，GetReturns（）可以输出一系列返回。这两种方法都将所需的特定返回序列以及接收值的数组作为输入参数。

//+------------------------------------------------------------------+
//|Gets the returns into array                                       |
//+------------------------------------------------------------------+
bool CReturns::GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[])
  {
//---
   CArrayDouble *returns,*equity;
   ZeroMemory(out_returns);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         returns=m_all_bars_returns;
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         returns=m_open_position_bars_returns;
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         if(m_trade_equity.Total()<2)
            ProcessHistory();
         returns=m_trade_returns;
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(equity.Total() < 2)
      return false;
//--- calculate average returns
   CalculateReturns(returns,equity);
//--- return the mean return
   if(returns.Total()<=0)
      return false;
//---
   if(ArraySize(out_returns)!=returns.Total())
      if(ArrayResize(out_returns,returns.Total()) < returns.Total())
         return false;
//---
   for(int i=0; i<returns.Total(); i++)
      out_returns[i]=returns[i];
//---
   return(true);
//---
  }



示例

下面的 EA 交易代码显示了如何使用CReturns收集一系列收益。在我们的例子中，返回序列被保存到一个二进制文件中。尽管可以在OnTester中使用CBootstrap进行置信区间计算。在我们的例子中，我们将从一个单独的程序中分析这个系列。 

//+------------------------------------------------------------------+
//|                                           MovingAverage_Demo.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <Bootstrap.mqh>
#include <Files\FileBin.mqh>
#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
input ENUM_RETURNS_TYPE rtypes  = ENUM_RETURNS_ALL_BARS; // return types to record
input uint BootStrapIterations  = 10000;
input double BootStrapConfidenceLevel = 0.975;
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input bool   SaveReturnsToFile = true;
input string ReturnsFileName = "MovingAverage_Demo";

//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;
CReturns ma_returns;
#define MA_MAGIC 1234501
//+------------------------------------------------------------------+
//| Calculate optimal lot size                                       |
//+------------------------------------------------------------------+
double TradeSizeOptimized(void)
  {
   double price=0.0;
   double margin=0.0;
//--- select lot size
   if(!SymbolInfoDouble(_Symbol,SYMBOL_ASK,price))
      return(0.0);
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,price,margin))
      return(0.0);
   if(margin<=0.0)
      return(0.0);

   double lot=NormalizeDouble(AccountInfoDouble(ACCOUNT_MARGIN_FREE)*MaximumRisk/margin,2);
//--- calculate number of losses orders without a break
   if(DecreaseFactor>0)
     {
      //--- select history for access
      HistorySelect(0,TimeCurrent());
      //---
      int    orders=HistoryDealsTotal();  // total history deals
      int    losses=0;                    // number of losses orders without a break

      for(int i=orders-1; i>=0; i--)
        {
         ulong ticket=HistoryDealGetTicket(i);
         if(ticket==0)
           {
            Print("HistoryDealGetTicket failed, no trade history");
            break;
           }
         //--- check symbol
         if(HistoryDealGetString(ticket,DEAL_SYMBOL)!=_Symbol)
            continue;
         //--- check Expert Magic number
         if(HistoryDealGetInteger(ticket,DEAL_MAGIC)!=MA_MAGIC)
            continue;
         //--- check profit
         double profit=HistoryDealGetDouble(ticket,DEAL_PROFIT);
         if(profit>0.0)
            break;
         if(profit<0.0)
            losses++;
        }
      //---
      if(losses>1)
         lot=NormalizeDouble(lot-lot*losses/DecreaseFactor,1);
     }
//--- normalize and check limits
   double stepvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   lot=stepvol*NormalizeDouble(lot/stepvol,0);

   double minvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   if(lot<minvol)
      lot=minvol;

   double maxvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX);
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);
  }
//+------------------------------------------------------------------+
//| Check for open position conditions                               |
//+------------------------------------------------------------------+
void CheckForOpen(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- check signals
   ENUM_ORDER_TYPE signal=WRONG_VALUE;

   if(rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=ORDER_TYPE_SELL;    // sell conditions
   else
     {
      if(rt[0].open<ma[0] && rt[0].close>ma[0])
         signal=ORDER_TYPE_BUY;  // buy conditions
     }
//--- additional checking
   if(signal!=WRONG_VALUE)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),
                               SymbolInfoDouble(_Symbol,signal==ORDER_TYPE_SELL ? SYMBOL_BID:SYMBOL_ASK),
                               0,0);
     }
//---
  }
//+------------------------------------------------------------------+
//| Check for close position conditions                              |
//+------------------------------------------------------------------+
void CheckForClose(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- positions already selected before
   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])
      signal=true;
//--- additional checking
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);
     }
//---
  }
//+------------------------------------------------------------------+
//| Position select depending on netting or hedging                  |
//+------------------------------------------------------------------+
bool SelectPosition()
  {
   bool res=false;
//--- check position in Hedging mode
   if(ExtHedging)
     {
      uint total=PositionsTotal();
      for(uint i=0; i<total; i++)
        {
         string position_symbol=PositionGetSymbol(i);
         if(_Symbol==position_symbol && MA_MAGIC==PositionGetInteger(POSITION_MAGIC))
           {
            res=true;
            break;
           }
        }
     }
//--- check position in Netting mode
   else
     {
      if(!PositionSelect(_Symbol))
         return(false);
      else
         return(PositionGetInteger(POSITION_MAGIC)==MA_MAGIC); //---check Magic number
     }
//--- result for Hedging mode
   return(res);
  }
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit(void)
  {
//--- prepare trade class to control positions if hedging mode is active
   ExtHedging=((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE)==ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
   ExtTrade.SetExpertMagicNumber(MA_MAGIC);
   ExtTrade.SetMarginMode();
   ExtTrade.SetTypeFillingBySymbol(Symbol());
//--- Moving Average indicator
   ExtHandle=iMA(_Symbol,_Period,MovingPeriod,MovingShift,MODE_SMA,PRICE_CLOSE);
   if(ExtHandle==INVALID_HANDLE)
     {
      printf("Error creating MA indicator");
      return(INIT_FAILED);
     }
//--- ok
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   ma_returns.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
   double returns[],confidence[],params[];
   ArrayResize(confidence,1);
   confidence[0]=BootStrapConfidenceLevel;
//---
   double ret=0.0;
//---
   if(ma_returns.GetReturns(rtypes,returns))
     {
      CBootstrap minreturn(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,returns);

      if(minreturn.CalculateConfidenceIntervals(confidence))
        {
         ret=confidence[0];
         string fname=ReturnsFileName+"_"+_Symbol+".returns";
         CFileBin file;
         if(SaveReturnsToFile && file.Open(fname,FILE_WRITE|FILE_COMMON)!=INVALID_HANDLE)
            file.WriteDoubleArray(returns);

        }

     }
//---
   return(ret);
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }


脚本读取保存的数据并将其传递给CBootstrap的实例。测试统计信息由MeanReturns（）函数计算，该函数的签名与BootStrapFunction函数指针的签名匹配。使用值为0.9、0.95、0.975的数组调用CalculateConfidenceIntervals（），这对应于90%、95%和97.5%的置信区间。

//+------------------------------------------------------------------+
//|                                       ApproximateMeanReturns.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Math.mqh>
#include<Files\FileBin.mqh>
#include<Bootstrap.mqh>
//--- input parameters
input string   FileName="MovingAverage_Demo_EURUSD.returns";//returns file name
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input uint BootStrapIterations=10000;
input string BootStrapProbability="0.975,0.95,0.90";
//---
CBootstrap *meanreturns;
double logreturns[],bounds[],bootstraps[];
string sbounds[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int done=StringSplit(BootStrapProbability,StringGetCharacter(",",0),sbounds);
//---
   if(done)
     {
      ArrayResize(bounds,done);
      for(int i=0; i<done; i++)
         bounds[i]=StringToDouble(sbounds[i]);
      if(ArraySort(bounds))
         for(int i=0; i<done; i++)
            sbounds[i]=DoubleToString(bounds[i]);
     }
//---
   if(!done)
     {
      Print("error parsing inputs ", GetLastError());
      return;
     }
//---
   if(!LoadReturns(FileName,logreturns))
      return;
//---
   meanreturns=new CBootstrap(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,logreturns);
//---
   if(meanreturns.CalculateConfidenceIntervals(bounds))
     {
      for(int i=0; i<done; i++)
         Print(EnumToString(AppliedBoostrapMethod)," ",sbounds[i],": ","(",bounds[i*2]," ",bounds[(i*2)+1],")");
     }
//---
   delete meanreturns;
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Load returns from file                                           |
//+------------------------------------------------------------------+
bool LoadReturns(const string fname,double &out_returns[])
  {
   CFileBin file;
//---
   if(file.Open(fname,FILE_READ|FILE_COMMON)==INVALID_HANDLE)
      return false;
//---
   if(!file.ReadDoubleArray(out_returns))
     {
      Print("File read error ",GetLastError());
      return false;
     }
//---
   return true;
  }
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }
//+------------------------------------------------------------------+



在查看计算区间的最终输出之前，最好在自举测试统计数据的分布图上取一个峰值。这可以通过绘制通过GetBootStrapStatistics（）访问的数据来完成。

自举的分布



查看移动平均EA结果。我们看到OnTester返回了一个负数，这表明尽管单个测试显示了正面的结果，但未来的性能可能会恶化。-0.12是我们可以预期的最坏情况下的平均回报率。  

结果


不同置信区间的结果如下所示。 

ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.90000000: (-0.07040966776550685 0.1134376873958945)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.95000000: (-0.09739322056041048 0.1397669758772337)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.97500000: (-0.12438450770122121 0.1619709975134838)

此示例演示了移动平均EA基于预测概率的平均回报的计算。对于其他效能指标也可以使用相同的原理。尽管已经非常谨慎，基于比率的性能指标可能还是会存在问题。这是因为分母在度量的计算中。如果它变得非常小，我们最终会得到非常大的数字

确定使用这些方法来估计特定指标的未来性能的适用性的最佳方法是研究加强样本统计的分布。我们要注意的是任何重尾，应谨慎使用从具有重尾的分布中获得的结果。

让我们看一个估计相同EA的最坏情况锐度比的示例。这是通过重写传递给CBootstrap构造函数的函数指针参数的函数来实现的。

测试的结果再次表明，相对于单个测试结果，性能差得多。

夏普比率估算


结论

了解我们未来的效能范围可以帮助我们在策略选择方面做出更好的投资决策。尽管所演示的方法是基于教科书统计数据，但用户应该意识到其固有的局限性。

计算出的置信区间仅与它们所基于的数据一样好。如果计算中使用的样本不足，我们最终会出现一个经典的垃圾输入-垃圾输出场景。选择能够代表未来可能遇到的情况的适当样本总是很重要的。

文件名
描述
Mql5files\include\Bootstrap.mqh
 包含CBootstrap类的定义
Mql5files\include\Returns.mqh
 包含CReturns类的定义
Mql5files\include\UniformRandom.mqh
这是一个用于生成0和1之间的均匀分布数的类
Mql5files\scripts\ApproximateMeanReturns.mq5
 从策略测试器读取文件保存并计算项目平均回报置信区间的脚本
Mql5files\experts\ MovingAverage_Demo.mq5
 用于演示 CBootstrap 和 CReturns 应用的 EA 交易。


本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/13426

附加的文件 |
下载ZIP
MovingAverage_Demo.mq5 (11.34 KB)
ApproximateMeanReturns.mq5 (3.59 KB)
Bootstrap.mqh (12.73 KB)
Returns.mqh (9.71 KB)
UniformRandom.mqh (2.84 KB)
mql5files.zip (10.97 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

前往讨论
价格走势模型及其主要规定。（第 3 部分）：计算股票证券博弈的最优参数 价格走势模型及其主要规定。（第 3 部分）：计算股票证券博弈的最优参数
在作者基于概率论开发的工程方式框架内，找到了开立盈利仓位的条件，并计算了最优（利润最大化）止盈和止损值。
DRAKON可视化编程语言 - 面向MQL开发人员和客户的通信工具 DRAKON可视化编程语言 - 面向MQL开发人员和客户的通信工具
DRAKON是一种可视化编程语言，旨在简化来自不同领域的专家（生物学家、物理学家、工程师…）与俄罗斯太空项目（例如，Buran可重复使用航天器项目）程序员之间的互动。在这篇文章中，我将讨论DRAKON如何使算法的创建变得容易和直观，即使你从未遇到过代码，以及客户在订购交易机器人时如何更容易解释他们的想法，以及程序员如何在复杂函数中减少错误。
为EA交易提供指标的现成模板（第3部分）：趋势指标 为EA交易提供指标的现成模板（第3部分）：趋势指标
在这篇参考文章中，我们将研究趋势指标类别中的标准指标。我们将创建现成的模板，用于EA中的指标使用——声明和设置参数、指标初始化和析构，以及从EA中的指示符缓冲区接收数据和信号。
开发回放系统 — 市场模拟（第 20 部分）：外汇（I） 开发回放系统 — 市场模拟（第 20 部分）：外汇（I）
本文的最初目标不是涵盖外汇交易的所有可能性，而更是出于适配系统，如此您就至少可以执行一次市场回放。我们把模拟留待其它时刻。不过，如果我们没有跳价而仅有柱线的话，稍加努力，我们就可以模拟外汇市场中可能发生的交易。直到我们研究如何适配模拟器之前，情况一直如此。不经修改就尝试在系统内处理外汇数据会导致一系列错误。