Vergleich verschiedener Typen gleitender Durchschnitte im Handel

MetaTrader 5 — Indikatoren | 22 November 2017, 08:57

3 266

Aleksey Zinovik

Inhaltsverzeichnis

Vergleich verschiedener Typen gleitender Durchschnitte

Fazit

Einleitung

Gleitender Durchschnitt (Moving Average, MA) ist einer der beliebtesten technischen Indikatoren auf dem Devisenmarkt. Unser Ziel ist es, verschiedene MA zu betrachten und diese beim Handel unter gleichen Bedingungen für Einstieg und Ausstieg zu vergleichen.

Wir betrachten sieben Typen gleitender Durchschnitte: Moving Average, Adaptive Moving Average, Double Exponential Moving Average, Fractal Adaptive Moving Average, Triple Exponential Moving Average, Variable Index Dynamic Average und Nick Rypock Moving Average.

Typen gleitender Durchschnitte

In diesem Abschnitt werden eine kurze Beschreibung der für uns interessanten gleitenden Durchschnitte und deren Berechnungsformel angeführt.

Der technische Indikator Moving Average

Moving Average ist einer der beliebtesten technischen Indikatoren auf dem Devisenmarkt. Er zeigt den durchschnittlichen Preis eines Symbols für den angegebenen Zeitraum. Es gibt verschiedene Varianten des Indikators Moving Average:

Simple Moving Average (SMA) — einfacher gleitender Durchschnitt
Exponential Moving Average (EMA) — exponentieller gleitender Durchschnitt
Smoothed Moving Average (SMMA) — geglätteter gleitender Durchschnitt
Linear Weighted Moving Average (LWMA) — linear gewichteter gleitender Durchschnitt

Führen wir die Formel für die Berechnung jeder Variante des Indikators Moving Average an:

Variante des Moving Average Indikators	Berechnungsformel	Kommentar
Simple Moving Average (SMA)		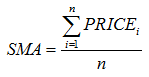n - Anzahl einzelner Perioden (z. B. wenn n=6 auf einem M15-Chart, wird der Indikator für die letzten 1,5 Stunden berechnet) PRICE — aktueller Preis, in den Einstellungen des Indikators kann man folgenden Varianten auswählen: high, low, open, close, median price ((high+Low)/2), typical price ((high+Low+Close)/3), weighted close ((high+Low+Close+Close)/4) oder Daten des vorherigen Indikators
Exponential Moving Average (EMA)		EMA(i-1) — vorheriger Wert F — Glättungsfaktor. Der Koeffizient F wird in einem Bereich von 0 bis 1 zufällig gewählt, zum Beispiel F=2/(n+1), wobei n - die Anzahl einzelner Perioden PRICE — aktueller Preise
Smoothed Moving Average (SMMA)		SMMA(i-1) — vorheriger Wert n — Anzahl einzelner Perioden PRICE — aktueller Preis
Linear Weighted Moving Average (LWMA)		PRICE — aktueller Preis n — Anzahl einzelner Perioden

Schauen wir uns verschiedene Varianten des Moving Average Indikators auf dem Preischart an. Auf der Abbildung 1 sind Varianten des Moving Average Indikators mit der Periode 12 dargestellt, der nach Schlusskursen berechnet wurde.

Der Moving Average Indikator

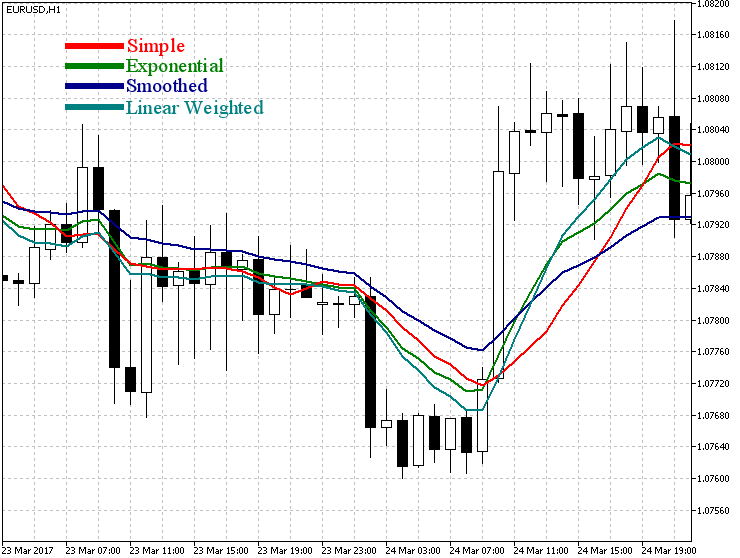
Abb. 1. Varianten des Moving Average Indiaktors

Wie man auf dem Bild sieht, schwankt Simple Moving Average ein wenig in der Seitwärtszone, was zur Erzeugung falscher Signale führen kann. Smoothed Moving Average, wie es aus dem Namen hervorgeht, sieht viel glätter aus. Exponential Moving Average und Linear Weighted Moving Average verhalten sich ungefähr gleich in der Seitwärtszone. Bei der Trendbewegung nähert sich Linear Weighted Moving Average den Preisen mehr als andere Linien und im Vergleich zu SMMA und EMA hängt nicht von seinem vorherigen Wert ab.

Technische Indikatoren basierend auf EMA

Der exponentielle gleitende Durchschnitt bildet die Grundlage für eine Reihe anderer technischer Indikatoren.

Indikator	Beschreibung	Erklärung der Berechnungsformel
Adaptive Moving Average (AMA)	ein MA, der wenig empfindlich gegenüber Rauschen ist. Im Vergleich zu anderen gleitenden Durchschnitten hat dieser Indikator minimale Verspätung bei der Erkennung von Trendwenden und Trendwechseln. Bei Schwankungen gibt es keine starken Fluktuationen, d.h. er erzeugt keine falschen Signale.	AMA(i-1) — vorheriger Wert des Indikators Price(i) — aktueller Preis SSC(i) — Glättungskonstante
Double Exponential Moving Average	Der Indikator wird für die Glättung des Preises oder der Werte anderer Indikatoren verwendet. Der wichtigste Vorteil besteht darin, dass der Indikator keine falschen Signale bei einer Preisbewegung im Zickzack erzeugt. Er hilft, Positionen bei einem starken Trend zu halten, und reduziert die Verzögerung des Signals im Vergleich zu einem einfachen EMA.	EMA(Price, n, i) — aktueller Wert des EMA vom Preis Price mit der Periode n EMA2(Price, n, i) = EMA(EMA(Price, n, i), n, i) — doppelter EMA vom Preis Price mit der Periode n
Triple Exponential Moving Average	Eine Synthese aus einem einzelnen, doppelten und dreifachen exponentiellen MA. Als Ergebnis ist die Verzögerung viel kleiner, als für jeden dieser MA einzeln. Der Indikator wird statt traditioneller gleitender Durchschnitte verwendet sowie für die Glättung eines Preischarts und der Werte anderer Indikatoren.	EMA(Price, n, i) — aktueller Wert des EMA vom Preis Price mit der Periode n EMA2(Price, n, i) = EMA(EMA(Price, n, i), n, i) — doppelter EMA vom Preis Price mit der Periode n EMA3(Price, n, i)=EMA(EMA2(Price, n, i), n, i) — dreifacher EMA vom Preis Price mit der Periode n
Fractal Adaptive Moving Average	Der Glättungsfaktor wird basierend auf der aktuellen fraktaler Dimension einer Preisreihe berechnet. Der Vorteil des Indikators besteht darin, dass er einem starken Trend folgt und sich in Konsolidierungsphasen verlangsamt.	Price(i) — aktueller Preis A(i) — aktueller Faktor der exponentiellen Glättung
Variable Index Dynamic Average	Dies ist ein EMA, dessen Periodenlänge sich dynamisch ändert und von der Volatilität auf dem Markt abhängt. Die Volatilität des Marktes wird mittels des Chande Momentum Oscillator (CMO) gemessen. Er misst die Relation zwischen den Summen der positiven und der negativen Inkremente innerhalb einer bestimmten Periode. Der CMO-Wert dient als Koeffizient für den Glättungsfaktor des EMA. Auf diese Weise werden zwei Parameter des Indikators eingestellt: die Periode des Oszillators CMO und die Glättungsperiode des EMA.	F=2/(n+1) — Glättungsfaktor, n — Anzahl einzelner Perioden ABS — mathematische Funktion, die den absoluten Wert einer Größe berechnet VIDYA(i-1) — vorheriger Wert des Indikators CMO(i) — Wert des CMO Oszillators
Nick Rypock Moving Average	Der Indikator ist nicht im Standard-Paket des MetaTrader 5 Terminals enthalten. Der Hauptvorteil ist, dass es fast keine Schwankungen bei im Seitwärtsmarkt gibt, der Indikator folgt einem Trend.	NRMA(i-1) — vorheriger Wert des Indikators Price(i) — aktueller Preis F=2/(n+1) — Glättungsfaktor, n — Anzahl einzelner Perioden NRratio - der Koeffizient des Glättungsfaktors

Unterscheide zwischen den Indikatoren und einem einfachen EMA

Vergleichen wir die oben betrachteten Indikatoren mit einem einfachen EMA. Auf der Abbildung 2 sehen wir:

Adaptive Moving Average (Periode — 12, schneller EMA — 2, langsamer EMA — 30, Verschiebung — 0)
Double Exponential Moving Average (Periode — 12, Verschiebung — 0)
Fractal Adaptive Moving Average (Periode — 12, Verschiebung — 0)
Exponential Moving Average (Periode — 12, Verschiebung — 0)
Triple Exponential Moving Average (Periode — 12, Verschiebung — 0)
Variable Index Dynamic Average (Periode CMO — 12, Periode EMA — 12, Verschiebung — 0)
Nick Rypock Moving Average (Methode der Durchschnittsbildung — SMA, Tiefe der Glättung — 3, Parameter der Glättung — 15 (wird nicht für SMA verwendet), Kf — 1, Fast — 12, Sharp — 2, horizontale und vertikale Verschiebung — 0).

Alle Indikatoren basieren auf Close-Kursen.

AMA, DEMA, TEMA, FRAMA, VIDYA, NRMA, EMA

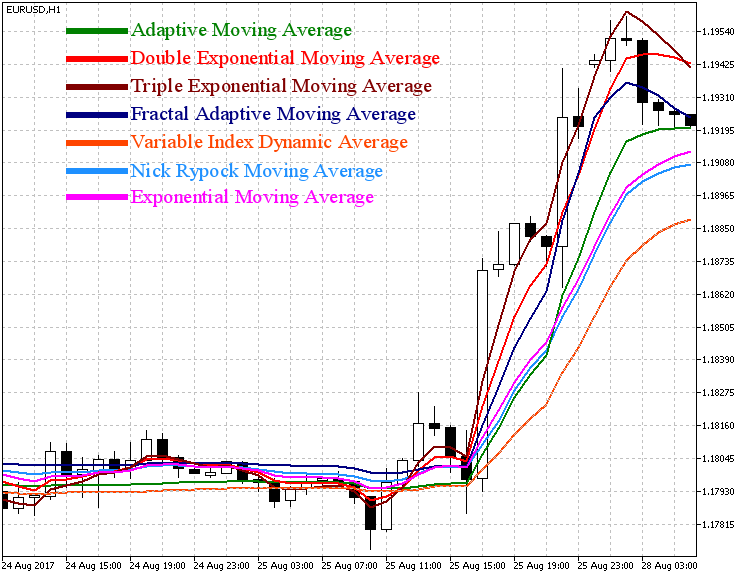
Abb. 2. Vergleich der Indikatoren, die auf dem exponentiellen gleitenden Durchschnitt (EMA) basieren

Wie man auf der Abbildung 2 sieht, wiederholen DEMA und TEMA im Vergleich zum einfachen EMA die Preisbewegung genauer, aber ihre Schwankungen in der Stagnation können falsche Handelssignale erzeugen. Weitere Indikatoren (FRAMA, AMA, VIDYA, NRMA) schwanken in der Stagnation fast nicht, sie reagieren nicht auf kleine Preisänderungen. Beim Trend verhalten sich fast alle Indikatoren gleich, TEMA und FRAMA haben schneller als alle anderen auf die Trendwende reagiert.

Vergleich verschiedener Typen gleitender Durchschnitte

Vergleichen wir die oben angeführten technischen Indikatoren mittels einer Handelsstrategie unter gleichen Bedingungen für Einstieg und Ausstieg.

Beschreibung der Handelsstrategie

Für das Testen wurde eine einfache Strategie mit klaren Bedingungen für den Einstieg und Ausstieg aus dem Markt ausgewählt.

Bedingungen für den Einstieg in den Markt.

Vorläufiges Kaufsignal: die Indikatorlinie kreuzt den Körper einer "bullischen" Kerze. Weiter, wenn die Differenz zwischen dem aktuellen und dem vorherigen Wert des Indikators größer als der angegebene Parameter Growth factor ist (der Indikator steigt), öffnen wir eine Buy-Position.
Vorläufiges Verkaufssignal: die Indikatorlinie kreuzt den Körper einer "bärischen" Kerze. Wenn die Differenz zwischen dem vorherigen und dem aktuellen Wert des Indikators größer als der angegebene Parameter Growth factor ist (der Indikator sinkt), öffnen wir eine Sell-Position.

Bedingungen für den Ausstieg aus dem Markt:

beim Erreichen von TakeProfit oder StopLoss;
wenn eine Buy-Position offen ist, und die Indikatorlinie den Körper einer "bärischen" Kerze gekreuzt hat;
wenn eine Sell-Position offen ist, und die Indikatorlinie den Körper einer "bärischen" Kerze gekreuzt hat.

Auf den Abbildungen 3 und 4 sind Handelsbeipiele für diese Strategie angeführt.

Buy

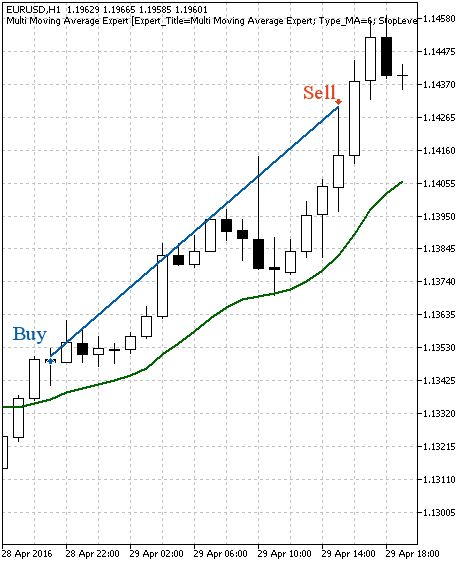
Abb. 3. Beispiel für eine Kaufposition

Sell

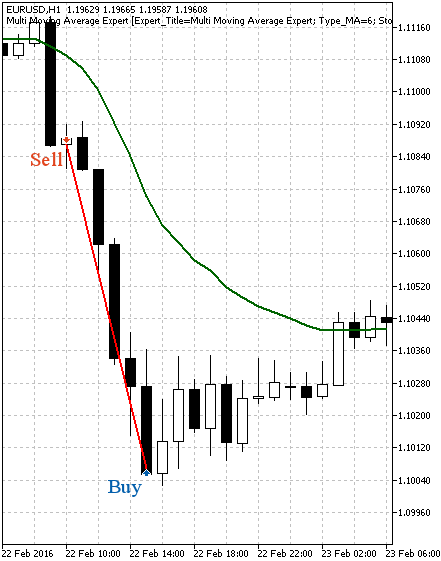
Abb. 4. Beispiel für eine Verkaufsposition

Eine ähnliche Strategie wurde im Moving Average Expert Advisor implementiert, welchen man im Navigator im MetaTrader 5 Terminal finden kann.

Erstellen des Expert Advisors

Schreiben wir einen Expert Advisor für den Handel nach der oben beschriebenen Strategie. Im Expert Advisor wird die Möglichkeit der Auswahl eines technischen Indikators implementiert: MA (mit den Methoden Simple, Exponential, Smoothed, Linear Weighted), DEMA, TEMA, FRAMA, AMA, VIDYA oder NRMA. Der ausgewählte Indikator wird im Chart dargestellt. Man kann auch die Inputparameter des Indikators angeben sowie TakeProfit und StopLoss, Lotgröße und den Growth factor setzen.

Die Bedingungen für Einstieg und Ausstieg überprüfen wir nur auf einem neuen Balken statt bei jedem Tick. Zuerst wird überprüft, ob es eine offene Position gibt (dafür wurde im Expert Advisor die Funktion SelectPosition erstellt). Wenn es keine offene Position gibt, prüfen wir die Bedingung für den Einstieg (die Funktion CheckForOpen), wenn sie vorhanden sind - prüfen wir die Bedingung für den Ausstieg (die Funktion CheckForClose).

Der komplette Code des Expert Advisors ist im Anhang zu finden (Datei MultiMovingAverageExpert.mq5). Betrachten wir nur die Implementierung der Bedingungen für Einstieg und Ausstieg. Die Bedingungen für den Einstieg werden in der Funktion CheckForOpen wie folgt überprüft:

   if(rt[0].open>ma[0] && rt[0].close<ma[0])               //Prüfung, ob der Körper einer "bärischen" Kerze gekreuzt wird
     {
      if(BuyCross)
         BuyCross=false;                                   //heben wir die vorläufige Bedingung für den Kauf auf (wenn die Indikatorlinie vorher eine "bullischen" Kerze gekreuzt hat)
      SellCross=true;                                      //setzen wir eine vorläufige Bedingung für den Verkauf
     }
   else
   if(rt[0].open<ma[0] && rt[0].close>ma[0])               //Prüfung, ob der Körper einer "bullischen" Kerze gekreuzt wird
     {
      if(SellCross)
         SellCross=false;                                 //heben wir die vorläufige Bedingung (wenn die Indikatorlinie vorher eine "bärische" Kerze gekreuzt hat) auf
      BuyCross=true;                                      //setzen wir eine vorläufige Bedingung für den Kauf
     }
   if(SellCross && ma[0]>ma[1] && ma[0]-ma[1]>GFactor)
     {
      signal=ORDER_TYPE_SELL;                             //wenn der Indikator sinkt, tritt die Bedingung für den Verkauf auf
      SellCross=false;                                    // heben wir die vorläufige Bedingung für den Verkauf auf
     }
   else
   if(BuyCross && ma[1]>ma[0] && ma[1]-ma[0]>GFactor)
     {
      signal=ORDER_TYPE_BUY;                             // wenn der Indikator steigt, tritt die Bedingung für den Kauf auf
      BuyCross=false;                                    //heben wir die vorläufige Bedingung für den Kauf auf
     }

Im Array rt[] werden historische Kursdaten gespeichert
Im Array ma[] — Werte des Indikators.
rt[0].close, rt[0].open — Wert des vorherigen Close/Open
ma[0] — vorheriger Wert des Indikators
ma[1] — aktueller Wert des Indikators.
GFactor — Wachstumsfaktor des Indikators.
Die Variable signal wird weiter für die Bildung einer Handelsanfrage verwendet.

Die Bedingungen werden in der Funktion CheckForClose wie folgt überprüft:

   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])       //wenn es eine offene Kaufposition gibt und
                                                                                    //die Linie des Indikators den Körper einer "bärischen" Kerze kreuzt 
      signal=true;                                                                  //wird ein Signal zum Schließen des Trades erzeugt
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])      //wenn es eine offene Verkaufsposition gibt und
                                                                                    //die Linie des Indikators den Körper einer "bullischen" Kerze kreuzt  
      signal=true;                                                                  //wird ein Signal zum Schließen des Trades erzeugt
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);                                         //den Trade schließen
     }

Testergebnisse des Expert Advisors

Der Expert Advisor wird auf den Währungspaaren EURUSD, GBPUSD, USDJPY, USDCAD, AUDUSD, im Zeitrahmen H1 getestet. TakeProfit — 80 Punkte, StopLoss — 50 Punkte, Lotgröße 0.1, Einlage — 10 000 USD, Testmodus — alle Ticks, Hebel 1:100, fünfstellige Kurse, Server: MetaQuotes-Demo.

Das Testen wurde für eine Periode von 01.01.2016 bis zum 09.09.2017 durchgeführt.

Für jeden Indikator wurden die Periode (Änderungsbereich 5 — 50, Schrittweite 1) und der Growth factor (Änderungsbereich 0,0001 — 0,0001, Schrittweite 0,001) optimiert.

Für Variable Index Dynamic Average wurde die EMA Periode (als Periode für die Berechnung des Indikators) und die Periode des CMO Oszillators (Änderungsbereich 5 — 50, Schrittweite 1) optimiert.

Für Nick Rypock Moving Average wurde der Parameter Fact optimiert, der die Berechnungsperiode des Indikators festlegt.

Die Indikatorenwerte wurden anhand Schlusskursen ohne horizontale und vertikale Verschiebung berechnet. Einige Indikatoren haben zusätzliche Parameter:

Bezeichnung des gleitenden Durchschnitts	Werte der Parameter
Adaptive Moving Average	Periode des schnellen EMA — 2 Periode des langsamen EMA — 30
Nick Rypock Moving Average	Methode der Durchschnittsbildung — SMA Glättungstiefe — 3 Glättungsparameter — 15 (wird nicht bei der Mittelungmethode SMA verwendet) KF=1 Sharp=2

Testergebnisse auf EURUSD

Die Ergebnisse des Testens auf dem Währungspaar EURUSD (die Varianten mit dem größten Nettogewinn) sind unten in der Tabelle angeführt:

Bezeichnung des gleitenden Durchschnitts	Zu optimierende Parameter und deren Werte	Anzahl der Trades	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity
Moving Average (Methode der Durchschnittsbildung Simple)	Periode —15, Growth factor — 0.0002	383	1309.82	1.32	3.14	0.1	397.29 (3.81%)	417.26 (3.99%)
Moving Average (Methode der Durchschnittsbildung Exponential)	Periode — 11, Growth factor — 0.0003	405	1109.72	1.22	3.02	0.08	346.35 (3.39%)	367.45 (3.6%)
Moving Average (Methode der Durchschnittsbildung Smoothed)	Periode — 6, Growth factor — 0.0003	405	1109.72	1.22	3.02	0.08	346.35 (3.39%)	367.45 (3.6%)
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	Periode — 22, Growth factor — 0.0002	351	1505.35	1.34	3.65	0.11	383.71 (3.41%)	412.88 (3.91%)
Adaptive Moving Average	Periode — 14, Growth factor — 0.0001	384	1024.19	1.19	1.63	0.07	600.06 (5.41%)	627.36 (5.64%)
Double Exponential Moving Average	Periode — 28, Growth factor — 0.0003	366	1676.43	1.39	3.49	0.12	460.33 (4.39%)	481.03 (4.58%)
Triple Exponential Moving Average	Periode — 44, Growth factor — 0.0002	482	1842.81	1.35	5.31	0.11	321.07 (3.14%)	347.27 (3.39%)
Fractal Adaptive Moving Average	Periode — 16, Growth factor — 0.0007	174	766.52	1.37	2.69	0.12	252.4 (2.5%)	285.08 (2.78%)
Variable Index Dynamic Average	EMA Periode— 12, CMO Periode — 2, Growth factor — 0.0003	333	1237.31	1.26	2.86	0.09	385.44 (3.43%)	432.81 (3.84%)
Nick Rypock Moving Average	Fact — 15, Growth factor — 0.0001	295	1669.62	1.42	4.14	0.14	376.22 (3.5%)	403.52 (3.75%)

Anhand der Testergebnisse kann man folgende Schlussfolgerungen ziehen:

Den höchsten Nettogewinn und Erholungsfaktor zeigte Triple Exponential Moving Average, aber die anderen Werte sind nicht die höchsten. Gute Ergebnisse lieferten auch Double Exponential Moving Average und Nick Rypock Moving Average.
Die schlechtesten Werte für Profitabilität, Erholungsfaktor und Sharpe-Ratio sowie den größten Rückgang von Kontostand und Equity wies Adaptive Moving Average auf.

Um den Vergleich der Testergebnisse besser zu veranschaulichen, normalisieren wir die Werte des Nettogewinns, der Profitablität, des Sharpe-Ratio, des Erholungsfaktors und der maximalen Rückgänge von Kontostand und Equity nach der folgenden Formel:

wobei:

nValue — normalisierter Wert des Parameters in einem Bereich von 0 bis 1,
Value — aktueller Wert des Parameters,
MaxValue — maximaler Wert des Parameters,
MinValue — minimaler Wert des Parameters.

Die Ergebnisse sind in der Tabelle dargestellt (die besten sind in Gelb hervorgehoben, die schlechtesten - in Rot):

Bezeichnung des gleitenden Durchschnitts	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity	Summe der Werte ohne Rückgänge	Summe der Werte mit Rückgängen
Moving Average (Methode der Durchschnittsbildung Simple)	0.50479	0.56522	0.41033	0.42857	0.41676	0.38618	1.9089	1.10597
Moving Average (Methode der Durchschnittsbildung Exponential)	0.31887	0.13043	0.37772	0.14286	0.27024	0.24065	0.96988	0.459
Moving Average (Methode der Durchschnittsbildung Smoothed)	0.31887	0.13043	0.37772	0.14286	0.27024	0.24065	0.96988	0.459
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	0.68646	0.65217	0.54891	0.57143	0.3777	0.37338	2.45898	1.7079
Adaptive Moving Average	0.23941	0	0	0	1	1	0.23941	-1.76059
Double Exponential Moving Average	0.84541	0.86957	0.50543	0.71429	0.59808	0.57248	2.9347	1.76413
Triple Exponential Moving Average	1	0.69565	1	0.57143	0.19572	0.18169	3.26708	2.88787
Fractal Adaptive Moving Average	0	0.78261	0.28804	0.71429	0	0	1.78494	1.78494
Variable Index Dynamic Average	0.43742	0.29631	0.33361	0.27656	0.38267	0.43161	1.34419	0.52992
Nick Rypock Moving Average	0.83909	1	0.68207	1	0.35615	0.34603	3.52115	2.81897

Die Werte des maximalen Rückgangs von Kontostand und Equity werden beim Addieren in der letzten Spalte der Tabellemit einem negativen Vorzeichen genommen (je kleiner der Rückgang, desto besser die Strategie). Auf diese Weise lieferten Triple Exponential Moving Average, Nick Rypock Moving Average und Double Exponential Moving Average die besten Werte für unsere Strategie (in der Tabelle in Gelb hervorgehoben). Die Testergebnisse für TEMA, NRMA und DEMA sind auf den Abbildungen 5-10 dargestellt.

Grafik für Triple Exponential MA

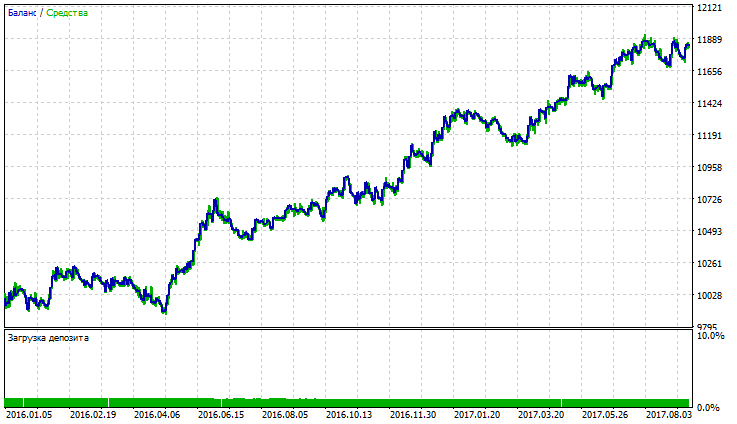
Abb. 5. Kontostand (Equity) Chart von Triple Exponential Moving Average

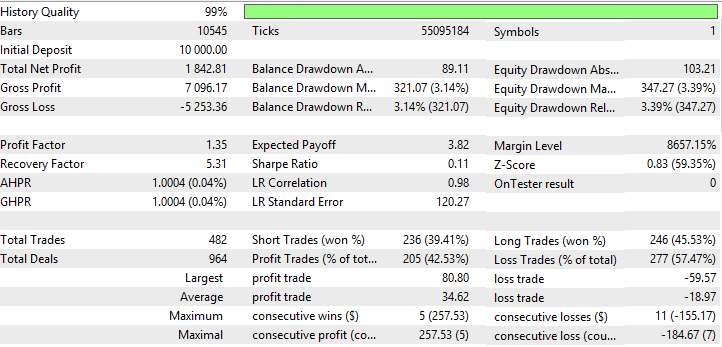
Abb. 6. Bericht für Triple Exponential Moving Average

Grafik für NRMA

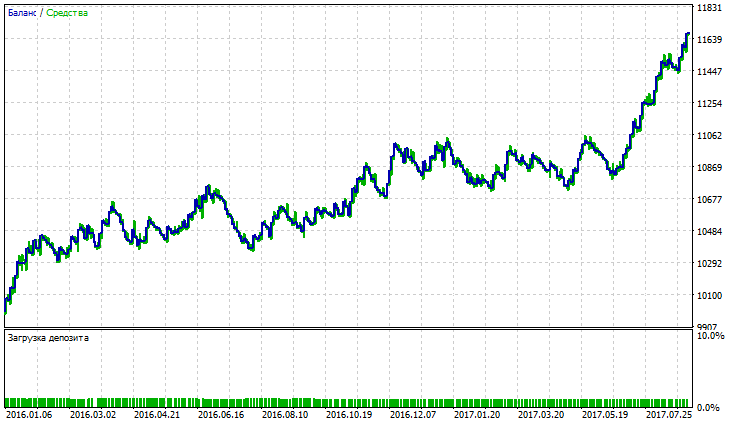
Abb. 7. Kontostand (Equity) Chart von Nick Rypock Moving Average

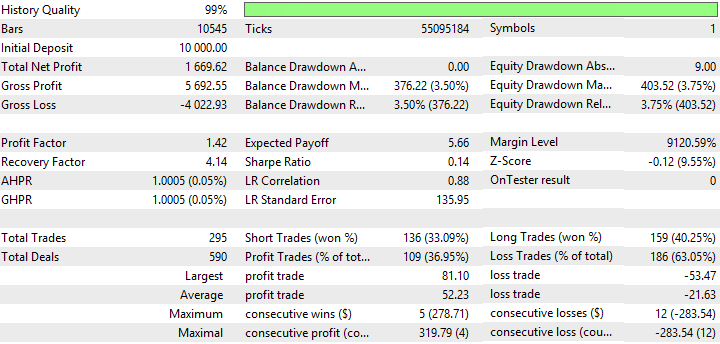
Abb. 8. Bericht für Nick Rypock Moving Average

DEMA Grafik

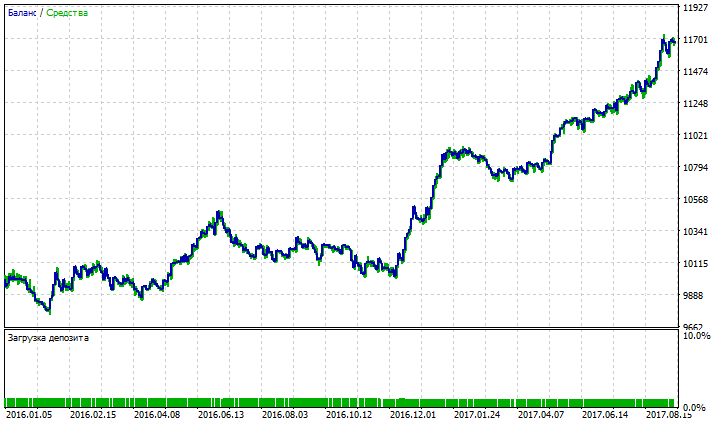
Abb. 9. Kontostand (Equity) Chart von Double Exponential Moving Average

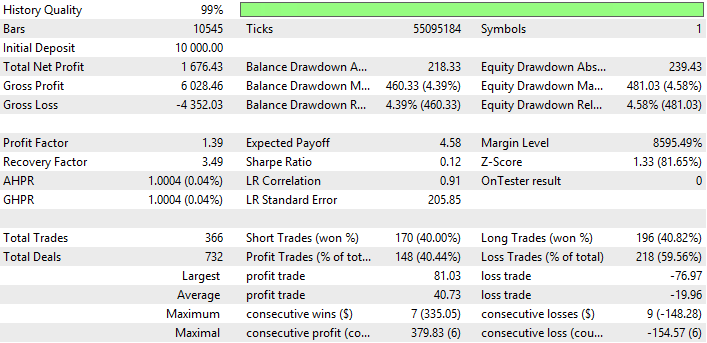
Abb. 10. Bericht für Double Exponential Moving Average

Aus den Abbildungen 5, 7 und 9 geht hervor, dass der Kontostand (Equity) Chart von NRMA und DEMA stabil aussieht, obwohl auch kleine Rückgänge aufweist. Auf dem Kontostand (Equity) Chart von NRMA ist ein Wachstum des Gewinns innerhalb der letzten 3 Handelsmonaten zu verzeichnen. Auf der dem Diagramm von DEMA beginnt das Wachstum des Gewinns (mit einem kleinen Rückgang) seit Dezember 2016.

Testergebnisse auf GBPUSD

Die Testerergebnisse auf dem Währungspaar GBPUSD sind in der Tabelle dargestellt:

Bezeichnung des gleitenden Durchschnitts	Zu optimierende Parameter und deren Werte	Anzahl der Trades	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity
Moving Average (Methode der Durchschnittsbildung Simple)	Periode —38, Growth factor — 0.0005	52	1013.56	1.98	3.82	0.32	207.04 (2.7%)	265.06 (2.65%)
Moving Average (Methode der Durchschnittsbildung Exponential)	Periode — 41, Growth factor — 0.0002	219	787.12	1.14	1.23	0.07	576.96 (5.21%)	639.44 (5.75%)
Moving Average (Methode der Durchschnittsbildung Smoothed)	Periode — 42, Growth factor — 0.0003	48	817.42	1.71	3.85	0.26	151.32 (1.51%)	212.24 (2.04%)
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	Periode — 50, Growth factor — 0.0001	328	1086.08	1.17	1.26	0.07	818.34 (7.45%)	861.04 (7.82%)
Adaptive Moving Average	Periode — 21, Growth factor — 0.001	100	1102.16	1.61	4.61	0.21	176.46 (1.71%)	239.12 (2.28%)
Double Exponential Moving Average	Periode — 23, Growth factor — 0.0007	263	1070.88	1.21	1.96	0.08	466.24 (4.42%)	547.58 (5.16%)
Triple Exponential Moving Average	Periode — 30, Growth factor — 0.0009	214	1443.90	1.39	4.11	0.14	322.76 (3.02%)	351.14 (3.28%)
Fractal Adaptive Moving Average	Periode — 38, Growth factor — 0.0001	819	651.54	1.05	0.85	0.02	747.98 (7.12%)	764.88 (7.28%)
Variable Index Dynamic Average	Periode EMA — 35, Periode CMO — 7, Growth factor — 0.0004	73	1606.98	1.99	5.20	0.34	251.94 (2.52%)	309 (3.08%)
Nick Rypock Moving Average	Fact — 45, Growth factor — 0.0005	53	978.30	1.80	3.86	0.29	200.64 (1.99%)	253.58 (2.51%)

Die normalisierten Ergebnisse sind in der Tabelle dargestellt (die besten Ergebnisse sind in Gelb hervorgehoben, die schlechtesten - in Rot):

Bezeichnung des gleitenden Durchschnitts	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity	Summe der Werte ohne Rückgänge	Summe der Werte mit Rückgängen
Moving Average (Methode der Durchschnittsbildung Simple)	0.3789	0.98929	0.68343	0.91799	0.08354	0.08141	2.96961	2.80467
Moving Average (Methode der Durchschnittsbildung Exponential)	0.1419	0.09351	0.08718	0.13465	0.63812	0.65845	0.45724	-0.8393
Moving Average (Methode der Durchschnittsbildung Smoothed)	0.17416	0.70302	0.69032	0.74598	0	0	2.31347	2.31347
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	0.45481	0.12036	0.09417	0.14629	1	1	0.81562	-1.1844
Adaptive Moving Average	0.47164	0.58999	0.86402	0.57613	0.03769	0.04143	2.50177	2.42265
Double Exponential Moving Average	0.4389	0.17142	0.25383	0.1936	0.47213	0.51686	1.05774	0.06875
Triple Exponential Moving Average	0.82931	0.36161	0.74969	0.36845	0.25702	0.21409	2.30906	1.83795
Fractal Adaptive Moving Average	0	0	0	0	0.89452	0.85179	0	-1.7463
Variable Index Dynamic Average	1	1	1	1	0.15085	0.14914	4	3.70001
Nick Rypock Moving Average	0.342	0.79826	0.69126	0.82047	0.07394	0.06372	2.65199	2.51433

Wie aus den Tabellen ersichtlich, liefert Variable Index Dynamic Average die besten Werte. Nick Rypock Moving Average und Moving Average mit der Methode der Durchschnittsbildung Simple haben auch gute Ergebnisse gezeigt. Die Testergebnisse für VIDYA, NRMA und SMA sind auf den Abbildungen 11-16 dargestellt.

Vidya_gbp_usd

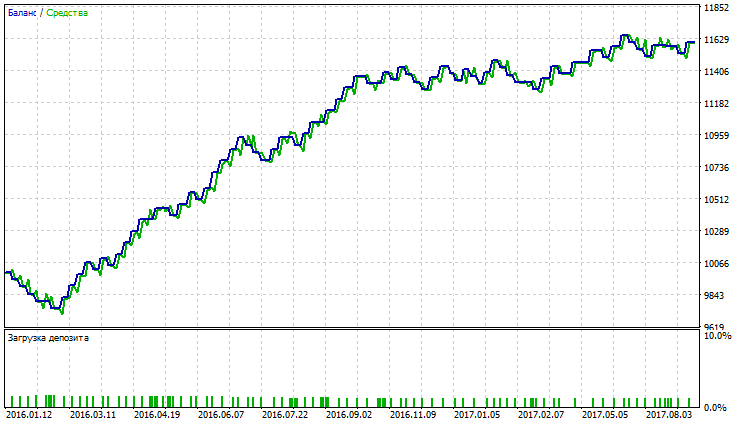
Abb. 11. Kontostand (Equity) Chart von Variable Index Dynamic Average

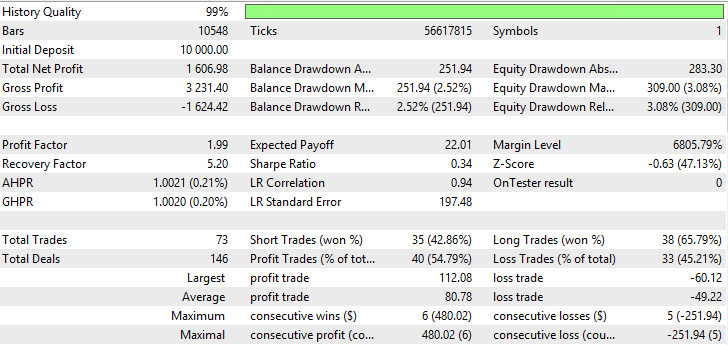
Abb. 12. Bericht für Variable Index Dynamic Average

NRMA GBPUSD

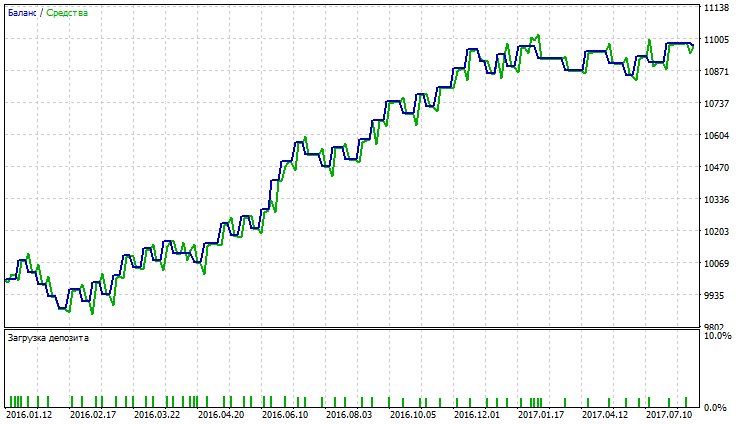
Abb. 13. Kontostand (Equity) Chart von Nick Rypock Moving Average

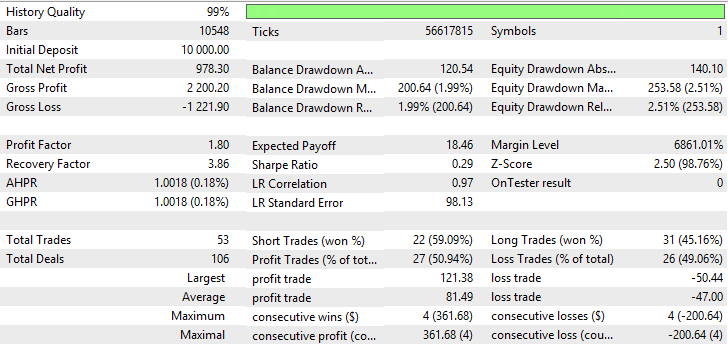
Abb. 14. Bericht für Variable Index Nick Rypock Moving Average

SMA GBPUSD

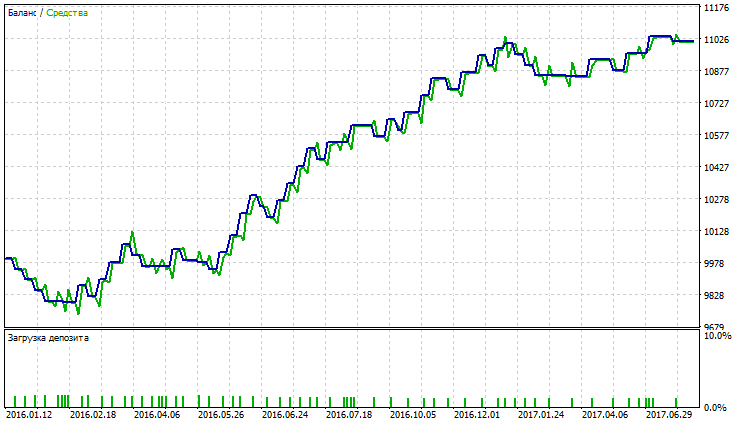
Abb. Kontostand (Equity) Chart von Simple Moving Average

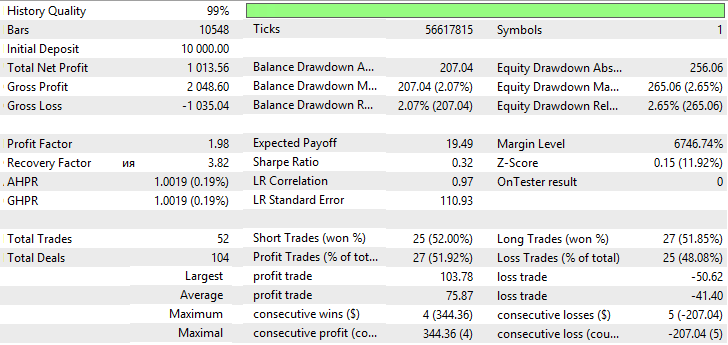
Abb. 16. Bericht für Simple Moving Average

Auf den Abbildungen 11-16 sehen wir, dass die Charts von VIDYA, NRMA und SMA ungefähr gleich aussehen, am Anfang ist ein kleiner Rückgang zu verzeichnen, weiter steigen die Kurven, die Anzahl der Trades bei VIDYA ist größer als bei NRMA und SMA. Der Anteil von Gewinntrades bei VIDYA ist größer als bei NRMA und SMA.

Testergebnisse auf USDJPY

Die Testergebnisse auf USDJPY sind in der Tabelle dargestellt:

Bezeichnung des gleitenden Durchschnitts	Zu optimierende Parameter und deren Werte	Anzahl der Trades	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity
Moving Average (Methode der Durchschnittsbildung Simple)	Periode —34, Growth factor — 0.0004	451	1784.95	1.32	3.69	0.1	465.52 (4.17%)	483.34 (4.32%)
Moving Average (Methode der Durchschnittsbildung Exponential)	Periode — 42, Growth factor — 0.0007	465	1135.23	1.20	2.21	0.07	461.52 (4.08%)	514.61 (4.53%)
Moving Average (Methode der Durchschnittsbildung Smoothed)	Periode — 33, Growth factor — 0.0008	372	1702.94	1.36	5.15	0.12	296.57 (2.58%)	330.6 (2.87%)
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	Periode — 50, Growth factor — 0.0005	477	1892.24	1.33	4.66	0.10	384.06 (3.68%)	406.1 (3.88%)
Adaptive Moving Average	Periode — 46, Growth factor — 0.0006	403	1460.51	1.26	2.56	0.09	527.75 (4.77%)	569.67 (5.13%)
Double Exponential Moving Average	Periode — 18, Growth factor — 0.001	1062	1459.18	1.15	3.55	0.05	366.24 (3.30%)	410.56 (3.69%)
Triple Exponential Moving Average	Periode — 50, Growth factor — 0.0003	657	1115.86	1.15	1.87	0.05	537.18 (4.68%)	597.71 (5.18%)
Fractal Adaptive Moving Average	Periode — 24, Growth factor — 0.0008	1030	615.92	1.06	0.8	0.02	734.03 (6.58%)	766.01 (6.85%)
Variable Index Dynamic Average	Periode EMA — 18, Periode CMO — 42, Growth factor — 0.001	238	2338.68	1.64	5.14	0.21	417.66 (3.62%)	454.69 (3.93%)
Nick Rypock Moving Average	Fact — 28, Growth factor — 0.0002	435	1465.32	1.27	3.00	0.09	456.65 (4.02%)	488.7 (4.29%)

Die normalisierten Ergebnisse sind in der Tabelle dargestellt (die besten Ergebnisse sind in Gelb hervorgehoben, die schlechtesten - in Rot):

Bezeichnung des gleitenden Durchschnitts	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity	Summe der Werte ohne Rückgänge	Summe der Werte mit Rückgängen
Moving Average (Methode der Durchschnittsbildung Simple)	0.67858	0.45316	0.66457	0.4324	0.38621	0.3508	2.22871	1.49171
Moving Average (Methode der Durchschnittsbildung Exponential)	0.30144	0.25001	0.32251	0.25216	0.37706	0.42261	1.12612	0.32645
Moving Average (Methode der Durchschnittsbildung Smoothed)	0.63098	0.51885	1	0.50010	0	0	2.64993	2.64993
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	0.74086	0.46535	0.88693	0.42881	0.2	0.1734	2.52195	2.14855
Adaptive Moving Average	0.49025	0.34559	0.40481	0.36951	0.52846	0.54907	1.61017	0.53264
Double Exponential Moving Average	0.48948	0.15054	0.63263	0.14711	0.15926	0.18364	1.41976	1.07686
Triple Exponential Moving Average	0.2902	0.15141	0.2445	0.15928	0.55002	0.61347	0.84538	-0.3181
Fractal Adaptive Moving Average	0	0	0	0	1	1	0	-2
Variable Index Dynamic Average	1	1	0.99825	1	0.2768	0.285	3.99825	3.43645
Nick Rypock Moving Average	0.49305	0.36549	0.50479	0.37182	0.36593	0.36311	1.73515	1.00611

Wie aus den Tabellen ersichtlich, zeigen Variable Index Dynamic Average und Moving Average mit den Methoden der Durchschnittsbildung Smoothed und Linear Weighted die besten Ergebnisse. Die Werte des Nettogewinns, der Profitabilität und des Sharpe-Ratio von VIDYA übersteigen die von SMMA und LWMA, aber SMMA und LWMA weisen den kleinsten Rückgang von Kontostand und Equity auf. Die Testergebnisse für VIDYA, SMMA und LWMA sind auf den Abbildungen 17-22 dargestellt.

Vidya USDJPY

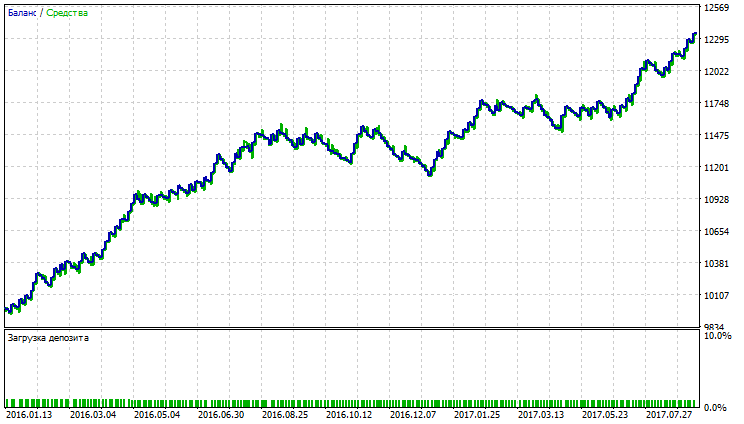
Abb. 17. Konstand (Equity) Chart von Variable Index Dynamic Average

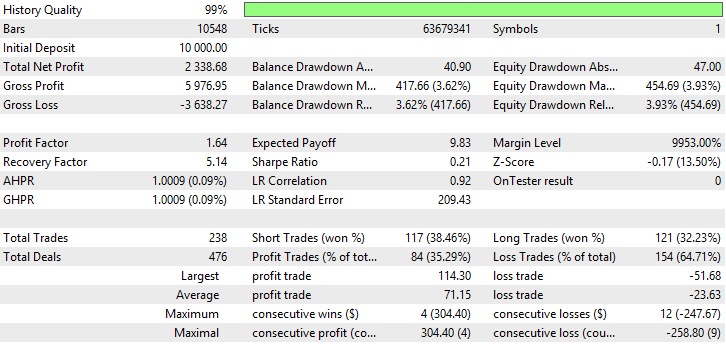
Abb. 18. Bericht für Variable Index Dynamic Average

LWMA

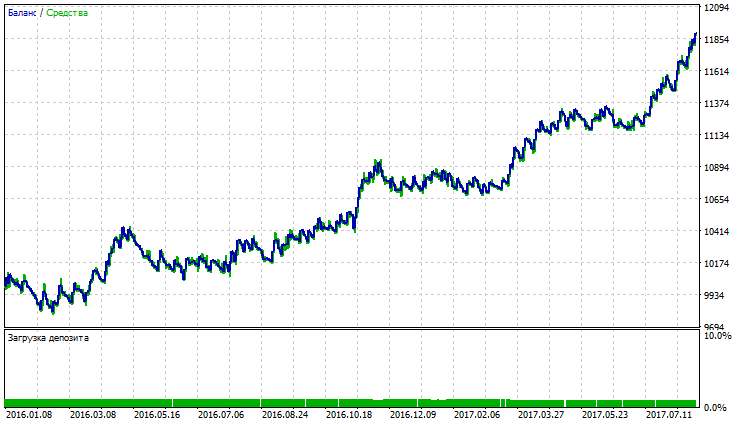
Abb. 19. Konstand (Equity) Chart von Linear Weighted Moving Average

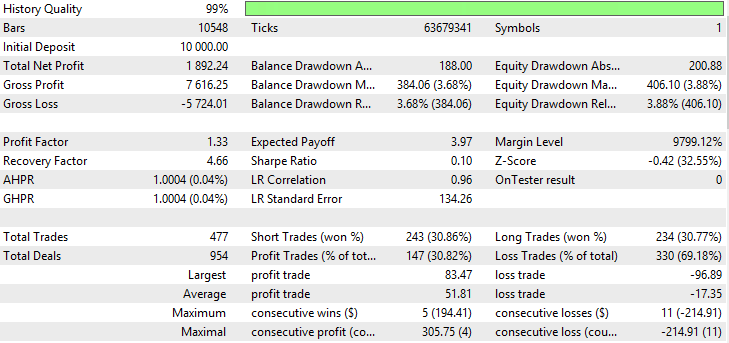
Abb. 20. Bericht für Linear Weighted Moving Average

SSMA

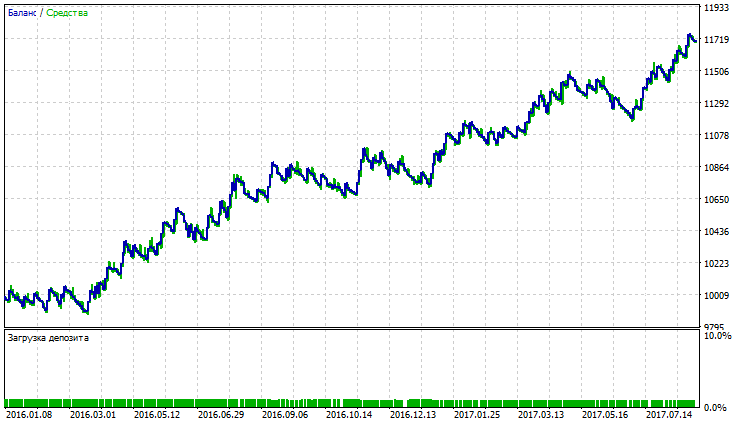
Abb. 21. Kontostand (Equity) Chart von Smoothed Moving Average

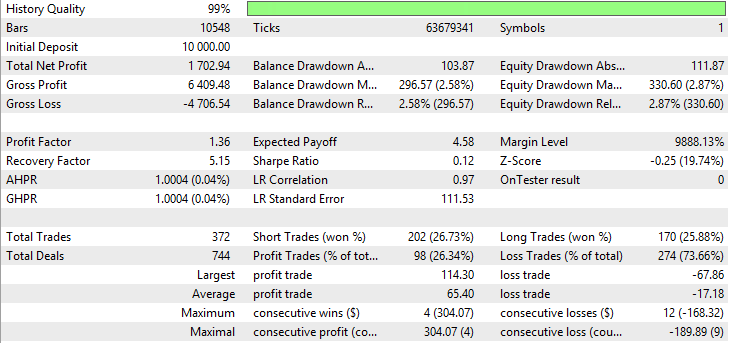
Abb. 22. Bericht für Smoothed Moving Average

Auf den Abbildungen 17-22 sehen wir, dass die Indikatoren trotz einem niedrigen Anteil der profitablen Trades einen hohen Nettogewinn liefern, das ist damit verbunden, dass USDJPY eine hohe Volatilität aufweist.

Testergebnisse auf USDCAD

Die Ergebnisse des Testens auf dem Währungspaar USDCAD sind in der Tabelle dargestellt:

Bezeichnung des gleitenden Durchschnitts	Zu optimierende Parameter und deren Werte	Anzahl der Trades	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity
Moving Average (Methode der Durchschnittsbildung Simple)	Periode —39, Growth factor — 0,0004	59	1101.44	2.30	7.11	0.40	133.44 (1.25%)	154.92 (1.45%)
Moving Average (Methode der Durchschnittsbildung Exponential)	Periode — 31, Growth factor — 0.0005	76	951.88	1.74	3.01	0.27	278.08 (2.56%)	316.57 (2.91%)
Moving Average (Methode der Durchschnittsbildung Smoothed)	Periode — 50, Growth factor — 0.0001	121	1262.26	1.57	3.07	0.22	343.76 (3.19%)	411.32 (3.81%)
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	Periode — 46, Growth factor — 0.0005	46	903.64	2.34	5.31	0.42	128.97 (1.22%)	170.05 (1.61%)
Adaptive Moving Average	Periode — 38, Growth factor — 0.0009	41	990.44	3.18	8.62	0.55	77.57 (0.73%)	114.96 (1.09%)
Double Exponential Moving Average	Periode — 44, Growth factor — 0.0007	73	941.93	2.07	5.33	0.32	137.28 (1.28%)	176.6 (1.64%)
Triple Exponential Moving Average	Periode — 49, Growth factor — 0.0009	76	559.18	1.62	3.28	0.20	122.21 (1.2%)	170.57 (1.66%)
Fractal Adaptive Moving Average	Periode — 15, Growth factor — 0.0009	185	504.26	1.27	2.44	0.09	197.12 (1.95%)	206.37 (2.04%)
Variable Index Dynamic Average	Periode EMA — 34, Periode CMO — 9, Growth factor — 0.0002	111	1563.99	1.86	6.17	0.30	185.64 (1.70%)	253.36 (2.32%)
Nick Rypock Moving Average	Fact — 41, Growth factor —0.0004	81	594.91	1.39	1.74	0.16	309.02 (2.88%)	342.16 (3.18%)

Die normalisierten Ergebnisse sind in der Tabelle dargestellt (die besten Ergebnisse sind in Gelb hervorgehoben, die schlechtesten - in Rot):

Bezeichnung des gleitenden Durchschnitts	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity	Summe der Werte ohne Rückgänge	Summe der Werte mit Rückgängen
Moving Average (Methode der Durchschnittsbildung Simple)	0.56352	0.53776	0.78104	0.67198	0.20989	0.13484	2.5543	2.20957
Moving Average (Methode der Durchschnittsbildung Exponential)	0.42239	0.24419	0.18441	0.37529	0.75326	0.68029	1.22628	-0.2073
Moving Average (Methode der Durchschnittsbildung Smoothed)	0.71528	0.15751	0.19342	0.26924	1	1	1.33545	-0.6646
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	0.37687	0.55859	0.5199	0.69827	0.1931	0.18589	2.15363	1.77465
Adaptive Moving Average	0.45878	1	1	1	0	0	3.45878	3.45878
Double Exponential Moving Average	0.413	0.42112	0.52277	0.48957	0.22431	0.20799	1.84645	1.41415
Triple Exponential Moving Average	0.05182	0.18256	0.22388	0.23681	0.1677	0.18764	0.69508	0.33974
Fractal Adaptive Moving Average	0	0	0.10249	0	0.44912	0.30844	0.10249	-0.6551
Variable Index Dynamic Average	1	0.30606	0.64482	0.43945	0.40599	0.467	2.39033	1.51734
Nick Rypock Moving Average	0.08554	0.06124	0	0.14059	0.86949	0.76664	0.28737	-1.3488

Aus der Tabelle wird deutlich, dass Adaptive Moving Average und Moving Average mit der Methode der Durchschnittsbildung Simple und Variable Index Dynamic Average die besten Werte zeigen. Adaptive Moving Average zeigt die besten Werte für Profitabilität, Erholungsfaktor und Sharpe-Ratio sowie hat den kleinsten Rückgang von Kontostand und Equity. Variable Index Dynamic Average weist den größten Nettogewinn auf, aber ihre anderen Werte sind nicht so hoch. Die Testergebnisse für AMA, SMA und VIDYA sind auf den Abb. 23-28 dargestellt.

AMA

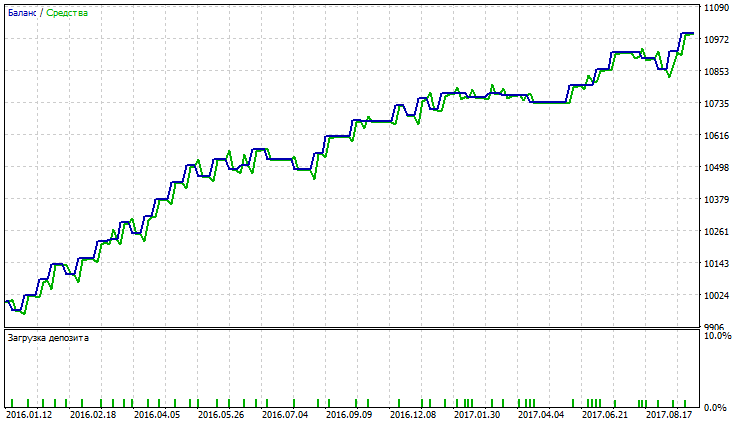
Abb. 23. Kontostand (Equity) Chart von Adaptive Moving Average

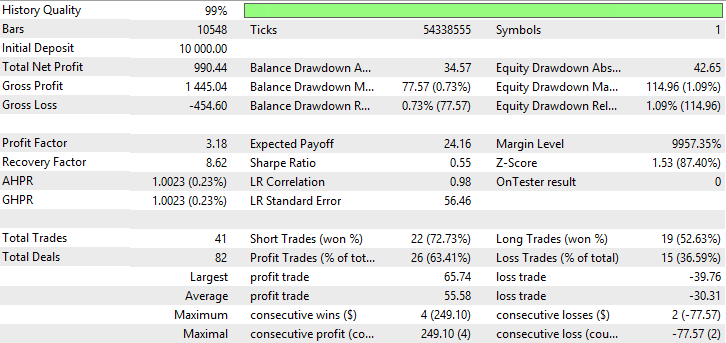
Abb. 24. Bericht für Adaptive Moving Average

SMA

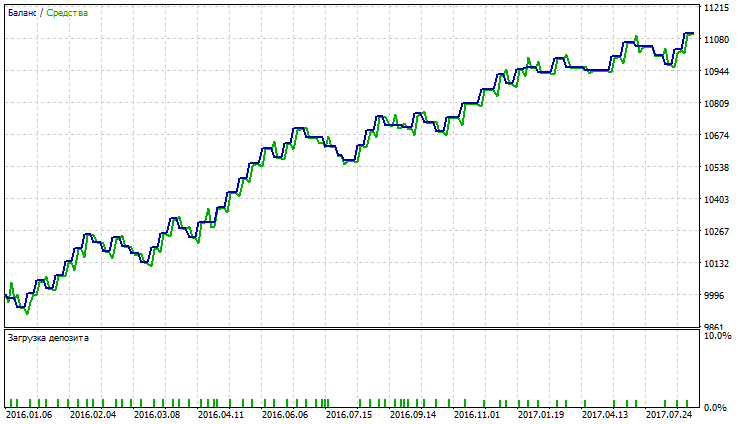
Abb. 25. Kontostand (Equity) Chart von Simple Moving Average

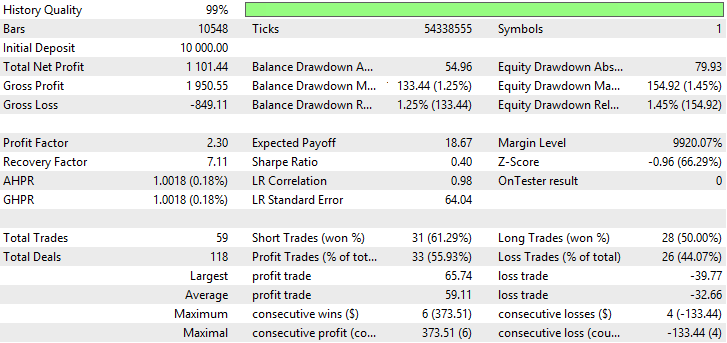
Abb. 26. Bericht für Simple Moving Average

VIDyA

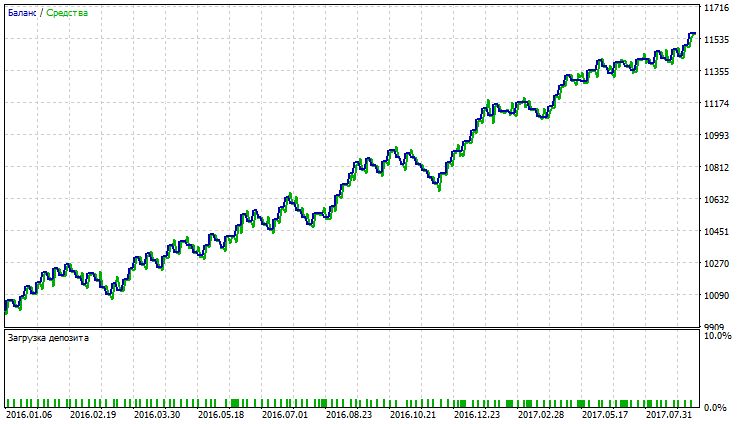
Abb. 27. Kontostand (Equity) Chart von Variable Index Dynamic Average

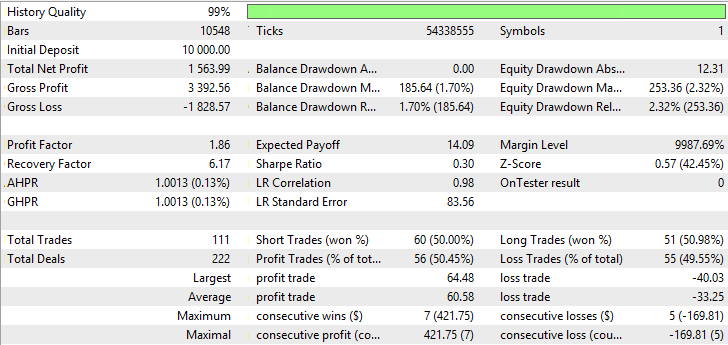
Abb. 28. Bericht für Variable Index Dynamic Average

Aus den Abbildungen 23-28 ist ersichtlich, dass AMA die kleinste Anzahl von Trades und den größten Anteil an profitablen Trades hat. SMA und VIDYA weisen einen größeren Profit durch eine größere Anzahl von Trades auf, dabei gibt es mehr profitable Trades als verlustbringende. Auf den Charts von AMA, SMA und VIDYA sind keine starken Rückgänge zu erkennen.

Testergebnisse auf AUDUSD

Die Testergebnisse auf AUDUSD sind in der Tabelle dargestellt:

Bezeichnung des gleitenden Durchschnitts	Zu optimierende Parameter und deren Werte	Anzahl der Trades	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity
Moving Average (Methode der Durchschnittsbildung Simple)	Periode —7, Growth factor — 0.0009	78	262.48	1.36	1.23	0.11	175.85 (1.74%)	214.18 (2.11%)
Moving Average (Methode der Durchschnittsbildung Exponential)	Periode — 40, Growth factor — 0.0004	24	652.88	2.62	2.82	0.47	206.76 (1.93%)	231.76 (2.16%)
Moving Average (Methode der Durchschnittsbildung Smoothed)	Periode — 21, Growth factor — 0.0004	24	651.18	2.61	2.81	0.47	206.76 (1.93%)	231.76 (2.16%)
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	Periode — 32, Growth factor — 0.0005	24	383.64	1.97	2.25	0.30	116.38 (1.11%)	170.24 (1.62%)
Adaptive Moving Average	Periode — 21, Growth factor — 0.0007	58	252.39	1.30	0.54	0.11	392.15 (3.80%)	464.47 (4.48%)
Double Exponential Moving Average	Periode — 40, Growth factor — 0.0006	39	296.15	1.70	1.53	0.20	156.62 (1.51%)	193.02 (1.86%)
Triple Exponential Moving Average	Periode — 21, Growth factor — 0.001	69	273.12	1.35	1.05	0.11	228.5 (2.20%)	259.71 (2.50%)
Fractal Adaptive Moving Average	Periode — 38, Growth factor — 0.0007	83	109.01	1.11	0.55	0.04	142.85 (1.42%)	196.47 (1.94%)
Variable Index Dynamic Average	Periode EMA — 26, Periode CMO — 5, Growth factor — 0.0006	23	697.59	2.99	2.96	0.53	151.35 (1.41%)	235.38 (2.19%)
Nick Rypock Moving Average	Fact — 22, Growth factor — 0.0006	34	509.27	1.90	2.55	0.28	94.58 (0.9%)	200 (1.89%)

Die normalisierten Ergebnisse sind in der Tabelle dargestellt (die besten Ergebnisse sind in Gelb hervorgehoben, die schlechtesten - in Rot):

Bezeichnung des gleitenden Durchschnitts	Nettogewinn	Profitabilität	Erholungsfaktor	Sharpe-Ratio	Maximaler Rückgang von Kontostand	Maximaler Rückgang von Equity	Summe der Werte ohne Rückgänge	Summe der Werte mit Rückgängen
Moving Average (Methode der Durchschnittsbildung Simple)	0.26075	0.12921	0.28183	0.13463	0.27311	0.14934	0.80642	0.38397
Moving Average (Methode der Durchschnittsbildung Exponential)	0.92404	0.80629	0.93942	0.86552	0.37699	0.20909	3.53527	2.94919
Moving Average (Methode der Durchschnittsbildung Smoothed)	0.92115	0.8006	0.93639	0.86226	0.37699	0.20909	3.5204	2.93433
Moving Average (Methode der Durchschnittsbildung Linear Weighted)	0.4666	0.45691	0.70658	0.52861	0.07326	0	2.1587	2.08544
Adaptive Moving Average	0.2436	0.10105	0	0.13347	1	1	0.47812	-1.5219
Double Exponential Moving Average	0.31795	0.31405	0.40942	0.31848	0.20849	0.07742	1.3599	1.07399
Triple Exponential Moving Average	0.27882	0.12776	0.20999	0.14014	0.45005	0.30408	0.75672	0.00259
Fractal Adaptive Moving Average	0	0	0.00473	0	0.16221	0.08915	0.00473	-0.2466
Variable Index Dynamic Average	1	1	1	1	0.19078	0.22139	4	3.58783
Nick Rypock Moving Average	0.68004	0.42124	0.82757	0.48773	0	0.10115	2.41659	2.31545

Wie aus der Tabelle hervorgeht, weisen Variable Index Dynamic Average und Moving Average mit den Methoden der Durchschnittsbildung Exponential und Smoothed die besten Ergebnisse auf. VIDYA zeigt die besten Werte für Nettogewinn, Profitabilität, Erholungsfaktor und Sharpe-Ratio. EMA und SMMA haben fast die gleichen Werte und die Anzahl von Trades. Die Testergebnisse für VIDYA, EMA und SMMA sind auf den Abb. 29-34 dargestellt.

VIDyA
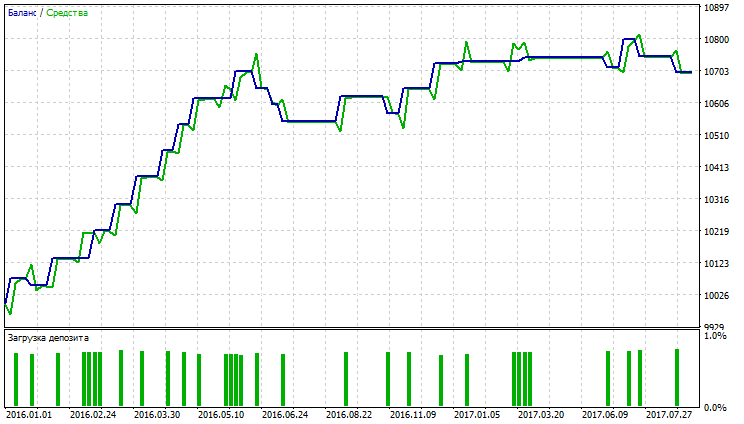
Abb. 29. Kontostand (Equity) Chart von Variable Index Dynamic Average

Abb. 30. Bericht für Variable Index Dynamic Average

EMA

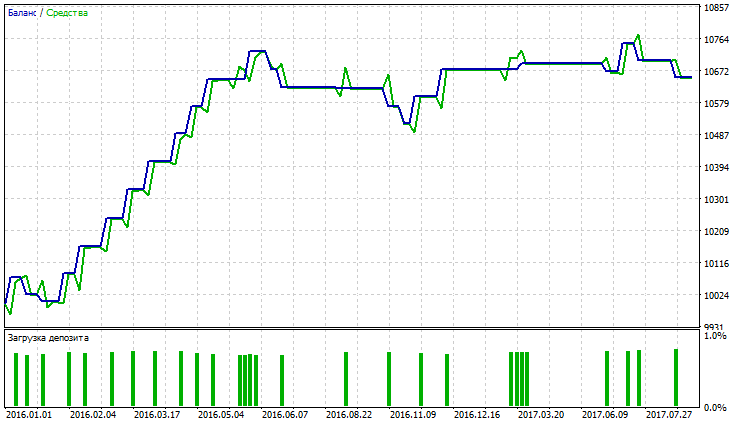
Abb. 31. Kontostand (Equity) Chart von Exponential Moving Average

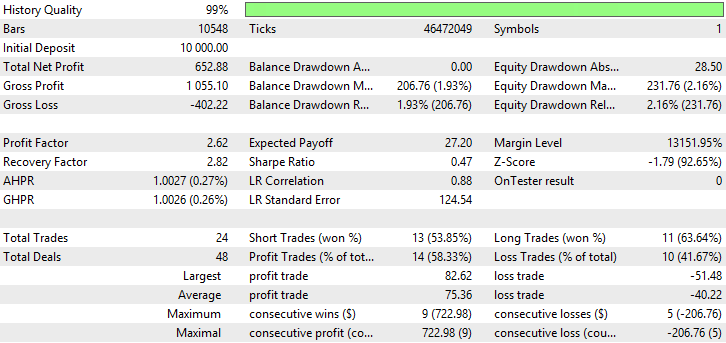
Abb. 32. Bericht für Exponential Moving Average

SSMA

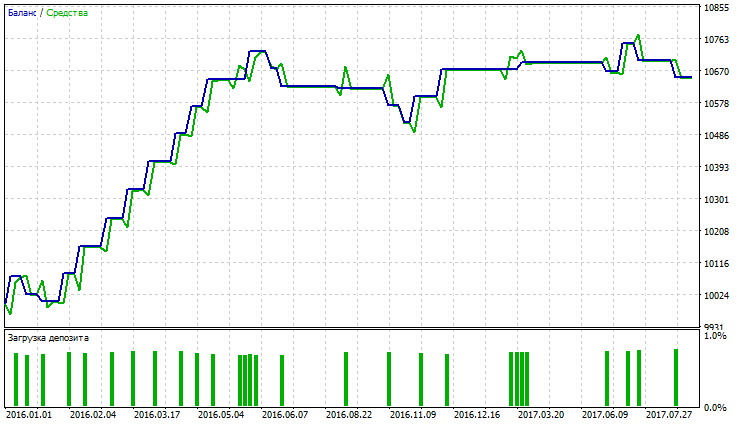
Abb. 33. Kontostand (Equity) Chart von Smoothed Moving Average

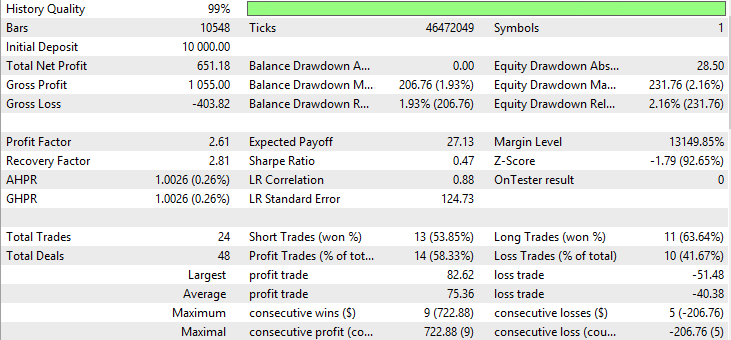
Abb. 34. Bericht für Smoothed Moving Average

Aus den Abbildungen 29-34 geht hervor, dass die Charts des Kontostandes (Equity) für VIDYA, EMA und SMMA ungefähr gleich sind; VIDYA weist mehr gewinnbringende Trades als EMA und SMMA auf. Das Währungsapaar AUDUSD weist eine niedrige Volatilität auf, was die erhaltenen Ergebnisse erklärt.

Aus den Testergebnissen auf EURUSD, GBPUSD, USDJPY, USDCAD und AUDUSD kann man folgende Schlussfolgerungen ziehen:

die besten Ergebnisse auf den Währungspaaren mit einer hohen (GBPUSD, USDJPY) und niedrigen (AUDUSD) Volatilität zeigte Variable Index Dynamic Average
die besten Ergebnisse auf USDCAD erzielte Adaptive Moving Average, aber auf EURUSD zeigt sie die schlechtesten Ergebnisse
die besten Ergebnisse auf EURUSD lieferte Triple Exponential Moving Average
die schlechtesten Ergebnisse auf GBPUSD, USDJPY, USDCAD und AUDUSD zeigte Fractal Adaptive Moving Average
gute Ergebnisse erzielte der Standardindikator Moving Average mit verschiedenen Mittelungsperioden.

Fazit

Wir betrachteten verschiedene gleitende Durchschnitte (MA (mit den Methoden Simple, Exponential, Smoothed, Linear Weighted), DEMA, TEMA, FRAMA, AMA, VIDYA und NRMA). Die Berechnung jedes gleitenden Durchschnitts wurde ausführlich beschrieben. Die gleitenden Durchschnitte wurden miteinander verglichen und unter gleichen Bedingungen für Einstieg und Ausstieg optimiert.

Basierend auf den erhaltenen Ergebnissen kann man folgende Schlussfolgerungen ziehen:

wenn man die Parameter eines der gleitenden Durchschnitten optimiert, kann man eine gewinnbringende Strategie erhalten;
die meisten gleitenden Durchschnitte sind Varianten des EMA Indikators;
der Hauptvorteil der gleitenden Durchschnitte auf Basis des EMA ist eine kleinere Anzahl falscher Signale in der Stagnation und eine schnellere Reaktion auf einen Trendwechsel;
die besten Ergebnisse zeigte der Indikator Variable Index Dynamic Average, er kann für Währungspaare sowohl mit einer hohen und als auch einer geringen Volatilität verwendet werden.

Der Artikel beschäftigt sich mit vier technischen Indikatoren (AMA, FRAMA, VIDYA, NRMA), die sich von EMA durch die Berechnungsmethode des Glättungsfaktors unterscheiden. Wahrscheinlich wird das jemandem einen Anstoß geben, eine neue effizientere Variante des EMA Indikators zu erstellen.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3791

Beigefügte Dateien |

ZIP herunterladen

MultiMovingAverageExpert.mq5 (38.17 KB)

MultiMovingAverageExpert.ex5 (81.08 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Mini Market Emulator oder ein manueller Strategie-Tester

Der Mini Market Emulator ist ein Indikator, der für die partielle Emulation des Handels am Terminal entwickelt wurde. Vielleicht möchte jemand damit "manuell" seine Strategie einer Marktanalyse oder des Handels testen.

Fuzzy-Logik in Handelsstrategien

Der Artikel befasst sich mit einem Beispiel für die Anwendung der Fuzzy-Logik, um ein einfaches Handelssystem unter Verwendung der Fuzzy-Bibliothek zu erstellen. Es werden Varianten zur Verbesserung des Systems durch Kombination von Fuzzy-Logik, genetischen Algorithmen und neuronalen Netzen vorgeschlagen.

Trianguläre Arbitrage

Der Artikel beschäftigt sich mit der populären Handelsmethode - dem Trianguläre Arbitrage. Wir analysieren hier das Thema so detailliert wie möglich, betrachten die positiven und negativen Aspekte der Strategie und entwickeln den fertigen Code für einen Expert Advisor.

Ein neuer Ansatz der Interpretation der klassischen und der versteckten Divergenz

Der Artikel untersucht die klassische Methode eine Divergenz zu erkennen und bietet eine zusätzliche Interpretation. Auf Basis dieser neuen Interpretation wurde eine Handelsstrategie entwickelt. Auch diese Strategie ist in diesem Artikel beschrieben.

Inhaltsverzeichnis

Einleitung

Typen gleitender Durchschnitte

Der technische Indikator Moving Average

Technische Indikatoren basierend auf EMA

Adaptive Moving Average (AMA)

Double Exponential Moving Average

Triple Exponential Moving Average

Fractal Adaptive Moving Average

Variable Index Dynamic Average

Nick Rypock Moving Average

Unterscheide zwischen den Indikatoren und einem einfachen EMA

Vergleich verschiedener Typen gleitender Durchschnitte

Beschreibung der Handelsstrategie

Erstellen des Expert Advisors

Testergebnisse des Expert Advisors

Fazit

Andere Artikel von diesem Autor