プライスアクション分析ツールキットの開発（第41回）：MQL5で統計的価格レベルEAを構築する

内容

• はじめに
• 戦略ロジック
• コード解説
• 結果
• 結論

はじめに

統計は、ノイズの多い市場データを測定可能で比較可能な量に変換するため、金融分析の中心的存在です。本記事では「Price Action Analysis Toolkit」の一貫として、この統計手法をローソク足に直接適用します。各バーを単なる情報の一つとして扱うのではなく、複数のバーを圧縮して再現可能な価格レベルや分布特徴に変換することで、市場の直近の動きをより明確に解釈できるようにします。

各ローソク足は、典型価格(TP: Typical Price)で要約できます。ここでは、典型価格をローソク足の主要3要素（高値、安値、終値）の算術平均として定義します。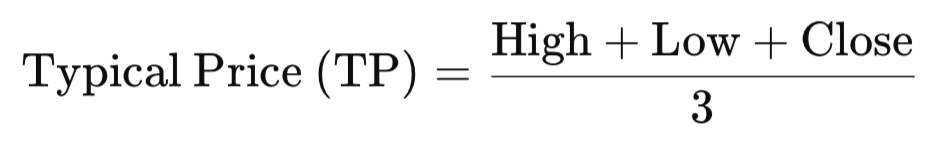

典型価格を用いることで平均値、中央値、最頻値、およびパーセンタイルレベルを算出することは不可欠です。最頻値は相場が最も集中する価格帯を示し、実務上のサポートやレジスタンスに対応することが多く、中央値は分布の頑健な中心を示し、価格が中央値を横切ることで方向性の変化を把握しやすくなります。平均値と派生するzスコアは大きな価格変動に敏感なバランスポイントとなり、ボラティリティ正規化されたシグナルに有用です。パーセンタイル(P25/P75)は価格変動の中央50%(IQR)を基準として、狭い範囲の保合いと広い分散を識別するのに役立ちます。つまり、典型価格に基づく統計は、統計的に意味があり、かつ日中の価格動向に直接関連する参照レベルを生成します。

本記事では、これらの指標をチャート上で実用的なシグナルに変換する方法を示します。水平参照線（平均、中央値、P25/P75、最頻値）として表示したり、ATRスケールの閾値として使用してブレイクアウトと反転を判別したり、zスコアシグナルエンジンの基礎として異常な価格変動をフラグ化します。今回紹介するKDE Level Sentinel EAは、再現性と使いやすさに重点を置いており、スナップショットで参照レベルを固定して将来の監視を可能にし、ラベルは安定的に配置され、重ならず、シグナルは対象価格に矢印として正確に描画されます。

続いて、各指標の数学的背景、MQL5における実装方法、EAの出力の解釈方法を学ぶことで、生のローソク足データから、明確で検証可能な取引仮説を構築できるようになります。

戦略ロジック

前述の通り、私たちは統計的手法をプライスアクションに適用しようとしており、すべての統計計算には典型価格を使用しています。典型価格は、ローソク足の高値、安値、終値を合計し、3で割ることで算出されます。これにより、取引範囲と終値のバランスを取り、単純な終値のみを用いる場合に比べて単発的なスパイクを平滑化し、より安定した系列を生成します。典型価格はローソク足内の極値を取り込むことで、始値を必要とせずに分布統計（平均、中央値、カーネル密度推定など）への入力を豊かにし、後続モデルの安定性とシグナル品質を向上させます。終値、HL/2、OHLC4などの代替指標と比較すると、典型価格は取引範囲と方向性の両方を適切に捉えた、プライスアクション統計分析に理想的な堅牢でコンパクトな入力値となります。

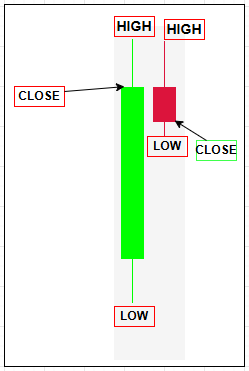
ここから、典型価格から導出される統計指標を説明します。各指標は時間に対する価格の振る舞いの異なる側面を浮き彫りにします。具体的には、中心傾向、ばらつき、頻度、構造などを理解するのに役立ちます。 

典型価格から得られる指標

• 平均値
• 中央値
• 最頻値
• 標準偏差
• 分散
• 範囲
• 歪度と尖度（オプション、上級）

次に、それぞれの指標を順に見ていきましょう。これにより、生のローソク足データがどのように意味のある価格レベルやプライスアクション分析を導くシグナルへと変換されるかを理解できます。

1. 平均値

平均は、サンプル内のすべての典型価格の中心的な値を表します。極端なスパイクには敏感ですが、価格が概ねどのあたりで推移しているかを把握する信頼できる概観を提供します。たとえば、ある人が3か月で1000ドル、1200ドル、1100ドルを稼いだ場合、平均給与は(1000+1200+1100)/3 = 1100ドルとなり、全体の所得水準を反映します。同様に、取引においても典型価格の平均は、市場が変動する平均的な価格帯を示します。

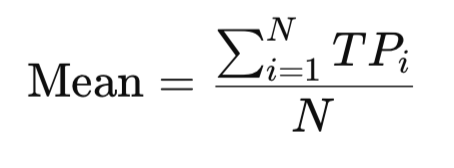
MQL5での実装

double Mean(const double &values[])
{
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += values[i];
   return sum / ArraySize(values);
}

2. 中央値

中央値は、順序付けされた典型価格の中間に位置する値です。平均値とは異なり、極端な高値や安値の影響を受けないため、中心傾向を示す堅牢な指標となります。たとえば、テストの点数が50、55、60、95、100の場合、中央値は60であり、実際のパフォーマンスの中間値を表します。取引においても、典型価格の中央値は、異常なスパイクに影響されずに価格のバランスの取れた中心を示します。

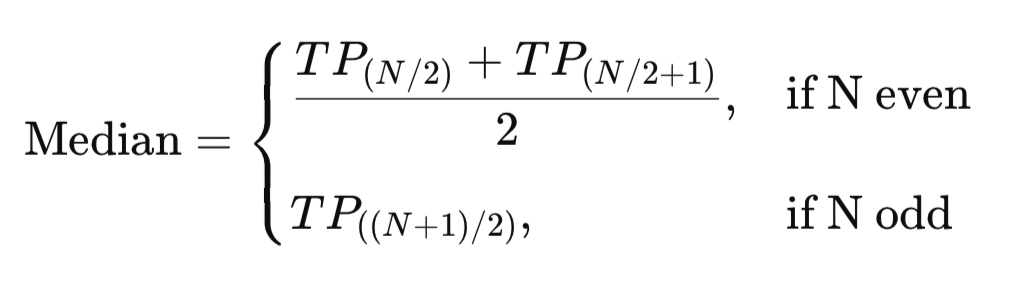
MQL5での実装

double Median(double &values[])
{
   ArraySort(values, WHOLE_ARRAY, 0, MODE_ASCEND);
   int size = ArraySize(values);
   if(size % 2 == 0)
      return (values[size/2 - 1] + values[size/2]) / 2.0;
   else
      return values[size/2];
}

3. 最頻値

最頻値は、データセット内で最も頻繁に出現する値を示し、自然なクラスタリングの傾向を把握するのに役立ちます。たとえば、靴のサイズが7、8、8、9、8、7、10、8、9、7の場合、最も多く出現するサイズは8であり、これが最頻値となります。同様に、取引においても典型価格の最頻値は、市場が最も長く滞在する価格帯を示し、強いサポートやレジスタンスのゾーンと一致することが多いです。

MQL5での実装

double Mode(const double &values[])
{
   double mode = values[0];
   int maxCount = 0;

   for(int i=0; i<ArraySize(values); i++)
   {
      int count = 0;
      for(int j=0; j<ArraySize(values); j++)
      {
         if(values[j] == values[i]) count++;
      }
      if(count > maxCount)
      {
         maxCount = count;
         mode = values[i];
      }
   }
   return mode;
}

4. 標準偏差

標準偏差は、各値が平均からどの程度離れているかを測定し、変動の大きさを示します。たとえば、2人が同じ平均歩数を記録しているとします。一方は7900、8000、8100歩、もう一方は2000、15,000、5000歩です。平均は両者ともほぼ8000歩ですが、後者のほうがはるかに変動が大きくなります。取引に応用すると、典型価格の標準偏差は、市場が落ち着いて安定しているか、あるいは変動が激しく不安定かを判別するのに役立ちます。

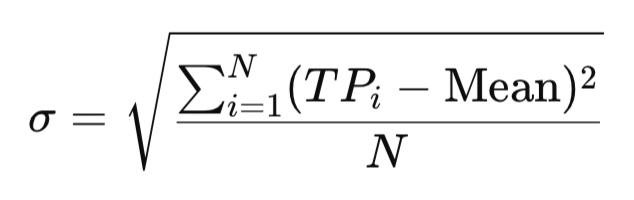
MQL5での実装

double StandardDeviation(const double &values[])
{
   double mean = Mean(values);
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += MathPow(values[i] - mean, 2);
   return MathSqrt(sum / ArraySize(values));
}

5. 分散

分散は標準偏差の二乗であり、値が平均からどの程度散らばっているかを二乗単位で定量化します。標準偏差ほど直感的ではありませんが、大きな偏差を強調し、異なる銘柄間でのボラティリティを比較するための一貫した基準を提供します。典型価格の文脈では、分散は価格がどの程度広く分布しているかを示し、市場の安定性を別の視点から把握することができます。

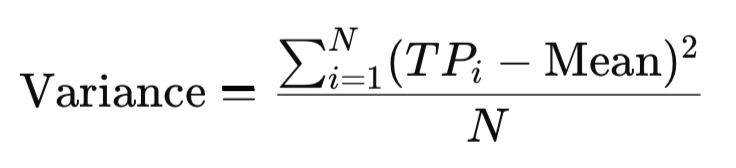
MQL5での実装

double Variance(const double &values[])
{
   double mean = Mean(values);
   double sum = 0.0;
   for(int i=0; i<ArraySize(values); i++)
      sum += MathPow(values[i] - mean, 2);
   return sum / ArraySize(values);
}

6. 範囲

範囲は、データセット内の最高値と最低値の差を示します。たとえば、週間の気温が20℃から35℃の範囲で変動する場合、範囲は15℃です。取引においては、典型価格(TP)の範囲が市場の値動きの幅を示し、トレーダーが狭い範囲での保ち合いと大きなスイングを素早く判別するのに役立ちます。

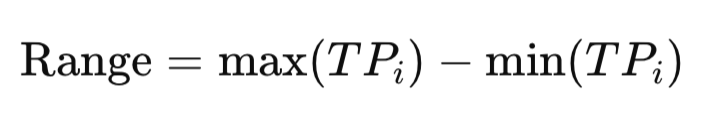
MQL5での実装

double Range(const double &values[])
{
   double minVal = values[ArrayMinimum(values)];
   double maxVal = values[ArrayMaximum(values)];
   return maxVal - minVal;
}

7. 歪度または尖度

歪度は分布の非対称性を測定します。

double Skewness(const double &values[])
{
   int n = ArraySize(values);
   double mean = Mean(values);
   double sd   = StandardDeviation(values);

   double sum = 0.0;
   for(int i=0; i<n; i++)
      sum += MathPow((values[i] - mean)/sd, 3);

   return (double)n / ((n-1)*(n-2)) * sum;
}

たとえば、従業員の大半が月収3,000ドルで、CEOが50,000ドルを稼いでいる会社を考えると、平均給与は高く引き上げられ、正の歪みが生じます。同様に、典型価格(TP)の歪度は価格が上方向または下方向の極端値に偏っているかを示し、市場構造における方向性の不均衡を捉える手がかりとなります。

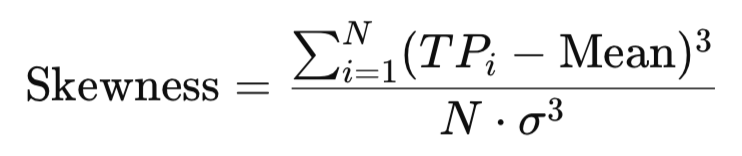
尖度は分布の「裾の厚さ」や極端な値が発生する可能性の度合いを評価します。たとえば、高速道路でほとんどの車が時速60〜70kmで走行している場合、尖度は低くなります。一方、通常はその範囲で走行しているが、時折時速20kmまで遅くなったり時速150kmまで急加速する場合、尖度は高くなります。

double Kurtosis(const double &values[])
{
   int n = ArraySize(values);
   double mean = Mean(values);
   double sd   = StandardDeviation(values);

   double sum = 0.0;
   for(int i=0; i<n; i++)
      sum += MathPow((values[i] - mean)/sd, 4);

   return ((double)n*(n+1) / ((n-1)*(n-2)*(n-3))) * sum
          - (3.0*MathPow(n-1,2) / ((n-2)*(n-3)));
}

取引において、典型価格(TP)の尖度が高い場合は、市場が大部分の時間は落ち着いているものの、突然の急激な値動きが発生しやすいことを示しています。

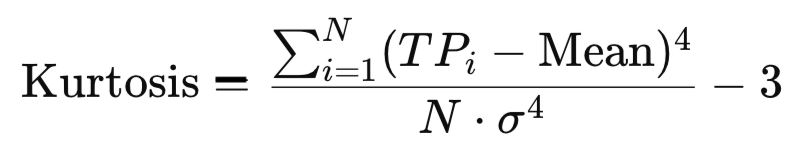
8. パーセンタイル（P25とP75）

パーセンタイルはデータセットを順位付きに分割し、値が分布内でどの位置にあるかを理解するのに役立ちます。第25パーセンタイル（P25）は典型価格の25％がその値以下にあるポイントを示し、第75パーセンタイル（P75）は75％がその値以下にあるレベルを示します。この2つの値は四分位範囲(IQR)を構成し、データの中央50％を表します。

double p25 = Percentile(values, 0.25);
double p75 = Percentile(values, 0.75);

Print("P25 = ", DoubleToString(p25, _Digits), 
      " | P75 = ", DoubleToString(p75, _Digits));

取引において、P25は価格活動の「下位クラスター」を示し、買い手が一貫して介入する水準を把握できます。一方、P75は「上位クラスター」を示し、売り手が支配的な水準を捉えます。この2つの境界を組み合わせることで、平均や中央値だけでは得られない市場の集中度をより精密に理解できます。IQRが狭い場合は保ち合いを示し、広い場合は市場の値動きが拡散していることを示します。

シグナル生成のロジックは、最新の典型価格のzスコアに基づきます。zスコアは(TP – mean) / stddevで計算されます。現在の統計ウィンドウを用いて標準化した偏差が設定されたエントリー閾値(ZScoreSignalEnter)を超えた場合、価格が平均より十分に下にある場合はロングシグナル（負のzスコア）、十分に上にある場合はショートシグナル（正のzスコア）が生成されます。シグナルはAllowLongSignalsまたはAllowShortSignalsが有効な場合にのみ確定します。シグナル状態中は、zスコアが定義された終了バンド(ZScoreSignalExit)内に戻るまで待ち、シグナルを解除して反転の可能性を通知します。各シグナルの変化時にはEmitAlertWithArrowが呼ばれ、チャート上に方向矢印を描画し、ユーザー設定に応じてポップアップ、音、プッシュ通知も送信されます。

コード解説

このセクションでは、KDE Level Sentinel.mq5の実装詳細について説明します。アーキテクチャ、データフロー、コアアルゴリズム、チャート上の可視化やレベル監視を支える重要な補助関数に焦点を当てています。読者が概念設計をコードの該当箇所や設定オプションにマッピングできるように構成しています。

設定と初期化

ユーザーが設定可能なすべてのオプションは、ソースコードの冒頭でinputパラメータとして宣言されています。これには、分析対象期間(Lookback)、現在形成中のバーを除外するかどうか、KDEおよびヒストグラム設定（ModeBins、KDEGridPoints、KDEBandwidthFactor）、シグナル用zスコア閾値、スナップショットおよび監視設定(AutoSnapshotLevels、MonitorBars、TouchTolerancePips、BreakoutPips、ReversalPips、UseATRforThresholds)、およびUI/クリーンアップのタイミング（TimerIntervalSeconds、CleanupIntervalSeconds）が含まれます。この単一のセクションがEAのコントロールパネルとして機能し、入力値を変更するだけで、コードを変更せずに統計的な解析視点や監視挙動を調整できます。

// ---------- user inputs (control panel) ----------
input int    Lookback               = 1000;
input bool   ExcludeCurrent         = true;
input bool   UseWeightedByVol       = true;
input int    ModeBins               = 30;
input int    KDEGridPoints          = 100;
input double KDEBandwidthFactor     = 1.0;
input bool   DrawHistogramOnChart   = false;
input int    RefreshEveryXTicks     = 1;
input double ZScoreSignalEnter      = 2.0;
input double ZScoreSignalExit       = 0.8;
input bool   AutoSnapshotLevels     = true;
input int    MonitorBars            = 20;
input double TouchTolerancePips     = 3.0;
input bool   UseATRforThresholds    = true;
input double ATRMultiplier          = 0.5;
input int    ATRperiod              = 14;
input int    TimerIntervalSeconds   = 60;
input int    CleanupIntervalSeconds = 3600;

// ---------- OnInit (build names, cleanup, placeholders, start timer) ----------
int OnInit()
  {
   S_base = StringFormat("CSTATS_%s_%d", _Symbol, (int)TF);
   S_mean = S_base + "_MEAN";
   S_p25  = S_base + "_P25";
   // remove leftovers from previous runs
   RemoveExistingEAObjects();
   // create panel + placeholder HLINEs
   CreatePanel();
   CreateHLine(S_mean, 0.0, clrBlack, 2);
   CreateHLine(S_p25,  0.0, clrTeal,  1);
   // optionally clear previous snapshot
   if(ClearSnapshotOnStart) ClearSnapshot();
   // start periodic timer for housekeeping
   EventSetTimer(TimerIntervalSeconds);
   return(INIT_SUCCEEDED);
  }

OnInit内では、EAは「S_base = StringFormat("CSTATS_%s_%d", _Symbol, (int)TF)」を使って標準化されたオブジェクト名およびグローバル変数名の接頭辞を構築します。この決定論的な命名により、複数チャートのインスタンス間での名前衝突を回避し、クリーンアップを集中管理できます。初期化処理では、以前のインスタンスの残留オブジェクトを削除し、コンパクトなコーナーパネル（統計サマリー用ラベル）を作成し、各主要統計（平均、±標準偏差、P25/P75、中央値、両最頻値）のためのプレースホルダー水平線を配置します。必要に応じて以前のスナップショットをクリアし、定期タイマーを開始してハウスキーピング処理をおこないます。

データ収集とメインループ

主要な計算はOnTick内で実行され、RefreshEveryXTicksによって処理頻度が調整され、高頻度ティックでもCPU負荷が過剰にならないようにしています。ルーチンはCopyRatesを使用して設定された時間足のLookbackバーをrates[]にコピーします。ここで「CopyRates, using start = ExcludeCurrent ?1 :0」により、形成中のローソク足を除外するかどうかを選択できます。rates[]から、各ローソク足の典型価格「vals[] = (high + low + close) / 3.0」およびティックボリュームvols[]（ボリューム加重が有効な場合）を計算します。

void OnTick()
  {
   tick_count++;
   if(tick_count < RefreshEveryXTicks) return;
   tick_count = 0;

   int start = ExcludeCurrent ? 1 : 0;
   int needed = Lookback;
   if(Bars(_Symbol, TF) - start < needed) return;

   MqlRates rates[];
   int copied = CopyRates(_Symbol, TF, start, needed, rates);
   if(copied <= 0) { Print("CopyRates failed: ", GetLastError()); return; }

   double vals[], vols[];
   ArrayResize(vals, copied);
   ArrayResize(vols, copied);
   for(int i = 0; i < copied; i++)
     {
      vals[i] = (rates[i].high + rates[i].low + rates[i].close) / 3.0; // typical price
      vols[i] = (double)rates[i].tick_volume;
     }

   // pass vals/vols into statistics routines...
  }

統計計算はすぐに続きます。算術平均、必要に応じてボリューム加重平均、標本分散および標準偏差、中央値、25パーセンタイル/75パーセンタイル、ビン分け最頻値(ModeBinned)、およびカーネル密度推定に基づく最頻値(ModeKDE)が計算されます。KDEの帯域幅はSilverman則に類似した「h = 1.06 * sd * n^-0.2」をKDEBandwidthFactorでスケーリングして決定され、均一グリッド(KDEGridPoints)上で密度を評価し、推定密度が最大となるグリッドポイントを返します。最新の典型価格(latest)を用いてzスコア「(latest - mean) / stddev」を計算し、これに基づき単純なzスコアのエントリー/エグジットシグナルが生成されます。
計算された統計値はチャート上の水平線やテキストラベルに表示されるとともにS_baseを接頭辞としたキーでグローバル変数としてエクスポートされ、他のスクリプトやインジケーターからも参照可能です。

スナップショットおよび参照レベルの監視

AutoSnapshotLevelsが有効な場合、EAは単一のスナップショットを固定し、現在のレベル推定値（平均、平均±標準偏差、P25、P75、中央値、最頻値）を保持します。そして、RefLevel構造体から成るrefLevels[]配列を作成します。各RefLevelにはname、price、touched、touchTime、monitorLeft、highest、lowest、result（0=不明、1=ブレイクアウト、-1=リバーサル、2=フォローなし）、およびresolvedTimeが格納されます。スナップショット用のHLINEはS_base + "REF" + nameという名前で管理され、既存のラベルが存在する場合は標準のTXTオブジェクトを更新し、そうでない場合はREF専用のラベルを使用します。

// take snapshot (single-shot)
void SnapshotReferenceLevels(double mean_val, double p25, double p75, double median_val, double mode_b, double mode_k)
  {
   snapshot_mean = mean_val;
   snapshot_p25  = p25;
   snapshot_p75  = p75;
   snapshot_median= median_val;
   // build refLevels
   ArrayResize(refLevels, 6);
   refLevels[0].name = "MEAN"; refLevels[0].price = snapshot_mean; refLevels[0].touched=false; refLevels[0].result=0;
   // ... fill others ...
   refSnapshotTaken = true;
   snapshotTakenTime = TimeCurrent();
  }

// monitor reference levels (called from OnTick)
void MonitorReferenceLevels(const MqlRates &rates[], int copied)
  {
   if(!refSnapshotTaken || copied <= 0) return;
   double barHigh = rates[0].high;
   double barLow  = rates[0].low;
   double barClose= rates[0].close;
   double pipPoints = pipToPointMultiplier();
   double touchTol = TouchTolerancePips * pipPoints;
   // compute thresholds (fixed or ATR-scaled)
   double breakoutThreshold = BreakoutPips * pipPoints;
   if(UseATRforThresholds)
     {
      int hATR = iATR(_Symbol, TF, ATRperiod);
      double atrBuf[];
      CopyBuffer(hATR,0,0,1,atrBuf);
      IndicatorRelease(hATR);
      breakoutThreshold = atrBuf[0] * ATRMultiplier;
     }

   for(int i=0;i<ArraySize(refLevels);i++)
     {
      RefLevel L = refLevels[i];
      if(L.result != 0) continue;
      if(!L.touched)
        {
         if(barHigh >= L.price - touchTol && barLow <= L.price + touchTol)
           {
            L.touched = true;
            L.touchTime = rates[0].time;
            L.monitorLeft = MonitorBars;
            L.highest = barHigh; L.lowest = barLow;
            refLevels[i] = L;
           }
        }
      else
        {
         // update highest/lowest and evaluate breakout/reversal
         if(barHigh > L.highest) L.highest = barHigh;
         if(barLow  < L.lowest)  L.lowest  = barLow;
         bool breakout = (L.highest >= L.price + breakoutThreshold);
         bool reversal = (L.lowest  <= L.price - breakoutThreshold);
         if(breakout && !reversal) { L.result = 1; L.resolvedTime = rates[0].time; DrawOutcome(L, true); }
         else if(reversal && !breakout) { L.result = -1; L.resolvedTime = rates[0].time; DrawOutcome(L, false); }
         else { if(--L.monitorLeft <= 0) { L.result = 2; L.resolvedTime = rates[0].time; DrawOutcome(L, false); } }
         refLevels[i] = L;
        }
     }
  }

監視はMonitorReferenceLevels関数で実装されています。未解決の参照ごとに、最新バーの高値/安値/終値をタッチ許容値（TouchTolerancePipsをpipToPointMultiplierで価格単位に変換した値）と比較します。タッチが発生するとmonitorLeftがMonitorBarsに設定され、初期の高値/安値が記録されます。監視期間中、EAは最高値と最低値を追跡し、ブレイクアウト/リバーサル条件を評価します。閾値は固定のpips値、またはUseATRforThresholdsがtrueの場合はATRに基づいて算出されます。ATRはiATRとCopyBufferで取得し、ATRMultiplierでスケーリングして適応的な閾値を生成します。バーの終値による確認(UseCloseForConfirm)もオプションでサポートされます。結果は確認時に即時確定するか、監視期間終了時に観測された極値を閾値と比較して確定され、DrawOutcomeにより記録および描画されます。

描画とラベル配置

EAは安定かつ重ならない注釈表示を優先します。統計値およびスナップショット参照の水平線はCreateHLineを使用して作成され、既存オブジェクトがある場合は更新され、メタデータのタイムスタンプが設定されます。テキストラベルはCreateOrUpdateLineTextで管理される配置ルーチンを通じて処理されます。

void CreateOrUpdateLineText(string name, datetime t, double price, string text)
  {
   long chart_id = ChartID();
   int x0 = 0, y0 = 0;
   bool ok = ChartTimePriceToXY(chart_id, 0, t, price, x0, y0);
   int fontSize = 10;
   int pixelThresh = MathMax(18, fontSize * 2);

   // collect used Y positions from existing OBJ_TEXT objects
   int usedYPositions[];
   ArrayResize(usedYPositions,0);
   int total = ObjectsTotal(0);
   for(int oi=0; oi<total; oi++)
     {
      string oname = ObjectName(0, oi);
      if(oname == name) continue;
      if(ObjectGetInteger(0, oname, OBJPROP_TYPE) != OBJ_TEXT) continue;
      long ot = (long)ObjectGetInteger(0, oname, OBJPROP_TIME);
      double op = ObjectGetDouble(0, oname, OBJPROP_PRICE);
      int xp=0, yp=0;
      if(ChartTimePriceToXY(chart_id,0,(datetime)ot,op,xp,yp))
        {
         ArrayResize(usedYPositions, ArraySize(usedYPositions)+1);
         usedYPositions[ArraySize(usedYPositions)-1] = yp;
        }
     }

   // attempt to find free Y slot
   int chosenY = y0;
   if(!IsYFree(chosenY, usedYPositions, pixelThresh))
     {
      int step = pixelThresh;
      bool found = false;
      for(int s=1; s<=20 && !found; s++)
        {
         int yUp = y0 - s*step;
         if(yUp >= 0 && IsYFree(yUp, usedYPositions, pixelThresh)) { chosenY = yUp; found = true; break; }
         int yDn = y0 + s*step;
         if(IsYFree(yDn, usedYPositions, pixelThresh)) { chosenY = yDn; found = true; break; }
        }
     }

   // convert chosen XY back to time/price; fallback if needed
   datetime tt = t; double pp = price;
   if(!ChartXYToTimePrice(chart_id, 0, x0, chosenY, tt, pp))
     { // fallback: nudge price slightly
      double point = SymbolInfoDouble(_Symbol, SYMBOL_POINT);
      int slotDelta = (chosenY - y0) / pixelThresh;
      pp = price + slotDelta * pixelThresh * point;
     }

   // create or update the OBJ_TEXT
   KeepSingleTextLabel(name);
   if(ObjectFind(0, name) >= 0)
     {
      ObjectSetInteger(0, name, OBJPROP_TIME, (long)tt);
      ObjectSetDouble(0, name, OBJPROP_PRICE, pp);
      ObjectSetString(0, name, OBJPROP_TEXT, text);
     }
   else
     {
      ObjectCreate(0, name, OBJ_TEXT, 0, tt, pp);
      ObjectSetString(0, name, OBJPROP_TEXT, text);
     }
   SetObjTimestamp(name);
  }

ChartTimePriceToXYを用いて、対象の時間＋価格を画面座標にマッピングしようとします。

既存のOBJ_TEXTオブジェクト（および統計値用のTXT正規ラベル）のYピクセル位置を取得し、新しいラベルが衝突しないようにします。

フォントサイズに基づくピクセルステップで上下に探索して空きスロットを探し(IsYFree)、選ばれたXYスロットをChartXYToTimePriceで時間＋価格に戻します。変換に失敗した場合は、クラッシュを避けるために近似位置を調整する堅牢なフォールバックを実行します。

さらに、KeepSingleTextLabelにより各HLINEに対して_TXTオブジェクトは1つだけに制限されます。

この方法により、チャートのスクロールやリサイズ時でも最小限のジッターで読みやすいラベルを表示できます。シグナルや結果を示す矢印はDrawArrowAtで描画され、矢印の価格位置に薄い正確なHLINEを作成して精密な整列を維持します。

ヒストグラムとKDE

DrawHistogramは、典型価格の分布をModeBinsに分けた頻度ヒストグラムを計算し、各ビンの中心にHLINEを描画、カウントに応じた幅を設定し、コンパクトなカウントラベルを作成します。ModeBinnedは、最もデータが集中しているビンの中心を返すことで高速に最頻値を推定します。ModeKDEは、ユーザー指定のグリッドに対して単純なカーネル密度推定をおこなうことで滑らかな最頻値推定を提供します。その計算量はO(n × gridPts)であり、選択したLookbackおよびバー内データ量に応じて調整する必要があります。

// histogram drawing (bin counts => HLINE widths)
void DrawHistogram(const double &arr[], int n, int bins, int maxWidth)
  {
   double minv = ArrayMin(arr, n);
   double maxv = ArrayMax(arr, n);
   double binw = (maxv - minv) / bins;
   int counts[]; ArrayResize(counts, bins); ArrayInitialize(counts,0);
   for(int i=0;i<n;i++)
     {
      int b = (int)MathFloor((arr[i]-minv)/binw);
      if(b < 0) b=0; if(b >= bins) b=bins-1;
      counts[b]++;
     }
   // draw HLINE per bin with width proportional to counts[b]
  }

// KDE-based modal estimate
double ModeKDE(const double &a[], int n, int gridPts, double bwFactor)
  {
   double mn = ArrayMin(a,n), mx = ArrayMax(a,n);
   double sd = MathSqrt(Variance(a, n, false));
   double h = 1.06 * sd * MathPow((double)n, -0.2);
   if(h <= 0) h = (mx - mn) / 20.0;
   h *= bwFactor;
   double bestX = mn, bestD = -1.0;
   const double SQRT2PI = 2.5066282746310002;
   for(int g=0; g<gridPts; g++)
     {
      double x = mn + (double)g/(gridPts-1) * (mx - mn);
      double s = 0.0;
      for(int i=0;i<n;i++)
        {
         double u = (x - a[i]) / h;
         s += MathExp(-0.5 * u * u);
        }
      double dens = s / (n * h * SQRT2PI);
      if(dens > bestD) { bestD = dens; bestX = x; }
     }
   return(bestX);
  }

メタデータとライフサイクル管理

作成されるすべてのチャートオブジェクトは、SetObjTimestampを用いてS_base + "_META_" + objectNameをキーとするグローバル変数にタイムスタンプ付きメタデータとして関連付けられます。これにより、OnTimer内で呼び出されるRemoveOldObjectsは候補オブジェクトをスキャンし、CleanupIntervalSecondsより古いものを削除でき、長時間稼働するチャートでの視覚的混雑を防ぎます。RemoveExistingEAObjectsとCleanupAllMetaGlobalsは、以前のオブジェクトとそのメタデータを削除することで、初期化や終了処理を制御可能にします。

// store timestamp meta
void SetObjTimestamp(string name)
  {
   string g = S_base + "_META_" + name;
   GlobalVariableSet(g, (double)TimeCurrent());
  }

// read meta timestamp
datetime GetObjTimestamp(string name)
  {
   string g = S_base + "_META_" + name;
   if(GlobalVariableCheck(g)) return (datetime)GlobalVariableGet(g);
   return 0;
  }

// remove objects older than ageSec
void RemoveOldObjects(int ageSec)
  {
   datetime now = TimeCurrent();
   string candidates[] = { S_mean, S_mean + "_TXT", S_p25, S_p25 + "_TXT", S_panel /* ... */ };
   for(int j=0;j<ArraySize(candidates);j++)
     {
      string nm = candidates[j];
      datetime ts = GetObjTimestamp(nm);
      if(ts == 0) continue;
      if((int)(now - ts) >= ageSec)
        {
         if(ObjectFind(0, nm) >= 0) ObjectDelete(0, nm);
         string g = S_base + "_META_" + nm;
         if(GlobalVariableCheck(g)) GlobalVariableDel(g);
        }
     }
  }

アラートとシグナル処理

Zスコアによるシグナルは各ティックで評価され、AllowLongSignals / AllowShortSignalsに従います。エントリー閾値はZScoreSignalEnter、エグジット閾値はZScoreSignalExitです。シグナル状態が変化した際には、EmitAlertWithArrowがチャート上に矢印を描画し、必要に応じてプラットフォームのアラート（Alert()）、サウンド(PlaySound())、プッシュ通知(SendNotification())を発動します。同時に、チャート上の反対シグナル矢印は削除され、視覚的ノイズを抑えます。

// z-score signal logic (called from OnTick after stats computed)
int newSig = currentSignal;
if(zscore >= ZScoreSignalEnter && AllowLongSignals) newSig = 1;
else if(zscore <= -ZScoreSignalEnter && AllowShortSignals) newSig = -1;
else if(currentSignal == 1 && zscore < ZScoreSignalExit) newSig = 0;
else if(currentSignal == -1 && zscore > -ZScoreSignalExit) newSig = 0;

if(newSig != currentSignal)
  {
   if(newSig == 1)
     EmitAlertWithArrow("CSTATS LONG " + _Symbol + " z=" + DoubleToString(zscore,3), t_now, latest, true, S_arrow_long);
   else if(newSig == -1)
     EmitAlertWithArrow("CSTATS SHORT " + _Symbol + " z=" + DoubleToString(zscore,3), t_now, latest, false, S_arrow_short);
   else // clear arrows on exit
     {
      if(ObjectFind(0, S_arrow_long) >= 0) ObjectDelete(0, S_arrow_long);
      if(ObjectFind(0, S_arrow_short) >= 0) ObjectDelete(0, S_arrow_short);
     }
   currentSignal = newSig;
  }

// emit alert helper
void EmitAlertWithArrow(string message, datetime when, double price, bool isBuy, string arrowName)
  {
   DrawArrowAt(arrowName, when, price, isBuy);
   if(SendAlertOnSignal) Alert(message);
   if(PlaySoundOnSignal) PlaySound(SoundFileOnSignal);
   if(SendPushOnSignal) SendNotification(message);
  }

統計ヘルパー関数と数値上の注意点

コードは標準的な配列ベースの統計処理を実装しており、平均、加重平均、標本分散、中央値（偶数サンプル時の平均値処理を含む）、および線形補間によるパーセンタイル計算がMQL5配列仕様に合わせて提供されています。ヘルパー関数として、必要に応じて歪度や尖度も計算可能です。実務上、KDEの解像度(KDEGridPoints)および帯域幅(KDEBandwidthFactor)は、滑らかさ、精度、CPUコストのバランスを考慮して設定すべきです。ATRハンドルの生成および解放は評価ごとにおこなわれますが、高頻度実行の場合は、ハンドルを再利用するか、新しいバーが形成されたタイミングでのみATRを計算することでオーバーヘッドを削減することが推奨されます。

double Mean(const double &a[], int n)
  {
   if(n<=0) return 0.0;
   double s=0.0;
   for(int i=0;i<n;i++) s += a[i];
   return s / n;
  }

double WeightedMean(const double &a[], const double &w[], int n)
  {
   if(n<=0) return 0.0;
   double sw=0.0, s=0.0;
   for(int i=0;i<n;i++) { s += a[i] * w[i]; sw += w[i]; }
   if(sw == 0.0) return Mean(a, n);
   return s / sw;
  }

double Variance(const double &a[], int n, bool sample)
  {
   if(n <= 1) return 0.0;
   double mu = Mean(a,n), s = 0.0;
   for(int i=0;i<n;i++) { double d = a[i] - mu; s += d * d; }
   return sample ? s / (n-1) : s / n;
  }

double Median(const double &a[], int n)
  {
   if(n <= 0) return 0.0;
   double tmp[]; ArrayResize(tmp, n); ArrayCopy(tmp, a); ArraySort(tmp);
   if((n % 2) == 1) return tmp[n/2];
   return (tmp[n/2 - 1] + tmp[n/2]) / 2.0;
  }

double Percentile(const double &a[], int n, double q)
  {
   if(n <= 0) return 0.0;
   double tmp[]; ArrayResize(tmp, n); ArrayCopy(tmp, a); ArraySort(tmp);
   if(q <= 0.0) return tmp[0];
   if(q >= 1.0) return tmp[n-1];
   double idx = q * (n - 1);
   int i0 = (int)MathFloor(idx); double frac = idx - i0;
   if(i0 + 1 < n) return tmp[i0] * (1.0 - frac) + tmp[i0+1] * frac;
   return tmp[i0];
  }

結果

このセクションでは、EAのチャート上でのパフォーマンスを検証します。システムを本番資金で運用する前に、バックテストおよびデモ口座で十分に検証することが重要です。リアルタイムのシグナルは、規律あるトレーダーでも早まった取引に誘う可能性があるためです。EAはコンパクトな統計パネルを表示し、計算された各統計値に対して水平ラインを描画します。それぞれのラインには意味を示すテキストラベル（平均、中央値、最頻値、P25/P75など）が付属しており、価格が統計的に意味のある水準とどのように相互作用しているかを容易に把握できます。これにより、過去および将来のテストでEAの動作を検証することが可能です。

下図は、Step Index (M5)上でのEAの統計パネルと水平ラインの例を示しています。平均値と加重平均は8114.8に収束し、安定した中心点を形成しています。標準偏差(15.6)はサンプル内の中程度の変動を示し、中央値(8113.3)は平均値付近に位置しており、価格分布が概ね対称であることを反映しています。離散最頻値(8112.4)およびKDE推定最頻値(8113.2)は平均の少し下に集まっており、密集した価格帯として自然なサポート/レジスタンス領域を示しています。パーセンタイル（P25 = 8105.7、P75 = 8121.6）は、16ポイントの四分位範囲(IQR)を示しており、データの中間50％の価格帯を明確に捉えています。この範囲は、価格が最も頻繁に振動する収束帯を浮き彫りにします。最後にzスコア(2.676)は価格が平均より標準偏差2以上上方に移動したことを示しており、一時的な過熱状態を示唆し、平均回帰の可能性を高めています。

これらの結果は、典型価格から導出した統計水準が実践的な参照ポイントとして活用できることを示しています。EAのチャート表示により、トレーダーは価格がこれらのゾーンを尊重するか、反発するか、突破するかを視覚的に確認でき、主観的な判断ではなく、客観的に測定された市場構造に沿った取引判断をおこないやすくなります。

結論

このEAは典型価格（TP = (高値 + 安値 + 終値) / 3）から統計的参照水準を算出し、チャート上に直接表示します。表示内容はラベル付き水平ライン（平均、加重平均、中央値、ビン分割による最頻値およびKDEによる最頻値、P25/P75）、コンパクトな統計パネル、視覚的シグナル（矢印、タッチ/結果マーカー）です。また、プログラムから利用可能なグローバル変数としても出力され、タッチを記録して結果をブレイクアウト、反転、ノーフォローに分類するモニタリングロジックも備えています。

これらの水準は、価格のクラスタリング、中心傾向、分散を客観的なチャート上の参照ポイントに変換します。一目で把握できる統計マップのように考え、意思決定の補助として利用してください。価格がこれらのゾーンとどのように相互作用するかを確認してから行動し、EAの出力は自動売買ではなく、あくまで状況判断のコンテキストとして扱うのが適切です。将来的なプロジェクトでは、より高度な統計手法やアンサンブル手法を導入して、参照水準の安定性や予測精度の向上を目指す予定です。

他の記事もご覧ください。