知っておくべきMQL5ウィザードのテクニック（第72回）：教師あり学習でMACDとOBVのパターンを活用する

はじめに

前回の記事では、MACDとOBVのインジケーターペアを紹介しました。MACDはトレンド系、OBVは出来高系のインジケーターであり、この2つは補完的なペアとなります。私たちは常に、2つのインジケーターの組み合わせから導かれる10種類のシグナルパターンを対象に、過去1年間でのトレーニングまたは最適化をおこない、その後の1年間でフォワードウォークテストを実施しています。前回の記事では、その中でPattern_7だけがフォワードウォークで利益を上げることができました。このインジケーターペアは、これまで取り上げた他のインジケーターと比べて成績が芳しくなかった理由についても検討しましたが、同時にこれは「機械学習によってこれらのシグナルパターンを改善できるのではないか」という機会でもありました。

そこで今回は、Rational Quadraticカーネルを用いた畳み込みニューラルネットワーク(CNN)を取り上げ、このインジケーターペアのシグナル解釈や適用を改善できるかどうかを検討します。Rational Quadratic (RQ)カーネルは次の式で定義されます。

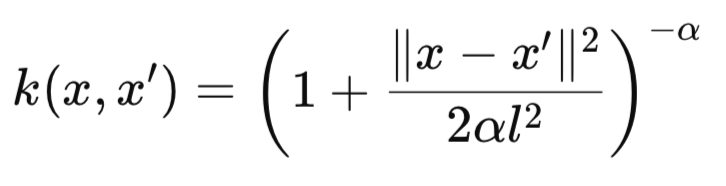
ここで

• k(x,x′)：2つの入力xとx′の間のカーネル類似度を表す値です。範囲は0から1で、1に近いほど高い類似度を示します。
  
  
• xとx′：2つの入力ベクトルです（例：1次元信号のスライス、特徴ベクトル、または時間上の位置など）。これらは1次元スカラー値(dim=1)の場合もあれば、多次元ベクトルの場合もあります。
  
  
• ∥x−x′∥2：入力ベクトル間の二乗ユークリッド距離です。これは特徴空間においてxとx′がどれだけ離れているかを測るもので、この距離は次の式から求められます。
• 
  

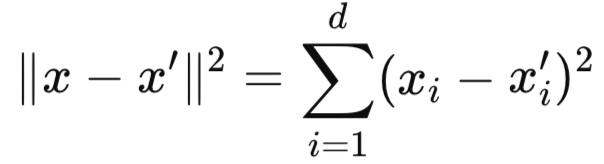
• l：カーネルの長さスケール、または特性スケールです。距離に応じて類似度がどの程度早く減衰するかを決定します。
• lが小さい場合：急激に減衰する（局所的な感度が高い）
• lが大きい場合：緩やかに減衰する（広範な類似性を持つ）
  
  
• α：スケール混合パラメータ。形状パラメータとも呼ばれます。大きなスケールと小さなスケールの変動に対する重み付けを制御します。
  
  
• α→∞の場合、このカーネルは二乗指数カーネル（RBFカーネル）と同等になります。
• αが小さい場合、テールが厚くなり、より長距離の相互作用を許容します。

私たちのCNNにおけるRational Quadratic Kernel (RQK)の実装では、このカーネルをCNNのカーネルサイズやチャンネル数の設定に利用しています。ただし、このカーネルをCNN内で利用する方法には他にも可能性があり、読者が別の応用を検討する余地があります。

RQカーネルの代替的な応用と利点

まず最初に挙げられるのはアダプティブアテンションマスキングです。このケースではRQカーネルがCNN内部で空間的または時間的なアテンションマスクを構築します。これによりセグメンテーションや時系列予測が助けられます。動作としては、セントロイドウィンドウのような参照に対して高い類似度を持つ領域を強調することによって機能します。RQカーネルのもう一つの利用法としては距離認識型プーリングがあります。このシナリオでは、すべてを平均する代わりに、RQカーネルの下で設定された類似度閾値内のネットワーク活性化のみをプーリングします。これにより特徴の近さを考慮した距離認識型の適応的プーリングが可能になります。

別の応用としては特徴量重要度スケーリングがあります。ここではCNNのチャンネルに対して学習によって得られる滑らかな重み付けを適用します。最後に、RQカーネルはCNN内で入力空間におけるカーネル評価で効果が最小な重みを減少または「剪定」するために利用できます。なぜこのカーネルをCNNで利用でき、また利用すべきかの理由は多岐に渡ります。以下にその要約を示します。

外れ値に対して堅牢	RQカーネルの長いテールにより空間的・時間的な異常値に対してアーキテクチャが影響を受けにくくなる。
スムーズな遷移	カーネルの滑らかな減衰によって層間の表現シフトが急激にならず、勾配フローに有利。
動的アーキテクチャ	類似度計測を用いてCNNのカーネルサイズやチャンネル拡張をデータ依存で選択できる。

このRQカーネルを用いたCNN(conv-1d)設計は、局所的な類似性が重要な1次元入力に最適です。本記事で扱っている金融時系列がその典型で、他にも音声信号やバイナリパターン検出などに適しています。このCNNを利用する際には、入力ベクトルを0–1範囲に正規化または標準化することが重要で、これは過去の記事でのネットワークでも実施してきたことです。入力の形状は通常(batch_size,input_length)であり、入力ベクトルは0や1で埋められています。 

RQカーネルには先に示した式の通り、いくつかの重要なハイパーパラメータが存在します。最初に挙げられるのはαで、これはテール減衰を制御します。値が大きいとカーネルは単一のRBFカーネルのように振る舞います。しかし値を小さくすると、RQカーネルは異なるスケールの複数RBFの組み合わせのように振る舞います。もう一つのハイパーパラメータは長さスケールで、距離に対する類似度の感度を決定します。

ネットワークが確率分布出力を持つ分類器である場合、学習にはBCE損失関数を利用できます。この非標準的なアーキテクチャでは適切な初期化や学習率スケジューリングも重要です。さらに拡張としては層間に残差接続を追加して勾配伝播を改善することが可能です。また、RQカーネルをゲーティングメカニズムとして統合したり、類似度に基づいたドロップアウトを層間で用いることもできます。

研究によればRQカーネルはConv1Dの重みを定義し、特定のデータパターンを捉えることが示されています。この応用は総パラメータ数を減らし解釈性を向上させますが、一方で学習カーネルに比べ適応性が制限される可能性があります。より良い結果の証拠は、このカーネルをガウス過程層やCNN設計におけるハイパーパラメータ最適化に用いることに傾いています。これは「畳み込みカーネルを用いたディープガウス過程」に関する研究で扱われています。 

固定サイズのカーネルを利用することは学習可能パラメータを減らし、特にデータが限られる場合の過学習を抑制します。これはキャッサバ病分類に関する研究で示されています。しかし、事前に設定されたカーネルを利用することで特徴抽出の理解が深まりブラックボックス的な学習カーネルとは対照的な利点がある一方で、適応性には懸念が残ります。固定カーネルは学習カーネルのようにデータにうまく適応せず、複雑なタスクでは性能が低下する可能性があります。前述のキャッサバ研究では、ハイブリッドカーネルが単一RQカーネルを上回る結果を示しました。その一部を以下に示します。

カーネルタイプ	精度
RQカーネル	88.5%
二乗指数カーネル	88.0%
ハイブリッドカーネル	90.1%

上記のキャッサバ病研究の表は、学習カーネルと固定カーネルの間でのパフォーマンス上のトレードオフを示しています。ハイブリッドアプローチが推奨されます。以前はRQカーネルの役割は曖昧でした。しかし、上記で触れた研究をはじめとする複数の研究（リンク、リンク、リンク）によって、その応用がディープガウス過程における画像データ利用やConv1Dへの適用で明らかにされました。キャッサバ病研究は、固定カーネルと学習カーネルのバランスを取る手段として事前定義された重みを利用する判断に影響を与えました。

ネットワーク設計においては、カーネルサイズはハイパーパラメータである長さスケールlに基づいて決定しました。複数のチャンネルが異なるスケールを捉えることで、CNNの受容野を変化させるという実践と一致しています。最終実装では柔軟性を持たせるためにグローバル平均プーリングを使用しました。これにより出力は任意の系列長から独立し、また0–1範囲に制限されたスカラー出力にも適していました。

ネットワーク

ネットワーク実装はPythonでおこなっています。過去の記事でも述べた通り、Pythonでコーディングおよび学習をおこなう方が、同じ作業をMQL5でおこなうよりも効率的だからです。Pythonでは、次のようにRQ-Kernelを用いてカーネルとチャネルのスケーリングをおこなうCNNを実装しています。

import torch
import torch.nn as nn
import torch.nn.functional as F

import pandas as pd
import numpy as np

class RationalQuadraticConv1D(nn.Module):
    def __init__(self, alpha=1.0, length_scale=1.0, input_length=100):
        super(RationalQuadraticConv1D, self).__init__()
        self.alpha = alpha
        self.length_scale = length_scale
        self.input_length = input_length

        # Deeper and wider design
        self.kernel_sizes, self.channels = self._design_architecture()

        self.conv_layers = nn.ModuleList()
        in_channels = 1

        for i, (out_channels, kernel_size) in enumerate(zip(self.channels, self.kernel_sizes)):
            layer = nn.Sequential(
                nn.Conv1d(in_channels, out_channels, kernel_size=kernel_size, padding=kernel_size // 2),
                nn.BatchNorm1d(out_channels),
                nn.ReLU(),
                nn.Dropout(0.2)
            )
            self.conv_layers.append(layer)
            in_channels = out_channels

        # Fully connected head to increase parameter count
        self.head = nn.Sequential(
            nn.AdaptiveAvgPool1d(1),
            nn.Flatten(),
            nn.Linear(in_channels, 128),
            nn.ReLU(),
            nn.Dropout(0.2),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )

    def _rq_kernel(self, x, x_prime):
        dist_sq = (x - x_prime) ** 2
        return (1 + dist_sq / (2 * self.alpha * self.length_scale ** 2)) ** -self.alpha

    def _design_architecture(self):
        x = torch.linspace(0, 1, self.input_length)
        center = 0.5
        responses = self._rq_kernel(x, center)
        thresholded = responses[responses > 0.01]  # allow more spread

        num_layers = 10
        kernel_sizes = [3 + (i % 4) * 2 for i in range(num_layers)]  # cyclic 3, 5, 7, 9
        channels = [32 * (i + 1) for i in range(num_layers)]  # 32, 64, ..., 320

        return kernel_sizes, channels

    def forward(self, x):
        x = x.unsqueeze(1)  # (B, 1, L)
        for layer in self.conv_layers:
            x = layer(x)
        return self.head(x)

まず、RQ-Kernelの式で示した重要なパラメータのいくつかを入力として受け取る、カスタムのPyTorchモジュールを定義します。私たちが「RationalQuadraticConv1D」と名付けたクラスは、過去の記事でも述べた通り、すべてのPyTorchニューラルネットワークモジュールの基底クラスである「nn.Module」を継承しています。コンストラクタでは、RQ-Kernelの重要な3つのパラメータであるα、長さスケール、入力長さを初期化します。αは前述の通りカーネルの形状を制御し、長さスケールはカーネルがどの距離で減衰するかを決定し、入力長さは入力ベクトルの期待サイズを反映するためのものです。

これらの初期設定は、モデルの基礎を確立し、カーネルの挙動をカスタマイズできるようにする上で重要です。また、アーキテクチャが入力ベクトルの次元に適合することを保証します。αや長さスケールの調整は、入力の違いに対するカーネルの感度を変更するためにおこないます。例えば、長さスケールを小さくすると局所的なパターンに焦点を当て、値を大きくすると広範な類似性を捉えることができます。入力長さについても、データサイズに一致していることを確認する必要があります。 

初期化の後、畳み込み層のカーネルサイズとチャンネル数を動的に割り当てます。このコード行では、「_design_architecture」メソッド（後述）を呼び出し、入力空間全体におけるRQカーネルの類似度プロファイルに基づいてカーネルサイズとチャンネル数を計算します。これが本ネットワークの中核的な考え方であり、固定構造のCNNとは異なり、この手法ではデータの特性に応じてモデル構造を適応させることができます。これにより、特徴量抽出の効率性および有効性が向上する可能性があります。この適応的アプローチによって、本モデルは類似度構造が多様なデータセットにも適したものとなります。「_design_architecture」メソッドの出力をモニタリングすることは、アーキテクチャがタスクの複雑さと整合しているかを確認するために重要です。

その後のコードでは、動的な性質を持つ柔軟な畳み込み層スタックを構築します。nn.ModuleList()関数は、可変数の畳み込み層を保持するコンテナを生成します。ループ処理では、self.channelsとself.kernel_sizeからそれぞれ読み取った出力チャンネル数(out-channels)とカーネルサイズ(kernel-size)のペアに対して反復をおこないます。各nn.Conv1D層は、最初の層では入力チャンネル(in-channels)を1とし、出力チャンネル(out-channels)および対応するカーネルサイズ(kernel-size)を使用します。入力長を維持するためにパディングを設定し、次の層におけるカーネルサイズを決定します。続く層では、in-channelsを前のout-channelsに更新して接続を形成します。

このような動的構築により、モデルはタスクに合わせた層数とパラメータ数を持つことができます。加えて、パディングにより出力長が入力長と一致することを保証し、これは時系列データなどを扱う際に極めて重要です。カーネルサイズが大きいほど入力データの広範なパターンを捉える傾向があり、出力チャンネル数が多いほど多様な特徴を抽出できます。出力長を完全に保持する必要がない場合（ダウンサンプリングなど）、パディングを0に調整することも可能です。

次に、「final」ネットワークを定義します。これは畳み込みの出力を単一の確率的な値に変換する部分です。この段階ではnn.AdaptiveAvgPool1D、nn.Flatten、nn.Linear、nn.Sigmoidといった操作の連鎖を定義します。これらは、系列全体で平均を取ることで空間次元を1に縮小すること、テンソルを1次元ベクトルに変換すること、平坦化された特徴を単一の出力に写像すること、そして0から1の範囲の値を出力し、2値分類や回帰にそれぞれ適した形にすることを担当します。 

この最終ステップによって、抽出された特徴を統合し、タスク固有の出力を生成します。これにより、モデルは2値分類や確率推定などに利用できるようになります。多クラス分類の場合は、nn.Linear(in_channels, num_classes)およびnn.Softmax()に置き換えることができます。回帰タスクでは、Sigmoidを削除する方が適切です。

クラス内には、データ点またはベクトル間の類似度を計算する関数「_rq_kernel」があります。この類似度は、期待されるとおりRQカーネルを用いて計算されます。この計算では、xとx’のユークリッド距離を測定し、先に共有したRQカーネルの式を適用します。距離が大きくなるほど、αおよびlength-scaleハイパーパラメータによって制御されつつ類似度は減少します。RQカーネルは入力データ全体における類似性を定量化し、CNNアーキテクチャ設計の基盤として機能します。

このカーネルは柔軟であり、局所的および大域的なパターンの両方を捉えることが可能です。αを大きくするとガウシアンカーネルに近づき、逆にαを小さくすると柔軟性が増します。また、length-scaleを調整することで減衰の速さを制御でき、値を小さくするほど局所的な類似度を重視します。

次に、前述した「_design_architecture」関数について説明します。この関数はRQカーネルの減衰プロファイルを利用して、CNNアーキテクチャを動的に設計します。まず、正規化された入力位置範囲「x」を生成します。次に、類似度計算の基準点を「center」として設定します。その後、各位置に対して「responses」（RQカーネル応答）を計算し、centerに対する相対的な類似度を求めます。次に、カーネル応答が0.2を超える位置をフィルタリングし、重要な領域に焦点を当てます。

これが完了したら、位置に基づいてカーネルサイズをスケーリングします。初期値を3とし、「中心」からの距離に応じてこれを増加させます。次に、類似度が低い領域により多くのチャンネルを割り当てます。初期値は4とします。最後に、ネットワーク設計を3層に制限するアーキテクチャ設定を返します。

この関数は、データの類似性構造に合わせてCNNを調整します。より大きなカーネルを使用することで広範なパターンを捉えることができ、チャンネル数を増やすことでより複雑な特徴抽出が可能になります。閾値0.2、およびカーネルとチャンネルに対するスケーリング係数（それぞれ4と60）はチューニング可能です。層の数は、より深い特徴抽出を必要とするタスクに応じて増やすことができますが、計算コストとのバランスを考慮する必要があります。

最後に、RationalQuadraticConv1Dクラスのforwardメソッドを定義します。これは、入力から出力までのモデル計算を実行します。まず、入力にチャネル次元を追加し、nn.Conv1Dと互換性を持たせます。その後、各畳み込み層を適用し、非線形性を導入するためにReLU活性化関数を使用します。最後に、出力層を通して最終的な出力を得ます。forwardパス関数は、動的に設計されたアーキテクチャを活用し、予測に使用される特徴量を抽出するためのデータフローを定義します。

入力形状は(batch_size, input_length)の形式であることを確認することが重要です。また、使用する活性化関数の種類はタスクに適したものを選ぶ必要があります。このネットワークでは形状の不一致が発生しやすいため、各ステップで入力データの形状を出力してデバッグすることが重要です。ここまででネットワーク入力の設定を確認できたため、次にPythonにおけるMACDおよびOBVのインジケーター実装を見ていきます。

MACD

私たちのインジケーターは、既存のライブラリやモジュールで代替可能なものもありますが、あえてPythonで一から実装しています。これは、よりスムーズでメモリ負荷の少ないコンパイルおよび実行を実現するためです。MACD（移動平均収束拡散法）は、MACDライン、シグナルライン、そしてヒストグラムを算出します。これらはいずれも資産価格の動向を分析するうえで有用な指標です。Pythonにおける実装例は以下のとおりです。

def MACD(df, fast_period: int = 12, slow_period: int = 26, signal_period: int = 9) -> pd.DataFrame:
    """
    Calculate Moving Average Convergence Divergence (MACD) and append it to the input DataFrame.

    The MACD line is the difference between a fast and slow EMA.
    The Signal line is an EMA of the MACD line.
    The Histogram is the difference between the MACD and Signal lines.
    
    Args:
        df (pd.DataFrame): DataFrame with a 'close' column.
        fast_period (int): Lookback period for the fast EMA. Default is 12.
        slow_period (int): Lookback period for the slow EMA. Default is 26.
        signal_period (int): Lookback period for the Signal line EMA. Default is 9.
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'MACD', 'Signal_Line', and 'MACD_Histogram' columns.
    """
    # Input validation
    if 'close' not in df.columns:
        raise ValueError("DataFrame must contain a 'close' column")
    if not all(p > 0 for p in [fast_period, slow_period, signal_period]):
        raise ValueError("All period values must be positive integers")
    if fast_period >= slow_period:
        raise ValueError("fast_period must be less than slow_period")

    # Create a copy to avoid modifying the original DataFrame
    result_df = df.copy()
    
    # Calculate Fast and Slow Exponential Moving Averages (EMA)
    ema_fast = result_df['close'].ewm(span=fast_period, adjust=False).mean()
    ema_slow = result_df['close'].ewm(span=slow_period, adjust=False).mean()
    
    # Calculate MACD line
    result_df['MACD'] = ema_fast - ema_slow
    
    # Calculate Signal line (EMA of MACD)
    result_df['Signal_Line'] = result_df['MACD'].ewm(span=signal_period, adjust=False).mean()
    
    # Calculate MACD Histogram
    result_df['MACD_Histogram'] = result_df['MACD'] - result_df['Signal_Line']
    
    return result_df

私たちの関数の形式は、これまで使用してきたものと同様で、終値列を含むpandasのデータフレームを入力とし、3つのオプションの整数パラメータを取ります。これらは、fast_period（デフォルト値：12）、slow_period（デフォルト値：26）、およびsignal_period（デフォルト値：9）です。入力にデータフレームを使用する形式は、これまでと同様にMT5のPythonモジュールを用いて価格データをインポートする手順を前提としています。関数の出力は、入力データフレームのコピーにMACD、MACDライン、シグナルラインの値を表す列を追加したものです。

コードの冒頭では、入力データフレームに終値列が存在するかを確認します。これは、EMAの計算に必要な終値データを取得するためです。さらに、各期間パラメータが正の整数であることを検証します。これらは過去の参照期間を示すため、妥当性確認が不可欠です。また、高速期間が低速期間よりも小さいことも確認します。これにより、MACDが短期トレンドと長期トレンドの差異を正確に反映するようにします。これらの検証ステップにより、実行時エラーを防ぎ、論理的一貫性を確保します。誤った設定によるトレンドの誤解釈は、不適切な取引判断を招くおそれがあるため、慎重さが求められます。 

次に、入力データフレームのコピーを作成します。これは、元データを保持しながら出力を格納するためです。この手法により、他の関数で再利用される可能性のある入力フレームの整合性を損なうことがありません。Pythonにおいては、このようなコピーの使用によりモジュール性と再利用性が高まります。コピーを作成した後、指数加重移動平均関数を使用して、高速期間および低速期間における終値のEMAを計算します。この際、パラメータ「adjust」をfalseに設定し、標準的なEMA式が適用されるようにします。また、spanはウィンドウサイズを指定するパラメータであり、その値によって感度が決まります。spanを小さく設定するとEMAは変化に敏感になり、大きく設定するとノイズを平滑化します。

高速EMAと低速EMAの計算が完了したら、最初の新しいpandasのSeriesを出力データフレームに追加します。  これを「MACD」とラベル付けし、高速EMAと低速EMAの差を計算してMACDラインを生成します。MACDラインは、短期および長期の価格変動の収束と発散を示す中心的な指標です。一般に、MACDが正の値であれば上昇トレンド（強気）、負の値であれば下降トレンド（弱気）を意味します。MACDラインの方向や変化量を監視することで、トレンドの強さを評価することができ、クロスオーバーはトレンド転換のシグナルとなることがあります。

続いて、出力データフレームにシグナルラインのSeriesを追加します。これは、MACDラインをsignal_periodのEMAによって平滑化する計算です。MACDとシグナルラインを平滑化することで、売買シグナルを判断する際の基準を提供します。MACDラインとシグナルラインのクロスオーバーは、取引判断における重要な転換点となります。デフォルトのsignal_period(9)は、感度と平滑性のバランスをとる設定ですが、取引する資産の特性に応じて調整することも可能です。

最後に、出力データフレームにMACDヒストグラムのSeriesを追加します。これは、MACDとシグナルラインの差を計算したもので、モメンタムの強さを視覚的に捉えるのに役立ちます。ヒストグラムの値が正であれば強気、負であれば弱気を示し、符号の変化はトレンドの転換を示唆します。これら3つのpandas Series（MACD、シグナルライン、ヒストグラム）を出力データフレームに追加した時点で、関数の処理は完了し、このデータフレームを返します。

OBV

この関数はオンバランスボリューム(OBV: On-Balance Volume)を計算するものであり、価格変動と出来高の関係を示すボリューム系指標です。Pythonにおける実装例は以下のとおりです。

def OBV(df) -> pd.DataFrame:
    """
    Calculate On-Balance Volume (OBV) and append it as an 'OBV' column 
    to the input DataFrame.

    OBV is a momentum indicator that uses volume flow to predict changes in stock price.
    
    Args:
        df (pd.DataFrame): DataFrame with 'close' and 'volume' columns.
        
    Returns:
        pd.DataFrame: Input DataFrame with a new 'OBV' column.
    """
    # Input validation
    if not all(col in df.columns for col in ['close', 'tick_volume']):
        raise ValueError("DataFrame must contain 'close' and 'volume' columns")

    # Create a copy to avoid modifying the original DataFrame
    result_df = df.copy()
    # print(result_df.columns)
    
    # Calculate the direction of price change
    # np.sign returns 1 for positive, -1 for negative, and 0 for zero change
    direction = np.sign(result_df['close'].diff())
    
    # Calculate the OBV
    # Multiply the volume by the direction of price movement
    # Then calculate the cumulative sum
    obv = (result_df['tick_volume'] * direction).cumsum()
    
    # The first value of diff() is NaN, so the first OBV will be NaN.
    # We can fill it with the first day's volume or 0. A common practice is to start at 0.
    result_df['OBV'] = obv.fillna(0)
    
    return result_df

上記のソースコードは、まずデータフレームを検証するところから始まります。これは、終値(close)およびティック出来高(tick_volume)の列が存在することを確認するためです。ティック出来高を使用しているのは、実際の出来高データが為替ペアのような分散型市場では入手しにくいのに対し、ティック出来高の方が多くの資産クラスで容易に利用可能だからです。この検証が完了した後、入力データフレームのコピーを作成します。これは、後ほどデータを追加するためであり、MACD関数の実装時にも述べたように、元の入力データの整合性を保つための措置です。 

次に、終値変化の方向(direction)を計算します。これらの計算は連続する期間ごとにおこなわれます。np.sign関数を用いて、価格が下落した場合は-1、上昇した場合は+1、変化がない場合は0を割り当てます。このステップは価格変動の方向を明確にするために重要であり、その結果、OBVにおいて出来高がどのように蓄積されるかが決まります。また、このステップによって価格トレンド分析が二値的な形式に簡略化され、出来高データとの統合が容易になります。 

directionベクトルが定義されたら、次にOBVを計算します。これは、出来高とdirectionの積を取り、それを累積和にして時間とともに追跡することで算出されます。OBVは、強気相場では出来高を加算し、弱気相場では出来高を減算することで、出来高に基づく価格変動を蓄積します。したがって、OBVの値は買い圧力や売り圧力を反映します。なお、OBVの絶対値そのものよりも、そのトレンドが重要です。OBVの方向と価格の動きを比較することで、トレンドの確認に役立ちます。

最後に、diff()計算の結果として最初のOBV値に生じるNaNを補完します。これは比較を妨げるため、この欠損値を埋める必要があります。この行では、新しいOBV値を出力データフレーム内のOBVシリーズとして追加します。このインジケーターにおけるOBVの選択は、実用的な理由によるものです。0という値は「どちらの方向にも出来高の偏りがない中立的な状態」を意味しており、移動平均のバッファに0を代入することとは異なります。

前回のメモ

前回の記事では、MACDとOBVの組み合わせによるインジケーターペアを紹介しましたが、その多くのシグナルパターンはフォワードウォークで良好な成績を上げることができませんでした。実際にフォワードウォークで利益を上げられたのはPattern_7だけであり、通常は10個のテストパターンのうち少なくとも6つ程度がフォワードウォークで良好な結果を示すことを考えると、これは大きなアンダーパフォーマンスです。そこで今回は、前回の記事で特に成績が悪かったパターンの一部を取り上げ、教師あり学習を適用することで、より良い結果が得られるかを検証します。具体的には、前回の9つの不調なパターンのうち、Pattern_2、Pattern_3、Pattern_5の3つを選択しました。

Pattern_2

MQL5でPattern_2を次のように実装します。

def feature_2(macd_df, obv_df, price_df):
    """

    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((price_df['low'] < price_df['low'].shift(1)) &
                     (macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((price_df['high'] > price_df['high'].shift(1)) &
                     (macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

要約すると、この手法は価格トレンドのダイバージェンスに基づいています。価格がより低い安値をつける一方でMACDが上昇している場合は隠れた上向きのダイバージェンスを示し、逆に価格がより高い高値をつけているのにMACDが低下している場合は隠れた下向きのダイバージェンスを示します。この考え方に加えて、出来高による確認も組み合わせます。OBVが上昇している場合は資金の蓄積を示し、これはポジティブなシグナルとなります。一方、OBVが低下している場合は資金の分配を示し、これはネガティブなシグナルとなります。要するに、このパターンは価格が極端な動きを示しているにもかかわらずモメンタムが弱まっている状況で検出されるダイバージェンスを、出来高の流れと照合して検証することを目的としています。

既存のトレンドにおける継続パターンを特定することを狙いとしており、確立された上昇トレンドや下降トレンドの中で最も信頼性が高くなります。通常、このシグナルを完全に判断するには、2本のローソク足による確認が必要です。私たちは、2023.01.01から2024.01.01の期間にわたってGBP/JPYペアでテストの設定としては、RQカーネルを組み込んだCNNネットワークを用いてモデルのアーキテクチャを定義し、このパターンから得られる入力シグナルを2023年1月1日から2025年1月1日までの期間で分析しました。学習および最適化は2023年1月1日から2024年1月1日までおこない、テスト対象はGBP/JPYで、4時間足のデータを使用しました。私たちのテストレポートは次のとおりです。

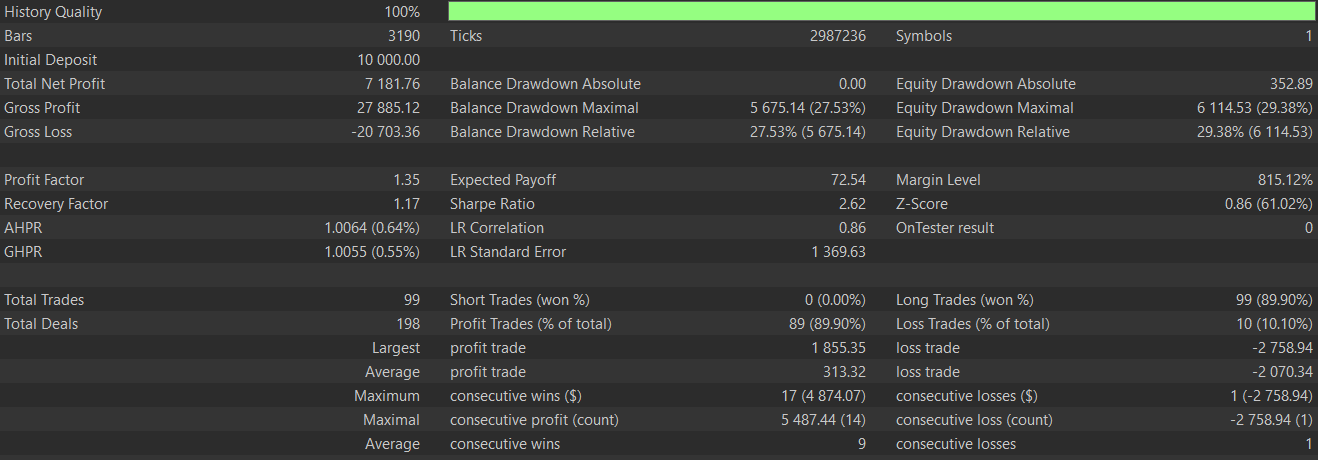
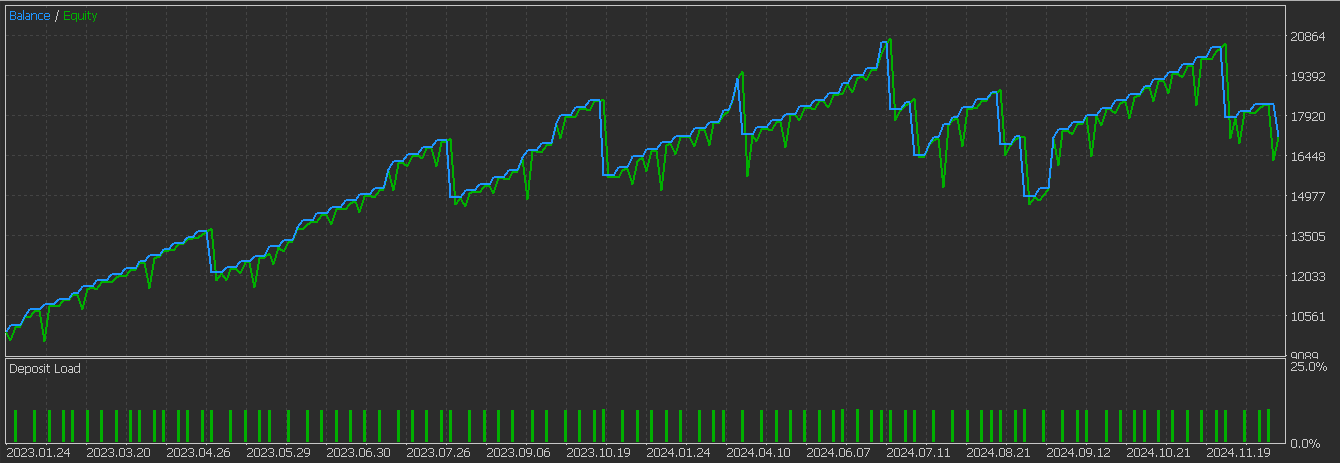
結果を見ると、前回の記事で得られた成績と比べて明らかに改善が見られます。したがって、今回の教師あり学習モデルは有効に機能したと言えます。とはいえ、ここで提示するアイデアを実際の運用に適用する前には、読者自身による慎重な検証と独立したテストが強く推奨されます。本連載は主に自動売買を念頭に置いていますが、実際のチャート上でこれらのパターンがどのように現れるかを理解することも、有益な洞察を得る上で役立ちます。以下に、このパターンにおけるポジティブシグナルの例を示します。

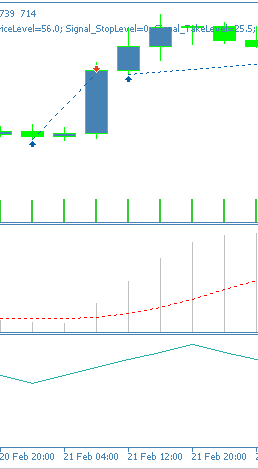
Pattern_3

このパターンをPythonで次のように実装します。

def feature_3(macd_df, obv_df, price_df):
    """
    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'].shift(1) < macd_df['MACD_Histogram'].shift(2)) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'].shift(1) > macd_df['MACD_Histogram'].shift(2)) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

このパターンは、MACDヒストグラムの反転を捉えることを目的としています。上向きのシグナルは、ヒストグラムが下降した後に上昇することで示される谷（トラフ）によって確認されます。一方、下向きのシグナルは、ヒストグラムが直前のバーで上昇していた後に下降することで示される山（ピーク）によって確認されます。ヒストグラムはモメンタムの転換点を捉えることを目的としており、谷や山のパターンを正確に定義し、誤ったシグナルを減らすために、少なくとも3本のバーが必要です。

これと同時に、OBVはトレンドの整合性を提供します。出来高の方向が価格トレンドと一致していることが望ましく、正の値は上向きシグナルを確認し、負の値は下向きシグナルを確認します。理論上、これは機関投資家の参加を示すことになります。Pattern_2と同様の条件でテストをおこなった結果、フォワードウォークテストでも良好な結果が期待できる以下のレポートが得られました。

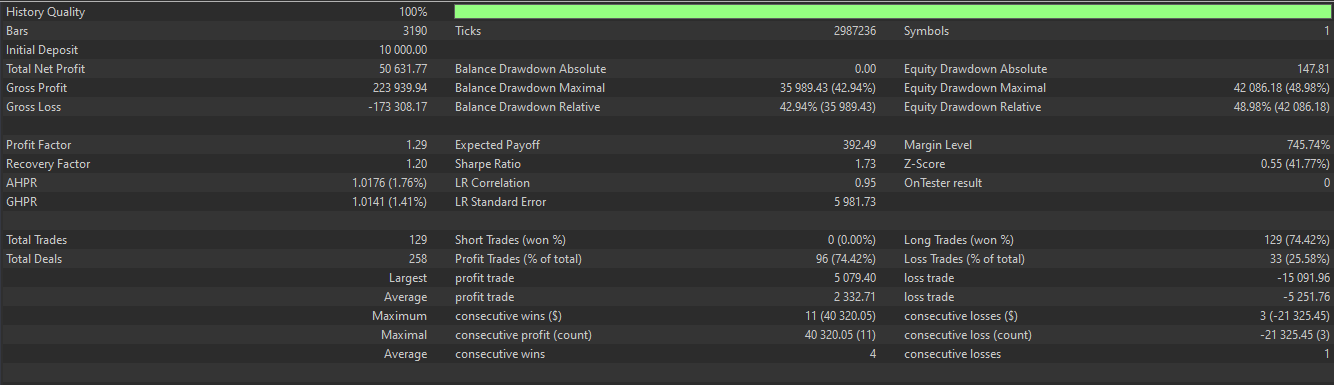
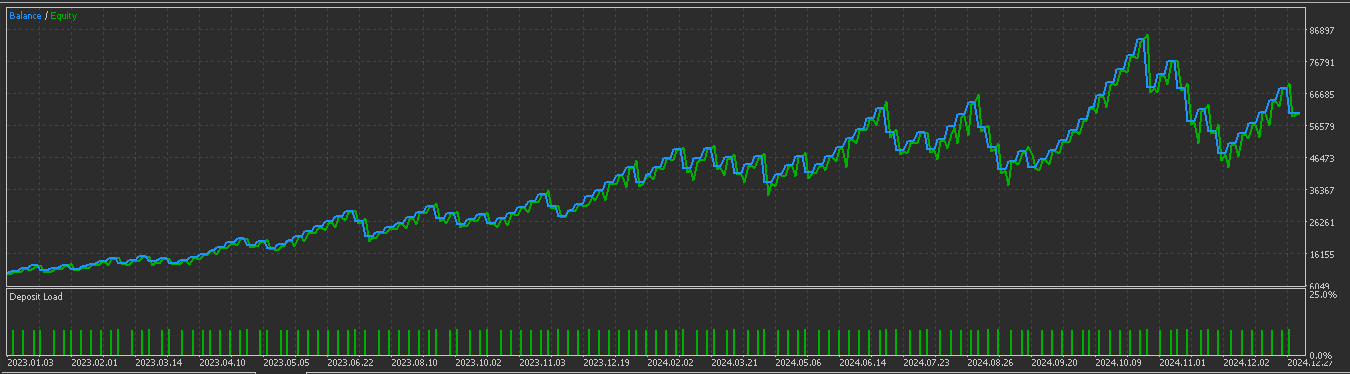
このシグナルパターンは、トレンドの反転を狙うのに適しており、過熱状態や売られすぎの局面におけるピボットで有効に機能することがあります。少なくとも3本のバーの価格履歴が必要なため、シリーズの最初の2本のバーは比較データがないためゼロとして扱われます。チャート上での表現例は、上向きシグナルの場合は次のようになります。

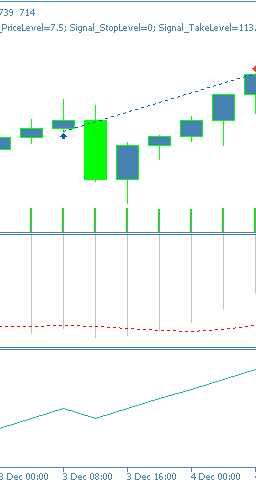
Pattern_5

このパターンはPythonで次のように実装します。

def feature_5(macd_df, obv_df, price_df):
    """

    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'] < 0.0) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'] > 0.0) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Pattern_5は、MACDのゼロラインの状況に基づいた手法です。このパターンは早期エントリーを狙うもので、MACDがゼロ以下の弱気領域にある場合に上向きシグナルが示され、逆にMACDがゼロ以上にある場合に下向きシグナルが示されます。このパターンで示されるモメンタムの変化を確認するために、サードパーティの指標を併用すると誤ったシグナルを回避するのに役立ちます。また、出来高の方向フィルタは、機関投資家の関心を確認する意味で、出来高のモメンタム変化と一致していることが望ましいです。

このパターンでは、強気のシグナルは売られ過ぎの状況で勢いが増している場合に弱まりやすく、弱気のシグナルは買われ過ぎの状況で勢いが弱まっている場合に弱まりやすい傾向があります。このパターンはレンジ相場でより効果的であり、MACDがピボットしているか回復中である必要があります。上記の2つのパターンと同様に、楽手と最適化後にこのパターンをテストした結果、以下のテストレポートが得られました。

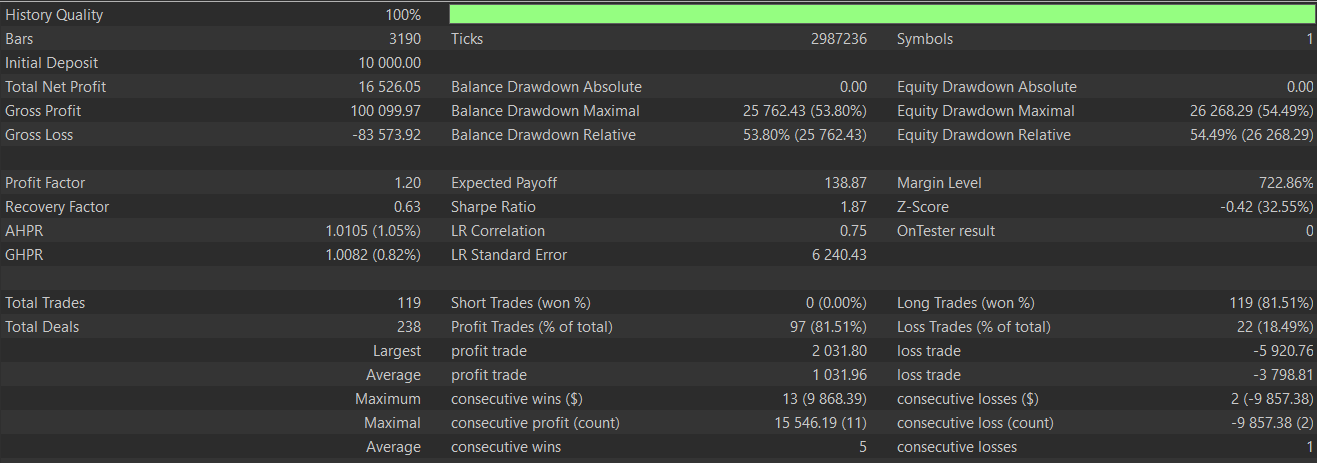
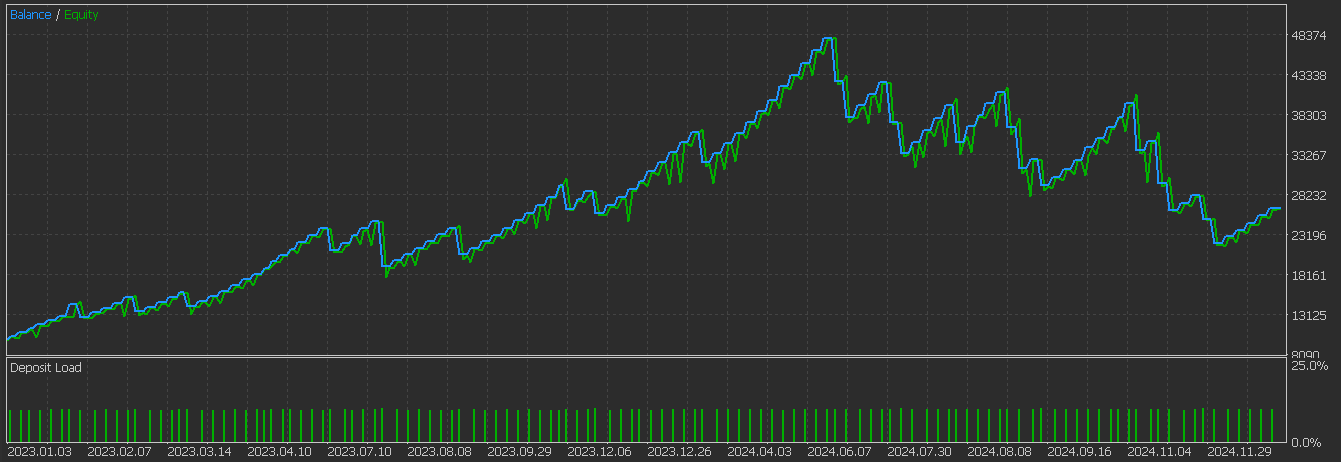
ここでテストした3つの中では、このパターンは依然としてフォワードテストで苦戦しているようです。これは、独立したモメンタムのピボットが確認されない早期タイミングでの偽のMACDシグナルが原因である可能性があります。チャート上のパターンは次のように示されます。

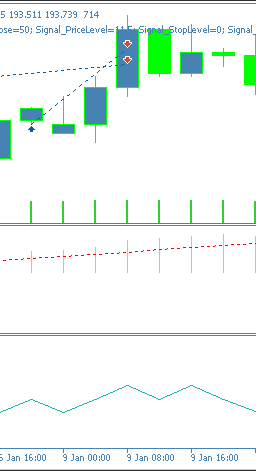
結論

要約すると、前回の記事で紹介したMACDとOBVの指標ペアリングを再確認し、いくつかのシグナルパターンのパフォーマンス低迷を改善できるかを検証しました。Rational Quadraticカーネルを用いてカーネルサイズとチャネルサイズを設定する監視学習CNNを使用したところ、再検討した3つのパターンのうち2つは改善が見られました。残る3つ目のパターン(Pattern_5)は、より多くの確認が必要な弱いエントリーポイントが原因で低迷しています。

名前	説明
WZ-72.mq5	ヘッダでインクルードファイルを示す、ウィザード作成EA
SignalWZ_72.mqh	ウィザードアセンブリで使用されるカスタムシグナルクラスファイル
72_2.onnx	Pattern_2用のPythonエクスポートネットワーク
72_3.onnx	Pattern_3用のPythonエクスポートネットワーク
72_5.onnx	Pattern_5用のPythonエクスポートネットワーク

添付のカスタムシグナルファイルは、MQL5ウィザードを使用してEAに組み込むことを想定しています。新しい読者向けに、その手順についてのガイドも用意されています。