MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 15): Support-Vektor-Maschinen mit dem Newtonschen Polynom

Einführung

Die Support Vector Machine (SVM) ist ein Klassifizierungsalgorithmus des maschinellen Lernens. Die Klassifizierung unterscheidet sich von der Clusterbildung, die wir in früheren Artikeln hier und hier behandelt haben. Der Hauptunterschied zwischen den beiden besteht darin, dass bei der Klassifizierung die Daten in vordefinierte Gruppen aufgeteilt werden (Überwachtes Lernen), während bei der Clusterbildung versucht wird, zu bestimmen, welche und wie viele dieser Gruppen es gibt (Unüberwachtes Lernen).

Kurz gesagt, SVM klassifiziert Daten, indem es die Beziehung zwischen jedem Datenpunkt und allen anderen berücksichtigt, wenn eine Dimension zu den Daten hinzugefügt wird. Eine Klassifizierung wird erreicht, wenn eine Hyperebene definiert werden kann, die die vordefinierten Datensätze sauber zerlegt.

Oft haben die betrachteten Datensätze mehrere Dimensionen, und genau diese Eigenschaft macht die SVM zu einem sehr leistungsfähigen Werkzeug bei der Klassifizierung solcher Datensätze, insbesondere wenn die Anzahl der Datensätze klein ist oder das relative Verhältnis der Datensätze schief ist. Der Quellcode für die Implementierung von SVMs, die mehr als zwei Dimensionen haben, ist sehr komplex, und in vielen Anwendungsfällen in Python oder C# werden immer Bibliotheken verwendet, sodass der Nutzer nur ein Minimum an Code eingeben muss, um ein Ergebnis zu erhalten.

Hochdimensionierte Daten neigen zu einer Kurvenanpassung der Trainingsdaten, was die Zuverlässigkeit der SVM bei Daten außerhalb der Stichprobe stark beeinträchtigt. Daten mit niedrigeren Dimensionen hingegen lassen sich viel besser kreuzvalidieren, und es gibt mehr allgemeine Anwendungsfälle.

In diesem Artikel betrachten wir einen sehr einfachen SVM-Fall, der 2-dimensionale Daten verarbeitet (auch bekannt als linear-SVM), da der komplette Quellcode der Implementierung ohne Bezug auf Bibliotheken Dritter gemeinsam genutzt werden soll. Normalerweise wird die trennende Hyperebene von einer der beiden Methoden abgeleitet: einem polynomial Kernel oder einem radialen Kernel. Letzteres ist komplexer und wird hier nicht behandelt, da wir uns nur mit dem ersten, dem Polynomkernel, beschäftigen.

Bei der Verwendung des Polynomkernels wird dies in der Regel durch die nachstehende Gleichung definiert:

die die idealen c- und d-Werte bestimmen und die Gleichung der Hyperebene festlegen. Es ist ein iterativer Prozess, der darauf abzielt, dass die Vektoren so weit wie möglich auseinander liegen, da sie den Abstand zwischen den beiden Datensätzen messen.

In diesem Artikel werden wir jedoch, wie im Titel angegeben, das Newtonsche Polynom zur Ableitung der Gleichung der Hyperebene auf 2-dimensionalen Datensätzen verwenden. Wir hatten uns in einem kürzlich erschienenen Artikel mit dem Newton'schen Polynom befasst und werden einen Teil seiner Umsetzung überfliegen.

Wir implementieren das Newtonsche Polynom (NP) in drei Szenarien. Zunächst werden die Mittelpunkte zwischen zwei vordefinierten Datensätzen interpoliert, um eine Reihe von Punkten zu erhalten, die zur Ableitung einer Geraden/Kurvengleichung verwendet werden, die unsere Hyperebene definiert. Nachdem diese Hyperebene definiert wurde, wird sie als Klassifikator bei der Ausführung von Handelsentscheidungen für eine zu verwendende Klasse von Testsignalen verwendet. Im zweiten Szenario fügen wir eine Regressionsfunktion hinzu, sodass die Expertensignalklasse nicht nur 0 oder 100 Werte ausgibt (wie im ersten Szenario), sondern auch Werte zwischen diesen beiden Werten liefert. Der Regressionswert errechnet sich daraus, wie nahe der nicht klassifizierte Vektor an den bekannten Vektorpunkten liegt. Drittens bauen wir auf dem zweiten Szenario auf, indem wir bei der Definition der Hyperebene nur eine kleine Anzahl von Punkten interpolieren. Die kleine Anzahl von Punkten, auch Support-Vektoren genannt, sind diejenigen, die näher am anderen Datensatz liegen und somit die Hyperebenengleichung „verfeinern“, während alles andere übernommen wird.

Hintergrund zum Polynom-Kernel

Für diesen Beitrag ziehen wir lineare SVMs in Betracht, da die gesamte Quellcode-Implementierung gemeinsam genutzt werden soll und wir die Verwendung von Bibliotheken vermeiden wollen, indem wir vollständige Transparenz über den gesamten Quellcode bieten. In realen Anwendungen der SVM werden jedoch die nichtlinearen Typen angesichts der inhärenten Komplexität und Multidimensionalität vieler Datensätze häufig verwendet. Der Umgang mit diesen Herausforderungen in SVMs hat sich durch Kernel-Trick als überschaubar erwiesen. Mit dieser Methode kann ein Datensatz in einer höheren Dimension untersucht werden, wobei seine ursprüngliche Struktur erhalten bleibt. Kernel-Trick verwendet das Punktprodukt von Vektoren, um die Werte von Vektoren niedrigerer Dimension zu erhalten. Indem man den Datensatz auf höhere Dimensionen ausrichtet, wird die Trennung der Datensätze leicht erreicht, und dies geschieht auch mit weniger Rechenressourcen.

Wie oben erwähnt, ist unsere Kernel-Funktion formal wie folgt definiert:

wobei x und y als Datenpunkte zwischen zwei beliebigen verglichenen Datenpunkten in jedem Satz dienen, c eine Konstante ist (deren Wert anfangs oft auf 1 gesetzt wird) und d der Polynomgrad ist. Mit zunehmendem d kann eine genauere Hyperebenengleichung definiert werden, was jedoch zu einer Überanpassung führt, sodass ein Gleichgewicht gefunden werden muss. Die Datenpunkte x und y liegen in vielen Fällen im Vektor- oder sogar Matrixformat vor, weshalb die Potenz T die Transponierung von x darstellt.

Die Implementierung eines Polynomkerns in MQL5 könnte zur Veranschaulichung folgendermaßen aussehen.

//+------------------------------------------------------------------+
//| Define a data point structure                                    |
//+------------------------------------------------------------------+
struct Sdatapoint
{  double      features[2];
   int               label;
                     Sdatapoint()
   {                 ArrayInitialize(features, 0.0);
      label = 0;
   };
                    ~Sdatapoint() {};

};

//+------------------------------------------------------------------+
//| Function to calculate the polynomial kernel value                |
//+------------------------------------------------------------------+
double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree)
{  double _kernel_sum = 0.0;
   for (int i = 0; i < 2; i++)
   {  _kernel_sum += (A.features[i] * B.features[i]);
   }
   _kernel_sum += Constant; // Add constant term
   return(pow(_kernel_sum, Degree));
}

Beziehungsgewichte zwischen Datenpunkten, die sich in separaten Sätzen befinden, werden berechnet und in einer Kernelmatrix gespeichert. Diese Kernelmatrix quantifiziert den Abstand der Datenpunkte und filtert daher für die Stützvektoren die Datenpunkte heraus, die sich am Rande jedes Datensatzes befinden und näher am Nachbarsatz liegen.

Quelle

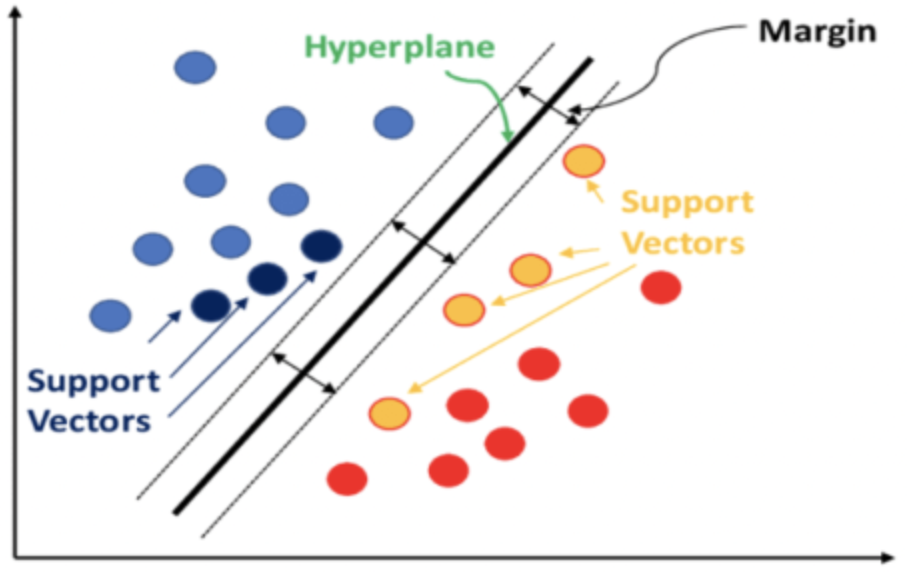
Diese Stützvektoren dienen dann als Eingabe für die Berechnung der Hyperebenengleichung. All dies wird in Bibliotheksfunktionen wie: PyLIBSVM, oder shogun für Python; oder kernlab oder SVMlight in R. Es sind Bibliotheksfunktionen wie diese, die angesichts der komplexen Natur der Ableitung der Hyperebenengleichung die Hyperebene berechnen und ausgeben.

Bei der Bestimmung der Kernelmatrix können verschiedene Konstanten- und Polynomgradwerte berücksichtigt werden, um eine optimale Lösung zu finden. Da dies aber den ohnehin schon komplexen Prozess der Ableitung einer Hyperebene aus nur einer Matrix noch komplizierter macht, indem man dies über mehrere Matrizen hinweg tut, ist es sinnvoller, zu Beginn immer eine definitive (oder aus Erfahrung suboptimale) Konstante und einen Polynomgrad zu wählen und damit zur Hyperebene zu gelangen. Zu diesem Zweck wird der konstante Wert auch oft auf 1 gesetzt. Wie zu erwarten, ist die Klassifizierung umso besser, je höher der Grad des Polynoms ist, aber dies birgt die bereits erwähnte Gefahr der Überanpassung.

Außerdem sind höhere Polynomgrade in der Regel rechenintensiver, sodass zu Beginn ein intuitiver Wert festgelegt werden muss, der nicht zu hoch ist.

Die hier betrachteten polynomialen Kernel sind relativ einfach zu verstehen, aber sie sind nicht der am häufigsten verwendete oder bevorzugte Kernel in vielen SVM-Implementierungen, da diese Rechte an den Radiale Basisfunktion gehen.

Der RBF-Kernel (Radial Base Function) wird am häufigsten gewählt, da der Vorteil der SVM in der Verarbeitung mehrdimensionaler Daten liegt und der RBF-Kernel dies besser kann als der Polynom-Kernel. Sobald ein Kernel gewählt ist, wird das duale Optimierungsproblem, bei dem, wie oben erwähnt, die Datensätze auf einen höherdimensionalen Raum abgebildet werden, in Angriff genommen, und dank der Punktproduktregeln, die im so genannten Kernel-Trick erfasst sind, kann diese Optimierung (hin und her) effizienter durchgeführt und gleichzeitig einfacher ausgedrückt werden. Die Komplexität der Hyperebenengleichungen für Datensätze mit mehr als 2 Dimensionen macht dies unerlässlich. Letztendlich hat die Hyperebenengleichung die folgende Form:

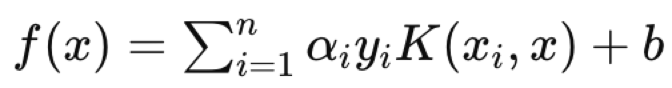
wobei:

• f(x) ist die Entscheidungsfunktion.
• αi​ sind die Koeffizienten, die sich aus dem Optimierungsprozess ergeben.
• yi​ sind die Klassenbezeichnungen.
• K(xi​,x) ist die Kernel-Funktion.
• b ist der Bias-Term.

Die Hyperebenengleichung legt fest, wie die beiden Datensätze durch die Entscheidungsfunktion getrennt werden, die eine Klassenbezeichnung zuweist, die definiert, zu welcher Seite ein beliebiger Abfragepunkt gehört. Ein Abfragedatenpunkt wäre also das x in der Gleichung, wobei xi und yi die Trainingsdaten bzw. deren Klassifikatoren sind.

Nebenbei bemerkt, die Anwendungsmöglichkeiten von SVM sind vielfältig und reichen von der Spam-Filterung, wenn man E-Mail-Kopfzeilen und -Inhalte in ein strukturiertes Format einbetten kann, bis hin zum Screening von Kreditantragstellern auf Zahlungsausfälle usw. Was SVM im Gegensatz zu anderen Alternativen des maschinellen Lernens ideal macht, ist die Robustheit bei der Entwicklung von Modellen aus kleinen oder sehr verzerrten Datensätzen.

Implementierung in MQL5

Die Modellstruktur, die wir für die Speicherung von x- und y-Werten verwenden, ist unseren bisherigen Implementierungen sehr ähnlich, mit dem Unterschied, dass hier ein Zähler für jeden Klassifikatortyp hinzugefügt wurde. SVM ist von Natur aus ein Klassifikator, und wir werden uns Beispiele aus der Praxis ansehen, bei denen diese Zähler nützlich sind.

Die Werte des x-Vektors sind also bei jedem Index 2, da wir die Mehrdimensionalität unserer Datensätze auf 2 beschränken, um das Newtonsche Polynom verwenden zu können. Mit zunehmender Dimensionalität besteht auch die Gefahr der Überanpassung. Die erste Dimension oder der erste Wert von x ist die Veränderung des Hochpreispuffers, während die zweite Dimension erwartungsgemäß die Veränderung des Niedrigpreispuffers sein wird. Die Auswahl der Eingabedaten ist heute ein entscheidender Aspekt beim maschinellen Lernen. Obwohl Transformatoren, CNNs und RNNs sehr einfallsreich sind, kann die Entscheidung über die Eingabedaten und die Art und Weise, wie sie eingebettet oder normalisiert werden, kritischer sein.

Wir haben einen sehr einfachen Datensatz gewählt, aber der Leser sollte sich darüber im Klaren sein, dass seine Wahl der Eingabedaten nicht auf rohe Preisdaten oder sogar Indikatorwerte beschränkt ist, sondern auch Werte von Wirtschaftsindikatoren umfassen kann. Und auch hier kann die Art und Weise, wie man dies normalisiert, den entscheidenden Unterschied ausmachen.

//+------------------------------------------------------------------+
//| Function to get and prepare data.                                |
//+------------------------------------------------------------------+
double CSignalSVM::GetOutput(int Index)
{  double _get = 0.0;
   

        ....
        ....

   int _x = StartIndex() + Index;
   for(int i = 0; i < m_length; i++)
   {  for(int ii = 0; ii < Dimensions(); ii++)
      {  if(ii == 0) //dim-1
         {  m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1);
         }
         else if(ii == 1) //dim-2
         {  m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1);
         }
      }
      if(i > 0) //assign classifier
      {  if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0)
         {  m_model.y[i - 1] = 1;
            m_model.y1s++;
         }
         else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0)
         {  m_model.y[i - 1] = 0;
            m_model.y0s++;
         }
      }
   }
//
   _get = SetOutput();
   return(_get);
}

Bei unserem y-Datensatz handelt es sich um vorwärts verzögerte Änderungen des Schlusskurses, wie es bisher der Fall war. Wir führen Zähler für die beiden Klassen ein, die mit „y0“ und „y1“ bezeichnet werden. Diese protokollieren einfach für jeden verarbeiteten Balken, dessen zwei x-Werte ermittelt wurden, ob die anschließende Veränderung des Schlusskurses nach oben gerichtet war (in diesem Fall wird eine 0 protokolliert) oder nach unten gerichtet war (in diesem Fall würde eine 1 aufgezeichnet werden).

Da y ein Vektor ist, könnten wir nebenbei diese 0- und 1-Zählungen abrufen, indem wir die aktuellen Werte mit Vektoren vergleichen, die mit Nullen und Vektoren, die mit Einsen gefüllt sind, da die zurückgegebenen Werte effektiv eine Zählung der vorhandenen Nullen bzw. Einsen im y-Vektor darstellen würden.

Die Funktion „set-output“ ist eine weitere Ergänzung zu den Funktionen, die wir für die Verarbeitung unserer Modellinformationen hatten. Es nimmt x Vektorwerte für jede Klasse und interpoliert einen Mittelpunkt zwischen den beiden Gruppen, der als Hyperebene der beiden Gruppen dienen könnte. Dies ist nicht der bereits erwähnte SVM-Ansatz, aber da wir eine Hyperebene durch das Newtonsche Polynom definieren wollen, gibt uns dies eine Reihe von Punkten, mit denen wir arbeiten können, um eine Hyperebenengleichung abzuleiten.

//+------------------------------------------------------------------+
//| Function to set and train data                                   |
//+------------------------------------------------------------------+
double CSignalSVM::SetOutput(void)
{  double _set = 0.0;
   matrix _a,_b;
   Classifier(_a,_b);
   if(_a.Rows() * _b.Rows() > 0)
   {  matrix _interpolate;
      _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions());
      for(int i = 0; i < int(_a.Rows()); i++)
      {  for(int ii = 0; ii < int(_b.Rows()); ii++)
         {  _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]);
            _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]);
         }
      }
      vector _w;
      vector _x = _interpolate.Col(0);
      vector _y = _interpolate.Col(1);
      _w.Init(m_model.y0s * m_model.y1s);
      _w[0] = _y[0];
      m_newton.Set(_w, _x, _y);
      double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0;
      m_newton.Get(_w, _xx, _zz);
      if(_yy < _zz)
      {  _set = 100.0;
      }
      else if(_yy > _zz)
      {  _set = -100.0;
      }
      _set *= Regressor(_x, _y, _xx, _yy);
   }
   return(_set);
}

Wir betrachten 3 Ansätze zur Ableitung der Hyperebene im Rahmen dieser Methode. Der erste Ansatz berücksichtigt alle Punkte in jeder Menge, um die Punkte der Hyperebene zu ermitteln, indem der Mittelwert jedes Punktes in einer Menge mit jedem Punkt in der anderen Menge interpoliert wird. Dieser Ansatz berücksichtigt natürlich keine Stützvektoren, wird aber hier zu Studienzwecken und zum Vergleich mit den anderen Ansätzen vorgestellt.

Die zweite Methode ähnelt der ersten, mit dem einzigen Unterschied, dass der prognostizierte y-Wert regressiert wird, d.h. anstatt ihn als 0 oder 1 zu haben, verwenden wir die Funktion „regulizer“, um die Ausgabeprognosen als Gleitkommawert im Bereich von 0,0 bis 1,0 zu transformieren oder zu normalisieren. Dadurch entsteht ein System, das im Prinzip noch weiter von SVMs entfernt ist, aber immer noch eine Hyperebene zur Unterscheidung von 2-dimensionalen Datenpunkten verwendet.

//+------------------------------------------------------------------+
//| Regressor for the model                                          |
//+------------------------------------------------------------------+
double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY)
{  double _x_max = fmax(X.Max(), XX);
   double _x_min = fmin(X.Min(), XX);
   double _y_max = fmax(Y.Max(), YY);
   double _y_min = fmin(Y.Min(), YY);
   return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min)))));
}

Wir sind in der Lage, einen stellvertretenden regressiven Wert zu erhalten, indem wir den Prognosewert mit dem Höchst- und Mindestwert in seiner Menge vergleichen, sodass bei Übereinstimmung mit dem Mindestwert 0 zurückgegeben wird, während bei Übereinstimmung mit dem Höchstwert 1 zurückgegeben werden würde.

Drittens und letztens verbessern wir die Methode in Teil 2, indem wir die Funktion „classifier“ hinzufügen, die die Punkte in jeder der Gruppen filtert, die bei der Ableitung der Hyperebene verwendet werden. Indem man die Punkte berücksichtigt, die am weitesten vom Schwerpunkt der eigenen Gruppe entfernt sind und gleichzeitig am nächsten zum Schwerpunkt der gegnerischen Gruppe liegen, erhält man zwei Teilmengen von Punkten, eine aus jeder Klasse, die zur Interpolation der Hyperebenengrenze zwischen den beiden Gruppen verwendet werden können.

//+------------------------------------------------------------------+
//| 'Classifier' for the model that identifies Support Vector points |
//|  for each set.                                                   |
//+------------------------------------------------------------------+
void CSignalSVM::Classifier(matrix &A, matrix &B)
{  if(m_model.y0s * m_model.y1s > 0)
   {  matrix _a_centroid, _b_centroid;
      _a_centroid.Init(1, Dimensions());
      _b_centroid.Init(1, Dimensions());
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  _a_centroid[0][0] += m_model.x[i][0];
            _a_centroid[0][1] += m_model.x[i][1];
         }
         else if(m_model.y[i] == 1)
         {  _b_centroid[0][0] += m_model.x[i][0];
            _b_centroid[0][1] += m_model.x[i][1];
         }
      }
      _a_centroid[0][0] /= m_model.y0s;
      _a_centroid[0][1] /= m_model.y0s;
      _b_centroid[0][0] /= m_model.y1s;
      _b_centroid[0][1] /= m_model.y1s;
      double _a_sd = 0.0, _b_sd = 0.0;
      double _ab_sd = 0.0, _ba_sd = 0.0;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _a_sd += sqrt(_0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _ab_sd += sqrt(_1);
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _b_sd += sqrt(_1);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _ba_sd += sqrt(_0);
         }
      }
      _a_sd /= m_model.y0s;
      _ab_sd /= m_model.y0s;
      _b_sd /= m_model.y1s;
      _ba_sd /= m_model.y1s;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1))
            {  A.Resize(A.Rows()+1,Dimensions());
               A[A.Rows()-1][0] = m_model.x[i][0];
               A[A.Rows()-1][1] = m_model.x[i][1];
            }
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0))
            {  B.Resize(B.Rows()+1,Dimensions());
               B[B.Rows()-1][0] = m_model.x[i][0];
               B[B.Rows()-1][1] = m_model.x[i][1];
            }
         }
      }
   }
}

Der oben geteilte Code, der dies tut, ist etwas langwierig, und ich bin sicher, dass effizientere Implementierungen davon gemacht werden können, insbesondere wenn man die eingebauten Funktionen der Vektor- und Matrix-Datentypen nutzen würde, die kürzlich in MQL5 eingeführt wurden. Wir suchen jedoch zunächst den Schwerpunkt (oder Durchschnitt) jedes Datensatzes. Sobald diese definiert ist, wird die Standardabweichung jedes Datensatzes berechnet, die durch die Variablen mit dem Suffix „_sd“ ermittelt wird. Sobald wir die Koordinaten des Schwerpunkts und die Größe der Standardabweichung haben, können wir für jeden Punkt messen und vergleichen, wie weit er von seinem Schwerpunkt entfernt ist und wie weit er vom Schwerpunkt des gegnerischen Datensatzes entfernt ist, wobei die berechneten Standardabweichungen als Schwellenwert für zu weit oder zu nah dienen.

Die interpolierten Punkte sind alles, was wir brauchen, um eine Gleichung mit dem Newtonschen Polynom zu definieren. Wie wir hier gesehen haben, ist der Gleichungsexponent umso höher, je mehr Punkte man angibt. Die maximale Anzahl der interpolierten Punkte, die wir mit dem Newtonschen Polynom verwenden können, wird durch die Größe der Datensätze gesteuert und ist direkt proportional zum Parameter „m_length“, einer Variablen, die festlegt, wie viele Datenpunkte in der Vergangenheit wir bei der Definition der beiden Datensätze im Modell zurückblicken müssen.

Von den drei Methoden zur Ableitung einer Hyperebene hat nur die letzte Ähnlichkeit mit den typischen SVM-Methoden. Durch das Screening der Punkte innerhalb jeder Menge, die der Grenze der Menge am nächsten liegen und daher für die Hyperebene relevanter sind, definieren wir die Stützvektoren. Diese Stützvektorpunkte dienen dann als Eingabe für unsere Newton-Polynomklasse zur Ableitung der Hyperebenengleichung. Im Gegensatz dazu würden wir bei einer strengen SVM unseren Datenpunkten eine zusätzliche Dimension für eine zusätzliche Differenzierung hinzufügen, während wir durch die Konstanten in der Polynom-Kernel-Gleichung iterieren, die dies ermöglicht. Selbst bei nur zweidimensionalen Daten ist es eindeutig um eine Größenordnung komplizierter, ganz zu schweigen von den erforderlichen Rechenressourcen. Der Einfachheit halber oder wegen der besten Praxis wird eine dieser Konstanten (das c) immer als 1 angenommen, während nur die Variable des Polynomgrades (das d in den obigen Gleichungen) optimiert wird. Und wie Sie sich vorstellen können, würde dies bei Datensätzen mit mehr als 2 Dimensionen eindeutig eine Bibliothek eines Drittanbieters erforderlich machen, da die gesuchte Gleichung mit 4, 5 oder n-ten Exponenten um einige Größenordnungen komplexer sein wird, als dies sonst der Fall wäre.

Die Implementierung des Newton-Polynoms ist sehr ähnlich zu dem, was wir im vorhergehenden Artikel behandelt haben, mit Ausnahme einiger Fehlersuche bei der Funktion „Get“, die die erstellte Gleichung ausführt, um den nächsten y-Wert zu bestimmen. Dieser ist unten beigefügt.

Testergebnisse

Die 3 Signalklassendateien, die am Ende dieses Artikels angehängt sind, können jeweils mit dem MQL5-Assistenten zu einem Expert Advisor zusammengestellt werden. Beispiele dafür, wie dies geschieht, finden Sie in den Artikeln hier und hier.

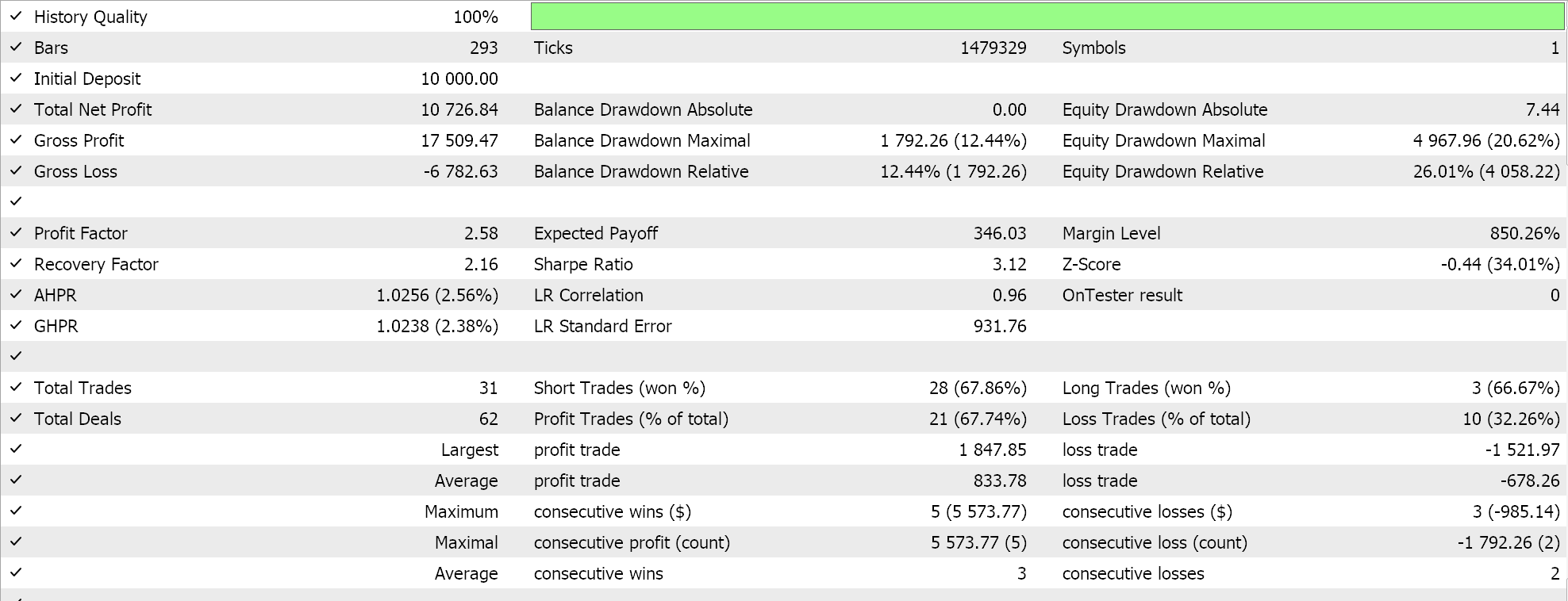
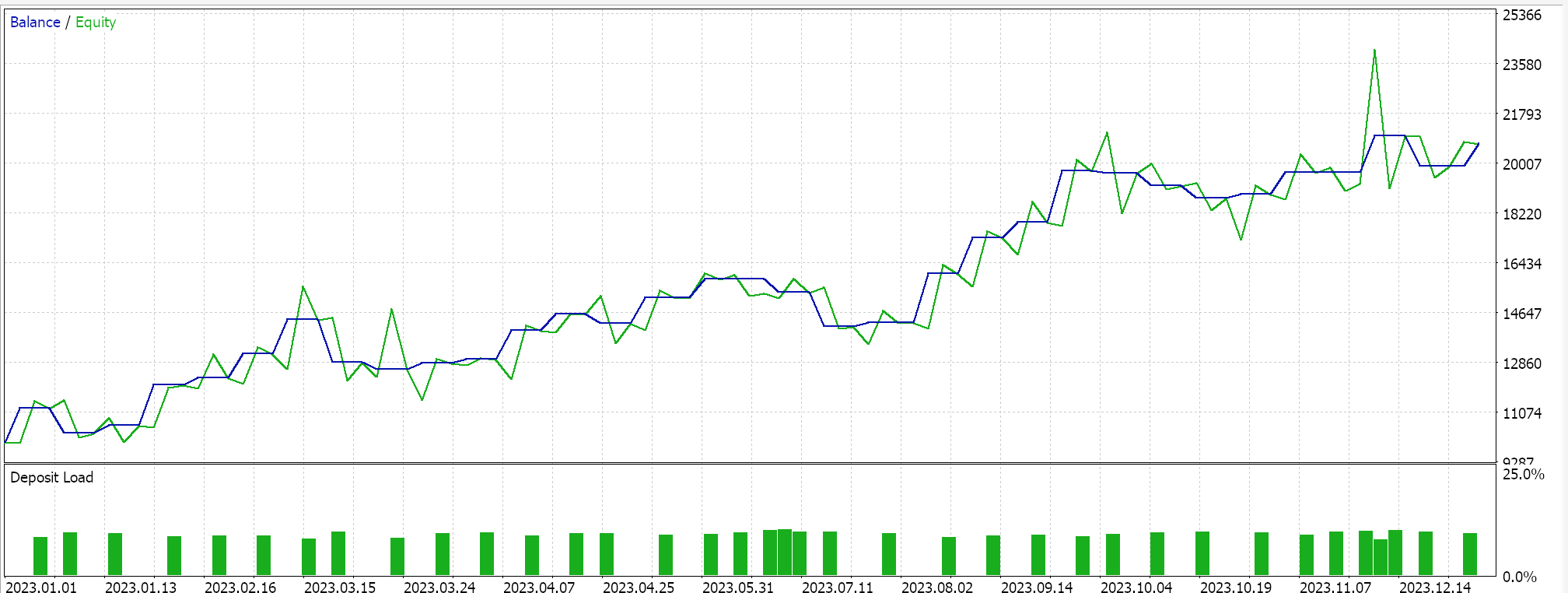
Wenn wir also Tests für die allererste Implementierung durchführen, bei der die Hyperebene durch Interpolation über alle Punkte in einer der beiden Mengen ohne Screening nach Stützvektoren ermittelt wird, erhalten wir die folgenden Ergebnisse:

Wenn wir ähnliche Testläufe wie oben durchführen, wobei unser Testsymbol EURJPY auf dem täglichen Zeitrahmen für das Jahr 2023 ist, ergibt sich für die zweite Methode, die nur die Regression zur obigen Methode hinzufügt, Folgendes:

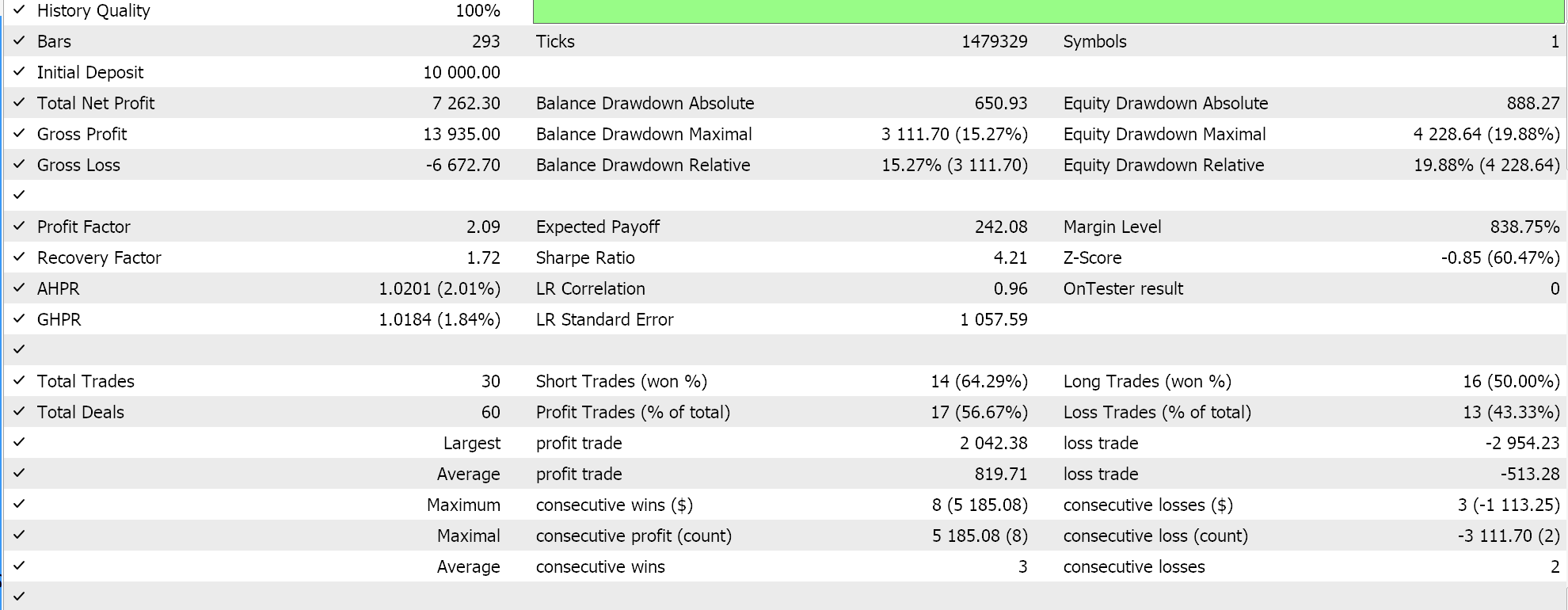
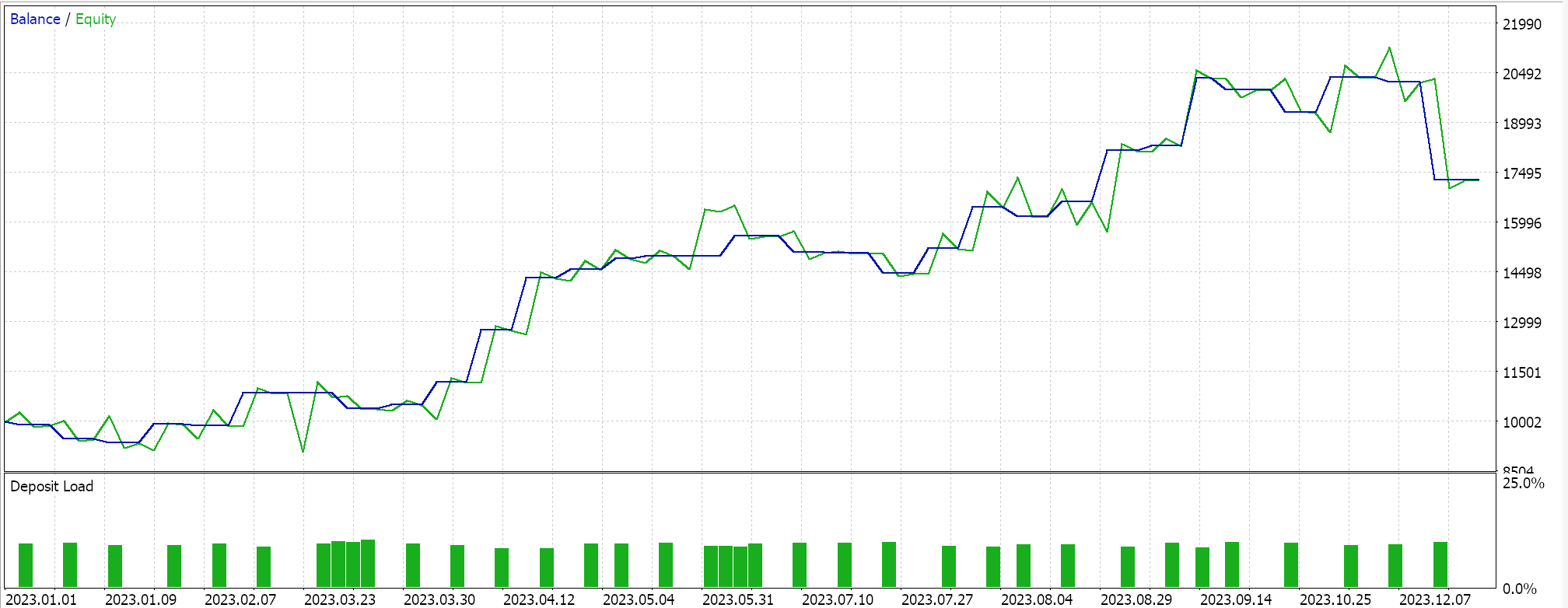
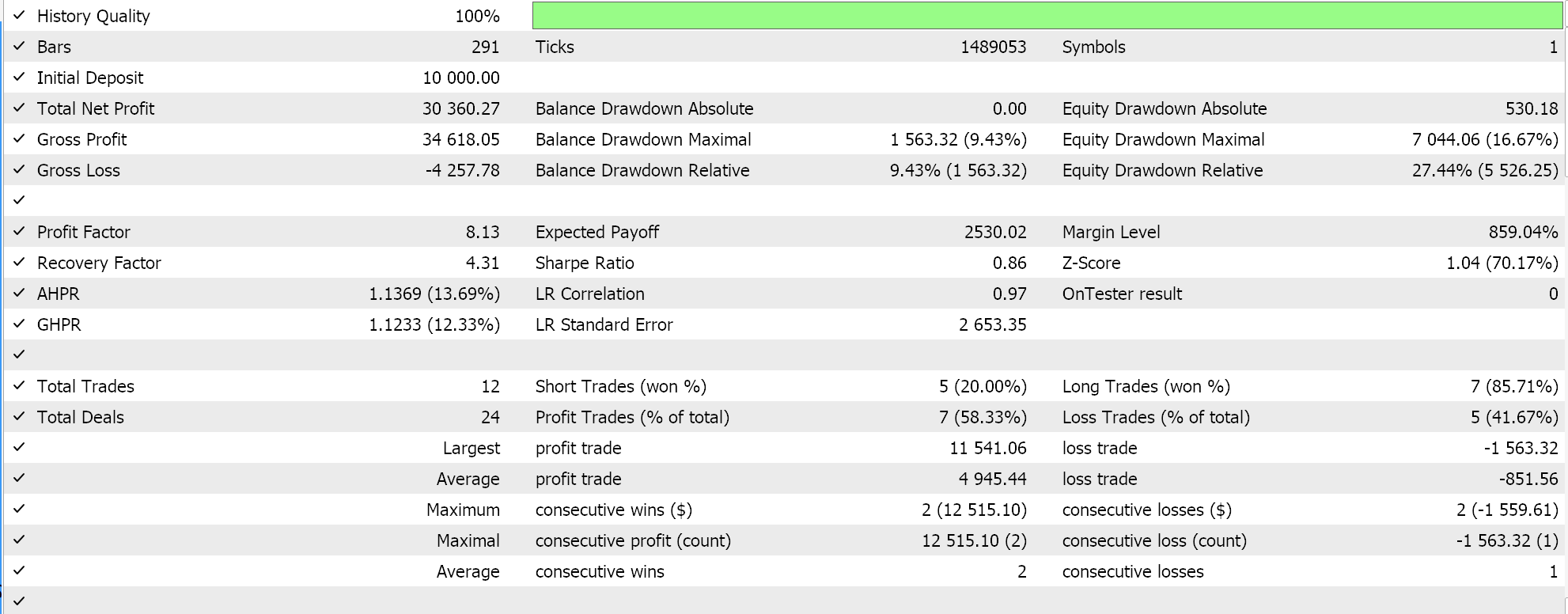
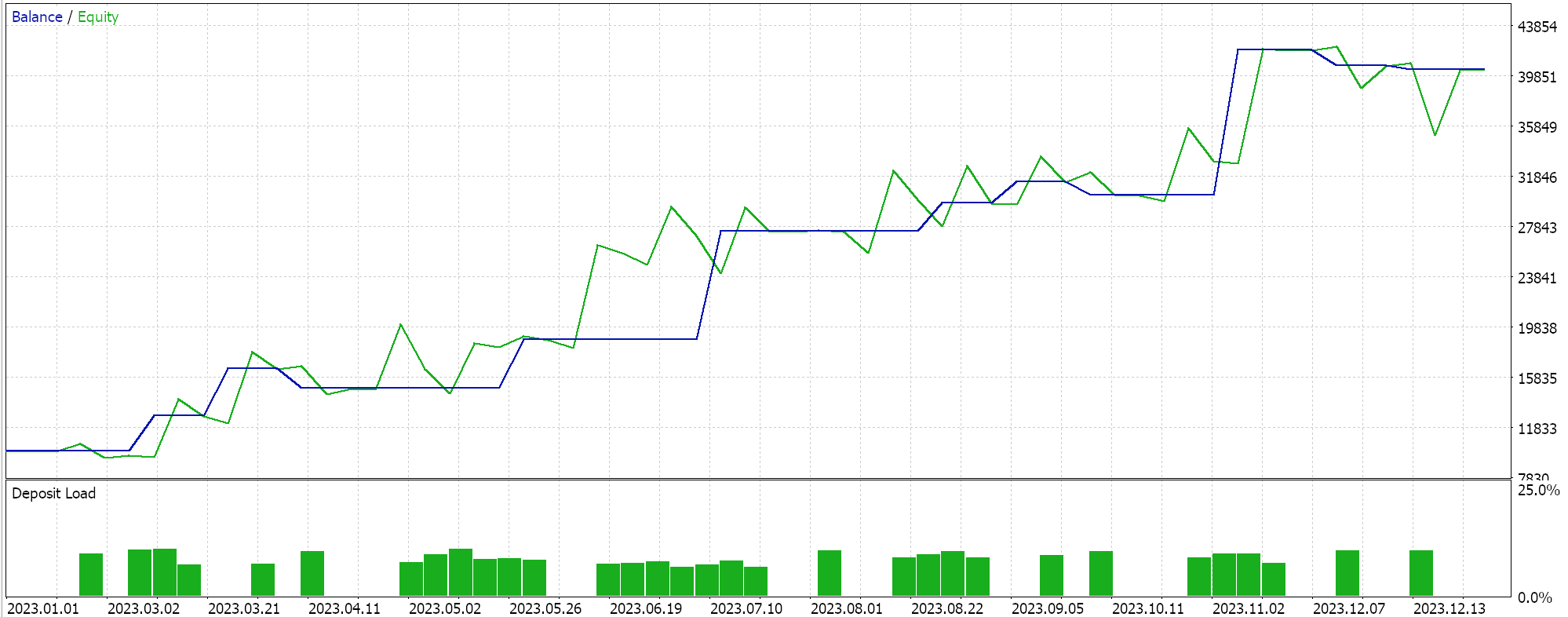
Der Ansatz, der der SVM am ähnlichsten ist und bei dem jeder Datensatz vor der Ableitung der Hyperebene nach Stützvektorpunkten durchsucht wird, führt im Test zu folgenden Ergebnissen:

Aus unseren obigen Berichten geht hervor, dass die Methode, die Stützvektoren verwendet, am vielversprechendsten ist, was angesichts der zusätzlichen Feinabstimmung (auch wenn die Anzahl der Parameter bei allen drei Methoden identisch ist) keine Überraschung sein dürfte.

Nebenbei bemerkt: Diese Tests werden mit echten Ticks und Limit-Orders durchgeführt, ohne dass Gewinnziele oder Stop-Losses verwendet werden. Wie immer sind weitere Tests erforderlich, bevor aussagekräftige Schlussfolgerungen gezogen werden können. Interessant ist jedoch, dass die Support-Vector-Methode bei der gleichen Anzahl von Eingabeparametern besser abschneidet. Es wurden weniger Trades getätigt, was zu einer drastisch besseren Performance führte als bei den anderen beiden Ansätzen.

Die Hinzufügung der Regression im zweiten Ansatz verbesserte die Leistung nur geringfügig, wie aus den Ergebnissen ersichtlich ist. Die Anzahl der Handelsgeschäfte war ebenfalls fast gleich, aber das Vorab-Screening der Datensatzpunkte nach Support-Vektoren vor der Definition der Hyperebene war eindeutig ein entscheidender Vorteil. MetaTrader-Berichte sind sehr subjektiv, und viele diskutieren darüber, was die kritischste Statistik ist, auf die man sich als Indikator dafür verlassen kann, ob das Handelssystem vorwärts gehen kann, und ich habe auch keine endgültige Antwort auf dieses Thema. Ich denke jedoch, dass ein Vergleich zwischen dem durchschnittlichen Gewinn und dem durchschnittlichen Verlust (pro Handel) unter Berücksichtigung des Verhältnisses zwischen durchschnittlichen aufeinanderfolgenden Gewinnen und durchschnittlichen aufeinanderfolgenden Verlusten aufschlussreich sein könnte. Alle diese Werte werden häufig kombiniert, um eine Kennzahl zu berechnen, die als Erwartungswert bezeichnet wird. Dies unterscheidet sich stark von der erwarteten Auszahlung, die einfach der Gewinn geteilt durch alle Abschlüsse ist. Vergleicht man die Erwartung aller Berichte, so ist die Methode, die Unterstützungsvektoren verwendet, im Vergleich zu den anderen beiden Ansätzen um fast 10 Prozent besser.

Schlussfolgerung

Zusammenfassend haben wir also ein weiteres Beispiel für die rasche Entwicklung und Prüfung einer möglichen Handelsidee betrachtet, um zu beurteilen, ob sie eine Verbesserung darstellt oder in die bestehende Strategie passt.

SVM ist ein ziemlich komplizierter Algorithmus, der nur selten, wenn überhaupt, ohne die Hilfe einer Bibliothek eines Drittanbieters implementiert wird, sei es PyLIBSVM für Python oder SVMlight für R. Darüber hinaus wird oft einer der optimierbaren Parameter mit 1 gleichgesetzt, um diesen Prozess zu vereinfachen. Bei diesem Verfahren wird eine Kopie eines untersuchten Datensatzes durch eine spezielle umkehrbare Formel, den so genannten Polynomkernel, vergrößert. Es ist die relative Einfachheit und Umkehrbarkeit dieses Polynomkernels, die ihm den Namen „Kernel-Trick“ einbrachte. Diese Einfachheit und Umkehrbarkeit, die dank der Punktprodukte möglich ist, wird in Fällen, in denen der Datensatz mehr als zwei Dimensionen hat, dringend benötigt, da, wie man sich vorstellen kann, in Fällen von Datensätzen mit sehr hoher Dimensionalität die Hyperebenengleichung, die solche Datensätze richtig klassifiziert, sehr komplex sein muss.

Durch die Einführung einer alternativen Methode zur Ableitung der Hyperebene über das Newton'sche Polynom, die erstens weniger rechenintensiv und zweitens viel besser zu verstehen und darzustellen ist, können alternative SVM-Implementierungen nicht nur getestet, sondern auch als Alternative zur bestehenden Strategie oder als Bereicherung betrachtet werden. Die MQL5 IDE erlaubt beide Szenarien, wobei Sie im ersten Fall ein völlig neues Handelssystem auf der Grundlage des hier geteilten Signalklassencodes entwickeln würden. Was aber vielleicht oft übersehen wird, ist das wachsende Potenzial des MQL5-Assistenten, der die gleichzeitige Erstellung und Prüfung mehrerer Strategien ermöglicht. Auch dies kann schnell und mit minimaler Codierung erfolgen, wenn in der Vorphase nach Ideen und Strategien gesucht wird. Und wie immer kann man nicht nur die Signalklasse der zusammengesetzten Klassen des Assistenten betrachten, sondern auch die Nachlaufklasse und die Geldmanagementklassen.