您应当知道的 MQL5 向导技术（第 15 部分）：协同牛顿多项式的支持向量机

概述

支持向量机（SVM）是一种机器学习分类算法。分类不同于我们之前在这里和这里文章中研究过的聚类，两者之间的主要区别在于，分类在有监督的情况下将数据分成预定义的集合，而聚类则寻求在无监督的情况下判定这些集合的内容和数量。

简言之，如果要向数据添加维度，SVM 通过参考每个数据点与所有其它数据点的关系，来进行数据分类。如果能够定义一个超平面来清晰地剖析预定义的数据集，则分类就能达成。

所参考的数据集往往拥有多个维度，正是这一属性令 SVM 成为针对此类数据集进行分类的非常强力的工具，尤其若是每个集合中的数字很小、或数据集合的相对比例偏斜的情况下。拥有 2 个以上维度的 SVM 的实现源代码非常复杂，并且 python 或 C# 中的用例往往都一直使用函数库，以至于用户只需输入最少的代码即可获得结果。

高维数据倾向于曲线拟合训练数据，这令其在样本数据以外不太可靠，这是 SVM 的一个主要缺陷。另一方面，低维数据能做到更好的交叉验证，并有更多常见的用例。

至于本文，我们将研究一个非常基础的 SVM 案例，它处理 2-维数据（也称为线性 SVM），而完整的实现源代码也会在不引用任何第三方函数库的情况下分享。通常，分离超平面来自以下两种方法之一：多项式内核、或径向内核。后者更复杂，这里不予讨论，故我们只与前者打交道，即多项式内核。

典型情况下，当使用多项式内核时，它的正式定义如下方程，

判定理想的 c 和 d 值，其为设置超平面方程，是一个迭代过程，旨在令支持向量尽可能远离，因为它们衡量的是两个数据集之间的间隙。

至于本文，如标题所示，我们将运用牛顿多项式来推导 2-维数据集上的超平面方程。我们在最近的一篇文章中已见识过牛顿多项式，故此将略过一些其实现。

我们按三种场景来实现牛顿多项式（NP）。首先，我们在两个预定义的数据集之间插入中点，以便获得点集的边界，这些点用于推导定义超平面的直线/曲线方程。定义该超平面之后，我们将其视为分类器，在测试所用智能信号类时执行交易决策。在第二个场景中，我们添加了一个回归函数，如此智能信号类的输出不光仅有 0 或 100 值（如第 1 个），且提供范围之间的数值。我们根据未分类向量与已知向量点的接近程度来计算回归值。第三，我们依据第二种场景构建时，仅在定义超平面时插入少量点。少量的点，又名支持向量，是那些更接近其它数据集的点，因此在适配其它所有项的同时“完善”了超平面方程。

多项式核的背景

至于该部分，我们正在研究线性 SVM，其完整的源代码实现是共享的，我们希望通过提供所有源代码的完全透明性来避免使用函数库。然而，在真实世界应用 SVM 时，鉴于许多数据集固有的复杂性和多维性，会更多采用非线性类型。多亏有内核技巧，证明与 SVM 中的这些挑战打交道是可控的。这种方法允许在保持其原始结构的同时，在更高维度上研究数据集。内核技巧使用向量的点积来保留低维向量值。通过将数据集指向更高的维度，可以轻松达成数据集的分离，而这也只需更少的计算资源即可做到。

如上所示，我们的内核函数正式定义为：

将 x 和 y 作为每个集合中任意两个比较数据点的数据点，c 是常数（其值通常设置为初值 1），d 是多项式次方数。随着 d 的增加，可以定义更精确的超平面方程，但这往往会导致过度拟合，需要设置一个平衡点。x 和 y 数据点在许多情况下是向量、甚至是矩阵格式，这就是为什么幂 T 表示 x 的转置。

为了便于说明，利用 MQL5 实现多项式内核可以采用以下形式。

//+------------------------------------------------------------------+
//| Define a data point structure                                    |
//+------------------------------------------------------------------+
struct Sdatapoint
{  double      features[2];
   int               label;
                     Sdatapoint()
   {                 ArrayInitialize(features, 0.0);
      label = 0;
   };
                    ~Sdatapoint() {};

};

//+------------------------------------------------------------------+
//| Function to calculate the polynomial kernel value                |
//+------------------------------------------------------------------+
double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree)
{  double _kernel_sum = 0.0;
   for (int i = 0; i < 2; i++)
   {  _kernel_sum += (A.features[i] * B.features[i]);
   }
   _kernel_sum += Constant; // Add constant term
   return(pow(_kernel_sum, Degree));
}

计算位于单独集中的数据点之间的关系权重，并将其存储在内核矩阵当中。该内核矩阵量化数据点间距，因此筛选出支持向量，即位于每个数据集边缘、且更接近相邻集的数据点。

源

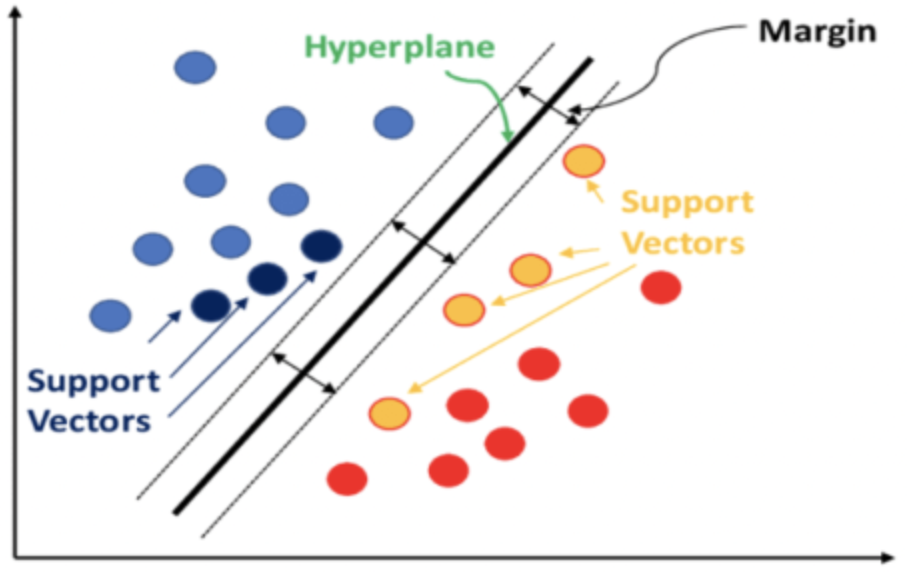
然后，这些支持向量用作计算超平面方程的输入。所有这些都在库函数中处理，例如：PyLIBSVM 或 python 的 shogun；或者 R 中的 kernlab 或 SVMlight。鉴于推导超平面方程的复杂性，正是由这些库函数计算并输出了超平面。

在判定内核矩阵时，在得出最优解过程中，可以考虑各种常数和多项式次方值。因为这令本已很复杂的仅自一个矩阵推导超平面的过程，因涵盖多个矩阵而变得越发复杂，所以更谨慎的做法是始终在开始时一次性选择一个确定的（或从专业角度看次优）常数和多项式次方，并用它来得出超平面。为此，常数值也通常设置为 1。正如人们所料，多项式的次方数越高，分类越好，但上面曾提到的过拟合风险也有所提升。

还有，较高的多项式阶数往往计算强度更高，如此这般需要在初立时建立一个不太高的直观值。

此处研究的多项式内核相对容易理解，但它们并不是许多 SVM 实现中最常用、或首选的内核，因为那些吹嘘的权利都属于径向基本函数内核。

径向基本函数（RBF）内核被选择更常见，因为 SVM 的优势在于处理多维数据，而 RBF 内核在这方面比多项式内核更擅长。一旦选择了内核，对偶优化问题，如上所述，数据集被映射到更高的维度空间，并且由于在所谓的内核技巧中捕获的点积规则，这种优化（来回）可以更有效地完成，同时也可以更清晰地表达。对于拥有 2 个以上维度的数据集，超平面方程的复杂性质令其不可或缺。所有言行之后，超平面方程采用了以下形式：

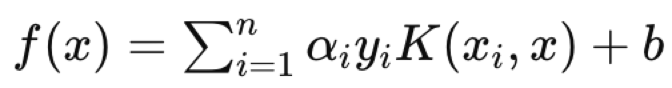
其中：

• f(x) 是决策函数。
• αi 是从优化过程中获得的系数。
• yi 是类标签。
• K(xi​,x) 是内核函数。
• b 是偏置项。

超平面方程定义了两个数据集如何由决策函数分隔，该决策函数会分配一个类标签，定义了任何查询点属于哪一侧。故此，一个查询数据点将是方程中的 x，其中 xi 和 yi 分别是训练数据、及其分类器。

插一句话，SVM 的应用广阔，它们的范围包括：垃圾邮件过滤，如您可以将电子邮件标题和内容嵌入到结构化格式中；筛选贷款申请人是否违约；等等。与其它机器学习替代方案相比，令 SVM 理想的原因在于能够依据小型或非常扭曲的数据集来开发稳健模型。

利用 MQL5 实现

我们存储 x 和 y 值的模型结构与我们最近的实现非常相似，此处的不同之处是为每个分类器类型添加了一个计数器。SVM 本质上是一个分类器，我们将见识一些动作示例，其中这些计数器将派上用场。

如此这般，在每个索引处 x 向量值为 2，因为我们将数据集的多维性限制为 2，这样就能够使用牛顿多项式。增加的维度也提高了过度拟合风险。x 的第一个维度的数值是最高价缓冲区的变化，而第二个维度则是人们所期望的最低价缓冲区的变化。输入数据的选择现在是机器学习的一个关键方面。尽管变换器、CNN 和 RNN 非常足智多谋，但依据输入数据决策，以及如何您要嵌入或规范化它们可能更为关键。

我们选择了一个非常简单的数据集，但读者应当意识到，他选择的输入数据不仅限于原始价格数据、甚至指标值，还可以包括新闻财经指标值。再次，您如何选择将其规范化能够造成很大的不同。

//+------------------------------------------------------------------+
//| Function to get and prepare data.                                |
//+------------------------------------------------------------------+
double CSignalSVM::GetOutput(int Index)
{  double _get = 0.0;
   

        ....
        ....

   int _x = StartIndex() + Index;
   for(int i = 0; i < m_length; i++)
   {  for(int ii = 0; ii < Dimensions(); ii++)
      {  if(ii == 0) //dim-1
         {  m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1);
         }
         else if(ii == 1) //dim-2
         {  m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1);
         }
      }
      if(i > 0) //assign classifier
      {  if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0)
         {  m_model.y[i - 1] = 1;
            m_model.y1s++;
         }
         else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0)
         {  m_model.y[i - 1] = 0;
            m_model.y0s++;
         }
      }
   }
//
   _get = SetOutput();
   return(_get);
}

我们的 y 数据集，将是前向收盘价的滞后变化，就像以前的案例一样。我们为标记为 'y0' 和 'y1' 的两个类引入了计数器。这些只是记录，至于每根处理过的柱线，已建立两个 x 值，收盘价的后续变化看涨（在这种情况下记录 0）、亦或看跌（记录 1）。

由于 y 是一个向量，将其当前值与填充有 0 和 1的向量进行比较，而作为返回的数值实际上是 y 向量中分别存在 0 和 1 的计数，我们提取这些 0 和 1 的计数值就能得到旁注。

'set-output' 函数是在处理模型信息时，为我们已有函数的另一个补充。它针对每个类取 x 向量值，并在两个集合之间插入一个中点，其可用作两个集合的超平面。这并非已提到的 SVM 方式，但它为我们所做的是，鉴于我们打算用牛顿多项式定义一个超平面，所以给我们一个点集合，来推导一个超平面方程。

//+------------------------------------------------------------------+
//| Function to set and train data                                   |
//+------------------------------------------------------------------+
double CSignalSVM::SetOutput(void)
{  double _set = 0.0;
   matrix _a,_b;
   Classifier(_a,_b);
   if(_a.Rows() * _b.Rows() > 0)
   {  matrix _interpolate;
      _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions());
      for(int i = 0; i < int(_a.Rows()); i++)
      {  for(int ii = 0; ii < int(_b.Rows()); ii++)
         {  _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]);
            _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]);
         }
      }
      vector _w;
      vector _x = _interpolate.Col(0);
      vector _y = _interpolate.Col(1);
      _w.Init(m_model.y0s * m_model.y1s);
      _w[0] = _y[0];
      m_newton.Set(_w, _x, _y);
      double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0;
      m_newton.Get(_w, _xx, _zz);
      if(_yy < _zz)
      {  _set = 100.0;
      }
      else if(_yy > _zz)
      {  _set = -100.0;
      }
      _set *= Regressor(_x, _y, _xx, _yy);
   }
   return(_set);
}

我们正研究的是在该方法中推导超平面的 3 种方式。最先的第一种方式，参考即将到来的超平面点中每个集合的所有点，即把集合中每个点的平均值插值到备选集合。这显然没有参考支持向量，但在此展示是出于研究、并与其它方式比较目的。

第二种方法与第一种方法类似，仅有的区别是预测 y 值是回归的，这意味着我们用 “regulizer” 函数将输出预测转换或归一化为 0.0 到 1.0 范围内的浮点值，优于 0 或 1 整数值。这有效地产生了一个系统，原则上其虽远离 SVM，但仍然使用超平面来区分 2-维数据点。

//+------------------------------------------------------------------+
//| Regressor for the model                                          |
//+------------------------------------------------------------------+
double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY)
{  double _x_max = fmax(X.Max(), XX);
   double _x_min = fmin(X.Min(), XX);
   double _y_max = fmax(Y.Max(), YY);
   double _y_min = fmin(Y.Min(), YY);
   return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min)))));
}

我们能够通过比较预测值与其集合中的最大值/最小值，来获得一个中转回归值，如此若它与最小值匹配，则返回 0，而若它与最大值匹配，则返回 1。

第三，也是最后，我们在第 2 部分中通过添加一个 “classifier” 函数来改进该方法，即筛选推导超平面用到的每个集合中的点。通过参考离自身集合的质心最远、但又最接近相反集合质心的点，我们得出了点的 2 个子集，每个类一个，可用于两个集合之间的超平面边界插值。

//+------------------------------------------------------------------+
//| 'Classifier' for the model that identifies Support Vector points |
//|  for each set.                                                   |
//+------------------------------------------------------------------+
void CSignalSVM::Classifier(matrix &A, matrix &B)
{  if(m_model.y0s * m_model.y1s > 0)
   {  matrix _a_centroid, _b_centroid;
      _a_centroid.Init(1, Dimensions());
      _b_centroid.Init(1, Dimensions());
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  _a_centroid[0][0] += m_model.x[i][0];
            _a_centroid[0][1] += m_model.x[i][1];
         }
         else if(m_model.y[i] == 1)
         {  _b_centroid[0][0] += m_model.x[i][0];
            _b_centroid[0][1] += m_model.x[i][1];
         }
      }
      _a_centroid[0][0] /= m_model.y0s;
      _a_centroid[0][1] /= m_model.y0s;
      _b_centroid[0][0] /= m_model.y1s;
      _b_centroid[0][1] /= m_model.y1s;
      double _a_sd = 0.0, _b_sd = 0.0;
      double _ab_sd = 0.0, _ba_sd = 0.0;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _a_sd += sqrt(_0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _ab_sd += sqrt(_1);
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _b_sd += sqrt(_1);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _ba_sd += sqrt(_0);
         }
      }
      _a_sd /= m_model.y0s;
      _ab_sd /= m_model.y0s;
      _b_sd /= m_model.y1s;
      _ba_sd /= m_model.y1s;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1))
            {  A.Resize(A.Rows()+1,Dimensions());
               A[A.Rows()-1][0] = m_model.x[i][0];
               A[A.Rows()-1][1] = m_model.x[i][1];
            }
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0))
            {  B.Resize(B.Rows()+1,Dimensions());
               B[B.Rows()-1][0] = m_model.x[i][0];
               B[B.Rows()-1][1] = m_model.x[i][1];
            }
         }
      }
   }
}

上面分享的执行该操作的代码有点长，且我确信能更有效地实现其所做，特别是若有人从事在 MQL5 中最近引入的向量和矩阵数据类型的内置函数。但我们要做的是首先找到每个数据集的质心（或平均值）。一旦这个定下，我们继续计算每个数据集的标准差，这是得自后缀为 “_sd” 的变量。一旦有了质心坐标和标准差大小，我们就可以衡量和比较每个点离其质心有多远，以及它离对方数据集的质心有多远，而计算出的标准差则作为太远或太近的阈值。

我们定义一个牛顿多项式方程所需的全部就是插值点。正如我们在这里看到的，提供的点越多，方程指数就越高。我们能搭配牛顿多项式所用的最大插值点数量，由数据集的大小控制，它与 “m_length” 参数成正比，在模型中定义两个数据集时，该变量设置我们需回顾多少历史数据点。

在推导超平面的三种方法中，只有最后一种貌似典型的 SVM 方法。我们正在定义的支持向量，通过筛选每个集合内的点，即最接近集合边界，且与超平面更相关。然后，这些支持向量点在推导超平面方程时当作牛顿多项式类的输入。对比之下，如果我们做到严格的 SVM，我们会在数据点中添加一个额外的维度，以便额外微分，同时迭代遍历多项式内核方程中的常数，令其成为可能。即使仅有 2-维数据，其复杂度显然多出一个数量级，更不用提所涉及的计算资源了。事实上，为了简化或最佳实践，这些常数之一（c）始终假定为 1，而近有多项式阶数变量（上面方程中的 d）得到优化。正如您能想象的那样，对于拥有 2 个以上维度的数据集，这显然需要一个第三方函数库，因为如果不出意外，所寻求的 4、5 或 n 个指数方程会复杂数个量级。

牛顿多项式实现与我们在上一篇文章中讲述的内容非常相似，除了对 'Get' 函数进行一些调试，该函数运行构建的方程来判定下一个 y 值。这个会附在下面。

测试结果

本文末尾附带的 3 个信号类文件都可以经由 MQL5 向导组装进一个智能交易系统当中。有关如何做到这一点的示例，请参阅此处和此处的文章。

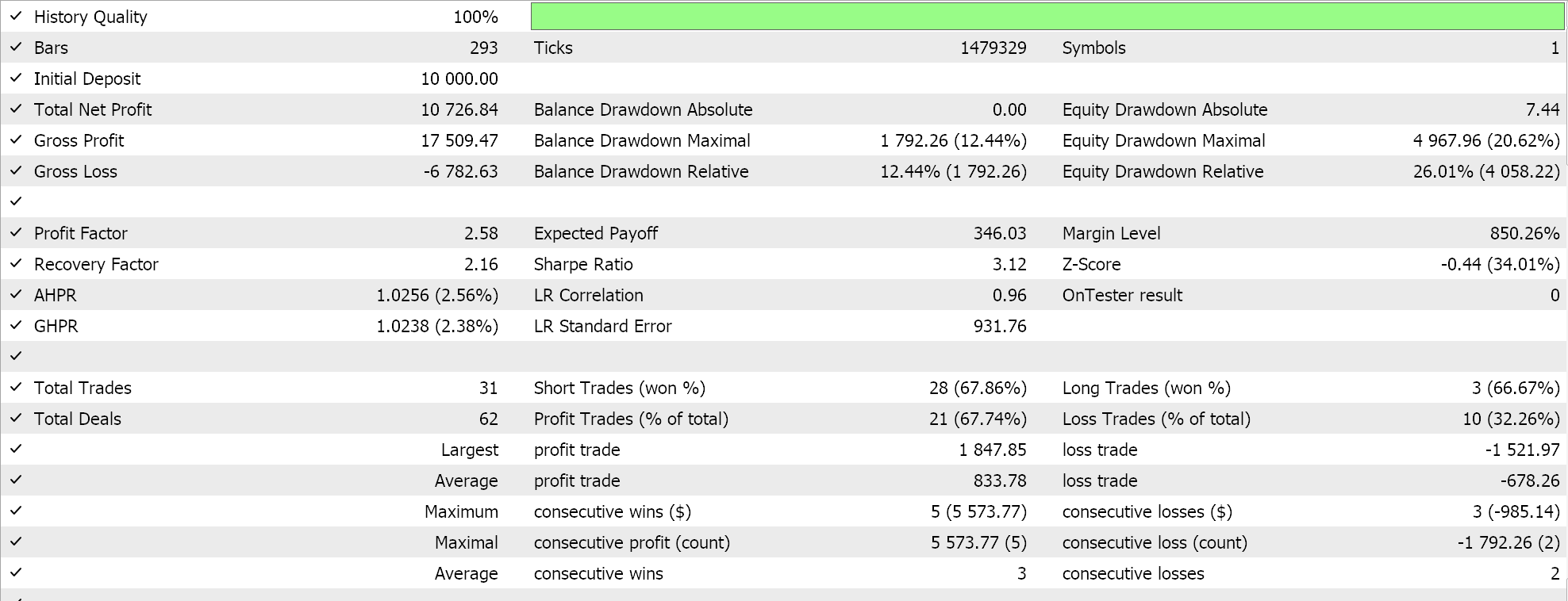
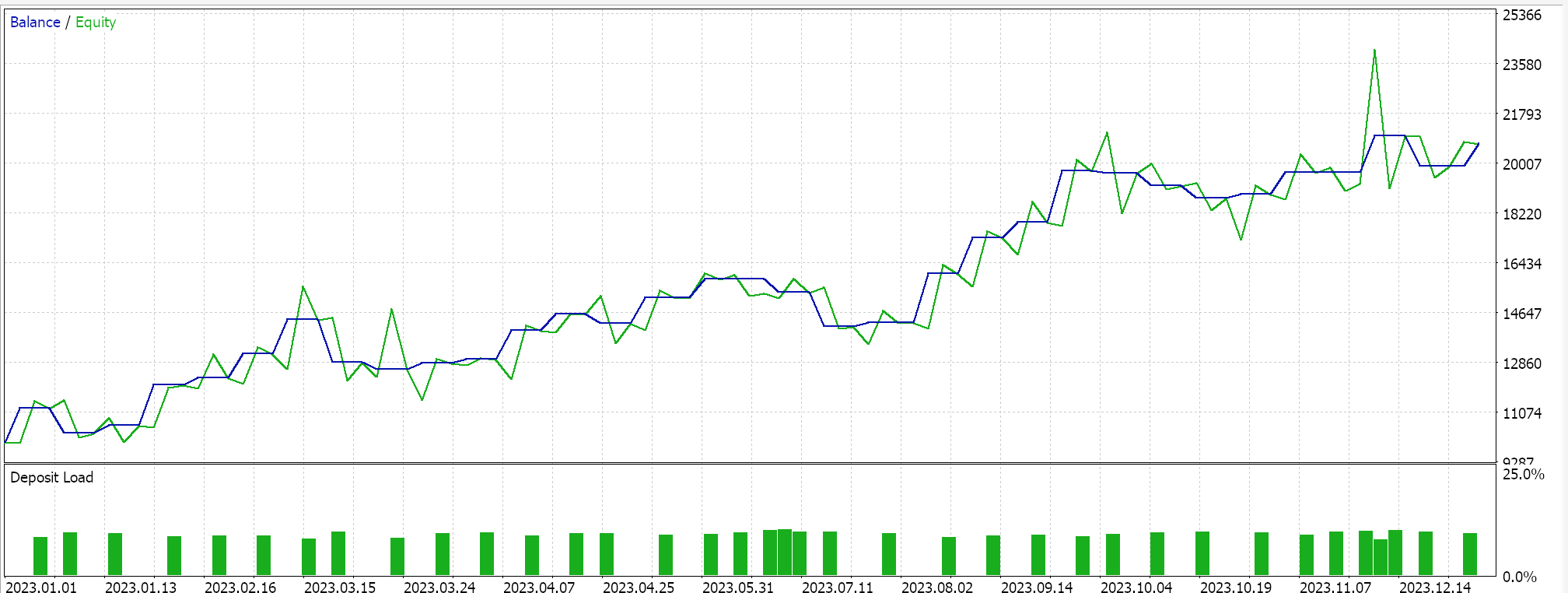
如此，最先一个实现运行测试时，其中得到的超平面是通过在任一集合中的所有点上插值，且不筛选支持向量，这为我们给出以下结果：

如果我们进行类似的测试运行，如上所述，我们的测试品种是 EURJPY、2023 年日线时间帧，对于第二种方法，它只在上述方法里添加了回归，我们所得如下：

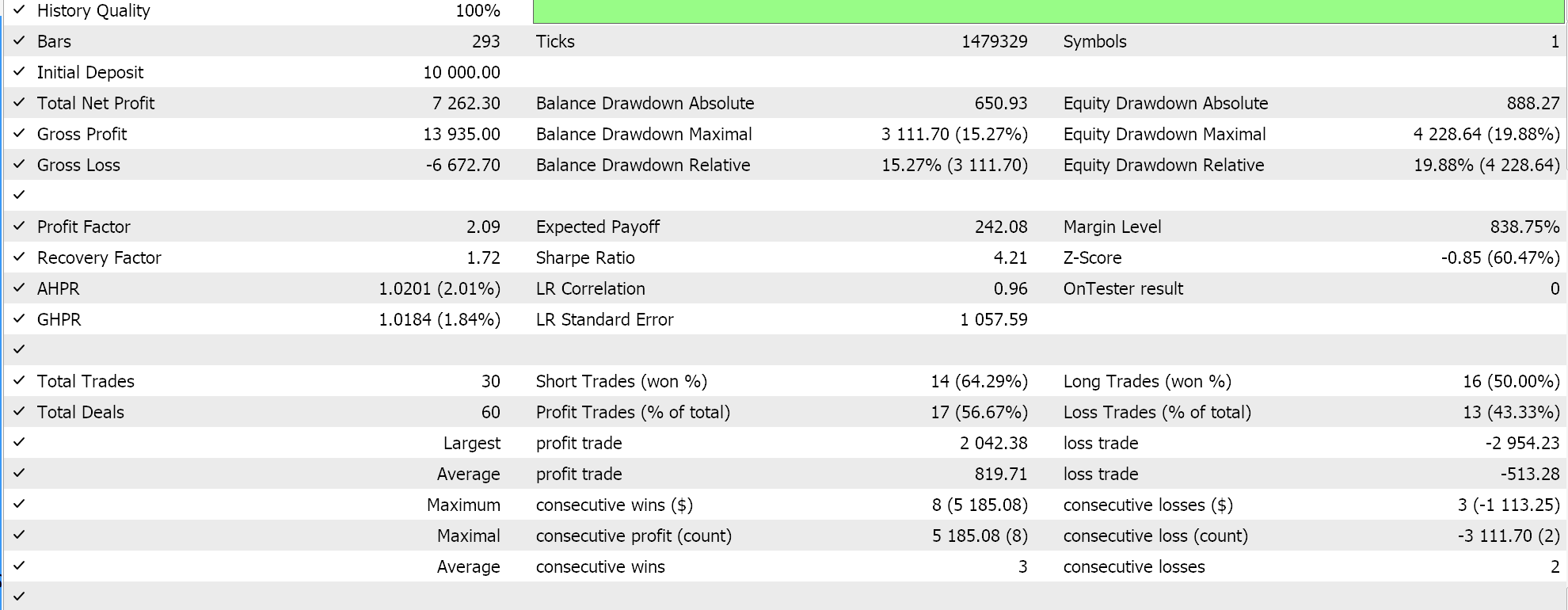
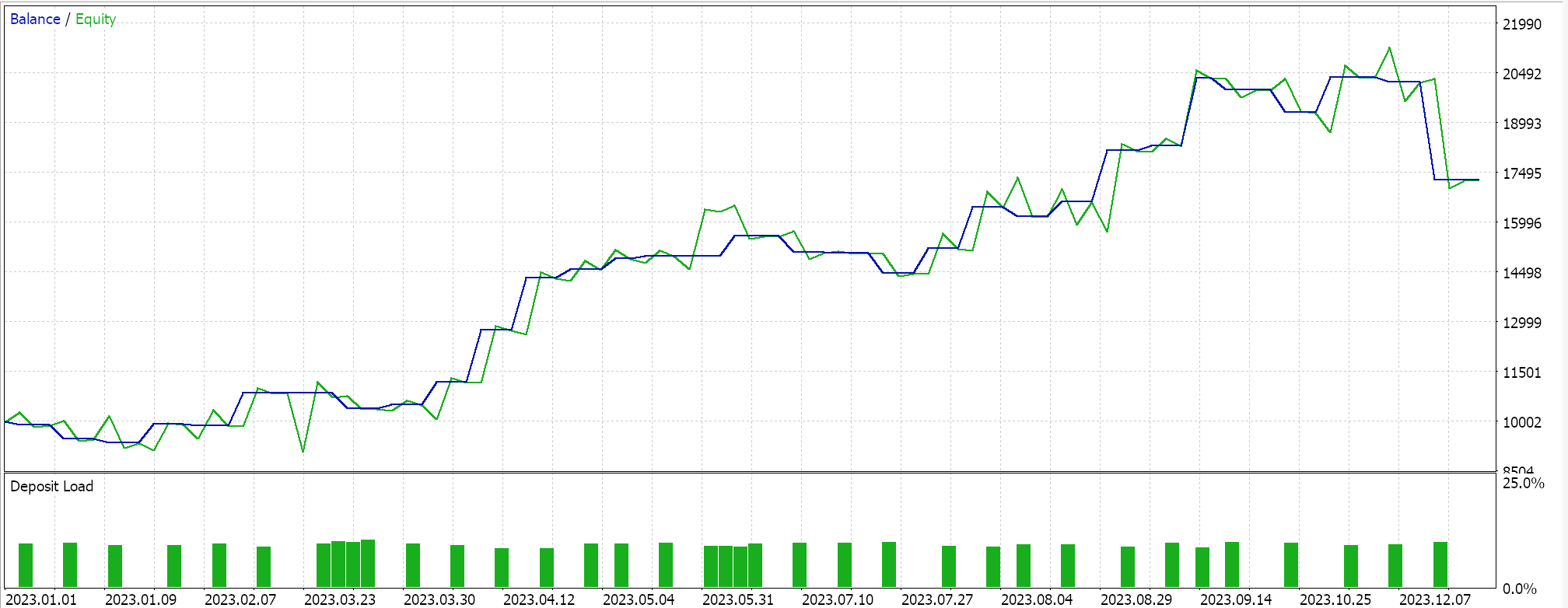
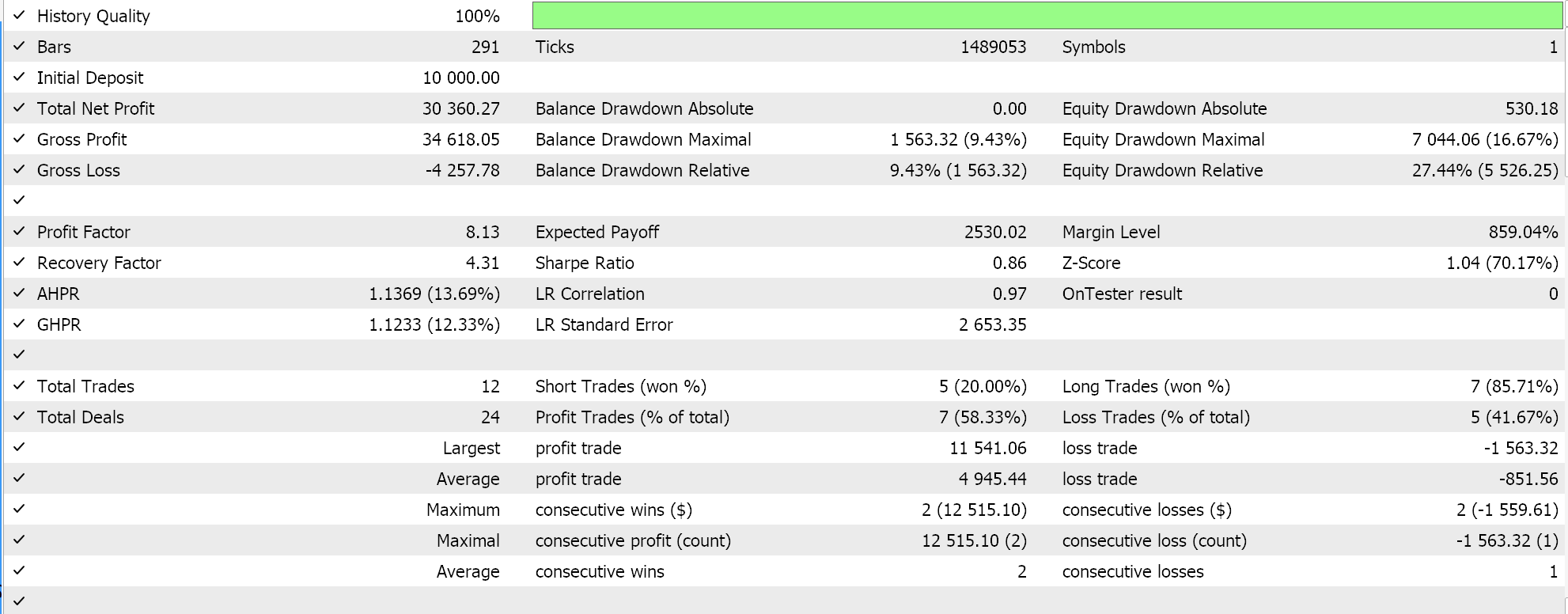
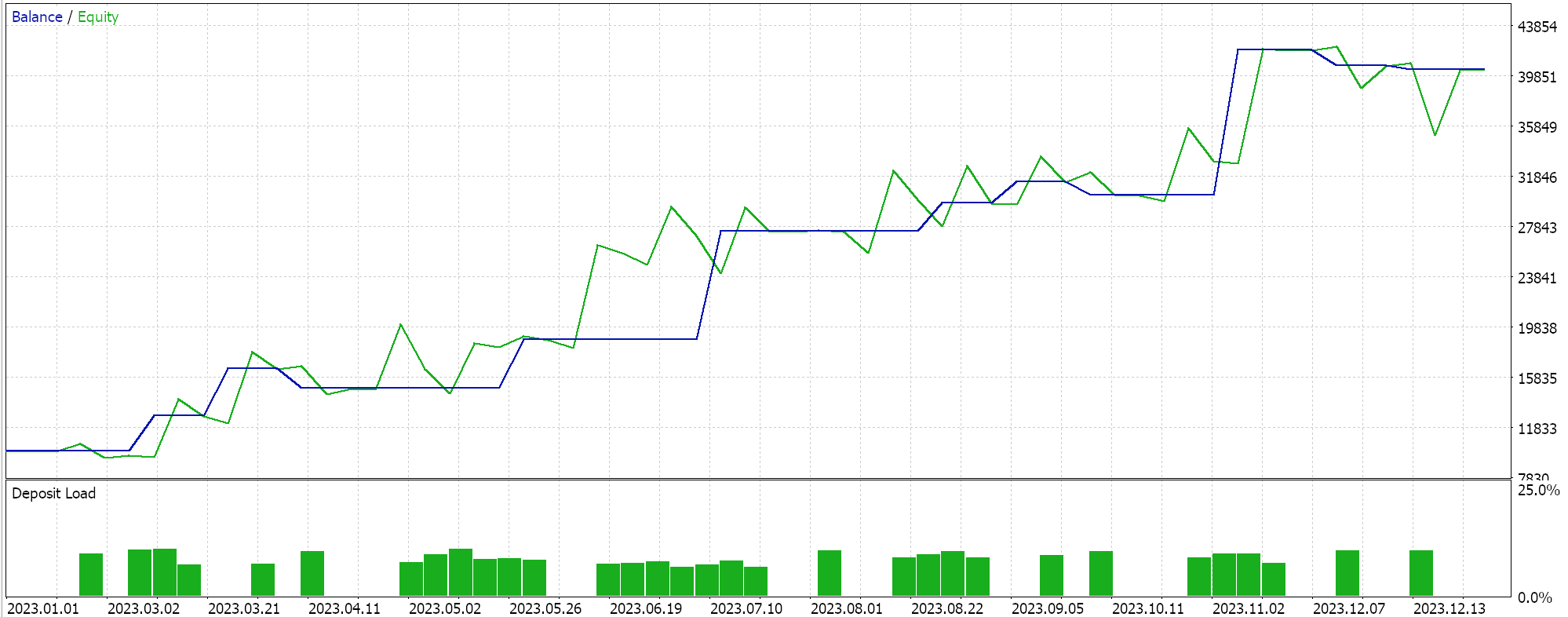
最后，与 SVM 最貌似的方式，在推导其超平面之前筛选支持向量点的数据集，当测试过后，我们得到了以下结果：

从我们上面的报告中，经快速扫视，可推测出使用支持向量的方法最有前途，且大概会给出额外优调（即使所有三种方法中的参数数量雷同）也不足为奇。

作为旁注，该测试是依据真实即时报价执行限价订单，并未使用止盈或止损目标。如常，在得出更有意义的结论之前，需要更多的测试。不过，有趣的是，在输入参数数量相同的情况下，支持向量方法的性能更佳。它造成的交易更少，且给出的性能比其它两种方式要好得多。

从结果中可以看出，在第二种方式中添加回归仅能略微提高性能。交易次数也几乎相同，然而在定义超平面之前，预先筛选支持向量的数据集点显然改变了游戏规则。MetaTrader 报告非常主观，许多人都在争论最关键统计依赖的指标，是否在于交易系统能够前向漫步，而我就这个话题也没有明确的答案。不过，我认为在比较平均盈利和平均亏损（每笔交易）的同时，还要留意平均连续胜绩与平均连续败绩的比率，这可能是有洞察力的。在计算称为“期望值”的比率时，往往会把所有这些数值组合在一起。这与预期收益非常不同，预期收益只是盈利除以所有交易。如果我们比较所有报告的期望值，那么与其它 2 种方式相比，采用支持向量方法更佳，量级近乎为 10。

结束语

如此这般，总而言之，我们见识到另一个快速开发和测试可能的交易思路的示例，来评估它是否是一种改进，或者是否适合一个人的现有策略。

SVM 是一种相当复杂的算法，如果没有第三方函数库的帮助，无论是用 python 的 PyLIBSVM、还是 R 的 SVMlight，它很少会实现，且为简化该过程，多个可优化参数往往会取值等于 1。回顾该过程，经由称为多项式内核的特定可逆公式，一个处于研究的数据集副本得以提升其维度。正是这个多项式内核的相对简单性、以及可逆性为其赢得了“内核技巧”的称号。这种简单性和可逆性，归因于点积而成为可能，在数据集拥有超过 2 个维度的情况下非常需要，因为可以想象，在数据集拥有极高维度的情况下，正确分类该类数据集的超平面方程必然非常复杂。

故此，通过引入一种由牛顿多项式推导超平面的替代方法，首先该方法不会是计算密集，但还更容易理解和表述；SVM 的多种实现不仅可被测试，且它们可被视为现有策略的备案或增值。这两种场景 MQL5 IDE 都允许，在前者中，您将基于此处共享的信号类代码开发一个全新的交易系统。但或许经常被忽视的是 MQL5 向导提供的增值潜力，它允许同时组装和测试多个策略。在初步阶段筛选思路和策略时，这可以快速完成，并且只需最少的编码。如常，除了查看向导组装类的信号类外，还可以探索尾随类和资金管理类。