通过分析组件评估交易系统的效益

简介

任何开始在金融市场上进行交易的人都会很快意识到，只有通过一些系统性方法才能获得成功，无意识地交易就是凭运气，中或者不中，是情绪化的，并不能获得好的结果。如果成功了，这基本上也是戏剧化的结果。所以，任何分析，不论是基于指标的图形化分析，还是任何其他类型的分析，都是在金融市场上成功交易的重要组成部分。在一定程度上，本文也是一项在联合应用程序中对其中几个简单独立的交易系统进行的研究，分析了它们的有效性和可用性。

设置评估交易系统有效性的标准

通常情况下，交易系统有效性的评估是由一系列指定参数，以及一些系统结果的数值定义的。指标的周期数，止损或者获利的大小，或者更加复杂一些的影响系统进入和退出市场的系数，都可以设置为参数。而结果数值是净利润，回撤，成功交易的百分比或者以存款货币为单位的平均交易利润等。

任何交易系统随着时间的推移效率都会下降，因为货币市场是不断变化的，从很多指标中可以看到这一点。所以，系统参数的设置必须要适应条件的改变而改变，在本文中，我们的目标是定义一个复杂交易系统的概念。

复杂交易系统是由一组独立的模块构成的，它们都有自己的算法和参数，并且相互之间联合工作。包含在系统中的这些模块的运行可以使用一组给定的标准进行评估，我们将会考虑如图1中所示的系统效益的评估框架。复杂系统由A,B,C三个模块构成，它们每个都有自己的运行参数，这个系统的运行和效益可以通过三个维度进行评估：1, 2, 3。一段时间之后，此系统交易的市场条件发生变化，而参数 1-3 向不令人满意的方向上发展了，这就意味着是时候重新配置系统了。这可以使用以下方法来做:

1. 开始优化全部九个参数，以便使系统适应当前的市场现状。但是这种方法会包含冗余 - 为什么要优化所有参数呢，是否可能发现是哪个模块开始工作得不好了呢？
2. 对应地，有了第二种方法。为这三个系统模块各创建一组评估标准C1, C2, C3，这使得可以独立为每个模块评估和比较它们的运行效益。

这种方法的优点:

• 避免冗余，如果模块运行得很好，就没有必要进行优化。
• 监控系统，可以在一段时间之后衡量 C1-C3 参数，从而把系统与它的单元分离和综合以观察它在不同市场时间段(交易期间，新闻发布，等等)的行为。
• 弱点分析，这使得可以确定是那个模块拖累了整个系统，从而可以优化、替代或提高特定的模块，而不是整个系统。

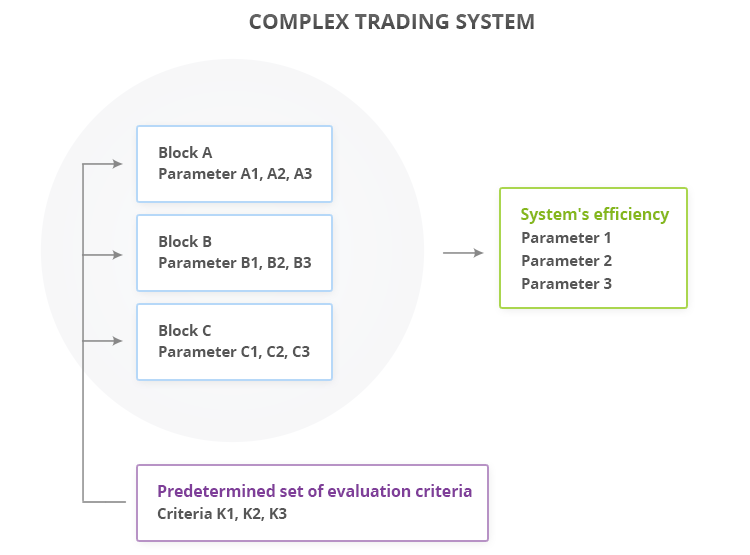
图1. 复杂交易系统

通过分析组件评估交易系统效益的示例

为了测试整个交易系统的效益，我们需要检查系统模块是如何相互独立运行以及如何一起工作的。测试的系统将包含两个模块:

1. 模块 A. 它是基于标准的抛物线状止损和反转指标(Parabolic SAR)信号的；
2. 模块 B. 它是基于标准的加速震荡指标(Accelerator Oscillator, AC)信号的。

我们马上就能定义评估这些模块的一组标准:

• 标准 C1 — 净利润；
• 标准 C2 — 最大回撤；
• 标准 C3 — 获利交易 (占总数百分比).

为了更加清楚，我们就选择这些标准作为效益的参数:

• 参数 1 — 净利润；
• 参数 2 — 最大回撤；
• 参数 3 — 获利交易 (占总数百分比).

这些指标的进场信号实例位于MQL5标准库的文档中: 抛物线状止损与反转指标信号 和 加速震荡指标信号 (第一条件)，对于它们中的每一个，我们都将描述进场条件并在预先测试中找到它们有效工作的条件，

测试EA交易的所有参数都按以下方式写下来: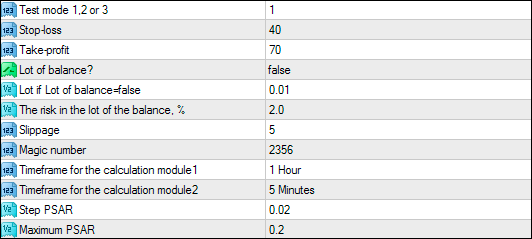

图2. EA交易的参数

//+------------------------------------------------------------------+
//|                                                                  |
//|                                                Alexander Fedosov |
//|                           https://www.mql5.com/ru/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property link      "https://www.mql5.com/ru/users/alex2356"
#property version   "1.00"
#property strict

#include "trading.mqh"

input int            tm = 1;                       //测试模式 1,2 或 3
input int            SL = 40;                      //止损
input int            TP = 70;                      //获利
input bool           lot_const = false;            //根据余额确定手数?
input double         lt=0.01;                      //如果lot_const=false的手数 
input double         Risk=2;                       //风险百分比, %
input int            Slippage= 5;                  //滑点
input int            magic = 2356;                 //幻数
input ENUM_TIMEFRAMES tf1 = PERIOD_H1;             //计算模块1的时段
input ENUM_TIMEFRAMES tf2 = PERIOD_M5;             //计算模块2的时段
input double         Step = 0.02;                  //PSAR步长
input double         Mxm = 0.2;                    //最大 PSAR

CTrading tr(magic,Slippage,lt,lot_const,Risk,5);
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(tm<1 || tm>3)
      return;
//--- Parabolic SAR 模块的进场条件 
   if(tm==1 && !tr.isOpened(magic))
     {
      double psar[],prc[];
      ArrayResize(psar,3);
      ArrayResize(prc,3);
      for(int i=0; i<3; i++)
        {
         psar[i]=iSAR(_Symbol,tf1,Step,Mxm,i);
         prc[i]=iClose(_Symbol,tf1,i);
        }

      if(psar[2]>prc[2] && psar[1]<prc[1] && psar[0]<prc[0])
         tr.OpnOrd(OP_BUY,lt,TP,SL);
      if(psar[2]<prc[2] && psar[1]>prc[1] && psar[0]>prc[0])
         tr.OpnOrd(OP_SELL,lt,TP,SL);

     }
//--- AC 模块的进场条件
   if(tm==2 && !tr.isOpened(magic))
     {
      double ac[];
      ArrayResize(ac,3);
      for(int i=0; i<3; i++)
         ac[i]=iAC(Symbol(),tf2,i);

      if(ac[2]>0 && ac[1]>0 && ac[1]>ac[2])
         tr.OpnOrd(OP_BUY,lt,TP,SL);
      if(ac[2]<0 && ac[1]<0 && ac[1]<ac[2])
         tr.OpnOrd(OP_SELL,lt,TP,SL);

     }
//--- 两个模块同时作用的进场条件
   if(tm==3 && !tr.isOpened(magic))
     {
      double psar[],prc[],ac[];
      ArrayResize(psar,3);
      ArrayResize(prc,3);
      ArrayResize(ac,3);
      for(int i=0; i<3; i++)
        {
         psar[i]=iSAR(_Symbol,tf1,Step,Mxm,i);
         prc[i]=iClose(_Symbol,tf1,i);
         ac[i]=iAC(Symbol(),tf2,i);
        }
      if((psar[2]>prc[2] && psar[1]<prc[1] && psar[0]<prc[0]) || (ac[2]>0 && ac[1]>0 && ac[1]>ac[2]))
         tr.OpnOrd(OP_BUY,lt,TP,SL);
      if((psar[2]<prc[2] && psar[1]>prc[1] && psar[0]>prc[0]) || (ac[2]<0 && ac[1]<0 && ac[1]<ac[2]))
         tr.OpnOrd(OP_SELL,lt,TP,SL);

     }

  }
//+------------------------------------------------------------------+

EA 交易的第一个参数是tm (测试模式，Test mode)，它的数值可以是 1, 2 或者 3，这些数值对应着三种模式的操作:

• tm = 1. 只使用抛物线状SAR 指标的进场条件，专门对应 A 模块的运行模式。
• tm = 2. 只使用加速震荡(AC)指标的进场条件,专门针对 B 模块的运行模式。
• tm = 3. 两个模块的联合运行，即整个系统的运行。

通过改变 Test Mode 参数我们可以找出我们所感兴趣的参数: 针对А和 B模块 - C1-C3, 针对整个系统 — 参数 1-3。以下是模块的测试结果，抛物线状SAR(图3), AC (图4) 和它们的联合运行(图5).

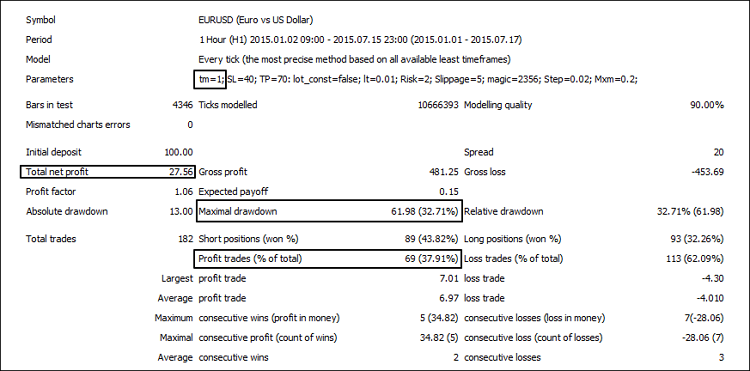
图3. 测试抛物线状SAR模块

图4. 测试AC模块

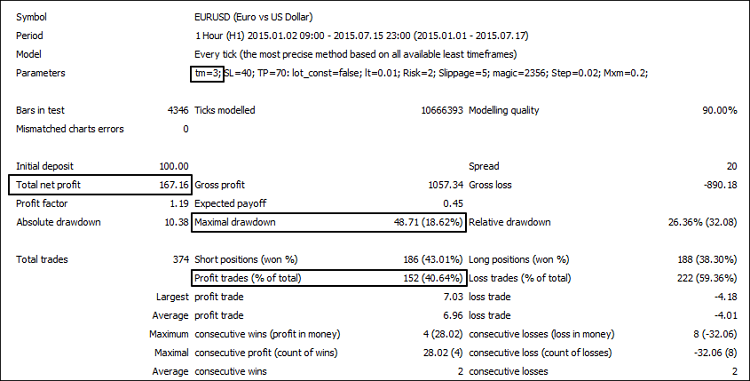
图5. 抛物线状SAR和AC模块的联合运行

基于三个不同运行模式的结果，比较出的表格将表现得更加清晰:

测试模式	净利润	获利交易,%	最大回撤
1	27,56	37,91	32,71
2	106,98	39,19	38,94
3	167,16	40,64	18,62

 

系统变坏的模拟

让我们修改模块A的运行参数 (Test Mode = 1) 以使它的效益降低，这将会告诉我们，如果一个模块变坏，系统将会发生什么。

为了模拟系统效益的降低，我们将修改一个与模块A运行有关的参数 - 计算模块1的时段 -，方法按以下图6所示。这将会改变它计算抛物线状SAR的周期数，会影响进场点，从而改变整个系统的效益。

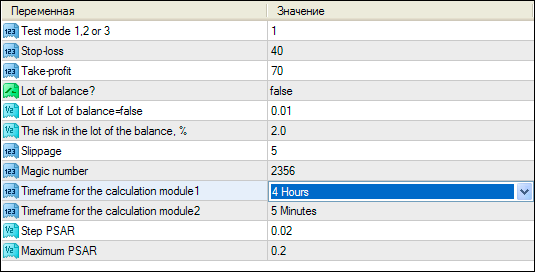
图6. 降低系统效益的模拟

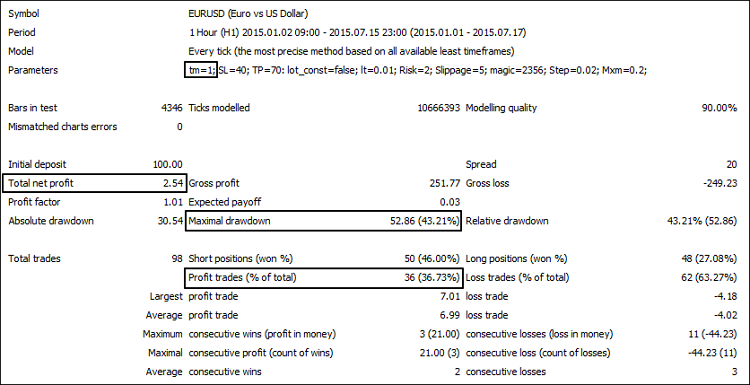
图7. 改变基于抛物线状SAR模块参数的结果

为了便于说明，我们将会比较模块A使用两个不同数值的计算模块1的时段参数的结果:

计算模块1的时段	净利润	获利交易,%	最大回撤
1 Hour	27.56	37.91	32.71
4 Hours	2.54	36.73	43.21

 

很明显，从三个评估标准看，4小时时段的计算给出了更差的结果。在图8中显示，在整个系统的测试中使用故意降低效益的组件参数值，也会减少参数 1-3 的效益：

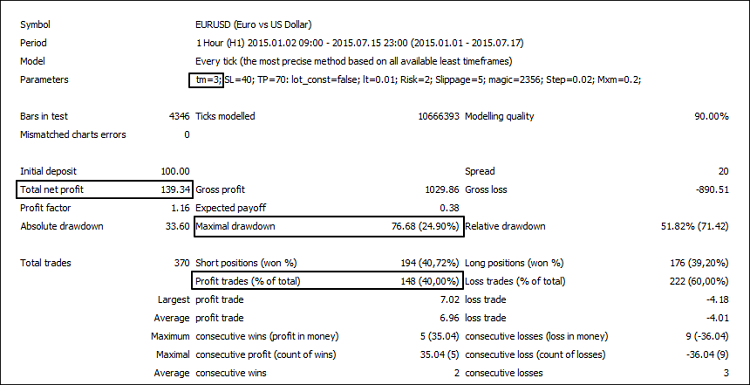
图8. 抛物线状 SAR (变坏的) 与 AC 的联合运行

现在我们把所有的测试结果放到一起，来确定模块A的变化是如何影响系统的整体效益的。

计算模块1的时段	净利润 (模块 1)	获利交易,% (模块 1)	最大回撤,% (模块 1)	净利润 (系统)	获利交易,% (系统)	最大回撤,% (系统)
4 Hours	2.54	36.73	43.21	139.34	40.00	24.9
1 Hour	27.56	37.91	32.71	167.16	40.64	18.62

结果显示，通过独立研究复杂系统的每个模块以便提高效率，在评估整个系统的参数时是有好的结果的，在本文的开始部分也已经确认，这种方法比把整个系统作为一个单独对象来优化有较少的冗余；另外，这种方法还提供了额外的监控系统的能力。

结论

本文探讨了通过分析组件来评估交易系统效益的方法，在测试和研究系统的组件和模块的基础上，我们得到了以下结论:

• 这种评估方法比优化全部系统参数的冗余较少，它可以识别出需要优化和提高的组件。
• 使用模块以组件的方式创建交易系统，就能通过设置标准对其进行评估，进行更好地管理，识别它的弱点并更加灵活地升级。

为了正确测试，必须创建一个独立的文件夹并把文件放入其中，例如 MQL4\Experts\article1924。